Leaf Carbon and Water Isotopes Correlate with Leaf Hydraulic Traits in Three Solanum Species (S. peruvianum, S. lycopersicum and S. chilense)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Plant Material
2.2. Leaf Hydraulics
2.3. Leaf Water Distillation and Isotope Composition
2.4. Modeling Isotopic Enrichment of Leaf Water
2.5. Leaf Carbon Isotope Composition
2.6. Leaf Vein Density
2.7. Statistical Analysis
3. Results
3.1. Leaf Vein Density
3.2. Leaf Hydraulic Conductance
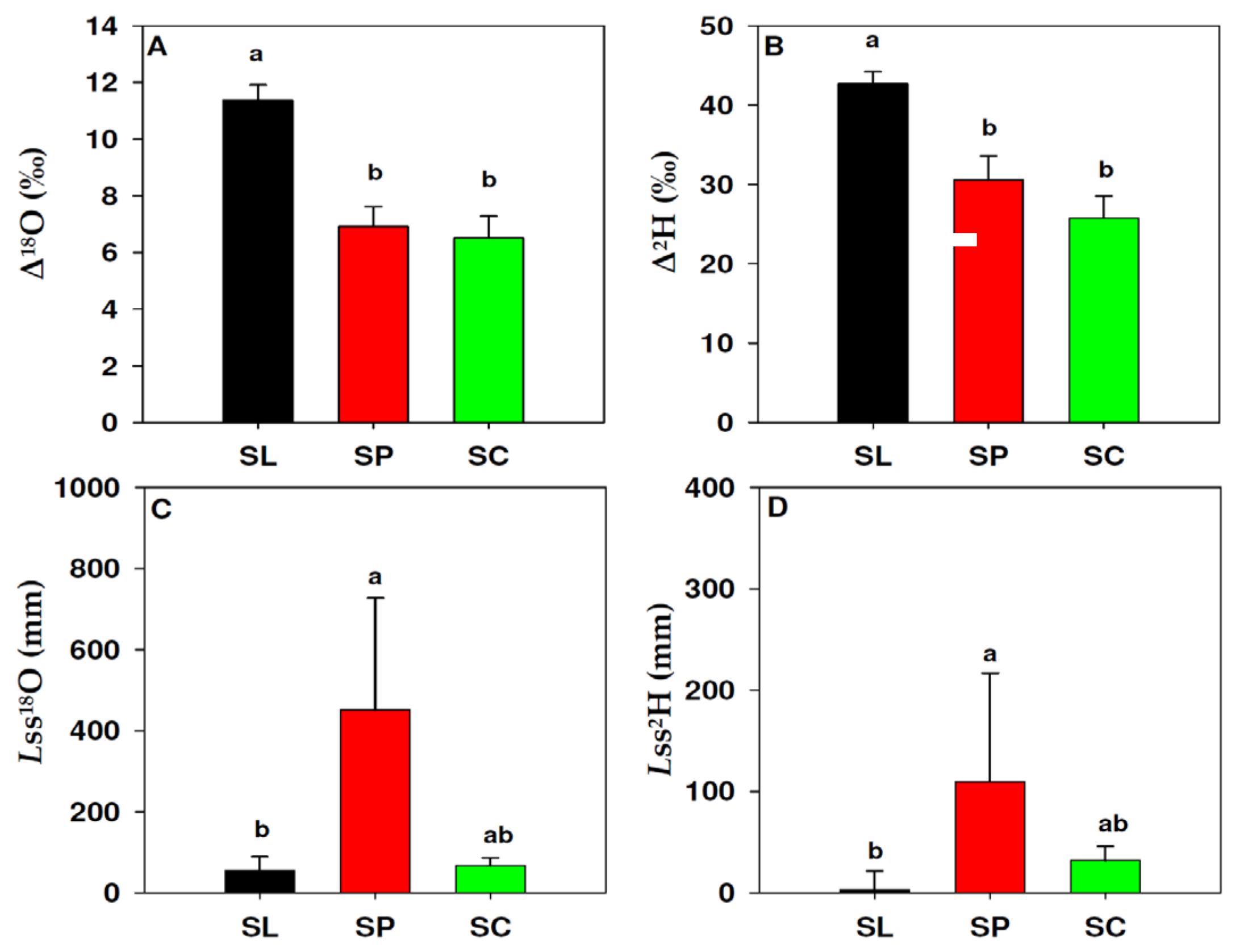
3.3. Leaf Water Isotopic Enrichment
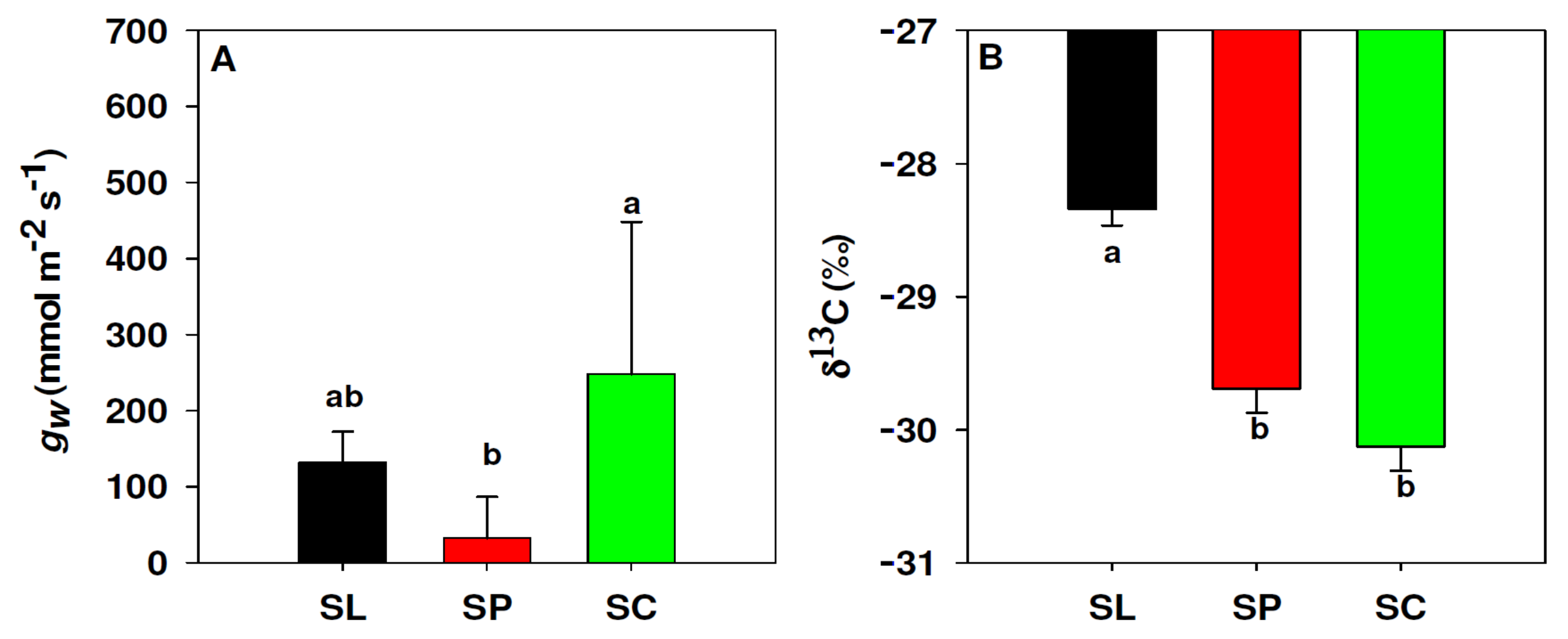
3.4. Leaf Conductance to Water Vapour and δ13C
3.5. Correlation Analysis
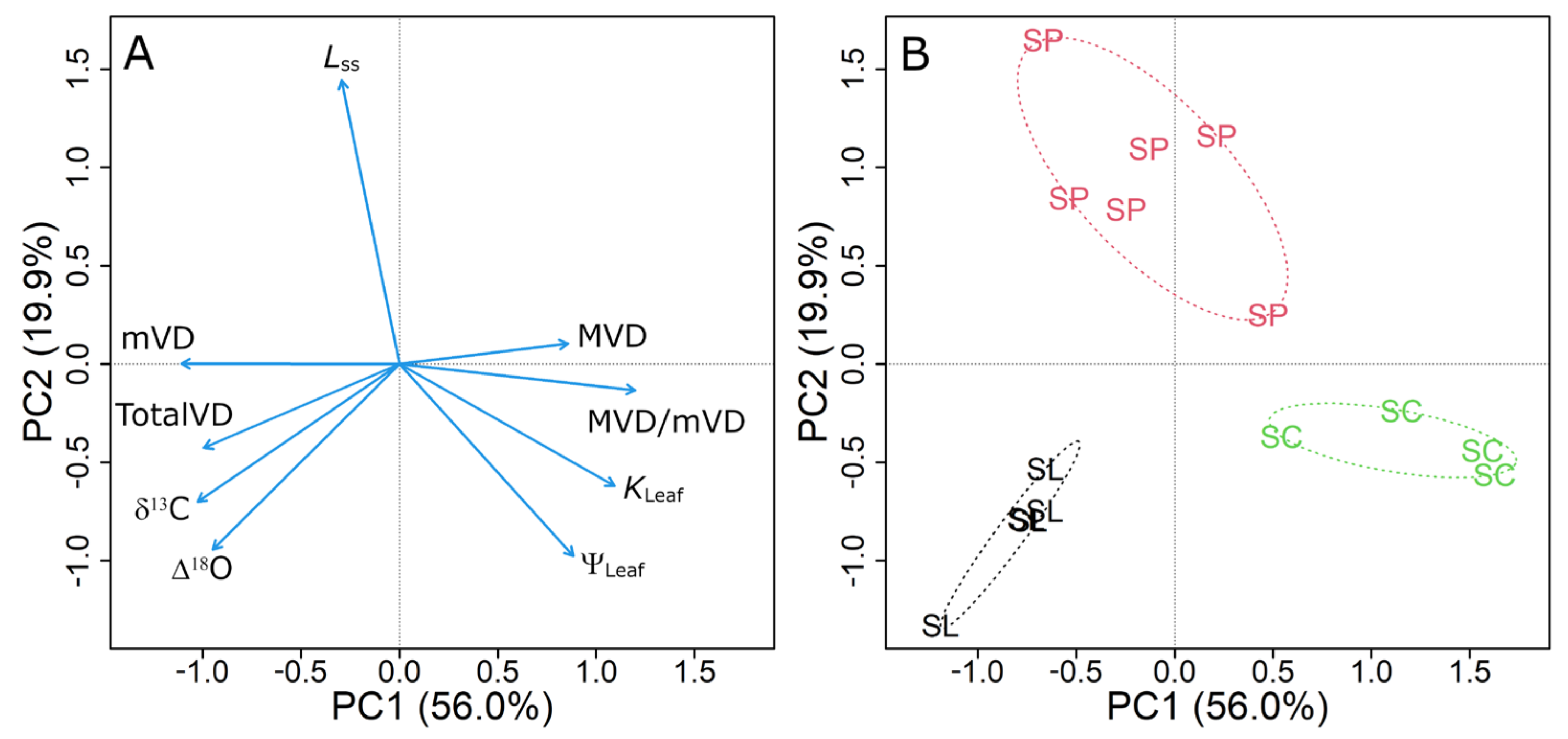
3.6. Principal Component Analysis
4. Discussion
4.1. Contrasting Hydraulic Strategies in Tomato Wild Relatives
4.2. Implications of Hydraulic Constraints for Water Use Efficiency
4.3. Potential and Limitations of Water Isotopes as Indicators of Hydraulic Constraints
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Accession Number | Taxon | Latitude | Longitude | Elevation (m.a.s.l) | Location-Country |
|---|---|---|---|---|---|
| Q958 | S. peruvianum | 18°14′31.9″ | 70°9′8.7″ | 355 | Tarapaca, Chile |
| Q966 | S. chilense | 18°16′52.7″ | 69°18′50.4″ | 3290 | Tarapaca, Chile |
References
- McDowell, N.; Pockman, W.T.; Allen, C.D.; Breshears, D.D.; Cobb, N.; Kolb, T.; Plaut, J.; Sperry, J.; West, A.; Williams, D.G. Mechanisms of plant survival and mortality during drought: Why do some plants survive while others succumb to drought? New Phytol. 2008, 178, 719–739. [Google Scholar] [CrossRef] [PubMed]
- Skelton, R.P.; West, A.G.; Dawson, T.E. Predicting plant vulnerability to drought in biodiverse regions using functional traits. Proc. Nat. Acad. Sci. USA 2015, 112, 5744–5749. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sack, L.; Holbrook, N.M. Leaf hydraulics. Annu. Rev. Plant Biol. 2006, 57, 361–381. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scoffoni, C.; Chatelet, D.S.; Pasquet-kok, J.; Rawls, M.; Donoghue, M.J.; Edwards, E.J.; Sack, L. Hydraulic basis for the evolution of photosynthetic productivity. Nat. Plants 2016, 2, 16072. [Google Scholar] [CrossRef]
- Brodribb, T.J.; Field, T.S.; Jordan, G.J. Leaf maximum photosynthetic rate and venation are linked by hydraulics. Plant Physiol. 2007, 144, 1890–1898. [Google Scholar] [CrossRef] [Green Version]
- McKown, A.D.; Cochard, H.; Sack, L. Decoding leaf hydraulics with a spatially explicit model: Principles of venation architecture and implications for its evolution. Am. Nat. 2010, 175, 447–460. [Google Scholar] [CrossRef] [Green Version]
- Sack, L.; Scoffoni, C. Leaf venation: Structure, function, development, evolution, ecology and applications in the past, present and future. New Phytol. 2013, 198, 983–1000. [Google Scholar] [CrossRef]
- Scoffoni, C.; Rawls, M.; McKown, A.; Cochard, H.; Sack, L. Decline of leaf hydraulic conductance with dehydration: Relationship to leaf size and venation architecture. Plant Physiol. 2011, 156, 832–843. [Google Scholar] [CrossRef] [Green Version]
- Cochard, H.; Nardini, A.; Coll, L. Hydraulic architecture of leaf blades: Where is the main resistance? Plant Cell Environ. 2004, 27, 1257–1267. [Google Scholar] [CrossRef]
- Ferrio, J.P.; Cuntz, M.; Offermann, C.; Siegwolf, R.; Saurer, M.; Gessler, A. Effect of water availability on leaf water isotopic enrichment in beech seedlings shows limitations of current fractionation models. Plant Cell Environ. 2009, 32, 1285–1296. [Google Scholar] [CrossRef]
- Ferrio, J.P.; Pou, A.; Florez-Sarasa, I.; Gessler, A.; Kodama, N.; Flexas, J.; Ribas-Carbó, M. The Péclet effect on leaf water enrichment correlates with leaf hydraulic conductance and mesophyll conductance for CO2. Plant Cell Environ. 2012, 35, 611–625. [Google Scholar] [CrossRef]
- Flexas, J.; Barbour, M.M.; Brendel, O.; Cabrera, H.M.; Carriquí, M.; Díaz-Espejo, A.; Douthe, C.; Dreyer, E.; Ferrio, J.P.; Gago, J.; et al. Mesophyll diffusion conductance to CO2: An unappreciated central player in photosynthesis. Plant Sci. 2012, 193–194, 70–84. [Google Scholar] [CrossRef]
- Farquhar, G.D.; Lloyd, J. Carbon and oxygen isotope effects in the exchange of carbon dioxide between terrestrial plants and the atmosphere. In Stable Isotopes and Plant Carbon-Water Relations; Ehleringer, J.R., Hall, A.E., Farquhar, G.D., Eds.; Academic Press, Inc.: San Diego, CA, USA, 1993; pp. 47–70. [Google Scholar] [CrossRef]
- Barbour, M.M.; Farquhar, G.D. Do pathways of water movement and leaf anatomical dimensions allow development of gradients in H218O between veins and the sites of evaporation within leaves? Plant Cell Environ. 2004, 27, 107–121. [Google Scholar] [CrossRef]
- Cernusak, L.A.; Barbeta, A.; Bush, R.T.; Eichstaedt, R.; Ferrio, J.P.; Flanagan, L.B.; Gessler, A.; Martín-Gómez, P.; Hirl, R.T.; Kahmen, A.; et al. Do 2H and 18O in leaf water reflect environmental drivers differently? New Phytol. 2022, 235, 41–51. [Google Scholar] [CrossRef]
- Cuntz, M.; Ogée, J.; Farquhar, G.D.; Peylin, P.; Cernusak, L.A. Modelling advection and diffusion of water isotopologues in leaves. Plant Cell Environ. 2007, 30, 892–909. [Google Scholar] [CrossRef]
- Loucos, K.E.; Simonin, K.A.; Song, X.; Barbour, M.M. Observed relationships between leaf H218O Péclet effective length and leaf hydraulic conductance reflect assumptions in Craig-Gordon model calculations. Tree Physiol. 2015, 35, 16–26. [Google Scholar] [CrossRef]
- Hommel, R.; Siegwolf, R.; Saurer, M.; Farquhar, G.D.; Kayler, Z.; Ferrio, J.P.; Gessler, A. Drought response of mesophyll conductance in forest understory species–impacts on water-use efficiency and interactions with leaf water movement. Physiol. Plant. 2014, 152, 98–114. [Google Scholar] [CrossRef]
- Sack, L.; Cowan, P.D.; Jaikumar, N.; Holbrook, N.M. The ‘hydrology’ of leaves: Co-ordination of structure and function in temperate woody species. Plant Cell Environ. 2003, 26, 1343–1356. [Google Scholar] [CrossRef] [Green Version]
- Flexas, J.; Scoffoni, C.; Gago, J.; Sack, L. Leaf mesophyll conductance and leaf hydraulic conductance: An introduction to their measurement and coordination. J. Exp. Bot. 2013, 64, 3965–3981. [Google Scholar] [CrossRef]
- Barbour, M.M. Understanding regulation of leaf internal carbon and water transport using online stable isotope techniques. New Phytol. 2017, 213, 83–88. [Google Scholar] [CrossRef]
- Fardusi, M.J.; Ferrio, J.P.; Comas, C.; Voltas, J.; Resco de Dios, V.; Serrano, L. Intra-specific association between carbon isotope composition and productivity in woody plants: A meta-analysis. Plant Sci. 2016, 251, 110–118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gyenge, J.; Fernández, M.E.; Sarasola, M.; Schlichter, T. Testing a hypothesis of the relationship between productivity and water use efficiency in Patagonian forests with native and exotic species. For. Ecol. Manag. 2008, 255, 3281–3287. [Google Scholar] [CrossRef]
- Araus, J.L.; Villegas, D.; Aparicio, N.; Del Moral, L.; El Hani, S.G.; Rharrabti, Y.; Ferrio, J.P.; Royo, C. Environmental factors determining carbon isotope discrimination and yield in durum wheat under Mediterranean conditions. Crop Sci. 2003, 43, 170–180. [Google Scholar] [CrossRef]
- Voltas, J.; Chambel, M.R.; Prada, M.A.; Ferrio, J.P. Climate-related variability in carbon and oxygen stable isotopes among populations of Aleppo pine grown in common-garden tests. Trees 2008, 22, 759–769. [Google Scholar] [CrossRef]
- Sack, L.; Tyree, M.T.; Holbrook, N.M. Leaf hydraulic architecture correlates with regeneration irradiance in tropical rainforest trees. New Phytol. 2005, 167, 403–413. [Google Scholar] [CrossRef]
- Du, Q.; Jiao, X.; Song, X.; Zhang, J.; Bai, P.; Ding, J.; Li, J. The response of water dynamics to long-term high vapor pressure deficit is mediated by anatomical adaptations in plants. Front. Plant Sci. 2020, 11, 758. [Google Scholar] [CrossRef]
- Moyle, L.C.; Muir, C.D. Reciprocal insights into adaptation from agricultural and evolutionary studies in tomato. Evol. Appl. 2010, 3, 409–421. [Google Scholar] [CrossRef]
- Bauchet, G.; Causse, M. Genetic diversity in Tomato (Solanum lycopersicum) and its wild relatives. In Genetic Diversity in Plants; InTech: London, UK, 2012; pp. 161–162. [Google Scholar] [CrossRef] [Green Version]
- Tapia, G.; Méndez, J.; Inostroza, L. Different combinations of morpho-physiological traits are responsible for tolerance to drought in wild tomatoes Solanum chilense and Solanum peruvianum. Plant Biol. 2016, 18, 406–416. [Google Scholar] [CrossRef]
- Muir, C.D.; Hangarter, R.P.; Moyle, L.C.; Davis, P.A. Morphological and anatomical determinants of mesophyll conductance in wild relatives of tomato (Solanum sect. Lycopersicon, sect. Lycopersicoides; Solanaceae). Plant Cell Environ. 2014, 37, 1415–1426. [Google Scholar] [CrossRef]
- Peralta, I.E.; Spooner, D.M. Classification of wild tomatoes: A review. Kurtziana 2000, 28, 45–54. [Google Scholar]
- Chetelat, R.; Pertuze, R.; Faundez, L.; Graham, E.; Jones, C. Distribution, ecology and reproductive biology of wild tomatoes and related nightshades from the Atacama Desert region of northern Chile. Euphytica 2009, 167, 77–93. [Google Scholar] [CrossRef] [Green Version]
- Palacio, S.; Azorín, J.; Montserrat-Martí, G.; Ferrio, J.P. The crystallization water of gypsum rocks is a relevant water source for plants. Nat. Commun. 2014, 5, 4660. [Google Scholar] [CrossRef] [Green Version]
- Martín-Gómez, P.; Barbeta, A.; Voltas, J.; Peñuelas, J.; Dennis, K.; Palacio, S.; Dawson, T.E.; Ferrio, J.P. Isotope-ratio infrared spectroscopy: A reliable tool for the investigation of plant-water sources? New Phytol. 2015, 207, 914–927. [Google Scholar] [CrossRef] [Green Version]
- Dongmann, G.; Nurnberg, H.W.; Forstel, H.; Wagener, K. On the enrichment of H218O in the leaves of transpiring plants. Radiat. Environ. Biophys. 1974, 11, 41–52. [Google Scholar] [CrossRef]
- Farquhar, G.D.; Richards, R.A. Isotopic Composition of Plant Carbon Correlates With Water-Use Efficiency of Wheat Genotypes. Funct. Plant Biol. 1984, 11, 539–552. [Google Scholar] [CrossRef]
- Loucos, K.E.; Simonin, K.A.; Barbour, M.M. Leaf hydraulic conductance and mesophyll conductance are not closely related within a single species. Plant Cell Environ. 2017, 40, 203–215. [Google Scholar] [CrossRef]
- Kahmen, A.; Simonin, K.; Tu, K.; Goldsmith, G.R.; Dawson, T.E. The influence of species and growing conditions on the 18-O enrichment of leaf water and its impact on ‘effective path length’. New Phytol. 2009, 184, 619–630. [Google Scholar] [CrossRef]
- Holloway-Phillips, M.; Cernusak, L.A.; Barbour, M.; Song, X.; Cheesman, A.; Munksgaard, N.; Stuart-Williams, H.; Farquhar, G.D. Leaf vein fraction influences the Péclet effect and 18O enrichment in leaf water. Plant Cell Environ. 2016, 39, 2414–2427. [Google Scholar] [CrossRef]
- Farquhar, G.D.; Gan, K.S. On the progressive enrichment of the oxygen isotopic composition of water along leaves. Plant Cell Environ. 2003, 26, 801–819. [Google Scholar] [CrossRef]


| 9 | KLeaf | Δ18O | Δ2H | Lss | δ13C | TotalVD | MVD | mVD | MVD/mVD |
|---|---|---|---|---|---|---|---|---|---|
| KLeaf | −0.47 | −0.59 * | −0.43 | −0.40 | −0.3 | 0.49 * | −0.67 *** | 0.77 *** | |
| Δ18O | −0.13 | 0.97 *** | −0.29 | 0.78 ** | 0.72 ** | −0.55 * | 0.73 ** | −0.66 ** | |
| Δ2H | −0.34 | 0.94 *** | −0.16 | 0.78 ** | 0.74 ** | −0.49 | 0.78 *** | 0.72 ** | |
| Lss | −0.61 * | −0.53 * | −0.36 | −0.20 | −0.18 | 0.21 | 0.06 | −0.10 | |
| δ13C | −0.21 | 0.68 ** | 0.68 ** | −0.42 | 0.66 ** | −0.464 | 0.67 ** | −0.58 * | |
| TotalVD | −0.17 | 0.54 * | 0.62 * | −0.25 | 0.61 * | −0.173 | 0.69 *** | −0.45 * | |
| MVD | 0.18 | −0.57 * | −0.51 * | 0.51 * | −0.51 * | −0.24 | −0.54 * | 0.78 *** | |
| mVD | −0.48 * | 0.63 * | 0.78 *** | −0.06 | 0.63 * | 0.70 *** | −0.54 * | −0.91 *** | |
| MVD/mVD | 0.42 | −0.71 ** | −0.76 *** | 0.29 | −0.72 ** | −0.59 ** | 0.83 *** | −0.83 *** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrera-Ayala, D.; Tapia, G.; Ferrio, J.P. Leaf Carbon and Water Isotopes Correlate with Leaf Hydraulic Traits in Three Solanum Species (S. peruvianum, S. lycopersicum and S. chilense). Agriculture 2023, 13, 525. https://doi.org/10.3390/agriculture13030525
Barrera-Ayala D, Tapia G, Ferrio JP. Leaf Carbon and Water Isotopes Correlate with Leaf Hydraulic Traits in Three Solanum Species (S. peruvianum, S. lycopersicum and S. chilense). Agriculture. 2023; 13(3):525. https://doi.org/10.3390/agriculture13030525
Chicago/Turabian StyleBarrera-Ayala, Diego, Gerardo Tapia, and Juan Pedro Ferrio. 2023. "Leaf Carbon and Water Isotopes Correlate with Leaf Hydraulic Traits in Three Solanum Species (S. peruvianum, S. lycopersicum and S. chilense)" Agriculture 13, no. 3: 525. https://doi.org/10.3390/agriculture13030525
APA StyleBarrera-Ayala, D., Tapia, G., & Ferrio, J. P. (2023). Leaf Carbon and Water Isotopes Correlate with Leaf Hydraulic Traits in Three Solanum Species (S. peruvianum, S. lycopersicum and S. chilense). Agriculture, 13(3), 525. https://doi.org/10.3390/agriculture13030525






