Robust Trajectory Tracking Control of an Autonomous Tractor-Trailer Considering Model Parameter Uncertainties and Disturbances
Abstract
:1. Introduction
2. Problem Statement
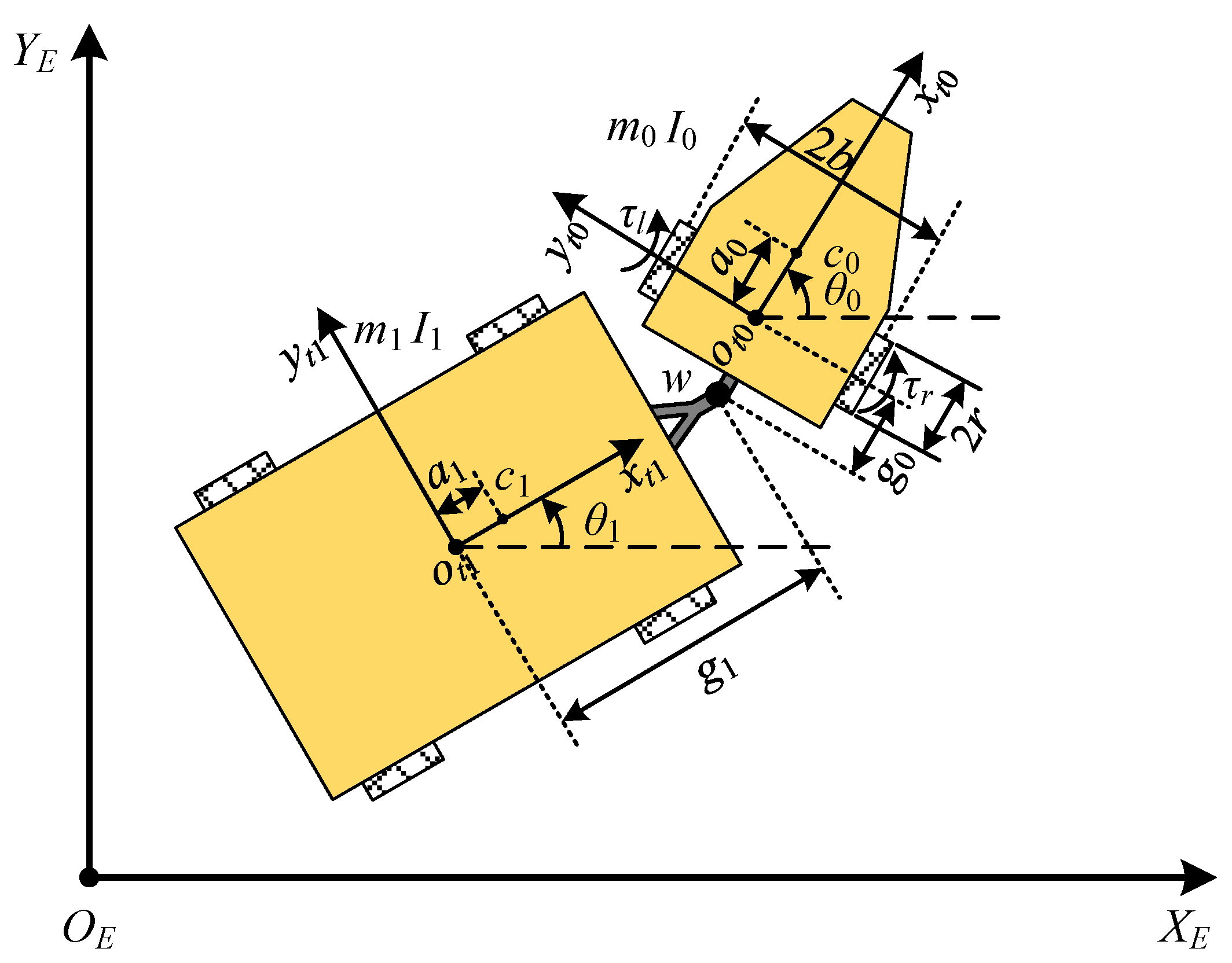
2.1. Kinematic Model of Tractor-Trailer
2.2. Dynamic Model of Tractor-Trailer
2.3. Coordinate Transformation
2.4. Prescribed Performance Function
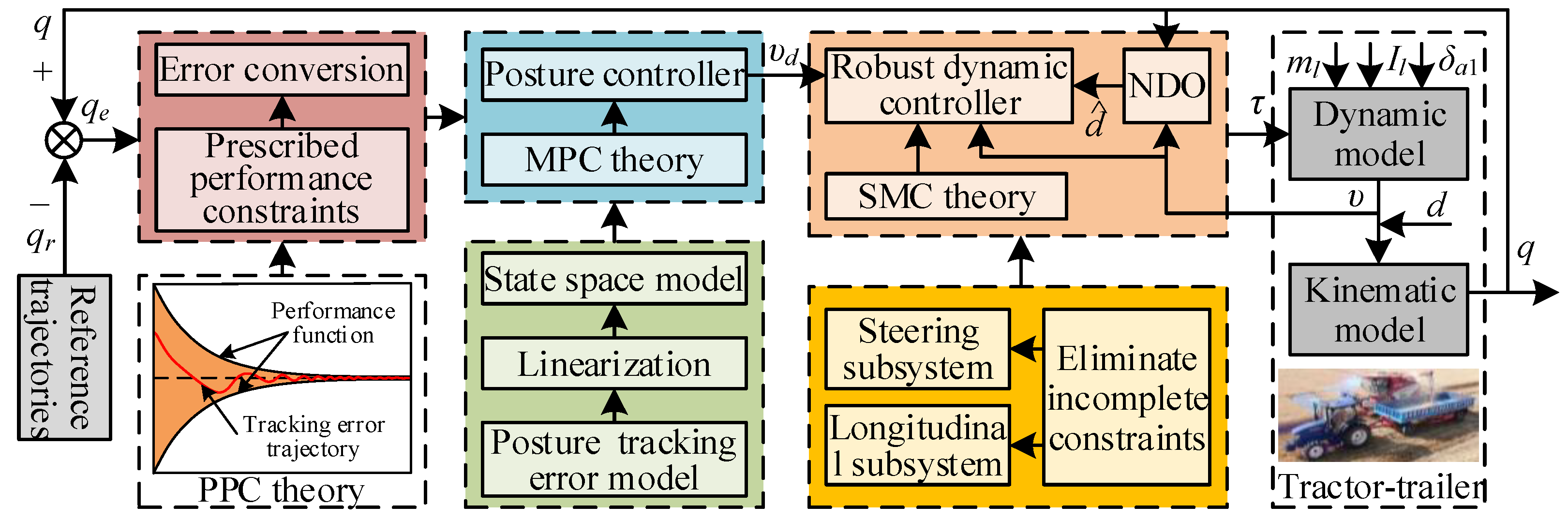
3. Main Results
3.1. Posture Controller
3.2. Dynamic Controller
3.2.1. Design of NDO
3.2.2. Design of Sliding Mode Controller
4. Results and Analysis
4.1. Simulation Description
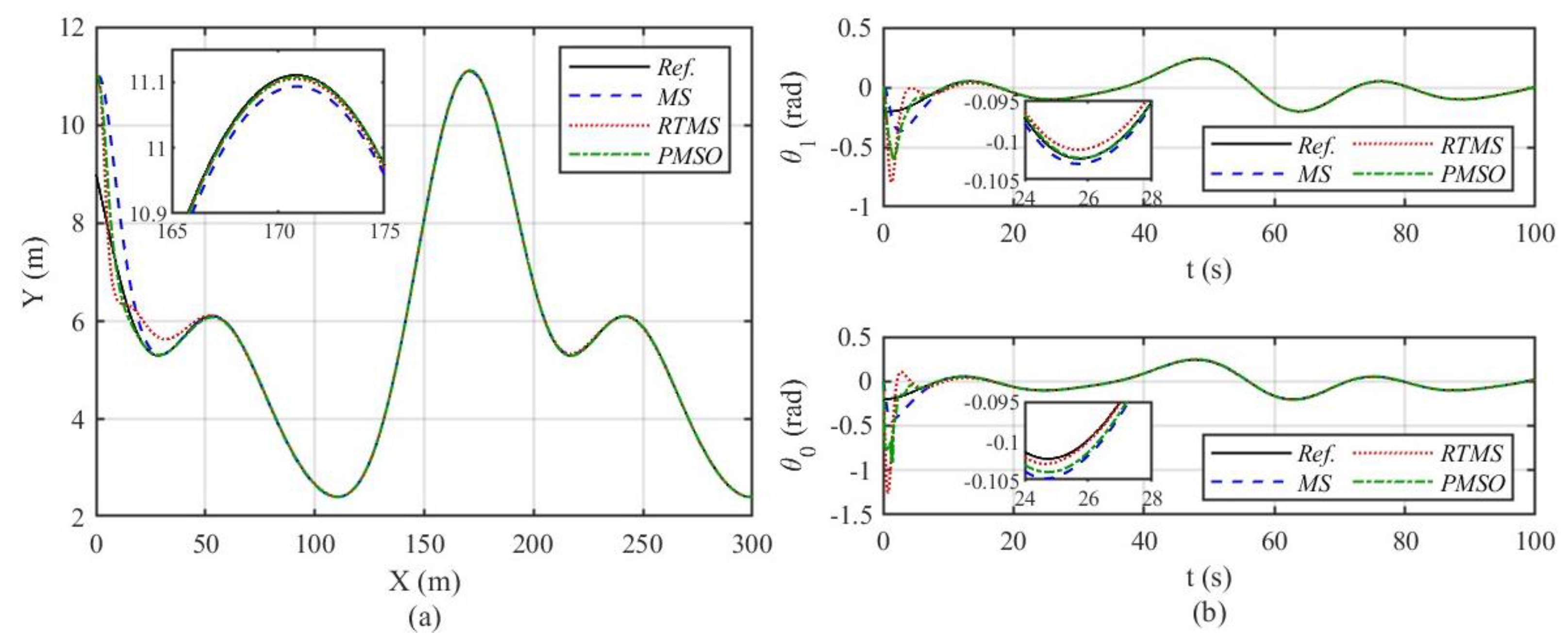
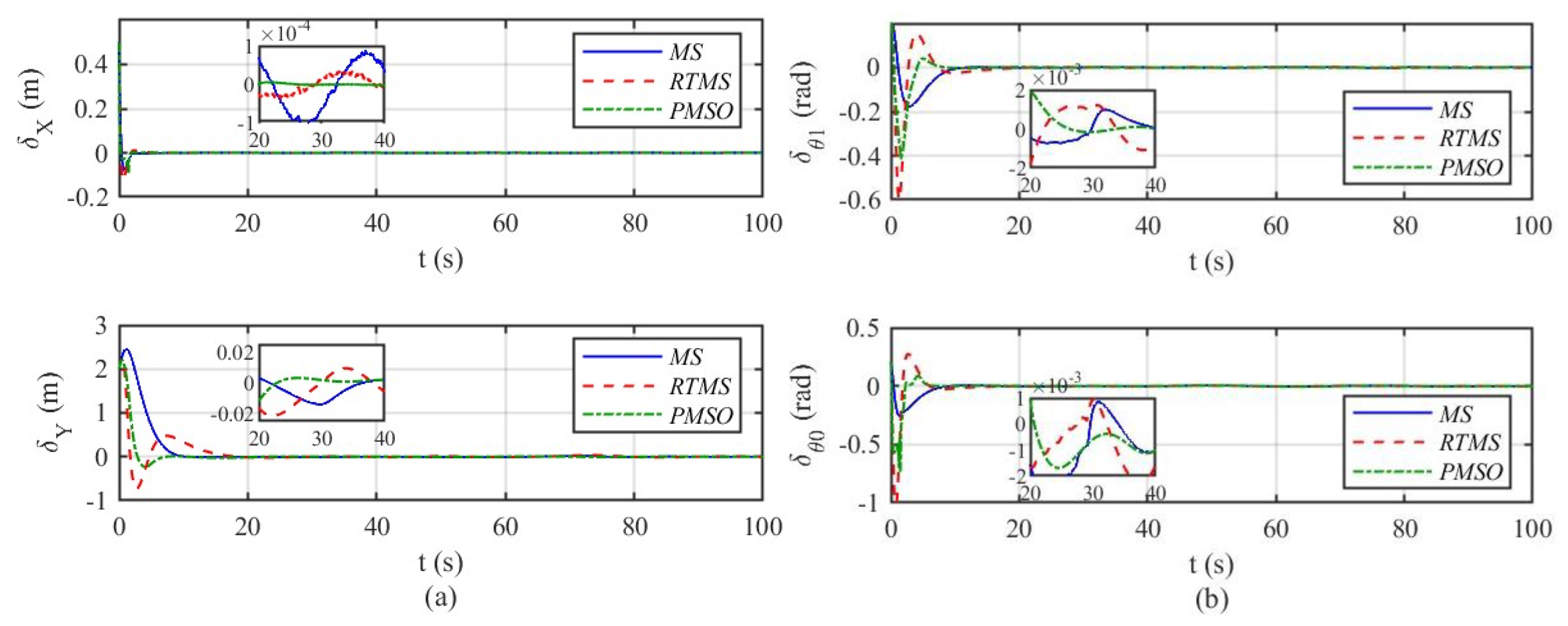
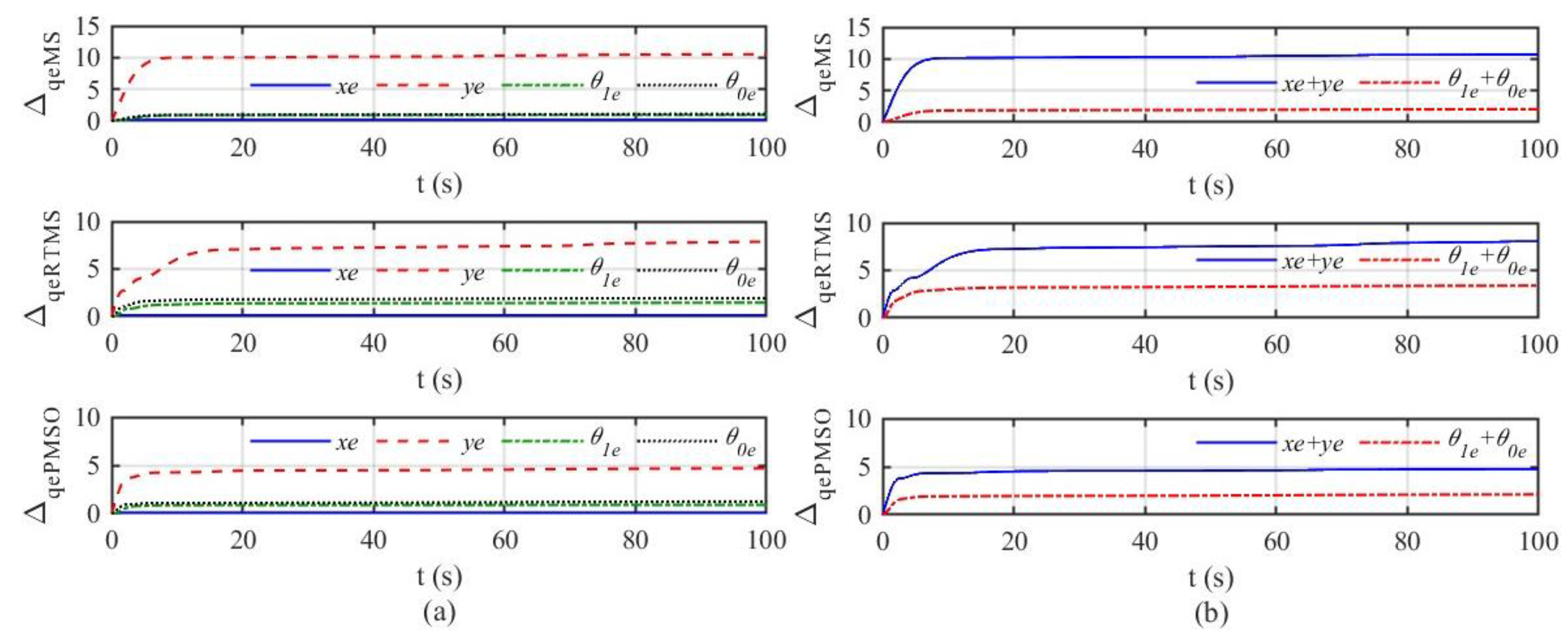
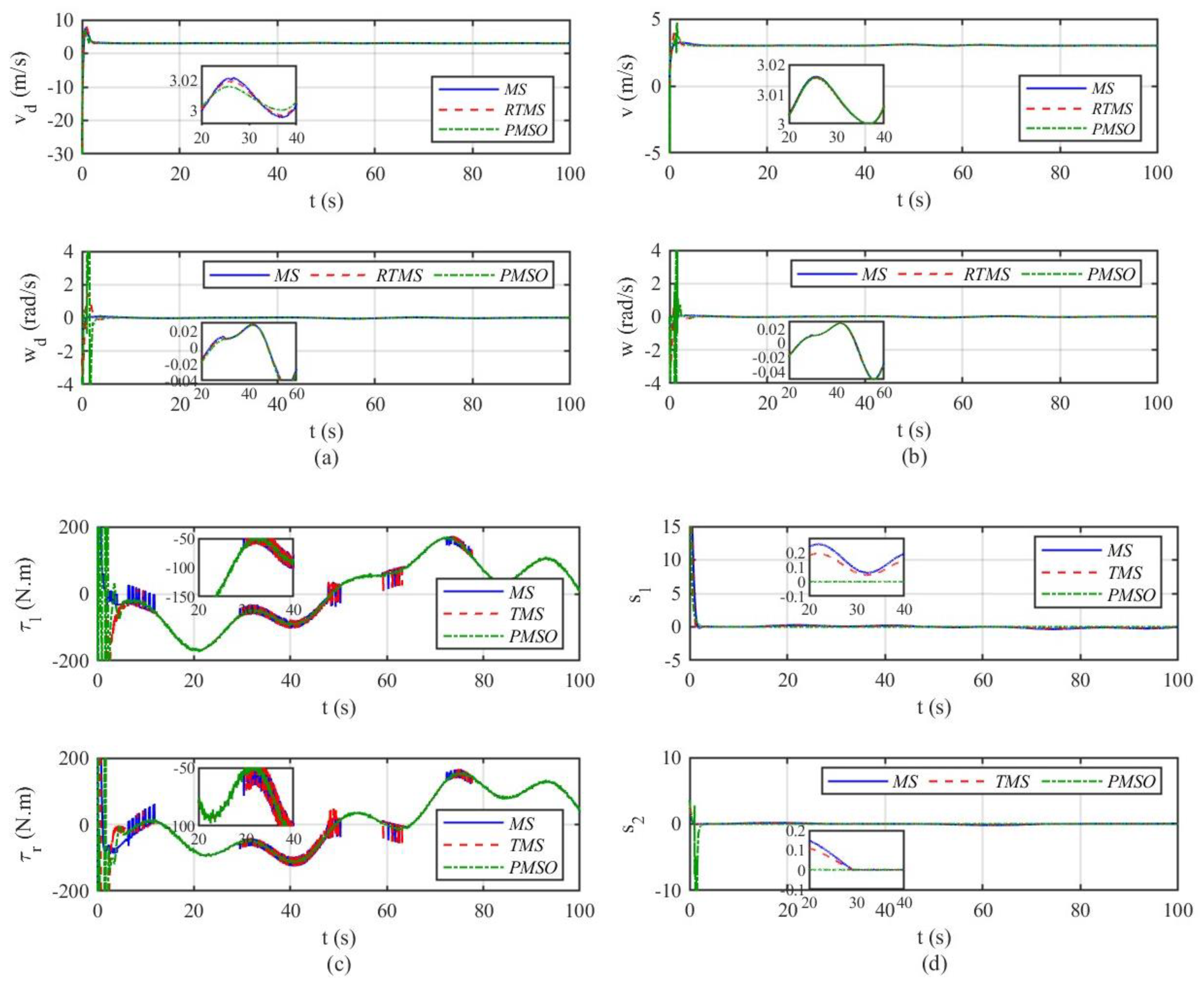
4.2. Simulation Results
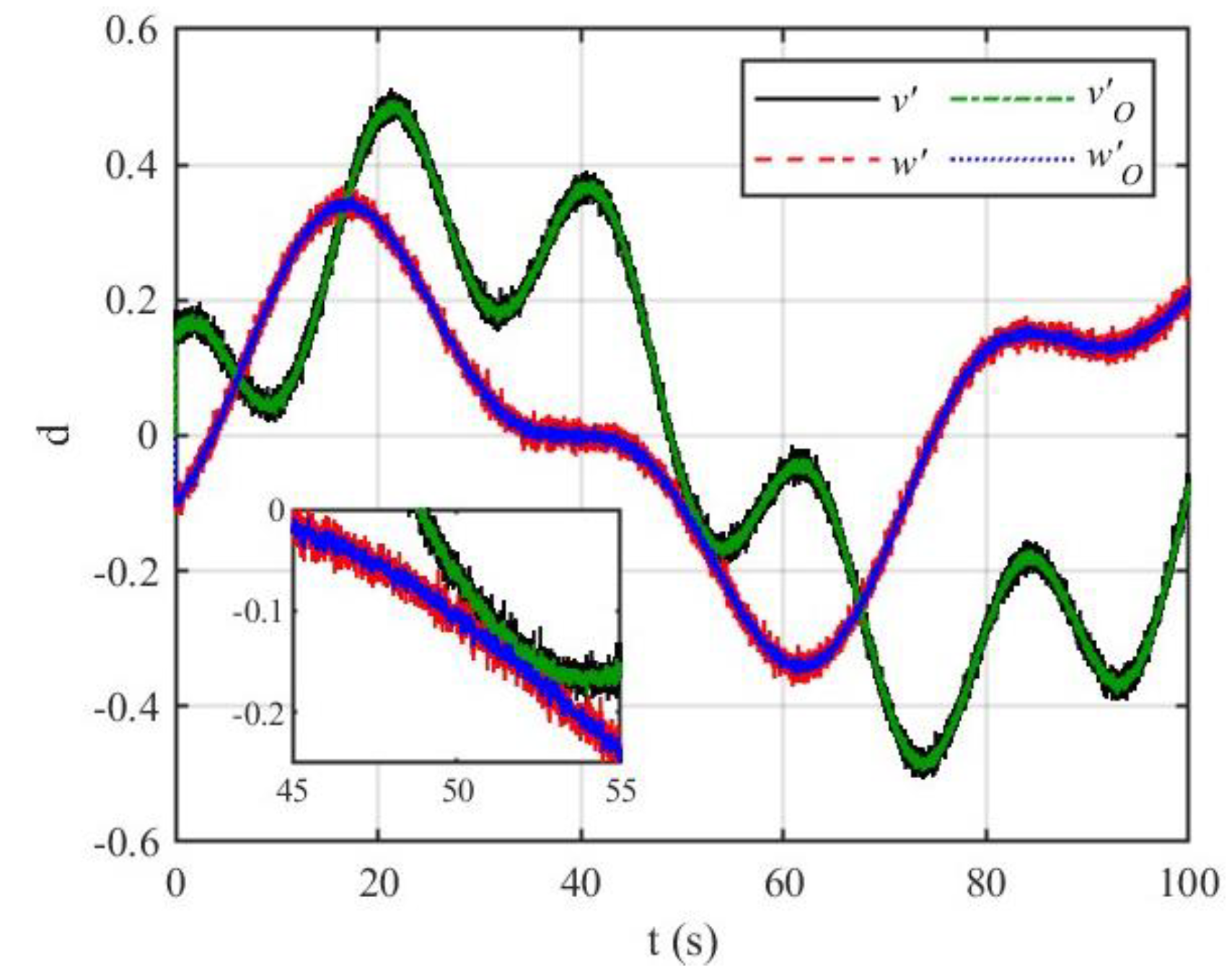
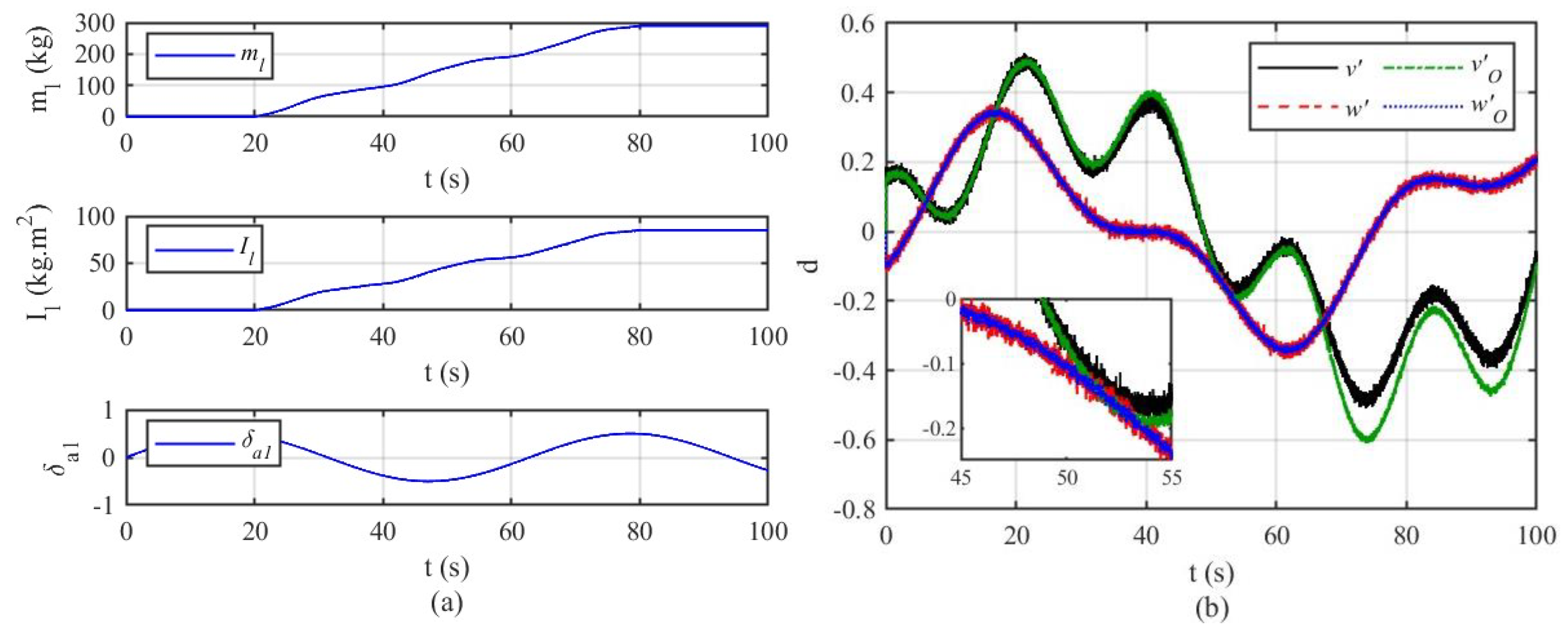
4.2.1. NDO
4.2.2. Robust Tracking Control
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bechar, A.; Vigneault, C. Agricultural robots for field operations: Concepts and components. Biosyst. Eng. 2016, 149, 94–111. [Google Scholar] [CrossRef]
- Lu, E.; Ma, Z.; Li, Y.M.; Xu, L.Z.; Tang, Z. Adaptive backstepping control of tracked robot running trajectory based on real-time slip parameter estimation. Int. J. Agric. Biol. Eng. 2020, 13, 178–187. [Google Scholar] [CrossRef]
- Shojaei, K. Intelligent coordinated control of an autonomous tractor-trailer and a combine harvester. Eur. J. Control. 2021, 59, 82–98. [Google Scholar] [CrossRef]
- Yuan, J.; Sun, F.C.; Huang, Y.L. Trajectory generation and tracking control for double-steering tractor-trailer mobile robots with on-axle hitching. IEEE Trans. Ind. Electron. 2015, 62, 7665–7677. [Google Scholar] [CrossRef]
- Yue, M.; Hou, X.Q.; Zhao, X.D.; Wu, X.M. Robust tube-based model predictive control for lane change maneuver of tractor-trailer vehicles based on a polynomial trajectory. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 5180–5188. [Google Scholar] [CrossRef]
- Alipour, K.; Robat, A.B.; Tarvirdizadeh, B. Dynamics modeling and sliding mode control of tractor-trailer wheeled mobile robots subject to wheels slip. Mech. Mach. Theory 2019, 138, 16–37. [Google Scholar] [CrossRef]
- Kassaeiyan, P.; Alipour, K.; Tarvirdizadeh, B. A full-state trajectory tracking controller for tractor-trailer wheeled mobile robots. Mech. Mach. Theory 2020, 150, 103872. [Google Scholar] [CrossRef]
- Murillo, M.; Sánchez, G.; Deniz, N.; Genzelis, L.; Giovanini, L. Improving path-tracking performance of an articulated tractor-trailer system using a non-linear kinematic model. Comput. Electron. Agric. 2022, 196, 106826. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Yue, M.; Guo, L.; Zhang, Y.S. Trajectory planning and robust tracking control for a class of active articulated tractor-trailer vehicle with on-axle structure. Eur. J. Control. 2020, 54, 87–98. [Google Scholar] [CrossRef]
- Zhang, R.X.; Xiong, L.; Yu, Z.P.; Bai, M.F.; Fu, Z.Q. Robust trajectory tracking control of autonomous vehicles based on conditional integration method. J. Mech. Eng. 2018, 54, 129–139. [Google Scholar] [CrossRef]
- Liao, J.F.; Chen, Z.; Yao, B. Model-based coordinated control of four-wheel independently driven skid steer mobile robot with wheel-ground interaction and wheel dynamics. IEEE Trans. Ind. Inform. 2019, 15, 1742–1752. [Google Scholar] [CrossRef]
- Elhaki, O.; Shojaei, K. Output-feedback robust saturated actor-critic multi-layer neural network controller for multi-body electrically driven tractors with n-trailer guaranteeing prescribed output constraints. Robot. Auton. Syst. 2022, 154, 104106. [Google Scholar] [CrossRef]
- Taghia, J.; Wang, X.; Lam, S.; Katupitiya, J. A sliding mode controller with a nonlinear disturbance observer for a farm vehicle operating in the presence of wheel slip. Auton. Robot. 2017, 41, 71–88. [Google Scholar] [CrossRef]
- Korayem, A.H.; Khajepour, A.; Fidan, B. Trailer mass estimation using system model-based and machine learning approaches. IEEE Trans. Veh. Technol. 2020, 69, 12536–12546. [Google Scholar] [CrossRef]
- Han, S.; Yoon, K.; Park, G.; Huh, K. Hybrid state observer design for estimating the hitch angles of tractor-multi unit trailer. IEEE Trans. Intell. Veh. 2022, 8, 1449–1458. [Google Scholar] [CrossRef]
- Guevara, L.; Jorquera, F.; Walas, K.; Auat-Cheein, F. Robust control strategy for generalized N-trailer vehicles based on a dual-stage disturbance observer. Control Eng. Pract. 2023, 131, 105382. [Google Scholar] [CrossRef]
- Guo, Y.K.; He, S.D.; Dai, S.L. Finite-time synchronization of nonlinear multi-agent systems with prescribed performance. In Proceedings of the 38th Chinese Control Conference, Guangzhou, China, 27–30 July 2019; pp. 5635–5640. [Google Scholar]
- Bechlioulis, C.P.; Rovithakis, G.A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance. IEEE Trans. Autom. Control 2008, 53, 2090–2099. [Google Scholar] [CrossRef]
- Shojaei, K.; Abdolmaleki, M. Output feedback control of a tractor with N-trailer with a guaranteed performance. Mech. Syst. Signal Process. 2020, 142, 106746. [Google Scholar] [CrossRef]
- Guo, G.; Zhang, Q.; Gao, Z.Y. Finite-time fixed configuration formation control of intelligent vehicles with prescribed transient and steady-state performance. China J. Highw. Transp. 2022, 35, 28–42. [Google Scholar]
- Yue, M.; Wu, X.M.; Guo, L.; Gao, J.J. Quintic polynomial-based obstacle avoidance trajectory planning and tracking control framework for tractor-trailer system. Int. J. Control. Autom. Syst. 2019, 17, 2634–2646. [Google Scholar] [CrossRef]
- Yin, Z.Y.; Suleman, A.; Luo, J.J.; Wei, C.S. Appointed-time prescribed performance attitude tracking control via double performance functions. Aerosp. Sci. Technol. 2019, 93, 105337. [Google Scholar] [CrossRef]
- Chen, L.S.; Ning, X.M. Nonlinear PI cascade attitude control with prescribed performance for a quadrotor UAV. J. Appl. Sci. 2019, 37, 137–150. [Google Scholar]
- Jin, Z.J.; Liu, S.; Zhang, L.H.; Lan, B.; Qin, H.R. Command-filtered backstepping control for stabilization of ship rolling based on nonlinear disturbance observer. Shipbuild. China 2019, 60, 121–130. [Google Scholar]
- Li, C.X.; Meng, X.Y.; Wang, J. Design of aircraft trajectory tracking controller based on disturbance observer. Syst. Eng. Electron. 2022, 44, 2593–2600. [Google Scholar]
- Li, P. Research and Application of Traditional and Higher-Order Sliding Mode Control; National University of Defense Technology: Changsha, China, 2011. [Google Scholar]
- Lu, E.; Li, W.; Yang, X.F.; Liu, Y.F. Anti-disturbance speed control of low-speed high-torque PMSM based on second-order non-singular terminal sliding mode load observer. ISA Trans. 2019, 88, 142–152. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, E.; Xue, J.; Chen, T.; Jiang, S. Robust Trajectory Tracking Control of an Autonomous Tractor-Trailer Considering Model Parameter Uncertainties and Disturbances. Agriculture 2023, 13, 869. https://doi.org/10.3390/agriculture13040869
Lu E, Xue J, Chen T, Jiang S. Robust Trajectory Tracking Control of an Autonomous Tractor-Trailer Considering Model Parameter Uncertainties and Disturbances. Agriculture. 2023; 13(4):869. https://doi.org/10.3390/agriculture13040869
Chicago/Turabian StyleLu, En, Jialin Xue, Tiaotiao Chen, and Song Jiang. 2023. "Robust Trajectory Tracking Control of an Autonomous Tractor-Trailer Considering Model Parameter Uncertainties and Disturbances" Agriculture 13, no. 4: 869. https://doi.org/10.3390/agriculture13040869
APA StyleLu, E., Xue, J., Chen, T., & Jiang, S. (2023). Robust Trajectory Tracking Control of an Autonomous Tractor-Trailer Considering Model Parameter Uncertainties and Disturbances. Agriculture, 13(4), 869. https://doi.org/10.3390/agriculture13040869







