Notes on Towed Self-Propulsion Experiments with Simulated Managed Ice in Traditional Towing Tanks
Abstract
1. Introduction
2. Testing Facilities and Ship Model
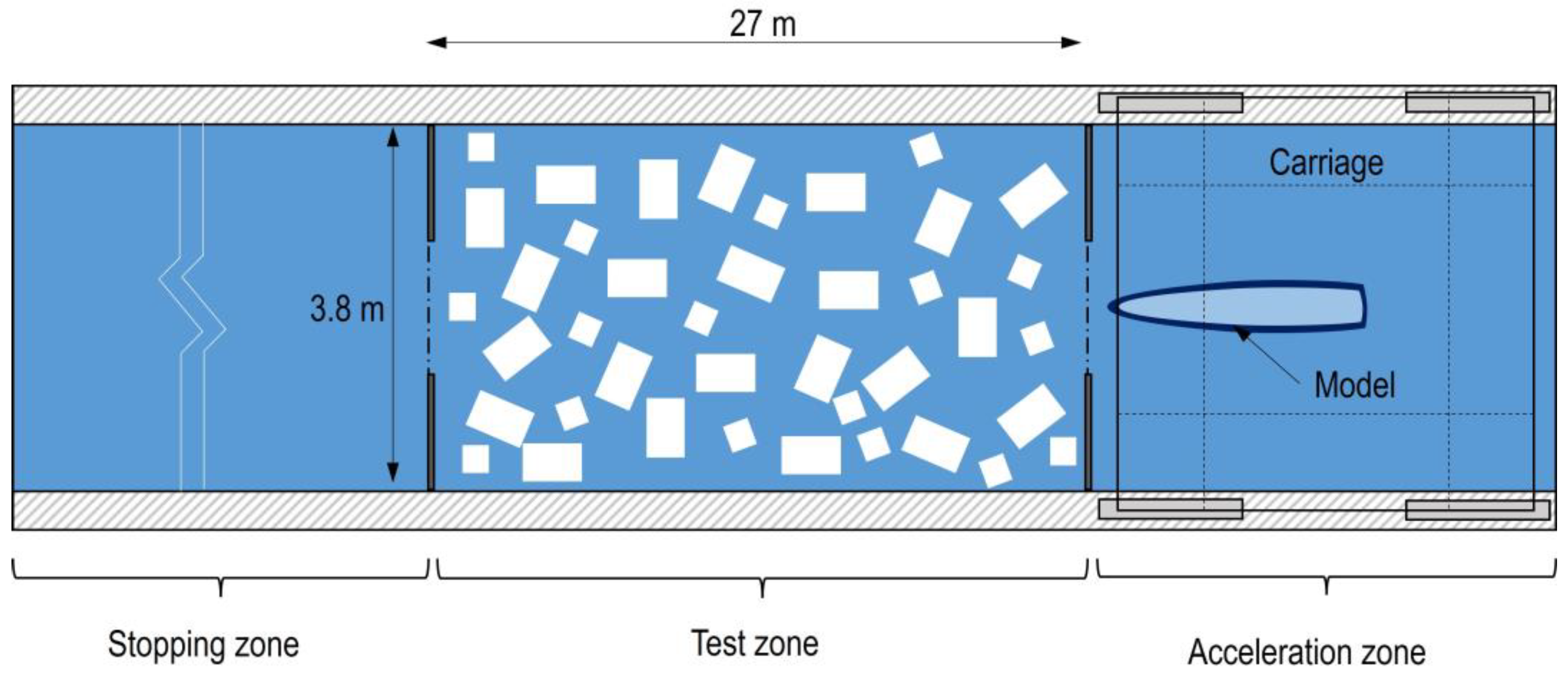
2.1. CEHINAV Testing Facilities
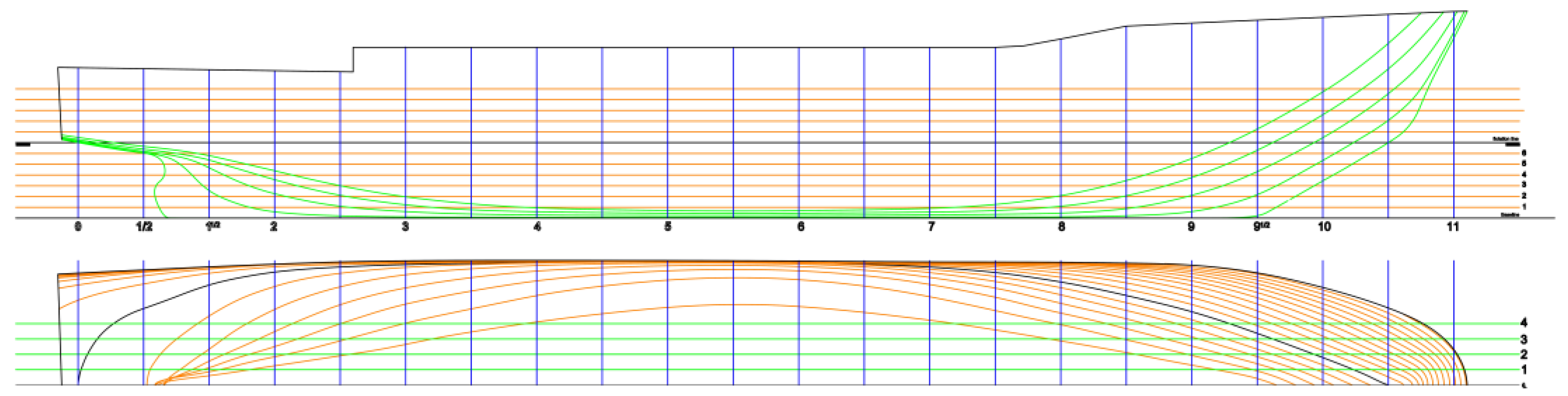
2.2. Hespérides Ship Model
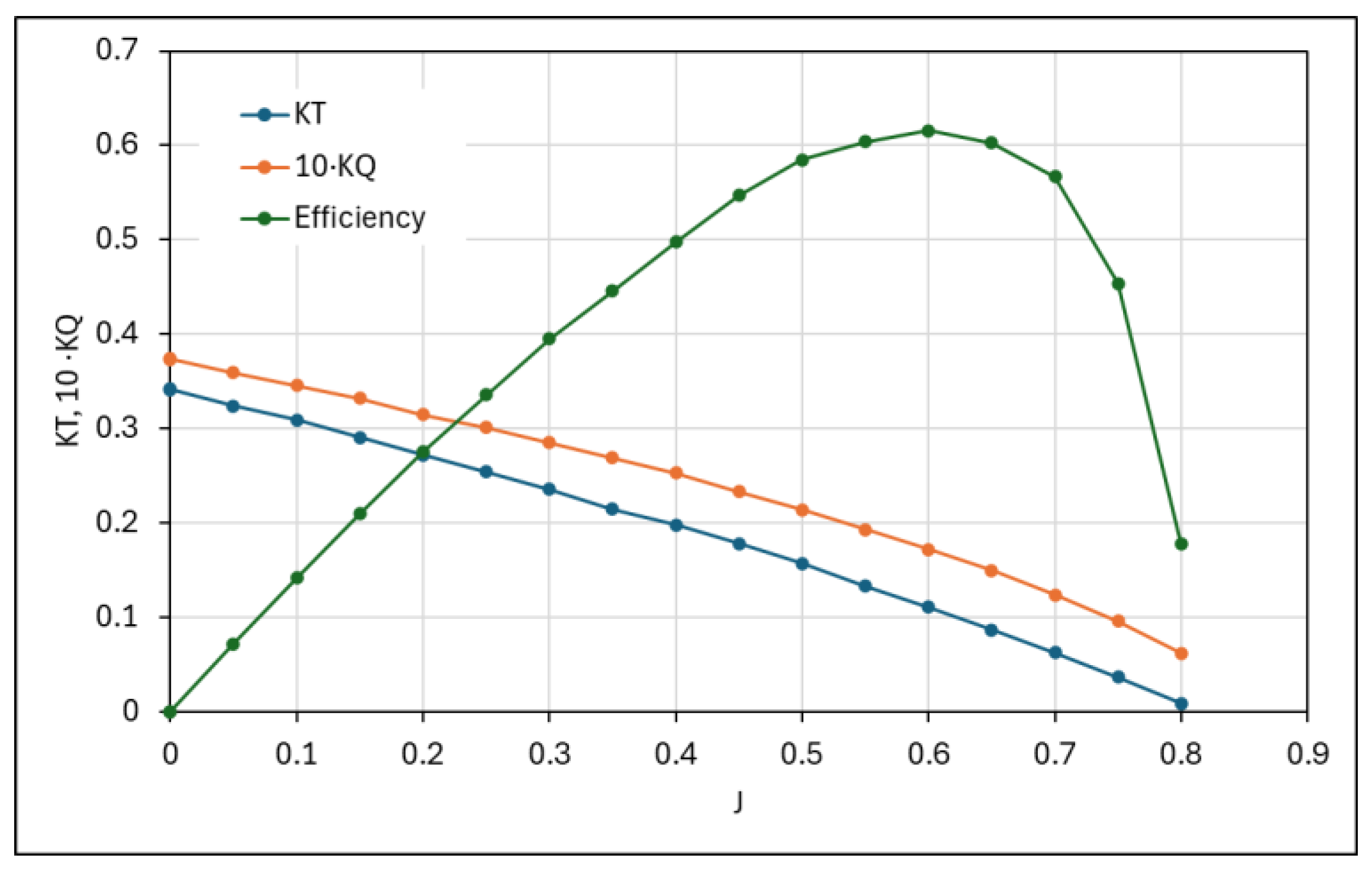
2.3. Features of the Propeller
3. Set-Up for the Experimental Campaign
3.1. Paraffin Wax as Floes
3.2. Free Surface Coverage Distribution for the Tests
3.3. Preliminary Isolated and Open Water Self-Propulsion Tests
4. Discussion of Results
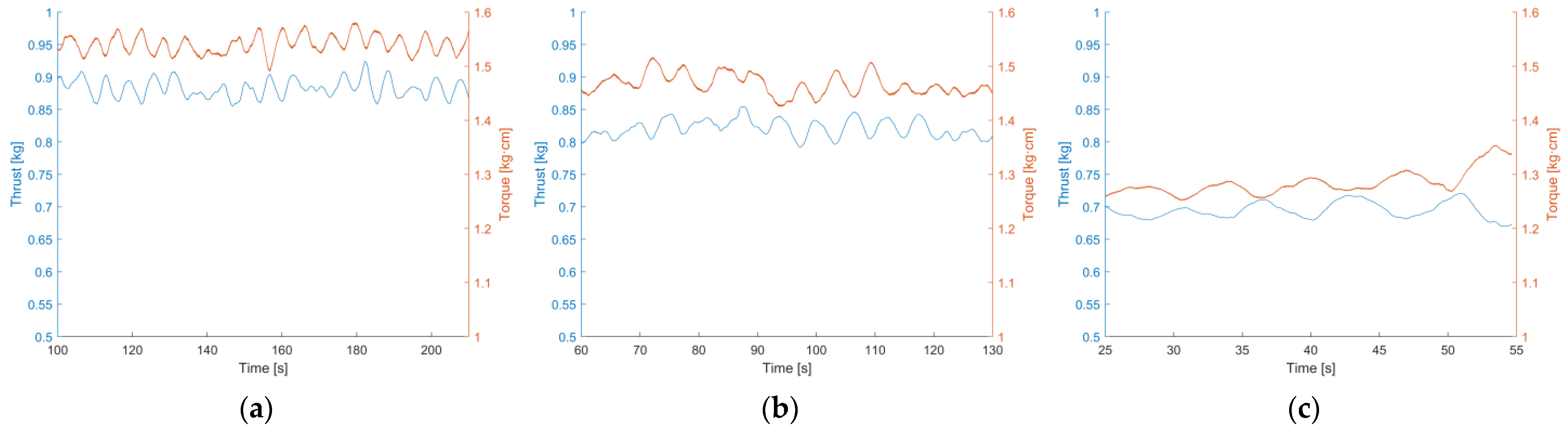
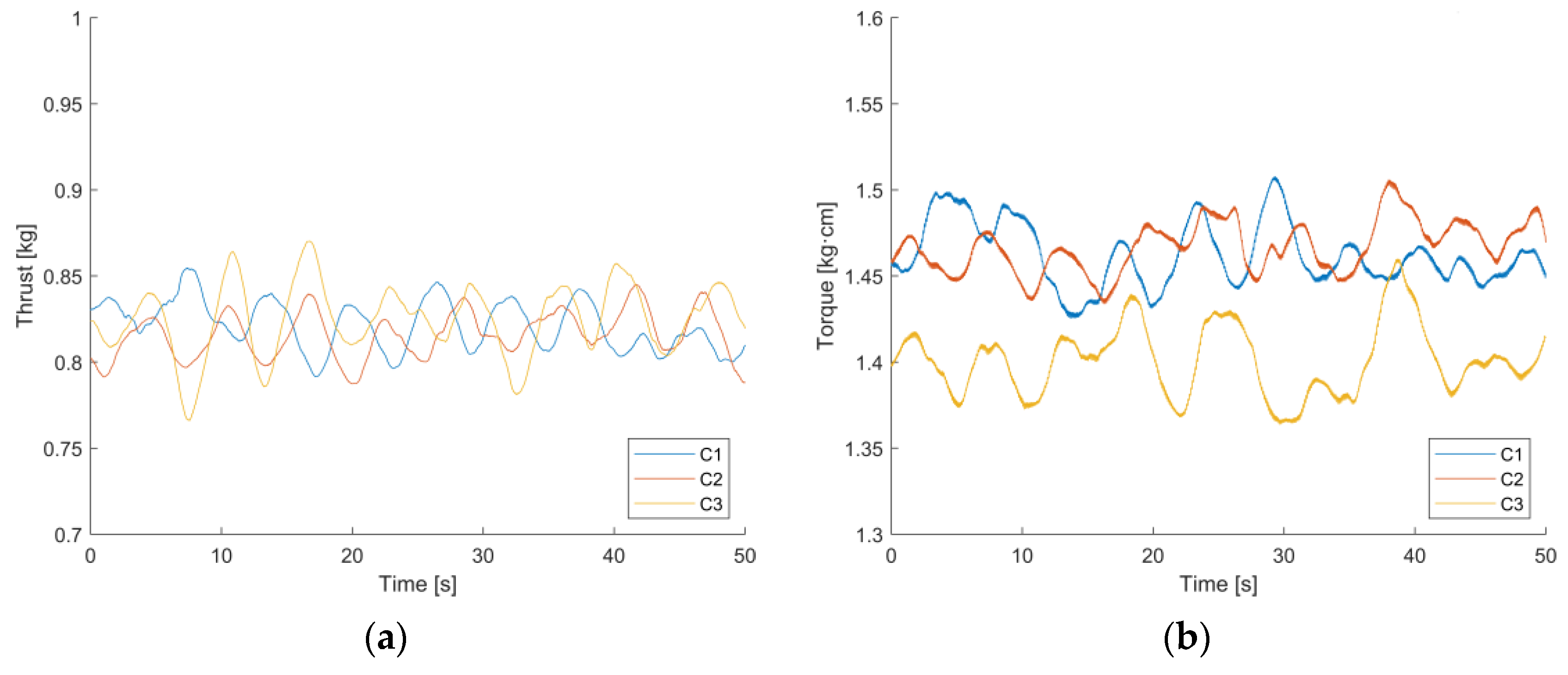
4.1. Thrust (T) Analysis
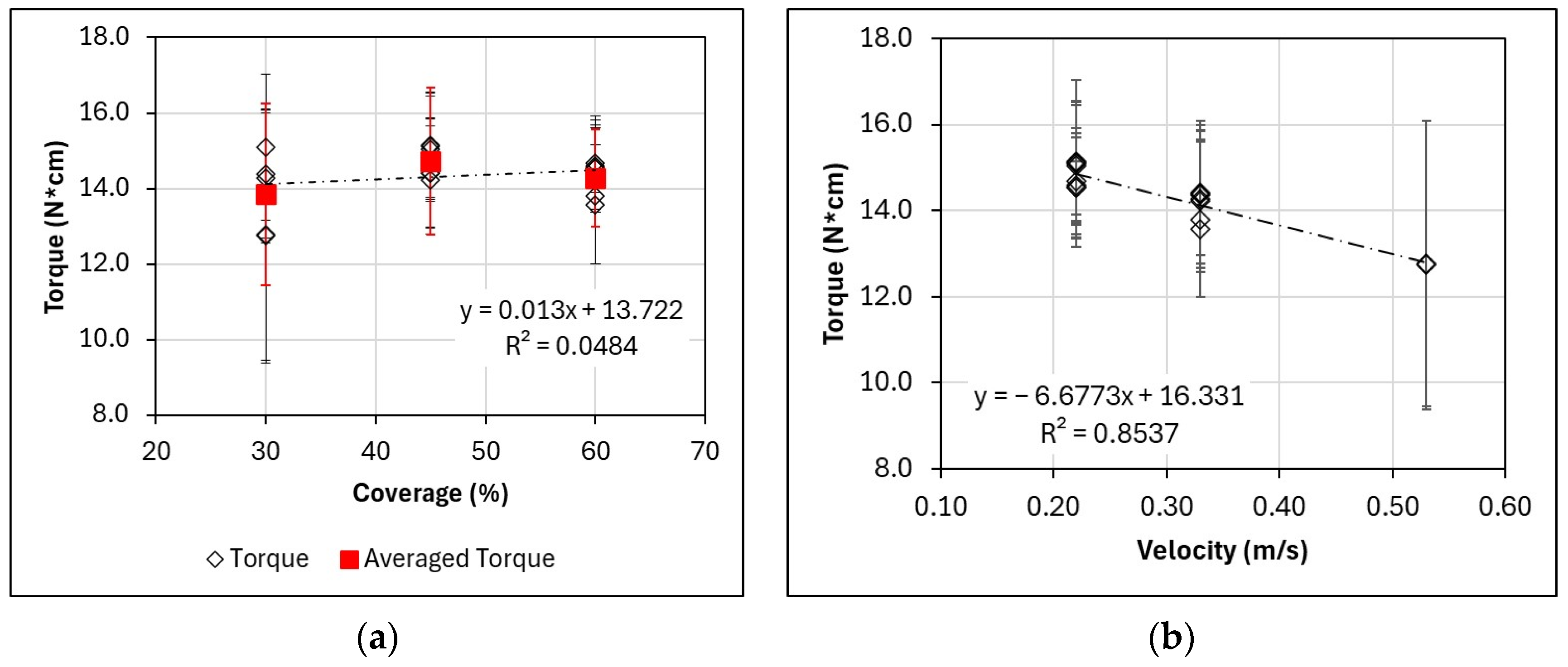
4.2. Torque (Q) Analysis
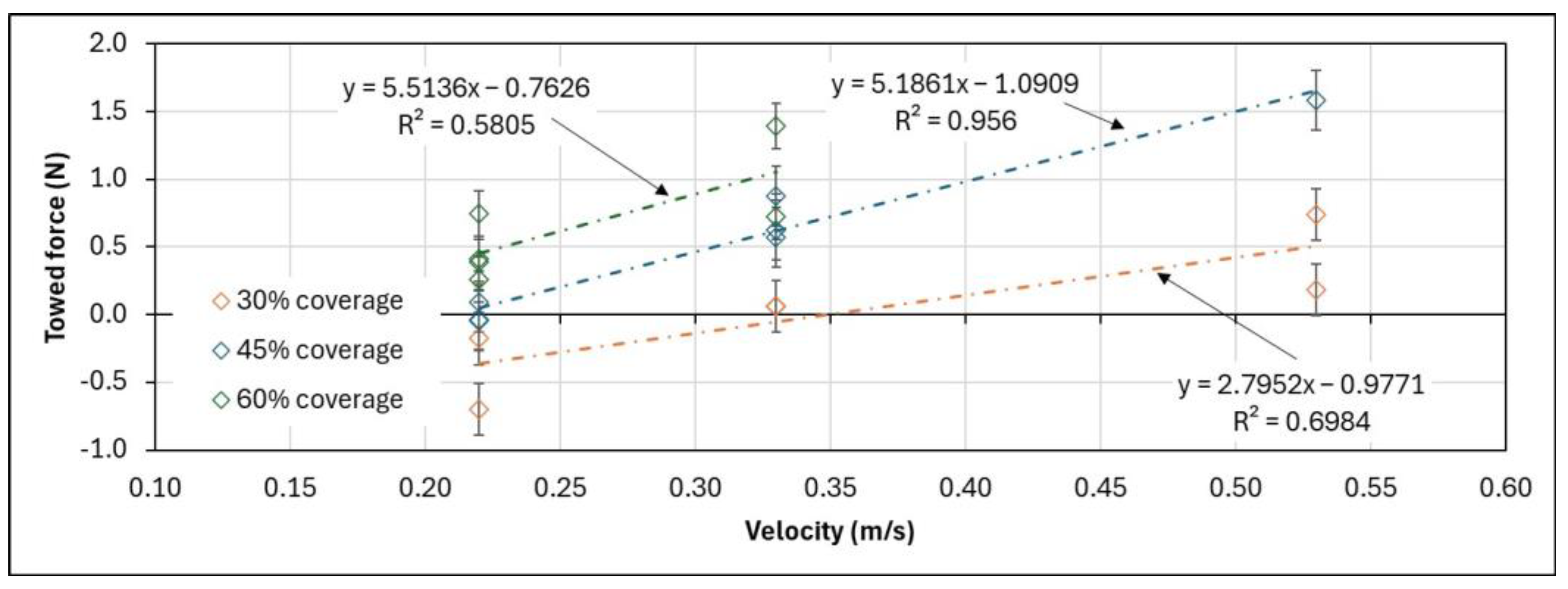
4.3. Towing Force (Fx) Analysis
4.4. Delivered Power (PD)
5. Testing Methodology
6. Conclusions
- –
- It is recommended that the model is pulled by a rod with a load cell placed inside it.
- –
- Increased coverage percentage reduces the variability of the results, for which it is advisable to perform tests within the range of medium-to-high coverage (40–65% coverage).
- –
- Removable front upper bounds should be installed to avoid an increase in coverage percentage in the final part of the tests, producing floe jams.
- –
- The length of the test channel can be reduced to increase the number of tests, significantly reducing the raw material needed to carry out the experimentation, as well as test costs. For instance, up to five ship lengths can be enough to recover valuable data.
- –
- High speeds are not recommended, since they significantly increase the order of magnitude of the towing force, leading to problems in the data collection system.
- –
- The segmentation hypothesis, combined with a large number of tests, is highly recommended to bound random uncertainties.
- –
- Paraffin wax can act as managed ice to model complex environments in ice experimentation, and it is suitable for numerical validation.
- –
- Attention to the trajectory of the blocks in the stern is a must when performing such tests, avoiding the collapse of the propulsion system, and the breaking of appendages. The suction effect can be fatal for the performance of the tests.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- GISTEMP Team. GISS Surface Temperature Analysis (GISTEMP). NASA Goddard Inst. Sp. Stud. Available online: https://data.giss.nasa.gov/gistemp/ (accessed on 28 August 2024).
- Comiso, J.C.; Bliss, A.C.; Gersten, R.; Parkinson, C.L.; Markus, T. Current state of sea ice cover. Available online: https://earth.gsfc.nasa.gov/cryo/data/current-state-sea-ice-cover (accessed on 28 August 2024).
- Corbett, J.J.; Lack, D.A.; Winebrake, J.J.; Harder, S.; Silberman, J.A.; Gold, M. Arctic shipping emissions inventories and future scenarios. Atmos. Chem. Phys. 2010, 10, 9689–9704. [Google Scholar] [CrossRef]
- Valsson, T.; Ulfarsson, G.F. Adaptation and change with global warming: Emerging spatial world structure and transportation impacts. Transp. Res. Rec. 2009, 2139, 117–124. [Google Scholar] [CrossRef]
- Cao, Y.; Liang, S.; Sun, L.; Liu, J.; Cheng, X.; Wang, D.; Feng, K. Trans-Arctic shipping routes expanding faster than the model projections. Glob. Environ. Chang. 2022, 73, 102488. [Google Scholar] [CrossRef]
- Gutiérrez-Romero, J.E.; Ruiz-Capel, S.; Esteve-Pérez, J.; Zamora-Parra, B.; Luna-Abad, J.P. Methodology Based on Photogrammetry for Testing Ship-Block Resistance in Traditional Towing Tanks: Observations and Benchmark Data. J. Mar. Sci. Eng. 2022, 10, 246. [Google Scholar] [CrossRef]
- Zong, Z.; Yang, B.Y.; Sun, Z.; Zhang, G.Y. Experimental study of ship resistance in artificial ice floes. Cold Reg. Sci. Technol. 2020, 176, 103102. [Google Scholar] [CrossRef]
- Jeong, S.Y.; Lee, C.J.; Cho, S.R. Ice resistance prediction for standard icebreaker model ship. In Proceedings of the Twentieth International Offshore and Polar Engineering Conference (ISOPE 2010), Beijing, China, 20–25 June 2010. [Google Scholar]
- Jeong, S.Y.; Choi, K.; Kim, H.S. Investigation of ship resistance characteristics under pack ice conditions. Ocean Eng. 2021, 219, 108264. [Google Scholar] [CrossRef]
- Jeong, S.Y.; Choi, K.; Kang, K.J.; Ha, J.S. Prediction of ship resistance in level ice based on empirical approach. Int. J. Naval Archit. Ocean Eng. 2017, 9, 613–623. [Google Scholar] [CrossRef]
- Lindqvist, G. A straightforward method for calculation of ice resistance of ships. In Proceedings of the 10th International Conference on Port and Ocean Engineering under Arctic Conditions (POAC’89), Lulea, Sweden, 12–16 June 1989; pp. 722–735. [Google Scholar]
- Riska, K. Performance of Merchant Vessels in Ice in the Baltic; Research Report/Winter Navigation Research Board, 52; Helsinki University of Technology, Ship Laboratory: Helsinki, Finland, 1997. [Google Scholar]
- WMO. Sea Ice Nomenclature. Volume 1—Terminology and Codes. In Proceedings of the 5th Session of JCOMM Expert Team on Sea Ice, Ottawa, ON, Canada, 25–28 March 2014; World Meteorological Organization: Geneva, Switzerland, 2014. [Google Scholar]
- Tan, X.; Riska, K.; Moan, T. Effect of dynamic bending of level ice on ship’s continuous-mode icebreaking. Cold Reg. Sci. Technol. 2014, 106, 82–95. [Google Scholar] [CrossRef]
- Zhou, L.; Riska, K.; von Bock und Polach, R.; Moan, T.; Su, B. Experiments on level ice loading on an icebreaking tanker with different ice drift angles. Cold Reg. Sci. Technol. 2013, 85, 79–93. [Google Scholar] [CrossRef]
- Huang, Y.; Sun, J.; Ji, S.; Tian, Y. Experimental study on the resistance of a transport ship navigating in level ice. J. Mar. Sci. Appl. 2016, 15, 105–111. [Google Scholar] [CrossRef]
- Dong, W.; Zhou, L.; Ding, S.; Ma, Q.; Li, F. Fast and Intelligent Ice Channel Recognition Based on Row Selection. J. Mar. Sci. Eng. 2023, 11, 1652. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Shang, Y.; Jin, Q.; Zhang, L. CFD-DEM based full-scale ship-ice interaction research under FSICR ice condition in restricted brash ice channel. Cold Reg. Sci. Technol. 2022, 194, 103454. [Google Scholar] [CrossRef]
- Sun, H.; Ni, X.; Zhang, Y.; Chen, K.; Ni, B. A Numerical Prediction of the Resistance of Bulk Carriers in Brash Ice Channels. J. Mar. Sci. Eng. 2023, 11, 1425. [Google Scholar] [CrossRef]
- Tian, Y.; Yang, D.; Gang, X.; Yu, C.; Ji, S.; Yue, Q. Development of a Numerical Ice Tank Based on DEM and Physical Model Testing: Methods, Validations and Applications. J. Mar. Sci. Eng. 2023, 11, 1455. [Google Scholar] [CrossRef]
- Wang, J. Prediction of Propeller Performance on a Model Podded Propulsor in Ice (Propeller-Ice Interaction). Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2007. [Google Scholar]
- Bach, C.; Myland, D. An experimental method for model propeller-ice interaction in air. Concept and first results. In Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering, OMAE 2017, Trondheim, Norway, 25–30 June 2017. [Google Scholar]
- Sampson, R.; Atlar, M.; Sasaki, N. Propeller ice interaction–effect of blockage proximity. In Proceedings of the First International Symposium on Marine Propulsors Smp’09, Trondheim, Norway, 22–24 June 2009. [Google Scholar]
- Xie, C.; Zhou, L.; Ding, S.; Lu, M.; Zhou, X. Research on self-propulsion simulation of a polar ship in a brash ice channel based on body force model. Int. J. Nav. Arch. Ocean Eng. 2023, 15, 100557. [Google Scholar] [CrossRef]
- Yang, D.; Liu, L.; Ji, S. Numerical analysis of interaction between sea ice and propeller based on coupled DEM-FEM model. Ocean Eng. 2023, 268, 113469. [Google Scholar] [CrossRef]
- Khan, A.G.; Hisette, Q.; Streckwall, H.; Liu, P. Numerical investigation of propeller-ice interaction. Ocean Eng. 2020, 216, 107716. [Google Scholar] [CrossRef]
- Huisman, T.J.; Bos, R.W.; Brouwer, J.; Hagesteijn, G.; de Koning-Gans, H.J. Interaction between warm model ice and a propeller. In Proceedings of the 33rd International Conference on Ocean, Offshore and Arctic Engineering, OMAE 2014, San Francisco, CA, USA, 13 June 2014. [Google Scholar] [CrossRef]
- Xiong, W.P.; Wang, C.; Wu, S.; Ye, L.Y.; Xu, P. Study of different load components during the propeller-ice interaction process. Ocean Eng. 2022, 247, 110787. [Google Scholar] [CrossRef]
- Tian, Y.F.; Huang, Y. Non-Frozen Model Ice Preparation Method with Columnar Texture Features. China Patent No. 110779250B, 10 October 2019. [Google Scholar]
- Van der Werff, S.; Brouwer, J.; Hagesteijn, G. Ship resistance validation using artificial ice. In Proceedings of the ASME 34th International Conference on Ocean, Offshore and Arctic Engineering, OMAE 2015, St. John’s, NL, Canada, 31 May–5 June 2015. [Google Scholar]
- Kim, M.-C.; Lee, S.-K.; Lee, W.-J.; Wang, J.-Y. Numerical and experimental investigation of the resistance performance of an icebreaking cargo vessel in pack ice conditions. Int. J. Nav. Archit. Ocean Eng. 2013, 5, 116–131. [Google Scholar] [CrossRef]
- Kim, M.-C.; Lee, W.-J.; Shin, Y.-J. Comparative study on the resistance performance of an icebreaking cargo vessel according to the variation of waterline angles in pack ice conditions. Int. J. Nav. Archit. Ocean Eng. 2014, 6, 876–893. [Google Scholar] [CrossRef]
- Xie, C.; Zhou, L.; Ding, S.; Liu, R.; Zheng, S. Experimental and numerical investigation on self-propulsion performance of polar merchant ship in brash ice channel. Ocean Eng. 2023, 269, 113424. [Google Scholar] [CrossRef]
- Wang, J.; Jones, S.J. Resistance and propulsion of CCGS Terry Fox in ice from model tests on full-scale correlation. In Proceedings of the 8th International Conference and Exhibition on Performance of Ships and Structures in Ice (ICETECH 2008), Banff, AB, Canada, 2–23 July 2008. [Google Scholar]
- Hellmann, J.H.; Rupp, K.H.; Kuehnlein, W.L. Model tests in brash ice channels. In Proceedings of the 24th International Conference on Offshore Mechanics and Arctic Engineering, OMAE 2005, Halkidiki, Greece, 12–17 June 2005. [Google Scholar] [CrossRef]
- ITTC Recommended Procedures and Guidelines. Testing and Extrapolation Methods Ice Testing Resistance Test in Level Ice. In Proceedings of the International Towing Tank Conference, Venice, Italy, 8–14 September 2002.
- CSIC. Unidad de Tecnología Marina. Consejo Superior de Investigación Científica. 2020. Available online: www.utm.csic.es (accessed on 15 July 2024).
- IACS. UR I1: Polar Class Descriptions and Application. Requirements Concerning Polar Class. International Association of Classification Societies. 2016. Available online: https://iacs.org.uk/resolutions/unified-requirements/ur-i (accessed on 30 August 2024).
- IACS. UR I2: Structural Requirements for Polar Class Ships. Requirements Concerning Polar Class. International Association of Classification Societies. 2019. Available online: https://iacs.org.uk/resolutions/unified-requirements/ur-i (accessed on 30 August 2024).
- ITTC Recommended Procedures and Guidelines. Experimental Uncertainty Analysis for Ship Resistance in Ice Tank Testing. In Proceedings of the International Towing Tank Conference, Edinburgh, UK, 4–10 September 2005.
- Timco, G.W. EG/AD/S: A new type of model ice for re-frigerated towing tanks. Cold Reg. Sci. Technol. 1986, 12, 175–195. [Google Scholar] [CrossRef]
- Zhang, Q.; Skjetne, R.; Metrikin, I.; Løset, S. Image Processing for Ice Floe Analyses in Broken-ice Model Testing. Cold Reg. Sci. Technol. 2015, 111, 27–38. [Google Scholar] [CrossRef]
- TRAFI. Ice Class Regulations and the Application Thereof. Finnish Transport Safety Agency, 2016. Available online: https://www.traficom.fi/en/transport/maritime/ice-classes-ships (accessed on 30 August 2024).
- Mas-Soler, J.; Uzunoglu, E.; Bulian, B.; Guedes Soares, C.; Souto-Iglesias, A. An experimental study on transporting a free-float capable tension leg platform for a 10 MW wind turbine in waves. Renew. Energy 2021, 179, 2158–2173. [Google Scholar] [CrossRef]
- ITTC Recommended Procedures and Guidelines. Propulsion test in ice. In Proceedings of the International Towing Tank Conference, Wuxi, China, 17–22 September 2017.









| Parameter | Value | Unit |
|---|---|---|
| Length overall, LOA | 82.588 | m |
| Length between perpendiculars, Lpp | 76.791 | m |
| Breadth | 14.591 | m |
| Draught | 4.421 | m |
| Displacement | 2725.86 | tons |
| Vertical position of the gravity center of the ship | 3.28 | m |
| Pitch radius of gyration, Ryy | 0.21 Lpp | m |
| Parameter | Value | Unit |
|---|---|---|
| Scale factor | 23.71 | – |
| Diameter, D | 0.14 | m |
| Number of blades | 4 | – |
| Pitch at 0.75 R | 0.11 | m |
| Cord length at 0.75 R | 0.0365 | m |
| Maximum thickness | 1.6 | mm |
| Blade ratio area | 0.437 | – |
| Coverage (%) | Number of Blocks |
|---|---|
| 30 | 207 |
| 45 | 291 |
| 60 | 876 |
| Speed VA (Knots) at Full-Scale | Advance Coefficient (J) | Wake Fraction Coefficient (w) | Thrust Deduction Coefficient (t) | Relative Rotative Efficiency (ηR) |
|---|---|---|---|---|
| 5.34 | 0.573 | 0.237 | 0.285 | 0.8553 |
| 6.94 | 0.581 | 0.226 | 0.241 | 0.8680 |
| 8.00 | 0.568 | 0.251 | 0.246 | 0.9233 |
| 9.34 | 0.558 | 0.248 | 0.256 | 0.9364 |
| VA (Knots) | Pd (kW) | n (r.p.m.) | Pe (kW) | η0 | T (kg) | Q (kg·m) | BHP (kW) |
|---|---|---|---|---|---|---|---|
| 5.34 | 60.7 | 73.1 | 30.1 | 0.47 | 1560 | 808.0 | 64 |
| 6.94 | 129.5 | 95.1 | 68.5 | 0.50 | 2576 | 1325.0 | 136 |
| 8.00 | 186.7 | 108.6 | 107.3 | 0.55 | 3522 | 1673.0 | 197 |
| 9.34 | 319.8 | 129.5 | 180.6 | 0.54 | 5150 | 2403.0 | 337 |
| Test Number | Model Speed, VA (m/s) | Coverage, C (%) | (N·cm) | (N) |
|---|---|---|---|---|
| 1 | 0.22 | 30 | 8.6466 | 15.0913 |
| 2 | 0.22 | 45 | 8.6088 | 15.1304 |
| 3 | 0.22 | 45 | 8.6098 | 15.1587 |
| 4 | 0.22 | 45 | 8.6234 | 15.0548 |
| 5 | 0.22 | 60 | 8.3775 | 16.1102 |
| 6 | 0.22 | 60 | 8.6835 | 14.5292 |
| 7 | 0.22 | 60 | 8.7759 | 14.6831 |
| 8 | 0.22 | 60 | 8.6824 | 14.5889 |
| 9 | 0.33 | 30 | 7.7152 | 14.3823 |
| 10 | 0.33 | 30 | 7.7070 | 14.2823 |
| 11 | 0.33 | 45 | 8.0185 | 14.4034 |
| 12 | 0.33 | 45 | 8.1134 | 14.2220 |
| 13 | 0.33 | 45 | 8.1058 | 14.4216 |
| 14 | 0.33 | 60 | 8.2417 | 13.7984 |
| 15 | 0.33 | 60 | 8.0152 | 13.5812 |
| 16 | 0.53 | 30 | 6.8410 | 12.7680 |
| 17 | 0.53 | 30 | 6.8280 | 12.7449 |
| 18 | 0.53 | 45 | 6.9324 | 12.5047 |
| Test Number | RMS Torque, Q (N·cm) | RMS Thrust, T (N) | Torque (N·cm) | Thrust (N) |
|---|---|---|---|---|
| 1 | 15.9250 | 8.7083 | 1.9423 | 0.3845 |
| 2 | 15.9301 | 8.6603 | 1.4082 | 0.2831 |
| 3 | 15.9631 | 8.6822 | 1.3961 | 0.2770 |
| 4 | 15.8671 | 8.7167 | 1.3938 | 0.2813 |
| 5 | 16.1630 | 8.5661 | 0.6203 | 0.4245 |
| 6 | 15.3387 | 8.7437 | 1.1677 | 0.2432 |
| 7 | 15.4887 | 8.8361 | 1.2324 | 0.2574 |
| 8 | 15.3831 | 8.7404 | 1.2196 | 0.2512 |
| Test Number | RMS Torque, Q (N·cm) | RMS Thrust, T (N) | Torque (N·cm) | Thrust (N) |
|---|---|---|---|---|
| 9 | 15.3831 | 8.7404 | 1.7019 | 0.3347 |
| 10 | 15.3831 | 8.7404 | 1.7124 | 0.3332 |
| 11 | 15.0525 | 8.0136 | 1.4391 | 0.2795 |
| 12 | 15.0020 | 8.1677 | 1.4395 | 0.2834 |
| 13 | 15.2034 | 8.1607 | 1.4509 | 0.2848 |
| 14 | 14.6192 | 8.3004 | 1.7075 | 0.3480 |
| 15 | 14.5015 | 8.1088 | 1.7973 | 0.4343 |
| Test Number | RMS Torque, Q (N·cm) | RMS Thrust, T (N) | Torque (N·cm) | Thrust (N) |
|---|---|---|---|---|
| 16 | 13.6047 | 6.8947 | 3.3216 | 0.6074 |
| 17 | 13.6000 | 6.8839 | 3.3562 | 0.6192 |
| 18 | 13.3379 | 6.9827 | 5.1311 | 2.6219 |
| Coverage (%) | VA (m/s) | RI + ROW (N) | Resistance (N) |
|---|---|---|---|
| 30 | 0.22 | 2.75 | 0.983 |
| 0.33 | 4.88 | 0.952 | |
| 0.53 | 6.55 | 0.791 | |
| 45 | 0.22 | 5.39 | 0.952 |
| 0.33 | 9.69 | 1.134 | |
| 0.53 | 14.40 | 1.896 | |
| 60 | 0.22 | 10.17 | 1.734 |
| 0.33 | 18.14 | 2.303 | |
| 0.53 | 21.93 | 2.707 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutiérrez-Romero, J.E.; Zamora-Parra, B.; Ruiz-Capel, S.; Esteve-Pérez, J.; López-Belchí, A.; Romero-Tello, P.; Lorente-López, A.J. Notes on Towed Self-Propulsion Experiments with Simulated Managed Ice in Traditional Towing Tanks. J. Mar. Sci. Eng. 2024, 12, 1691. https://doi.org/10.3390/jmse12101691
Gutiérrez-Romero JE, Zamora-Parra B, Ruiz-Capel S, Esteve-Pérez J, López-Belchí A, Romero-Tello P, Lorente-López AJ. Notes on Towed Self-Propulsion Experiments with Simulated Managed Ice in Traditional Towing Tanks. Journal of Marine Science and Engineering. 2024; 12(10):1691. https://doi.org/10.3390/jmse12101691
Chicago/Turabian StyleGutiérrez-Romero, José Enrique, Blas Zamora-Parra, Samuel Ruiz-Capel, Jerónimo Esteve-Pérez, Alejandro López-Belchí, Pablo Romero-Tello, and Antonio José Lorente-López. 2024. "Notes on Towed Self-Propulsion Experiments with Simulated Managed Ice in Traditional Towing Tanks" Journal of Marine Science and Engineering 12, no. 10: 1691. https://doi.org/10.3390/jmse12101691
APA StyleGutiérrez-Romero, J. E., Zamora-Parra, B., Ruiz-Capel, S., Esteve-Pérez, J., López-Belchí, A., Romero-Tello, P., & Lorente-López, A. J. (2024). Notes on Towed Self-Propulsion Experiments with Simulated Managed Ice in Traditional Towing Tanks. Journal of Marine Science and Engineering, 12(10), 1691. https://doi.org/10.3390/jmse12101691








