Study on Hydroelastic Responses of Membrane-Type LNG Cargo Containment Structure under Impulsive Sloshing Loads of Different Media
Abstract
1. Introduction
2. Sloshing Experiment and Pressure Measurement
2.1. Model-Scale Experiment
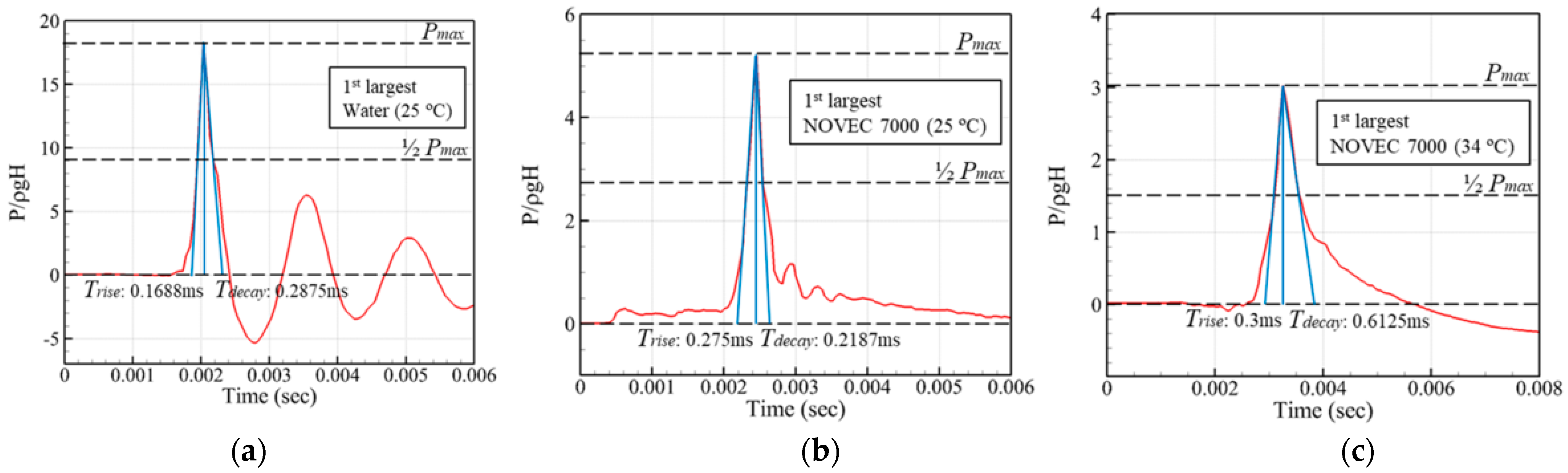
2.2. Measured Impact Pressures
3. Modeling of Hydroelasticity for LNG CCS Structure
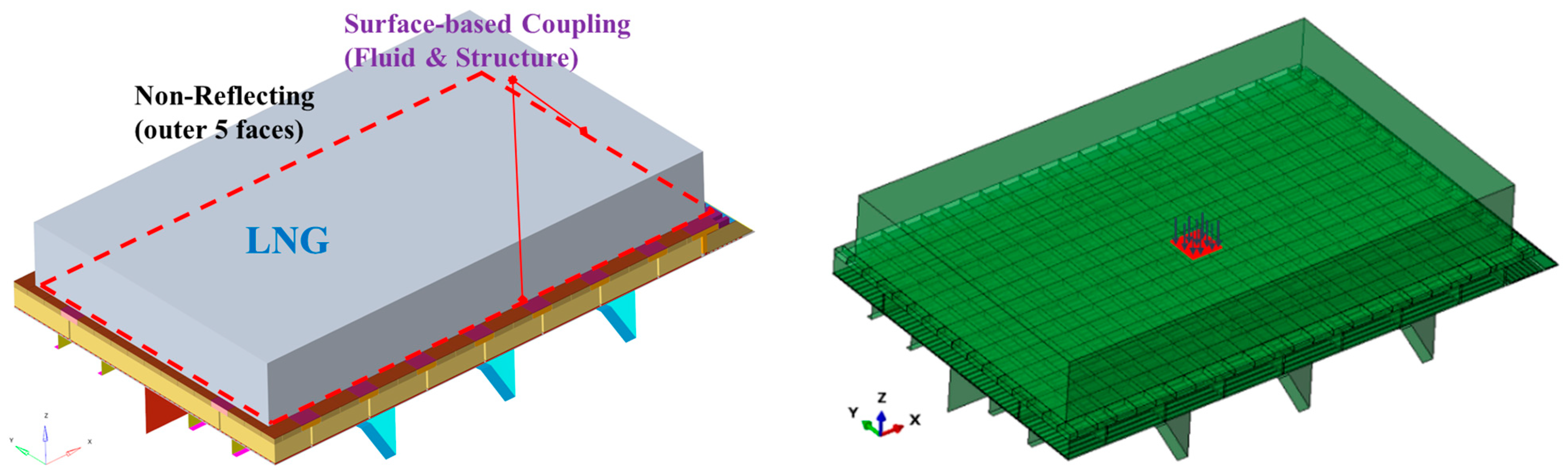
3.1. LNG CCS and Hull FE Modeling
3.2. Fluid–Structure Interaction in Coupled Analysis
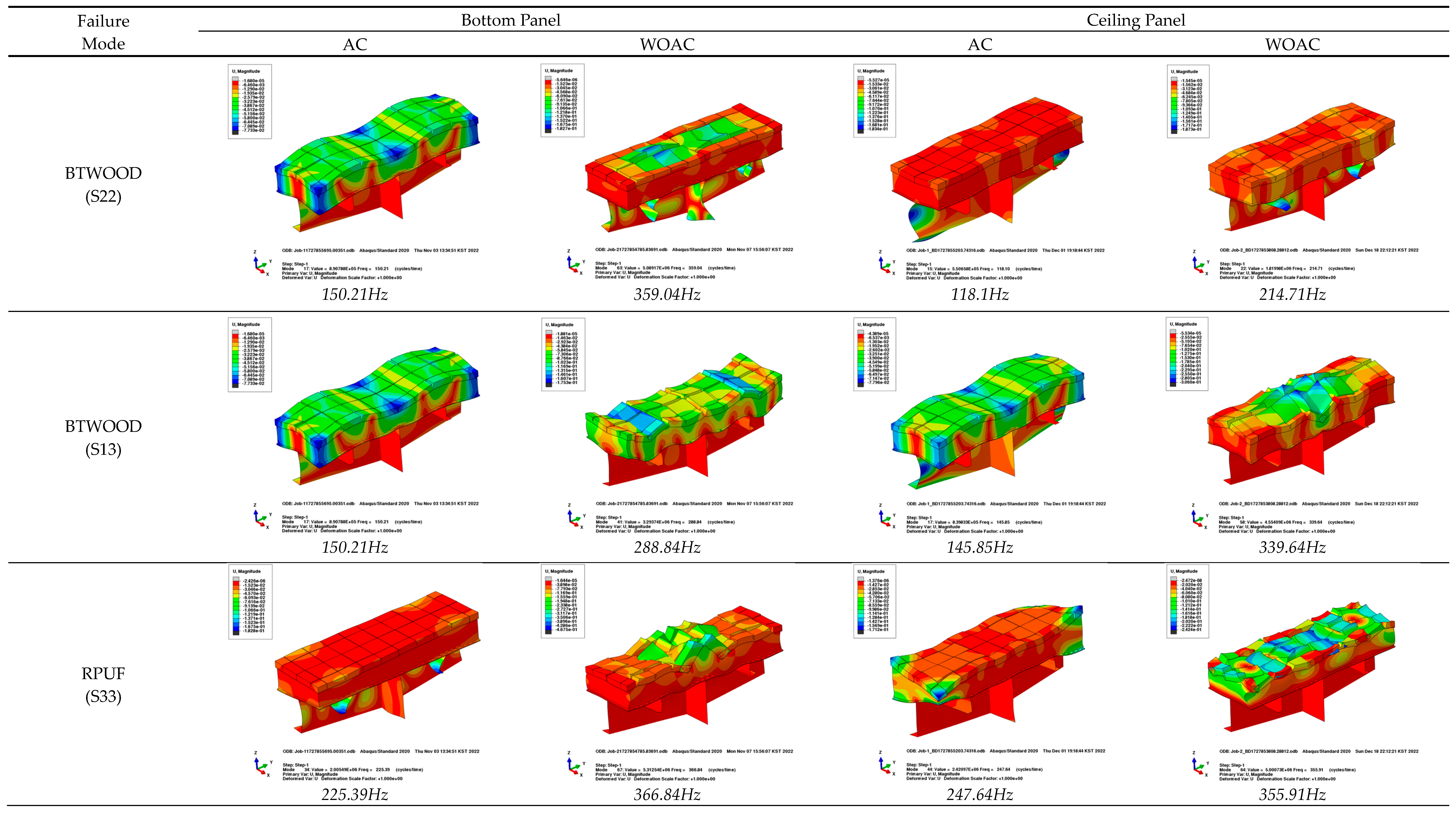
3.3. Failure Modes
4. Analysis Results of Hydroelastic Structural Responses
5. Results of Normal Mode Analysis
6. Dynamic Structural Responses Using Impulse Superposition Method
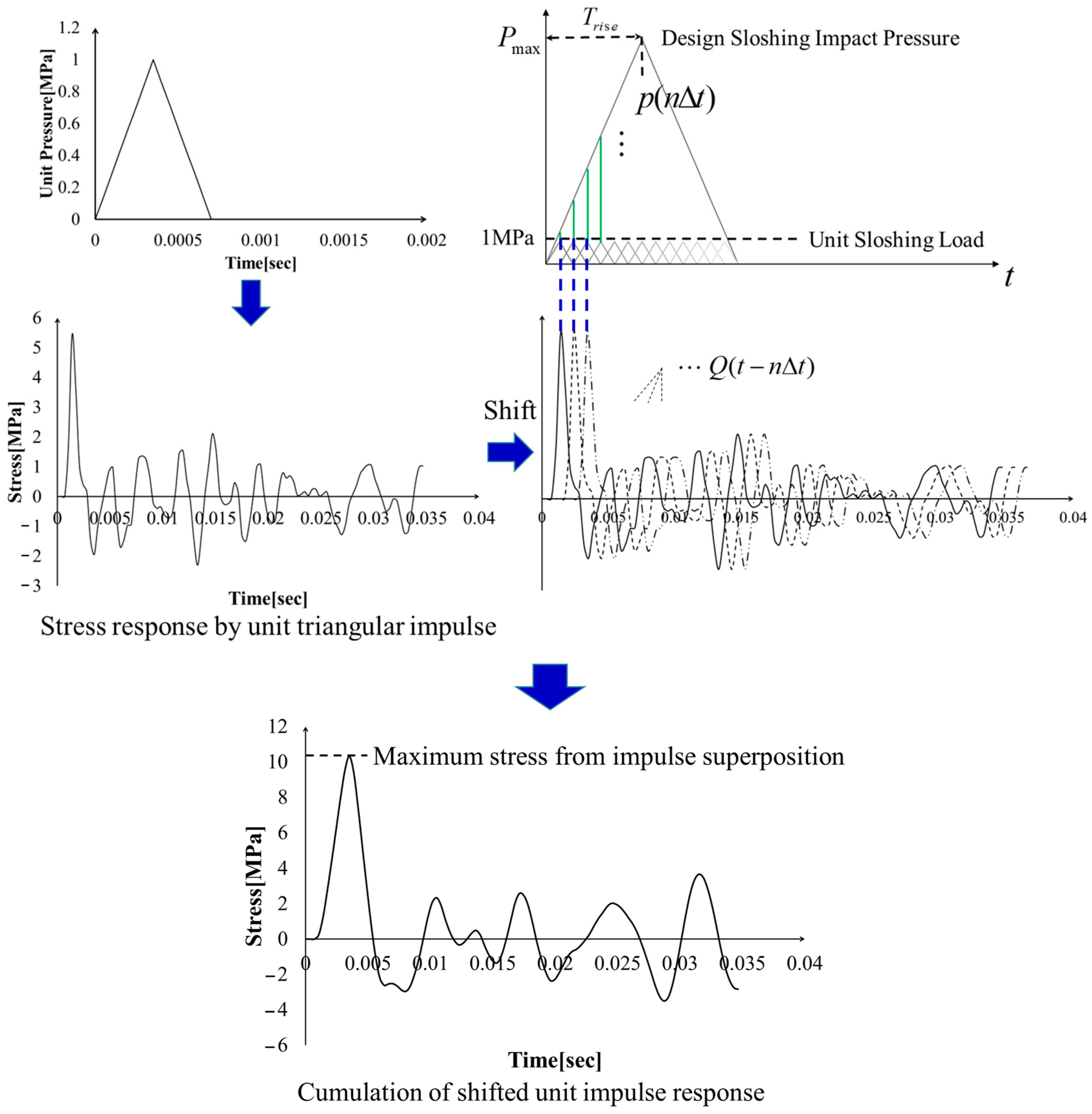
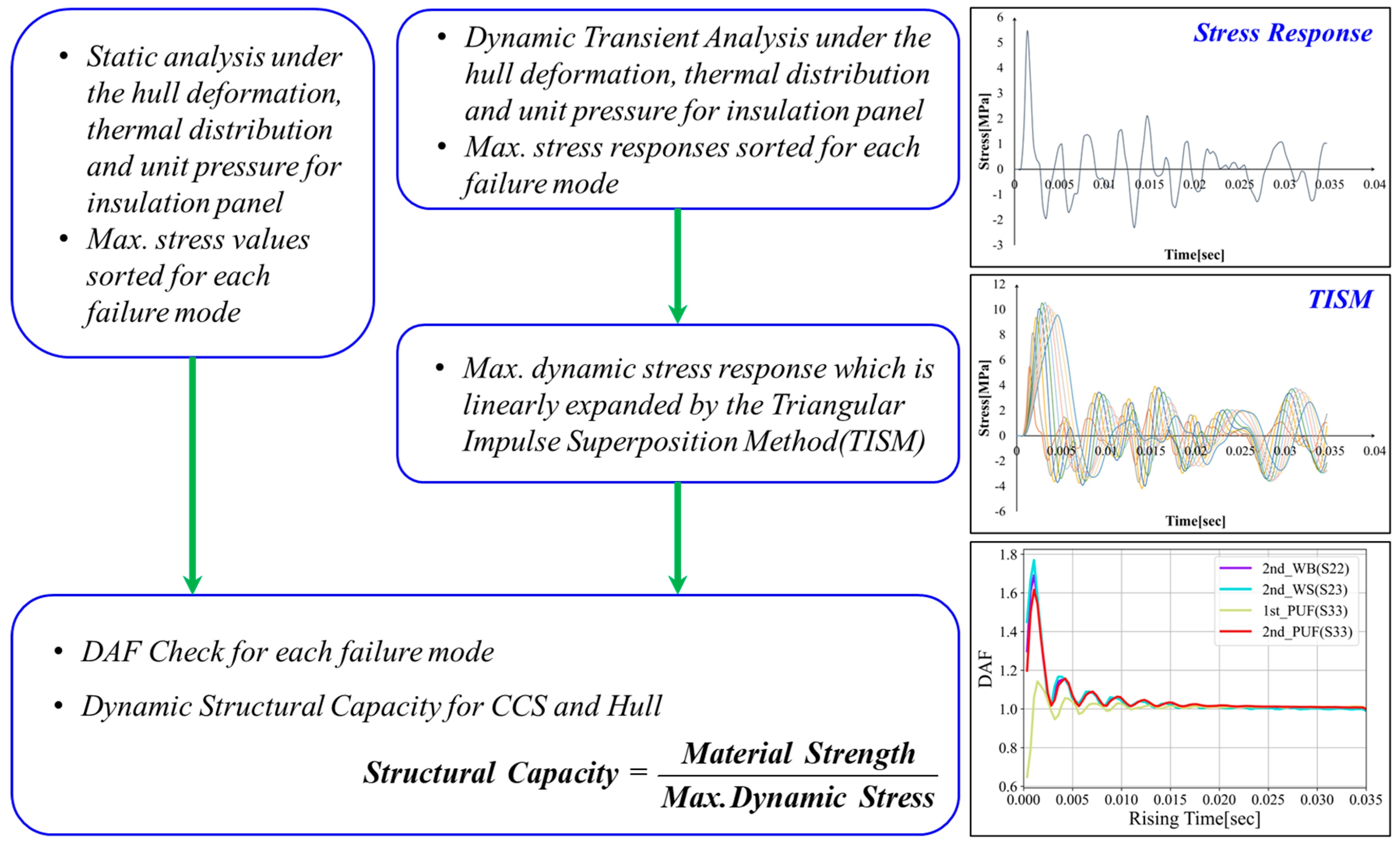
6.1. Triangular Impulse Superposition Method (TISM)
6.2. Dynamic Structural Capacity of the CCS and Hull
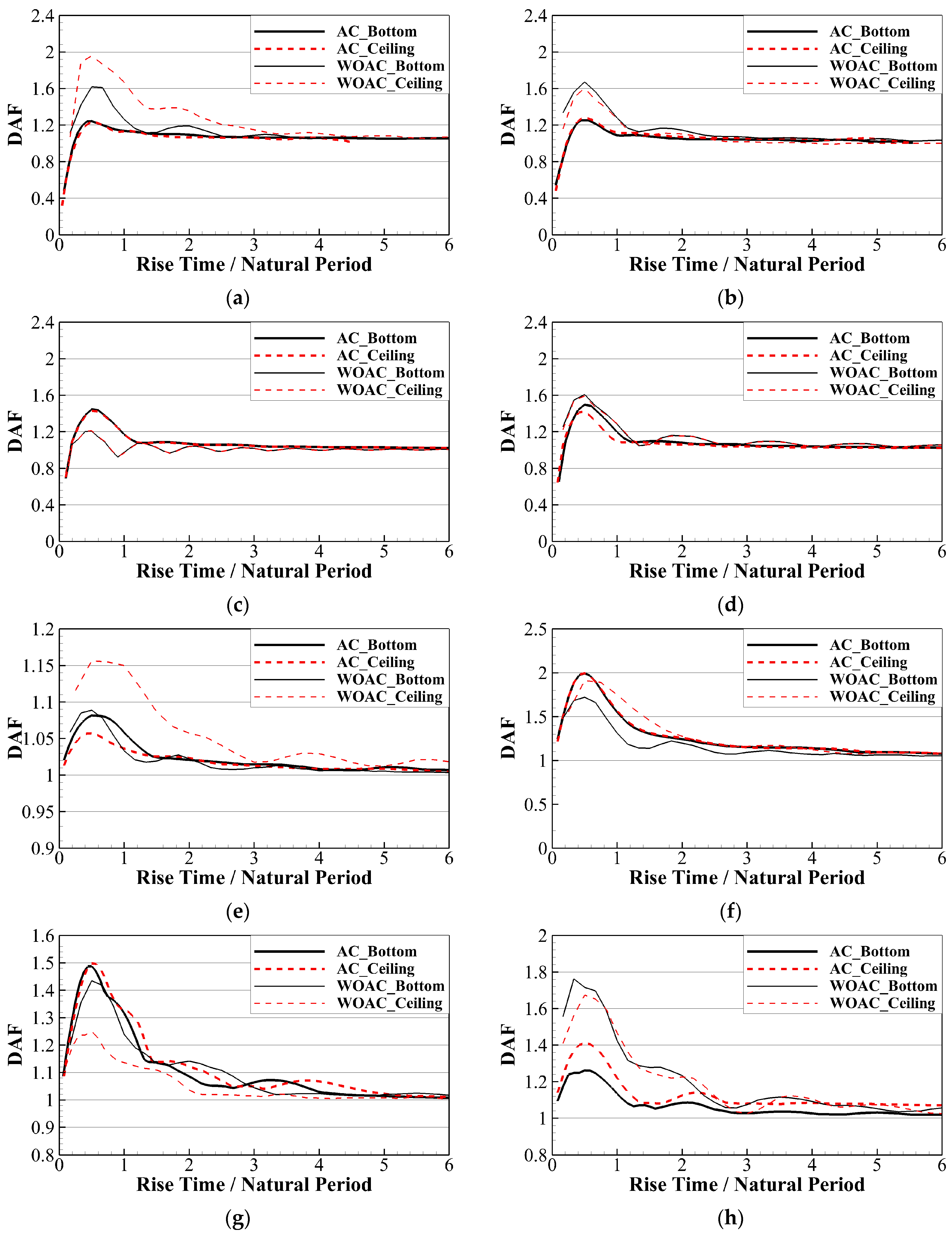
6.3. Dynamic Amplification Factor of CCS and Hull
7. Results of Sloshing Assessment
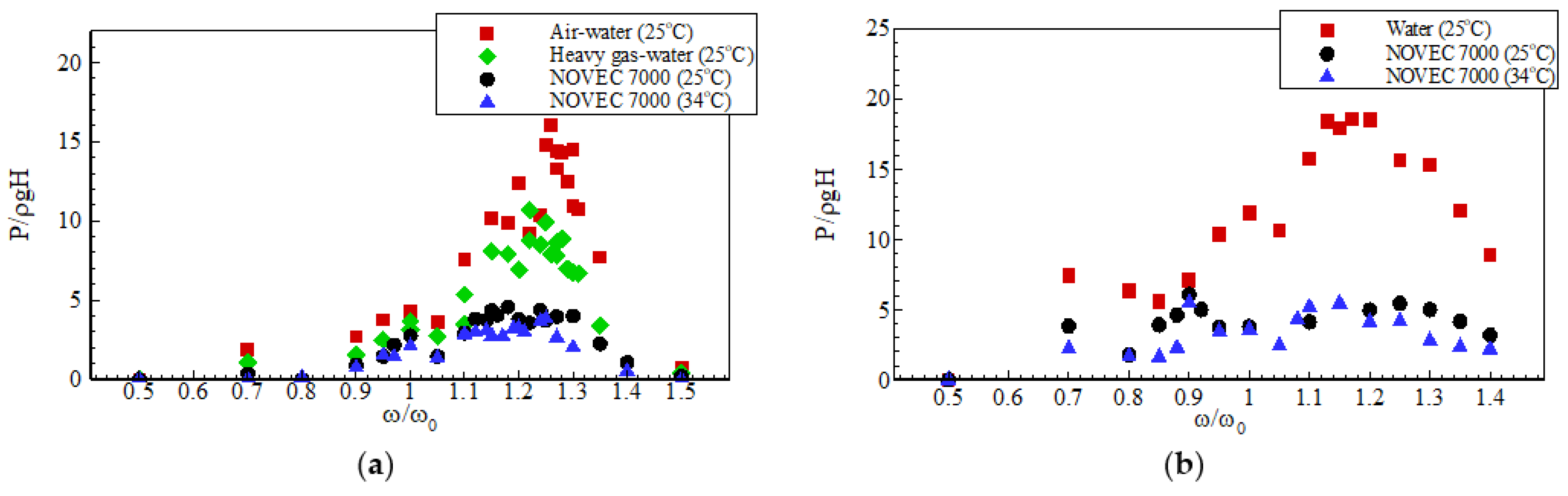
7.1. Conditions of Sloshing Assessment
7.2. Definition of the Utilization Factors
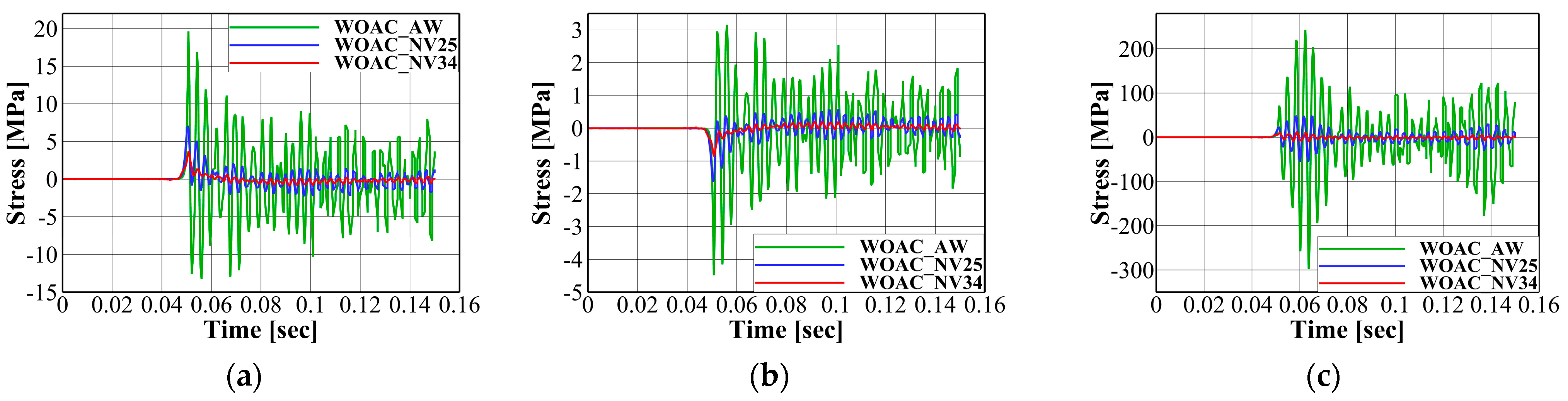
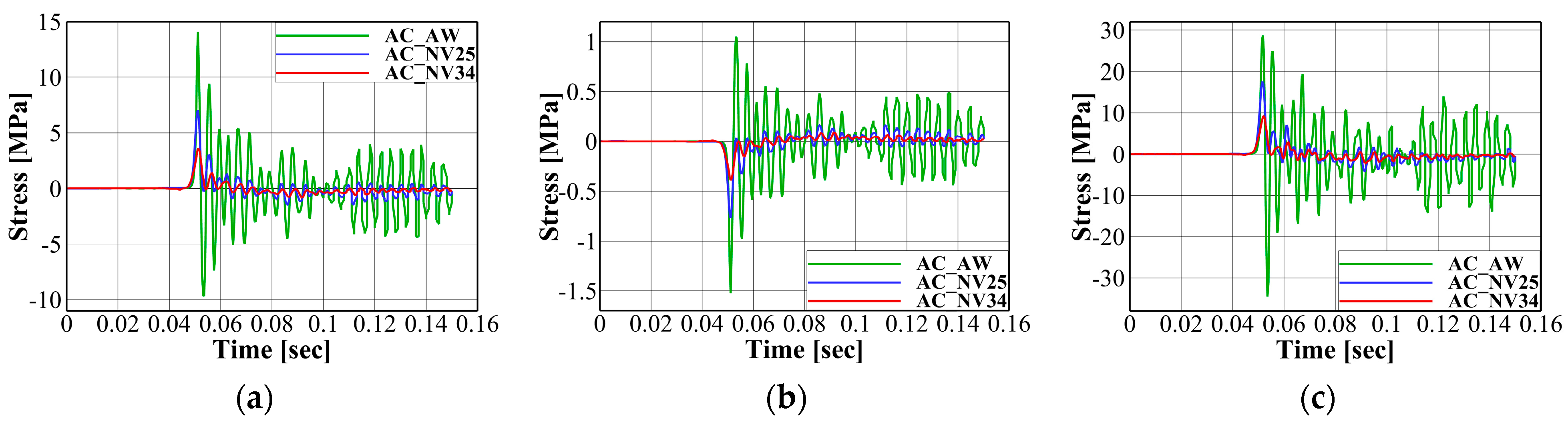
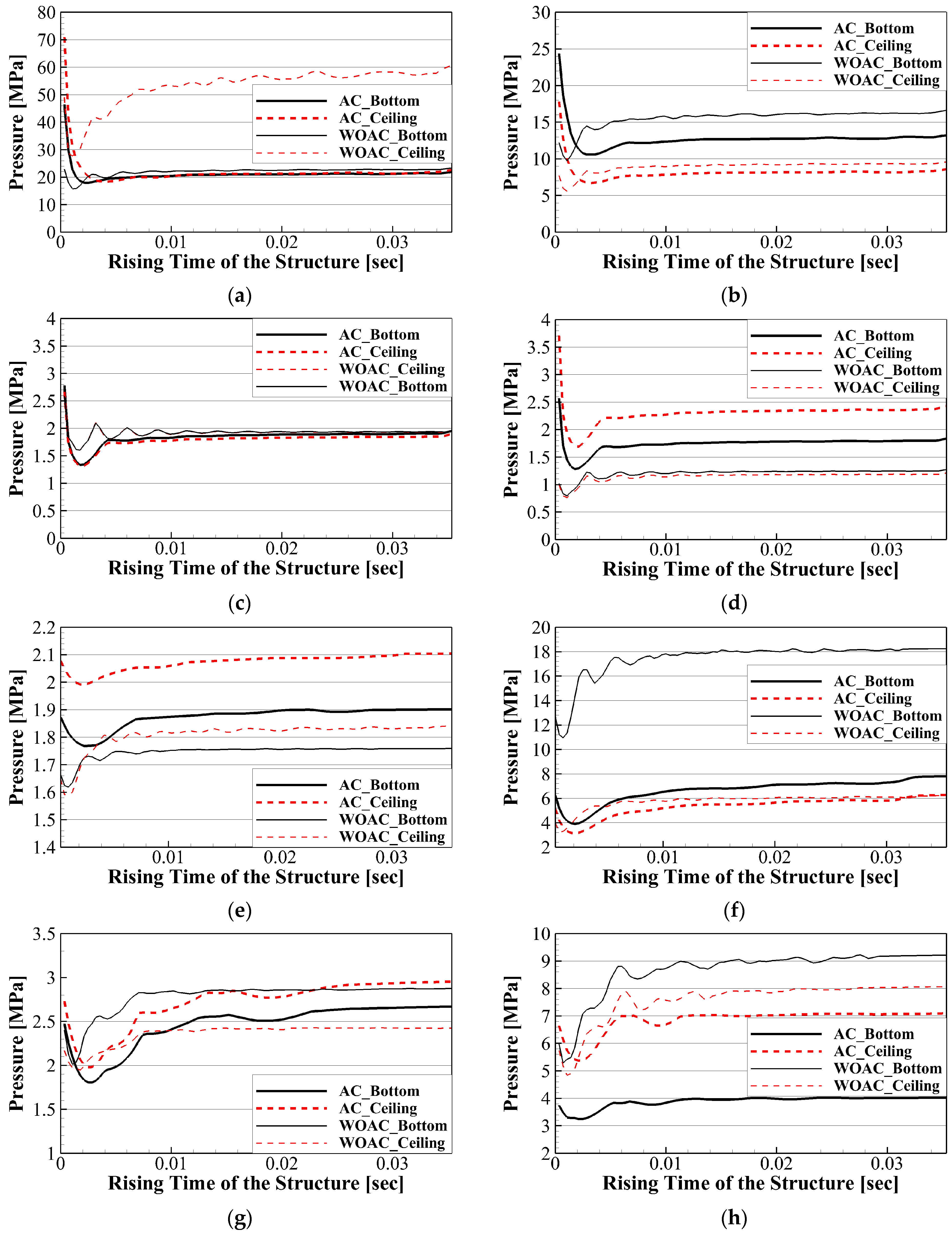
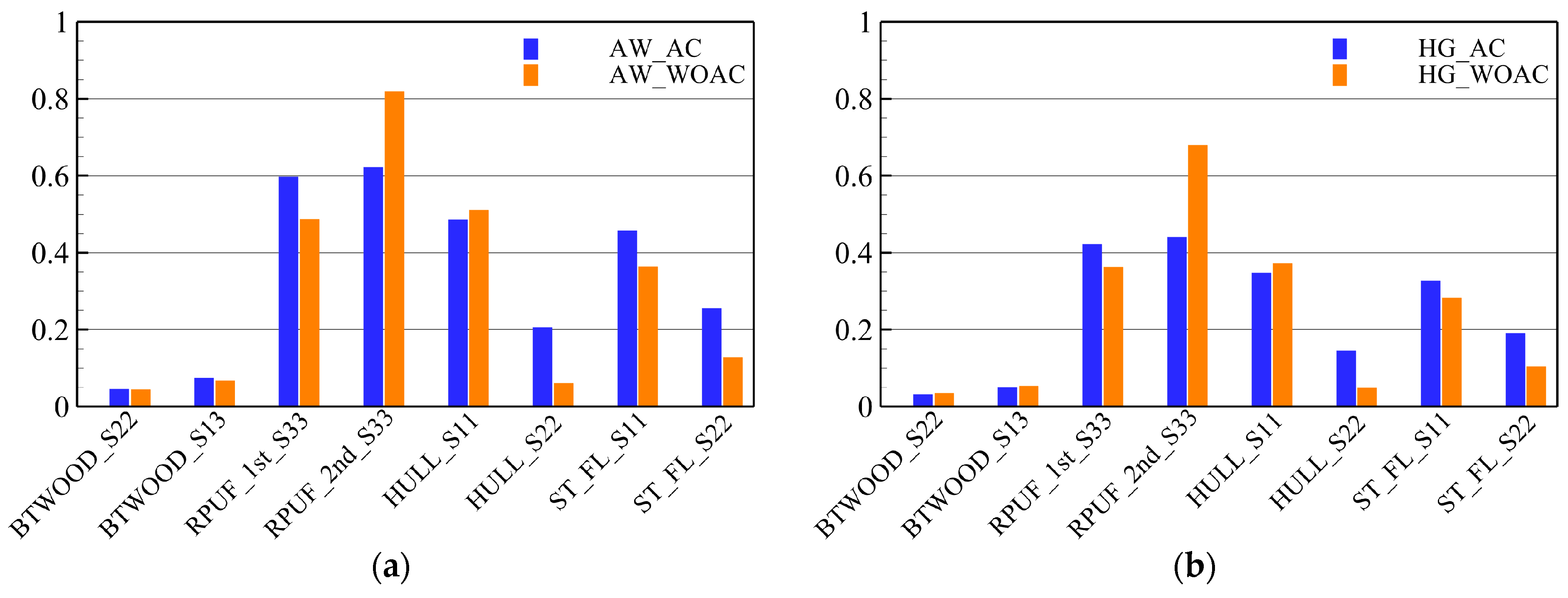
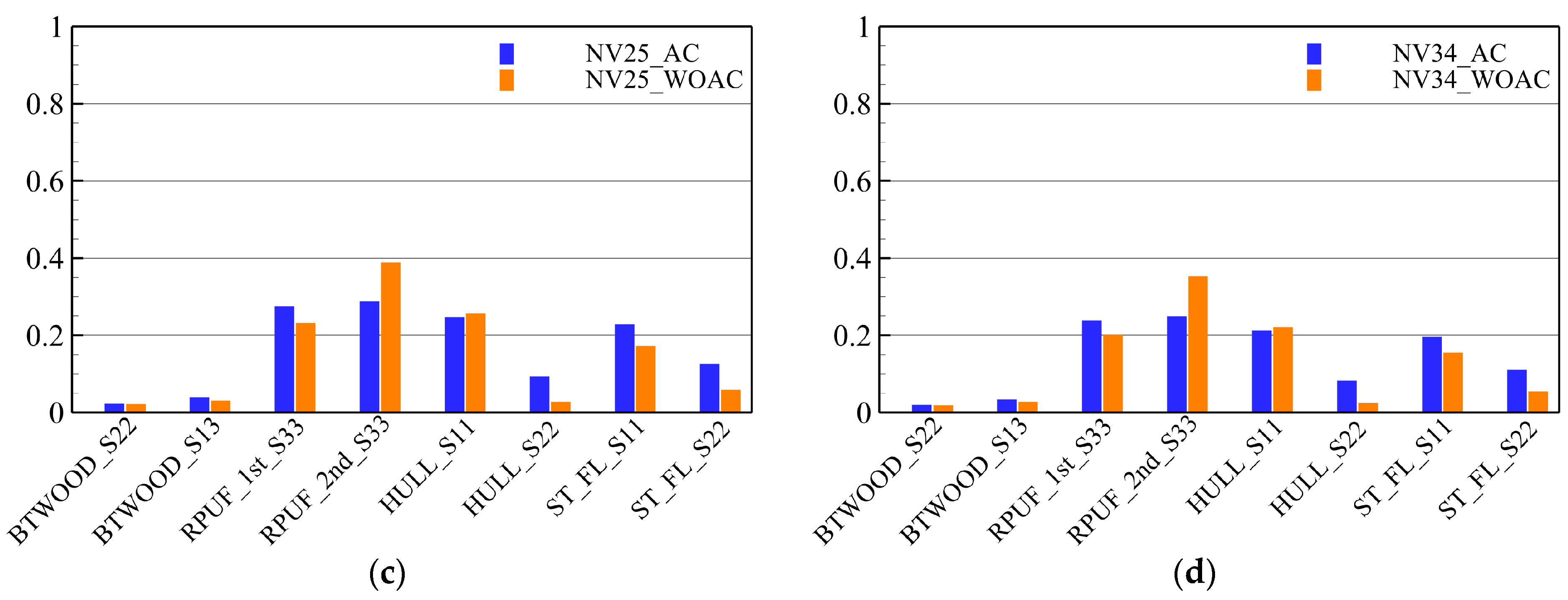
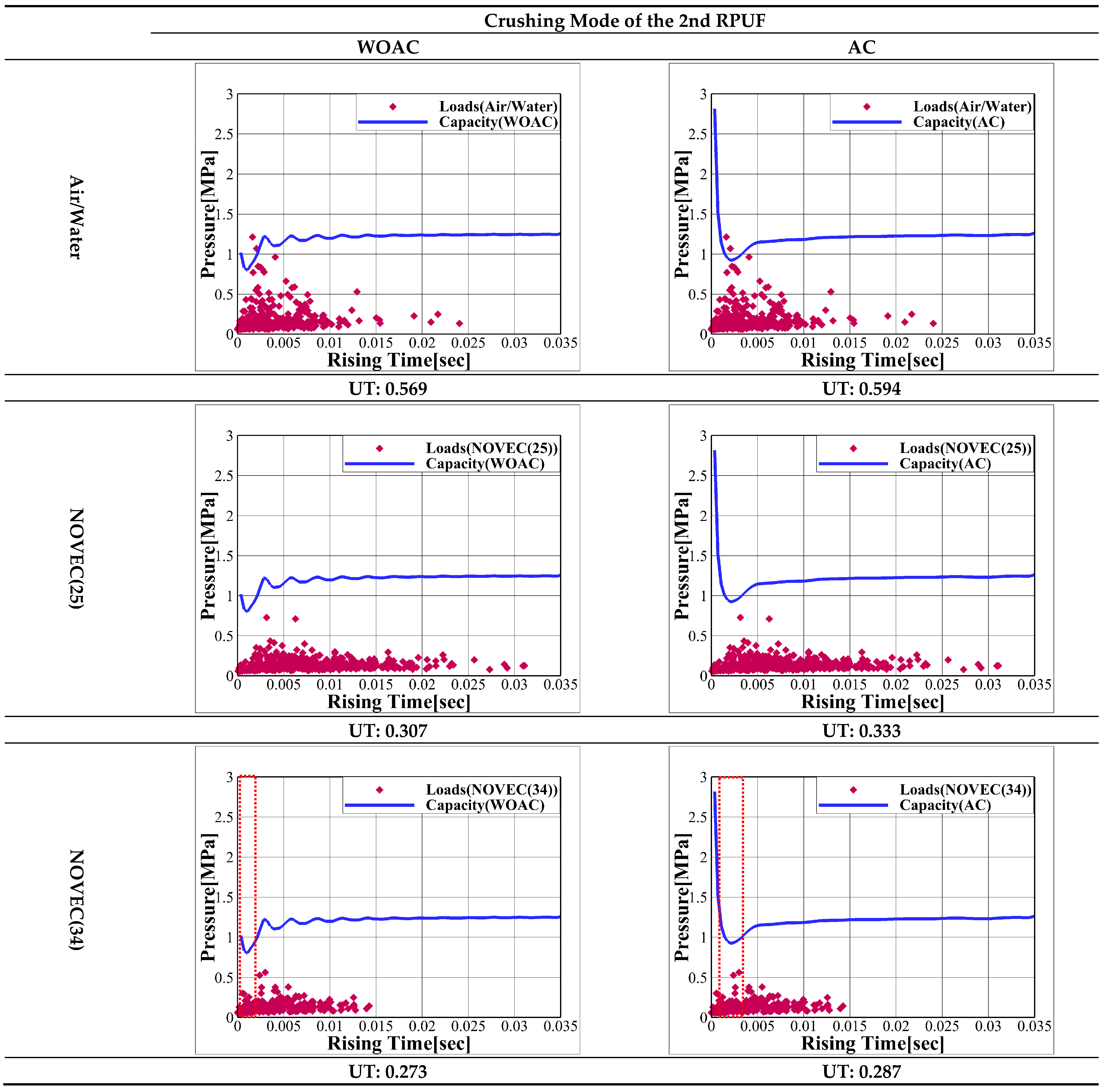
7.3. Utilization Factors with and without Fluid–Structure Interaction
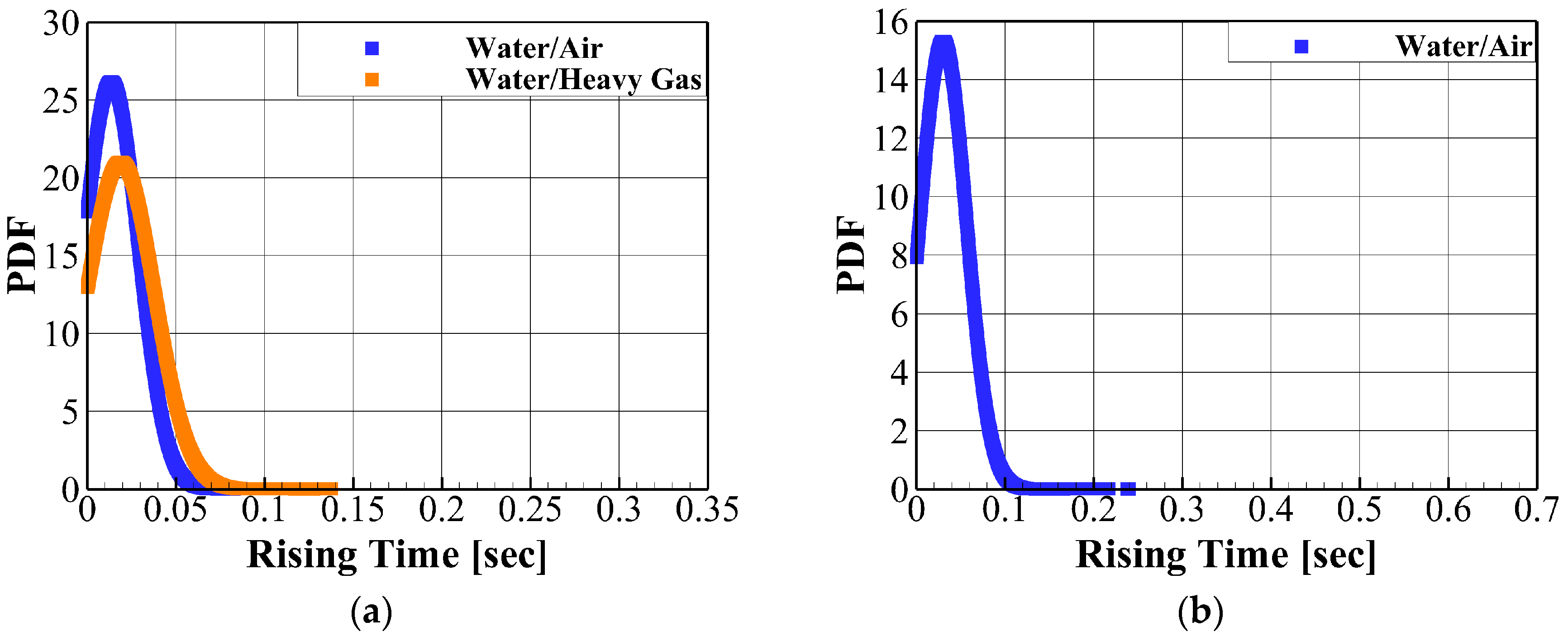
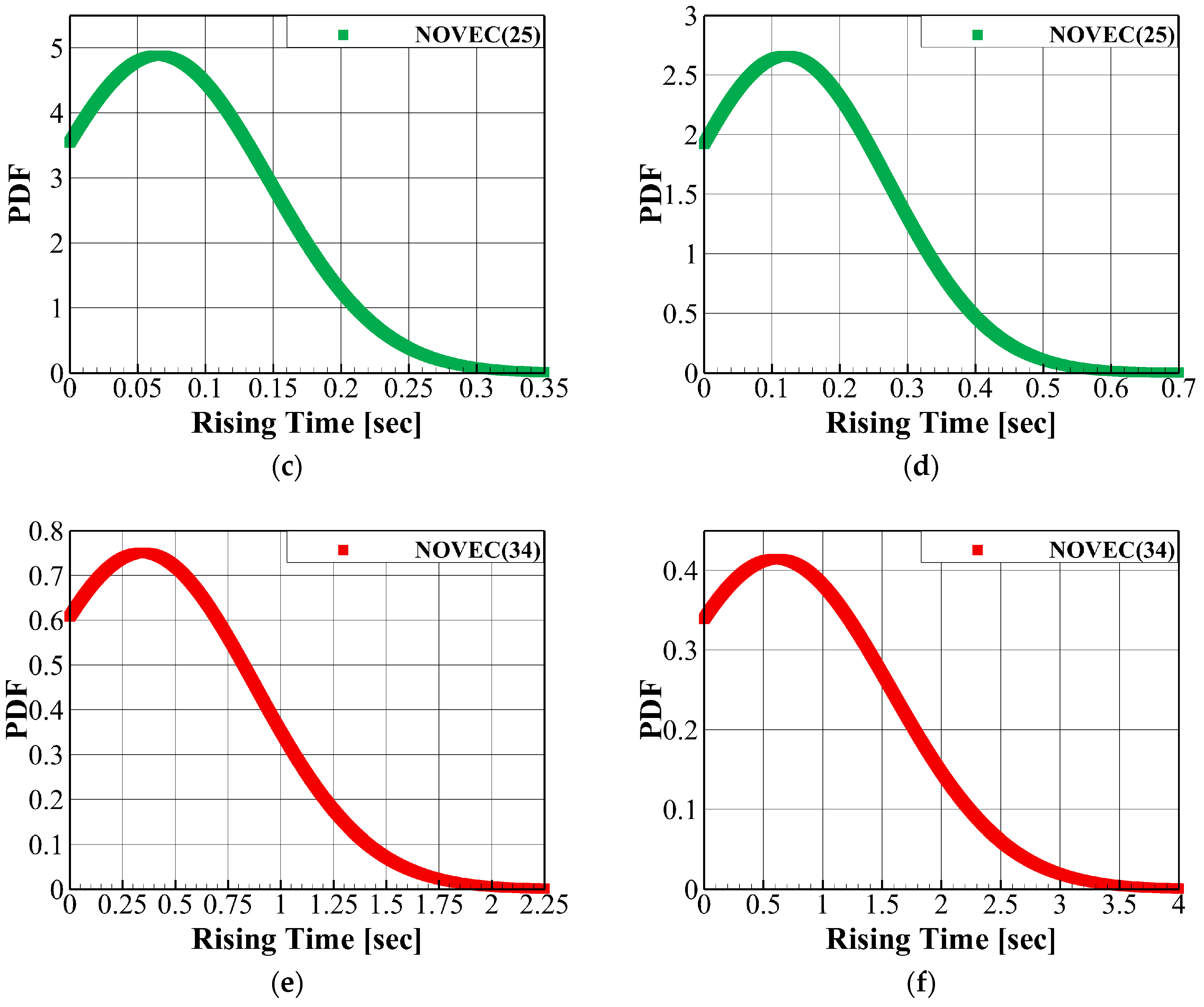
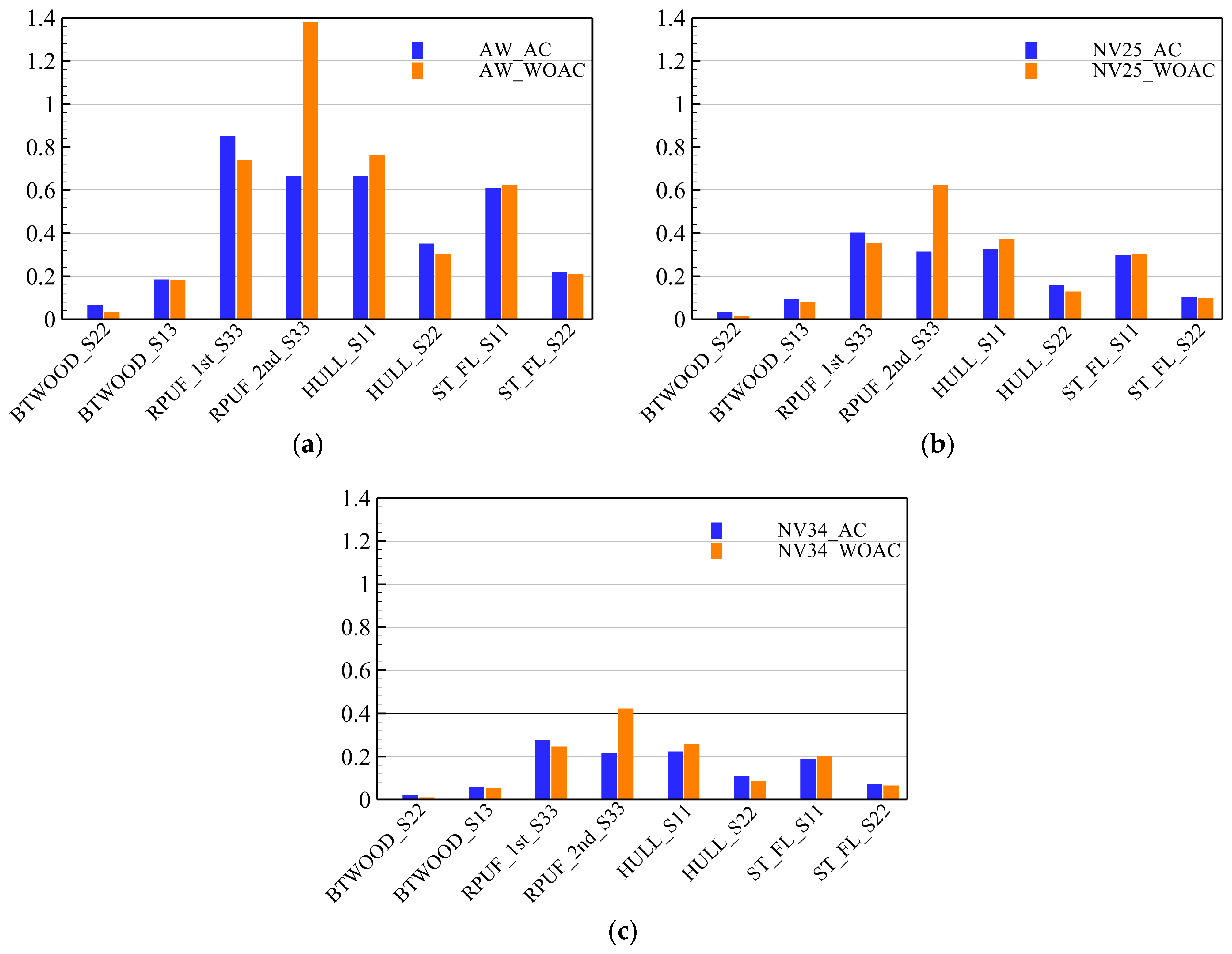
7.4. Consideration of the Lagging Rising Time
7.5. Evaluations with Hydroelasticity and Phase Transition
7.6. Limitations and Future Research
- It is necessary to concretize the definition of dynamic structural capacity that accounts for the nonlinearity of foam and to establish a corresponding absolute assessment methodology.
- The sloshing assessment for special areas, such as corner panels, needs to be conducted using various footprints based on load combinations derived from pressure sensor data.
- Given that the hull is significantly affected by hydroelastic effects, it is essential to establish guidelines for hull reinforcement by local sloshing impact pressures at the upper part of LNG carrier tanks.
- The potential for extending this research appears substantial for vessels that require consideration of partial filling conditions, such as LNG fuel tanks, floating LNG (FLNG) units, and bunkering vessels.
8. Conclusions
- In the sloshing model tests, the water–air combination provided the highest peak impact pressure. In contrast, the NOVEC test at the boiling point showed the lowest peak impact pressure, with a relatively longer rise time. Different pressure patterns induced different structural responses of the LNG CCS, significant dynamic responses with oscillations during the decay time for the water–air case, and relatively smaller and smoother structural responses in NOVEC 7000 at the boiling temperature.
- As a result of fluid–structure interactions, a time lag phenomenon can be observed in the dynamic structural capacity curves. A significantly longer time lag occurred in the ceiling structure than in the bottom structure. Moreover, under AC conditions, stress responses were predominant in the low-frequency range (below 200 Hz) compared to the WOAC conditions. The dominant failure mode was observed in the lower plywood bending and shear failure modes of the structure components.
- The DAF value under the WOAC condition increased at the furthest component from the point where the load was applied, and the maximum value was observed in the lower plywood bending mode. However, under AC conditions, the DAF in the RPUF increased compared to that in the lower plywood, and the maximum value was observed in the hull bending mode. In particular, DAF was most pronounced in the ceiling structure, where the hull was relatively thin. This indicates that when considering the hydroelastic effects, there can be an increase in the dynamic stress response in the foam material, and the dynamic stress response in the hull of the ceiling structure may be greater than that in the bottom structure.
- The sloshing assessment results showed a decreasing trend in UT values in the following order: water–air, water–heavy gas, NOVEC at 25 °C, and NOVEC at boiling temperature. The UT values were significantly higher in the ceiling structure than in the bottom structure. This was because of the higher sloshing loads in the high-filling condition than in the low-filling condition. Moreover, it was observed that both the bottom and ceiling structural components, specifically BTWOOD_S13, 1st RPUF Crushing, and Hull_S22, experienced an increase in UT values owing to hydroelastic effects.
- The structural responses were dependent on the distribution of structural capacity and sloshing loads over different rise times. Therefore, in the sloshing assessment, both the maximum sloshing impact pressure and distribution of rise times should be considered simultaneously. Furthermore, the delay in the dynamic structural responses due to hydroelasticity and phase transition can change the UT values.
- The significant dynamic structural responses observed in the water–air test indicate the limitations of the absolute assessment; therefore, a more realistic sloshing assessment considering the phase transition and hydroelastic effects is needed, rather than relying on conventional conservative approaches. More research is needed, but the method applied in this study can be efficient for practical sloshing assessment of LNG CCSs at the present stage.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviation
| AC | Acoustic field |
| CCS | Cargo Containment System |
| BTWOOD_S22 | Stress component of Bottom plywood in the y-direction |
| BTWOOD_S13 | Stress component of Bottom plywood in the xz plane |
| DAF | Dynamic Amplification Factor |
| FE | Finite Element |
| FEA | Finite Element Analysis |
| FFT | Fast Fourier Transform |
| FSI | Fluid Structure Interactions |
| GHG | Greenhouse Gas |
| HULL_S11 | Stress component of Hull plate in the x-direction |
| HULL_S22 | Stress component of Hull plate in the y-direction |
| IMO | International Maritime Organization |
| LNG | Liquefied Natural Gas |
| NG | Natural Gas |
| NOx | Nitrogen Oxides |
| RPUF | Reinforced Polyurethane Foam |
| RPUF_1st_S33 | Stress component of 1st RPUF in the z-direction |
| RPUF_2nd_S33 | Stress component of 2nd RPUF in the z-direction |
| SOx | Sulfur Oxides |
| ST_FL_S11 | Stress component of flange at stiffener in the x-direction |
| ST_FL_S22 | Stress component of flange at stiffener in the y-direction |
| TISM | Triangular Impulse Superposition Method |
| UT | Utilization factor |
| WOAC | Without Acoustic filed |
References
- Joung, T.H.; Kang, S.G.; Lee, J.K.; Ahn, J. The IMO initial strategy for reducing Greenhouse Gas (GHG) emissions, and its follow-up actions towards 2050. J. Int. Marit. Saf. Environ. Aff. Shipp. 2020, 4, 1–7. [Google Scholar] [CrossRef]
- Al-Aboosi, F.Y.; El-Halwagi, M.M.; Moore, M.; Nielsen, R.B. Renewable ammonia as an alternative fuel for the shipping industry. Curr. Opin. Chem. Eng. 2021, 31, 100670. [Google Scholar] [CrossRef]
- Faltinsen, O.M.; Timokha, A.N. Sloshing; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Gavory, T.; De Seze, P.E. Sloshing in membrane LNG carriers and its consequences from a designer’s perspective. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, ISOPE, Osaka, Japan, 21−26 July 2009; p. ISOPE-I-09-041. [Google Scholar]
- Malenica, S.; Diebold, L.; Kwon, S.H.; Cho, D.-S. Sloshing assessment of the LNG floating units with membrane type containment system where we are? Mar. Struct. 2017, 56, 99–116. [Google Scholar] [CrossRef]
- Ahn, Y.; Kim, S.-Y.; Kim, K.-H.; Lee, S.-W.; Kim, Y.; Jong-Jin, P. Study on the Effect of Density Ratio of Liquid and Gas in Sloshing Experiment. In Proceedings of the Twenty-Second International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012; p. ISOPE-I-12-398. [Google Scholar]
- Dias, F.; Ghidaglia, J.-M.; Le Coq, G. On the Fluid Dynamics Models for Sloshing. In Proceedings of the Seventeenth International Offshore and Polar Engineering Conference, Lisbon, Portugal, 1–6 July 2007; p. ISOPE-I-07-565. [Google Scholar]
- Bogaert, H.; Léonard, S.; Brosset, L.; Kaminski, M.L. Sloshing and scaling: Results from the Sloshel project. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, ISOPE, Beijing, China, 20–25 June 2010; p. ISOPE-I-10-030. [Google Scholar]
- Yung, T.-W.; Sandström, R.E.; He, H.; Minta, M.K. On the Physics of Vapor/Liquid Interaction During Impact on Solids. J. Ship Res. 2010, 54, 174–183. [Google Scholar] [CrossRef]
- Maillard, S.; Brosset, L. Influence of DR between liquid and gas on sloshing model test results. Int. J. Offshore Polar Eng. 2009, 19, ISOPE-09-19-4-271. [Google Scholar]
- Ahn, Y.; Kim, Y. Data mining in sloshing experiment database and application of neural network for extreme load prediction. Mar. Struct. 2021, 80, 103074. [Google Scholar] [CrossRef]
- Karimi, M.R.; Brosset, L.; Ghidaglia, J.M.; Kaminski, M.L. Effect of ullage gas on sloshing, Part I: Global effect of gas—liquid density ratio. Eur. J. Mech. B Fluid. 2015, 53, 213–228. [Google Scholar] [CrossRef]
- Karimi, M.R.; Brosset, L.; Ghidaglia, J.M.; Kaminski, M.L. Effect of ullage gas on sloshing, Part II: Local effects of gas—liquid density ratio. Eur. J. Mech. B Fluid. 2016, 57, 82–100. [Google Scholar] [CrossRef]
- Kim, S.-Y.; Kim, Y.; Lee, J. Comparison of sloshing-induced pressure in different scale tanks. Ships Offshore Struct. 2016, 12, 244–261. [Google Scholar] [CrossRef]
- Karimi, M.; Brosset, L.; Kaminski, M.; Ghidaglia, J.-M. Effects of ullage gas and scale on sloshing loads. Eur. J. Mech.B Fluids 2016, 62, 59–85. [Google Scholar] [CrossRef]
- Karimi, M.R.; Brosset, L.; Ghidaglia, J.-M.; Kaminski, M.L. A Study on Conservatism of Froude Scaling for Sloshing Model Tests. In Proceedings of the Twenty-fourth International Ocean and Polar Engineering Conference, Busan, Korea, 15–20 June 2014; p. ISOPE-I-14-322. [Google Scholar]
- Ancellin, M.; Ghidaglia, J.-M.; Laurent, B. Influence of Phase Transition on Sloshing Impact Pressures Described By a Generalized Bagnold′s Model. In Proceedings of the Twenty-second International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012; p. ISOPE-I-12-372. [Google Scholar]
- Braeunig, J.-P.; Brosset, L.; Dias, F.; Ghidaglia, J.-M. On the Effect of Phase Transition on Impact Pressures Due to Sloshing. In Proceedings of the Twentieth International Offshore and Polar Engineering Conference, Beijing, China, 20–25 June 2010; p. ISOPE-I-10-182. [Google Scholar]
- Kim, Y.; Lee, J.; Kim, J. Experimental Observation of the Effects of Liquid Temperature and Bubbles on Impact Pressure Inside Gas Pocket. Int. J. Offshore Polar Eng. 2017, 27, 1–10. [Google Scholar] [CrossRef]
- Lee, J.; Ahn, Y.; Kim, Y. Experimental study on effect of density ratio and phase transition during sloshing impact in rectangular tank. Ocean. Eng. 2021, 242, 11010. [Google Scholar] [CrossRef]
- Lloyd’s Register. Sloshing Assessment Guidance Document for Membrane Tank LNG Operations; Additional Design Procedures: London, UK, 2009. [Google Scholar]
- Bureau Veritas. Strength Assessment of LNG Membrane Tanks under Sloshing Loads; Guidance Note. NI564; Bureau Veritas: Neuilly sur Seine, France, 2011. [Google Scholar]
- American Bureau of Shipping. Strength Assessment of Membrane-type LNG Containment Systems under Sloshing Loads; Guidance Notes; American Bureau of Shipping: Houston, TX, USA, 2009. [Google Scholar]
- DNVGL. Sloshing Analysis of LNG Membrane Tanks, Class Guidance, DNVGL-CG-0158. 2016. Available online: https://rules.dnv.com/docs/pdf/dnvpm/cn/2016-02/CN30-9.pdf (accessed on 29 September 2024).
- Chun, S.E.; Hwang, J.O.; Chun, M.S.; Suh, Y.S.; Hwangbo, S.M.; Lee, J.M.; White, N.; Wang, Z.H. Direct Assessment of Structural Capacity Against Sloshing Loads Using Nonlinear Dynamic FE Analysis Including Hull Structural Interactions. In Proceedings of the Twenty-first International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011; p. ISOPE-I-11-473. [Google Scholar]
- Pillon, B.; Marhem, M.; Leclère, G.; Canler, G. Numerical Approach for Structural Assessment of LNG Containment Systems. In Proceedings of the Nineteenth International Offshore and Polar Engineering Conference, Osaka, Japan, 12–17 July 2009; p. ISOPE-I-09-044. [Google Scholar]
- Sang-Gab, L.; Jin-Kyung, K.; Hong-Anh, N.; Jae-Hyung, N. Structural Safety Assessment of LNGC MARK III Membrane Type CCS Under Sloshing Impact Loading. In Proceedings of the Twenty-Second International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012; p. ISOPE-I-12-409. [Google Scholar]
- Wang, B.; Kim, J.W. Strength Evaluation of LNG Containment System Considering Fluid-Structure Interaction Under Sloshing Impact Pressure. In Proceedings of the ASME 2007 26th International Conference on Offshore Mechanics and Arctic Engineering. Volume 1: Offshore Technology; Special Symposium on Ocean Measurements and Their Influence on Design, San Diego, CA, USA, 10–15 June 2007; pp. 545–552. [Google Scholar]
- Malenica, S.; Mravak, Z.; Besse, P.; Kaminski, M.L.; Bogaert, H. Full scale experiments and new methodology to assess the structural behaviour of a membrane LNGC containment system under breaking waves project “SLOSHEL”. In Proceedings of the 24th International Conference & Exhibition for the LNG, LPG & Natural Gas Industries, Abu Dabi, United Arab Emirates, 25–28 May 2009. [Google Scholar]
- Nho, I.S.; Ki, M.S.; Kim, S.C. A study on simplified sloshing impact response analysis for membrane-type LNG cargo con-tainment system. J. Soc. Nav. Archit. Korea 2011, 48, 451–456. [Google Scholar] [CrossRef]
- Lee, J. Experimental Study on the Effect of Liquid-Gas Phase Transition during Sloshing Impact. Ph.D. Thesis, Seoul National University, Seoul, Republic of Korea, 2020. [Google Scholar]
- GTT Mark III Systems. Available online: https://gtt.fr/technologies/markiii-systems (accessed on 25 August 2024).
- Abaqus. 6.14 User’s Documentation, Getting Started with Abaqus Interactive Edition. Available online: http://62.108.178.35:2080/v6.14/books/stm/default.htm (accessed on 25 August 2024).
- Crawford, D.B.; Durr, C.A. Design of LNG Receiving Terminals. In Advances in Cryogenic Engineering; Springer: Boston, MA, USA, 1995; pp. 261–268. [Google Scholar]
- Ju, H.-B.; Jang, B.-S.; Yim, K.-H. Prediction of sloshing pressure and structural response of LNG CCS. Ocean Eng. 2022, 266, 112298. [Google Scholar] [CrossRef]


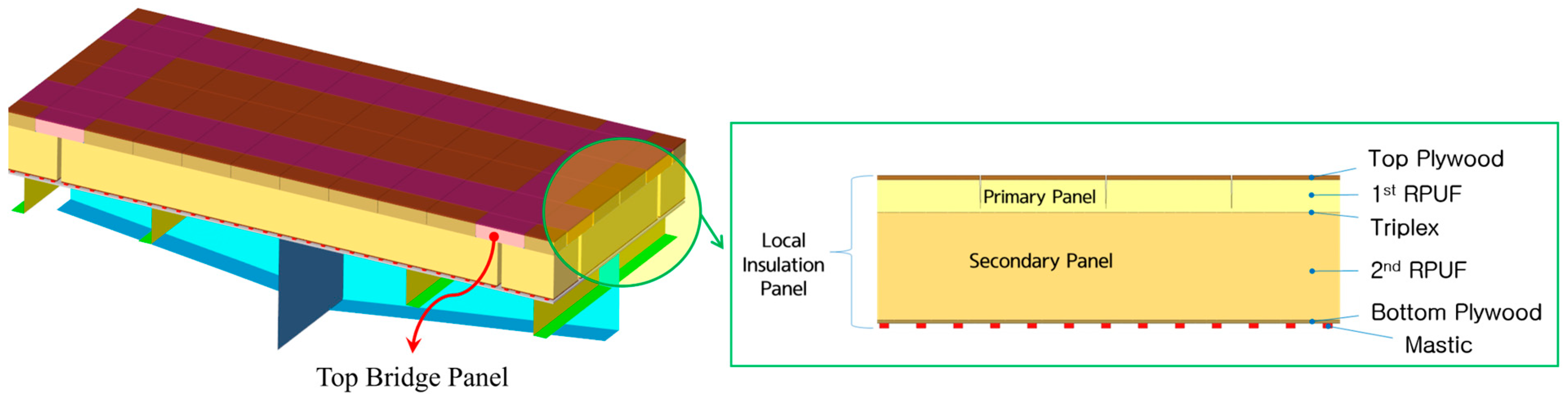
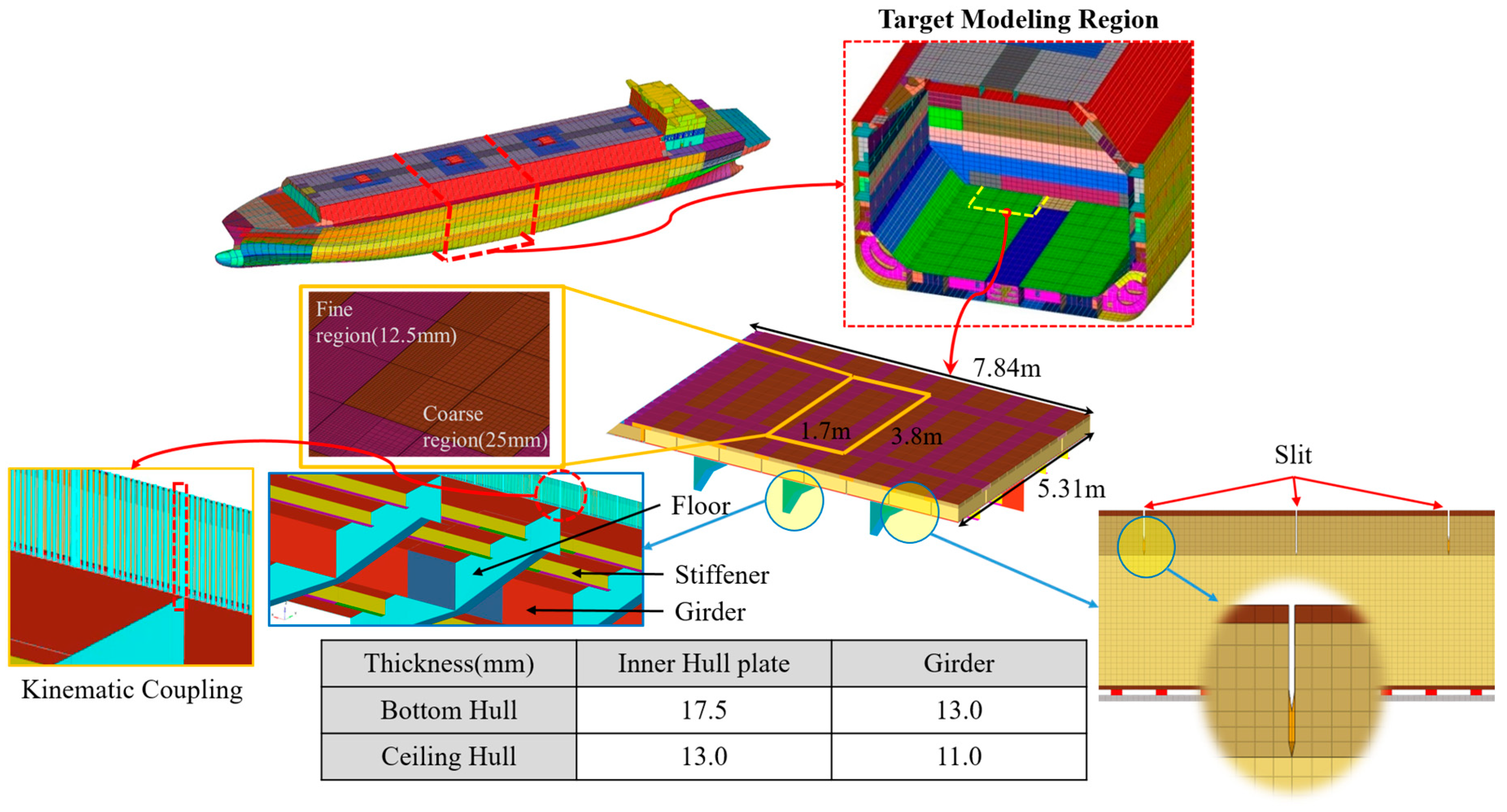
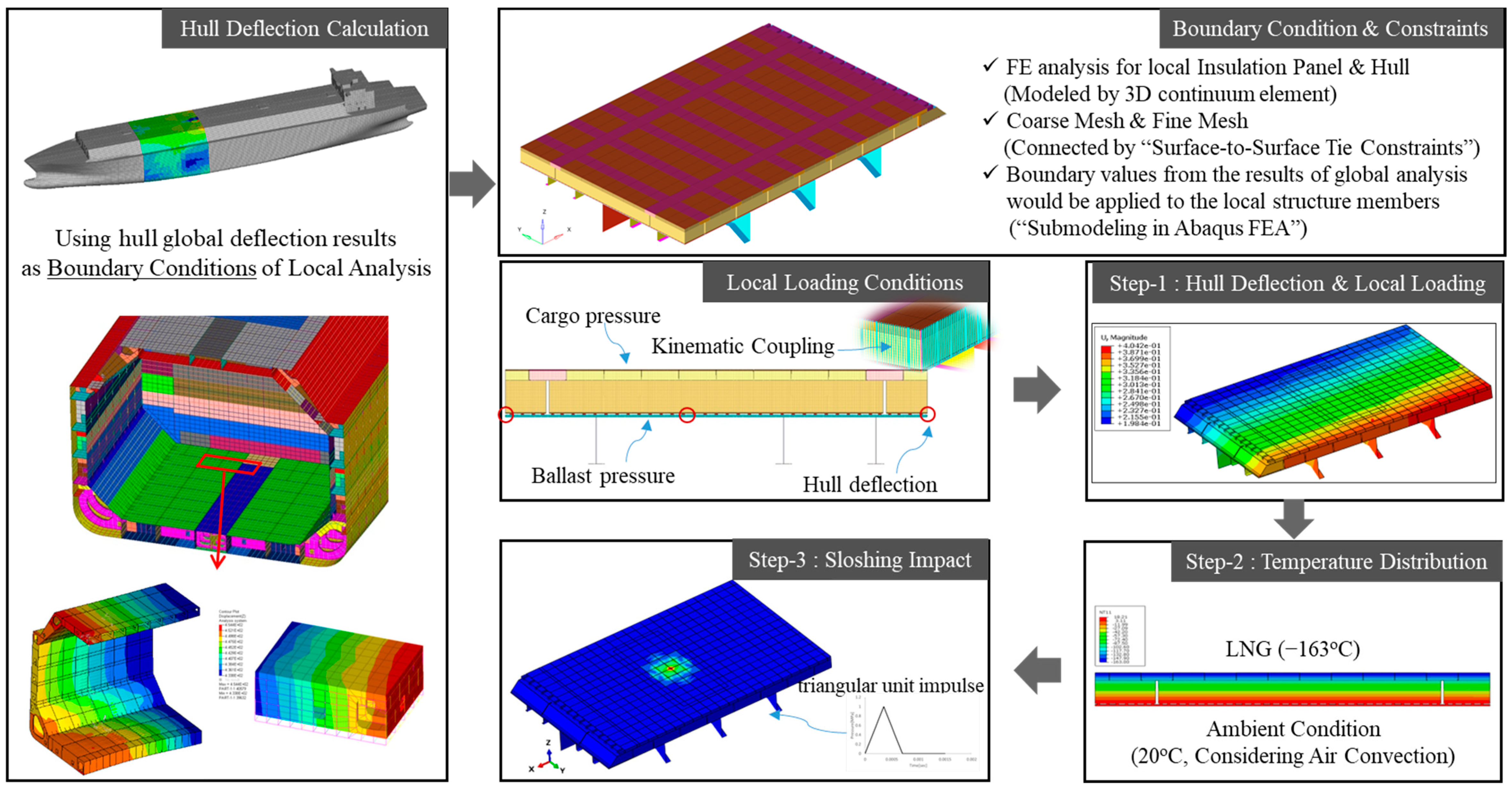
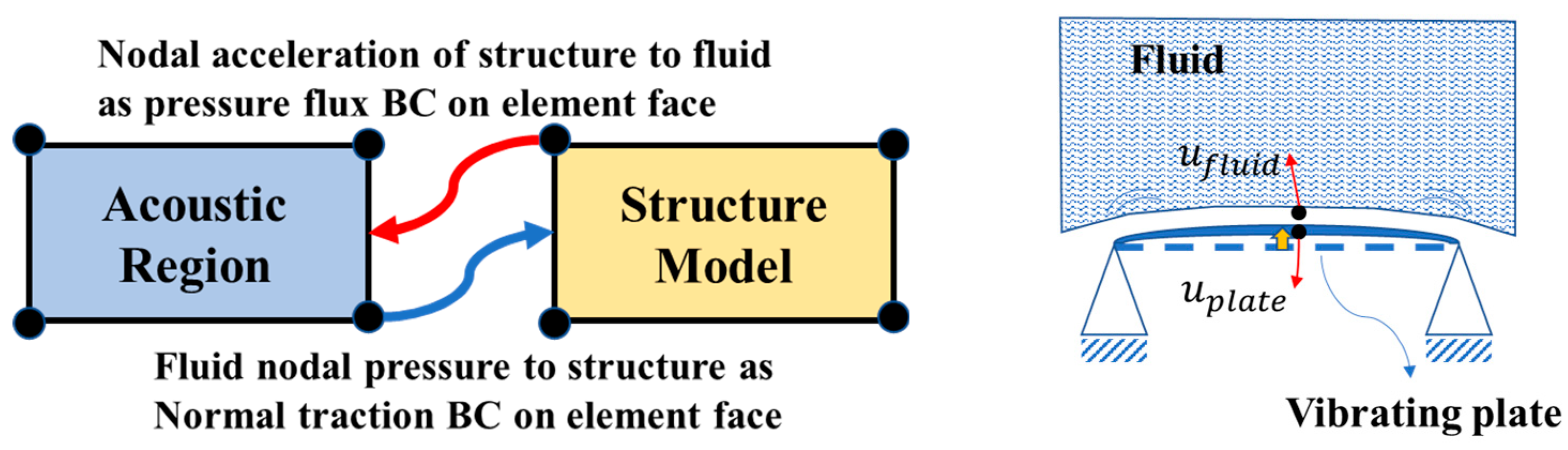




| Material | Plywood | RPUF | Secondary Barrier | Mastic | Hull |
|---|---|---|---|---|---|
| Material property | orthotropic | orthotropic | orthotropic | isotropic | isotropic |
| Density (kg/m3) | 680 | 130 | 2700 | 950 | 7850 |
| Elastic Modulus (MPa) −170 °C | E11 = 13,800 E22 = 7200 E33 = 170 | E11 = 68 E22 = 79 E33 = 80 | E11 = E33 = 7500 E22 = 9900 | - | - |
| Elastic Modulus (MPa) 20 °C | E11 = E22 = 8030 E33 = 70 | E11 = 30.4 E22 = 50.8 E33 = 47.6 | E11 = E33 = 5400 E22 = 7050 | 680 | 206,000 |
| Poisson’s Ratio −170 °C | v12, v13, v23 = 0.1 | v12 = 0.4 v13 = v23 = 0.2 | v12, v13, v23 = 0.3 | 0.3 | 0.3 |
| Poisson’s Ratio 20 °C | v12, v13, v23 = 0.1 | v12 = 0.4 v13 = v23 = 0.2 | v12, v13, v23 = 0.3 | 0.3 | 0.3 |
| Natural Gas at −163 °C | Density (kg/m3) | Bulk Modulus [Gpa] |
|---|---|---|
| LNG | 470 | 0.848 |
| No. | Index | Failure Mode | Stress Component |
|---|---|---|---|
| 1 | BTWOOD_S22 | Bending failure of bottom plywood in direction of mastic spacing | S22 |
| 2 | BTWOOD_S13 | Shearing failure of bottom plywood in way of mastics | S13 |
| 3 | RPUF_1st_S33 | Crushing failure of 1st RPUF in the z-direction | S33 |
| 4 | RPUF_2nd_S33 | Crushing failure of 2nd RPUF in the z-direction | S33 |
| 5 | HULL_S11 | Hull bending failure along the mastic ropes | S11 |
| 6 | HULL_S22 | Hull bending failure across the mastic ropes | S22 |
| 7 | ST_FL_S11 | Bending failure of the flange at stiffener in the x-direction | S11 |
| 8 | ST_FL_S22 | Bending failure of the flange at stiffener in the y-direction | S22 |
| Bottom | Ceiling | AC/WOAC [Times] | ||||
|---|---|---|---|---|---|---|
| Failure Mode | AC | WOAC | AC | WOAC | Bottom | Ceiling |
| BTWOOD_S22 | 2.47 | 1.06 | 3.89 | 1.06 | 2.33 | 3.67 |
| BTWOOD_S13 | 3.18 | 1.06 | 3.18 | 1.06 | 3.00 | 3.00 |
| RPUF_1st_S33 | 1.77 | 1.77 | 1.77 | 1.77 | 1.00 | 1.00 |
| RPUF_2nd_S33 | 1.77 | 1.06 | 2.12 | 1.06 | 1.67 | 2.00 |
| HULL_S11 | 2.47 | 1.06 | 2.47 | 0.71 | 2.33 | 3.50 |
| HULL_S22 | 2.12 | 1.06 | 2.12 | 0.71 | 2.00 | 3.00 |
| ST_FL_S11 | 2.83 | 1.06 | 2.47 | 1.77 | 2.67 | 1.40 |
| ST_FL_S22 | 2.12 | 1.06 | 2.12 | 1.06 | 2.00 | 2.00 |
| Bottom | Ceiling | |||
|---|---|---|---|---|
| Failure Mode | AC | WOAC | AC | WOAC |
| BTWOOD_S22 | 152.16 | 360.68 | 118.35 | 214.15 |
| BTWOOD_S13 | 152.16 | 287.41 | 146.52 | 338.13 |
| RPUF_1st_S33 | 225.42 | 366.31 | 247.96 | 355.04 |
| RPUF_2nd_S33 | 225.42 | 360.68 | 247.96 | 355.04 |
| HULL_S11 | 129.62 | 360.68 | 135.25 | 417.03 |
| HULL_S22 | 163.43 | 360.68 | 157.80 | 338.13 |
| ST_FL_S11 | 123.98 | 343.77 | 118.35 | 293.05 |
| ST_FL_S22 | 163.43 | 338.13 | 157.80 | 321.23 |
| Bottom | Ceiling | |||
|---|---|---|---|---|
| Failure Mode | AC | WOAC | AC | WOAC |
| BTWOOD_S22 | 1.2425 | 1.6189 | 1.2312 | 1.9582 |
| BTWOOD_S13 | 1.2511 | 1.6728 | 1.2787 | 1.6055 |
| RPUF_1st_S33 | 1.4444 | 1.2064 | 1.4294 | 1.2104 |
| RPUF_2nd_S33 | 1.4984 | 1.6066 | 1.4190 | 1.5934 |
| HULL_S11 | 1.0816 | 1.0888 | 1.0571 | 1.1563 |
| HULL_S22 | 1.9925 | 1.7203 | 1.9959 | 1.9107 |
| ST_FL_S11 | 1.4876 | 1.4344 | 1.4978 | 1.2506 |
| ST_FL_S22 | 1.2392 | 1.7159 | 1.3208 | 1.6736 |
| Test Cases | Low-Filling (20%H) | High-Filling (80%H) |
|---|---|---|
| Air/Water (ω/ω0) | 1.26 | 1.17 |
| Heavy Gas/Water (ω/ω0) | 1.22 | - |
| NOVEC 25 °C (ω/ω0) | 1.18 | 0.9 |
| NOVEC 34 °C (ω/ω0) | 1.25 | 0.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, C.-J.; Lee, J.-K.; Kim, Y. Study on Hydroelastic Responses of Membrane-Type LNG Cargo Containment Structure under Impulsive Sloshing Loads of Different Media. J. Mar. Sci. Eng. 2024, 12, 1794. https://doi.org/10.3390/jmse12101794
Park C-J, Lee J-K, Kim Y. Study on Hydroelastic Responses of Membrane-Type LNG Cargo Containment Structure under Impulsive Sloshing Loads of Different Media. Journal of Marine Science and Engineering. 2024; 12(10):1794. https://doi.org/10.3390/jmse12101794
Chicago/Turabian StylePark, Cheon-Jin, Jeoung-Kyu Lee, and Yonghwan Kim. 2024. "Study on Hydroelastic Responses of Membrane-Type LNG Cargo Containment Structure under Impulsive Sloshing Loads of Different Media" Journal of Marine Science and Engineering 12, no. 10: 1794. https://doi.org/10.3390/jmse12101794
APA StylePark, C.-J., Lee, J.-K., & Kim, Y. (2024). Study on Hydroelastic Responses of Membrane-Type LNG Cargo Containment Structure under Impulsive Sloshing Loads of Different Media. Journal of Marine Science and Engineering, 12(10), 1794. https://doi.org/10.3390/jmse12101794







