AI-Driven Model Prediction of Motions and Mooring Loads of a Spar Floating Wind Turbine in Waves and Wind
Abstract
1. Introduction
2. Case Study
2.1. Floating Wind Turbine Model
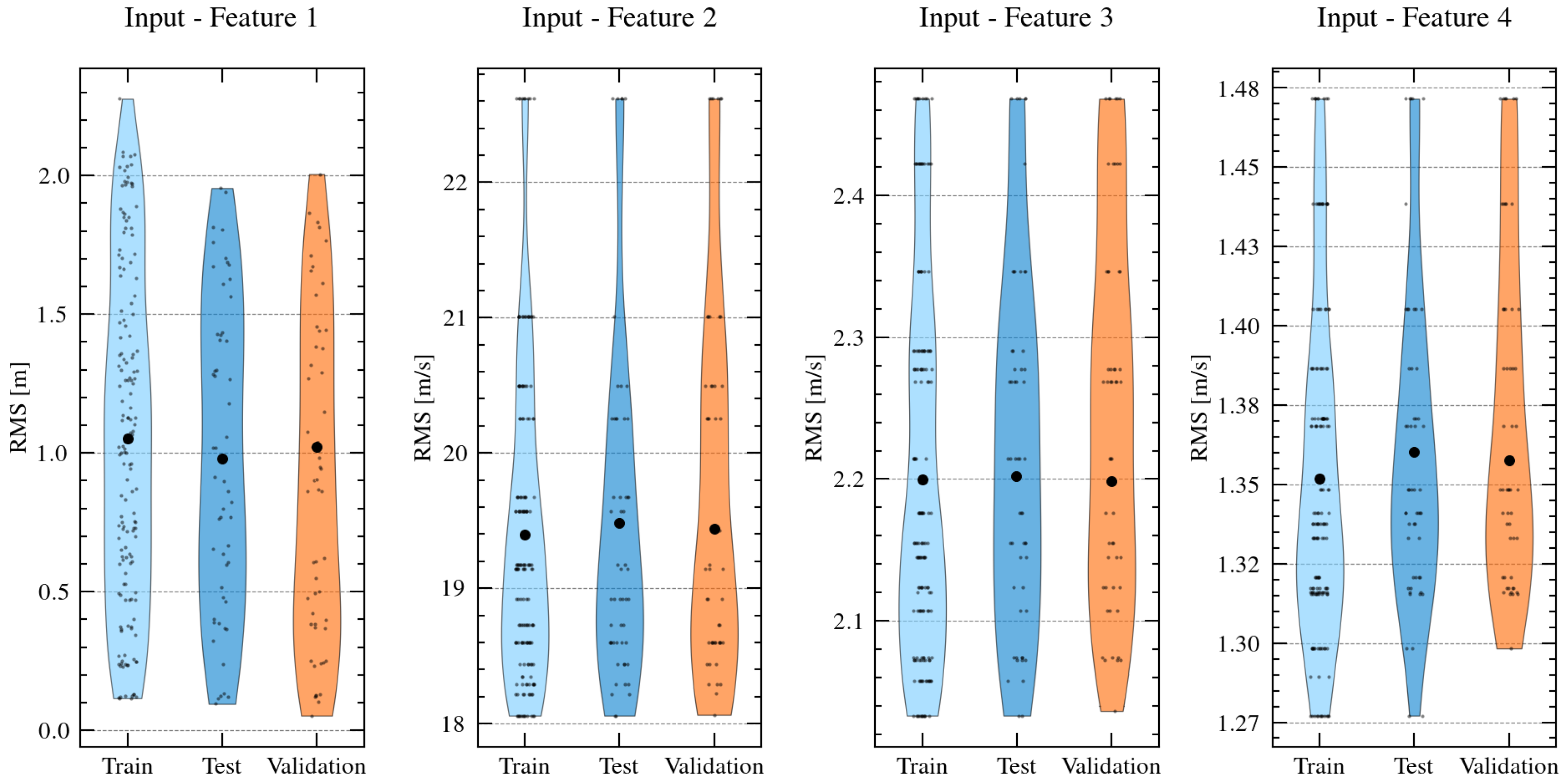
2.2. Database Generation for Training and Validation of the Neural Network Model
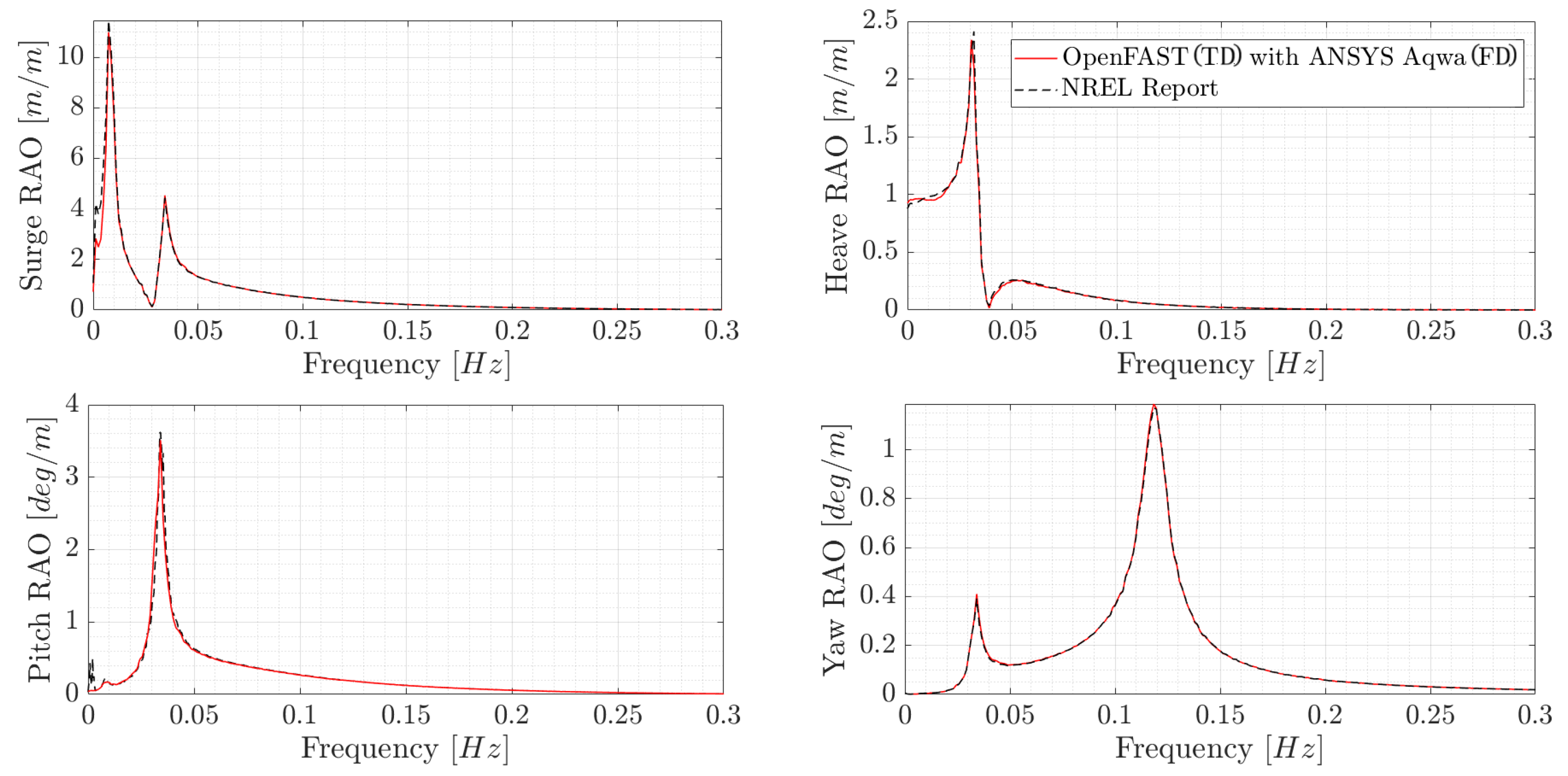
3. Numerical Simulations
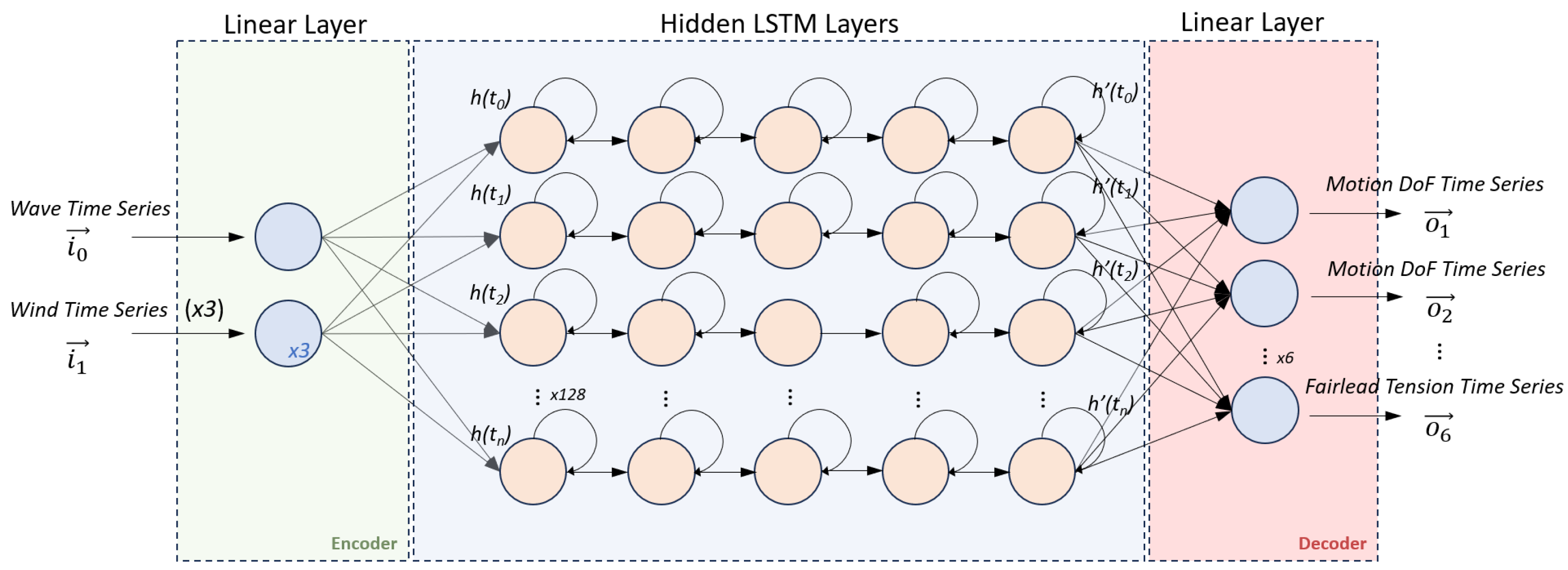
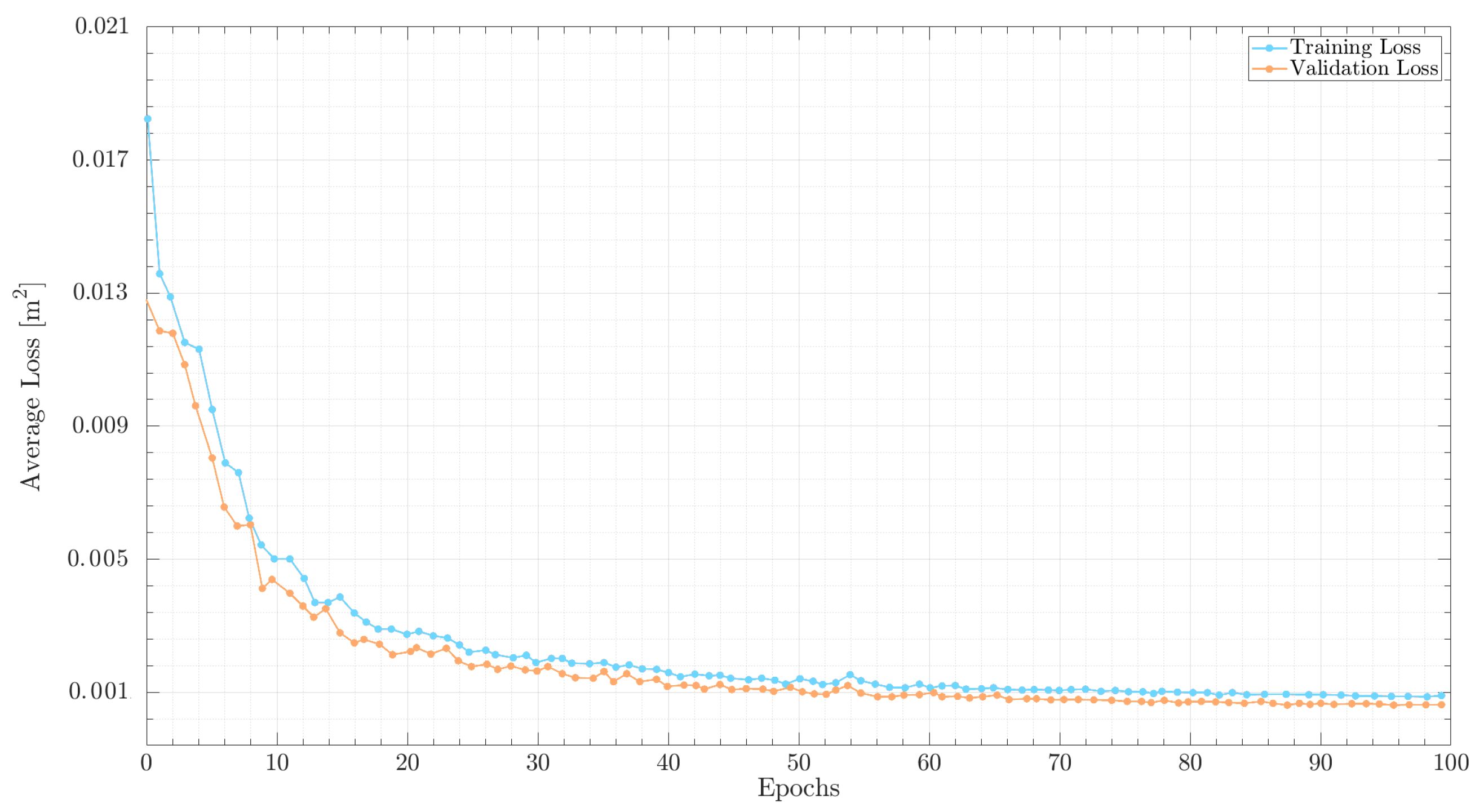
4. Neural Network Model
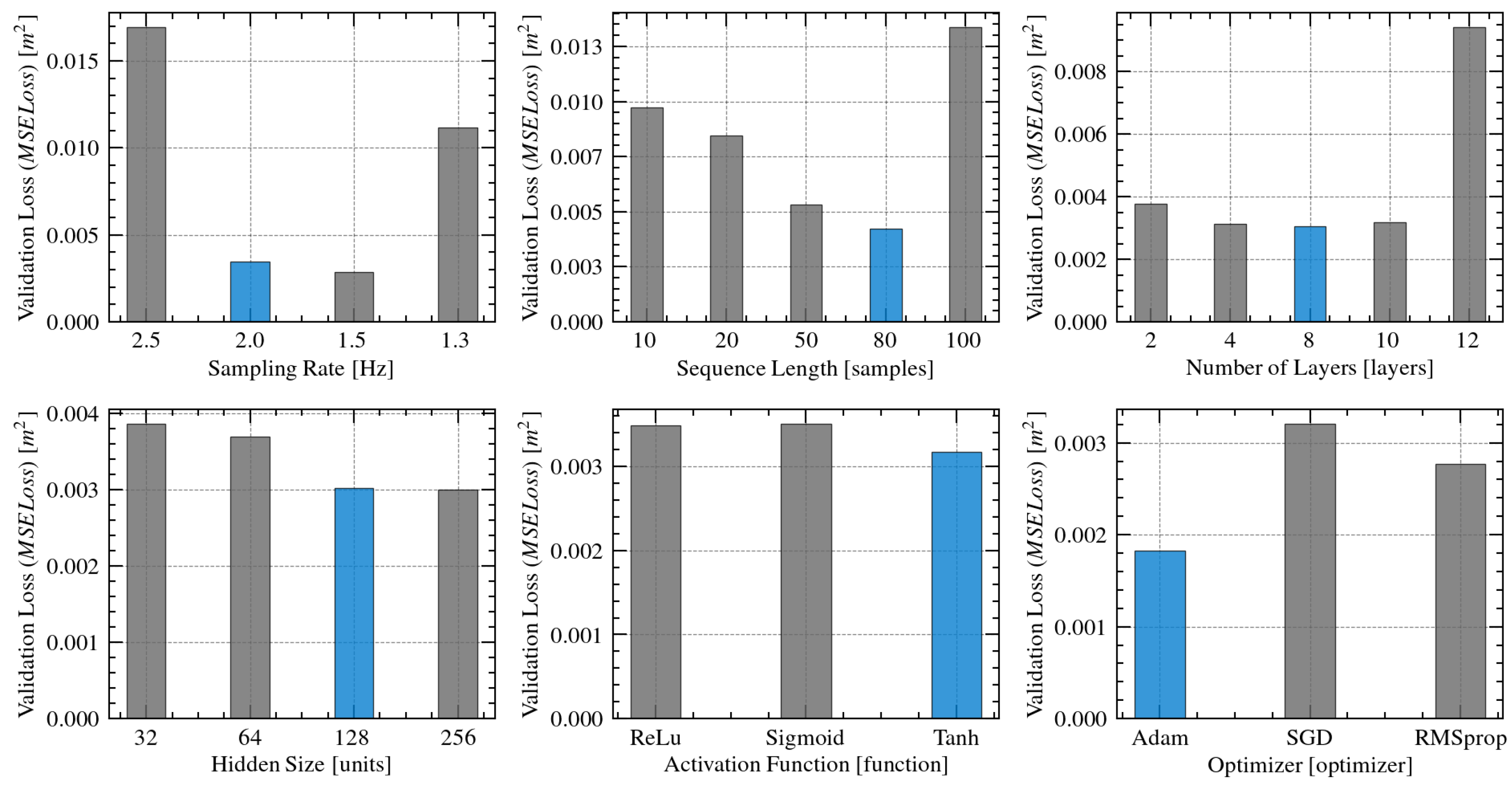
4.1. Model Architecture and Set-Up
5. Results and Discussion
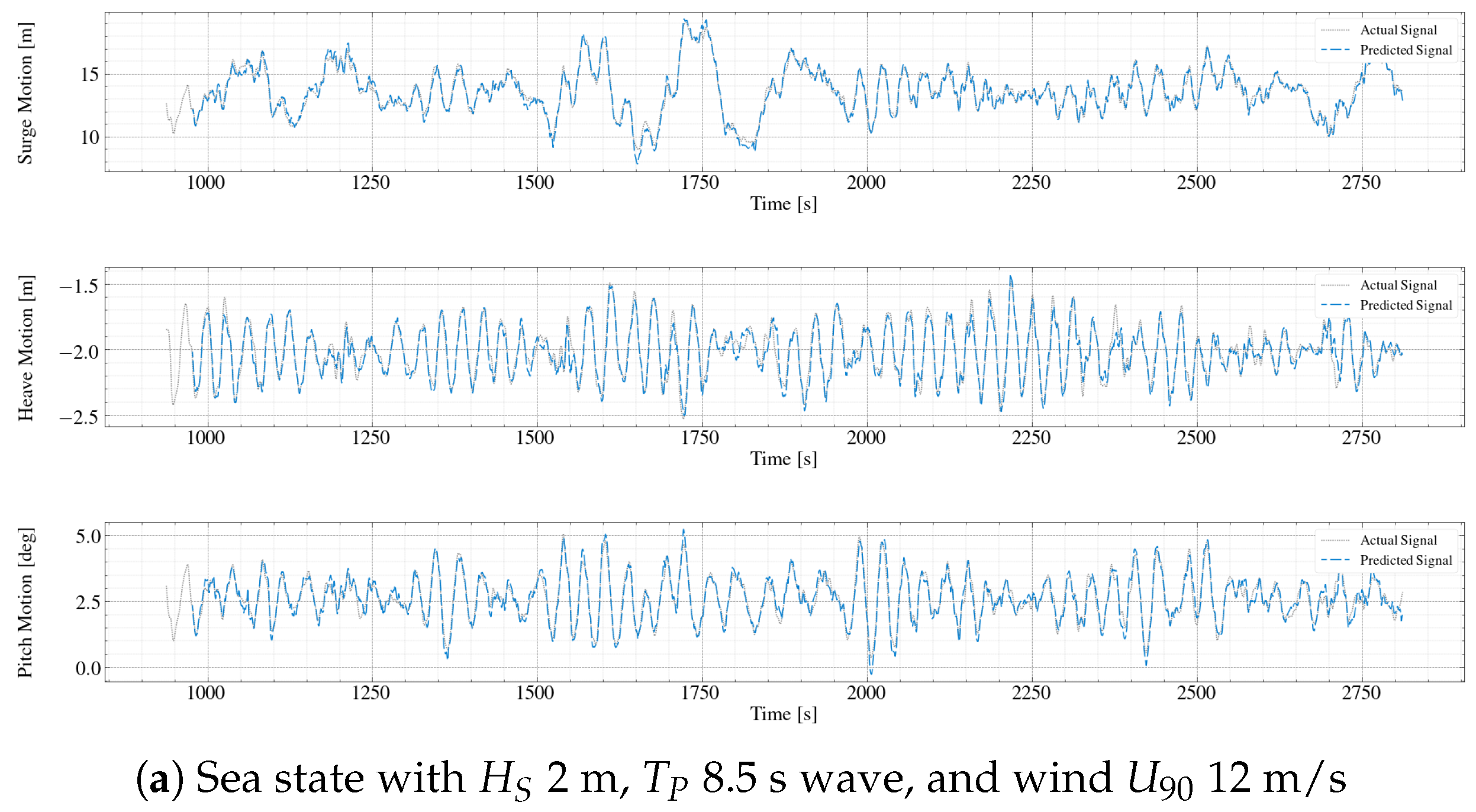
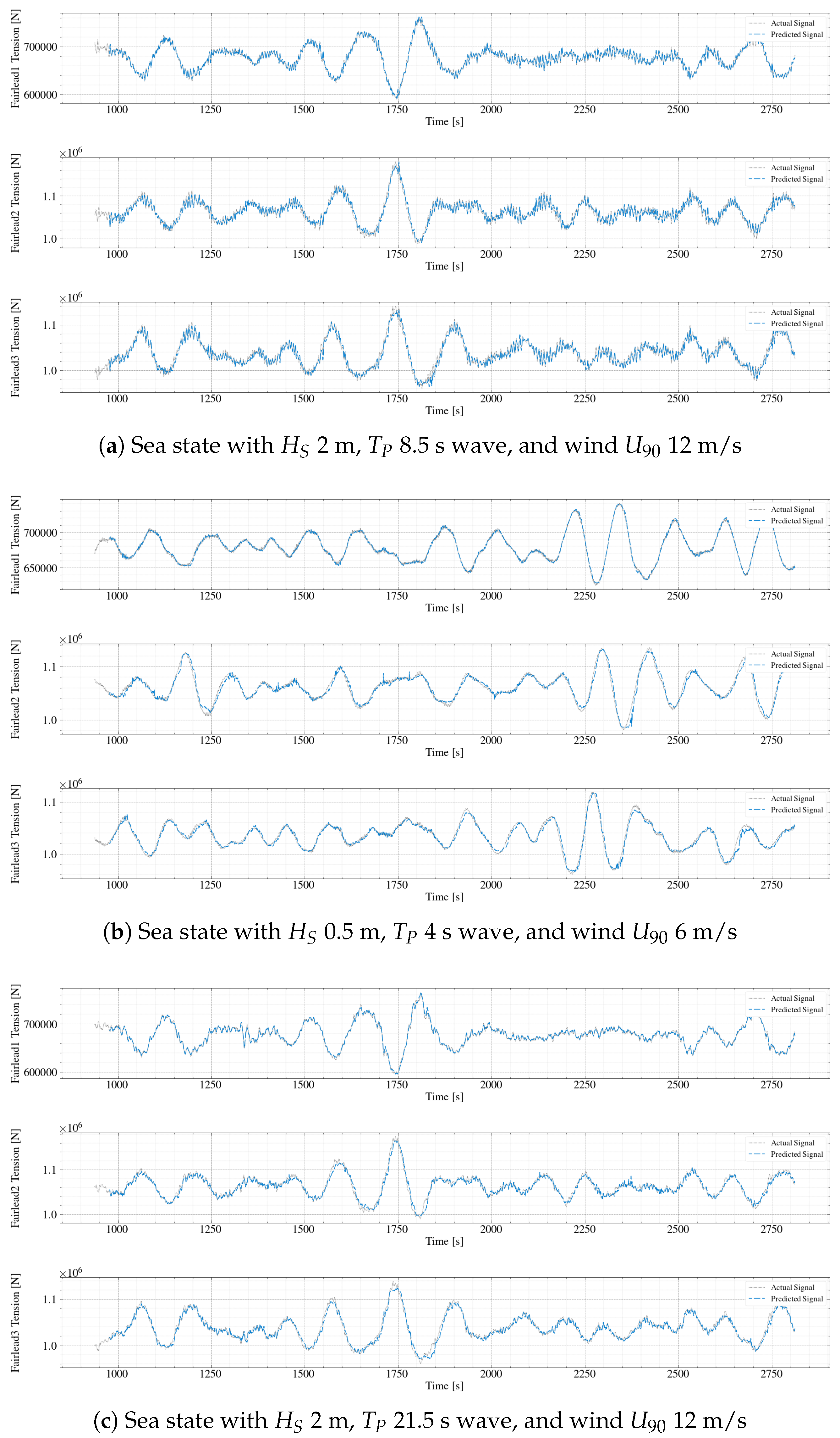
5.1. Discussion of Selected Test Cases through Analysis of Time Histories
- (a)
- Irregular wave case with 2 m, 8.5 s, and turbulent wind with 12 m/s represents the operational wave with higher occurrence probability.
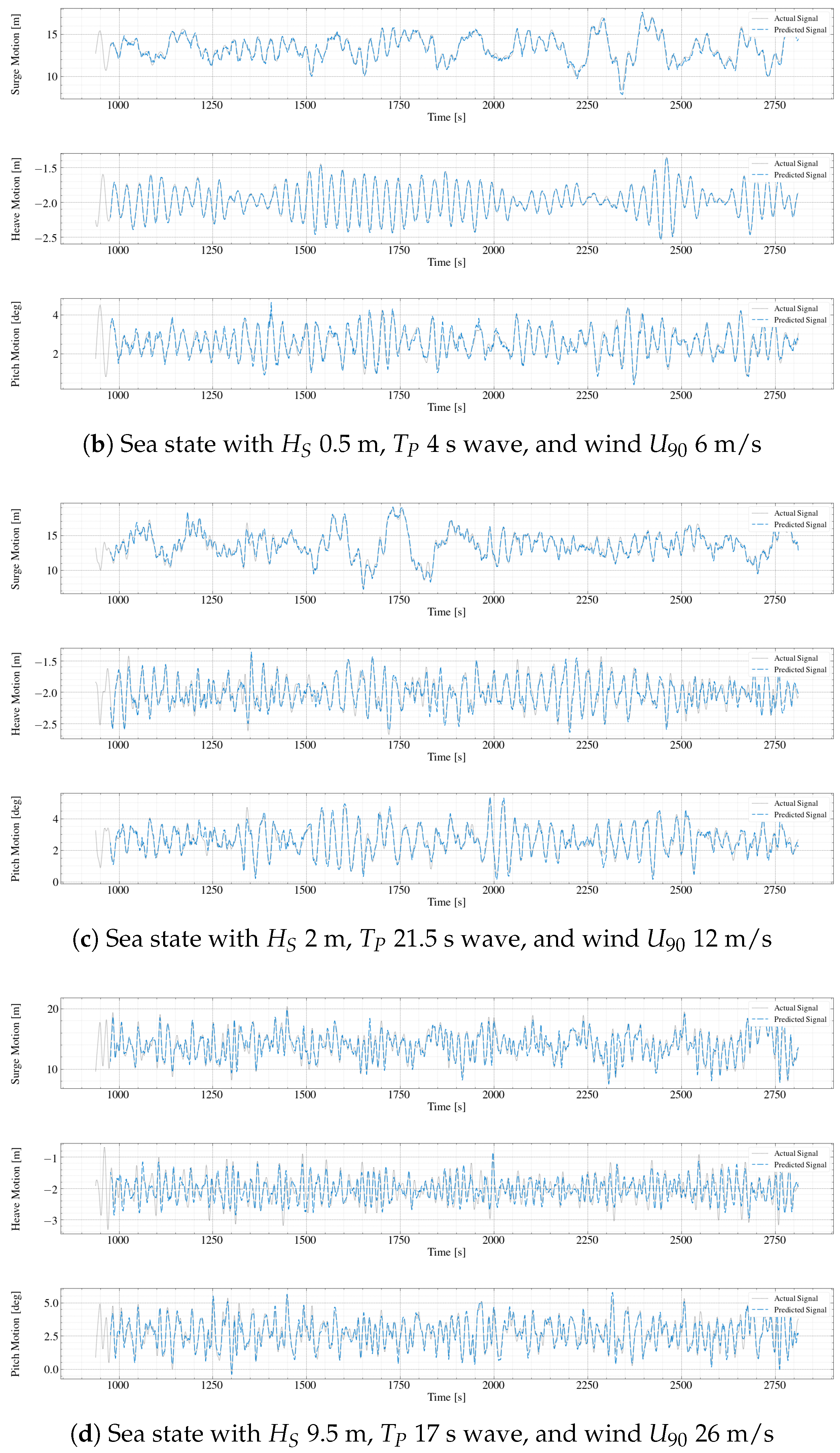
- (b)
- On the other hand, the case corresponding to an irregular wave with 3 m, 7 s, and a wind speed of 6 m/s for corresponds to the lowest peak period from the test dataset.
- (c)
- In addition, the case with 2 m, 21.5 s, and 12 m/s is within the highest peak period limits, with low observed events.
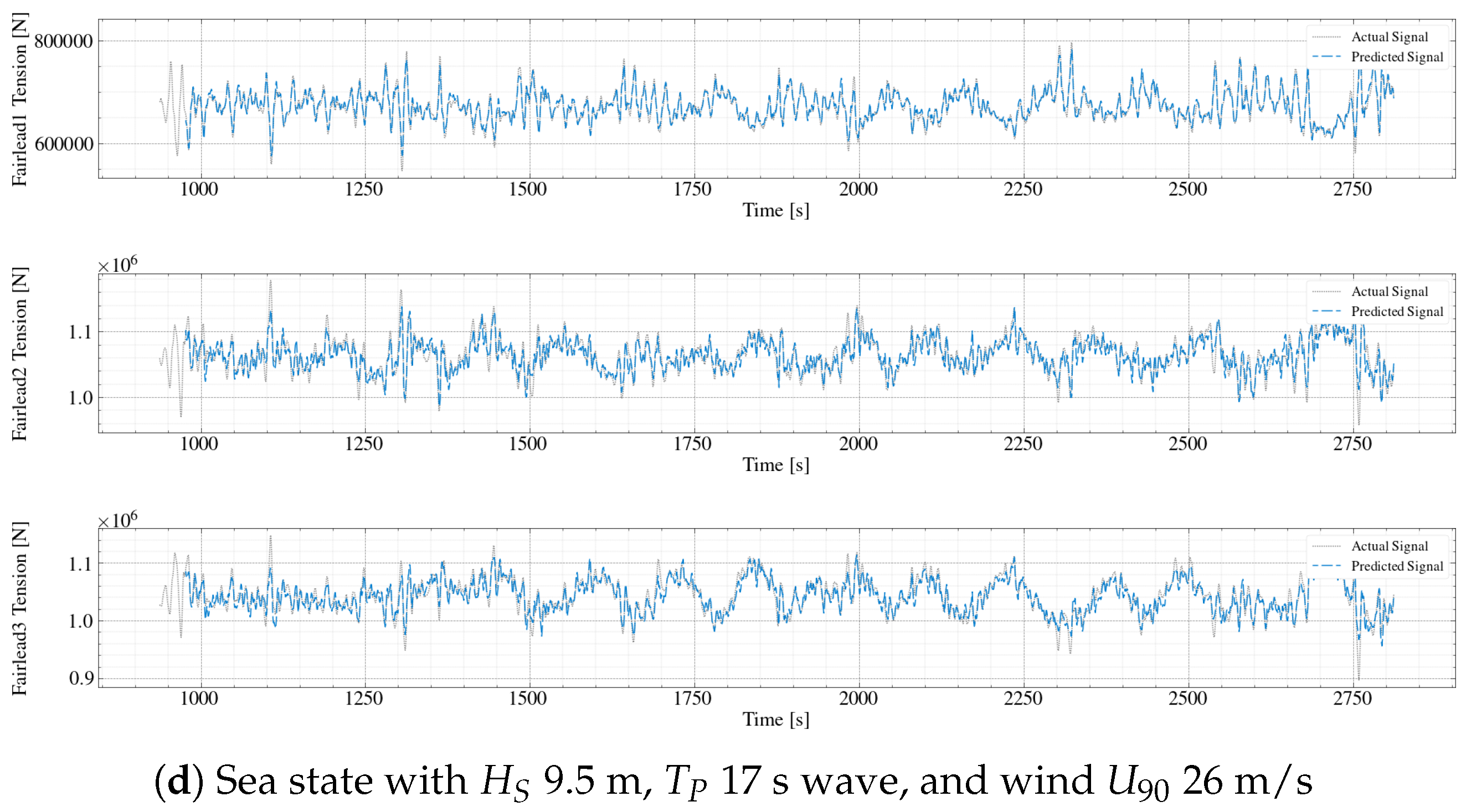
- (d)
- Finally, the irregular wave case with 9.5 m, 17 s, and a wind speed for of 26 m/s exemplifies the extreme sea state for the utilized scatter. In such a condition, the turbine is parked/idling.
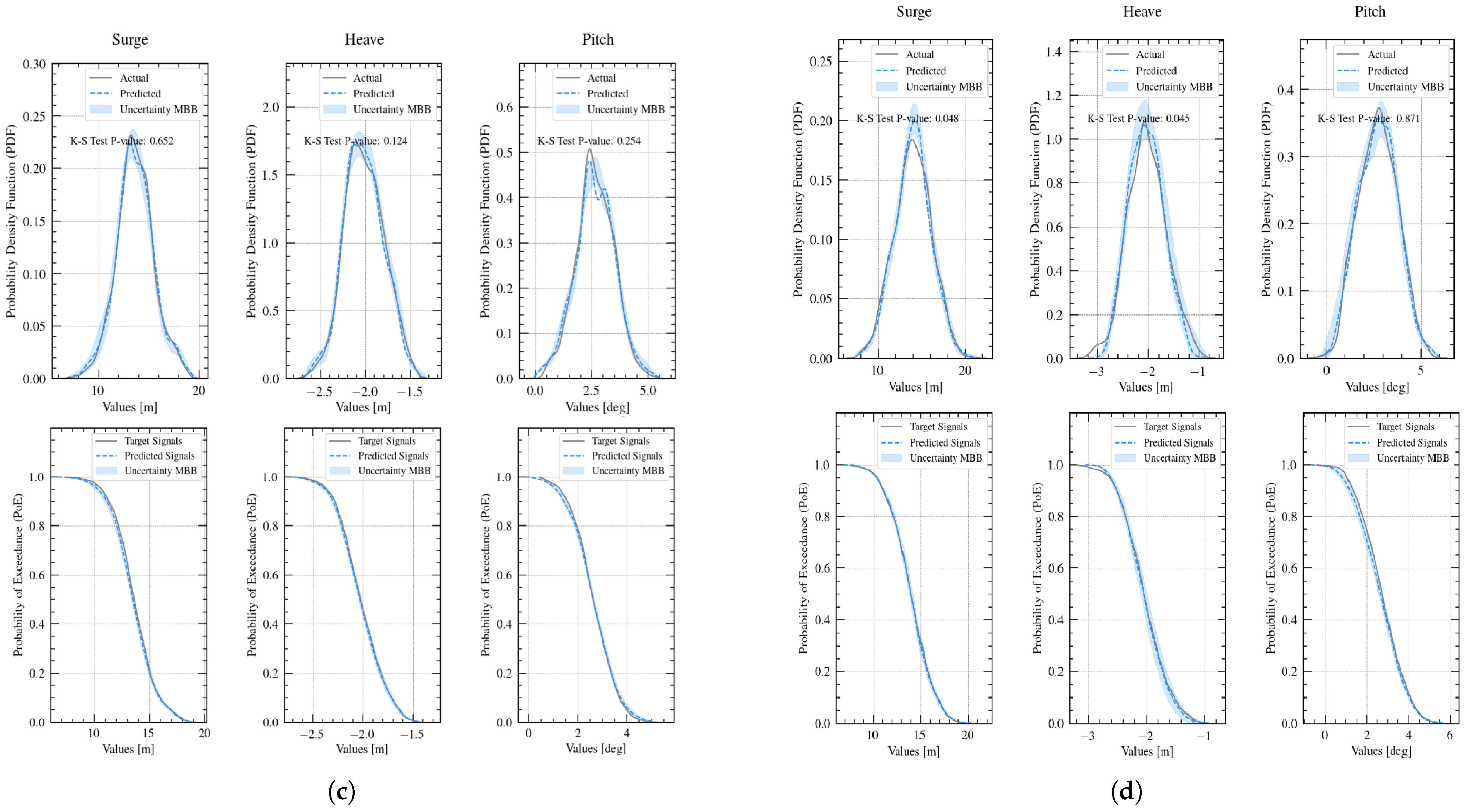
5.2. Evaluation of Selected Test Cases Using a Probabilistic Approach
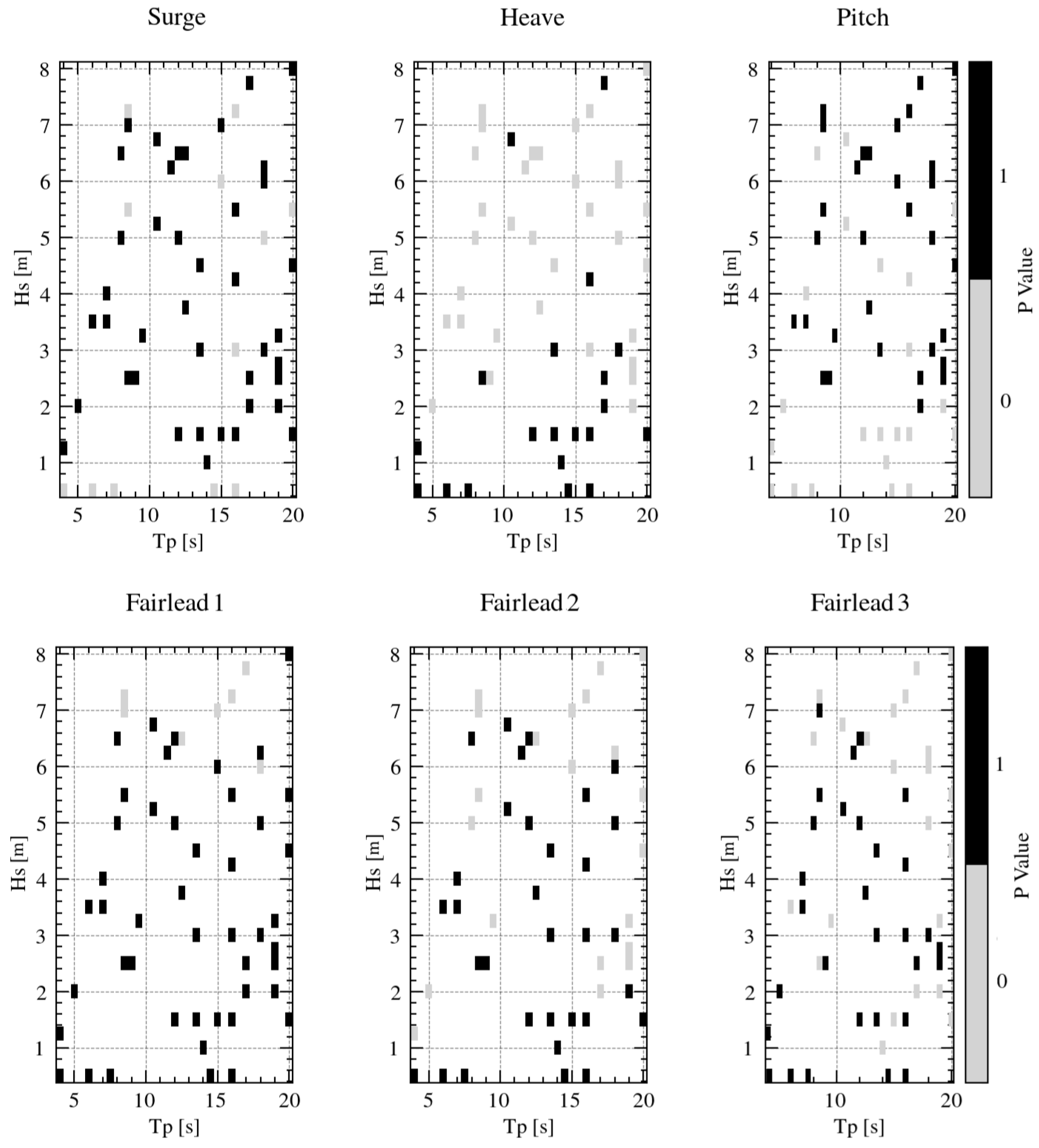
5.3. Global Evaluation of All Test Cases Using a Probabilistic Approach
6. Conclusions
- The LSTM model effectively predicted time series for surge, heave, and pitch motions, as well as fairlead tensions under both operational and extreme wind and wave conditions. The model demonstrated high predictive accuracy, particularly for surge and pitch motions, with values generally above .
- Statistical evaluations, including Probability Density Functions (PDFs), Cumulative Distribution Functions (CDFs), and Kolmogorov–Smirnov (K–S) Tests, confirmed the reliability of the model’s predictions. The majority of the cases passed the K–S Test, indicating that the predicted and actual distributions are very similar.
- Although the model performed well overall, the heave motion predictions were less accurate compared to surge and pitch. This discrepancy is attributed to the smaller amplitude of heave motions and their higher frequency response, indicating the need for further adjustments in sampling frequency and sequence length.
- The model significantly reduced the computational time required for predicting FOWT dynamics. While traditional numerical simulations could take more than 10 min to compute, the LSTM model inferred 30 min of time series data in less than 5 s. This reduction makes the present proposed approach relevant mainly for fatigue analysis, with aiming to discard preliminary designs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IRENA. Renewable Energy Statistics 2023; Technical Report; International Renewable Energy Agency: Masdar City, United Arab Emirates, 2023. [Google Scholar]
- DNV. Fatigue Design of Offshore Steel Structures; Technical Report; DNV: Høvik, Norway, 2021. [Google Scholar]
- Jonkman, J.; Sclavounos, P. Development of Fully Coupled Aeroelastic and Hydrodynamic Models for Offshore Wind Turbines: Preprint. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; Volume 16. [Google Scholar] [CrossRef]
- Bauduin, C.; Naciri, M. A Contribution on Quasi-Static Mooring Line Damping. J. Offshore Mech. Arct. Eng.-Trans. 2000, 122, 125–133. [Google Scholar] [CrossRef]
- Senra, S.; Corrêa, F.; Jacob, B.; Mourelle, M.; Masetti, I. Towards the Integration of Analysis and Design of Mooring Systems and Risers: Part I—Studies on a Semisubmersible Platform. In Proceedings of the OMAE 2022, Oslo, Norway, 23–28 June 2002. [Google Scholar] [CrossRef]
- Low, Y.; Langley, R. A hybrid time/frequency domain approach for efficient coupled analysis of vessel/mooring/riser dynamics. Ocean Eng. 2008, 35, 433–446. [Google Scholar] [CrossRef]
- Mushtaq, M.; Akram, U.; Aamir, M.; Ali, H.; Zulqarnain, M. Neural Network Techniques for Time Series Prediction: A Review. JOIV Int. J. Inform. Vis. 2019, 3, 314–320. [Google Scholar] [CrossRef]
- Wu, H.; Luo, Q.; Abdel-Basset, M. Training Feedforward Neural Networks Using Symbiotic Organisms Search Algorithm. Comput. Intell. Neurosci. 2016, 2016, 1–14. [Google Scholar] [CrossRef]
- Abdulkarim, S.; Garko, A. Evaluating feedforward and elman recurrent neural network in time series forecasting. Indian J. Pure Appl. Math. 2015, 1, 145–151. [Google Scholar]
- Serrano-Cinca, C. Feedforward Neural Networks in the Classification of Financial Information. Eur. J. Financ. 1998, 3, 183–202. [Google Scholar] [CrossRef]
- Chen, M.; Jiang, J.; Zhang, W.; Li, C.B.; Zhou, H.; Jiang, Y.; Sun, X. Study on Mooring Design of 15 MW Floating Wind Turbines in South China Sea. J. Mar. Sci. Eng. 2023, 12, 33. [Google Scholar] [CrossRef]
- Jiang, Y.; Duan, Y.; Li, J.; Chen, M.; Zhang, X. Optimization of mooring systems for a 10MW semisubmersible offshore wind turbines based on neural network. Ocean Eng. 2024, 296, 117020. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation. In Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Volume 1: Foundations; Rumelhart, D.E., Mcclelland, J.L., Eds.; MIT Press: Cambridge, MA, USA, 1986; pp. 318–362. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A Review on the Long Short-Term Memory Model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Bjørni, F.; Lien, S.; Midtgarden, T.; Kulia, G.; Verma, A.; Jiang, Z. Prediction of dynamic mooring responses of a floating wind turbine using an artificial neural network. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1201, 012023. [Google Scholar] [CrossRef]
- Silva, K.M.; Maki, K.J. Data-Driven system identification of 6-DoF ship motion in waves with neural networks. Appl. Ocean Res. 2022, 125, 103222. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, J.; Kim, Y.; Ahn, Y. Prediction of wave-induced ship motions based on integrated neural network system and spatiotemporal wave-field data. Phys. Fluids 2023, 35, 097127. [Google Scholar] [CrossRef]
- Park, H.J.; Kim, J.S.; Nam, B.; Kim, J.S. ANN-based prediction models for green water events around a FPSO in irregular waves. Ocean Eng. 2024, 291, 116408. [Google Scholar] [CrossRef]
- Jonkman, J.; Musial, W. Offshore Code Comparison Collaboration (OC3) for IEA Wind Task 23 Offshore Wind Technology and Deployment; Technical Report; NREL: Golden, CO, USA, 2010. [Google Scholar]
- Xu, X.; Day, S. Experimental investigation on dynamic responses of a spar-type offshore floating wind turbine and its mooring system behaviour. Ocean Eng. 2021, 236, 109488. [Google Scholar] [CrossRef]
- Yang, J.; He, Y.P.; Zhao, Y.S.; Shao, Y.L.; Han, Z.L. Experimental and numerical studies on the low-frequency responses of a spar-type floating offshore wind turbine. Ocean Eng. 2021, 222, 108571. [Google Scholar] [CrossRef]
- Browning, J.; Jonkman, J.; Robertson, A.; Goupee, A. Calibration and validation of a spar-type floating offshore wind turbine model using the FAST dynamic simulation tool. J. Phys. Conf. Ser. 2014, 555, 012015. [Google Scholar] [CrossRef]
- JM, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009. [Google Scholar] [CrossRef]
- Burns, R.D.; Martin, S.B.; Wood, M.A.; Wilson, C.C.; Lumsden, E.; Pace, F. Hywind Scotland Floating Offshore Wind Farm; Technical Report; JASCO Applied Sciences: Silver Spring, MD, USA, 2022. [Google Scholar]
- IEC 61400-3-2; Wind Energy Generation Systems-Part 3-2: Design Requirements for Floating Offshore Wind Turbines. Technical Report; International Electrotechnical Commission (IEC): Geneva, Switzerland, 2023.
- Reistad, M.; Breivik, O.; Haakenstad, H.; Aarnes, O.; Furevik, B.; Bidlot, J. A high-resolution hindcast of wind and waves for The North Sea, The Norwegian Sea and The Barents Sea. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Cummins, W.; Taylor, D.W. The Impulse Response Function and Ship Motions; Report (David W. Taylor Model Basin); Department of the Navy, David Taylor Model Basin: Bethesda, MD, USA, 1962. [Google Scholar]
- Oglive, T. Recent progress toward the understanding and prediction of ship motions. In Proceedings of the 5th Symposium on Navan Hydrodynamics, Bergen, Norway, 10–12 September 1964; Volume 1, p. 80. [Google Scholar]
- Duarte, T.; Alves, M.; Jonkman, J.; Sarmento, A. State-Space Realization of the Wave-Radiation Force Within FAST. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Nantes, France, 8–13 June 2013. OMAE2013-10375. [Google Scholar] [CrossRef]
- Jonkman, J.M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine; NREL/TP-500-41958; National Renewable Energy Laboratory: Golden, CO, USA, 2007. [Google Scholar] [CrossRef]
- Tomasicchio, G.R.; D’Alessandro, F.; Avossa, A.M.; Riefolo, L.; Musci, E.; Ricciardelli, F.; Vicinanza, D. Experimental modelling of the dynamic behaviour of a spar buoy wind turbine. Renew. Energy 2018, 127, 412–432. [Google Scholar] [CrossRef]
- Lopez-Olocco, T.; Liang, G.; Medina-Manuel, A.; Ynocente, L.S.; Jiang, Z.; Souto-Iglesias, A. Experimental comparison of a dual-spar floating wind farm with shared mooring against a single floating wind turbine under wave conditions. Eng. Struct. 2023, 292, 116475. [Google Scholar] [CrossRef]
- Jonkman, J. Definition of the Floating System for Phase IV of OC3; Number NREL/TP-500-47535; National Renewable Energy Laboratory: Golden, CO, USA, 2010. [Google Scholar]
- Hall, M.; Goupee, A. Validation of a lumped-mass mooring line model with DeepCwind semisubmersible model test data. Ocean Eng. 2015, 104, 590–603. [Google Scholar] [CrossRef]
- Jonkman, J.M. TurbSim User’s Guide v2.00.00. Revised June 1, 2016 (Draft Version); Technical Report; National Renewable Energy Lab (NREL): Golden, CO, USA, 2016. [Google Scholar]
- Jonkman, J.M.; Buhl, M.L., Jr. Fast User’s Guide-Updated August 2005; Technical Report; National Renewable Energy Lab (NREL): Golden, CO, USA, 2005. [Google Scholar]
- National Renewable Energy Lab. OpenFAST Documentation-Release v2.3.0; Technical Report; National Renewable Energy Lab (NREL): Golden, CO, USA, 2020. [Google Scholar]
- Liaw, R.; Liang, E.; Nishihara, R. Tune: A Research Platform for Distributed Model Selection and Training. arXiv 2018, arXiv:1807.05118. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Shannon, C. Communication in the Presence of Noise. Proc. IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Goda, Y. Random Seas and Design of Maritime Structures; University of Tokyo Press: Tokyo, Japan, 1985. [Google Scholar]
- ROM 1.0-09; Recommendations for the Project Design and Construction of Breakwaters (Part I: Calculation and Project Factors. Climate Agents). Technical Report; Puertos del Estado (PdE): Madrid, Spain, 2009.
- Nowlan, S.J.; Hinton, G.E. Simplifying Neural Networks by Soft Weight-Sharing. Neural Comput. 1992, 4, 473–493. [Google Scholar] [CrossRef]
- Dietterich, T. Overfitting and undercomputing in machine learning. ACM Comput. Surv. 1995, 27, 326–327. [Google Scholar] [CrossRef]
- Bejani, M.M.; Ghatee, M. A systematic review on overfitting control in shallow and deep neural networks. Artif. Intell. Rev. 2021, 54, 6391–6438. [Google Scholar] [CrossRef]
- Serfling, R. Approximation Theorems of Mathematical Statistics; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar] [CrossRef]
- Smirnov, N.V. Estimate of deviation between empirical distribution functions in two independent samples. Bull. Mosc. Univ. 1939, 2, 3–16. [Google Scholar]
- Fitzenberger, B. The moving blocks bootstrap and robust inference for linear least squares and quantile regressions. J. Econ. 1998, 82, 235–287. [Google Scholar] [CrossRef]






| Properties | Value |
|---|---|
| Total Platform Mass | 7,466,330 kg |
| Vertical Position of Center of Gravity (Below SWL) | 89.9 m |
| Platform Roll Inertia (about Center of Gravity) | 4,229,230,000 |
| Platform Pitch Inertia (about Center of Gravity) | 4,229,230,000 |
| Platform Yaw Inertia (about Center of Gravity) | 164,230,000 |
| Number of Mooring Lines | 3 |
| Angle Between Adjacent Lines | 120° |
| Unstretched Mooring Line Length | 902.2 m |
| Equivalent Mooring Line Weight in Water | 698.09 N/m |
| Equivalent Mooring Line Extensional Stiffness | 384,243,000 N |
| Properties | Value |
|---|---|
| Number of layers | 8 |
| Hidden size | 128 |
| Initial learning rate | 0.005 |
| Learning rate schedule | StepLR ( = 0.9) |
| Optimizer | Adam |
| Loss function | MSELoss |
| Sequence length | 80 |
| Epochs | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medina-Manuel, A.; Molina Sánchez, R.; Souto-Iglesias, A. AI-Driven Model Prediction of Motions and Mooring Loads of a Spar Floating Wind Turbine in Waves and Wind. J. Mar. Sci. Eng. 2024, 12, 1464. https://doi.org/10.3390/jmse12091464
Medina-Manuel A, Molina Sánchez R, Souto-Iglesias A. AI-Driven Model Prediction of Motions and Mooring Loads of a Spar Floating Wind Turbine in Waves and Wind. Journal of Marine Science and Engineering. 2024; 12(9):1464. https://doi.org/10.3390/jmse12091464
Chicago/Turabian StyleMedina-Manuel, Antonio, Rafael Molina Sánchez, and Antonio Souto-Iglesias. 2024. "AI-Driven Model Prediction of Motions and Mooring Loads of a Spar Floating Wind Turbine in Waves and Wind" Journal of Marine Science and Engineering 12, no. 9: 1464. https://doi.org/10.3390/jmse12091464
APA StyleMedina-Manuel, A., Molina Sánchez, R., & Souto-Iglesias, A. (2024). AI-Driven Model Prediction of Motions and Mooring Loads of a Spar Floating Wind Turbine in Waves and Wind. Journal of Marine Science and Engineering, 12(9), 1464. https://doi.org/10.3390/jmse12091464








