Research on the Effect of a Heave Plate on the Dynamics of the Floating Wind Turbine Using Model Tests
Abstract
:1. Introduction
2. Experiment Setup
2.1. Floating Wind Turbine Model
2.2. The Test Equipment
2.3. Test Cases
3. Results and Discussion
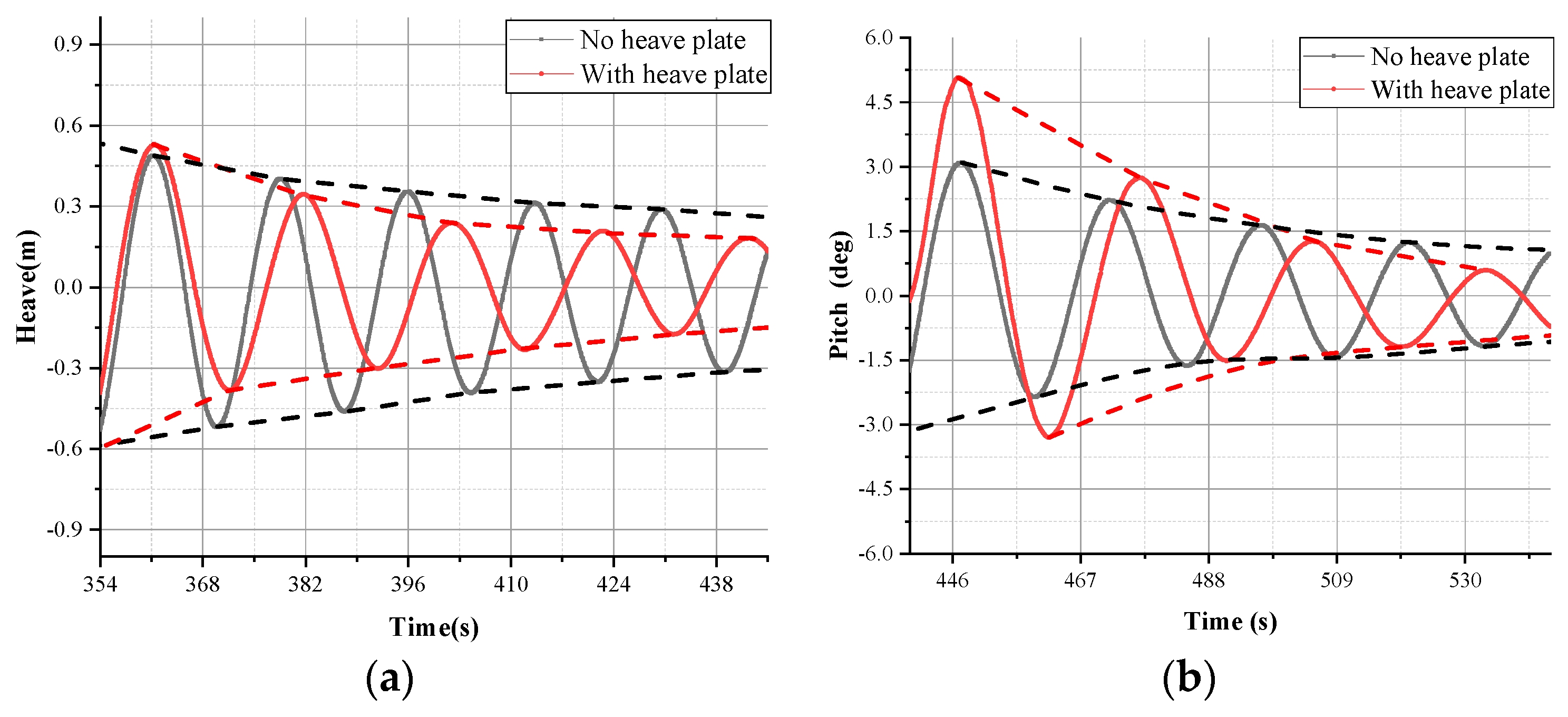
3.1. The Decay Tests
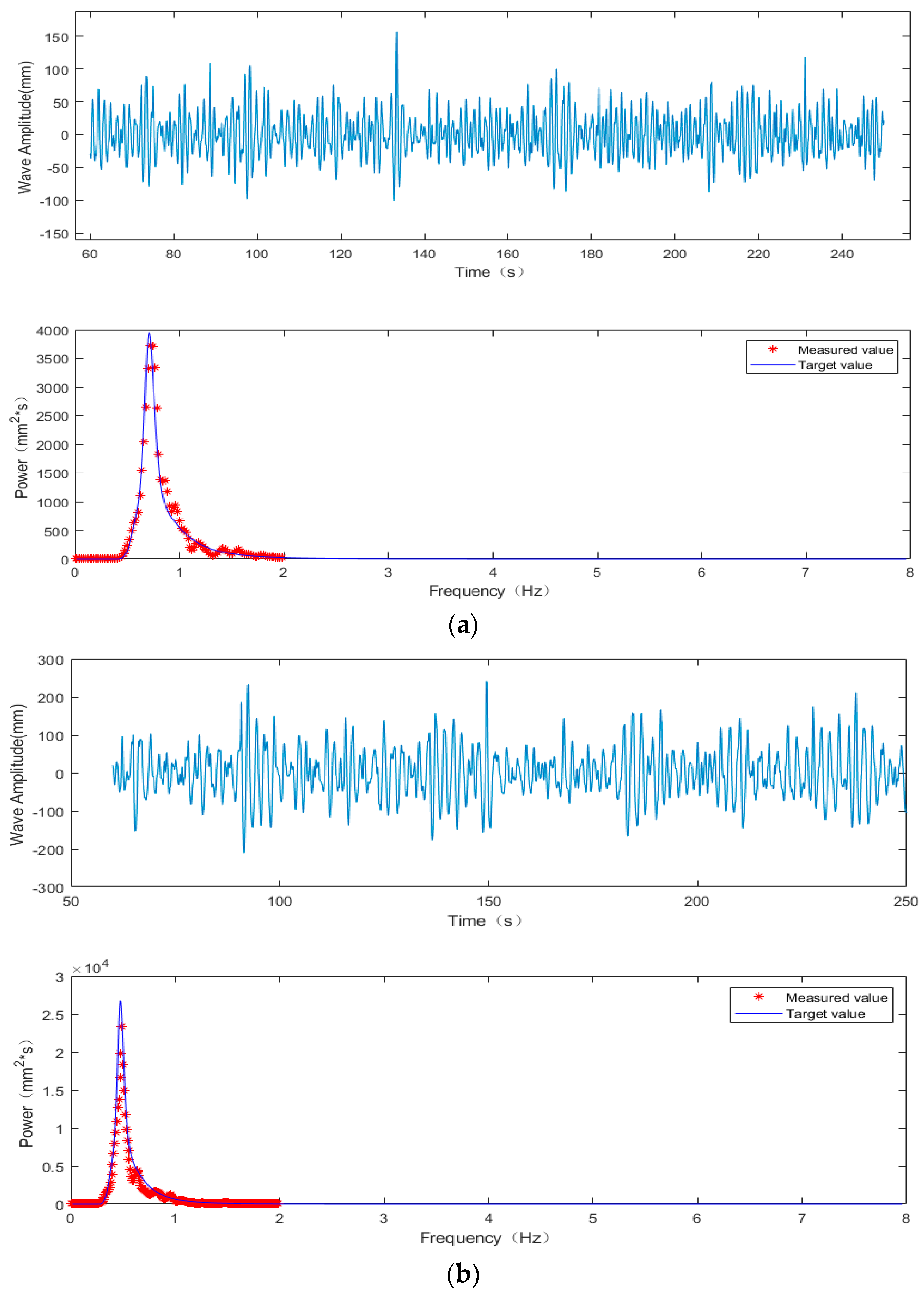
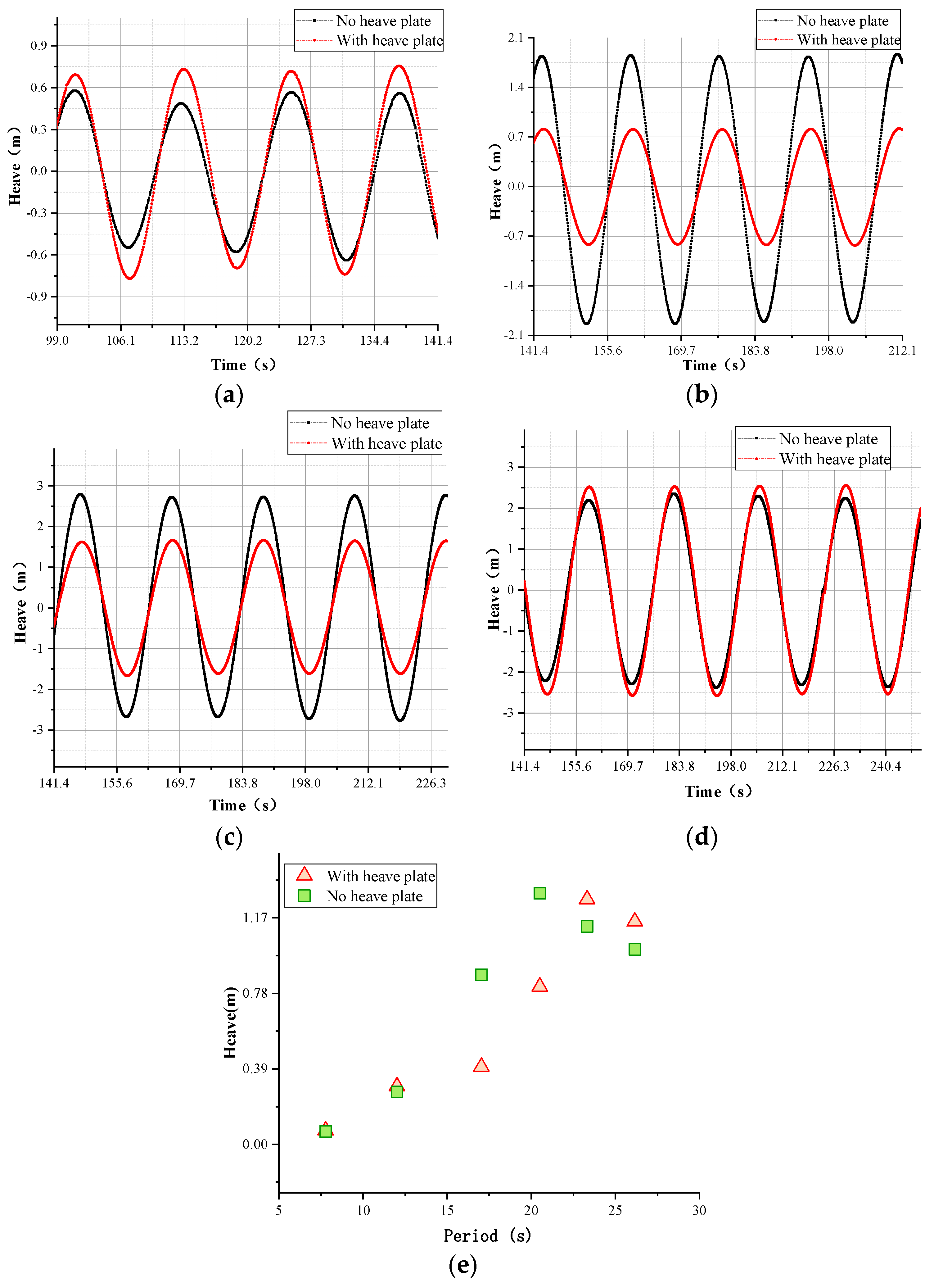
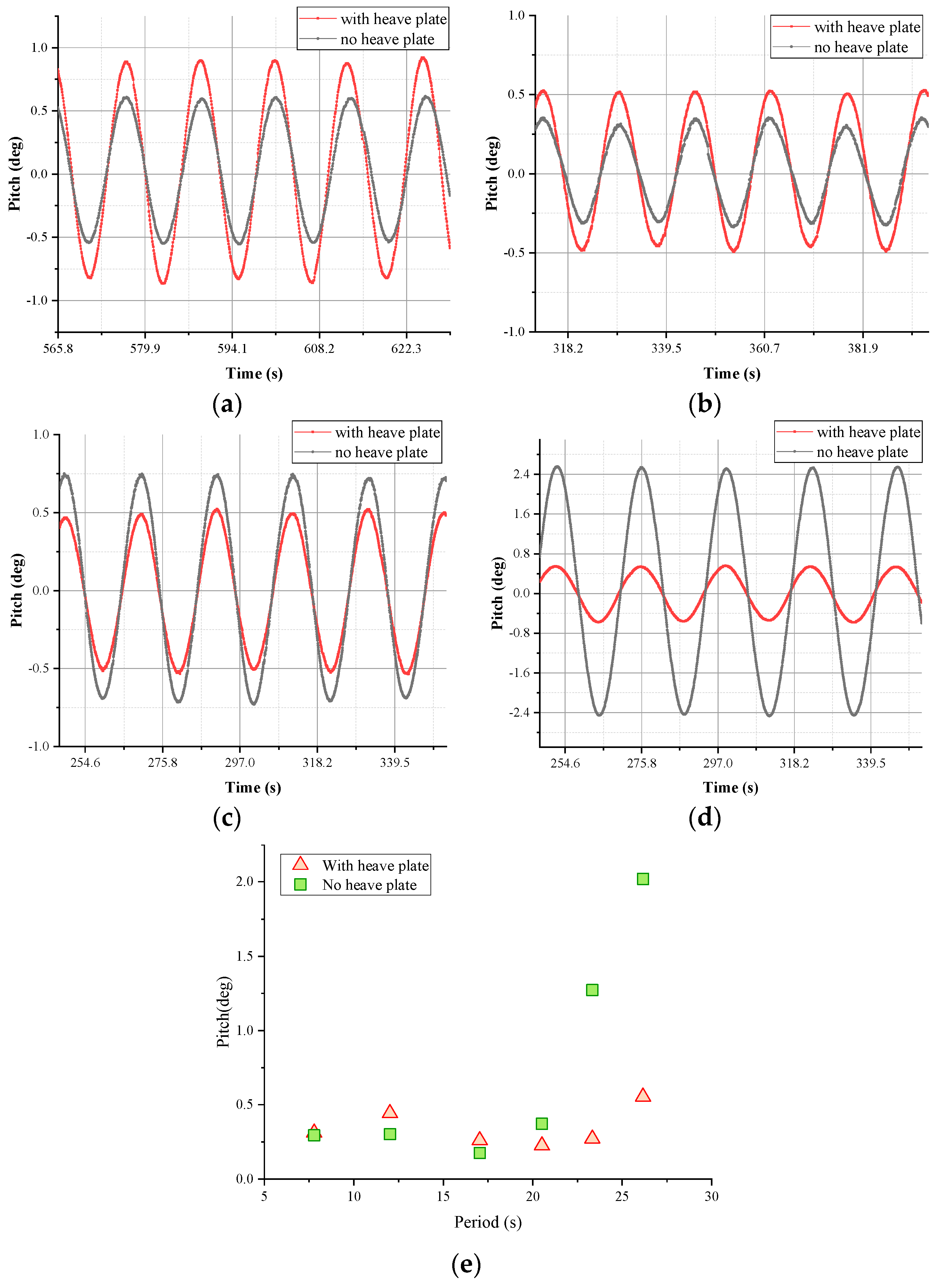
3.2. Regular Wave without Wind Tests
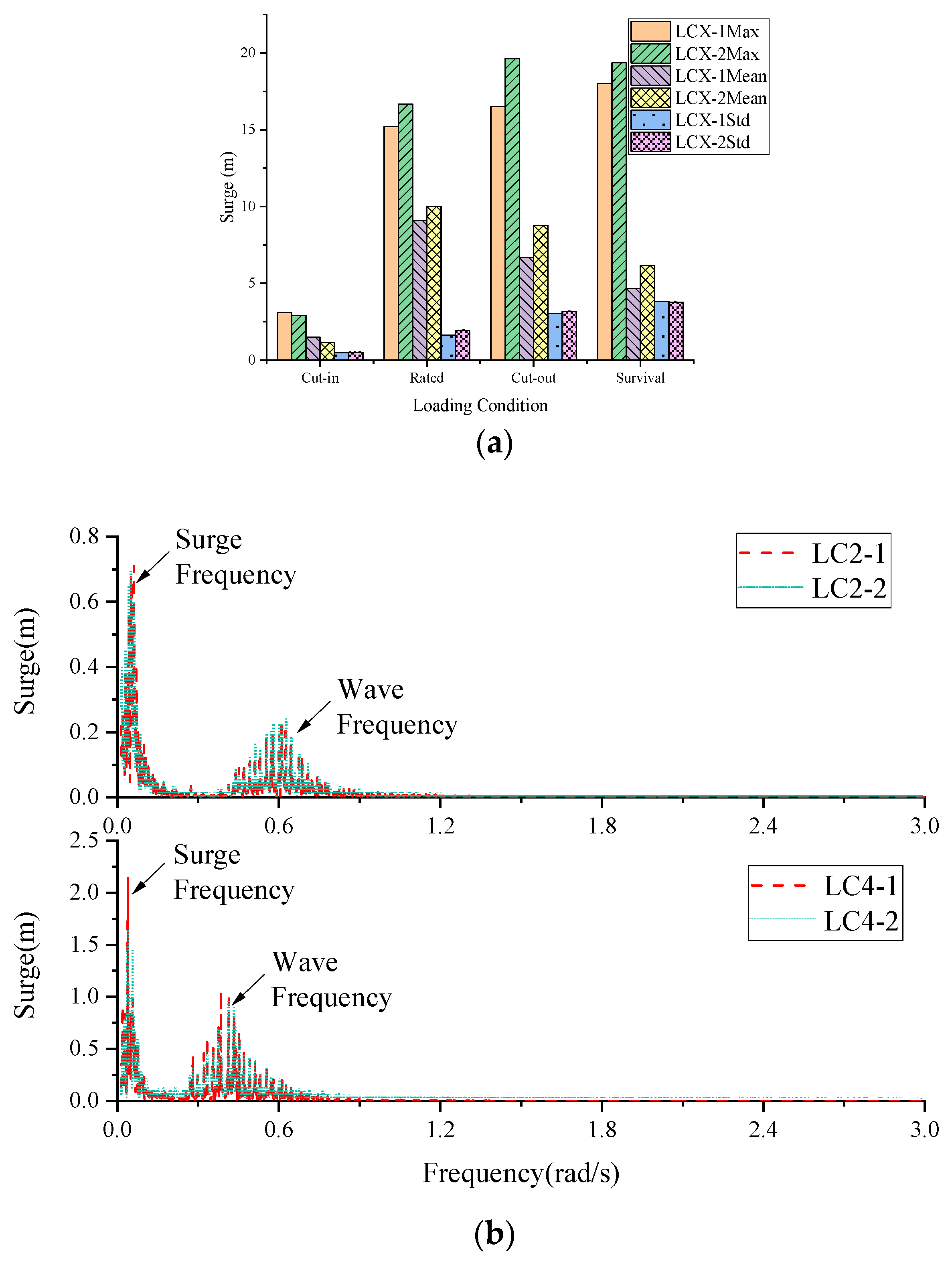
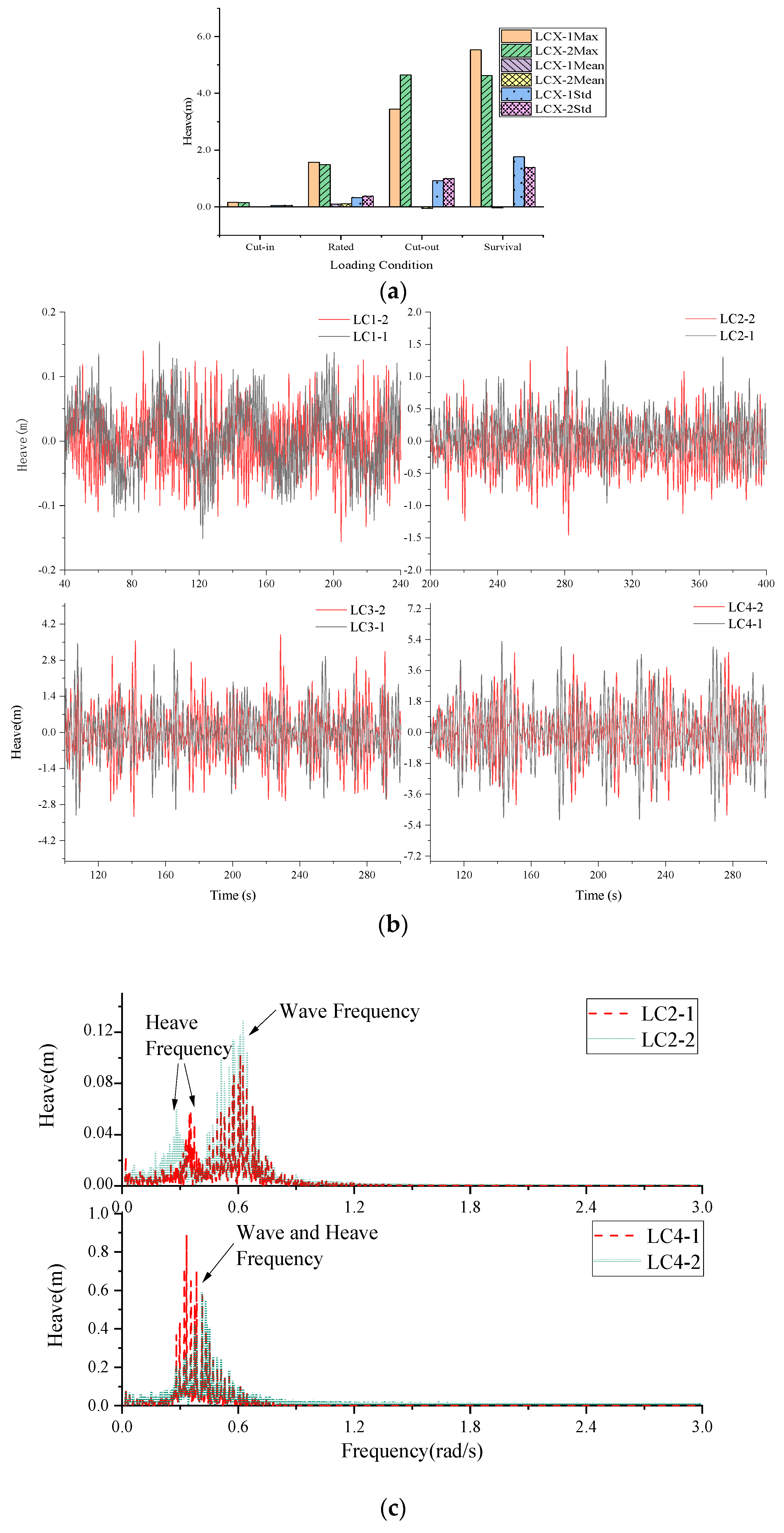
3.3. Irregular Wave with Steady Wind Tests
4. Conclusions
- (1)
- The heave plate significantly enhances the damping of both the heave and pitch motions of the floater. For the heave damping, especially, it is three times greater than that of the original floater without the heave plate. The natural period of the floater surge, heave, and pitch are also increased by altering the hydrodynamic interaction and increasing the added mass and damping properties of the system.
- (2)
- The RC cases show that when the wave period is in the range of 15–20 s, the weakening effect of the heave plate on the heave motion is obvious; when the wave period is in the range of 20–27 s, the weakening effect of the heave plate on the pitch motion is obvious.
- (3)
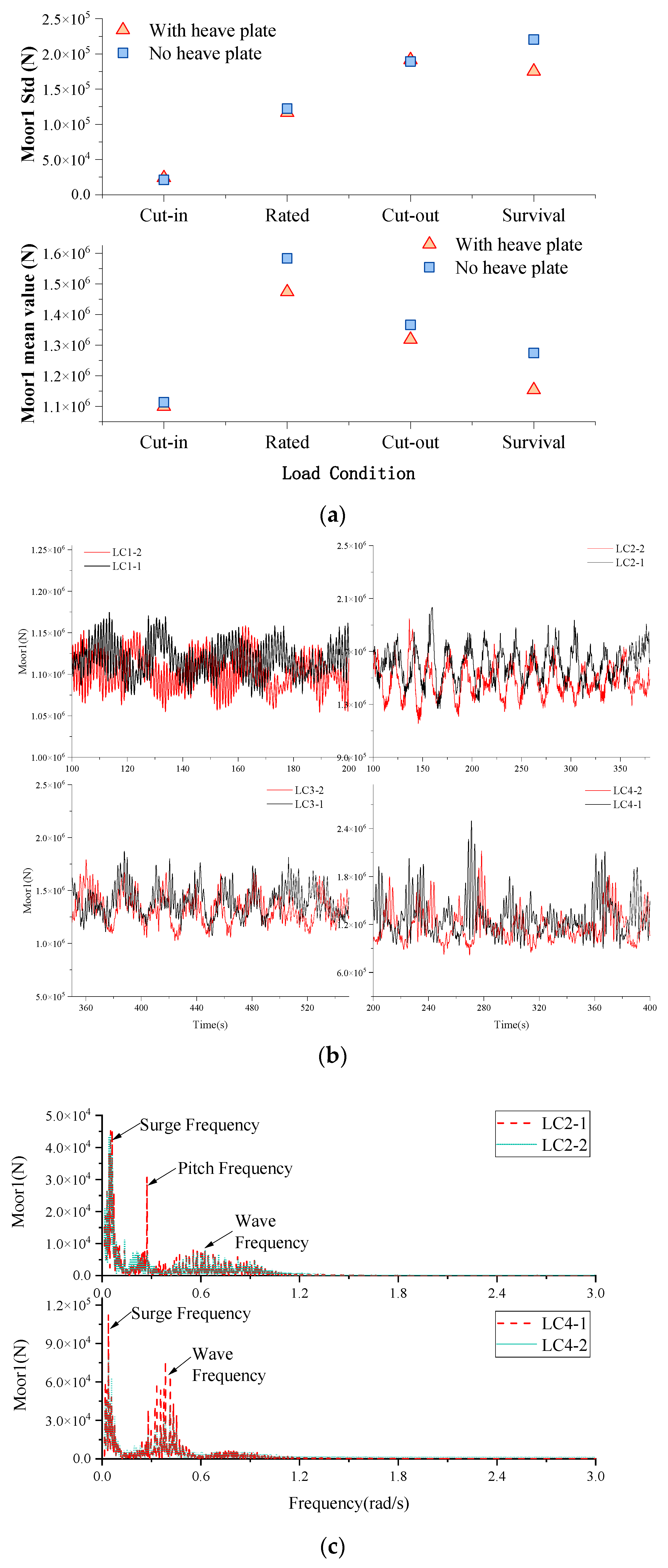
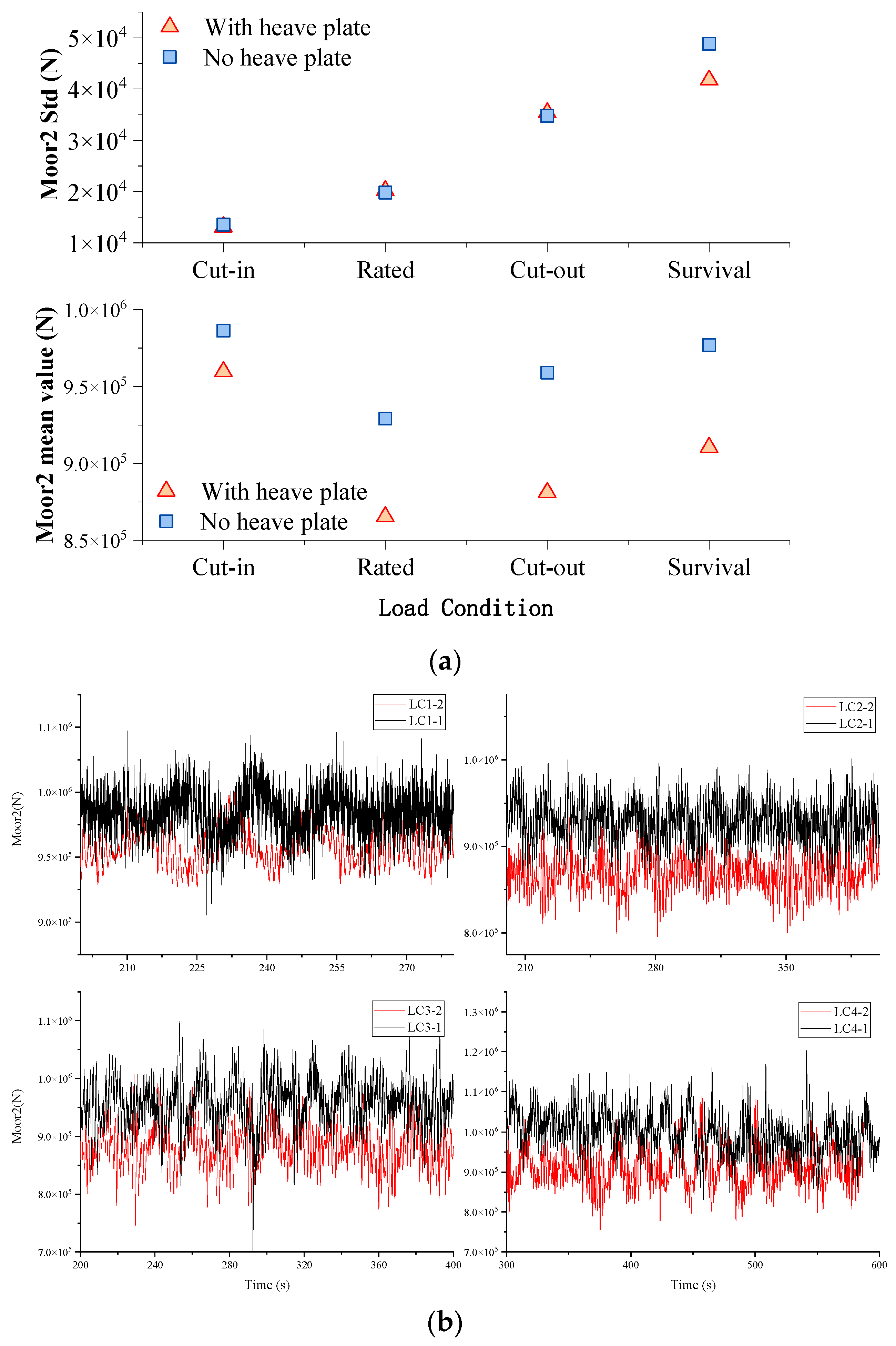
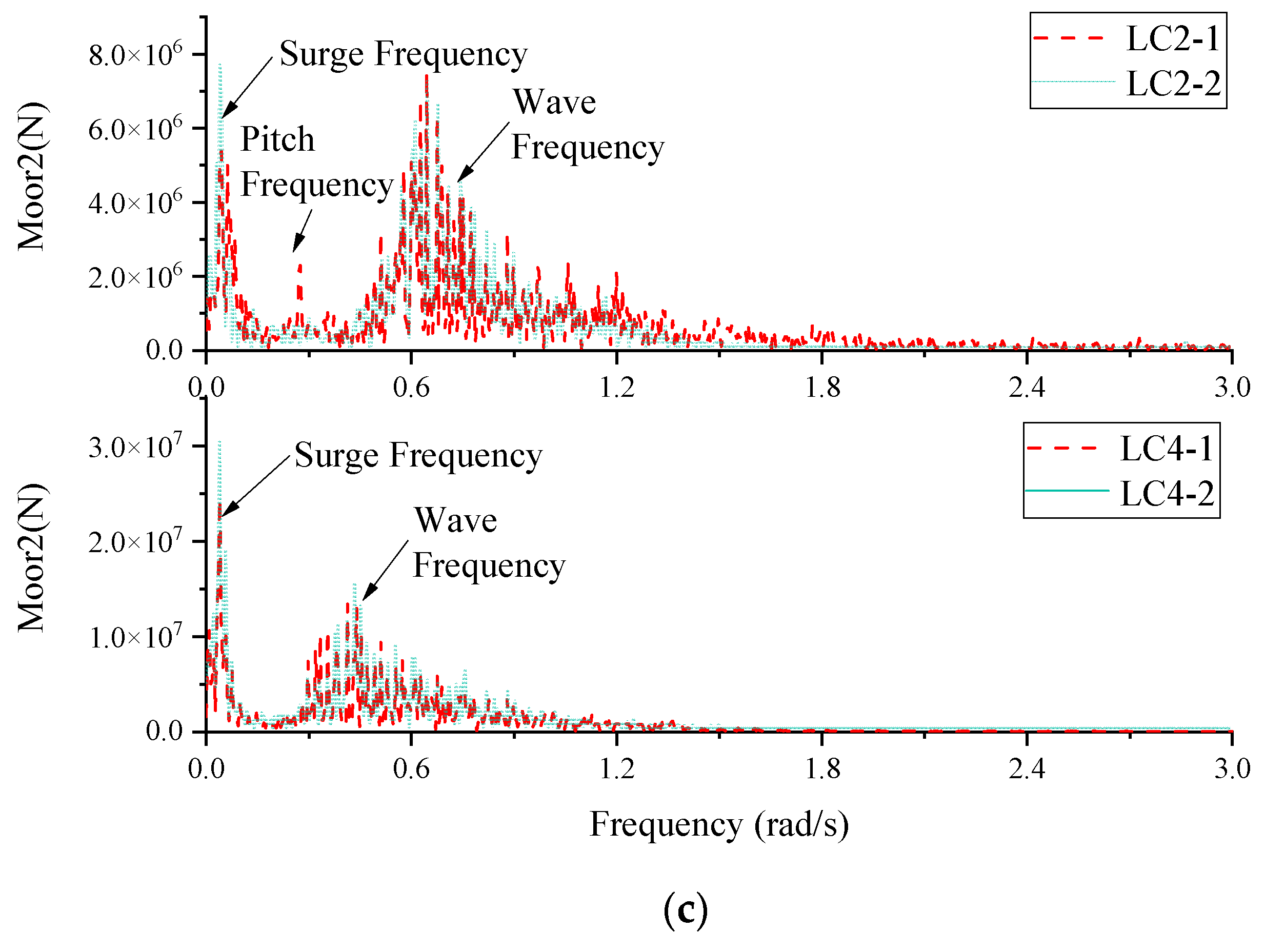
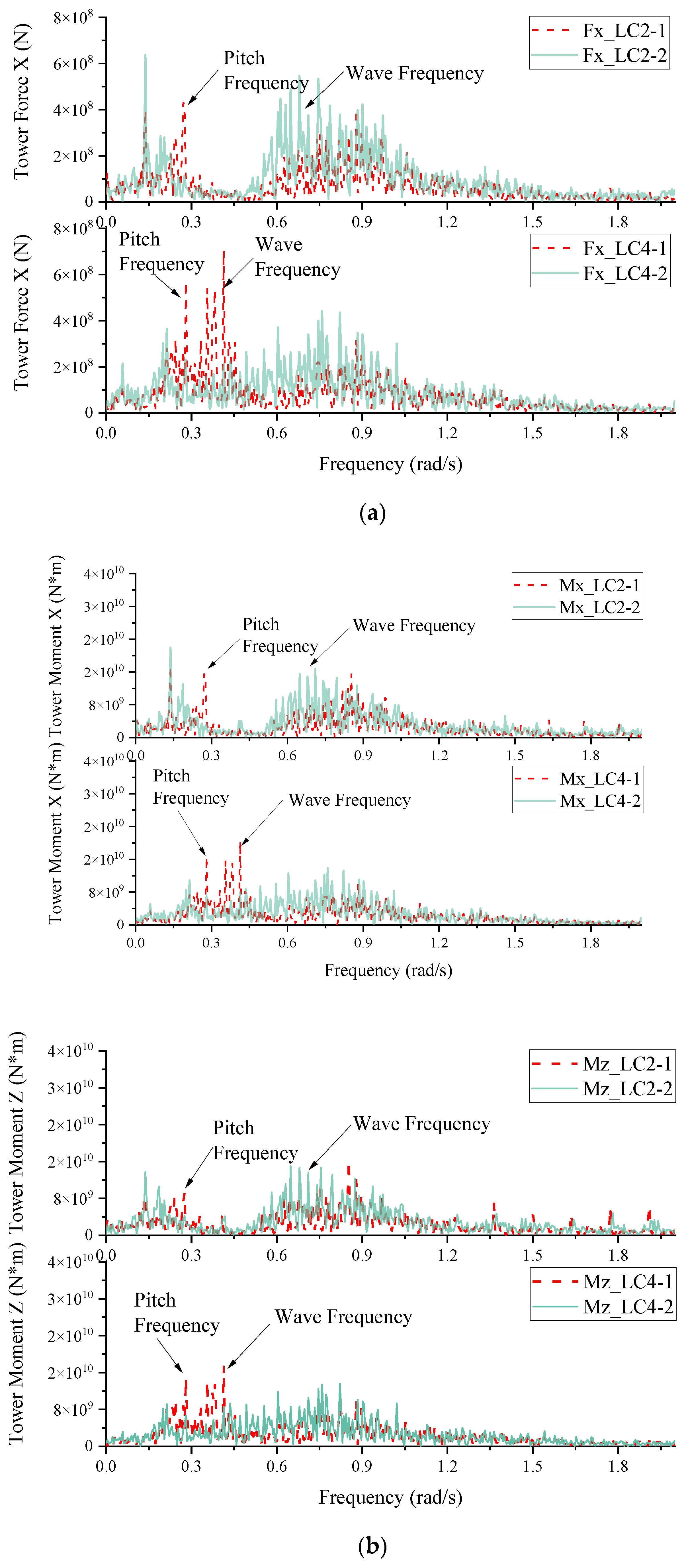
- For the irregular cases, the heave plate failed to reduce the surge and pitch of the floater. However, the heave response of the floater with the heave plate is significantly reduced for the survival case, with the maximum and standard deviation decreasing by 16% and 21%, respectively. The surge response of the floater with the heave plate becomes larger, and the mean value of the No.2 mooring line force decreases accordingly. In addition, the heave plate increases the fluctuations of force and moment at the bottom of the tower.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Blanco, H.; Nijs, W.; Ruf, J.; Faaij, A. Potential of Power-to-Methane in the EU energy transition to a low carbon system using cost optimization. Energy 2018, 232, 323–340. [Google Scholar] [CrossRef]
- Musial, W.; Butterfield, S.; Ram, B. Energy from offshore wind. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1–4 May 2006. [Google Scholar]
- Musial, W.; Butterfield, S. Future for Offshore Wind Energy in the United States; National Renewable Energy Laboratory: Golden, CO, USA, 2004. [Google Scholar]
- Jonkman, J.M. Loads Analysis of A Floating Offshore Wind Turbine Using Fully Coupled Simulation; National Renewable Energy Laboratory: Golden, CO, USA, 2007. [Google Scholar]
- Robertson, A.N.; Jonkman, J.M. Loads analysis of several offshore floating wind turbine concepts. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Luxcey, N.; Ormberg, H.; Passano, E. Global analysis of a floating wind turbine using an aero-hydro-elastic numerical model: Part 2—Benchmark study. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011. [Google Scholar]
- Liu, Y.; Xiao, Q.; Incecik, A.; Wan, D.-C. Investigation of the effects of platform motion on the aerodynamics of a floating offshore wind turbine. J. Hydrodyn. 2016, 28, 95–101. [Google Scholar] [CrossRef]
- Boo, S.Y.; Shelly, S.A.; Kim, D. Design and dynamic performances of Y-wind floating offshore wind turbine platform. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25−30 June 2017. [Google Scholar]
- Hegde, P.; Nallayarasu, S. Hydrodynamic response of buoy form spar with heave plate near the free surface validated with experiments. Ocean Eng. 2023, 269, 113580. [Google Scholar] [CrossRef]
- Li, Q. Hydrodynamic Performance of A New Semi-Spar Offshore Wind Turbine Platform and Its Mooring System. Master’s Thesis, Dalian University of Technology, Dalian, China, 2019. [Google Scholar]
- Cai, X.; Zhang, H.; Wang, H.; Xie, J.; Wang, Y. Research on the Hydrodynamic Performance of a Novel Floating Platform of the Offshore Wind Turbine in Deep Water. Proc. CSEE 2022, 42, 4339–4352. [Google Scholar] [CrossRef]
- Subbulakshmi, A.; Sundaravadivelu, R. Heave damping of spar platform for offshore wind turbine with heave plate. Ocean Eng. 2016, 121, 24–36. [Google Scholar] [CrossRef]
- Zheng, J.; Zhao, W.; Wan, D. Effects of heave plate on coupling aero-hydrodynamic performances of floating offshore wind turbine. Ocean Eng. 2022, 40, 65–73. [Google Scholar]
- Martin, H.R. Development of a Scale Model Wind Turbine for Testing of Offshore Floating Wind Turbine Systems. Master’s Thesis, The University of Maine, Orono, ME, USA, 2011. [Google Scholar]
- Jonkman, J. Definition of A 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]
- Jonkman, J.; Robertson, A.; Masciola, A.; Song, H.; Goupee, A.; Coulling, A.; Luan, C. Definition of the Semisubmersible Floating System for Phase II of OC4; National Renewable Energy Laboratory: Golden, CO, USA, 2014. [Google Scholar]

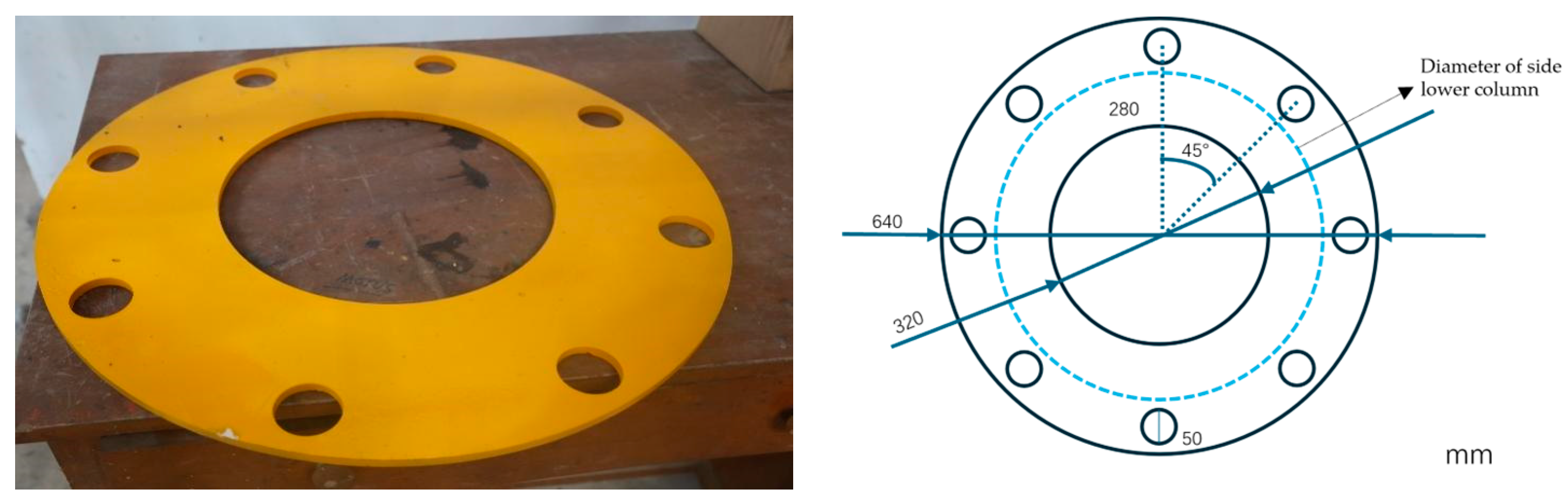

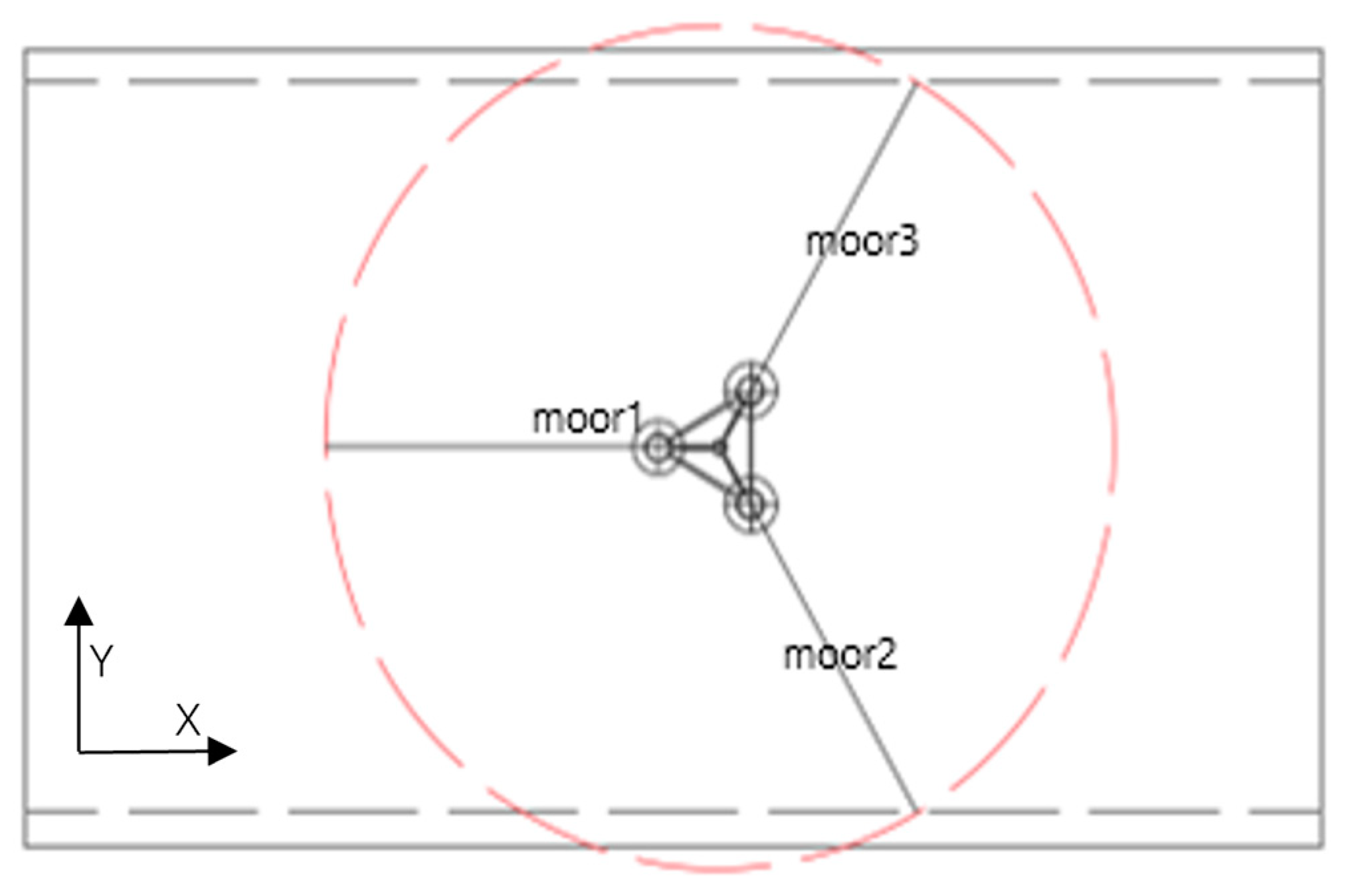

| Full Scale/m | Scale Value/mm | |
|---|---|---|
| Column spacing | 50 | 1000 |
| Middle column diameter | 6.5 | 130 |
| Total height of side column | 32 | 640 |
| Diameter of side upper column | 12 | 240 |
| Diameter of side lower column | 24 | 480 |
| Draft | 20 m | 40 cm |
| Total mass | 13,917 t | 109.4 kg |
| Height of center of gravity | 10.12 m | 20.24 cm |
| Ryy | 28.369 m | 56.74 cm |
| Conditions | Wind Speed | Wave Height/Significant Wave Height | Wave Period/Peak Period | Spectral Peak Factor | Heave Plate | |
|---|---|---|---|---|---|---|
| The Decay test | / | / | / | / | Yes/No | |
| RC1-3 | / | 4.0 m | 7.78/12.02/17.04 s | / | Yes/No | |
| RC4-6 | / | 4.0 m | 20.51/23.33/26.16 s | / | Yes/No | |
| LC1-1 | Cut-in | 3 m/s | 2.0 m | 7.5 s | 2.2 | No |
| LC1-2 | Yes | |||||
| LC2-1 | Rated | 11.4 m/s | 6.0 m | 10 s | 3 | No |
| LC2-2 | Yes | |||||
| LC3-1 | Cut-out | 25 m/s | 10.5 m | 13 s | 3.3 | No |
| LC3-2 | Yes | |||||
| LC4-1 | Survival | 50 m/s once in a hundred years | 13.1 m | 14.9 s | 3.3 | No |
| LC4-2 | Yes | |||||
| DOF | Natural Period (s) | Damping | ||
|---|---|---|---|---|
| Without Heave Plate | With Heave Plate | Without Heave Plate | With Heave Plate | |
| Surge | 123.2 | 132.8 | 0.143 | 0.17 |
| Pitch | 23.9 | 28.5 | 0.038 | 0.1113 |
| Heave | 17.4 | 20.5 | 0.01/0.084 (linear/nonlinear) | 0.0318/0.241 (linear/nonlinear) |
| Cases | Heave Plate | Force X | Moment X | Moment Z |
|---|---|---|---|---|
| LC1 (Cut-in) | VN | 8.43 × 104 N | 4.44 × 106 N·m | 7.51 × 106 N·m |
| VW | 1.00 × 105 N | 4.43 × 106 N·m | 7.49 × 106 N·m | |
| Df | 18.62% | −0.23% | −0.27% | |
| LC2 (Rated) | VN | 1.70 × 105 N | 7.22 × 106 N·m | 1.02 × 107 N·m |
| VW | 2.35 × 105 N | 7.98 × 106 N·m | 1.13 × 107 N·m | |
| Df | 38.24% | 10.53% | 10.78% | |
| LC3 (Cut-out) | VN | 1.64 × 105 N | 6.98 × 106 N·m | 1.01 × 107 N·m |
| VW | 2.26 × 105 N | 8.11 × 106 N·m | 1.20 × 107 N·m | |
| Df | 37.80% | 16.19% | 18.81% | |
| LC4 (Survival) | VN | 1.65 × 105 N | 5.02 × 106 N·m | 4.78 × 106 N·m |
| VW | 1.67 × 105 N | 5.37 × 106 N·m | 5.16 × 106 N·m | |
| Df | 1.21% | 6.97% | 7.95% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Jiang, Y.; Guo, S.; Lin, Z.; Deng, W.; Liu, L. Research on the Effect of a Heave Plate on the Dynamics of the Floating Wind Turbine Using Model Tests. J. Mar. Sci. Eng. 2024, 12, 1808. https://doi.org/10.3390/jmse12101808
Yang L, Jiang Y, Guo S, Lin Z, Deng W, Liu L. Research on the Effect of a Heave Plate on the Dynamics of the Floating Wind Turbine Using Model Tests. Journal of Marine Science and Engineering. 2024; 12(10):1808. https://doi.org/10.3390/jmse12101808
Chicago/Turabian StyleYang, Lidong, Yuting Jiang, Shibo Guo, Zihe Lin, Wanru Deng, and Liqin Liu. 2024. "Research on the Effect of a Heave Plate on the Dynamics of the Floating Wind Turbine Using Model Tests" Journal of Marine Science and Engineering 12, no. 10: 1808. https://doi.org/10.3390/jmse12101808
APA StyleYang, L., Jiang, Y., Guo, S., Lin, Z., Deng, W., & Liu, L. (2024). Research on the Effect of a Heave Plate on the Dynamics of the Floating Wind Turbine Using Model Tests. Journal of Marine Science and Engineering, 12(10), 1808. https://doi.org/10.3390/jmse12101808






