Nonparametric Modelling of Ship Dynamics Using Puma Optimizer Algorithm-Optimized Twin Support Vector Regression
Abstract
1. Introduction
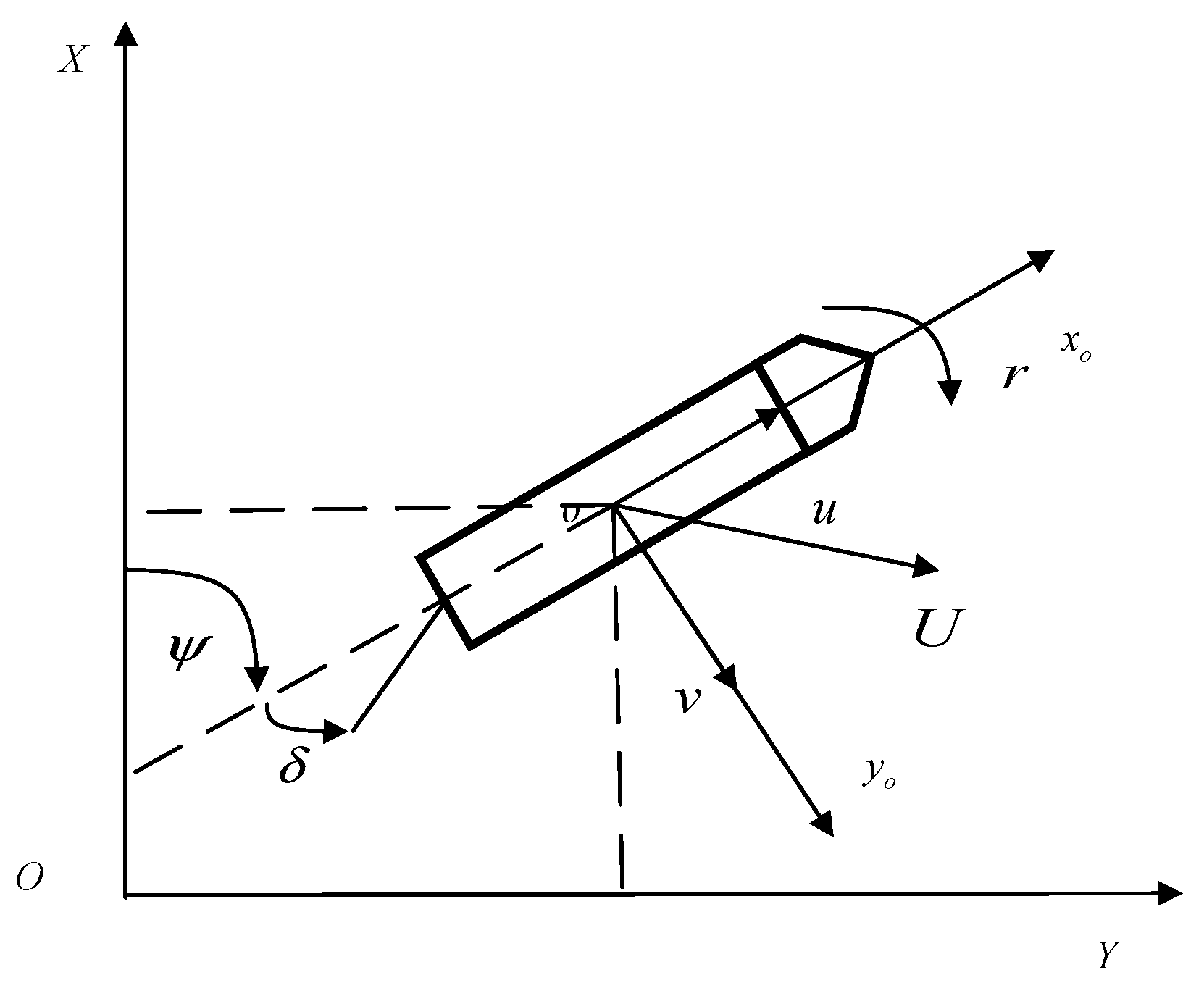
2. Problem Formulation
3. Twin Support Vector Regression Method
3.1. Support Vector Regression Method
3.2. TSVR Method
3.3. Hyperparameter Optimization
3.4. Modelling Process
4. Case Study
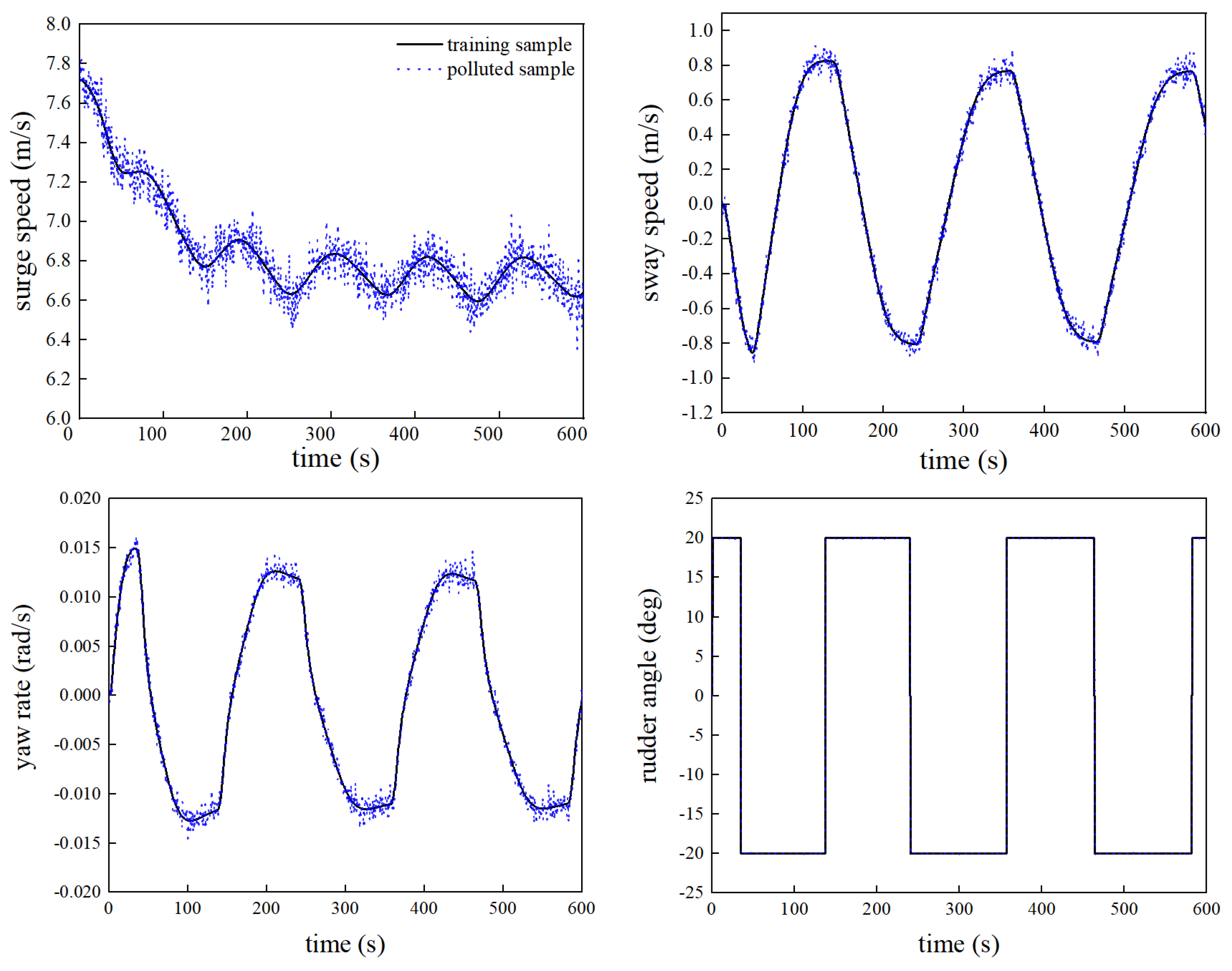
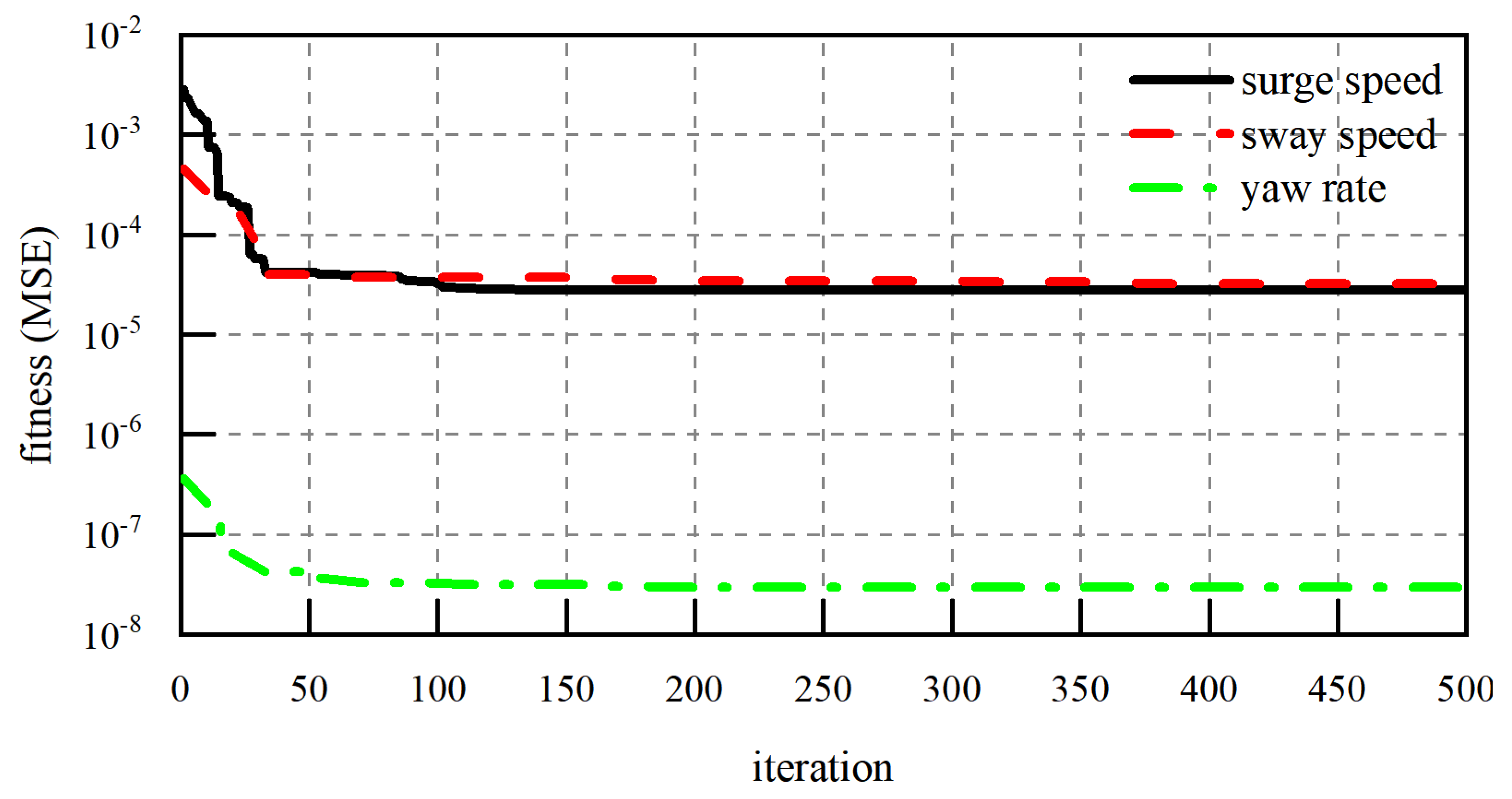
4.1. Modelling Data, Preprocessing, and Optimization Results
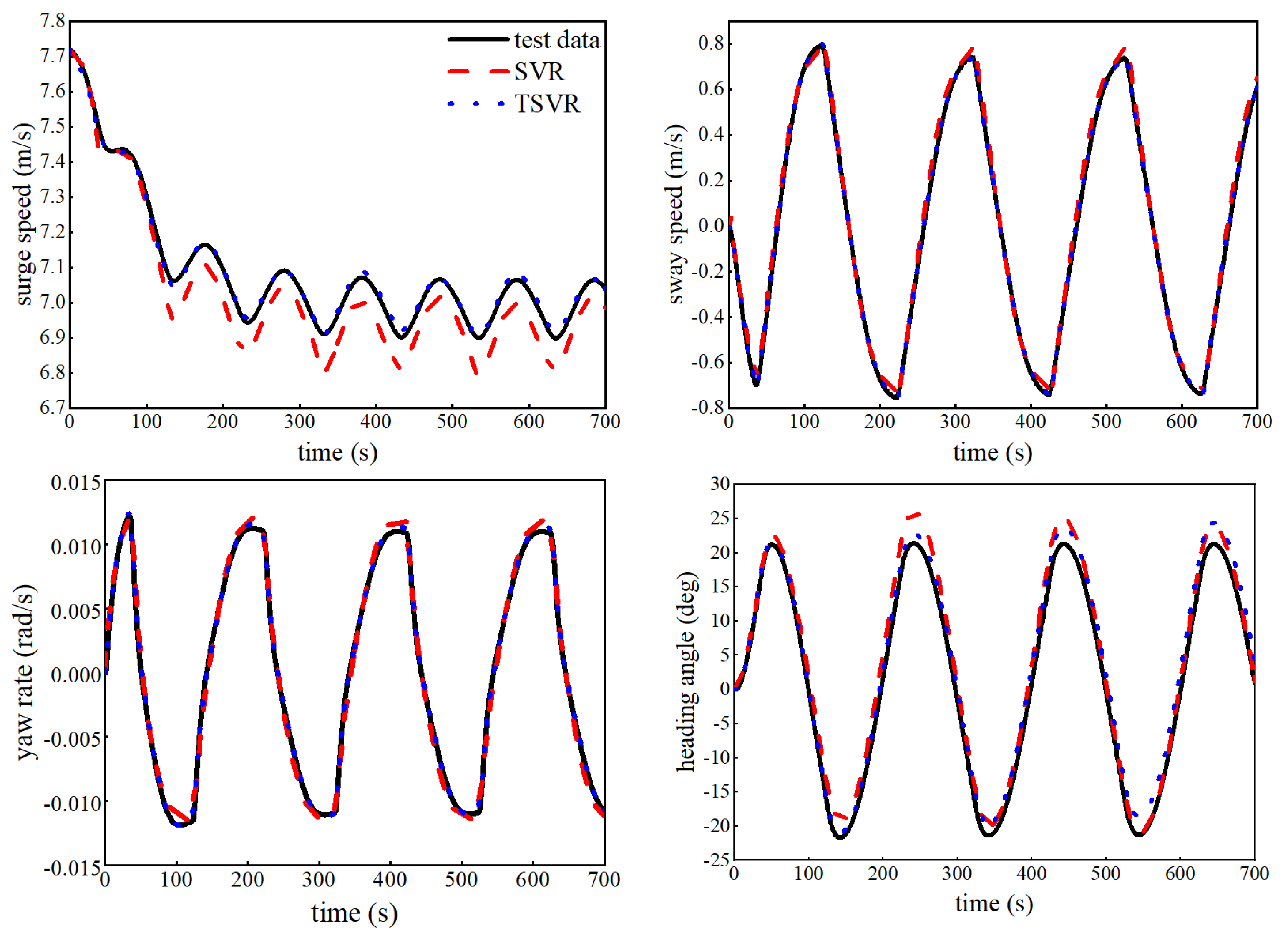
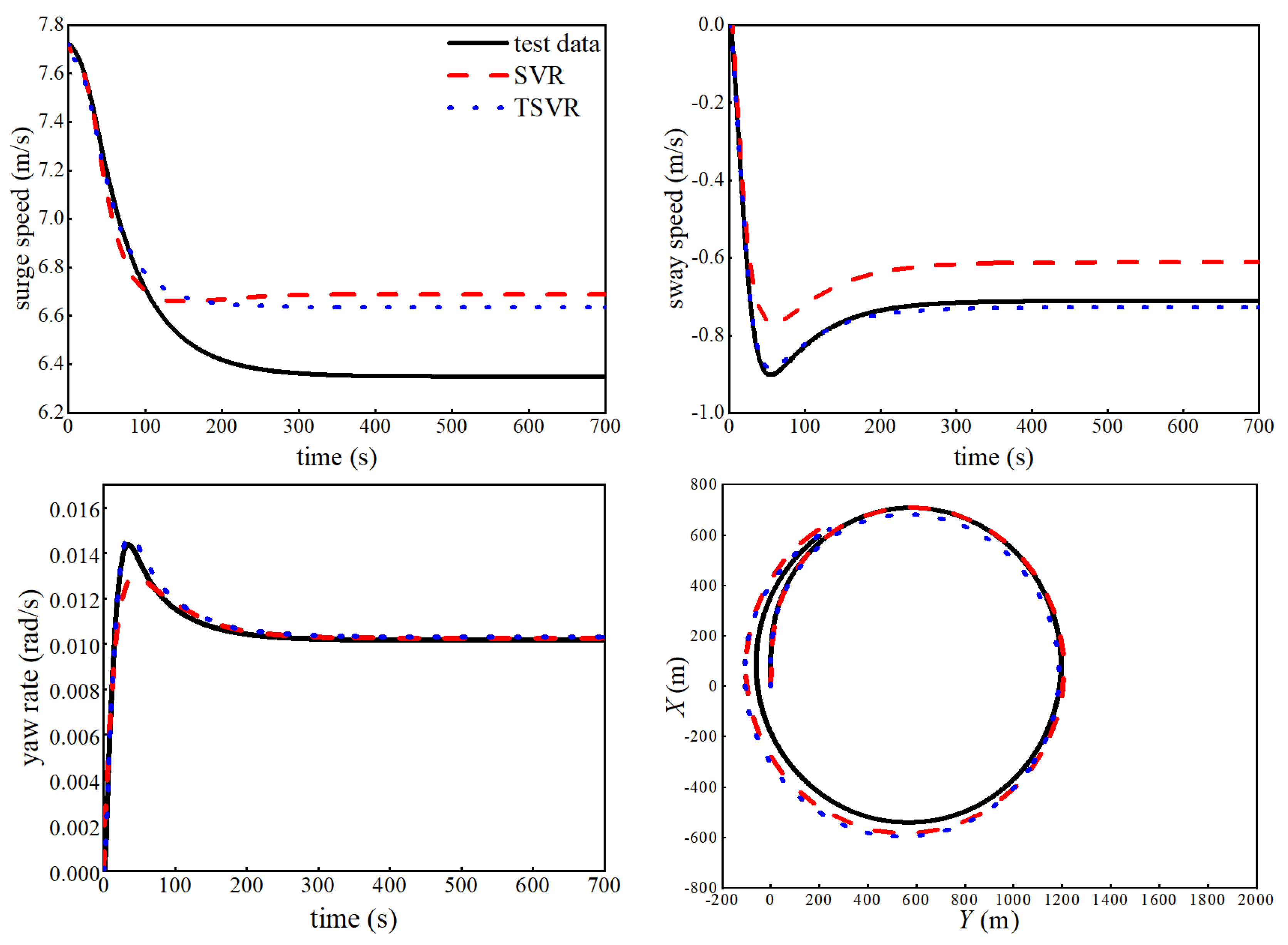
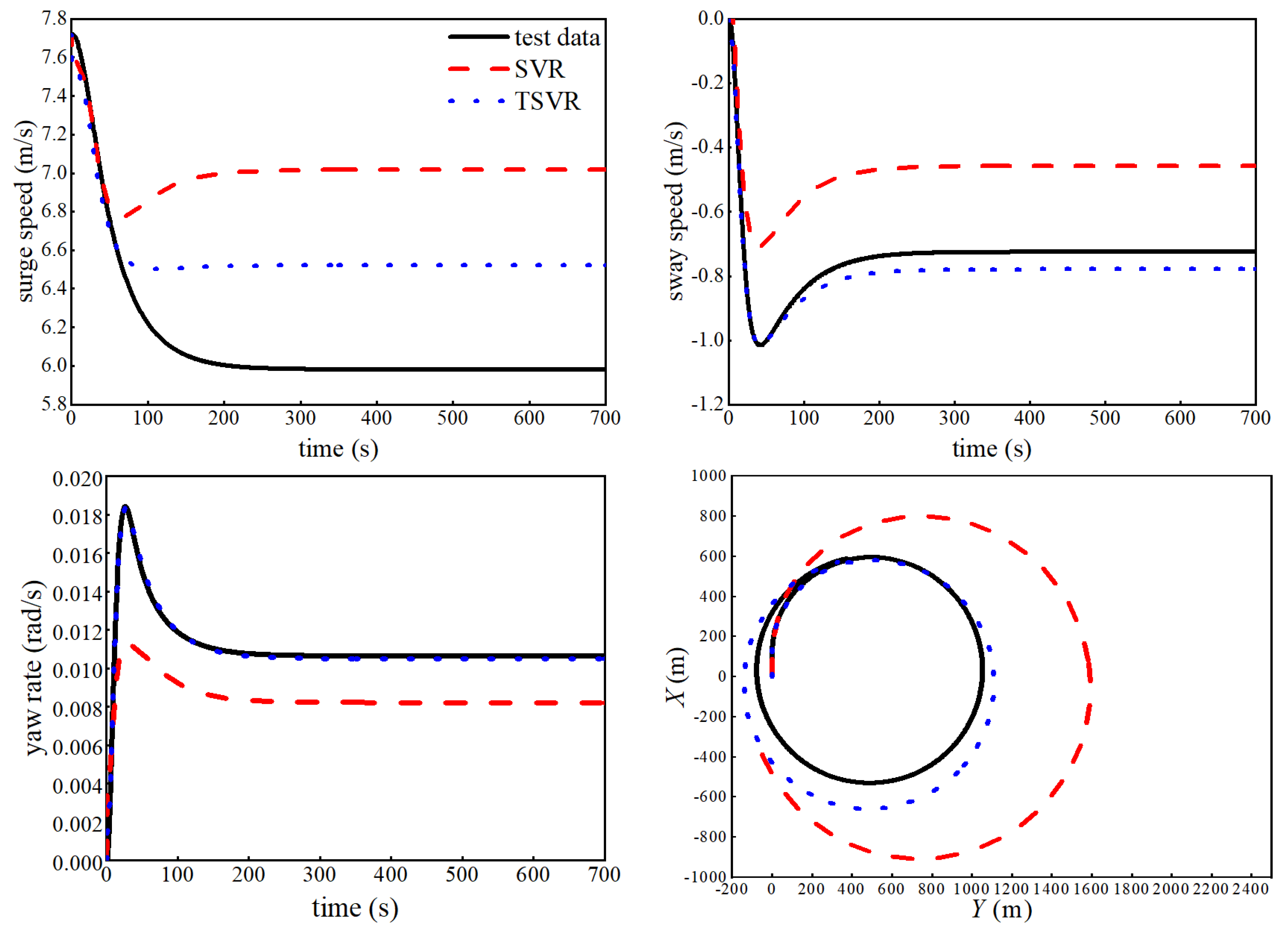
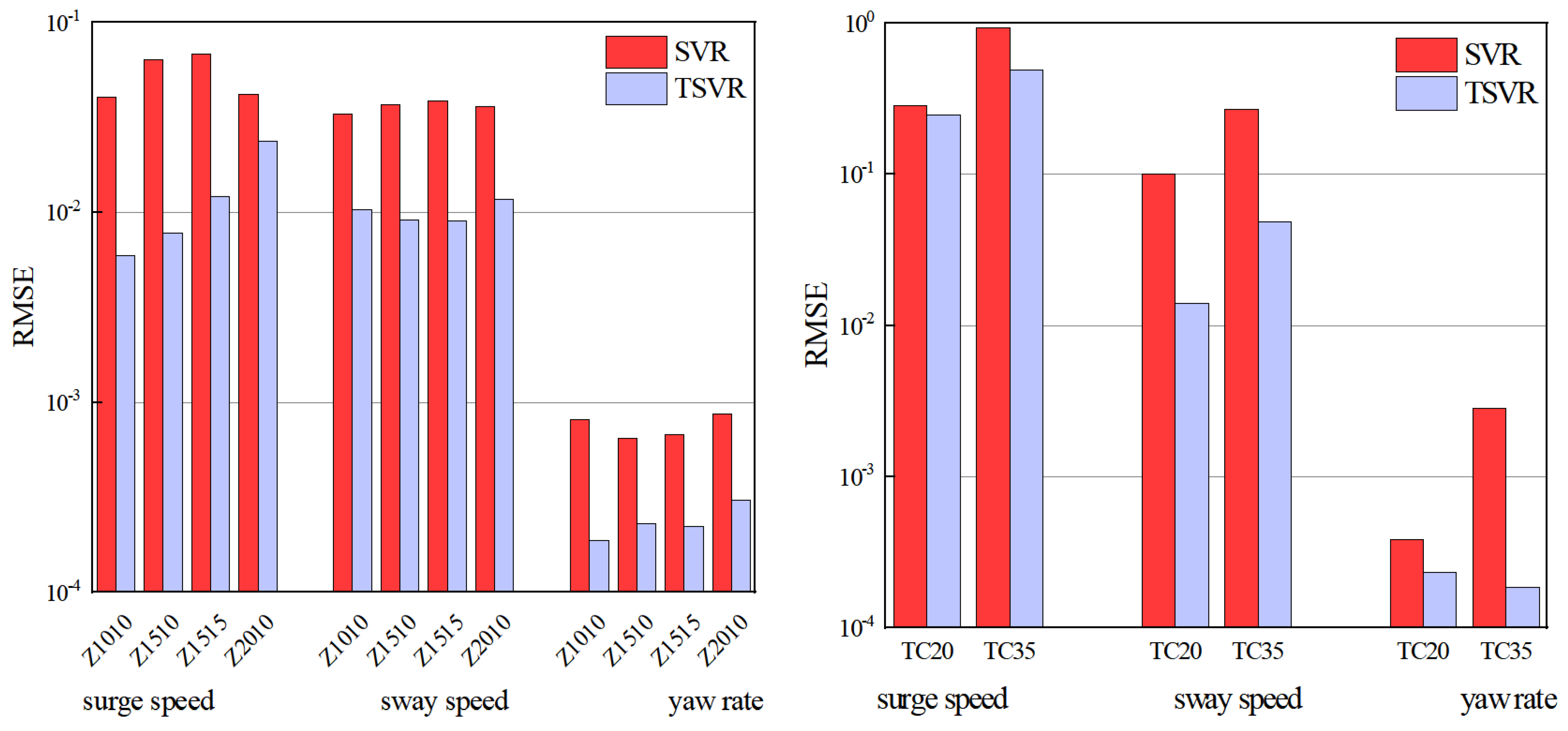
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, M.; Tian, K.; Wen, Y.Q.; Cao, J.N.; Huang, L. Improved PER-DDPG based nonparametric modeling of ship dynamics with uncertainty. Ocean Eng. 2023, 286, 115513. [Google Scholar] [CrossRef]
- Xue, Y.F.; Chen, G.; Li, Z.T.; Xue, G.; Wang, W.; Liu, Y. Online identification of a ship maneuvering model using a fast noisy input Gaussian process. Ocean Eng. 2022, 250, 110704. [Google Scholar] [CrossRef]
- Zhu, M.; Hahn, A.; Wen, Y.Q.; Sun, W.Q. Optimized support vector regression algorithm-based modeling of ship dynamics. Ocean Eng. 2019, 90, 101842. [Google Scholar] [CrossRef]
- Luo, W.L.; Guedes Soares, C.; Zou, Z.J. Parameter identification of ship maneuvering model based on support vector machines and particle swarm optimization. J. Offshore Mech. Arct. 2016, 138, 031101. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Ouyang, Z.L.; Zou, Z.J. Nonparametric modeling of ship maneuvering motion based on Gaussian process regression optimized by genetic algorithm. Ocean Eng. 2021, 238, 109699. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, H.; Xia, L.; Zou, Z.; Soares, C.G. Kernel-based support vector regression for nonparametric modeling of ship maneuvering motion. Ocean Eng. 2020, 216, 107994. [Google Scholar] [CrossRef]
- Jiang, L.C.; Shang, X.B.; Qi, X.Y.; Ouyang, Z.L.; Zhang, Z. Adaptive ensemble of multi-kernel Gaussian process regressions based on heuristic model screening for nonparametric modeling of ship maneuvering motion. J. Offshore Mech. Arct. Eng. 2025, 147, 011204. [Google Scholar] [CrossRef]
- Wu, T.; Li, R.; Chen, Q.; Pi, G.; Wan, S.; Liu, Q. A numerical study on modeling ship maneuvering performance using twin azimuth thrusters. J. Mar. Sci. Eng. 2023, 11, 2167. [Google Scholar] [CrossRef]
- Zhang, Z.; Ren, J. Locally weighted non-parametric modeling of ship maneuvering motion based on sparse Gaussian process. J. Mar. Sci. Eng. 2021, 9, 606. [Google Scholar] [CrossRef]
- Zhang, X.; Meng, Y.; Liu, Z.; Zhu, J. Modified grey wolf optimizer-based support vector regression for ship maneuvering identification with full-scale trial. J. Mar. Sci. Tech. 2022, 27, 576–588. [Google Scholar] [CrossRef]
- Luo, W.; Li, X. Measures to diminish the parameter drift in the modeling of ship manoeuvring using system identification. Appl. Ocean Res. 2017, 67, 9–20. [Google Scholar] [CrossRef]
- Liu, A.; Xue, Y.F.; Qin, H.D.; Zhu, Z.B. Physics-informed identification of marine vehicle dynamics using hydrodynamic dictionary library-inspired adaptive regression. Ocean Eng. 2024, 296, 117013. [Google Scholar] [CrossRef]
- Zhu, M.; Hahn, A.; Wen, Y.Q.; Bolles, A. Identification-based simplified model of large container ships using support vector machines and artificial bee colony algorithm. Appl. Ocean Res. 2017, 68, 249–261. [Google Scholar] [CrossRef]
- Chen, L.; Yang, P.; Li, S.; Tian, Y.; Liu, G.; Hao, G. Grey-box identification modeling of ship maneuvering motion based on LS-SVM. Ocean Eng. 2022, 266, 112957. [Google Scholar] [CrossRef]
- Sutulo, S.; Guedes Soares, C. An algorithm for offline identification of ship manoeuvring mathematical models from free-running tests. Ocean Eng. 2014, 79, 10–25. [Google Scholar] [CrossRef]
- Sajedi, Y.; Bozorg, M. Robust estimation of hydrodynamic coefficients of an AUV using Kalman and H∞ filters. Ocean Eng. 2019, 182, 386–394. [Google Scholar] [CrossRef]
- Perera, L.P.; Oliveira, P.; Guedes Soares, C. System identification of vessel steering with unstructured uncertainties by persistent excitation maneuvers. IEEE J. Ocean. Eng. 2015, 41, 515–528. [Google Scholar] [CrossRef]
- Padilla, A.; Yuz, J.L.; Herzer, B. Continuous-time system identification of the steering dynamics of a ship on a river. Int. J. Control 2014, 87, 1387–1405. [Google Scholar] [CrossRef]
- Muske, K.R.; Ashrafiuon, H.; Haas, G.; McCloskey, R.; Flynn, T. Identification of a control oriented nonlinear dynamic USV model. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 1–12. [Google Scholar]
- Haro Casado, M.; Ferreiro, R.; Velasco, F.J. Identification of nonlinear ship model parameters based on the turning circle test. J. Ship. Res. 2007, 51, 174–181. [Google Scholar] [CrossRef]
- Lbrahim, R.A.; Grace, I.M. Modeling of ship roll dynamics and its coupling with heave and pitch. Math. Probl. Eng. 2010, 2010, 934714. [Google Scholar]
- Phairoh, T.; Huang, J.K. Adaptive ship roll mitigation by using a U-tube tank. Ocean Eng. 2007, 34, 403–415. [Google Scholar] [CrossRef]
- Jiang, L.C.; Shang, X.B.; Jin, B.; Zhang, Z.; Zhang, W. Black-box modeling of ship maneuvering motion using multi-output least-squares support vector regression based on optimal mixed kernel function. Ocean Eng. 2024, 293, 116663. [Google Scholar] [CrossRef]
- Lewis, E.V. Principles of Naval Architecture Second Revision; SNAME: London, UK, 1988. [Google Scholar]
- Yasukawa, H.; Yoshimura, Y. Introduction of MMG standard method for ship maneuvering predictions. J. Mar. Sci. Technol. 2015, 20, 37–52. [Google Scholar] [CrossRef]
- Johan Åström, K. Design of fixed gain and adaptive ship steering autopilots based on the Nomoto model. In Proceedings of the Symposium on Ship Steering Automatic Control, Genoa, Italy, 15 January 1980. [Google Scholar]
- Luo, W.; Cong, H. Control for ship course-keeping using optimized support vector machines. Algorithms 2016, 9, 52. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Wang, Z.H.; Zou, Z.J. Black-box modeling of ship maneuvering motion based on multi-output nu-support vector regression with random excitation signal. Ocean Eng. 2022, 257, 111279. [Google Scholar] [CrossRef]
- Wang, Z.; Kim, J.; Im, N. Non-parameterized ship maneuvering model of Deep Neural Networks based on real voyage data-driven. Ocean Eng. 2023, 284, 115162. [Google Scholar] [CrossRef]
- Moreno, R.; Moreno-Salinas, D.; Aranda, J. Black-box marine vehicle identification with regression techniques for random manoeuvres. Electronics 2019, 8, 492. [Google Scholar] [CrossRef]
- Moreno-Sallnas, D.; Moreno, R.; Pereira, A.; Aranda, J.; de la Cruz, J.M. Modelling of a surface marine vehicle with kernel ridge regression confidence machine. Appl. Soft Comput. 2019, 76, 237–250. [Google Scholar] [CrossRef]
- Skulstad, R.; Li, G.; Fossen, T.I.; Vik, B.; Zhang, H. A hybrid approach to motion prediction for ship docking-integration of a neural network model into the ship dynamic model. IEEE Trans. Instrum. Meas. 2021, 70, 2501311. [Google Scholar] [CrossRef]
- Diez, M.; Serani, A.; Campana, E.F.; Stern, F. Time-series forecasting of ships maneuvering in waves via dynamic mode decomposition. J. Ocean Eng. Mar. Energy 2022, 8, 471–478. [Google Scholar] [CrossRef]
- Xue, Y.; Liu, Y.; Xue, G.; Chen, G. Identification and prediction of ship maneuvering motion based on a Gaussian process with uncertainty propagation. J. Mar. Sci. Eng. 2021, 9, 804. [Google Scholar] [CrossRef]
- Luo, W.; Moreira, L.; Guedes Soares, C. Manoeuvring simulation of catamaran by using implicit models based on support vector machines. Ocean Eng. 2014, 82, 150–159. [Google Scholar] [CrossRef]
- Ouyang, Z.L.; Zou, Z.J.; Zou, L. Nonparametric modeling and control of ship steering motion based on local Gaussian process regression. J. Mar. Sci. Eng. 2023, 11, 2161. [Google Scholar] [CrossRef]
- Liu, S.-Y.; Ouyang, Z.-L.; Chen, G.; Zhou, X.; Zou, Z.-J. Black-box modeling of ship maneuvering motion based on Gaussian process regression with wavelet threshold denoising. Ocean Eng. 2023, 271, 113765. [Google Scholar] [CrossRef]
- Shuai, Y.H.; Li, G.Y.; Cheng, X.; Skulstad, R.; Xu, J.; Liu, H.; Zhang, H. An efficient neural-network based approach to automatic ship docking. Ocean Eng. 2019, 191, 106514. [Google Scholar] [CrossRef]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef]
- Gu, B.; Fang, J.; Pan, F.; Bai, Z. Fast clustering-based weighted twin support vector regression. Soft Comput. 2020, 24, 6101–6117. [Google Scholar] [CrossRef]
- Platt, J. Fast Training of Support Vector Machines Using Sequential Minimal Optimization; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Xu, P.L.; Qin, H.D.; Ma, J.G.; Deng, Z.C.; Xue, Y.F. Data-driven model predictive control for ships with Gaussian process. Ocean Eng. 2023, 268, 113420. [Google Scholar] [CrossRef]
- Peng, X. TSVR: An efficient twin support vector machine for regression. Neural Netw. 2010, 23, 365–372. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, L. A weighted twin support vector regression. Knowl.-Based Syst. 2012, 33, 92–101. [Google Scholar] [CrossRef]
- Tanveer, M.; Shubham, K.; Aldhaifallah, M.; Ho, S. An efficient regularized K-nearest neighbor based weighted twin support vector regression. Knowl.-Based Syst. 2016, 94, 70–87. [Google Scholar] [CrossRef]
- Houssein, E.H. Particle swarm optimization-enhanced twin support vector regression for wind speed forecasting. J. Intell. Syst. 2019, 28, 905–914. [Google Scholar] [CrossRef]
- Cheng, H.X.; Huang, Z.; Luo, X.L. PH Prediction desulfurization system in thermal power plant based on improved twin support vector machine. J. Qingdao Univ. Sci. Technol. 2019, 40, 101–106. [Google Scholar]
- Gómez, D.; Salvador, P.; Sanz, J.; Casanova, J.L. Potato yield prediction using machine learning techniques and sentinel 2 data. Remote Sens. 2019, 11, 1745. [Google Scholar] [CrossRef]
- Gupta, D.; Pratama, M.; Ma, Z.; Li, J.; Prasad, M. Financial time series forecasting using twin support vector regression. PLoS ONE 2019, 14, e0211402. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Zhang, H.Y. Feature selection based on twin support vector regression. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019. [Google Scholar]
- Abdollahzadeh, B.; Khodadadi, N.; Barshandeh, S.; Trojovský, P.; Gharehchopogh, F.S.; El-Kenawy, E.-S.M.; Abualigah, L.; Mirjalili, S. Puma optimizer (PO): A novel metaheuristic optimization algorithm and its application in machine learning. Cluster Comput. 2024. [Google Scholar] [CrossRef]
- Chislett, M.S.; Strøm-Tejsen, J. Planar Motion Mechanism Tests and Full-Scale Steering and Maneuvering Predictions for a Mariner Class Vessel; Technical Report Hy-6. Hydro- and Aerodynamics Laboratory: Lyngby, Denmark, 1965. [Google Scholar]
- Wang, Z.H.; Zou, Z.J.; Guedes Soares, C. Identification of ship manoeuvring motion based on nu-support vector machine. Ocean Eng. 2019, 183, 270–281. [Google Scholar] [CrossRef]



| Particulars | Unit | Value |
|---|---|---|
| Length overall | m | 171.8 |
| Length between perpendiculars | m | 160.93 |
| Design waterline length | m | 158.72 |
| Maximum beam | m | 23.17 |
| Design draft | m | 8.23 |
| Design displacement | m3 | 18,541 |
| Number of propellers | -- | 1 |
| Number of blades | -- | 4 |
| Propeller diameter | m | 6.706 |
| Propeller pitch ratio | -- | 0.964 |
| Developed area ratio | -- | 0.565 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Zhang, Z.; Lu, L.; Shang, X.; Wang, W. Nonparametric Modelling of Ship Dynamics Using Puma Optimizer Algorithm-Optimized Twin Support Vector Regression. J. Mar. Sci. Eng. 2024, 12, 754. https://doi.org/10.3390/jmse12050754
Jiang L, Zhang Z, Lu L, Shang X, Wang W. Nonparametric Modelling of Ship Dynamics Using Puma Optimizer Algorithm-Optimized Twin Support Vector Regression. Journal of Marine Science and Engineering. 2024; 12(5):754. https://doi.org/10.3390/jmse12050754
Chicago/Turabian StyleJiang, Lichao, Zhi Zhang, Lingyun Lu, Xiaobing Shang, and Wei Wang. 2024. "Nonparametric Modelling of Ship Dynamics Using Puma Optimizer Algorithm-Optimized Twin Support Vector Regression" Journal of Marine Science and Engineering 12, no. 5: 754. https://doi.org/10.3390/jmse12050754
APA StyleJiang, L., Zhang, Z., Lu, L., Shang, X., & Wang, W. (2024). Nonparametric Modelling of Ship Dynamics Using Puma Optimizer Algorithm-Optimized Twin Support Vector Regression. Journal of Marine Science and Engineering, 12(5), 754. https://doi.org/10.3390/jmse12050754






