Modal Decomposition of Internal Tides in the Luzon Strait through Two-Dimensional Fourier Bandpass Filtering
Abstract
1. Introduction
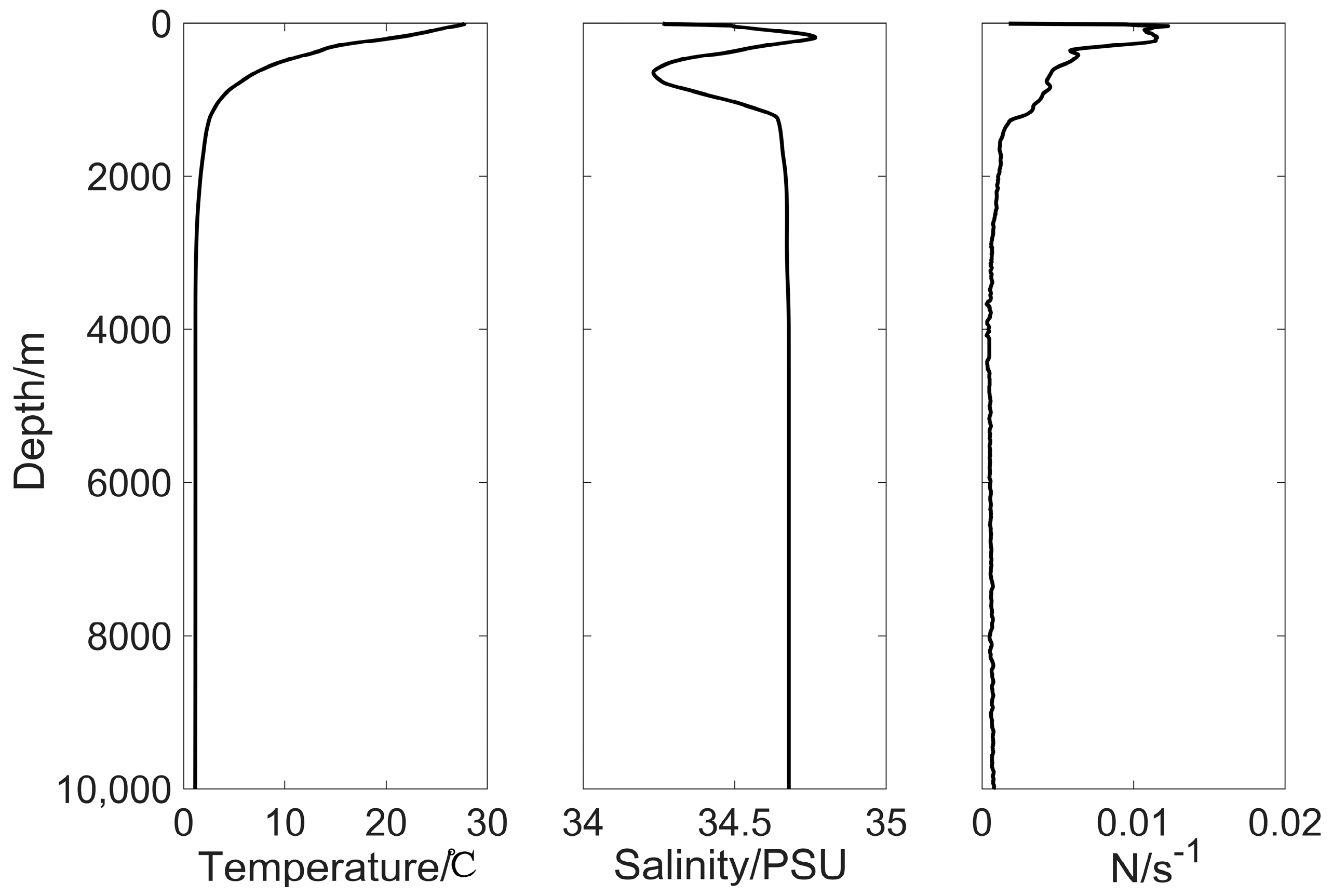
2. Materials and Methods
2.1. Internal Tide Model: MIOST-IT
2.2. Two-Dimensional Fourier Bandpass Filtering
2.3. The Directional Fourier Filter Method
3. Results
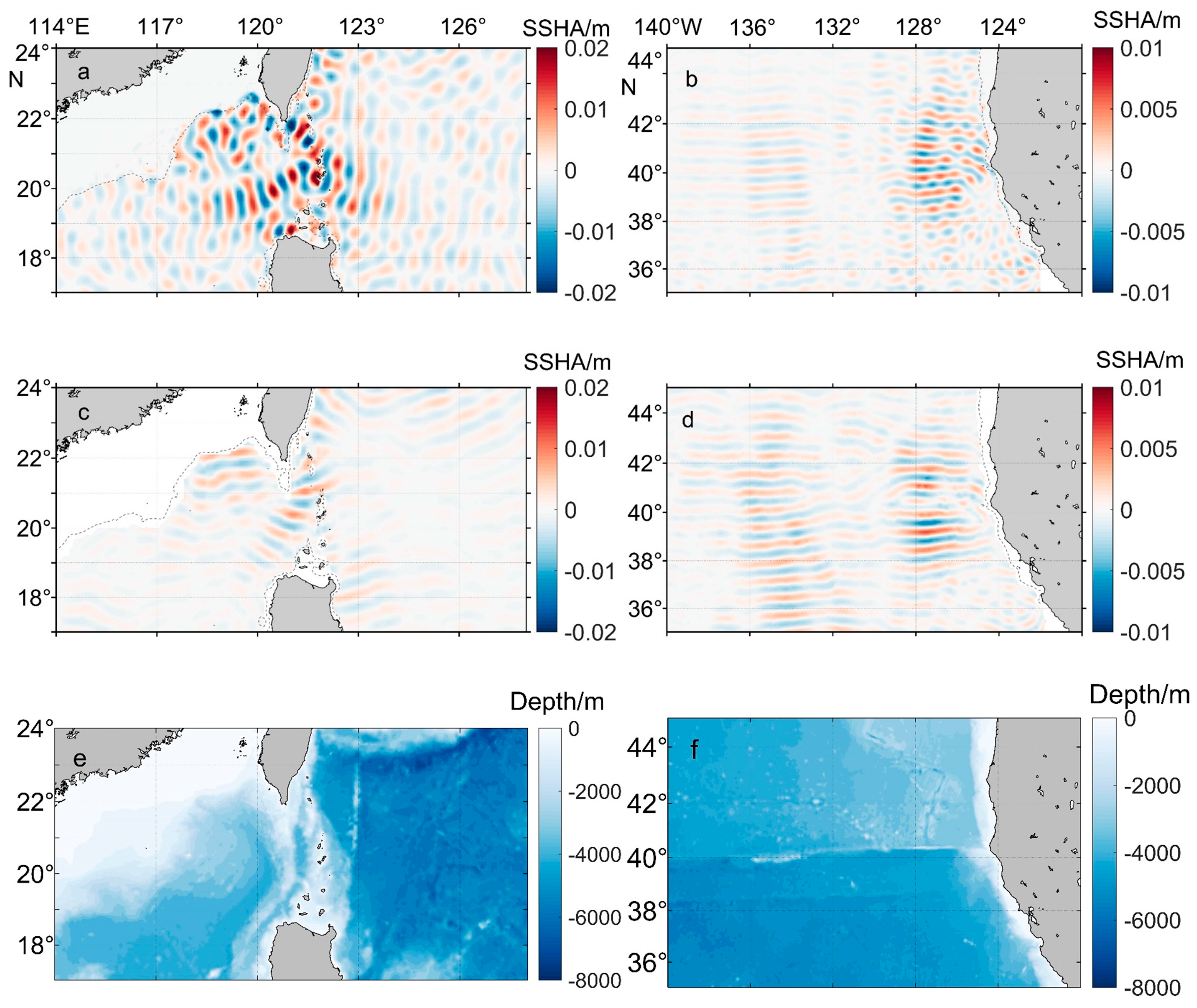
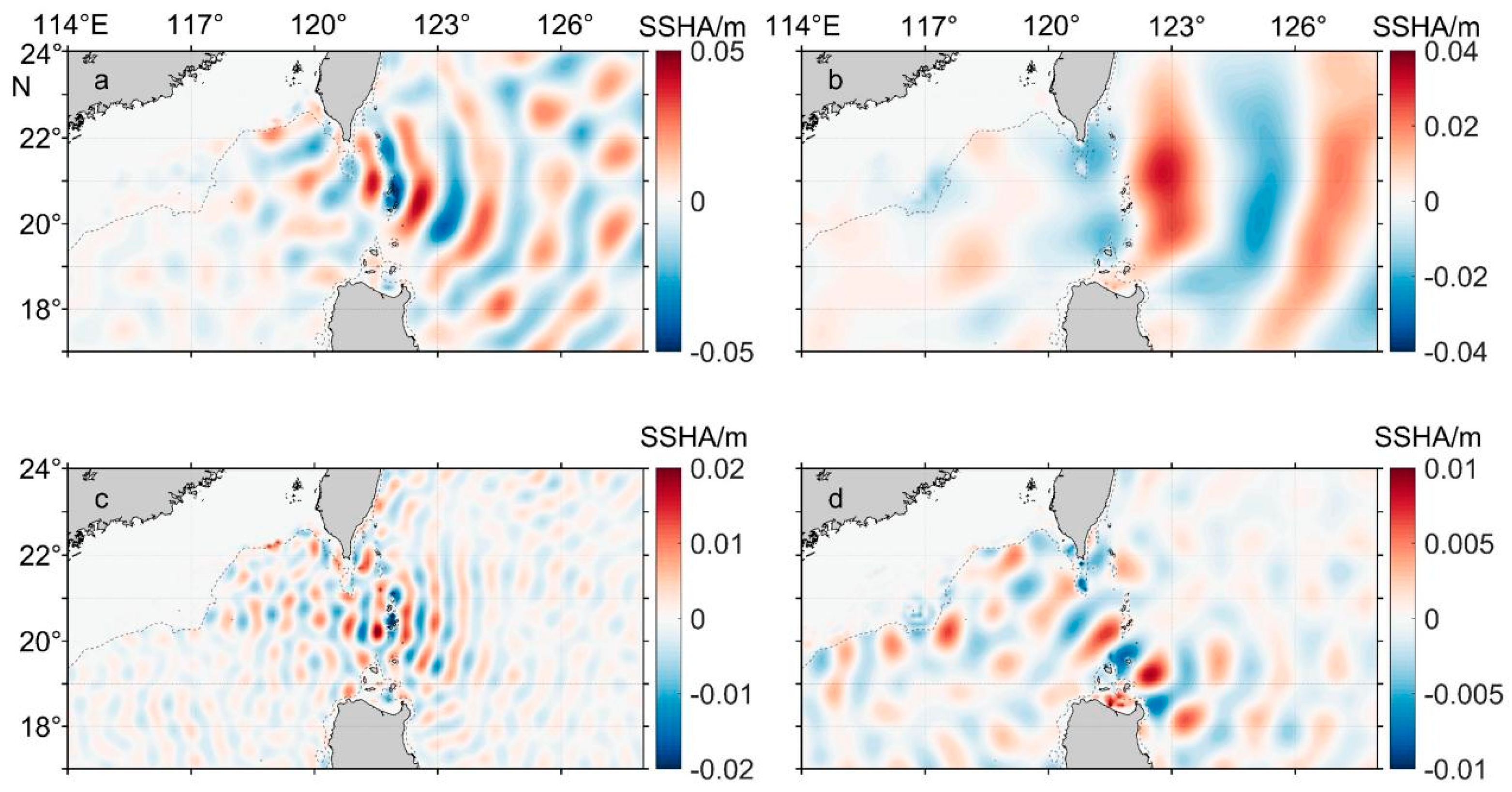
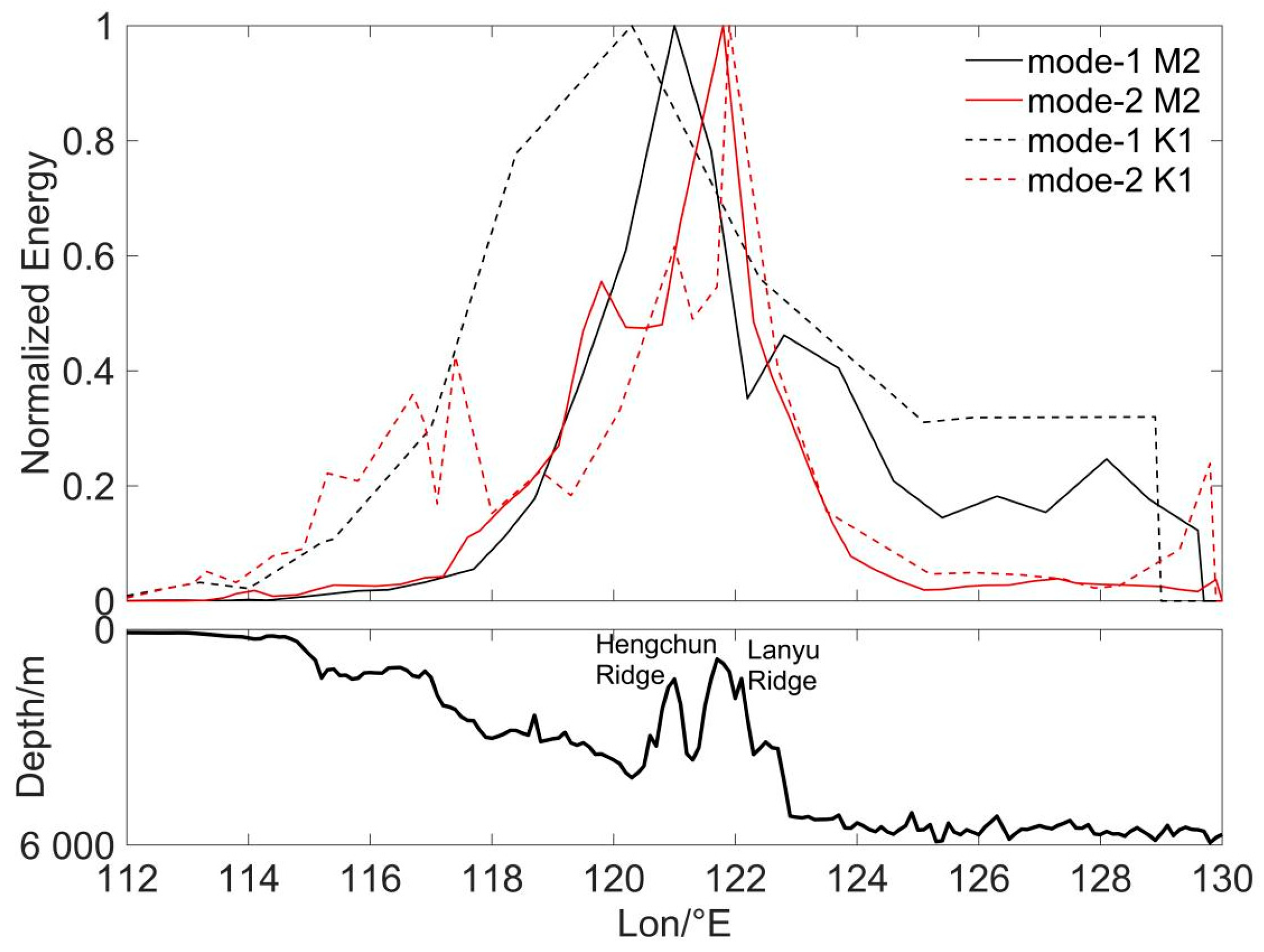
3.1. Modal Decomposition of Internal Tides within the Luzon Strait
3.2. Directional Decomposition of the Internal Tides in the Luzon Strait
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| List of Variables | |
| η1 | sea surface height elevation of internal tide. |
| η | elevation of internal tide below the sea surface. |
| a | amplitude. |
| k | wave number of internal tide. |
| g | gravity acceleration. |
| ω | tidal frequency. |
| N | buoyancy frequency. |
| ρ0 | average density of seawater. |
| Π | vertical structure of pressure perturbations. |
| W | vertical structure of vertical velocity of the internal wave. |
| c | linear phase velocity. |
| H | the maximum water depth. |
| f | Coriolis parameter. |
| cn | linear phase velocity of the n-th mode. |
| cp | group velocity of the internal tide. |
References
- Alford, M.H. Redistribution of energy available for ocean mixing by long-range propagation of internal waves. Nature 2003, 423, 159–162. [Google Scholar] [CrossRef]
- Egbert, G.D.; Ray, R.D. Tidal prediction. J. Mar. Res. 2017, 75, 189–237. [Google Scholar] [CrossRef]
- Wunsch, C. Internal tides in the ocean. Rev. Geophys. 1975, 13, 167–182. [Google Scholar] [CrossRef]
- Yadidya, B.; Rao, A.D. Interannual variability of internal tides in the Andaman Sea: An effect of Indian ocean dipole. Sci. Rep. 2022, 12, 11104. [Google Scholar] [CrossRef]
- Baines, P.G. On internal tide generation models. Deep. Sea Res. Part A Oceanogr. Res. Pap. 1982, 29, 307–338. [Google Scholar] [CrossRef]
- Rudnick, D.L.; Boyd, T.J.; Brainard, R.E.; Carter, G.S.; Egbert, G.D.; Gregg, M.C.; Holloway, P.E.; Klymak, J.M.; Kunze, E.; Lee, C.M.; et al. From tides to mixing along the Hawaiian Ridge. Science 2003, 301, 355–357. [Google Scholar] [CrossRef]
- Munk, W.; Wunsch, C. Abyssal recipes II: Energetics of tidal and wind mixing. Deep. Sea Res. Part I Oceanogr. Res. Pap. 1998, 45, 1977–2010. [Google Scholar] [CrossRef]
- Wunsch, C.; Ferrari, R. Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 2004, 36, 281–314. [Google Scholar] [CrossRef]
- Cui, Z.; Jin, W.; Ding, T.; Liang, C.; Lin, F.; Zhou, B.; Guo, B.; Liang, Q. Observations of anomalously strong mode-2 internal solitary waves in the central Andaman Sea by a mooring system. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2024, 208, 104300. [Google Scholar] [CrossRef]
- Yang, Q.; Tian, J.; Zhao, W. Observation of Luzon Strait transport in summer 2007. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2010, 57, 670–676. [Google Scholar] [CrossRef]
- Lefauve, A.; Muller, C.; Melet, A. A three-dimensional map of tidal dissipation over abyssal hills. J. Geophys. Res. Ocean. 2015, 120, 4760–4777. [Google Scholar] [CrossRef]
- Arbic, B.K.; Richman, J.G.; Shriver, J.F.; Timko, P.G.; Metzger, E.J.; Wallcraft, A.J. Global modeling of internal tides: Within an eddying ocean general circulation model. Oceanography 2012, 25, 20–29. [Google Scholar] [CrossRef]
- Buijsman, M.C.; Arbic, B.K.; Richman, J.G.; Shriver, J.F.; Wallcraft, A.J.; Zamudio, L. Semidiurnal internal tide incoherence in the equatorial pacific. J. Geophys. Res. Ocean. 2017, 122, 5286–5305. [Google Scholar] [CrossRef]
- Buijsman, M.C.; Stephenson, G.R.; Ansong, J.K.; Arbic, B.K.; Mattias, J.A.; Richman, J.G.; Shriver, J.F.; Vic, C.; Wallcraft, A.J.; Zhao, Z. On the interplay between horizontal resolution and wave drag and their effect on tidal baroclinic mode waves in realistic global ocean simulations. Ocean Model. 2020, 152, 101656. [Google Scholar] [CrossRef]
- Savage, A.C.; Arbic, B.K.; Alford, M.H.; Ansong, J.K.; Thomas, J.; Menemenlis, D.; O’Rourke, A.K.; Richman, J.G.; Shriver, J.F.; Voet, G.; et al. Spectral decomposition of internal gravity wave sea surface height in global models. J. Geophys. Res. Ocean. 2017, 122, 7803–7821. [Google Scholar]
- Cui, Z.; Liang, C.; Lin, F.; Chen, S.; Ding, T.; Zhou, B.; Jin, W.; Yang, W. Construction of a wavefront model for internal solitary waves and its application in the Northern South China Sea. Ocean Model. 2024, 189, 102366. [Google Scholar] [CrossRef]
- Zhao, Z.; Alford, M.H.; Girton, J.B.; Rainville, L.; Simmons, H.L. Global observations of open-ocean mode-1 M2 internal tides. J. Phys. Oceanogr. 2016, 46, 1657–1684. [Google Scholar] [CrossRef]
- Zaron, E.D. Baroclinic tidal sea level from exact-repeat mission altimetry. J. Phys. Oceanogr. 2019, 49, 193–210. [Google Scholar] [CrossRef]
- Ubelmann, C.; Carrere, L.; Durand, C.; Dibarboure, G.; Faugère, Y.; Ballarotta, M.; Briol, F.; Lyard, F. Simultaneous estimation of ocean mesoscale and coherent internal tide sea surface height signatures from the global altimetry record. Ocean Sci. 2022, 18, 469–481. [Google Scholar] [CrossRef]
- Zhao, Z. The global mode-2 M2 internal tide. J. Geophys. Res. Ocean. 2018, 123, 7725–7746. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Z.; Hibiya, T.; Yin, B.; Wang, F. Radiation path of diurnal internal tides in the northwestern Pacific controlled by refraction and interference. J. Geophys. Res. Ocean. 2021, 126, e2020JC016972. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, K.; Yin, B.; Zhao, Z.; Wang, Y.; Li, Q. Long-range propagation and associated variability of internal tides in the South China Sea. J. Geophys. Res. Ocean. 2016, 121, 8268–8286. [Google Scholar] [CrossRef]
- Warn-Varnas, A.; Hawkins, J.; Lamb, K.G.; Piacsek, S.; Chin-Bing, S.; King, D.; Bur-gos, G. Solitary wave generation dynamics at Luzon Strait. Ocean Model. 2010, 31, 9–27. [Google Scholar] [CrossRef]
- Zheng, K.; Zhang, Z.; Yang, Z.; Sun, H.; Guan, S.; Huang, X.; Zhou, C.; Zhao, W.; Tian, J. Influence of Lee Wave Breaking on Far-Field Mixing in the Deep Ocean. J. Geophys. Res. Ocean. 2024, 129, e2023JC020386. [Google Scholar] [CrossRef]
- Sheu, W.; Wu, C.; Oey, L. Blocking and westward passage of eddies in the Luzon Strait. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2010, 57, 1783–1791. [Google Scholar] [CrossRef]
- Hsin, Y.; Wu, C.; Chao, S. An updated examination of the Luzon Strait transport. J. Geophys. Res. Ocean. 2012, 117, C03022. [Google Scholar] [CrossRef]
- Chiswell, S.M. Altimeter and current meter observations of internal tides: Do they agree? J. Phys. Oceanogr. 2006, 36, 1860–1872. [Google Scholar] [CrossRef]
- Gill, A.E. Atmosphere-Ocean Dynamics; Academic Press: London, UK, 1982. [Google Scholar]
- Zhou, X.; Grimshaw, R. The effect of variable currents on internal solitary waves. Dyn. Atmos. Ocean. 1989, 14, 17–39. [Google Scholar] [CrossRef]
- Doblas-Reyes, F.J.; Déqué, M. A flexible bandpass filter design procedure applied to midlatitude intraseasonal variability. Mon. Weather. Rev. 1998, 126, 3326–3335. [Google Scholar] [CrossRef]
- Bleck, R.; Boudra, D. Initial testing of a numerical ncean circulation model using a hybrid (quasi-isopycnic) vertical coordinate. J. Phys. Oceanogr. 1981, 11, 755–770. [Google Scholar] [CrossRef]
- Gong, Y.; Rayson, M.D.; Jones, N.L.; Ivey, G.N. Directional decomposition of internal tides propagating from multiple generation sites. Ocean Model. 2021, 162, 101801. [Google Scholar] [CrossRef]
- Alford, M.H.; Peacock, T.; MacKinnon, J.A.; Nash, J.D.; Buijsman, M.C.; Centurioni, L.C.; Chao, S.-Y.; Chang, M.-H.; Farmer, D.M.; Fringer, O.B.; et al. The formation and fate of internal waves in the South China Sea. Nature 2015, 521, 65–69. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Yin, B.; Hou, Y.; Xu, Y. Variability of internal tides and near-inertial waves on the continental slope of the northwestern South China Sea. J. Geophys. Res. Ocean. 2013, 118, 197–211. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, B.; Zhang, Q.; Lin, F.; Jin, W.; Cui, Z. Modal Decomposition of Internal Tides in the Luzon Strait through Two-Dimensional Fourier Bandpass Filtering. J. Mar. Sci. Eng. 2024, 12, 1477. https://doi.org/10.3390/jmse12091477
Xie B, Zhang Q, Lin F, Jin W, Cui Z. Modal Decomposition of Internal Tides in the Luzon Strait through Two-Dimensional Fourier Bandpass Filtering. Journal of Marine Science and Engineering. 2024; 12(9):1477. https://doi.org/10.3390/jmse12091477
Chicago/Turabian StyleXie, Botao, Qi Zhang, Feilong Lin, Weifang Jin, and Zijian Cui. 2024. "Modal Decomposition of Internal Tides in the Luzon Strait through Two-Dimensional Fourier Bandpass Filtering" Journal of Marine Science and Engineering 12, no. 9: 1477. https://doi.org/10.3390/jmse12091477
APA StyleXie, B., Zhang, Q., Lin, F., Jin, W., & Cui, Z. (2024). Modal Decomposition of Internal Tides in the Luzon Strait through Two-Dimensional Fourier Bandpass Filtering. Journal of Marine Science and Engineering, 12(9), 1477. https://doi.org/10.3390/jmse12091477





