Magnetic, Electronic Structure and Micromagnetic Properties of Ferrimagnetic DyCo3 as a Platform for Ferrimagnetic Skyrmions
Abstract
:1. Introduction
2. Materials and Methods
3. Results
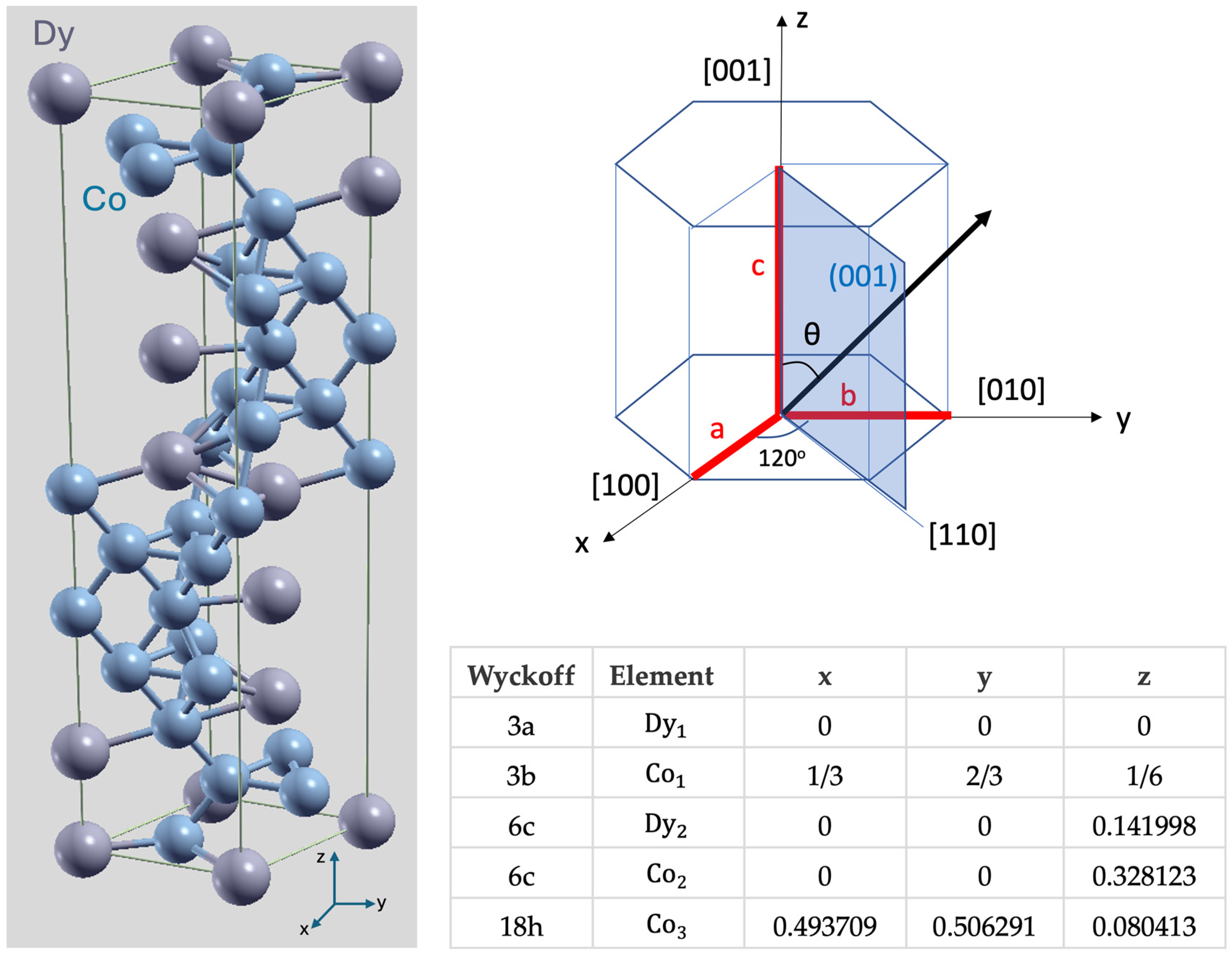
3.1. Ab Initio Calculations of DyCo3
- (i)
- finding the theoretical atomic equilibrium position by performing a structure relaxation to minimize total energy and force;
- (ii)
- a careful convergence in k point meshing;
- (iii)
- a study concerning a choice of the Hubbard U parameter further used for calculations. The choice criterium for the U was a value larger than the one that maximizes the orbital momentum of Dy. As illustrated by Figure 2, the adjunction of the Hubbard correlations leads to an increase of the Dy orbital moment which eventually saturates after a certain value of U. As expected, the Hubbard correlation influence is negligible for Co: the magnetic moment of the Co atoms is mostly independent on U. Moreover, as expected for a transition metal, the orbital contribution to the total magnetic moment is negligible as compared to the spin one.
3.2. Comparison with the Experiments
3.3. Structural Properties of the Bulk DyCo3
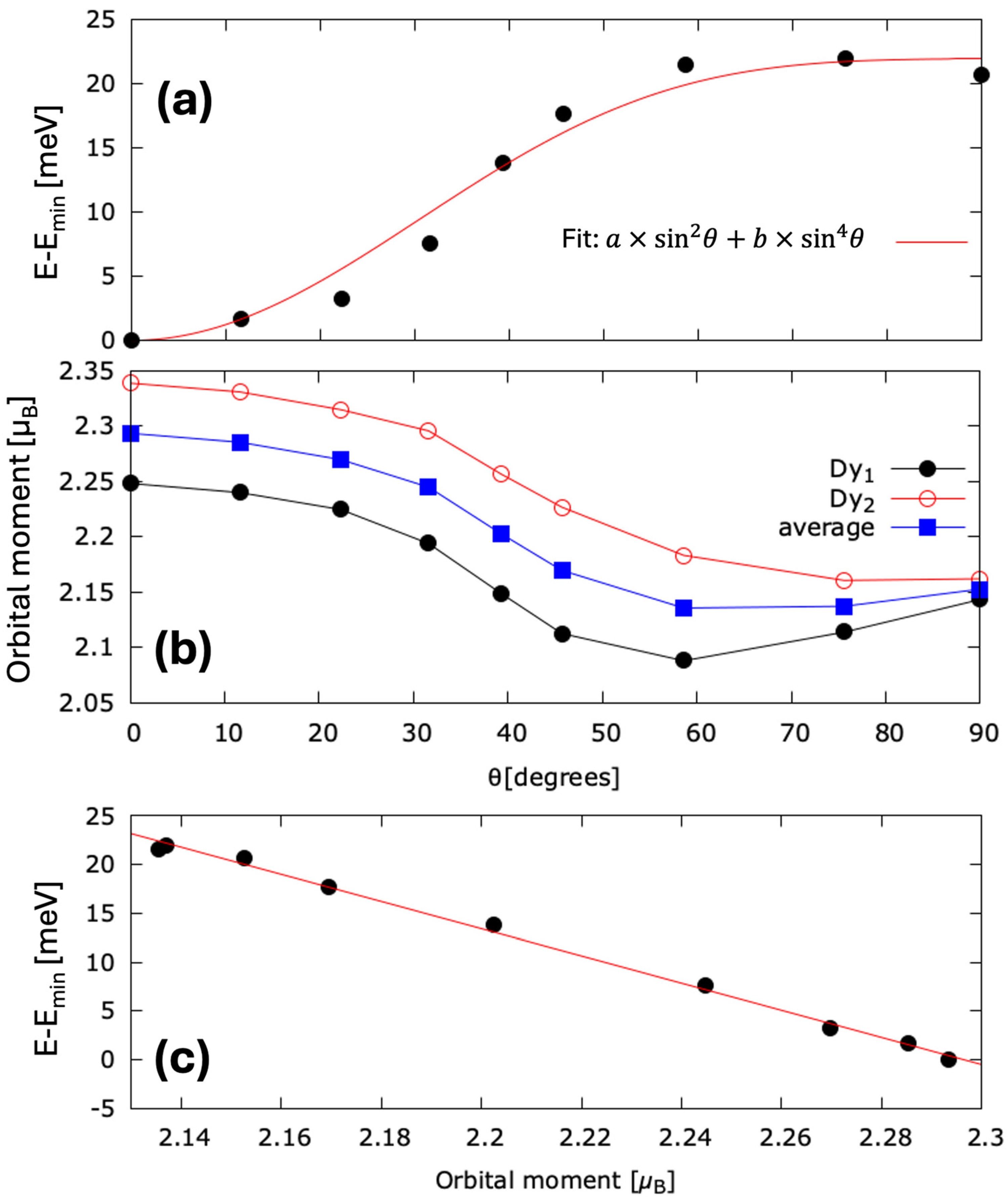
3.4. Magnetic Properties of the Bulk DyCo3 Systems
3.5. DyCox Thin Film Systems
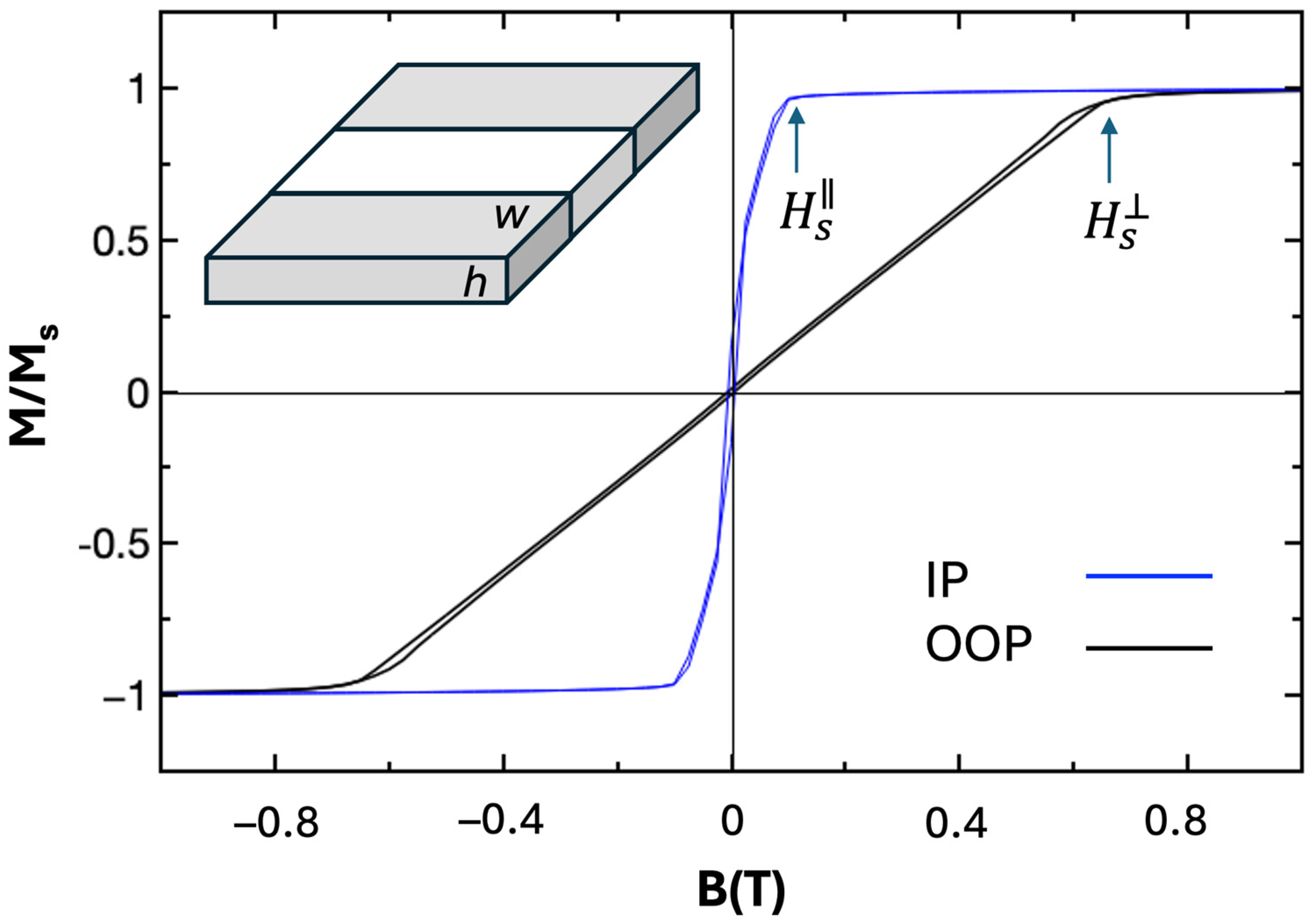
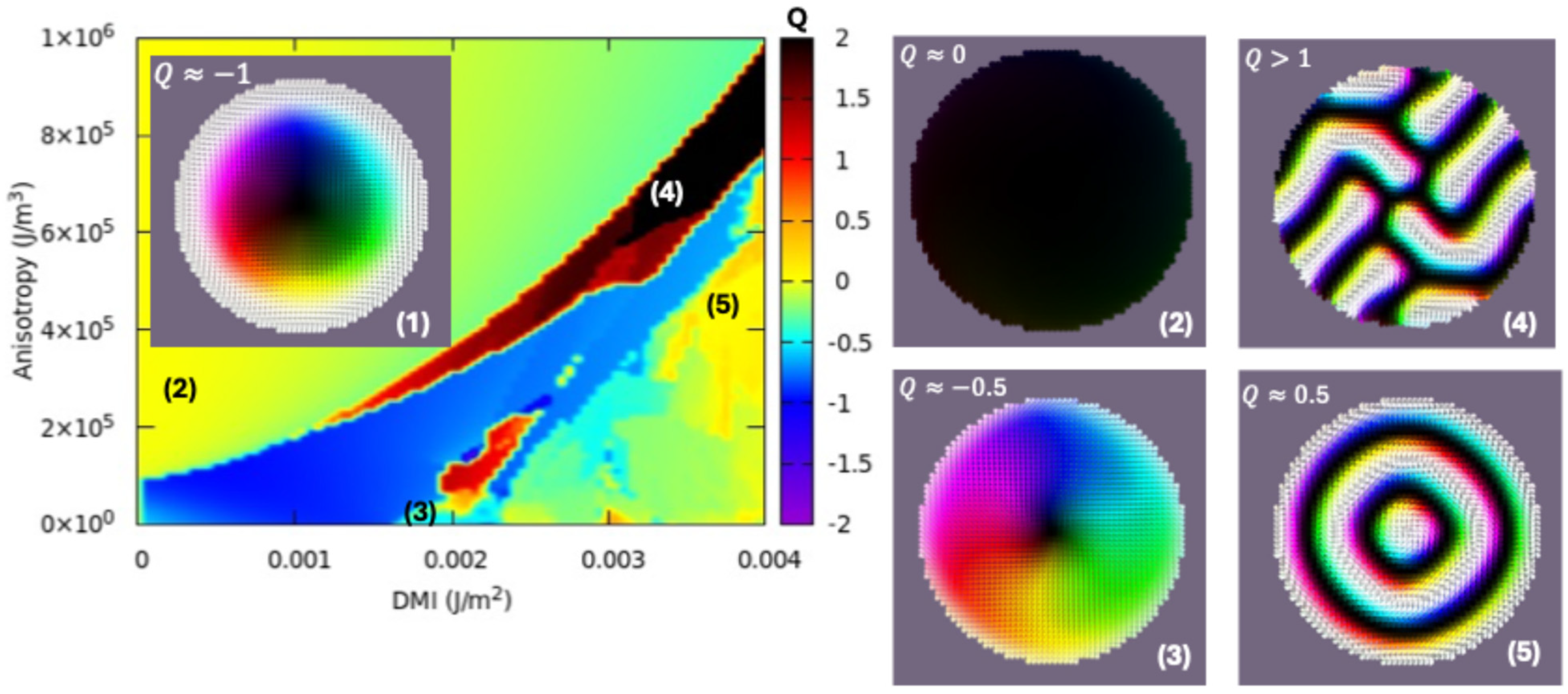
3.6. Micromagnetic Properties of DyCox Thin Films and Patterned Structures
4. Discussion and Conclusions
4.1. Intrinsic and Extrinsic Origin of the DMI in DyCo3 Samples
4.2. Prospects
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AF | Antiferromagnetic |
| AFM | Atomic Force Microscopy |
| DFT | Density Functional Theory |
| DMI | Dzyaloshinskii–Moriya interaction |
| FPLAPW | Full Potential Linearized Augmented Plane-Wave |
| IP | In-plane |
| LSDA | Local Spin Density Approach |
| MAE | Magnetic Anisotropy Energy |
| MFM | Magnetic Force Microscopy |
| OOP | Out-of-plane |
| PMA | Perpendicular Magnetic Anisotropy |
| RE | Rare Earth |
| SkHE | Skyrmion Hall Effect |
| SQUID | Superconducting Quantum Interference Device |
| STT | Spin Transfer Torque |
| TM | Transition Metal |
| UHV | Ultra-High-Vacuum |
| VSM | Vibrating Sample Magnetometer |
References
- Fert, A. The present and the future of spintronics. Thin Solid Films 2008, 517, 2–5. [Google Scholar] [CrossRef]
- Mitchell Waldrop, M. The chips are down for Moore’s law. Nature 2016, 530, 144. [Google Scholar] [CrossRef] [PubMed]
- Jungwirth, T.; Marti, X.; Wadley, P.; Wunderlich, J. Antiferromagnetic spintronics. Nat. Nanotechnol. 2016, 11, 231–241. [Google Scholar] [CrossRef]
- Fert, A.; Cros, V.; Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 2013, 8, 152–156. [Google Scholar] [CrossRef]
- Grollier, J.; Querlioz, D.; Camsari, K.Y.; Everschor-Sitte, K.; Fukami, S.; Stiles, M.D. Neuromorphic Spintronics. Nat. Electron. 2020, 3, 360–370. [Google Scholar] [CrossRef] [PubMed]
- Psaroudaki, C.; Panagopoulos, C. Skyrmion Qubits: A New Class of Quantum Logic Elements Based on Nanoscale Magnetization. Phys. Rev. Lett. 2021, 127, 067201. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Zhang, X.; Liu, X.; Zhou, Y.; Ezawa, M. Universal Quantum Computation Based on Nanoscale Skyrmion Helicity Qubits in Frustrated Magnets. Phys. Rev. Lett. 2023, 130, 106701. [Google Scholar] [CrossRef]
- Xia, J.; Zhang, X.; Liu, X.; Zhou, Y.; Ezawa, M. Qubits based on merons in magnetic nanodisks. Commun. Mater. 2022, 3, 88. [Google Scholar] [CrossRef]
- One, R.-A.; Mican, S.; Cimpoeșu, A.; Joldos, M.; Tetean, R.; Tiusan, C.V. Micromagnetic Design of Skyrmionic Materials and Chiral Magnetic Configurations in Patterned Nanostructures for Neuromorphic and Qubit Applications. Nanomaterials 2022, 12, 4411. [Google Scholar] [CrossRef]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 2013, 8, 899–911. [Google Scholar] [CrossRef]
- Legrand, W.; Maccariello, D.; Ajejas, F.; Collin, S.; Vecchiola, A.; Bouzehouane, K.; Reyren, N.; Cros, V.; Fert, A. Room-temperature stabilization of antiferromagnetic skyrmions in synthetic antiferromagnets. Nat. Mater. 2020, 19, 34–42. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Lott, D.; Philippi-Kobs, A.; Weigand, M.; Luo, C.; Radu, F. Observation of compact ferrimagnetic skyrmions in DyCo3 film. Nanoscale 2020, 12, 18137–18143. [Google Scholar] [CrossRef]
- Kim, S.K.; Beach, G.S.D.; Lee, K.J.; Ono, T.; Rasing, T.; Yang, H. Ferrimagnetic spintronics. Nat. Mater. 2022, 21, 24–34. [Google Scholar] [CrossRef]
- Mangin, S.; Gottwald, M.; Lambert, C.H.; Steil, D.; Uhlíř, V.; Pang, L.; Hehn, M.; Alebrand, S.; Cinchetti, M.; Malinowski, G.; et al. Engineered materials for all-optical helicity-dependent magnetic switching. Nat. Mater. 2014, 13, 286–292. [Google Scholar] [CrossRef] [PubMed]
- Woo, S.; Song, K.M.; Zhang, X.; Zhou, Y.; Ezawa, M.; Liu, X.; Finizio, S.; Raabe, J.; Lee, N.J.; Kim, S.I.; et al. Current-driven dynamics and inhibition of the skyrmion Hall effect of ferrimagnetic skyrmions in GdFeCo films. Nat. Commun. 2018, 9, 959. [Google Scholar] [CrossRef]
- Hirata, Y.; Kim, D.H.; Kim, S.K.; Lee, D.K.; Oh, S.H.; Kim, D.Y.; Nishimura, T.; Okuno, T.; Futakawa, Y.; Yoshikawa, H.; et al. Vanishing skyrmion Hall effect at the angular momentum compensation temperature of a ferrrimagnet. Nat. Nanotechnol. 2019, 14, 232. [Google Scholar] [CrossRef]
- Ye, C.; Li, L.L.; Shu, Y.; Li, Q.-R.; Xia, J.; Hou, Z.-P.; Zhou, Y.; Liu, X.X.; Yang, Y.Y.; Zhao, G.-P. Generation and manipulation of skyrmions and other topological spin structures with rare metals. Rare Met. 2022, 41, 2200–2216. [Google Scholar] [CrossRef]
- Chen, K.; Lott, D.; Radu, F.; Choueikani, F.; Otero, E.; Ohresser, P. Observation of an atomic exchange bias effect in DyCo4 film. Sci. Rep. 2015, 5, 18377. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Lott, D.; Radu, F.; Choueikani, F.; Otero, E.; Ohresser, P. Temperature-dependent magnetic properties of ferrimagnetic DyCo3 alloy films. Phys. Rev. B 2015, 91, 024409. [Google Scholar] [CrossRef]
- Kim, D.H.; Haruta, M.; Ko, H.W.; Go, G.; Park, H.J.; Nishimura, T.; Kim, D.Y.; Okuno, T.; Hirata, Y.; Futakawa, Y.; et al. Bulk Dzyaloshinskii–Moriya interaction in amorphous ferrimagnetic alloys. Nat. Mater. 2019, 18, 685–690. [Google Scholar] [CrossRef]
- Streubel, R.; Lambert, C.-H.; Kent, N.; Ercius, P.; N’Diaye, A.T.; Ophus, C.; Salahuddin, S.; Fischer, P. Experimental evidence of chiral ferrimagnetism in amorphous GdCo films. Adv. Mat. 2018, 30, 1800199. [Google Scholar] [CrossRef] [PubMed]
- Fert, A. Magnetic and transport properties of metallic multilayers. Mater. Sci. Forum. 1991, 59–60, 439–480. [Google Scholar] [CrossRef]
- Zhou, H.-A.; Liu, J.; Wang, Z.; Zhang, Q.; Xu, T.; Dong, Y.; Zhao, L.; Je, S.-G.; Im, M.-Y.; Xu, K.; et al. Rare-Earth Permanent Magnet SmCo5 for Chiral Interfacial Spin-Orbitronics. Adv. Funct. Mater. 2021, 31, 2104426. [Google Scholar] [CrossRef]
- Xiao, Y.; Morvan, F.J.; He, A.N.; Wang, M.K.; Luo, H.B.; Jiao, R.B.; Xia, W.X.; Zhao, G.P.; Liu, J.P. Spin-reorientation transition induced magnetic skyrmion in Nd2Fe14B magnet. Appl. Phys. Lett. 2020, 117, 132402. [Google Scholar] [CrossRef]
- Yakinthos, J.K.; Chappert, J. Crystal field and Mossbauer spectroscopy of the intermetallic compound DyCo3. Solid State Commun. 1975, 17, 979–981. [Google Scholar] [CrossRef]
- Coey, J.M.D.; Chappert, J.; Rebouillat, J.P.; Wang, T.S. Magnetic Structure of an Amorphous Rare-Earth Transition-Metal Alloy. Phys. Rev. Lett. 1976, 36, 1061. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B Condens. Matter 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Aldarawsheh, A.; Sallermann, M.; Abusaa, M.; Lounis, S. Current-driven dynamics of antiferromagnetic skyrmions: From skyrmion Hall effects to hybrid inter-skyrmion scattering. Npj Spintron. 2024, 2, 41. [Google Scholar] [CrossRef]
- Correia, M.V.; Velásquez, J.C.P.; de Souza Silva, C.C. Stability and dynamics of synthetic antiferromagnetic skyrmions in asymmetric multilayers. Phys. Rev. B 2024, 110, 094430. [Google Scholar] [CrossRef]
- Pham, V.T.; Sisodia, N.; Di Manici, I.; Urrestarazu-Larrañaga, J.; Bairagi, K.; Pelloux-Prayer, J.; Guedas, R.; Buda-Prejbeanu, L.D.; Auffret, S.; Locatelli, A.; et al. Fast current-induced skyrmion motion in synthetic antiferromagnets. Science 2024, 384, 307–312. [Google Scholar] [CrossRef]
- Shen, L.; Xia, J.; Zhao, G.; Zhang, X.; Ezawa, M.; Tretiakov, O.A.; Liu, X.; Zhou, Y. Spin torque nano-oscillators based on antiferromagnetic skyrmions. Appl. Phys. Lett. 2019, 114, 042402. [Google Scholar] [CrossRef]
- Gerasimchuk, V.S.; Gorobets, Y.I.; Gorobets, O.Y.; Gerasimchuk, I.V. Spatial antiferromagnetic spin texture as a nano-oscillator. Sci. Rep. 2023, 13, 6613. [Google Scholar] [CrossRef]
- Cullity, B.D.; Graham, C.D. Introduction to Magnetic Materials; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2008; Chapter 9; pp. 275–333. [Google Scholar] [CrossRef]
- Thiele, A.A. Theory of the Static Stability of Cylindrical Domains in Uniaxial Platelets. J. Appl. Phys. 1970, 41, 1139–1145. [Google Scholar] [CrossRef]
- Chen, D.-X.; Prados, C.; Pardo, E.; Sanchez, A.; Hernando, A. Transverse demagnetizing factors of long rectangular bars: I. Analytical expressions for extreme values of susceptibility. J. Appl. Phys. 2002, 91, 5254–5259. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Tran, F.; Laskowski, R.; Madsen, G.K.H.; Marks, L.D. WIEN2k: An APW+lo program for calculating the properties of solids. J. Chem. Phys. 2020, 152, 074101. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, D.-S.; Wu, R.; Freeman, A. Validity of the force theorem for magnetocrystalline anisotropy. J. Magn. Magn. Mater. 1996, 159, 337–341. [Google Scholar] [CrossRef]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Van Waeyenberge, B. The design and verification of MuMax3. AIP Adv. 2014, 4, 107133. [Google Scholar] [CrossRef]
- Bruno, P. Tight-binding approach to the orbital magnetic moment and magnetocrystalline anisotropy of transition-metal monolayers. Phys. Rev. B 1989, 39, 865–868. [Google Scholar] [CrossRef]
- Jin, L.; James, W.J.; Lemaire, R.; Rhyne, J. Magnetic structure of DyCo3. J. Less Common. Met. 1987, 130, 259. [Google Scholar] [CrossRef]
- Lemaire, R.; Pauthenet, R.; Schweizer, J.; Silvera, I.S. Proprietes Magnetiques Des Alliages De Formule Tco3, Dans Laquelle T Designe L’yttrium Ou Une Terre Rare. J. Phys. Chem. Solids 1967, 28, 2471. [Google Scholar] [CrossRef]
- Malik, S.K.; Boltich, E.B.; Wallace, W.E. Magnetization studies on ErCo3-hydride and TmCo3-hydride. Solid State Commun. 1981, 37, 329. [Google Scholar] [CrossRef]
- Narasimhan, K.S.V.L.; Butera, R.A.; Craig, R.S.J. Magnetic properties of RT3−x′Nix compounds (R = Dy or Ho and T′ = Fe or Co). Appl. Phys. 1973, 44, 879. [Google Scholar] [CrossRef]
- Burzo, E.; Chelkowski, L.; Kirchmayr, H.R. Compounds Between Rare Earth Elements and 3d, 4d, or 5d Elements, Landolt Börnstein Handbuch; Springer: Berlin, Germany, 1990; Volume 19. [Google Scholar] [CrossRef]
- Buschow, K.H.J. Intermetallic compounds of rare-earth and 3d transition metals. Rep. Prog. Phys. 1977, 40, 1179–1256. [Google Scholar] [CrossRef]
- Hassan, M.; Koraltan, S.; Ullrich, A.; Bruckner, F.; Serha, R.O.; Levchenko, K.V.; Varvaro, G.; Kiselev, N.S.; Heigl, M.; Abert, C.; et al. Dipolar skyrmions and antiskyrmions of arbitrary topological charge at room temperature. Nat. Phys. 2024, 20, 615–622. [Google Scholar] [CrossRef] [PubMed]
- Hehn, M.; Ounadjela, K.; Bucher, J.-P.; Rousseaux, F.; Decanini, D.; Bartenlian, B.; Chappert, C. Nanoscale Magnetic Domains in Mesoscopic Magnets. Science 1996, 272, 1782–1785. [Google Scholar] [CrossRef]
- Luo, C.; Chen, K.; Ukleev, V.; Wintz, S.; Weigand, M.; Abrudan, R.-M.; Prokeš, K.; Radu, F. Direct observation of Néel-type skyrmions and domain walls in a ferrimagnetic DyCo3 thin film. Commun. Phys. 2023, 6, 218. [Google Scholar] [CrossRef]
- Yang, H.; Liang, J.; Cui, Q. First-principles calculations for Dzyaloshinskii–Moriya interaction. Nat. Rev. Phys. 2023, 5, 43–61. [Google Scholar] [CrossRef]
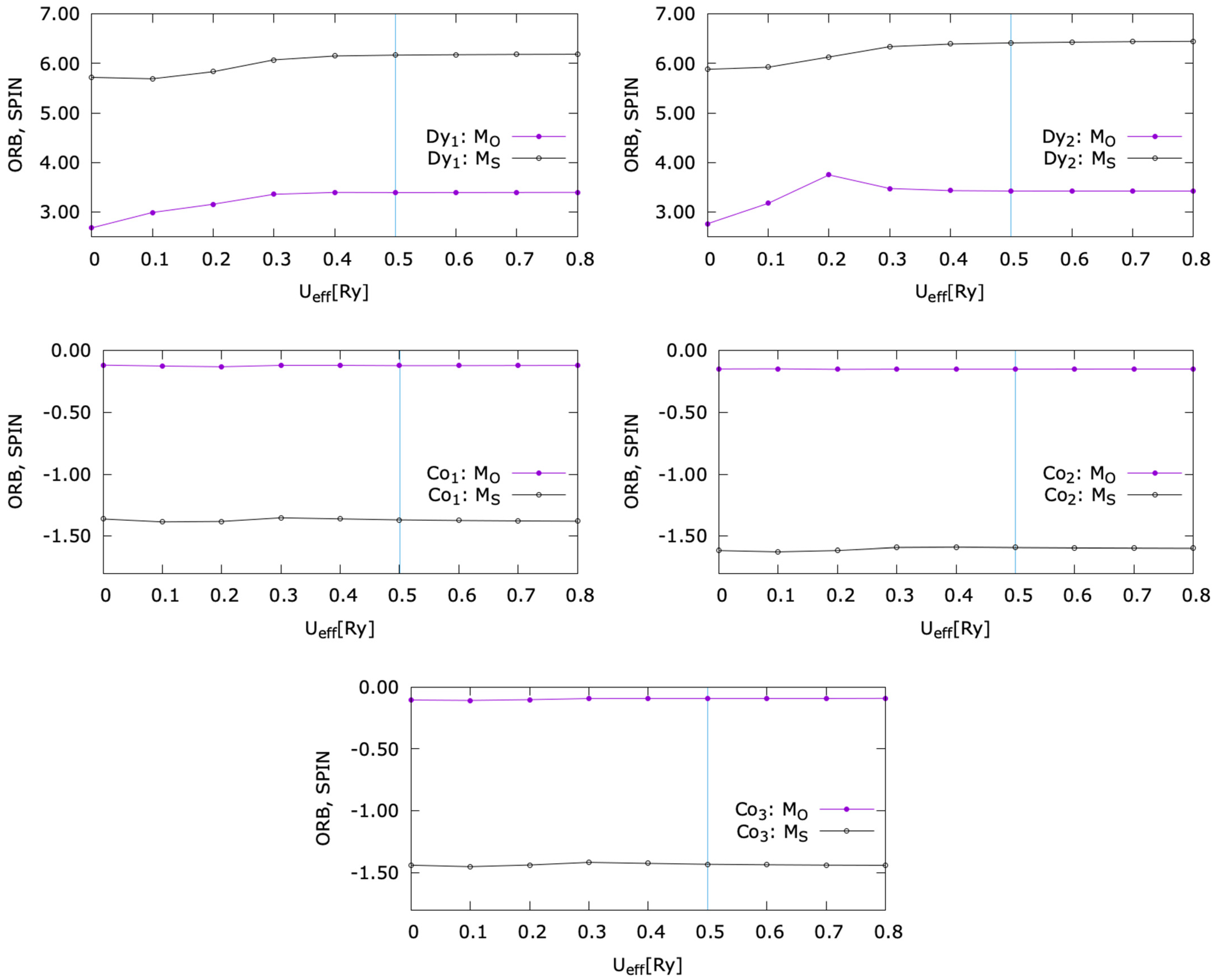



| ORB [μB] | SPIN [μB] | ORB [μB] | SPIN [μB] | ORB [μB] | SPIN [μB] | ORB [μB] | SPIN [μB] | ORB [μB] | SPIN [μB] |
|---|---|---|---|---|---|---|---|---|---|
| 3.54 | 6.07 | 3.56 | 6.42 | −0.12 | −1.37 | −0.15 | −1.59 | −0.09 | −1.43 |
| 9.61 | 9.98 | −1.49 | −1.74 | −1.52 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hategan, R.G.; Aldea, A.; Miclea, R.D.; Hirian, R.; Botiz, I.; Dudric, R.; Rasabathina, L.; Hellwig, O.; Salvan, G.; Zahn, D.R.T.; et al. Magnetic, Electronic Structure and Micromagnetic Properties of Ferrimagnetic DyCo3 as a Platform for Ferrimagnetic Skyrmions. Nanomaterials 2025, 15, 606. https://doi.org/10.3390/nano15080606
Hategan RG, Aldea A, Miclea RD, Hirian R, Botiz I, Dudric R, Rasabathina L, Hellwig O, Salvan G, Zahn DRT, et al. Magnetic, Electronic Structure and Micromagnetic Properties of Ferrimagnetic DyCo3 as a Platform for Ferrimagnetic Skyrmions. Nanomaterials. 2025; 15(8):606. https://doi.org/10.3390/nano15080606
Chicago/Turabian StyleHategan, Radu George, Andrei Aldea, Razvan Dan Miclea, Razvan Hirian, Ioan Botiz, Roxana Dudric, Lokesh Rasabathina, Olav Hellwig, Georgeta Salvan, Dietrich R. T. Zahn, and et al. 2025. "Magnetic, Electronic Structure and Micromagnetic Properties of Ferrimagnetic DyCo3 as a Platform for Ferrimagnetic Skyrmions" Nanomaterials 15, no. 8: 606. https://doi.org/10.3390/nano15080606
APA StyleHategan, R. G., Aldea, A., Miclea, R. D., Hirian, R., Botiz, I., Dudric, R., Rasabathina, L., Hellwig, O., Salvan, G., Zahn, D. R. T., Tetean, R., & Tiusan, C. (2025). Magnetic, Electronic Structure and Micromagnetic Properties of Ferrimagnetic DyCo3 as a Platform for Ferrimagnetic Skyrmions. Nanomaterials, 15(8), 606. https://doi.org/10.3390/nano15080606








