Surface Acoustic Wave (SAW) Sensors for Hip Implant: A Numerical and Computational Feasibility Investigation Using Finite Element Methods
Abstract
1. Introduction
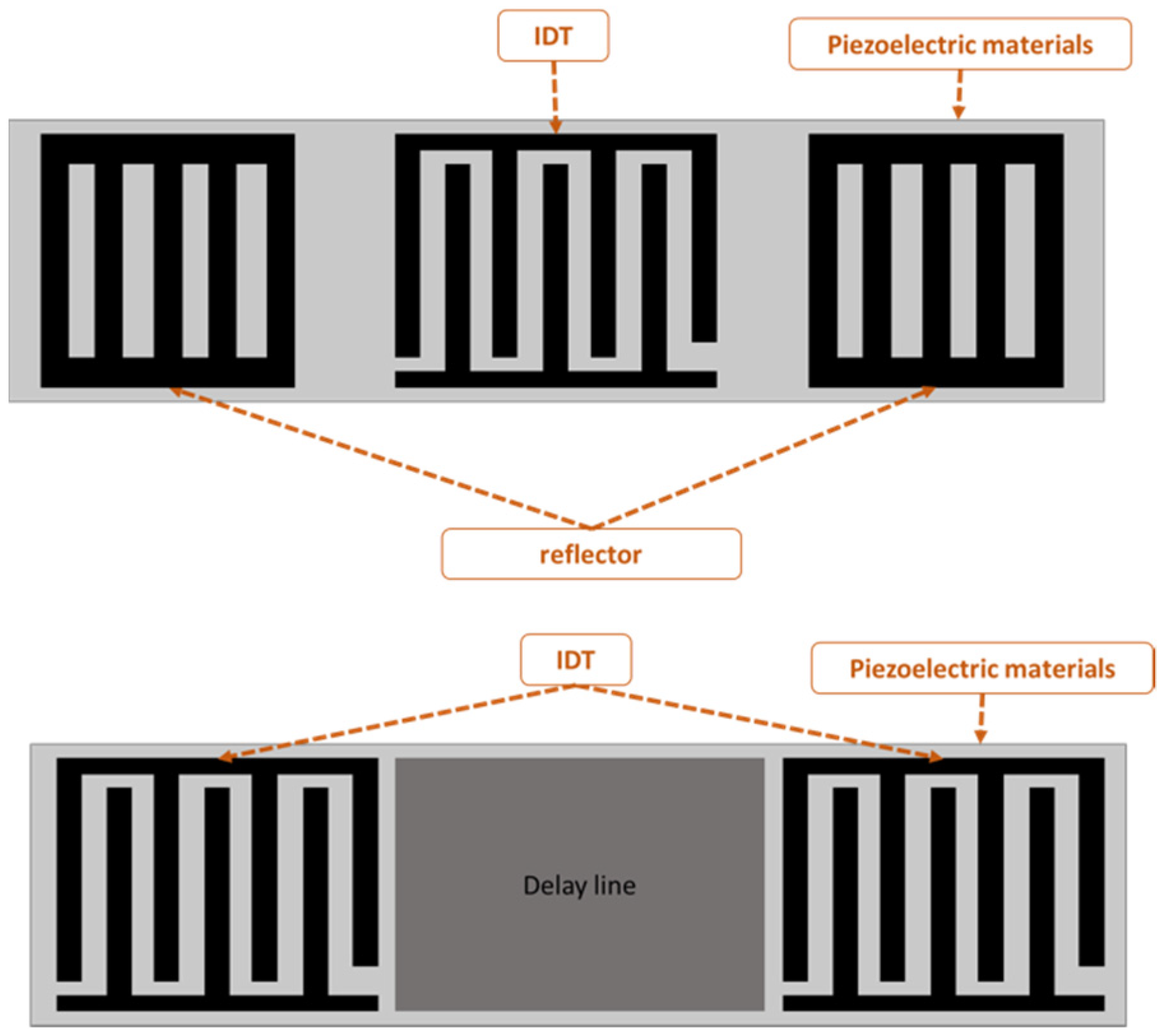
2. Numerical Analysis of a SAW Sensor
Impulse Response
3. Finite Element Analysis (FEA) of SAW Sensor
3.1. Electrical Potential of SAW Sensor
3.2. Modal Analysis of SAW Sensor
3.3. Frequency Analysis
3.4. Stationary Analysis of SAW Sensor
3.5. Performance Extension for Cantilever
4. Finite Element Analysis (FEA) of Hip Implant
4.1. Simulation Setup
4.2. Sensitivity Analysis
4.3. Results of FEA of Hip Implant
4.4. Integration of Hip Implant with SAW Sensor
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ben-Shlomo, Y.; Blom, A.; Boulton, C.; Brittain, R.; Clark, E.; Dawson-Bowling, S.; Deere, K.; Esler, C.; Espinoza, O.; Goldberg, A.; et al. The National Joint Registry 18th Annual Report 2021; National Joint Registry: London, UK, 2021. [Google Scholar]
- Baumann, A.P.; O’Neill, C.; Owens, M.C.; Weber, S.C.; Sivan, S.; D’Amico, R.; Carmody, S.; Bini, S.; Sawyer, A.J.; Lotz, J.C.; et al. FDA Public Workshop: Orthopaedic Sensing, Measuring, and Advanced Reporting Technology (SMART) Devices. J. Orthop. Res. 2021, 39, 22–29. [Google Scholar] [CrossRef] [PubMed]
- Temmerman, O.P.P.; Raijmakers, P.G.H.M.; Berkhof, J.; Hoekstra, O.S.; Teule, G.J.J.; Heyligers, I.C. Accuracy of Diagnostic Imaging Techniques in the Diagnosis of Aseptic Loosening of the Femoral Component of a Hip Prosthesis. J. Bone Jt. Surg. Br. 2005, 87, 781–785. [Google Scholar] [CrossRef] [PubMed]
- Temmerman, O.P.; Raijmakers, P.G.; David, E.F.; Pijpers, R.; Molenaar, M.A.; Hoekstra, O.S.; Berkhof, J.; Manoliu, R.A.; Teule, G.J.; Heyligers, I.C. A Comparison of Radiographic and Scintigraphic Techniques to Assess Aseptic Loosening of the Acetabular Component in a Total Hip Replacement. J. Bone Jt. Surg. Am. 2004, 86, 2456–2463. [Google Scholar] [CrossRef] [PubMed]
- Ives, L.; Pace, A.; Bor, F.; Jing, Q.; Wade, T.; Cama, J.; Khanduja, V.; Kar-Narayan, S. Conformable and robust microfluidic force sensors to enable precision joint replacement surgery. Mater. Des. 2022, 219, 110747. [Google Scholar] [CrossRef]
- Xie, B.; Ding, F.; Dong, Z.; Shang, H.; Huang, D.; Gu, H. FEM analysis of piezoelectric film as IDT on the diamond substrate to enhance the quality factor of SAW devices. Diam. Relat. Mater. 2019, 102, 107659. [Google Scholar] [CrossRef]
- Liu, X.-C.; Li, K.; Xuan, X.-W.; Cao, Y.; Teng, J.-F. SAW filter manufacture and piezoelectric materials evaluation based on printed electronics technology. Optoelectron. Lett. 2014, 10, 340–342. [Google Scholar] [CrossRef]
- Hamsch, M.; Hoffmann, R.; Buff, W.; Binhack, M.; Klett, S. An interrogation unit for passive wireless SAW sensors based on Fourier transform. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2004, 51, 1449–1456. [Google Scholar] [CrossRef] [PubMed]
- Stoney, R.; O’Donnell, G.E.; Geraghty, D. Dynamic wireless passive strain measurement in CNC turning using surface acoustic wave sensors. Int. J. Adv. Manuf. Technol. 2013, 69, 1421–1430. [Google Scholar] [CrossRef]
- Zalnezhad, E.; Musharavati, F.; Chen, T.; Jaber, F.; Uzun, K.; Chowdhury, M.E.H.; Khandakar, A.; Liu, J.; Bae, S. Tribo-mechanical properties evaluation of HA/TiO2/CNT nanocomposite. Sci. Rep. 2021, 11, 1867. [Google Scholar] [CrossRef] [PubMed]
- Nezhad, E.Z.; Qu, X.; Musharavati, F.; Jaber, F.; Appleford, M.R.; Bae, S.; Uzun, K.; Struthers, M.; Chowdhury, M.E.; Khandakar, A. Effects of titanium and carbon nanotubes on nano/micromechanical properties of HA/TNT/CNT nanocomposites. Appl. Surf. Sci. 2021, 538, 148123. [Google Scholar] [CrossRef]
- Abughanam, N.; Gaben, S.S.M.; Chowdhury, M.E.H.; Khandakar, A. Investigating the effect of materials and structures for negative pressure ventilators suitable for pandemic situation. Emergent Mater. 2021, 4, 313–327. [Google Scholar] [CrossRef] [PubMed]
- Mujahid, A.; Dickert, F.L. Surface Acoustic Wave (SAW) for Chemical Sensing Applications of Recognition Layers. Sensors 2017, 17, 2716. [Google Scholar] [CrossRef] [PubMed]
- Reindl, L.; Shrena, I. Wireless measurement of temperature using surface acoustic waves sensors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2004, 51, 1457–1463. [Google Scholar] [CrossRef] [PubMed]
- Le, X.; Liu, Y.; Peng, L.; Pang, J.; Xu, Z.; Gao, C.; Xie, J. Surface acoustic wave humidity sensors based on uniform and thickness controllable graphene oxide thin films formed by surface tension. Microsyst. Nanoeng. 2019, 5, 36. [Google Scholar] [CrossRef] [PubMed]
- Mandal, D.; Banerjee, S. Surface Acoustic Wave (SAW) Sensors: Physics, Materials, and Applications. Sensors 2022, 22, 820. [Google Scholar] [CrossRef] [PubMed]
- Qiblawey, Y.; Chowdhury, M.E.H.; Musharavati, F.; Zalnezhad, E.; Khandakar, A.; Islam, M.T. Instrumented Hip Implant: A Review. IEEE Sens. J. 2020, 21, 7179–7194. [Google Scholar] [CrossRef]
- Ren, L.; Yu, K.; Tan, Y. Applications and Advances of Magnetoelastic Sensors in Biomedical Engineering: A Review. Materials 2019, 12, 1135. [Google Scholar] [CrossRef] [PubMed]
- Zou, L.; McLeod, C.; Bahmanyar, M.R. Wireless Interrogation of Implantable SAW Sensors. IEEE Trans. Biomed. Eng. 2020, 67, 1409–1417. [Google Scholar] [CrossRef] [PubMed]
- Bao, Z.; Hara, M.; Kuwano, H. Highly Sensitive Strain Sensors Using Surface Acoustic Wave on Aluminum Nitride Thin Film for Wireless Sensor Networks. In Proceedings of the 2015 Transducers—2015 18th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Anchorage, AK, USA, 21–25 June 2015; pp. 1239–1242. [Google Scholar]
- Ren, J.; Anurakparadorn, K.; Gu, H.; Zhao, M.; Wei, X. Design of SAW sensor for longitudinal strain measurement with improved sensitivity. Microsyst. Technol. 2018, 25, 351–359. [Google Scholar] [CrossRef]
- Gopalsami, N.; Osorio, I.; Kulikov, S.; Buyko, S.; Martynov, A.; Raptis, A.C. SAW Microsensor Brain Implant for Prediction and Monitoring of Seizures. IEEE Sens. J. 2007, 7, 977–982. [Google Scholar] [CrossRef]
- Konno, R.; Mitsui, M.; Kuwano, H.; Nagasawa, S.; Sano, K.; Hayasaka, J. A Highly Sensitive Strain Sensor Using Surface Acoustic Wave and Its Evaluation for Wireless Battery-Less Sensor Network. In Proceedings of the SENSORS, 2007 IEEE, Atlanta, GA, USA, 28–31 October 2007; pp. 796–799. [Google Scholar]
- Fischerauer, A.; Schwarzmuller, C.; Fischerauer, G. Experimental investigation of a novel SAW strain sensor with inbuilt temperature measurement capability. In Proceedings of the 2013 IEEE International Ultrasonics Symposium (IUS), Prague, Czech Republic, 21–25 July 2013; pp. 1949–1952. [Google Scholar] [CrossRef]
- Bergmann, G.; Graichen, F.; Dymke, J.; Rohlmann, A.; Duda, G.N.; Damm, P. High-Tech Hip Implant for Wireless Temperature Measurements In Vivo. PLoS ONE 2012, 7, e43489. [Google Scholar] [CrossRef] [PubMed]
- Rodgers, G.W.; Welsh, R.; King, L.J.; FitzPatrick, A.J.; Woodfield, T.B.; Hooper, G.J. Signal processing and event detection of hip implant acoustic emissions. Control. Eng. Pract. 2017, 58, 287–297. [Google Scholar] [CrossRef]
- Mavrogordato, M.; Taylor, M.; Taylor, A.; Browne, M. Real time monitoring of progressive damage during loading of a simplified total hip stem construct using embedded acoustic emission sensors. Med. Eng. Phys. 2011, 33, 395–406. [Google Scholar] [CrossRef] [PubMed]
- Marschner, U.; Grätz, H.; Jettkant, B.; Ruwisch, D.; Woldt, G.; Fischer, W.-J.; Clasbrummel, B. Integration of a wireless lock-in measurement of hip prosthesis vibrations for loosening detection. Sens. Actuators A Phys. 2009, 156, 145–154. [Google Scholar] [CrossRef]
- Sauer, S.; Kirsten, S.; Storck, F.; Grätz, H.; Marschner, U.; Ruwisch, D.; Fischer, W.-J. A Medical Wireless Measurement System for Hip Prosthesis Loosening Detection Based on Vibration Analysis. Sens. Transducers J. 2013, 18, 134–144. [Google Scholar]
- Burton, A.R.; Sun, P.; Lynch, J.P. Bio-compatible wireless inductive thin-film strain sensor for monitoring the growth and strain response of bone in osseointegrated prostheses. Struct. Health Monit. 2019, 20, 749–767. [Google Scholar] [CrossRef]
- Ramachandran, R.A.; Lee, C.; Zhang, L.; H, S.M.; Bijukumar, D.; Pai, P.S.; Foucher, K.; Chi, S.-W.; Ozevin, D.; Mathew, M.T. Total hip replacement monitoring: Numerical models for the acoustic emission technique. Med. Biol. Eng. Comput. 2022, 60, 1497–1510. [Google Scholar] [CrossRef]
- Alshuhri, A.A.; Holsgrove, T.P.; Miles, A.W.; Cunningham, J.L. Non-invasive vibrometry-based diagnostic detection of acetabular cup loosening in total hip replacement (THR). Med. Eng. Phys. 2017, 48, 188–195. [Google Scholar] [CrossRef] [PubMed]
- Yousef, M.; Hafizh, M.; Sassi, S.; Adeli, G. Development of a Wearable Wireless Sensing Device for Characterization of Hand Tremors Through Vibration Frequency Analysis. J. Vib. Eng. Technol. 2022, 1–12. [Google Scholar] [CrossRef]
- Poon, C.C.Y.; Lo, B.P.L.; Yuce, M.R.; Alomainy, A.; Hao, Y. Body Sensor Networks: In the Era of Big Data and Beyond. IEEE Rev. Biomed. Eng. 2015, 8, 4–16. [Google Scholar] [CrossRef]
- Chávez, P.A.S.; Bonhomme, J.; Bellaredj, M.L.F.; Olive, L.; Beyssen, D.; Oudich, M.; Charette, P.G.; Sarry, F. Love Wave Sensor with High Penetration Depth for Potential Application in Cell Monitoring. Biosensors 2022, 12, 61. [Google Scholar] [CrossRef] [PubMed]
- Länge, K. Bulk and Surface Acoustic Wave Biosensors for Milk Analysis. Biosensors 2022, 12, 602. [Google Scholar] [CrossRef] [PubMed]
- Waqar, T.; Ersoy, S. Design and Analysis Comparison of Surface Acoustic Wave-Based Sensors for Fabrication Using Additive Manufacturing. J. Nanomater. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Hamandi, F.; Tsatalis, J.T.; Goswami, T. Retrospective Evaluation and Framework Development of Bone Anisotropic Material Behavior Compared with Elastic, Elastic-Plastic, and Hyper-Elastic Properties. Bioengineering 2022, 9, 9. [Google Scholar] [CrossRef] [PubMed]
- Merola, M.; Affatato, S. Materials for Hip Prostheses: A Review of Wear and Loading Considerations. Materials 2019, 12, 495. [Google Scholar] [CrossRef] [PubMed]
- Grimal, Q.; Laugier, P. Quantitative Ultrasound Assessment of Cortical Bone Properties Beyond Bone Mineral Density. IRBM 2019, 40, 16–24. [Google Scholar] [CrossRef]
- Geng, W.; Zhao, C.; Xue, F.; Qiao, X.; He, J.; Xue, G.; Liu, Y.; Wei, H.; Bi, K.; Mei, L.; et al. Influence of Structural Parameters on Performance of SAW Resonators Based on 128° YX LiNbO3 Single Crystal. Nanomaterials 2022, 12, 2109. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. A Distributed Parameter Electromechanical Model for Cantilevered Piezoelectric Energy Harvesters. J. Vib. Acoust. 2008, 130, 041002. [Google Scholar] [CrossRef]
- Kuang, Y.; Zhu, M. Evaluation and validation of equivalent properties of macro fibre composites for piezoelectric transducer modelling. Compos. Part B Eng. 2019, 158, 189–197. [Google Scholar] [CrossRef]
- Muthalif, A.G.; Hafizh, M.; Renno, J.; Paurobally, M.R. An enhanced hybrid piezoelectric–electromagnetic energy harvester using dual-mass system for vortex-induced vibrations. J. Vib. Control 2021, 27, 2848–2861. [Google Scholar] [CrossRef]
- Soliman, M.; Chowdhury, M.E.H.; Islam, M.T.; Musharavati, F.; Nabil, M.; Hafizh, M.; Khandakar, A.; Mahmud, S.; Nezhad, E.Z.; Shuzan, N.I.; et al. A Review of Biomaterials and Associated Performance Metrics Analysis in Pre-Clinical Finite Element Model and in Implementation Stages for Total Hip Implant System. Polymers 2022, 14, 4308. [Google Scholar] [CrossRef] [PubMed]
- Chethan, K.N.; Bhat, S.; Zuber, M.; Shenoy, S. Finite Element Analysis of Different Hip Implant Designs along with Femur under Static Loading Conditions. J. Biomed. Phys. Eng. 2019, 9, 507–516. [Google Scholar] [CrossRef] [PubMed]
- Cyganik, Ł.; Binkowski, M.; Kokot, G.; Rusin, T.; Popik, P.; Bolechała, F.; Nowak, R.; Wróbel, Z.; John, A. Prediction of Young’s modulus of trabeculae in microscale using macro-scale’s relationships between bone density and mechanical properties. J. Mech. Behav. Biomed. Mater. 2014, 36, 120–134. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Isaksson, P.; Ferguson, S.J.; Persson, C. Young’s modulus of trabecular bone at the tissue level: A review. Acta Biomater. 2018, 78, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Safaei, M.; Sodano, H.A.; Anton, S.R. A review of energy harvesting using piezoelectric materials: State-of-the-art a decade later (2008–2018). Smart Mater. Struct. 2019, 28, 113001. [Google Scholar] [CrossRef]
- Lange, H.-E.; Bader, R.; Kluess, D. Design Study on Customised Piezoelectric Elements for Energy Harvesting in Total Hip Replacements. Energies 2021, 14, 3480. [Google Scholar] [CrossRef]
- Lange, H.-E.; Hohlfeld, D.; Bader, R.; Kluess, D. A piezoelectric energy harvesting concept for an energy-autonomous instrumented total hip replacement. Smart Mater. Struct. 2020, 29, 115051. [Google Scholar] [CrossRef]
- Graichen, F.; Arnold, R.; Rohlmann, A.; Bergmann, G. Implantable 9-Channel Telemetry System for In Vivo Load Measurements With Orthopedic Implants. IEEE Trans. Biomed. Eng. 2007, 54, 253–261. [Google Scholar] [CrossRef] [PubMed]
- Ruther, C.; Timm, U.; Fritsche, A.; Ewald, H.; Mittelmeier, W.; Bader, R.; Kluess, D. A New Approach for Diagnostic Investigation of Total Hip Replacement Loosening BT—Biomedical Engineering Systems and Technologies; Fred, A., Filipe, J., Gamboa, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 74–79. [Google Scholar]














| Parameter | Value |
|---|---|
| Operating frequency | 872 MHz |
| IDT finger pairs | 25 |
| Piezoelectric substance | Lithium niobate (LiNbO3) |
| Acoustic velocity in the medium | 3800 m/s |
| 0.053 | |
| Load resistance | 50 Ω |
| Electrode pair capacitance per unit length | 0.55 pf/cm |
| N | Bandwidth (MHz) | IDT Length (μm) |
|---|---|---|
| 25 | 69 | 54.4 |
| 50 | 35 | 108.9 |
| 75 | 23 | 163.4 |
| 100 | 17 | 217.8 |
| Material Properties | Cortical Bone | Titanium Alloy | Polyethene |
|---|---|---|---|
| Density (kg/m3) | 1700 | 4429 | 950 |
| Young’s Modulus (GPa) | 11 | 111 | 1.1 |
| Poisson’s Ratio | 0.25 | 0.339 | 0.42 |
| Ultimate Tensile Strength (MPa) | 100 | - | 33 |
| Ultimate Compressive Strength (MPa) | 100 | - | - |
| Mesh Resolution | Element Sizing (mm) | Element Count | Average Mesh Quality | Max. Stress (MPa) | Avg. Stress (MPa) |
|---|---|---|---|---|---|
| Mesh 1 | - | 3129 | 0.51 | 163.2 | 4.34 |
| Mesh 2 | - | 5133 | 0.64 | 283.5 | 6.42 |
| Mesh 3 | 2.80 | 16,947 | 0.76 | 304.3 | 8.76 |
| Mesh 4 | 2.45 | 21,099 | 0.76 | 308.7 | 9.02 |
| Mesh 5 | 2.00 | 31,728 | 0.76 | 298.1 | 8.96 |
| Mesh 6 | 1.70 | 43,188 | 0.77 | 328.1 | 9.14 |
| Mesh 7 | 1.40 | 67,677 | 0.77 | 358.9 | 9.22 |
| Loading Forces | Boundary Type | Simulated Scenario | Setup |
|---|---|---|---|
| 1270N Axial Load (Ball Head) 1.13N mm Torsional Load (Ball Head) | Hip implant fix bounded | Upper-body loading and leg extension | Figure 11a |
| 600N Axial Load (Body Shaft) | Ball head fix bounded | Lower-body loading | Figure 11b |
| 1270N Axial Load (Ball Head) 1.13N mm Torsional Load (Ball Head) | Femur tip fix bounded along medial condyle and lateral Condyle | Upper-body loading and leg extension | Figure 11c |
| Current Work (2022) | Lange & Kluess (2021) [50] | Lange et al. (2020) [51] | |
|---|---|---|---|
| Substrate Material | LiNbO3 | PZT Ceramic | |
| Piezoelectric Young’s Modulus (GPa) | 70 | 52.4 | |
| Maximum Voltage Output (V) | 17.88 | 7.64 * | 2.88 * |
| Reference | Monitoring Method | Implant Type | Operating Frequency |
|---|---|---|---|
| Bergmann et al. [25] | Temperature | Cementless | N/A |
| Graichen et al. [52] | Temperature and force | Cementless | 47 to 220 MHz |
| Marschner et al. [28] | Vibration | N/A | 125 KHz |
| Ruther et al. [53] | Vibration | N/A | N/A |
| Burton et al. [30] | Strain | N/A | 10 to 14 MHz |
| Rodgers et al. [26] | Acoustic Emission | Cement/Cementless | N/A |
| Current Work | SAW Sensor | Cementless | 872 MHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hafizh, M.; Soliman, M.M.; Qiblawey, Y.; Chowdhury, M.E.H.; Islam, M.T.; Musharavati, F.; Mahmud, S.; Khandakar, A.; Nabil, M.; Nezhad, E.Z. Surface Acoustic Wave (SAW) Sensors for Hip Implant: A Numerical and Computational Feasibility Investigation Using Finite Element Methods. Biosensors 2023, 13, 79. https://doi.org/10.3390/bios13010079
Hafizh M, Soliman MM, Qiblawey Y, Chowdhury MEH, Islam MT, Musharavati F, Mahmud S, Khandakar A, Nabil M, Nezhad EZ. Surface Acoustic Wave (SAW) Sensors for Hip Implant: A Numerical and Computational Feasibility Investigation Using Finite Element Methods. Biosensors. 2023; 13(1):79. https://doi.org/10.3390/bios13010079
Chicago/Turabian StyleHafizh, Muhammad, Md Mohiuddin Soliman, Yazan Qiblawey, Muhammad E. H. Chowdhury, Mohammad Tariqul Islam, Farayi Musharavati, Sakib Mahmud, Amith Khandakar, Mohammad Nabil, and Erfan Zal Nezhad. 2023. "Surface Acoustic Wave (SAW) Sensors for Hip Implant: A Numerical and Computational Feasibility Investigation Using Finite Element Methods" Biosensors 13, no. 1: 79. https://doi.org/10.3390/bios13010079
APA StyleHafizh, M., Soliman, M. M., Qiblawey, Y., Chowdhury, M. E. H., Islam, M. T., Musharavati, F., Mahmud, S., Khandakar, A., Nabil, M., & Nezhad, E. Z. (2023). Surface Acoustic Wave (SAW) Sensors for Hip Implant: A Numerical and Computational Feasibility Investigation Using Finite Element Methods. Biosensors, 13(1), 79. https://doi.org/10.3390/bios13010079








