Understanding the Mechanism of Bent DNA Amplifying Sensors Using All-Atom Molecular Dynamics Simulations
Abstract
:1. Introduction
2. Materials and Methods
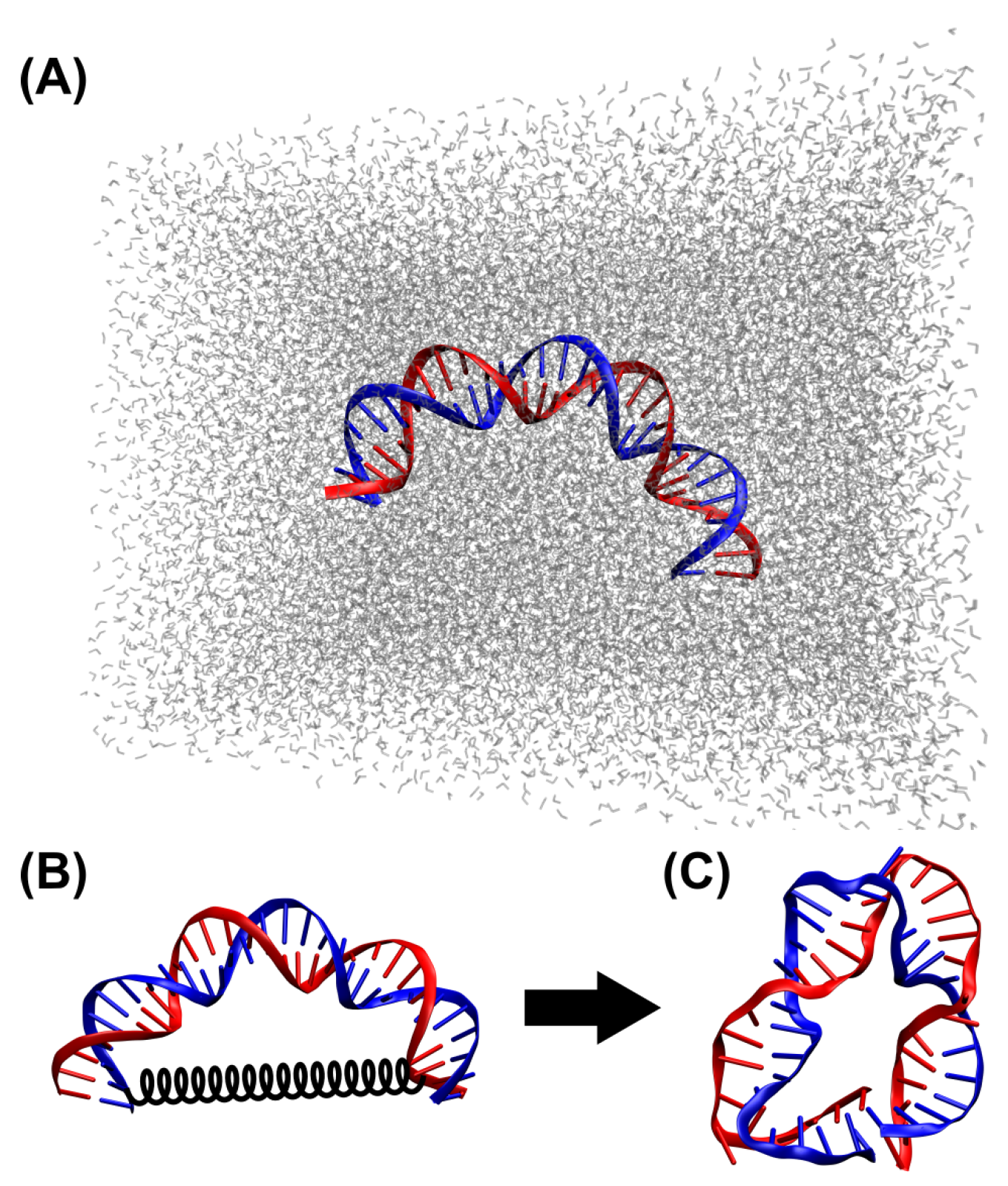
2.1. DNA Sequence and Initial Conformation for MD Simulations
2.2. MD Simulations
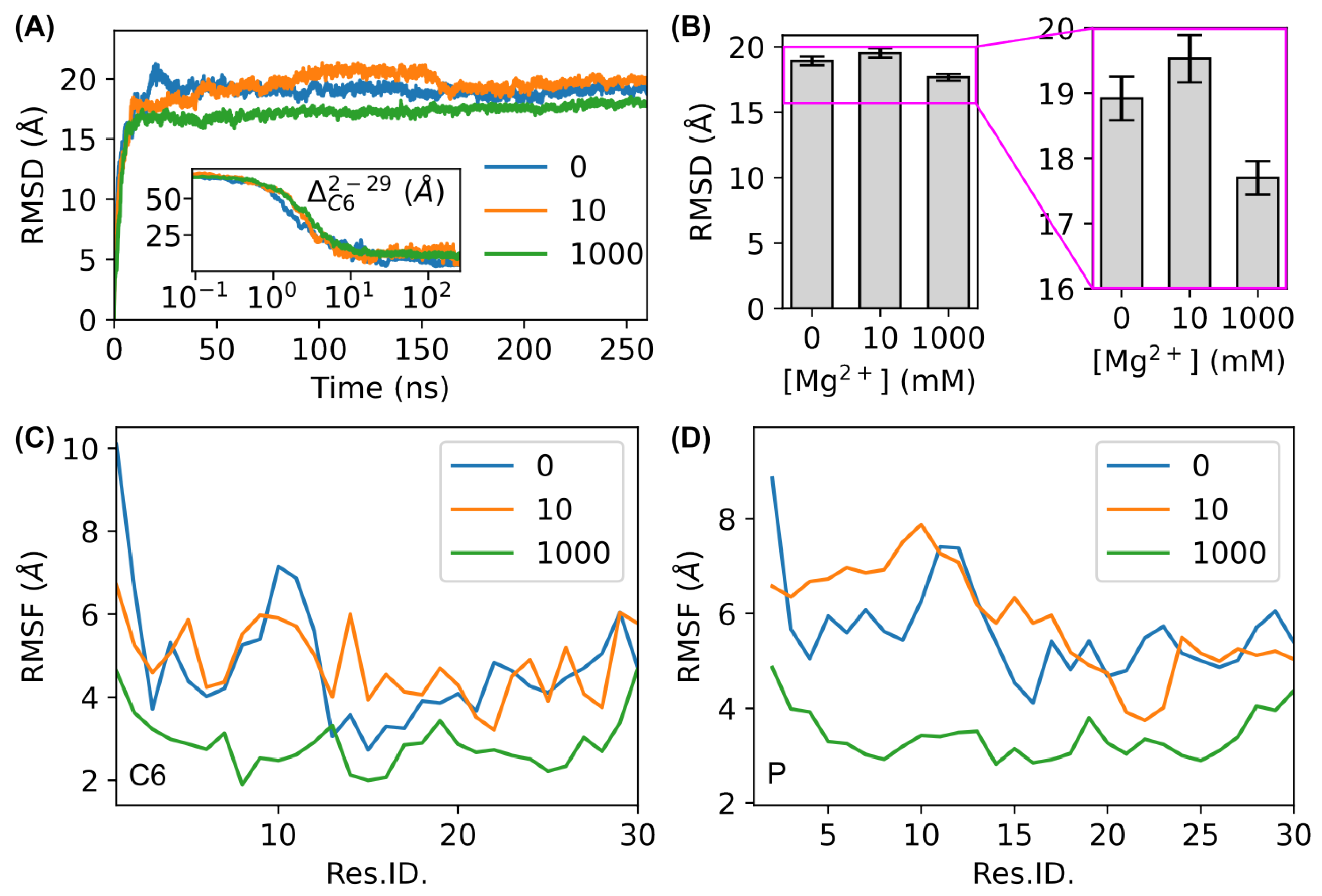
2.3. Trajectory Analysis
2.4. Melting Curve Experiments
2.5. FRET Measurements
3. Results
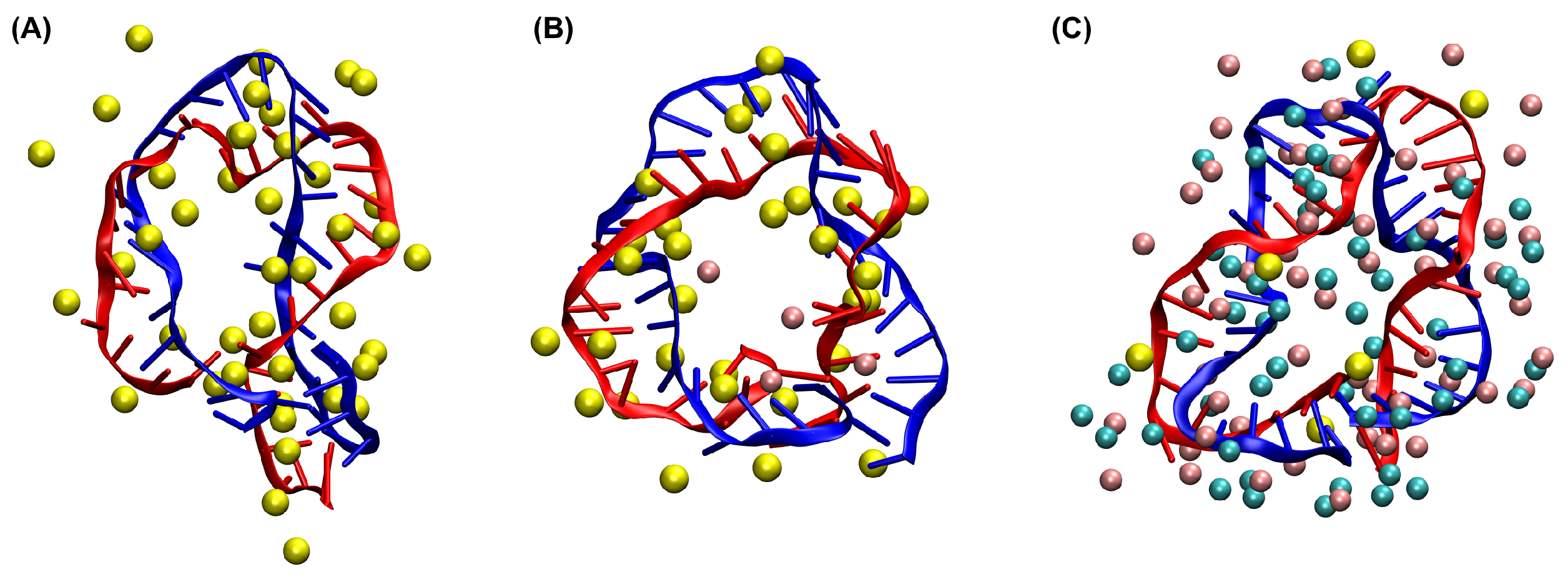
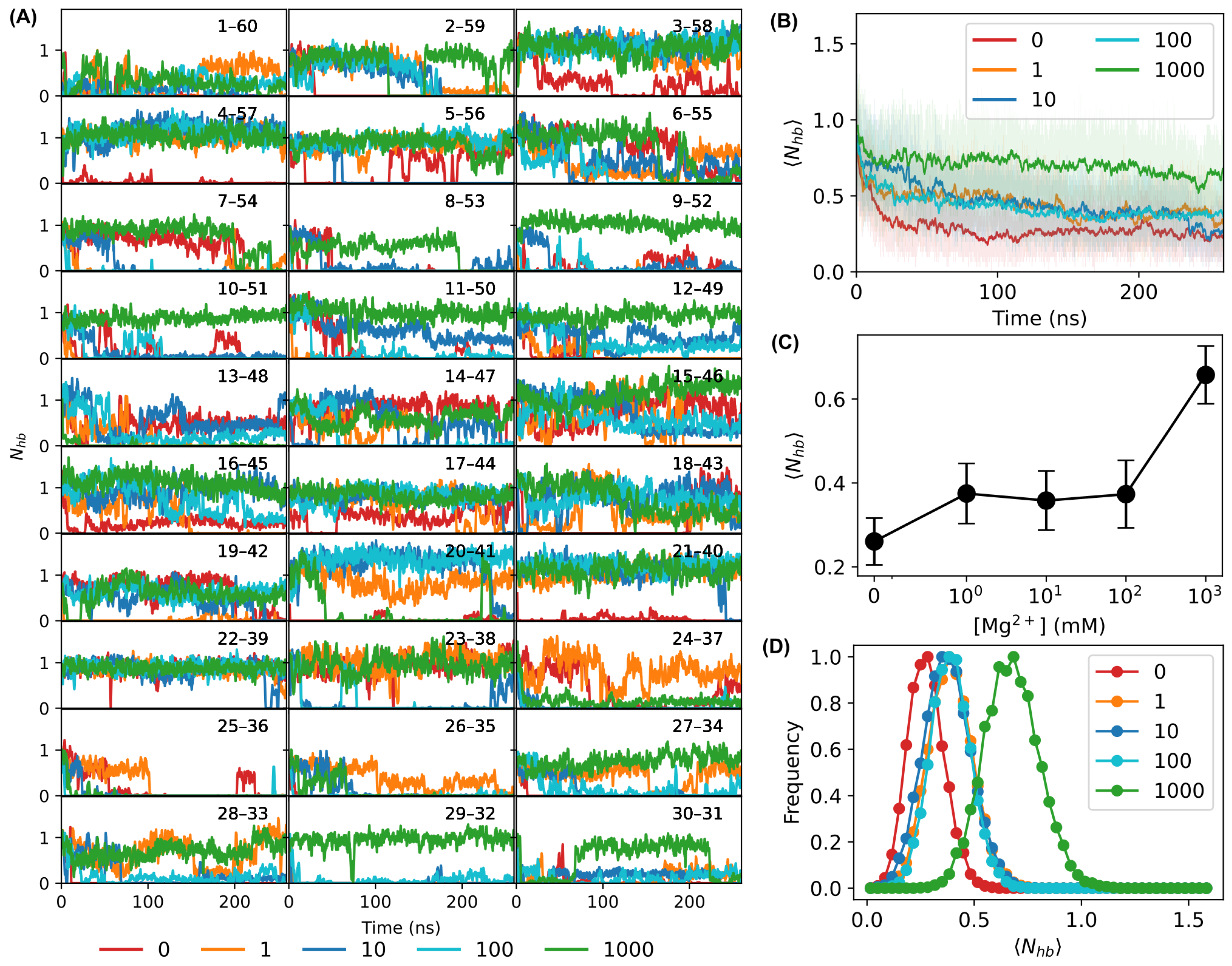
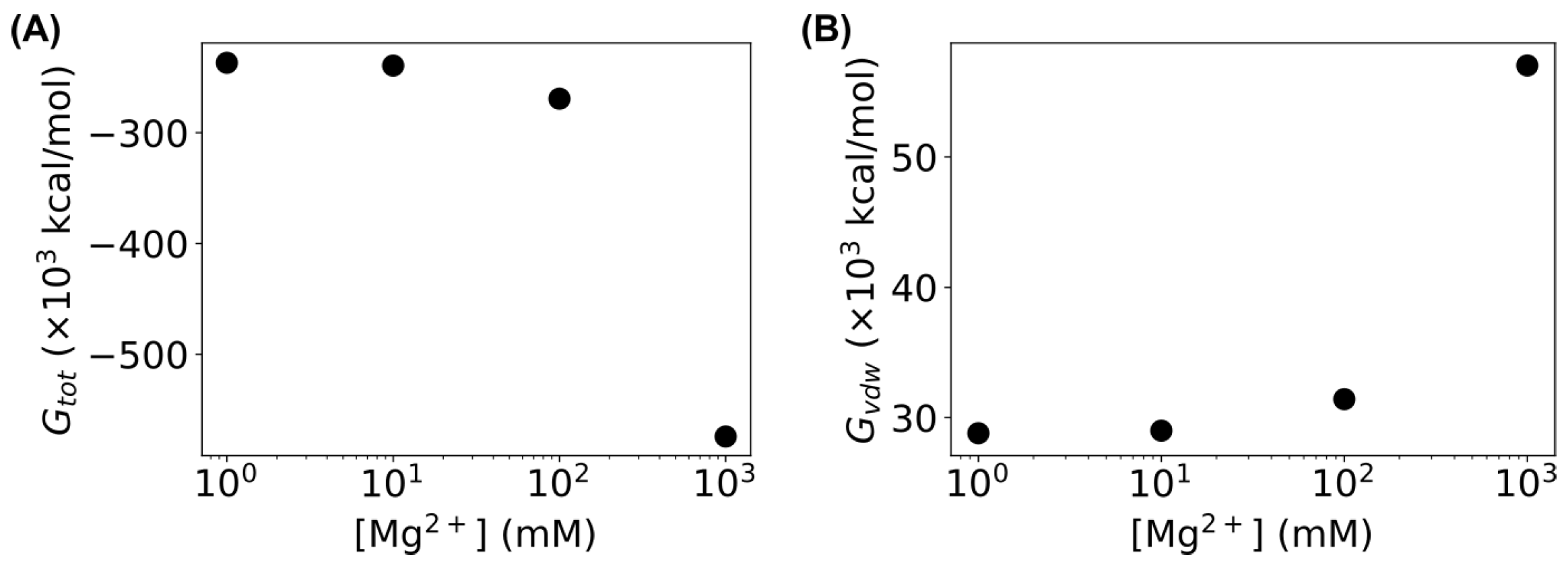
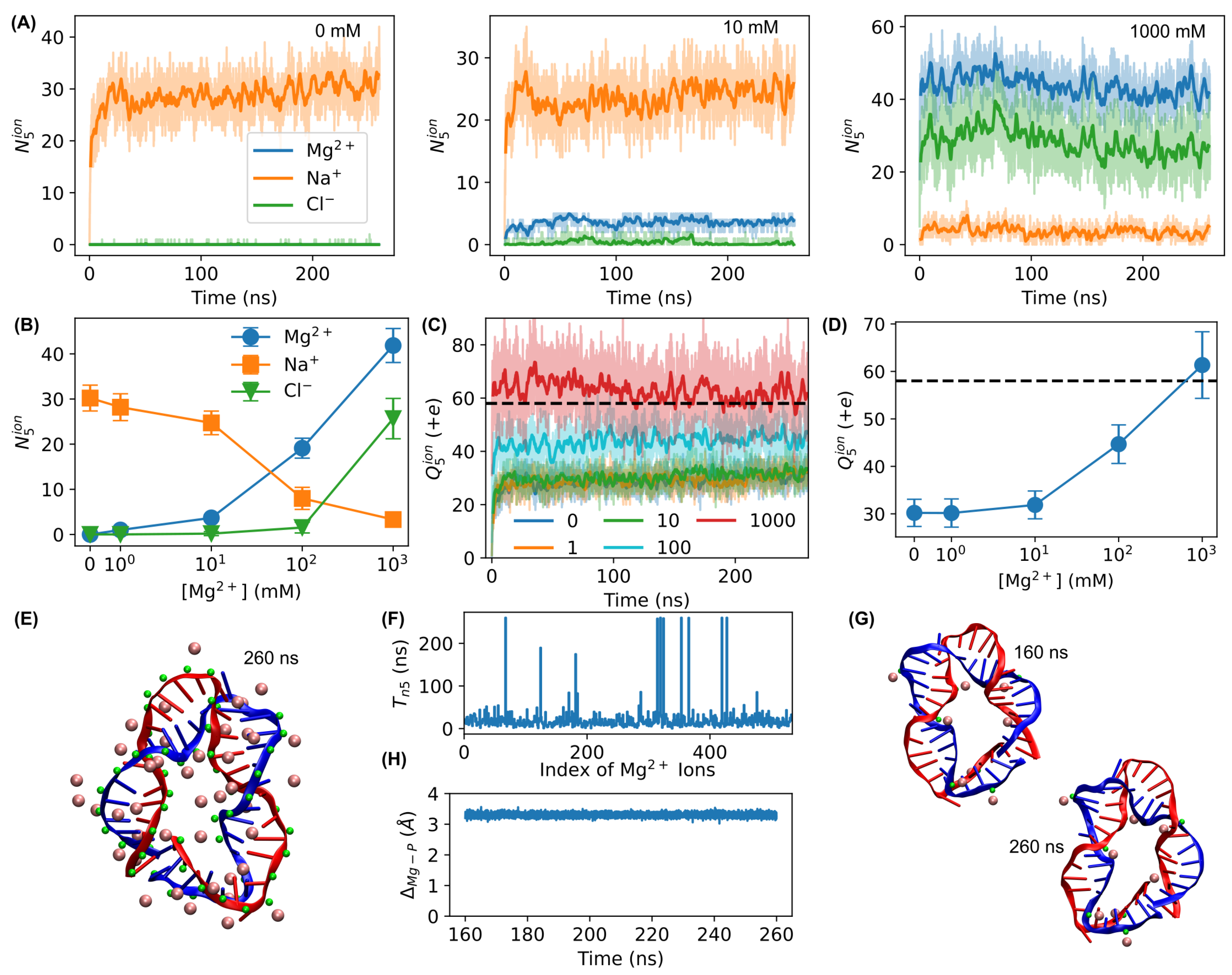
3.1. MD Simulations
3.2. Melting Curve Experiments
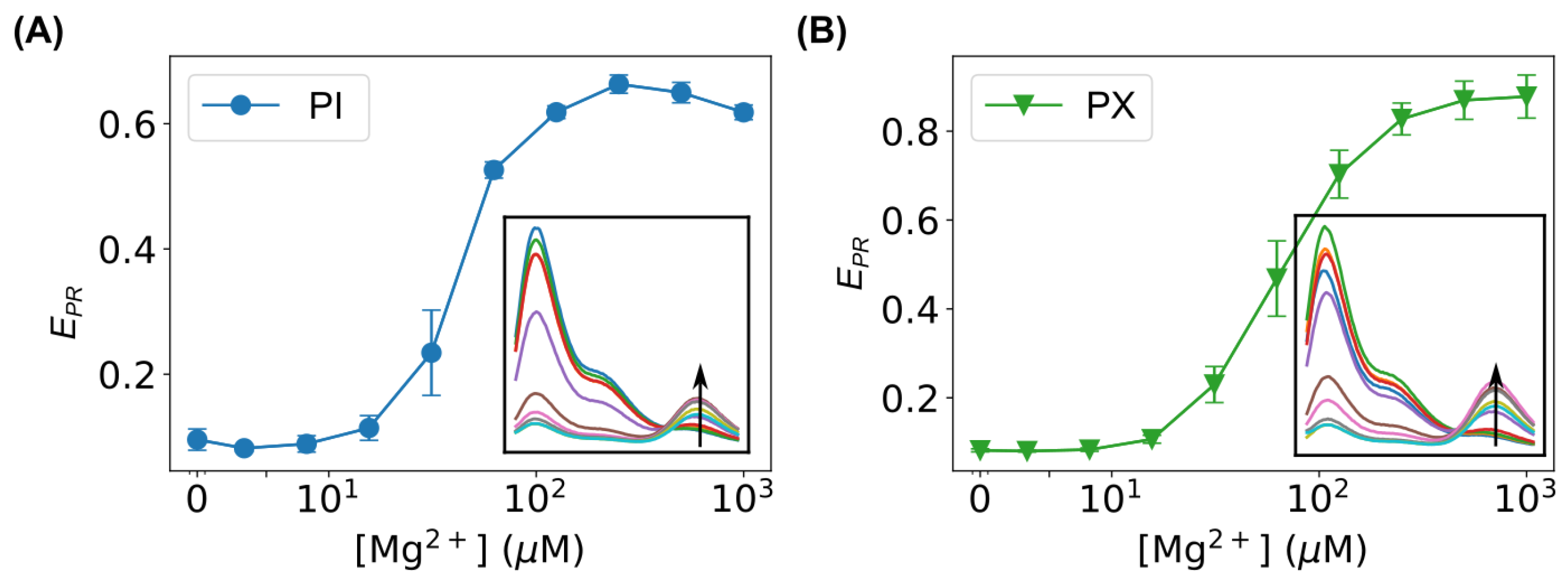
3.3. FRET Measurements
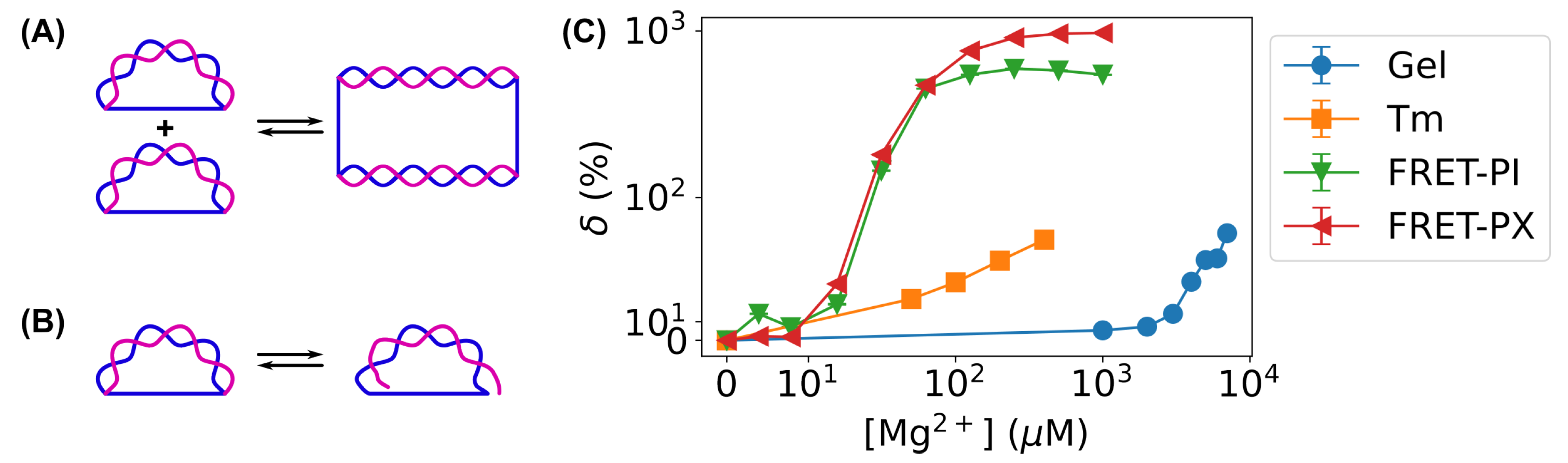
3.4. Improvement in Sensitivity of Bent DNA Amplifying Sensors Using FRET-Based Measurements Compared to Gel Electrophoresis
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lipfert, J.; Doniach, S.; Das, R.; Herschlag, D. Understanding Nucleic Acid-Ion Interactions. Annu. Rev. Biochem. 2014, 83, 813–841. [Google Scholar] [CrossRef] [PubMed]
- Wanunu, M.; Tor, Y. Methods for Studying Nucleic Acid/Drug Interactions, 1st ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Bui, V.C.; Nguyen, T.H. DNA Aggregation Induced by Mg2+ Ions under Different Conditions. J. Mol. Recognit. 2018, 31, e2721. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.J.; Choi, S.; Sang Cho, Y.; Yang, S.J.; Cho, Y.S.; Kim, K.K. Magnesium Ions Enhance Infiltration of Osteoblasts in Scaffolds via Increasing Cell Motility. J. Mater. Sci. Mater. Med. 2017, 28, 96. [Google Scholar] [CrossRef] [PubMed]
- Draper, D.E.; Grilley, D.; Soto, A.M. Ions and RNA Folding. Annu. Rev. Biophys. Biomol. Struct. 2005, 34, 221–243. [Google Scholar] [CrossRef]
- Yang, L.; Arora, K.; Beard, W.A.; Wilson, S.H.; Schlick, T. Critical Role of Magnesium Ions in DNA Polymerase Beta’s Closing and Active Site Assembly. J. Am. Chem. Soc. 2004, 126, 8441–8453. [Google Scholar] [CrossRef]
- Ivanov, I.; Tainer, J.A.; McCammon, J.A. Unraveling the Three-Metal-Ion Catalytic Mechanism of the DNA Repair Enzyme Endonuclease IV. Proc. Natl. Acad. Sci. USA 2007, 104, 1465–1470. [Google Scholar] [CrossRef]
- Hartwig, A. Role of Magnesium in Genomic Stability. Mutat. Res. 2001, 475, 113–121. [Google Scholar] [CrossRef]
- Anastassopoulou, J.; Theophanides, T. Magnesium-DNA Interactions and the Possible Relation of Magnesium to Carcinogenesis. Irradiation and Free Radicals. Crit. Rev. Oncol. Hematol. 2002, 42, 79–91. [Google Scholar] [CrossRef]
- Fei, B.L.; Xu, W.S.; Tao, H.W.; Li, W.; Zhang, Y.; Long, J.Y.; Liu, Q.B.; Xia, B.; Sun, W.Y. Effects of Copper Ions on DNA Binding and Cytotoxic Activity of a Chiral Salicylidene Schiff Base. J. Photochem. Photobiol. B Biol. 2014, 132, 36–44. [Google Scholar] [CrossRef]
- Tchounwou, P.B.; Yedjou, C.G.; Patlolla, A.K.; Sutton, D.J. Heavy Metal Toxicity and the Environment. EXS 2012, 101, 133–164. [Google Scholar] [CrossRef]
- Liang, L.; Shen, J.W.; Wang, Q. Molecular Dynamics Study on DNA Nanotubes as Drug Delivery Vehicle for Anticancer Drugs. Colloids Surf. B Biointerfaces 2017, 153, 168–173. [Google Scholar] [CrossRef] [PubMed]
- Palchaudhuri, R.; Hergenrother, P.J. DNA as a Target for Anticancer Compounds: Methods to Determine the Mode of Binding and the Mechanism of Action. Curr. Opin. Biotechnol. 2007, 18, 497–503. [Google Scholar] [CrossRef] [PubMed]
- Hurley, L.H. DNA and Its Associated Processes as Targets for Cancer Therapy. Nat. Rev. Cancer 2002, 2, 188–200. [Google Scholar] [CrossRef]
- Agudelo, D.; Bourassa, P.; Bérubé, G.; Tajmir-Riahi, H.A. Intercalation of Antitumor Drug Doxorubicin and Its Analogue by DNA Duplex: Structural Features and Biological Implications. Int. J. Biol. Macromol. 2014, 66, 144–150. [Google Scholar] [CrossRef]
- Richmond, T.J.; Davey, C.A. The Structure of DNA in the Nucleosome Core. Nature 2003, 423, 145–150. [Google Scholar] [CrossRef]
- Luger, K.; Mäder, A.W.; Richmond, R.K.; Sargent, D.F.; Richmond, T.J. Crystal Structure of the Nucleosome Core Particle at 2.8 A Resolution. Nature 1997, 389, 251–260. [Google Scholar] [CrossRef]
- Oehler, S.; Amouyal, M.; Kolkhof, P.; von Wilcken-Bergmann, B.; Müller-Hill, B. Quality and Position of the Three Lac Operators of E. Coli Define Efficiency of Repression. Embo J. 1994, 13, 3348–3355. [Google Scholar] [CrossRef]
- White, C.L.; Suto, R.K.; Luger, K. Structure of the Yeast Nucleosome Core Particle Reveals Fundamental Changes in Internucleosome Interactions. EMBO J. 2001, 20, 5207–5218. [Google Scholar] [CrossRef]
- Leforestier, A.; Livolant, F. Structure of Toroidal DNA Collapsed inside the Phage Capsid. Proc. Natl. Acad. Sci. USA 2009, 106, 9157–9162. [Google Scholar] [CrossRef]
- Ben-Shaul, A. Entropy, Energy, and Bending of DNA in Viral Capsids. Biophys. J. 2013, 104, L15–L17. [Google Scholar] [CrossRef]
- Evilevitch, A.; Lavelle, L.; Knobler, C.M.; Raspaud, E.; Gelbart, W.M. Osmotic Pressure Inhibition of DNA Ejection from Phage. Proc. Natl. Acad. Sci. USA 2003, 100, 9292–9295. [Google Scholar] [CrossRef] [PubMed]
- Grayson, P.; Evilevitch, A.; Inamdar, M.M.; Purohit, P.K.; Gelbart, W.M.; Knobler, C.M.; Phillips, R. The Effect of Genome Length on Ejection Forces in Bacteriophage Lambda. Virology 2006, 348, 430–436. [Google Scholar] [CrossRef] [PubMed]
- Tzlil, S.; Kindt, J.T.; Gelbart, W.M.; Ben-Shaul, A. Forces and Pressures in DNA Packaging and Release from Viral Capsids. Biophys. J. 2003, 84, 1616–1627. [Google Scholar] [CrossRef] [PubMed]
- Gelbart, W.M.; Knobler, C.M. Virology. Pressurized Viruses. Science 2009, 323, 1682–1683. [Google Scholar] [CrossRef]
- Wang, M.D.; Yin, H.; Landick, R.; Gelles, J.; Block, S.M. Stretching DNA with Optical Tweezers. Biophys. J. 1997, 72, 1335–1346. [Google Scholar] [CrossRef]
- Bustamante, C.; Smith, S.B.; Liphardt, J.; Smith, D. Single-Molecule Studies of DNA Mechanics. Curr. Opin. Struct. Biol. 2000, 10, 279–285. [Google Scholar] [CrossRef]
- Baumann, C.G.; Smith, S.B.; Bloomfield, V.A.; Bustamante, C. Ionic Effects on the Elasticity of Single DNA Molecules. Proc. Natl. Acad. Sci. USA 1997, 94, 6185–6190. [Google Scholar] [CrossRef]
- McCauley, M.; Hardwidge, P.R.; Maher, L.J.; Williams, M.C. Dual Binding Modes for an HMG Domain from Human HMGB2 on DNA. Biophys. J. 2005, 89, 353–364. [Google Scholar] [CrossRef]
- Rouzina, I.; Bloomfield, V.A. Force-Induced Melting of the DNA Double Helix 1. Thermodynamic Analysis. Biophys. J. 2001, 80, 882–893. [Google Scholar] [CrossRef]
- Rouzina, I.; Bloomfield, V.A. Force-Induced Melting of the DNA Double Helix. 2. Effect of Solution Conditions. Biophys. J. 2001, 80, 894–900. [Google Scholar] [CrossRef]
- Scipioni, A.; Anselmi, C.; Zuccheri, G.; Samori, B.; De Santis, P. Sequence-Dependent DNA Curvature and Flexibility from Scanning Force Microscopy Images. Biophys. J. 2002, 83, 2408–2418. [Google Scholar] [CrossRef] [PubMed]
- Tinoco, I.; Li, P.T.X.; Bustamante, C. Determination of Thermodynamics and Kinetics of RNA Reactions by Force. Q. Rev. Biophys. 2006, 39, 325–360. [Google Scholar] [CrossRef] [PubMed]
- Ceglarek, J.A.; Revzin, A. Studies of DNA-protein Interactions by Gel Electrophoresis. Electrophoresis 1989, 10, 360–365. [Google Scholar] [CrossRef] [PubMed]
- Garner, M.M.; Revzin, A. A Gel Electrophoresis Method for Quantifying the Binding of Proteins to Specific DNA Regions: Application to Components of the Escherichia Coli Lactose Operon Regulatory System. Nucleic Acids Res. 1981, 9, 3047–3060. [Google Scholar] [CrossRef]
- Guédin, A.; Lacroix, L.; Mergny, J.L. Thermal Melting Studies of Ligand DNA Interactions. Methods Mol. Biol. 2010, 613, 25–35. [Google Scholar] [CrossRef]
- LiCata, V.J.; Wowor, A.J. Applications of Fluorescence Anisotropy to the Study of Protein–Dna Interactions. In Biophysical Tools for Biologists, Volume One: In Vitro Techniques; Methods in Cell Biology; Elsevier: Amsterdam, The Netherlands, 2008; Volume 84, pp. 243–262. [Google Scholar] [CrossRef]
- Cary, P.D.; Kneale, G.G. Circular Dichroism for the Analysis of Protein-DNA Interactions. Methods Mol. Biol. 2009, 543, 613–624. [Google Scholar] [CrossRef]
- Garbett, N.C.; Ragazzon, P.A.; Chaires, J.B. Circular Dichroism to Determine Binding Mode and Affinity of Ligand-DNA Interactions. Nat. Protoc. 2007, 2, 3166–3172. [Google Scholar] [CrossRef]
- Buurma, N.J.; Haq, I. Advances in the Analysis of Isothermal Titration Calorimetry Data for Ligand-DNA Interactions. Methods 2007, 42, 162–172. [Google Scholar] [CrossRef]
- Czapla-Masztafiak, J.; Kwiatek, W.M.; Sá, J.; Szlachetko, J. X-ray Spectroscopy on Biological Systems. In X-Ray Scattering; Ares, A.E., Ed.; IntechOpen: London, UK, 2017. [Google Scholar] [CrossRef]
- Prosser, K.E.; Walsby, C.J. Electron Paramagnetic Resonance as a Tool for Studying the Mechanisms of Paramagnetic Anticancer Metallodrugs. Eur. J. Inorg. Chem. 2017, 2017, 1573–1585. [Google Scholar] [CrossRef]
- Duguid, J.G.; Bloomfield, V.A.; Benevides, J.M.; Thomas, G.J. Raman Spectroscopy of DNA-metal Complexes. II. The Thermal Denaturation of DNA in the Presence of Sr2+, Ba2+, Mg2+, Ca2+, Mn2+, Co2+, Ni2+, and Cd2+. Biophys. J. 1995, 69, 2623–2641. [Google Scholar] [CrossRef]
- Campagne, S.; Gervais, V.; Milon, A. Nuclear Magnetic Resonance Analysis of Protein-DNA Interactions. J. R. Soc. Interface 2011, 8, 1065–1078. [Google Scholar] [CrossRef] [PubMed]
- Peters, J.P.; Maher, L.J. DNA Curvature and Flexibility in Vitro and in Vivo. Q. Rev. Biophys. 2010, 43, 23–63. [Google Scholar] [CrossRef] [PubMed]
- Qu, H.; Tseng, C.Y.; Wang, Y.; Levine, A.J.; Zocchi, G. The Elastic Energy of Sharply Bent Nicked DNA. Europhys. Lett. 2010, 90, 18003. [Google Scholar] [CrossRef]
- Qu, H.; Zocchi, G. The Complete Bending Energy Function for Nicked DNA. EPL 2011, 94, 18003. [Google Scholar] [CrossRef]
- Qu, H.; Wang, Y.; Tseng, C.Y.; Zocchi, G. Critical Torque for Kink Formation in Double-Stranded DNA. Phys. Rev. X 2011, 1, 021008. [Google Scholar] [CrossRef]
- Vafabakhsh, R.; Ha, T. Extreme Bendability of DNA Less than 100 Base Pairs Long Revealed by Single-Molecule Cyclization. Science 2012, 337, 1097–1101. [Google Scholar] [CrossRef]
- Le, T.T.; Kim, H.D. Probing the Elastic Limit of DNA Bending. Nucleic Acids Res. 2014, 42, 10786–10794. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, H.D. Base-Pair Mismatch Can Destabilize Small DNA Loops through Cooperative Kinking. Phys. Rev. Lett. 2019, 122, 218101. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, H.D. Determinants of Cyclization–Decyclization Kinetics of Short DNA with Sticky Ends. Nucleic Acids Res. 2020, 48, 5147–5156. [Google Scholar] [CrossRef]
- Choi, B.; Zocchi, G. Mimicking cAMP-Dependent Allosteric Control of Protein Kinase A through Mechanical Tension. J. Am. Chem. Soc. 2006, 128, 8541–8548. [Google Scholar] [CrossRef]
- Choi, B.; Zocchi, G.; Wu, Y.; Chan, S.; Jeanne Perry, L. Allosteric Control through Mechanical Tension. Phys. Rev. Lett. 2005, 95, 078102. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, A.; Qu, H.; Zocchi, G. Protein-DNA Chimeras: Synthesis of Two-Arm Chimeras and Non-Mechanical Effects of the DNA Spring. J. Phys. Condens. Matter. 2009, 21, 335103. [Google Scholar] [CrossRef] [PubMed]
- Tseng, C.Y.; Zocchi, G. Mechanical Control of Renilla Luciferase. J. Am. Chem. Soc. 2013, 135, 11879–11886. [Google Scholar] [CrossRef] [PubMed]
- Tseng, C.Y.; Zocchi, G. Equilibrium Softening of an Enzyme Explored with the DNA Spring. Appl. Phys. Lett. 2014, 104, 153702. [Google Scholar] [CrossRef]
- Qu, H.; Ma, Q.; Wang, L.; Mao, Y.; Eisenstein, M.; Soh, H.T.; Zheng, L. Measuring Aptamer Folding Energy Using a Molecular Clamp. J. Am. Chem. Soc. 2020, 142, 11743–11749. [Google Scholar] [CrossRef]
- Freeland, J.; Khadka, P.; Wang, Y. Mechanical-Energy-Based Amplifiers for Probing Interactions of DNA with Metal Ions. Phys. Rev. E 2018, 98, 062403. [Google Scholar] [CrossRef]
- Freeland, J.; Zhang, L.; Wang, S.T.; Ruiz, M.; Wang, Y. Bent DNA Bows as Sensing Amplifiers for Detecting DNA-Interacting Salts and Molecules. Sensors 2020, 20, 3112. [Google Scholar] [CrossRef]
- Laughton, C.A.; Harris, S.A. The Atomistic Simulation of DNA. WIREs Comput. Mol. Sci. 2011, 1, 590–600. [Google Scholar] [CrossRef]
- Pérez, A.; Luque, F.J.; Orozco, M. Frontiers in Molecular Dynamics Simulations of DNA. Acc. Chem. Res. 2012, 45, 196–205. [Google Scholar] [CrossRef]
- Agarin, C.J.M.; Mascareñas, D.R.; Nolos, R.; Chan, E.; Senoro, D.B. Transition Metals in Freshwater Crustaceans, Tilapia, and Inland Water: Hazardous to the Population of the Small Island Province. Toxics 2021, 9, 71. [Google Scholar] [CrossRef]
- Blake, R.D.; Delcourt, S.G. Thermodynamic Effects of Formamide on DNA Stability. Nucleic Acids Res. 1996, 24, 2095–2103. [Google Scholar] [CrossRef] [PubMed]
- Zerze, G.H.; Stillinger, F.H.; Debenedetti, P.G. Thermodynamics of DNA Hybridization from Atomistic Simulations. J. Phys. Chem. B 2021, 125, 771–779. [Google Scholar] [CrossRef] [PubMed]
- Cong, P.; Dai, L.; Chen, H.; van der Maarel, J.R.C.; Doyle, P.S.; Yan, J. Revisiting the Anomalous Bending Elasticity of Sharply Bent DNA. Biophys. J. 2015, 109, 2338–2351. [Google Scholar] [CrossRef]
- Brunet, A.; Tardin, C.; Salomé, L.; Rousseau, P.; Destainville, N.; Manghi, M. Dependence of DNA Persistence Length on Ionic Strength of Solutions with Monovalent and Divalent Salts: A Joint Theory–Experiment Study. Macromolecules 2015, 48, 3641–3652. [Google Scholar] [CrossRef]
- Murugesapillai, D.; Bouaziz, S.; Maher, L.J.; Israeloff, N.E.; Cameron, C.E.; Williams, M.C. Accurate Nanoscale Flexibility Measurement of DNA and DNA-protein Complexes by Atomic Force Microscopy in Liquid. Nanoscale 2017, 9, 11327–11337. [Google Scholar] [CrossRef]
- Li, S.; Olson, W.K.; Lu, X.J. Web 3DNA 2.0 for the Analysis, Visualization, and Modeling of 3D Nucleic Acid Structures. Nucleic Acids Res. 2019, 47, W26–W34. [Google Scholar] [CrossRef]
- Lu, X.J.; Olson, W.K. 3DNA: A Software Package for the Analysis, Rebuilding and Visualization of Three-dimensional Nucleic Acid Structures. Nucleic Acids Res. 2003, 31, 5108–5121. [Google Scholar] [CrossRef]
- Lu, X.J.; Olson, W.K. 3DNA: A Versatile, Integrated Software System for the Analysis, Rebuilding and Visualization of Three-Dimensional Nucleic-Acid Structures. Nat. Protoc. 2008, 3, 1213–1227. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Moomaw, A.S.; Maguire, M.E. The Unique Nature of Mg2+ Channels. Physiology 2008, 23, 275–285. [Google Scholar] [CrossRef]
- Li, W.; Nordenskiöld, L.; Mu, Y. Sequence-Specific Mg2+–DNA Interactions: A Molecular Dynamics Simulation Study. J. Phys. Chem. B 2011, 115, 14713–14720. [Google Scholar] [CrossRef] [PubMed]
- MacKerell, A.D. Influence of Magnesium Ions on Duplex DNA Structural, Dynamic, and Solvation Properties. J. Phys. Chem. B 1997, 101, 646–650. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kalé, L.; Schulten, K. Scalable Molecular Dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef]
- Brooks, B.R.; Brooks, C.L.; Mackerell, A.D.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The Biomolecular Simulation Program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef] [PubMed]
- Michaud-Agrawal, N.; Denning, E.J.; Woolf, T.B.; Beckstein, O. MDAnalysis: A Toolkit for the Analysis of Molecular Dynamics Simulations. J. Comput. Chem. 2011, 32, 2319–2327. [Google Scholar] [CrossRef]
- Gowers, R.J.; Linke, M.; Barnoud, J.; Reddy, T.J.E.; Melo, M.N.; Seyler, S.L.; Domański, J.; Dotson, D.L.; Buchoux, S.; Kenney, I.M.; et al. MDAnalysis: A Python Package for the Rapid Analysis of Molecular Dynamics Simulations. In Proceedings of the 15th Python in Science Conference (Scipy2016), Austin, TX, USA, 11–17 July 2016; pp. 98–105. [Google Scholar] [CrossRef]
- Cowan, J.A. (Ed.) The Biological Chemistry of Magnesium, 1st ed.; Wiley-VCH: Weinheim, Germany, 1996. [Google Scholar]
- Every, A.E.; Russu, I.M. Influence of Magnesium Ions on Spontaneous Opening of DNA Base Pairs. J. Phys. Chem. B 2008, 112, 7689–7695. [Google Scholar] [CrossRef]
- Manning, G.S. The Molecular Theory of Polyelectrolyte Solutions with Applications to the Electrostatic Properties of Polynucleotides. Q. Rev. Biophys. 1978, 11, 179–246. [Google Scholar] [CrossRef]
- Nir, E.; Michalet, X.; Hamadani, K.M.; Laurence, T.A.; Neuhauser, D.; Kovchegov, Y.; Weiss, S. Shot-Noise Limited Single-Molecule FRET Histograms: Comparison between Theory and Experiments. J. Phys. Chem. B 2006, 110, 22103–22124. [Google Scholar] [CrossRef]
- McCann, J.J.; Choi, U.B.; Zheng, L.; Weninger, K.; Bowen, M.E. Optimizing Methods to Recover Absolute FRET Efficiency from Immobilized Single Molecules. Biophys. J. 2010, 99, 961–970. [Google Scholar] [CrossRef]
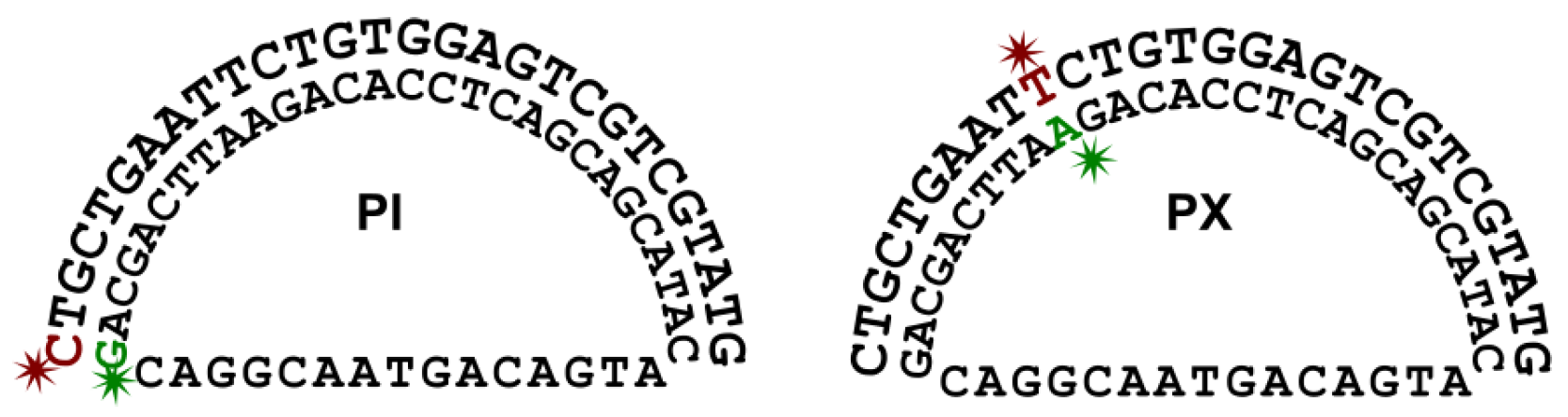


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bullard, K.; Okyere, D.; Foster, S.J.; Sadoon, A.A.; Li, J.; Chen, J.; Wang, Y. Understanding the Mechanism of Bent DNA Amplifying Sensors Using All-Atom Molecular Dynamics Simulations. Biosensors 2025, 15, 272. https://doi.org/10.3390/bios15050272
Bullard K, Okyere D, Foster SJ, Sadoon AA, Li J, Chen J, Wang Y. Understanding the Mechanism of Bent DNA Amplifying Sensors Using All-Atom Molecular Dynamics Simulations. Biosensors. 2025; 15(5):272. https://doi.org/10.3390/bios15050272
Chicago/Turabian StyleBullard, Kaitlin, Deborah Okyere, Shelbi J. Foster, Asmaa A. Sadoon, Jiali Li, Jingyi Chen, and Yong Wang. 2025. "Understanding the Mechanism of Bent DNA Amplifying Sensors Using All-Atom Molecular Dynamics Simulations" Biosensors 15, no. 5: 272. https://doi.org/10.3390/bios15050272
APA StyleBullard, K., Okyere, D., Foster, S. J., Sadoon, A. A., Li, J., Chen, J., & Wang, Y. (2025). Understanding the Mechanism of Bent DNA Amplifying Sensors Using All-Atom Molecular Dynamics Simulations. Biosensors, 15(5), 272. https://doi.org/10.3390/bios15050272




