Towards Quantitative Interpretation of Fourier-Transform Photocurrent Spectroscopy on Thin-Film Solar Cells
Abstract
1. Introduction
2. Materials and Methods
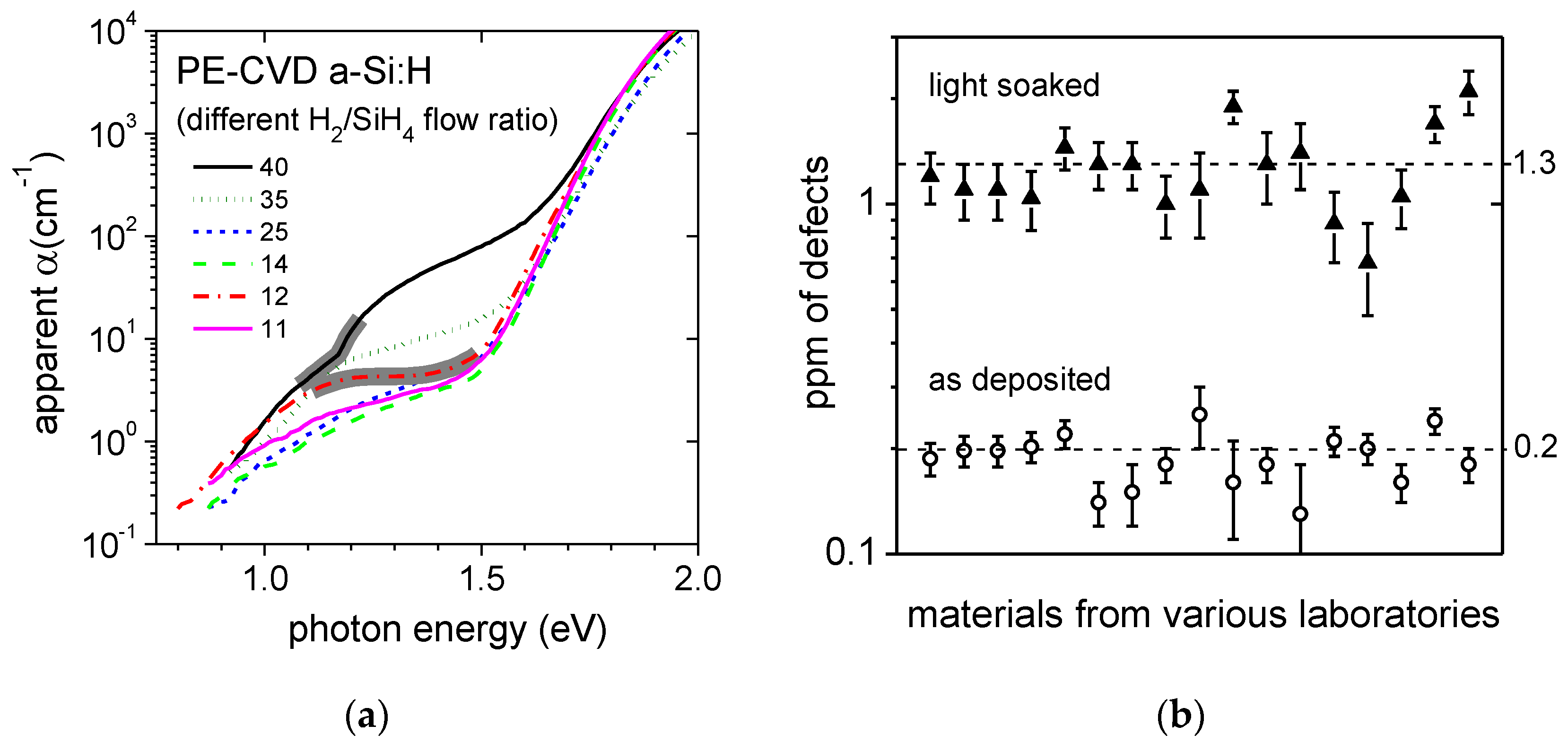
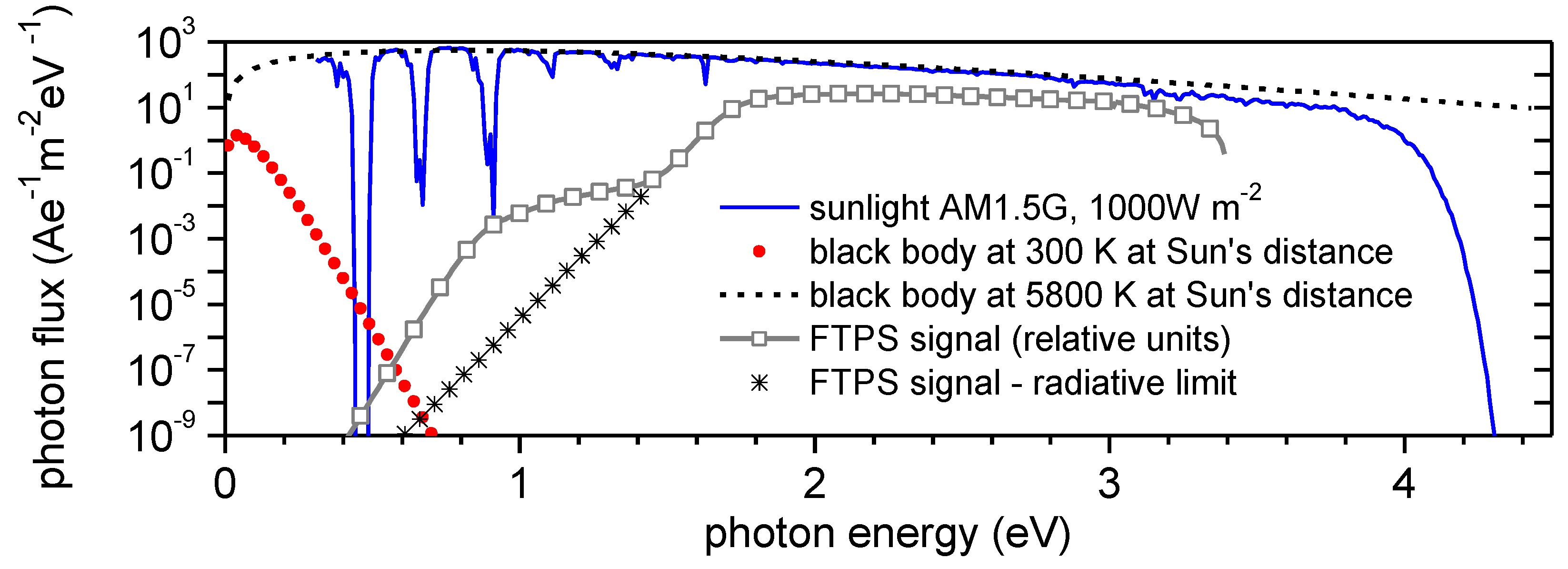
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vanecek, M.; Poruba, A. Fourier-transform photocurrent spectroscopy of microcrystalline silicon for solar cells. Appl. Phys. Lett. 2002, 80, 719–721. [Google Scholar] [CrossRef]
- Melskens, J.; Vanelzakker, G.; Li, Y.; Zeman, M. Analysis of hydrogenated amorphous silicon thin films and solar cells by means of Fourier Transform Photocurrent Spectroscopy. Thin Solid Films 2008, 516, 6877–6881. [Google Scholar] [CrossRef]
- Vandewal, K.; Goris, L.; Haeldermans, I.; Nesladek, M.; Haenen, K.; Wagner, P.; Manca, J. Fourier-transform photocurrent spectroscopy for a fast and highly sensitive spectral characterization of organic and hybrid solar cells. Thin Solid Films 2008, 516, 7135–7138. [Google Scholar] [CrossRef]
- De Wolf, S.; Holovsky, J.; Moon, S.-J.; Löper, P.; Niesen, B.; Ledinsky, M.; Haug, F.-J.; Yum, J.-H.; Ballif, C. Organometallic halide perovskites: Sharp optical absorption edge and its relation to photovoltaic performance. J. Phys. Chem. Lett. 2014, 5, 1035–1039. [Google Scholar] [CrossRef]
- Tang, X.; Brandl, M.; May, B.; Levchuk, I.; Hou, Y.; Richter, M.; Chen, H.; Chen, S.; Kahmann, S.; Osvet, A.; et al. Photoinduced degradation of methylammonium lead triiodide perovskite semiconductors. J. Mater. Chem. A 2016, 4, 15896–15903. [Google Scholar] [CrossRef]
- Holovský, J.; De Wolf, S.; Werner, J.; Remeš, Z.; Müller, M.; Neykova, N.; Ledinský, M.; Černá, L.; Hrzina, P.; Löper, P.; et al. Photocurrent Spectroscopy of Perovskite Layers and Solar Cells: A sensitive probe of material degradation. J. Phys. Chem. Lett. 2017, 8, 838–843. [Google Scholar] [CrossRef]
- Holovský, J.; Peter Amalathas, A.; Landová, L.; Dzurňák, B.; Conrad, B.; Ledinský, M.; Hájková, Z.; Pop-Georgievski, O.; Svoboda, J.; Yang, T.C.-J.; et al. Lead halide residue as a source of light-induced reversible defects in hybrid perovskite layers and solar cells. ACS Energy Lett. 2019, 4, 3011–3017. [Google Scholar] [CrossRef]
- Tomm, J.W.; Jaeger, A.; Bärwolff, A.; Elsaesser, T.; Gerhardt, A.; Donecker, J. Aging properties of high power laser diode arrays analyzed by Fourier-transform photocurrent measurements. Appl. Phys. Lett. 1997, 71, 2233. [Google Scholar] [CrossRef]
- Holovský, J. Fourier transform photocurrent spectroscopy on non-crystalline semiconductors. In Fourier Transforms–New Analytical Approaches and FTIR Strategies; InTech Publishing: London, UK, 2011; pp. 257–282. ISBN 978–953-307-232-6. [Google Scholar]
- Curtins, H.; Favre, M. Surface and bulk states determined by photothermal deflection spectroscopy. In Amorphous Silicon and Related Materials; Fritzsche, H., Ed.; World Scientific Publishing Company: Singapore, 1988; pp. 329–363. [Google Scholar]
- Holovský, J.; Ballif, C. Thin-film limit formalism applied to surface defect absorption. Opt. Express 2014, 22, 31466. [Google Scholar] [CrossRef]
- Bidiville, A.; Matsui, T.; Matsubara, K. Analysis of bulk and interface defects in hydrogenated amorphous silicon solar cells by Fourier transform photocurrent spectroscopy. J. Appl. Phys. 2015, 118, 184506. [Google Scholar] [CrossRef]
- Ritter, D.; Weiser, K. Suppression of interference fringes in absorption measurements on thin films. Opt. Commun. 1986, 57, 336–338. [Google Scholar] [CrossRef]
- Vaněček, M.; Kočka, J.; Poruba, A.; Fejfar, A. Direct measurement of the deep defect density in thin amorphous silicon films with the “absolute” constant photocurrent method. J. Appl. Phys. 1995, 78, 6203–6210. [Google Scholar] [CrossRef]
- Holovský, J.; Schmid, M.; Stuckelberger, M.; Despeisse, M.; Ballif, C.; Poruba, A.; Vaněček, M. Time evolution of surface defect states in hydrogenated amorphous silicon studied by photothermal and photocurrent spectroscopy and optical simulation. J. Non-Cryst. Solids 2012, 358, 2035–2038. [Google Scholar] [CrossRef]
- Wyrsch, N.; Finger, F.; Mcmahon, T.; Vanecek, M. How to reach more precise interpretation of subgap absorption spectra in terms of deep defect density in a-Si:H. J. Non-Cryst. Solids 1991, 137, 347–350. [Google Scholar] [CrossRef]
- van Elzakker, G.; Šutta, P.; Tichelaar, F.D.; Zeman, M. Phase control and stability of thin silicon films deposited from silane diluted with hydrogen. Mrs Proc. 2007, 989. [Google Scholar] [CrossRef]
- Poruba, A.; Fejfar, A.; Remeš, Z.; Špringer, J.; Vaněček, M.; Kočka, J.; Meier, J.; Torres, P.; Shah, A. Optical absorption and light scattering in microcrystalline silicon thin films and solar cells. J. Appl. Phys. 2000, 88, 148. [Google Scholar] [CrossRef]
- Benagli, S. High performance LPCVD-ZnO TCO used in p-i-n amorphous silicon & Micromorph® tandem deviced prepared in industrial KAI R&D reactor. In Proceedings of the 23rd European Photovoltaic Solar Energy Conference, Valencia, Spain, 1–5 September 2008; pp. 2414–2418. [Google Scholar]
- Stuckelberger, M.; Shah, A.; Krc, J.; Despeisse, M.; Meillaud, F.; Ballif, C. Internal electric field and fill factor of amorphous silicon solar cells. In Proceedings of the 2010 35th IEEE Photovoltaic Specialists Conference, Honolulu, HI, USA, 20–25 June 2010; pp. 1569–1574. [Google Scholar]
- Melskens, J.; Schouten, M.; Mannheim, A.; Vullers, A.S.; Mohammadian, Y.; Eijt, S.W.H.; Schut, H.; Matsui, T.; Zeman, M.; Smets, A.H.M. The nature and the kinetics of light-induced defect creation in hydrogenated amorphous silicon films and solar cells. IEEE J. Photovolt. 2014, 4, 1331–1336. [Google Scholar] [CrossRef]
- Stuckelberger, M.; Billet, A.; Riesen, Y.; Boccard, M.; Despeisse, M.; Schüttauf, J.-W.; Haug, F.-J.; Ballif, C. Comparison of amorphous silicon absorber materials: Kinetics of light-induced degradation: Comparison of amorphous silicon absorber materials: Kinetics of light-induced degradation. Prog. Photovolt. Res. Appl. 2014, 24, 446–457. [Google Scholar] [CrossRef]
- Stuckelberger, M.; Biron, R.; Wyrsch, N.; Haug, F.-J.; Ballif, C. Review: Progress in solar cells from hydrogenated amorphous silicon. Renew. Sustain. Energy Rev. 2017, 76, 1497–1523. [Google Scholar] [CrossRef]
- Staebler, D.L.; Wronski, C.R. Reversible conductivity changes in discharge-produced amorphous Si. Appl. Phys. Lett. 1977, 31, 292. [Google Scholar] [CrossRef]
- Stuckelberger, M. Hydrogenated Amorphous Silicon: Impact of Process Conditions on Material Properties and Solar Cell Efficiency; Ecole Polytechnique Federale de Lausanne: Neuchâtel, Switzerland, 2014. [Google Scholar]
- Springer, J.; Poruba, A.; Vanecek, M. Improved three-dimensional optical model for thin-film silicon solar cells. J. Appl. Phys. 2004, 96, 5329. [Google Scholar] [CrossRef]
- Holovský, J.; Dagkaldiran, Ü.; Remeš, Z.; Purkrt, A.; Ižák, T.; Poruba, A.; Vaněček, M. Fourier transform photocurrent measurement of thin silicon films on rough, conductive and opaque substrates. Phys. Status Solidi 2010, 207, 578–581. [Google Scholar] [CrossRef]
- Tiedje, T. Band tail recombination limit to the output voltage of amorphous silicon solar cells. Appl. Phys. Lett. 1982, 40, 627–629. [Google Scholar] [CrossRef]
- Kirchartz, T.; Rau, U. Detailed balance and reciprocity in solar cells. Phys. Status Solidi 2008, 205, 2737–2751. [Google Scholar] [CrossRef]
- Jean, J.; Mahony, T.S.; Bozyigit, D.; Sponseller, M.; Holovský, J.; Bawendi, M.G.; Bulović, V. Radiative efficiency limit with band tailing exceeds 30% for quantum dot solar cells. ACS Energy Lett. 2017, 2, 2616–2624. [Google Scholar] [CrossRef]
- Mahesh, S.; Ball, J.M.; Oliver, R.D.J.; McMeekin, D.P.; Nayak, P.K.; Johnston, M.B.; Snaith, H.J. Revealing the origin of voltage loss in mixed-halide perovskite solar cells. Energy Environ. Sci. 2020, 13, 258–267. [Google Scholar] [CrossRef]
- Sládek, P.; Thèye, M.L.; Chahed, L. Analysis of the temperature dependence of the CPM-derived optical absorption spectra of hydrogenated amorphous silicon films. J. Non-Cryst. Solids 1993, 164, 363–366. [Google Scholar] [CrossRef]
- Varache, R.; Leendertz, C.; Gueunier-Farret, M.E.; Haschke, J.; Muñoz, D.; Korte, L. Investigation of selective junctions using a newly developed tunnel current model for solar cell applications. Sol. Energy Mater. Sol. Cells 2015, 141, 14–23. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holovský, J.; Stuckelberger, M.; Finsterle, T.; Conrad, B.; Peter Amalathas, A.; Müller, M.; Haug, F.-J. Towards Quantitative Interpretation of Fourier-Transform Photocurrent Spectroscopy on Thin-Film Solar Cells. Coatings 2020, 10, 820. https://doi.org/10.3390/coatings10090820
Holovský J, Stuckelberger M, Finsterle T, Conrad B, Peter Amalathas A, Müller M, Haug F-J. Towards Quantitative Interpretation of Fourier-Transform Photocurrent Spectroscopy on Thin-Film Solar Cells. Coatings. 2020; 10(9):820. https://doi.org/10.3390/coatings10090820
Chicago/Turabian StyleHolovský, Jakub, Michael Stuckelberger, Tomáš Finsterle, Brianna Conrad, Amalraj Peter Amalathas, Martin Müller, and Franz-Josef Haug. 2020. "Towards Quantitative Interpretation of Fourier-Transform Photocurrent Spectroscopy on Thin-Film Solar Cells" Coatings 10, no. 9: 820. https://doi.org/10.3390/coatings10090820
APA StyleHolovský, J., Stuckelberger, M., Finsterle, T., Conrad, B., Peter Amalathas, A., Müller, M., & Haug, F.-J. (2020). Towards Quantitative Interpretation of Fourier-Transform Photocurrent Spectroscopy on Thin-Film Solar Cells. Coatings, 10(9), 820. https://doi.org/10.3390/coatings10090820





