Simulation of Cold Atmospheric Plasma Generated by Floating-Electrode Dielectric Barrier Pulsed Discharge Used for the Cancer Cell Necrosis
Abstract
:1. Introduction
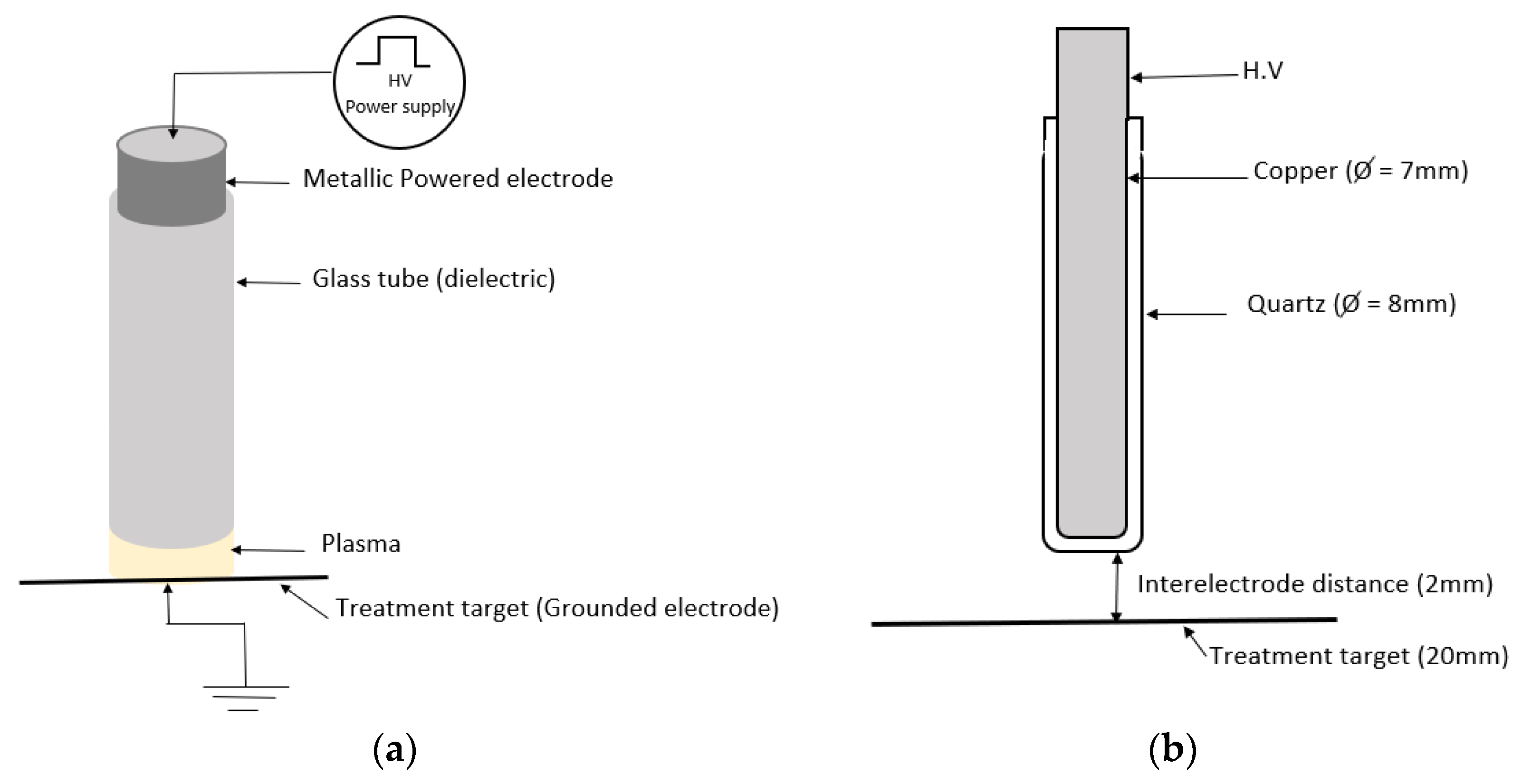
2. Configuration of Argon FE-DBD Plasma Generator
3. Simulation Model
3.1. Elementary Process and Basic Equations
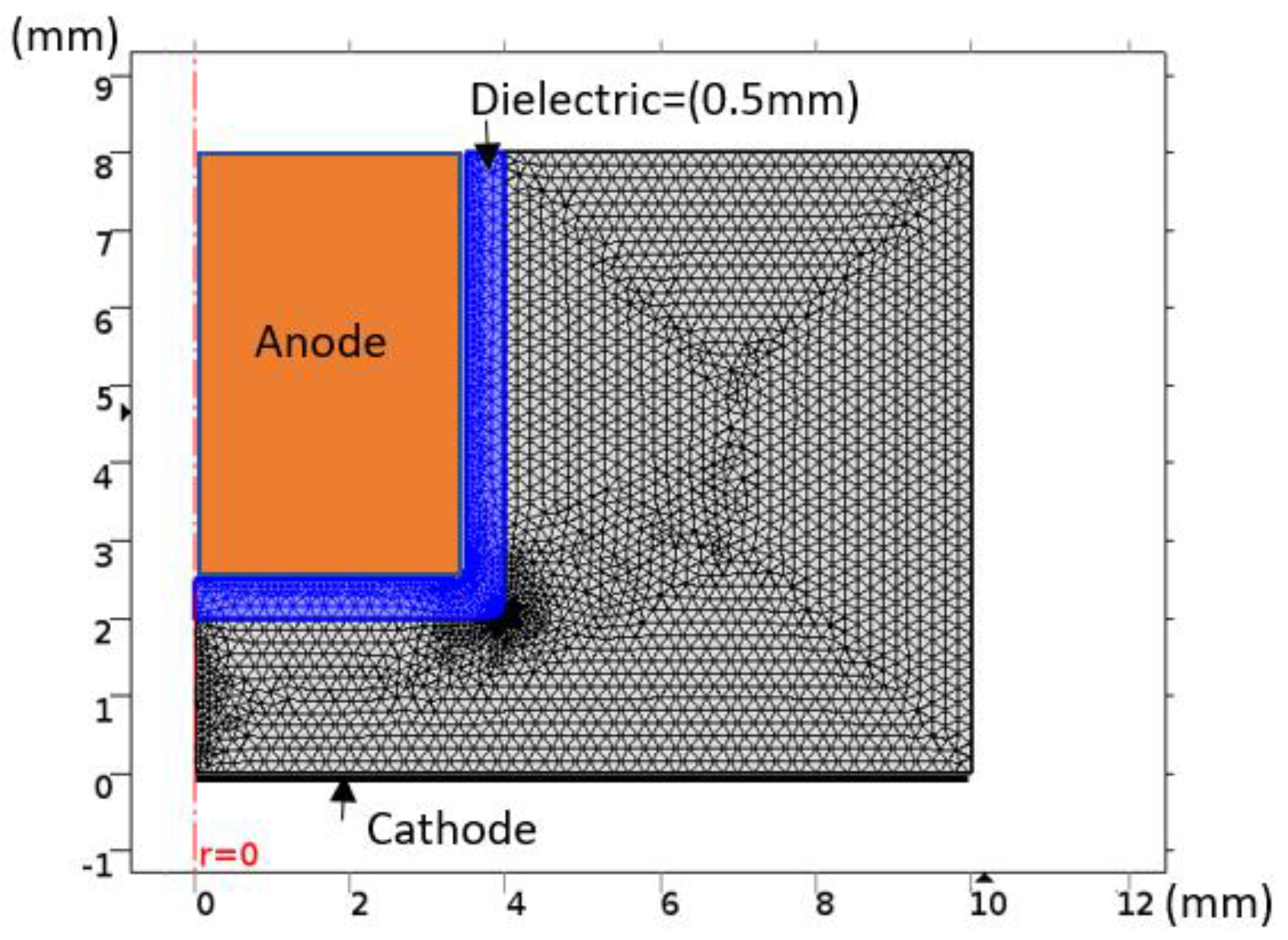
3.2. Initial and Boundary Conditions
3.3. Computational Method
4. Results and Discussion
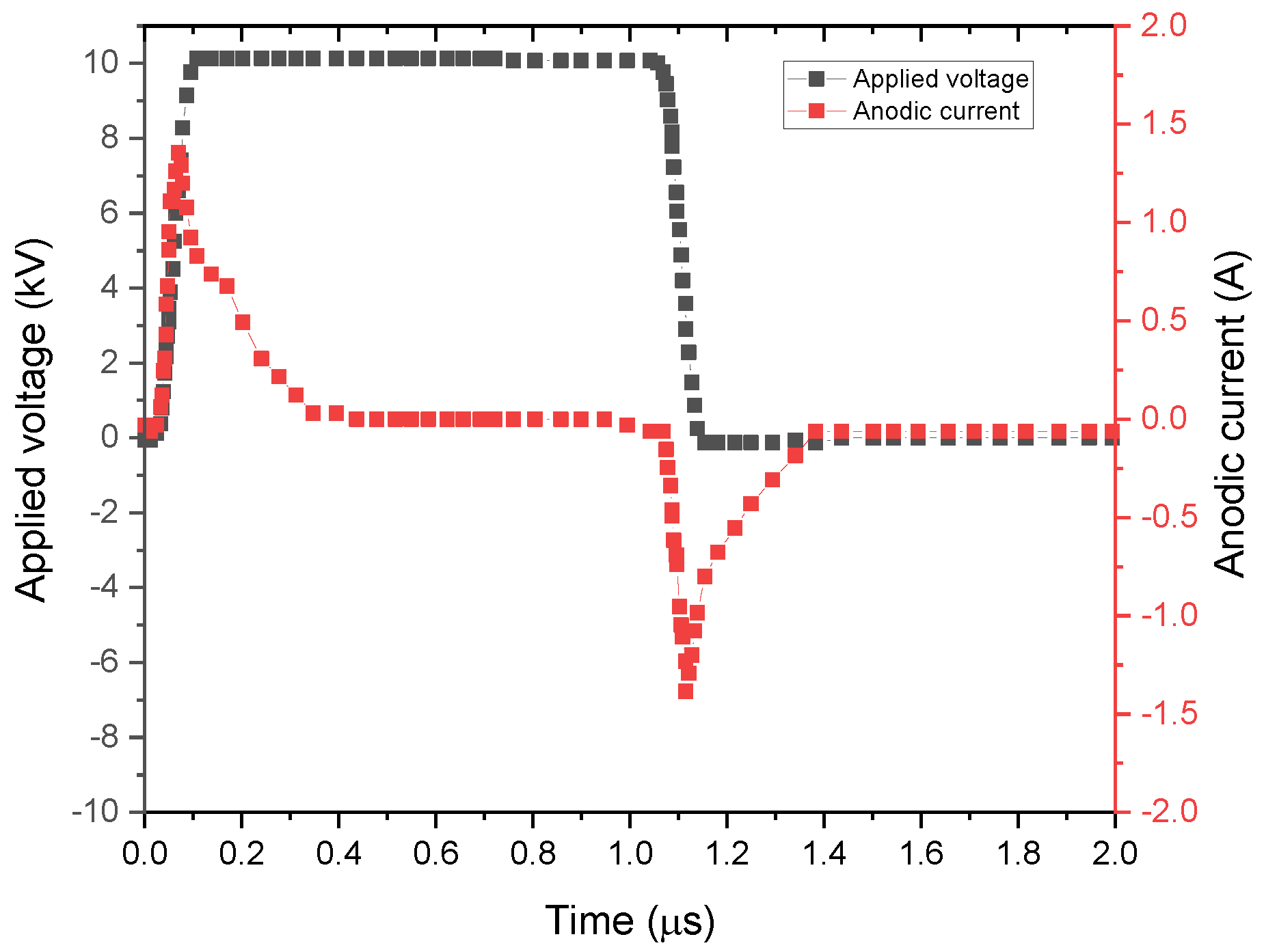
4.1. Electric Discharge Characteristics (Current-Voltage Waveform)
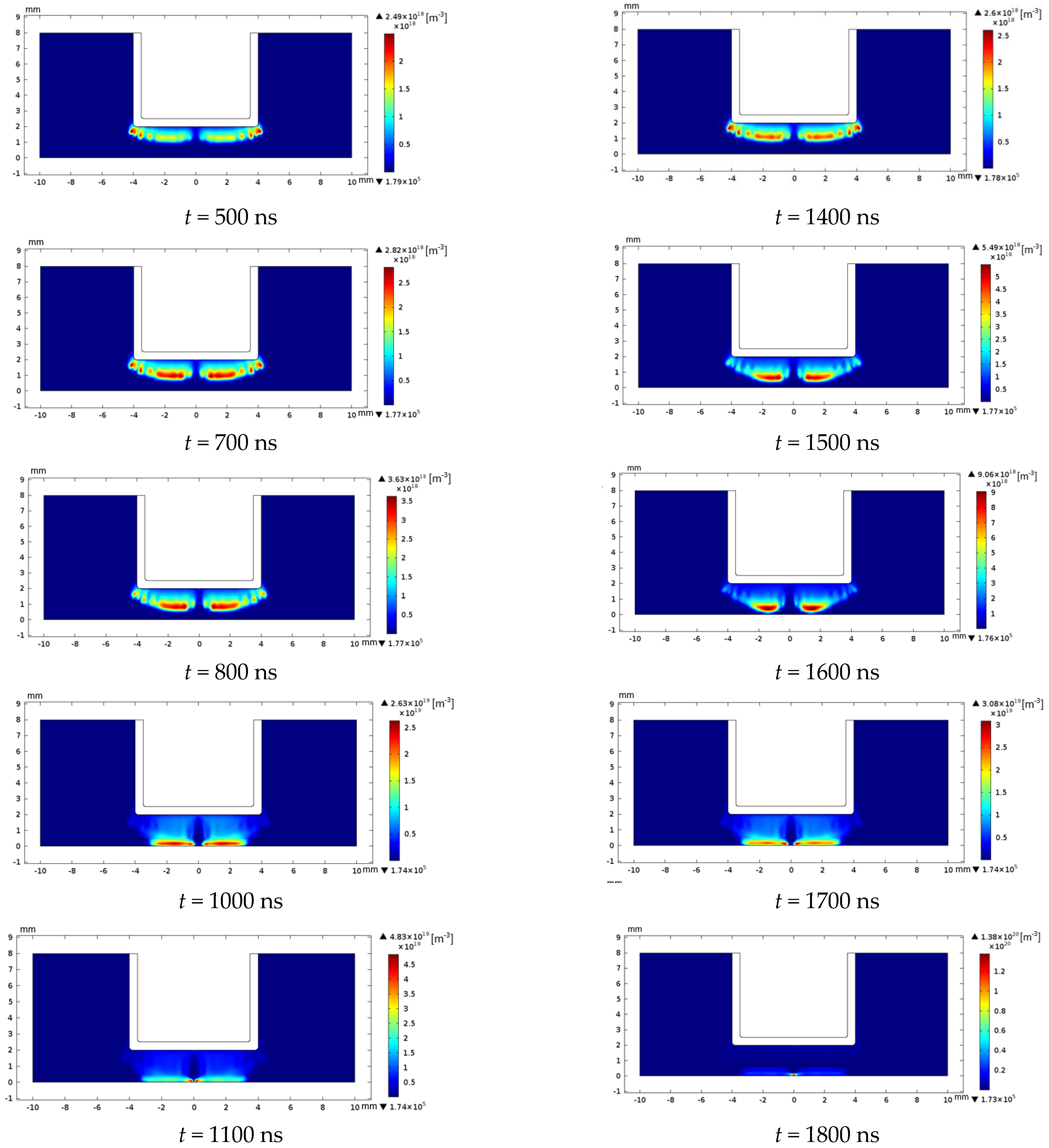
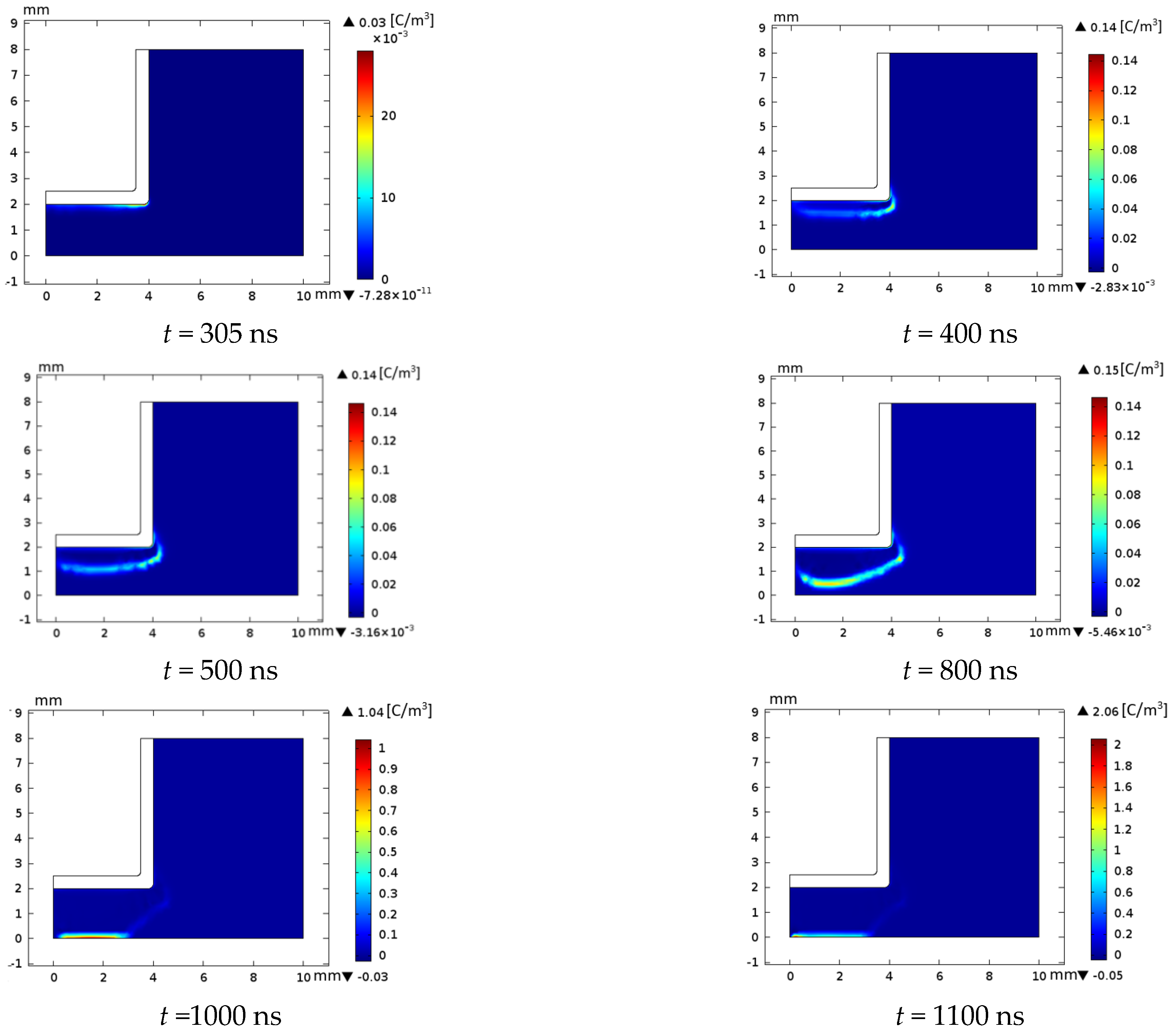
4.2. Dynamic of the Discharge Formation
4.3. Electric Field Distribution
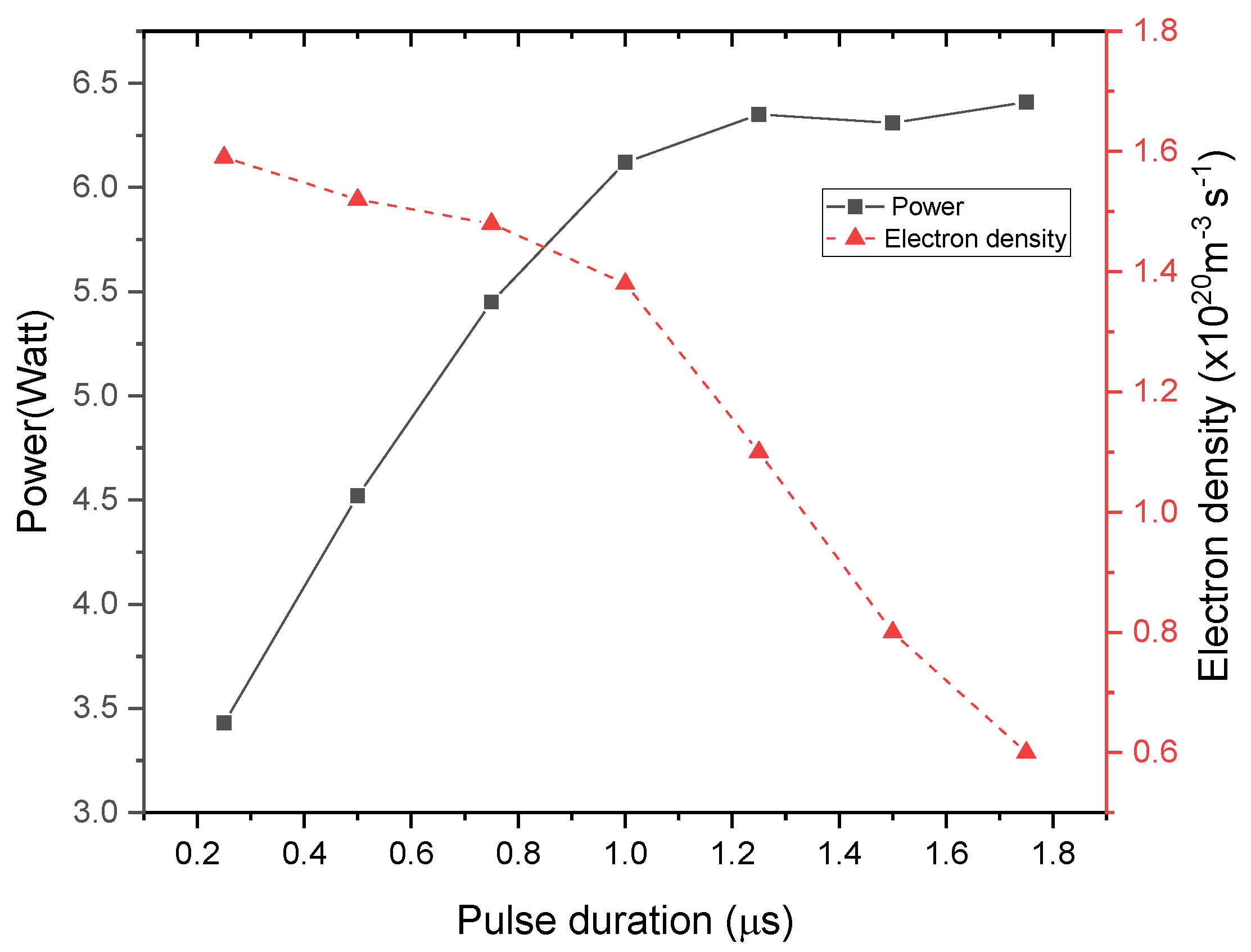
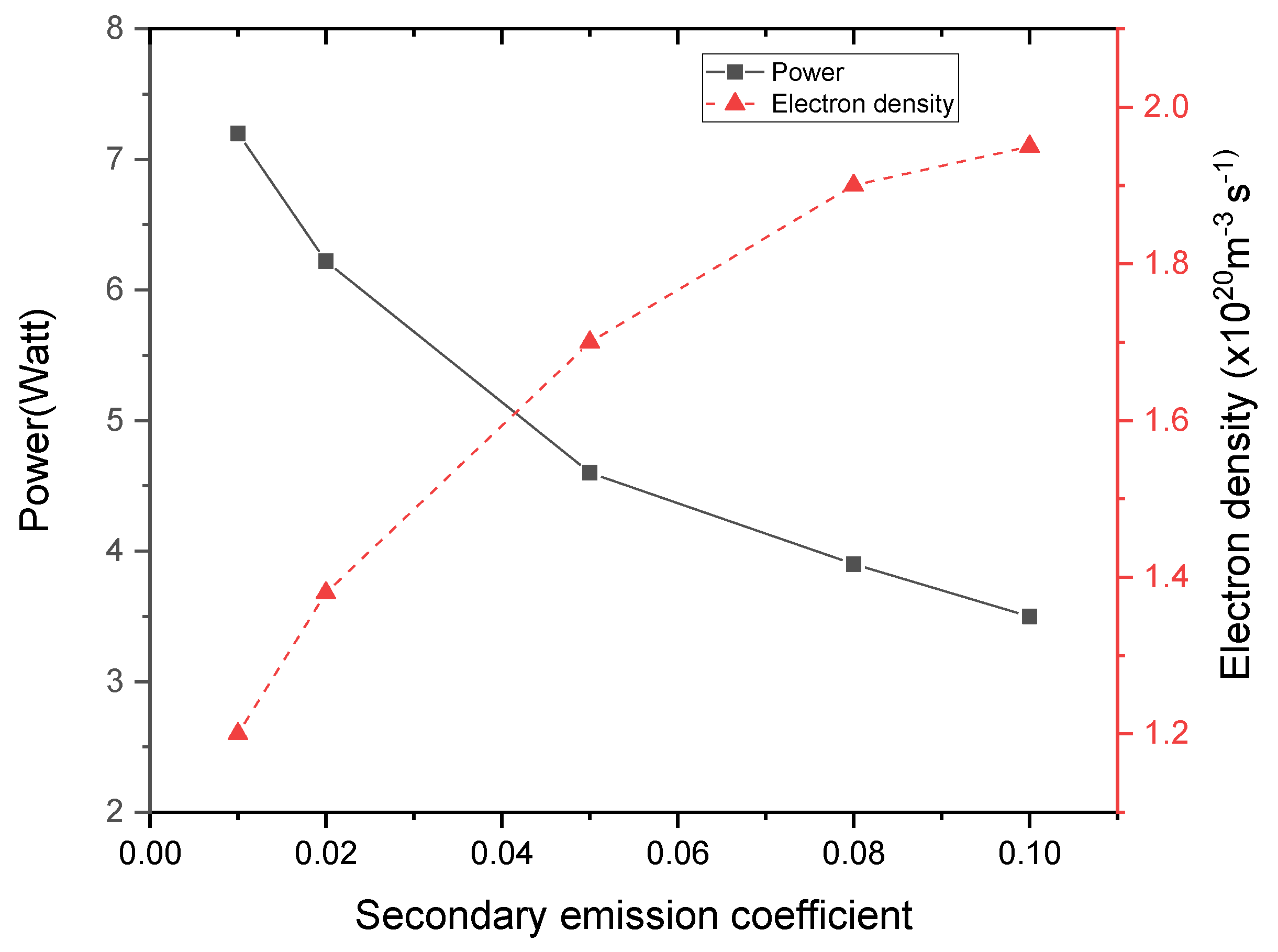
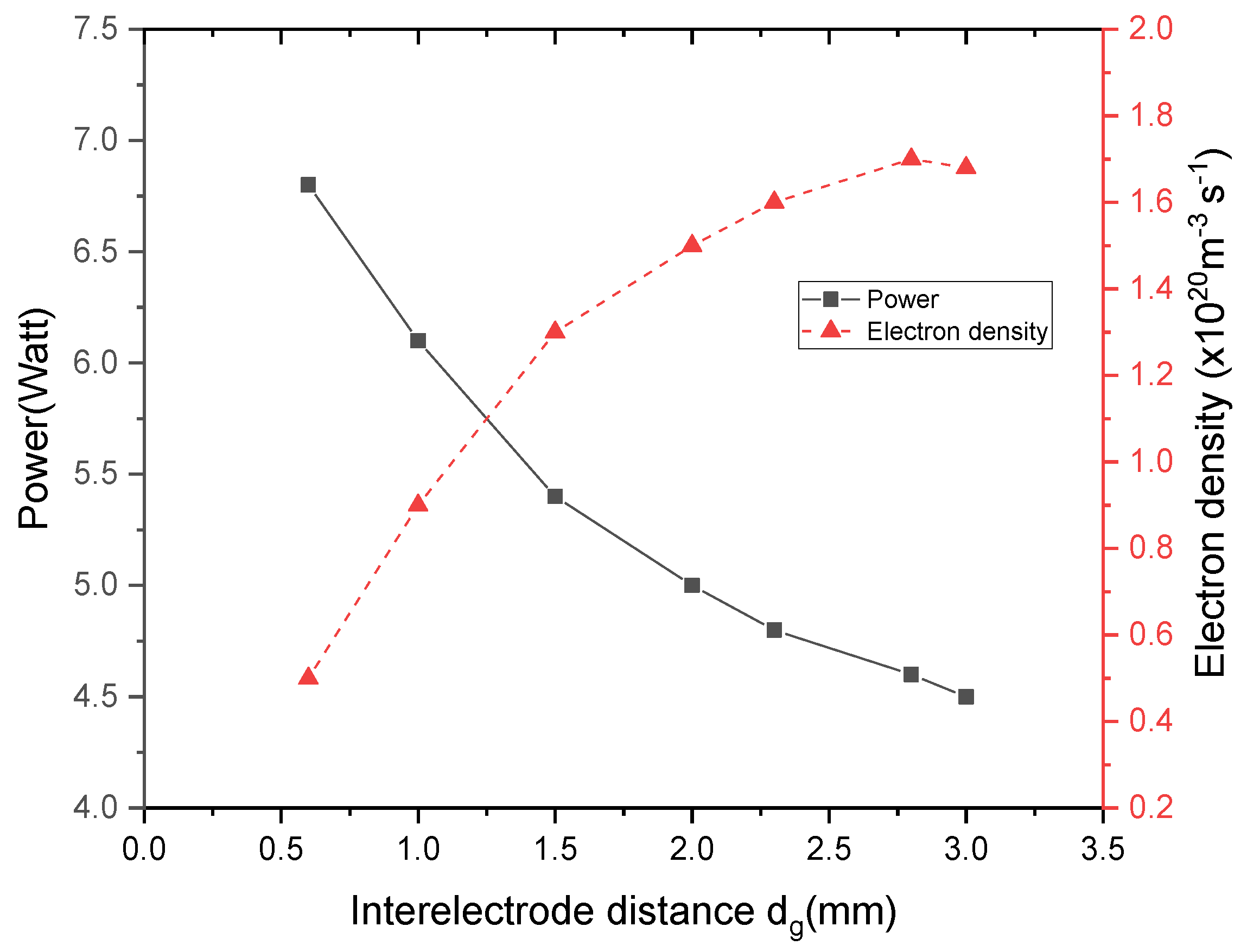
4.4. Effects of Model Parameters
4.5. Discussion
5. Conclusions
- –
- The electrical diagnostics revealed a higher consumed power with higher applied voltage.
- –
- The pulse width plays a crucial role in the development of the discharge due to the charge accumulation over the dielectric barrier covering the high voltage rod electrode.
- –
- The large electron number density with small-consumed power is obtained through the increasing of the secondary electron emission coefficient.
- –
- For small interelectrode distance, the breakdown of the gap occurs earlier, thus a wide area of the quasi-neutral plasma bulk is obtained, and a peak value of electron density is achieved.
- –
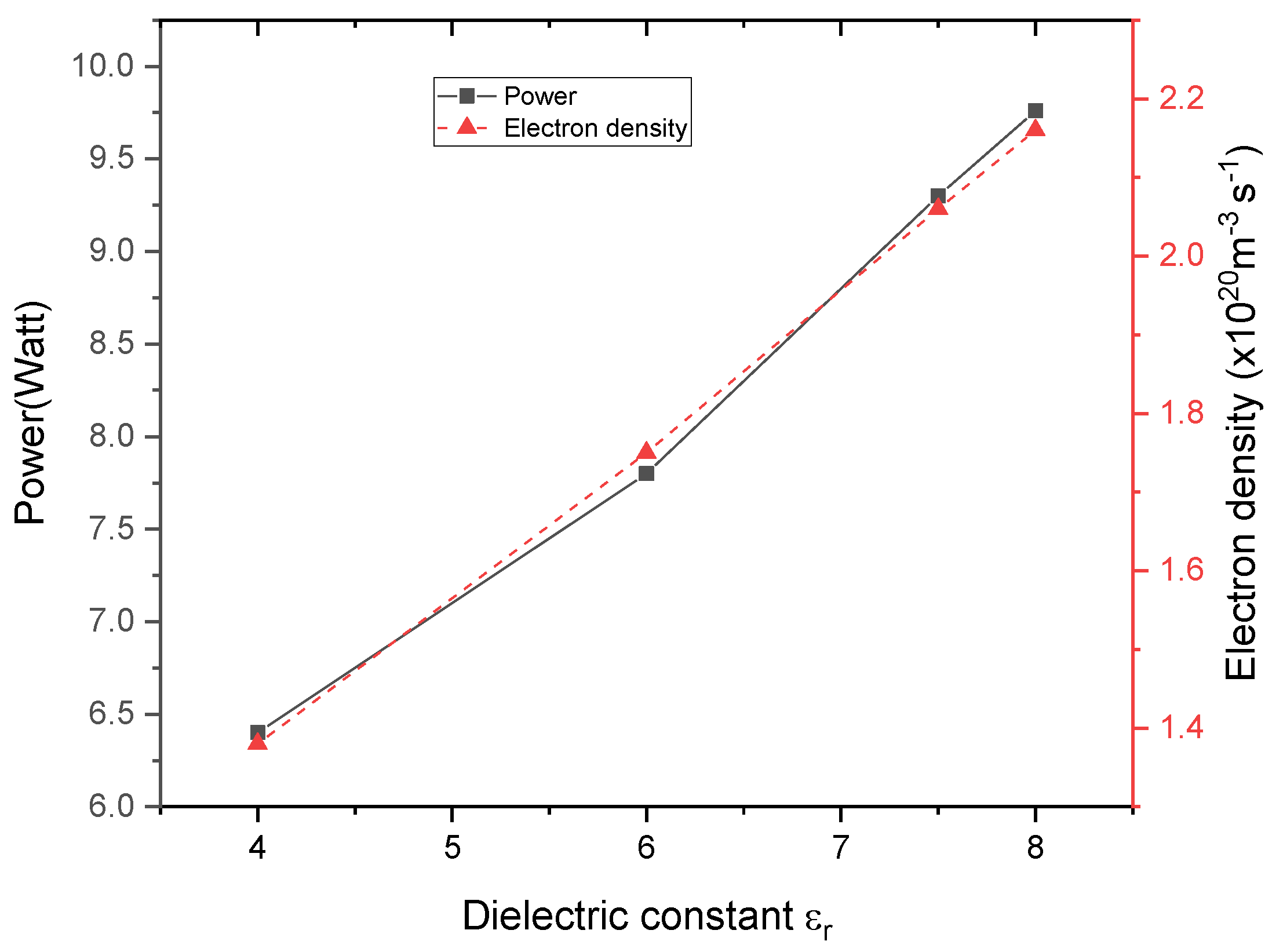
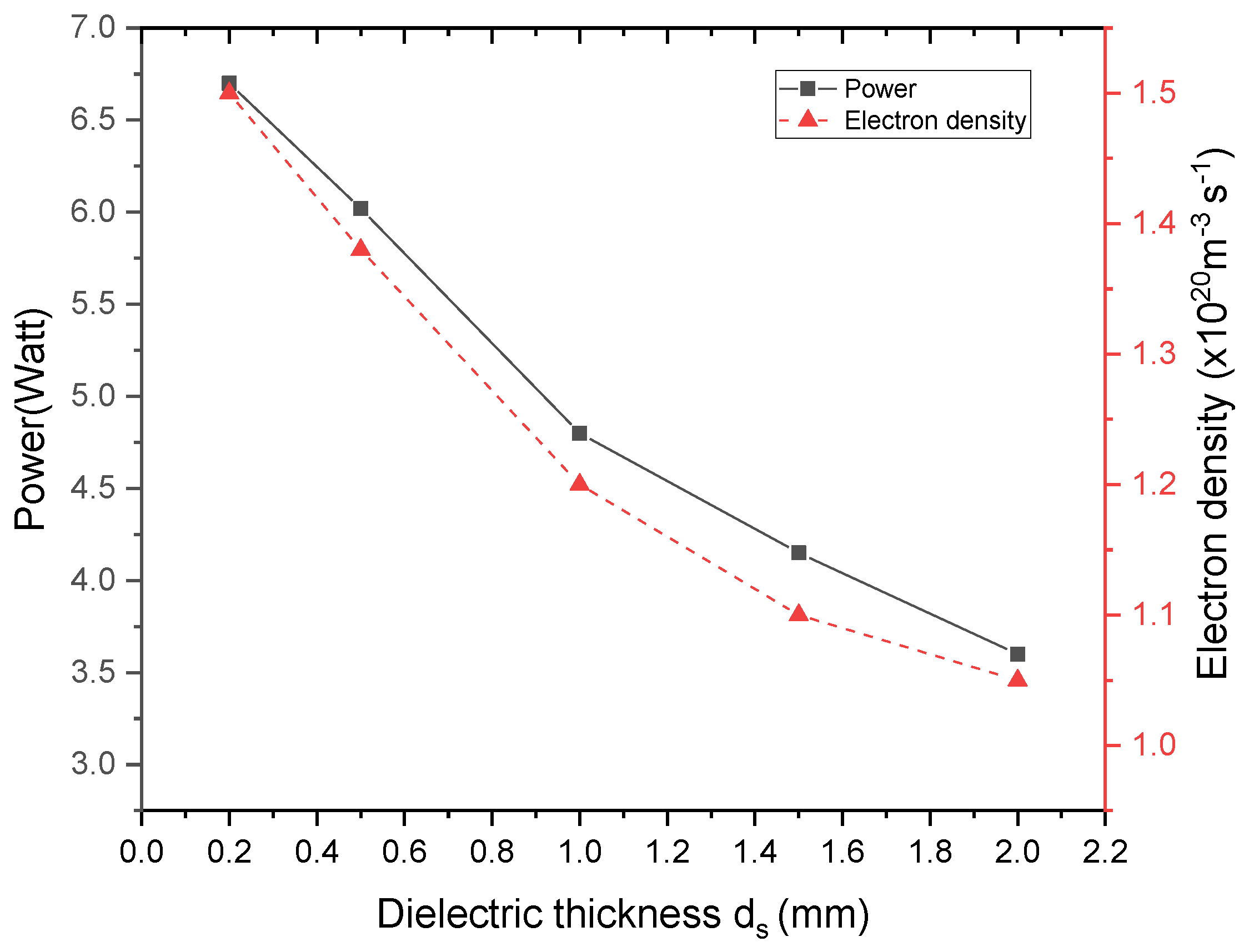
- The production of electrons is proportional to the barrier capacity, whereas the influence of the capacity on the dynamics of the discharge is negligible small: when εr decreases or ds increases, or V and Ne decrease, the peak value of electron density nearby the cathode gets smaller.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aminia, M.; Momeni, M.; Jahandideh, A. Floating Discharge Plasma for Healing of Tendon Injury. High Temp. 2020, 58, 795–799. [Google Scholar] [CrossRef]
- Pavelic, B.; Svarc, Z.; Segovic, S.; Bago, I. Cold atmospheric plasma for bleaching endodontically treated tooth: A new clinical approach. Quintessence Int. 2020, 1, 364–371. [Google Scholar] [CrossRef]
- Tanaka, H.; Hori, M. Medical applications of non-thermal atmospheric pressure plasma. J. Clin. Biochem. 2017, 60, 29–32. [Google Scholar] [CrossRef] [Green Version]
- Friedman, P.C. Cold atmospheric pressure (physical) plasma in dermatology: Where are we today? Int. J. Dermatol. 2020, 59, 1171–1184. [Google Scholar] [CrossRef]
- Cheng, X.; Murthy, S.R.K.; Zhuang, T.; Ly, L.; Jones, O.; Basadonna, G.; Keidar, M.; Kanaan, Y.; Canady, J. Canady Helios Cold Plasma Induces Breast Cancer Cell Death by Oxidation of Histone mRNA. Int. J. Mol. Sci. 2021, 22, 9578. [Google Scholar] [CrossRef]
- Alimohammadi, M.; Golpour, M.; Sohbatzadeh, F.; Hadavi, S.; Bekeschus, S.; Niaki, H.A.; Valadan, R.; Rafiei, A. Cold Atmospheric Plasma Is a Potent Tool to Improve Chemotherapy in Melanoma In Vitro and In Vivo. Biomolecules 2020, 10, 1011. [Google Scholar] [CrossRef]
- Subramanian, P.S.G.; Jain, A.; Shivapuji, A.M.; Sundaresan, N.R.; Dasappa, S.; Rao, L. Plasma-activated water from a dielectric barrier discharge plasma source for the selective treatment of cancer cells. Plasma Process. Polym. 2020, 17, 1900260. [Google Scholar] [CrossRef]
- Tian, W.; Kushner, M.J. Atmospheric pressure dielectric barrier discharges interacting with liquid covered tissue. J. Phys. D Appl. Phys. 2014, 47, 165201. [Google Scholar] [CrossRef] [Green Version]
- Galmiz, O.; Pavlinak, D.; Zemanek, M.; Brablec, A.; Cernak, M. Study of surface dielectric barrier discharge generated using liquid electrodes in different gases. J. Phys. D Appl. Phys. 2016, 49, 065201. [Google Scholar] [CrossRef]
- Song, J.; Tang, J.; Wang, Y.; Wei, L.; Ren, C.; Yu, D. Role of ambient dielectric in propagation of Ar atmospheric pressure nonequilibrium plasma jets. Phys. Plasmas 2015, 22, 050703. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Q.; Yao, C.; Zhang, X.; Sun, C. Dielectric Barrier Discharge Characteristics of Multineedle-to-Cylinder Configuration. Energies 2011, 4, 2133–2150. [Google Scholar] [CrossRef] [Green Version]
- Fridman, G.; Shereshevsky, A.; Jost, M.M.; Brooks, A.D.; Fridman, A.; Gutsol, A.; Vasilets, V.; Friedman, G. Floating Electrode Dielectric Barrier Discharge Plasma in Air Promoting Apoptotic Behavior in Melanoma Skin Cancer Cell Lines. Plasma Chem. Plasma Process. 2007, 27, 163–176. [Google Scholar] [CrossRef]
- Graves, D.B. Low temperature plasma biomedicine: A tutorial review. Phys. Plasma 2014, 21, 080901. [Google Scholar] [CrossRef] [Green Version]
- Asimakoulas, L.; Katsafadou, M.; Svarnas, U.P.; Pachis, K.; Kostazos, N.; Gazeli, K.; Mitronikas, E.; Antimisiaris, S.G. Hand-sized dielectric barrier discharge reactor of floating potential electrode for cell model studies. In Proceedings of the ICPIG 32nd Conference, Iasi, Romania, 26–31 July 2015. [Google Scholar]
- Fridman, G.; Peddinghaus, M.; Ayan, H.; Fridman, A.; Balasubramanian, M.; Gutsol, A.; Brooks, A.; Friedman, G. Blood Coagulation and Living Tissue Sterilization by Floating-Electrode Dielectric Barrier Discharge in Air. Plasma Chem. Plasma Process. 2006, 26, 425–442. [Google Scholar] [CrossRef]
- Judée, F.; Fongia, C.; Ducommun, B.; Yousfi, M.; Lobjois, V.; Merbahi, N. Short and long-time effects of low temperature Plasma Activated Media on 3D multicellular tumor Spheroids. Sci. Rep. 2016, 6, 21421. [Google Scholar] [CrossRef]
- Lee, J.H.; Choi, E.H.; Kim, K.M.; Kim, K.N. Effect of non-thermal air atmospheric pressure plasma jet treatment on gingival wound healing. J. Phys. D Appl. Phys. 2016, 49, 075402. [Google Scholar] [CrossRef]
- Fridman, G.; Friedman, G.; Gutsol, A.; Shekhter, A.B.; Vasilets, V.N.; Fridman, A. Applied Plasma Medicine. Plasma Process. Polym. 2008, 5, 503–533. [Google Scholar] [CrossRef]
- Hu, J.T.; Wang, J.G.; Liu, X.Y.; Liu, D.W.; Lu, X.P.; Shi, J.J.; Ostrikov, K. Effect of a floating electrode on a plasma jet. Phys. Plasmas 2013, 20, 083516. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Zhuang, J.; Woedtke, T.V.; Kolb, J.F.; Weltmann, K.D.; Zhang, J.; Fang, J. Combination of pulsed electric fields and non-thermal plasma jet for more effective bacterial decontamination. In Proceedings of the 2015 IEEE International Conference on Plasma Sciences (ICOPS), Antalya, Turkey, 24–28 May 2015; IEEE: Antalya, Turkey, 2015. [Google Scholar] [CrossRef]
- Bekeschus, S.; Lin, A.; Fridman, A.; Wende, K.; Weltmann, K.D.; Miller, V. A Comparison of Floating-Electrode DBD and kINPen Jet: Plasma Parameters to Achieve Similar Growth Reduction in Colon Cancer Cells Under Standardized Conditions. Plasma Chem. Plasma Process. 2018, 38, 1–12. [Google Scholar] [CrossRef]
- Adil, B.H.; Al-Shammari, A.M.; Murbat, H.H. Breast cancer treatment using cold atmospheric plasma generated by the FE-DBD scheme. Clin. Plasma Med. 2020, 19, 100103. [Google Scholar] [CrossRef]
- Bak, M.S.; Cappelli, M.A. Simulations of nanosecond-pulsed dielectric barrier discharges in atmospheric pressure air. J. Appl. Phys. 2013, 113, 113301. [Google Scholar] [CrossRef]
- Komuro, A.; Ono, R.; Oda, T. Effects of pulse voltage rise rate on velocity, diameter and radical production of an atmospheric-pressure streamer discharge. Plasma Sources Sci. Technol. 2013, 22, 045002. [Google Scholar] [CrossRef]
- Pan, G.; Tan, Z.; Pan, J.; Wang, X.; Shan, C. A comparative study on the frequency effects of the electrical characteristics of the pulsed dielectric barrier discharge in He/O2 and in Ar/O2 at atmospheric pressure. Phys. Plasma 2016, 23, 043508. [Google Scholar] [CrossRef]
- Joo, J. Numerical modelling of floating electrodes in a plasma processing system. Appl. Sci. Converg. Technol. 2015, 24, 102–110. [Google Scholar] [CrossRef] [Green Version]
- Viegas, P.; Hofmans, M.; Rooij, O.V.; Obrusnik, A.; Klarenaar, B.L.M.; Bonaventura, Z.; Guaitella, O.; Sobota, A.; Bourdon, A. Interaction of an atmospheric pressure plasma jet with grounded and floating metallic targets: Simulations and experiments. Plasma Sources Sci. Technol. 2020, 29, 095011. [Google Scholar] [CrossRef]
- Arserim, E.H.; Salvi, D.; Fridman, G.; Schafner, D.W.; Karwe, M.V. Microbial Inactivation by Non equilibrium Short Pulsed Atmospheric Pressure Dielectric Barrier Discharge (Cold Plasma): Numerical and Experimental Studies. Food Eng. Rev. 2021, 13, 136–147. [Google Scholar] [CrossRef]
- Shihab, A.M.; Murbat, H.H.; Hussein, M.U.; Muhamed, S.D. The influence of argon gas flow in the killing of staphylococcus epidermidis bacteria. Iraqi J. Phys. 2018, 16, 134–139. [Google Scholar] [CrossRef]
- Cooper, M.; Fridman, G.; Fridman, A.; Joshi, S.G. Biological responses of bacillus stratosphericus to floating electrode- dielectric barrier discharge plasma treatment. J. Appl. Microbiol. 2010, 109, 2039–2048. [Google Scholar] [CrossRef] [PubMed]
- Bafoil, M.; Ru, A.; Merbahi, N.; Eichwald, O.; Dunand, C.; Yousfi, M. New insights of low-temperature plasma effects on germination of three genotypes of Arabidopsis thaliana seeds under osmotic and saline stresses. Sci. Rep. 2019, 9, 8649. [Google Scholar] [CrossRef] [Green Version]
- Sharma, N.K.; Misra, S.; Varun, D.; Pal, U.N. Experimental and simulation analysis of dielectric barrier discharge based pulsed cold atmospheric pressure plasma jet. Phys. Plasmas 2020, 27, 113502. [Google Scholar] [CrossRef]
- COMSOL. Multiphysics V5.4. Plasma Module, User’s Guide; COMSOL AB: Stockholm, Sweden, 2019. [Google Scholar]
- Hagelaar, G.J.M.; Pitchford, L.C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sources Sci. Technol. 2005, 14, 722–733. [Google Scholar] [CrossRef]
- Dickinson, E.J.F.; Ekstrom, H.; Fontes, E. COMSOL Multiphysics®: Finite element software for electrochemical analysis. A mini review. Electrochem. Commun. 2014, 40, 71–74. [Google Scholar] [CrossRef]
- Mohamed, A.A.H.; Aljuhani, M.M.; Almarashi, J.Q.M.; Alhazime, A.A. The effect of a second grounded electrode on the atmospheric pressure argon plasma jet. Plasma Res. Express 2020, 2, 015011. [Google Scholar] [CrossRef]
- Guedah, H.; Abahazem, A.; Merbahi, N.; Yousfi, M.; Saber, K.; Ihlal, A. Experimental Investigation of Effects of Electric Operating Parameters on Pulsed Corona Discharges in Humid Air at Atmospheric Pressure. J. Anal. Sci. Methods Instrum. 2018, 8, 49–64. [Google Scholar] [CrossRef] [Green Version]
- Judée, F.; Merbahi, N.; Wattieaux, G.; Yousfi, M. Analysis of Ar plasma jets induced by single and double dielectric barrier discharges at atmospheric pressure. J. Appl. Phys. 2016, 120, 114901. [Google Scholar] [CrossRef]
- Yurgelenas, Y.V.; Wagner, H.E. A computational model of a barrier discharge in air at atmospheric pressure: The role of residual surface charges in micro discharges formation. J. Phys. D Appl. Phys. 2006, 39, 4031–4043. [Google Scholar] [CrossRef] [Green Version]
- Steinle, G.; Neundorf, D.; Hiller, W.; Pietralla, M. Two-dimensional simulation of filaments in barrier discharges. J. Phys. D Appl. Phys. 1999, 32, 1350–1356. [Google Scholar] [CrossRef] [Green Version]
- Abahazem, A.; Merbahi, N.; Guedah, H.; Yousfi, M. Electric and Spectroscopic Studies of Pulsed Corona Discharges in Nitrogen at Atmospheric Pressure. J. Anal. Sci. Methods Instrum. 2017, 7, 57–74. [Google Scholar] [CrossRef] [Green Version]
- Qian, M.; Ren, C.; Wang, D.; Zhang, J.; Wei, G. Stark broadening measurement of the electron density in an atmospheric pressure argon plasma jet with double-power electrodes. J. Appl. Phys. 2010, 107, 063303. [Google Scholar] [CrossRef]
- Xiong, Q.; Nikiforov, A.Y.; Gonzalez, M.A.; Leys, C.; Lu, X.P. Characterization of an atmospheric helium plasma jet by relative and absolute optical emission spectroscopy. Plasma Sources Sci. Technol. 2013, 22, 015011. [Google Scholar] [CrossRef]
- Chen, B.; Tan, Z.; Song, X. Effects of the Operating Conditions on the Electrical Characteristics of Pulse Discharges in Atmospheric-Pressure Pure Helium. IEEE Trans. Plasma Sci. 2012, 40, 1103–1109. [Google Scholar] [CrossRef]
- Braný, D.; Dvorská, D.; Halašová, E.; Škovierová, H. Cold Atmospheric Plasma: A Powerful Tool for Modern Medicine. Int. J. Mol. Sci. 2020, 21, 2932. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tanaka, H.; Mizuno, M.; Ishikawa, K.; Kondo, H.; Takeda, K.; Hashizume, H.; Nakamura, K.; Utsumi, F.; Kajiyama, H.; Kano, H.; et al. Plasma with high electron density and plasma-activated medium for cancer treatment. Clin. Plasma Med. 2015, 3, 72–76. [Google Scholar] [CrossRef]



| R. No | Formula | Rate Coefficient | Ref |
|---|---|---|---|
| 1 | e + Ar → e + Ar | Boltzmann equation | [32] |
| 2 | e + Ar → e + Ars | Boltzmann equation | [32] |
| 3 | e + Ars → e + Ar | Boltzmann equation | [32] |
| 4 | e + Ar → 2e + Ar+ | Boltzmann equation | [32] |
| 5 | e + Ars → 2e + Ar+ | Boltzmann equation | [32] |
| 6 | Ars + Ars → e + Ar + Ar+ | 5 × 10−10 cm3 s−1 | [33] |
| 7 | Ars + Ar → Ar + Ar | 3 × 10−15 cm3 s−1 | [33] |
| 8 | Ar+ + 2Ar → Ar2+ + Ar | 2.5 × 10−31 cm3 s−1 | [33] |
| 9 | e + Ar2+ → 2Ars | 5.4 × 10−8 Te0.66 cm3 s−1 | [33] |
| 10 | 2e + Ar+ → Ars + e | 5 × 10−27 Te4.5 cm6 s−1 | [33] |
| 11 | Ar2 + Ar → 3Ar | 10−14 cm3 s−1 | [33] |
| 12 | Ars + 2Ar → Ar2 + Ar | 10−31 cm6 s−1 | [33] |
| R. No | Formula | Sticking Coefficient |
|---|---|---|
| 1 | Ars ⇒ Ar | 1 |
| 2 | Ar+ ⇒ Ar | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elaissi, S.; Charrada, K. Simulation of Cold Atmospheric Plasma Generated by Floating-Electrode Dielectric Barrier Pulsed Discharge Used for the Cancer Cell Necrosis. Coatings 2021, 11, 1405. https://doi.org/10.3390/coatings11111405
Elaissi S, Charrada K. Simulation of Cold Atmospheric Plasma Generated by Floating-Electrode Dielectric Barrier Pulsed Discharge Used for the Cancer Cell Necrosis. Coatings. 2021; 11(11):1405. https://doi.org/10.3390/coatings11111405
Chicago/Turabian StyleElaissi, Samira, and Kamel Charrada. 2021. "Simulation of Cold Atmospheric Plasma Generated by Floating-Electrode Dielectric Barrier Pulsed Discharge Used for the Cancer Cell Necrosis" Coatings 11, no. 11: 1405. https://doi.org/10.3390/coatings11111405
APA StyleElaissi, S., & Charrada, K. (2021). Simulation of Cold Atmospheric Plasma Generated by Floating-Electrode Dielectric Barrier Pulsed Discharge Used for the Cancer Cell Necrosis. Coatings, 11(11), 1405. https://doi.org/10.3390/coatings11111405






