Coupled Resonance Mechanism of Interface Stratification of Thin Coating Structures Excited by Horizontal Shear Waves
Abstract
:1. Introduction
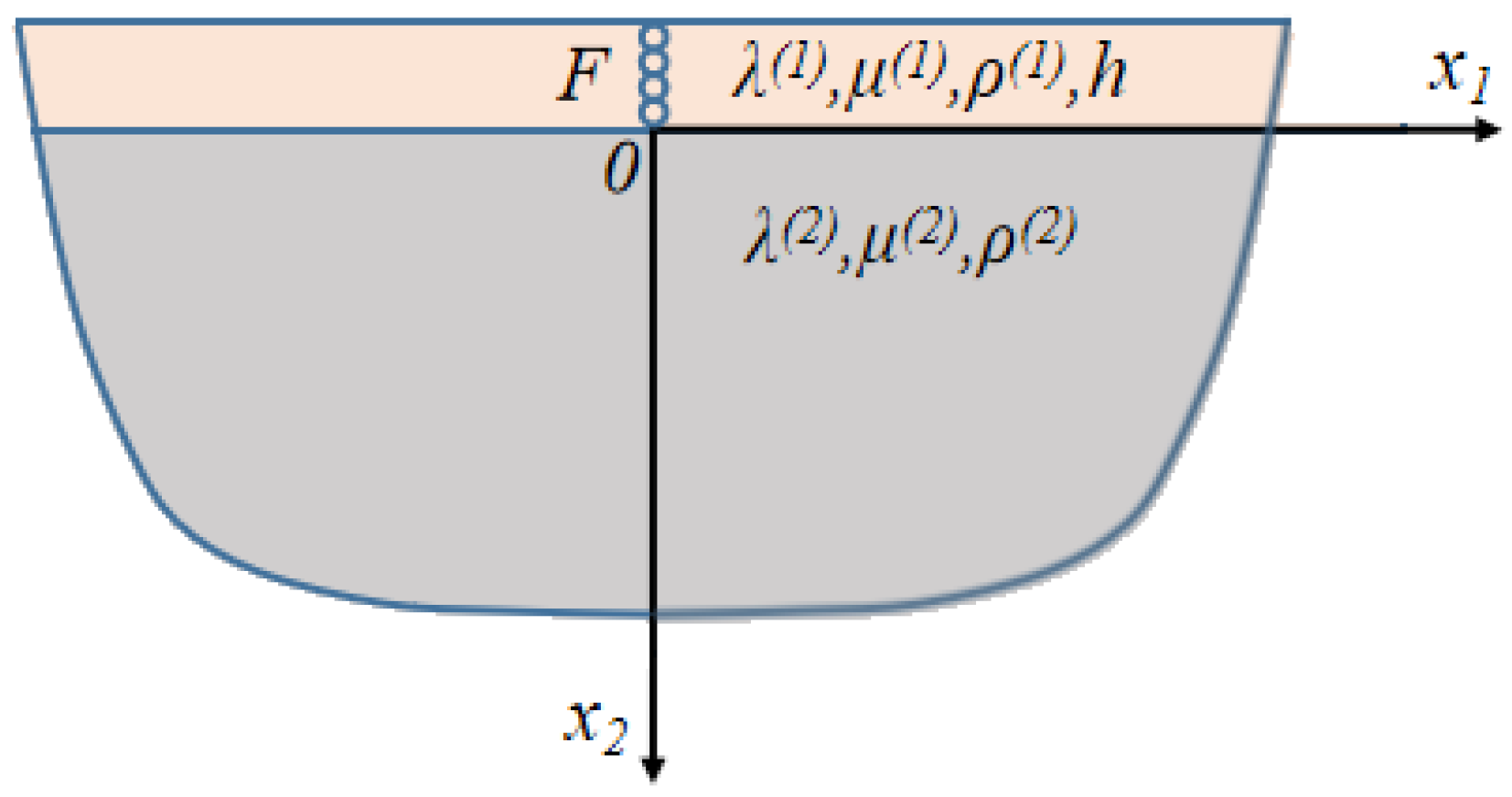
2. The Forced Vibration Solution and the Necessary Condition of Interfacial Stratification of Thin Coating Structures Excited by Horizontal Shear Waves
2.1. The Forced Vibration Solution of Interface Shear Stress of Thin Coating Structures Excited by Horizontal Shear Waves
2.2. The Necessary Condition of Interface Delamination of the Thin Coating Structure Excited by Horizontal Shear Waves
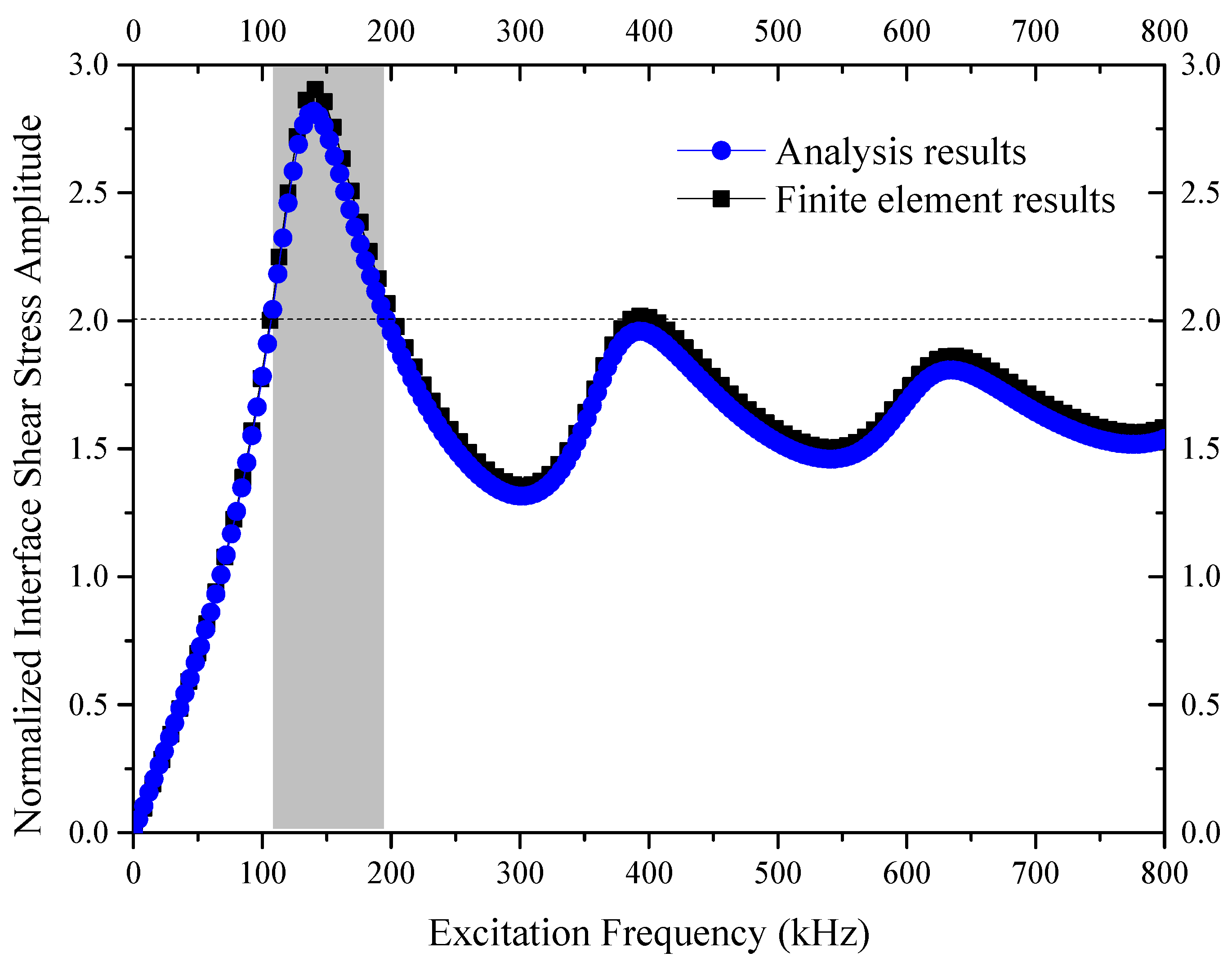
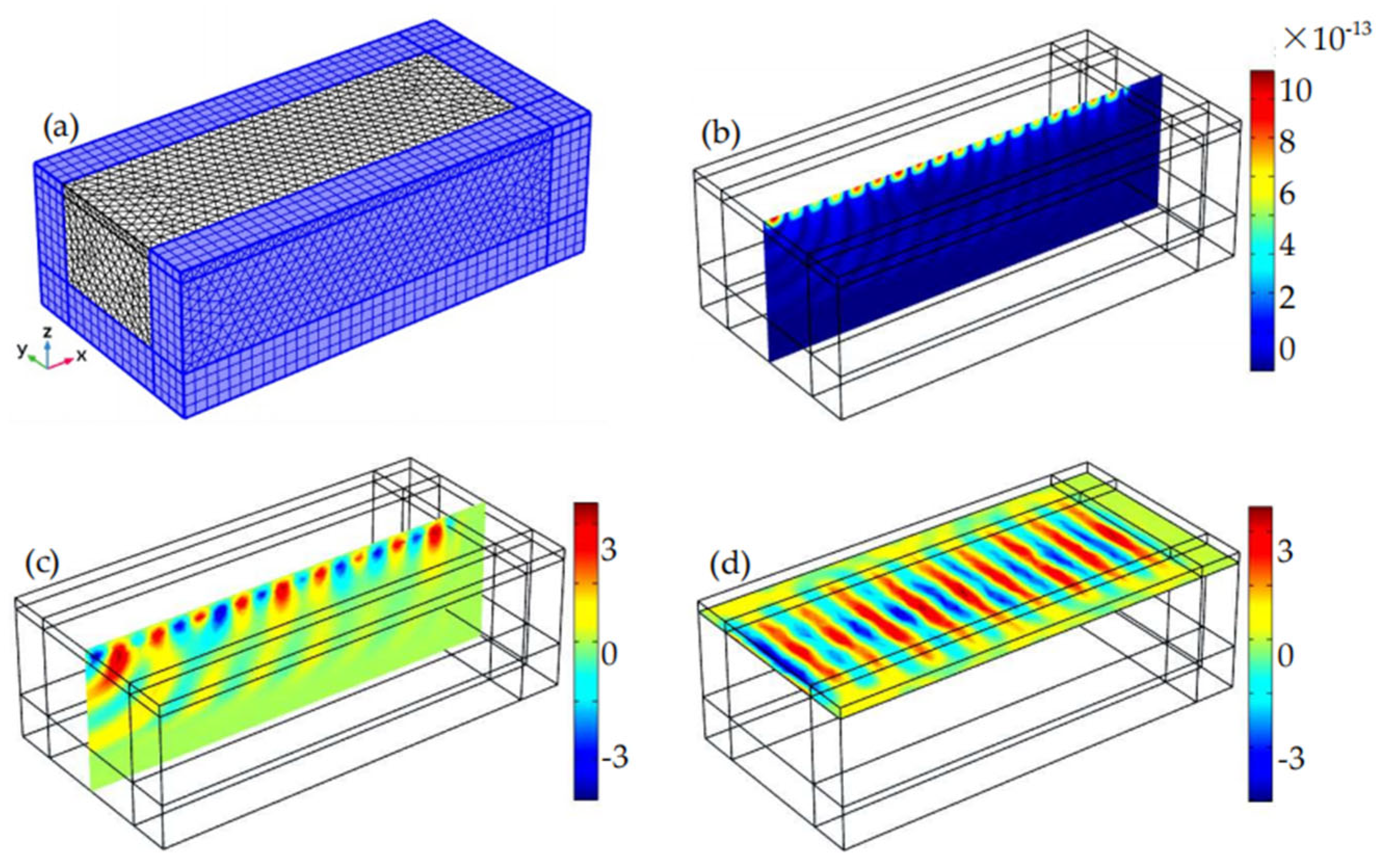
3. Coupled Resonance Mechanism of Interfacial Delamination of Thin Coating Structures Excited by Horizontal Shear Waves
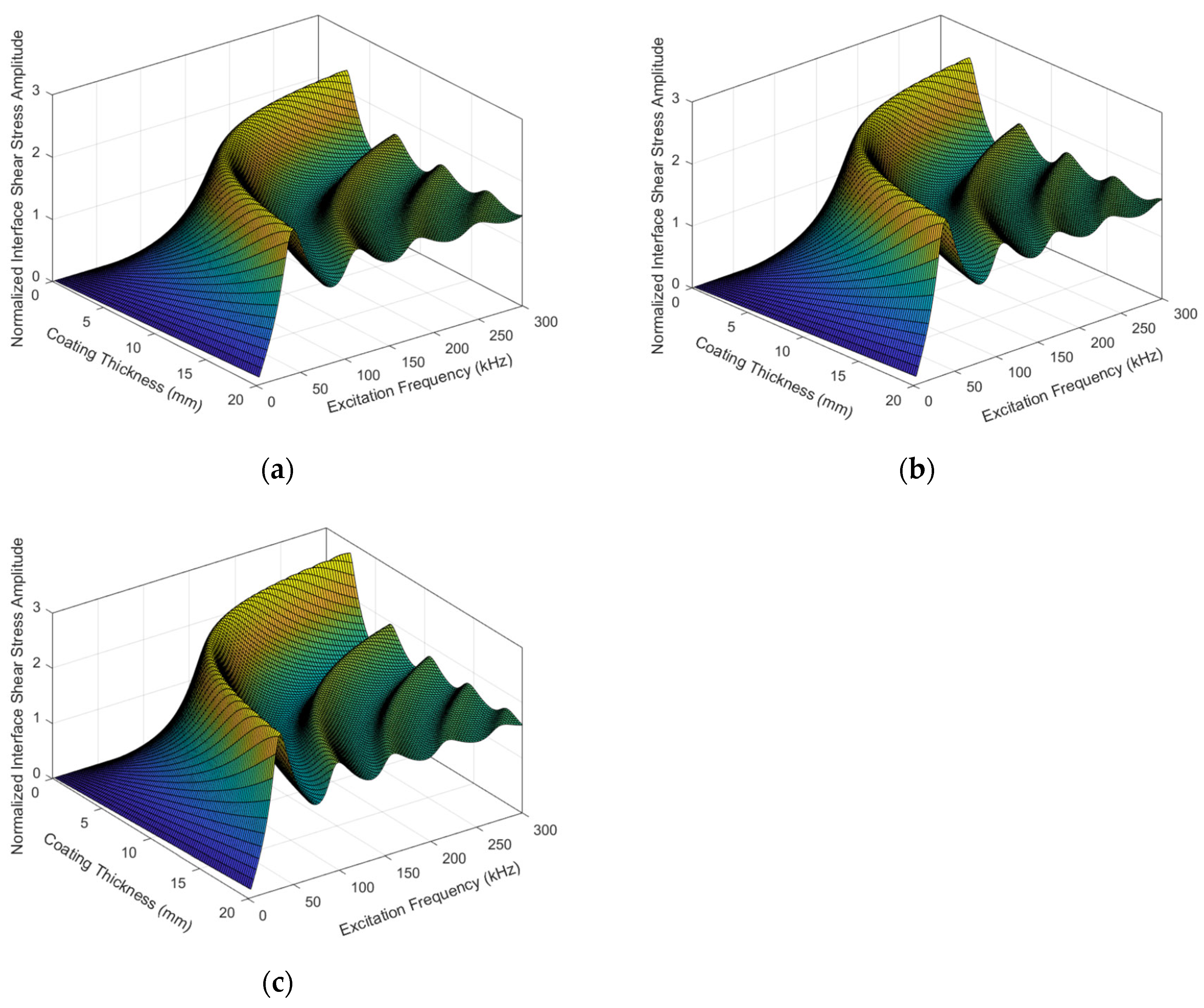
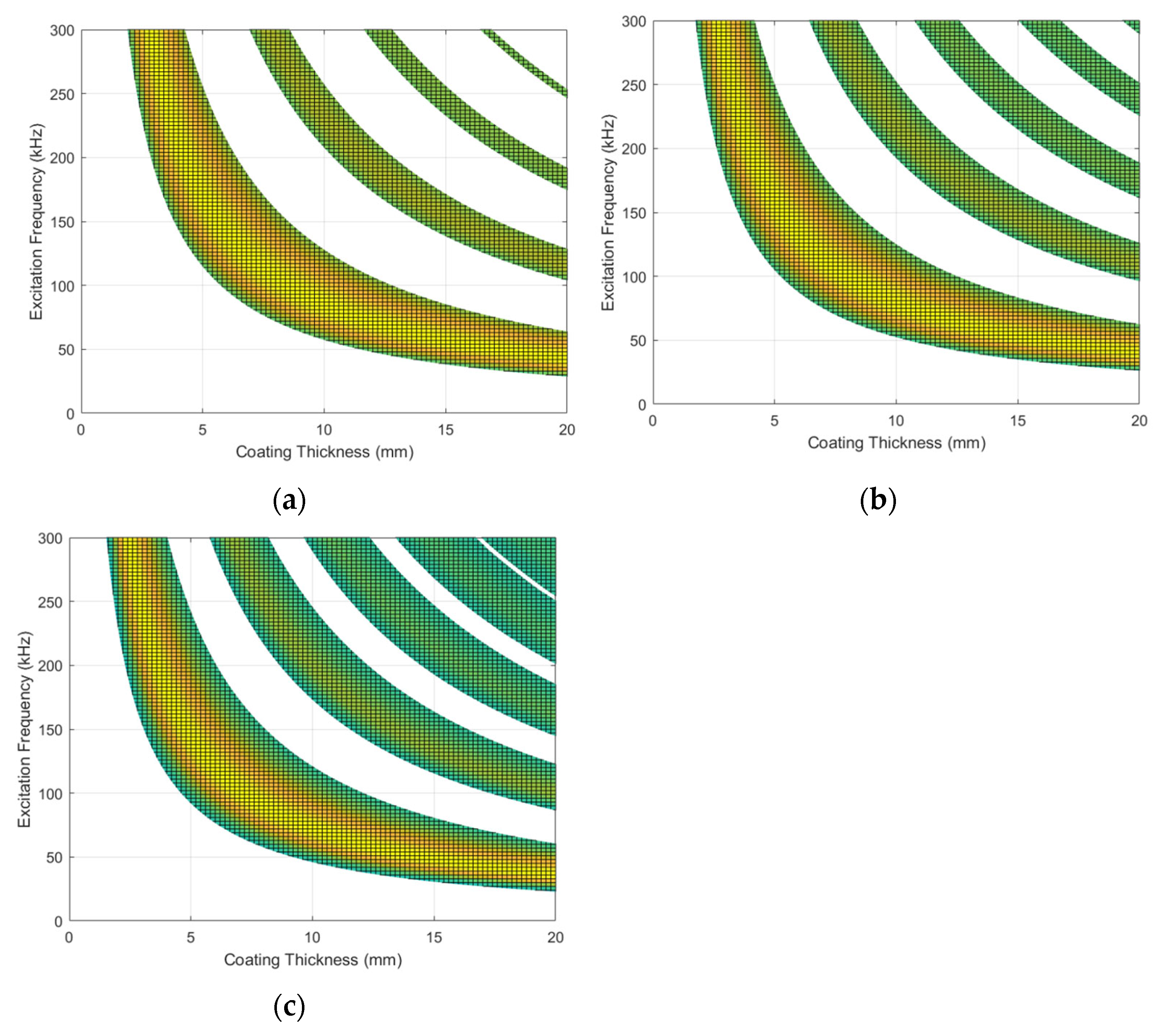
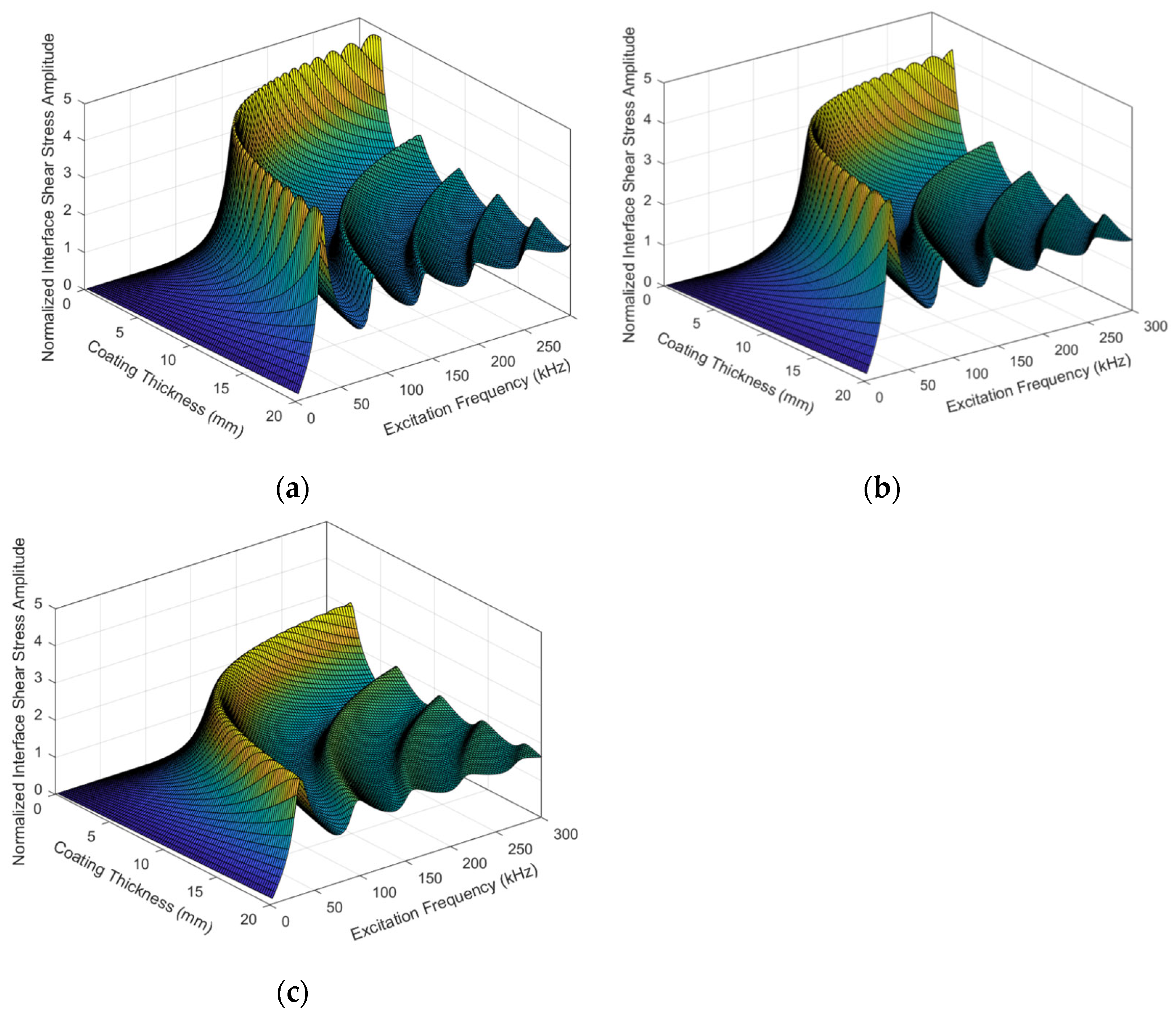
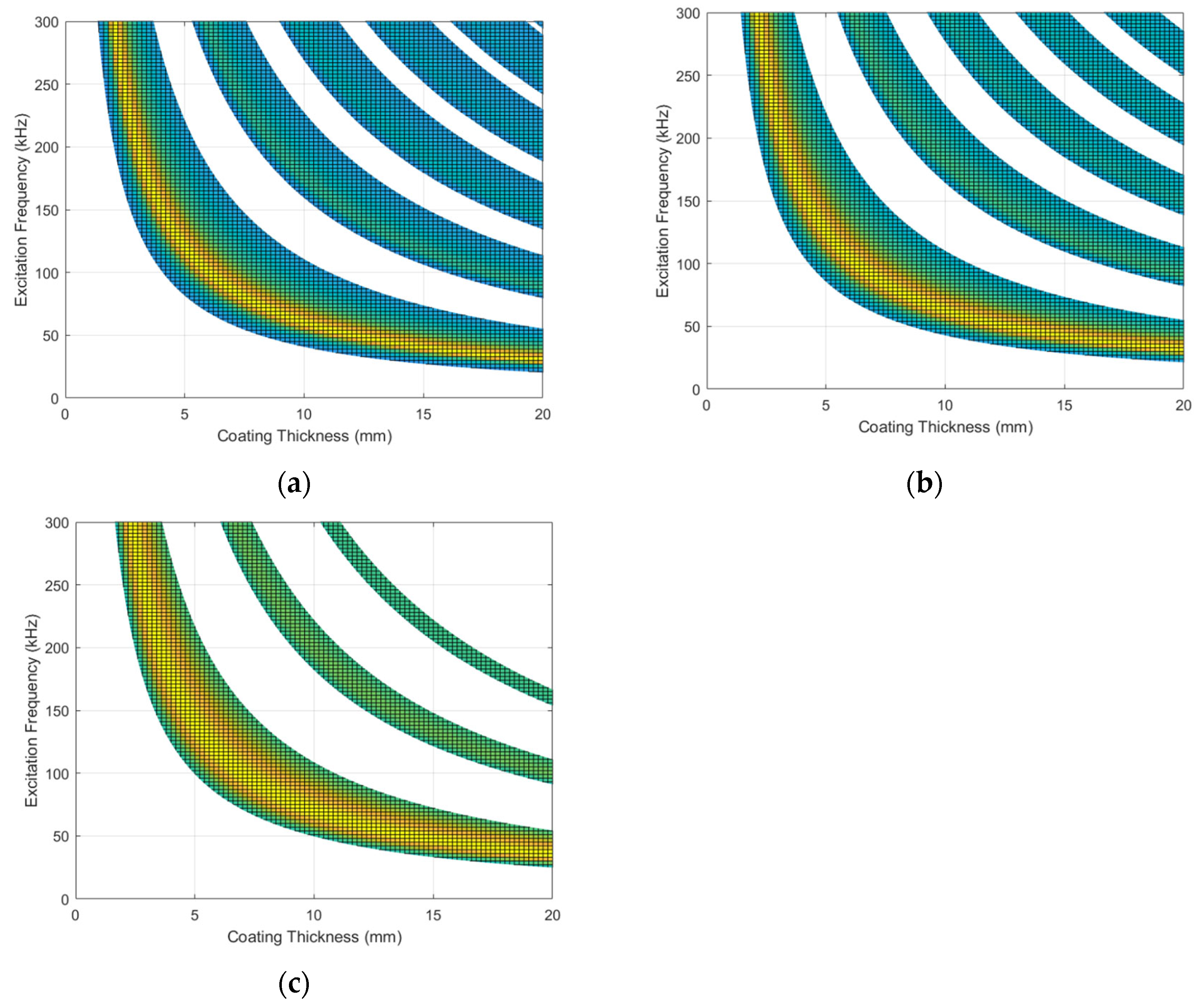
4. The Influence of Thin Coating Material on Coupling Resonance Characteristic and Interfacial Shear Delamination Interval
5. The Influence of Matrix Material on Coupling Resonance Characteristic and Interfacial Shear Delamination Interval
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pickering, S.J. Recycling technologies for thermoset composite materials-current status. Compos. Part A-Appl. Sci. Manuf. 2006, 37, 1206–1215. [Google Scholar] [CrossRef]
- Tan, H.; Xu, G.; Tao, T. Experimental investigation on the defrosting performance of a finned-tube evaporator using intermittent ultrasonic vibration. Appl. Energy 2015, 158, 220–232. [Google Scholar] [CrossRef]
- Palacios, J.; Smith, E.; Rose, J.; Royer, R. Ultrasonic de-icing of wind-tunnel impact icing. J. Aircr. 2011, 48, 1020–1027. [Google Scholar] [CrossRef]
- Bednarik, M.; Cervenka, M.; Lotton, P.; Simon, L. Analytical solutions for elastic SH-waves propagating through an isotropic inhomogeneous layer. Compos. Struct. 2019, 220, 875–887. [Google Scholar] [CrossRef]
- Golub, M.V.; Fomenko, S.I.; Bui, T.Q.; Zhang, C.; Wang, Y.S. Transmission and band gaps of elastic SH waves in functionally graded periodic laminates. Int. J. Solids Struct. 2012, 49, 344–354. [Google Scholar] [CrossRef] [Green Version]
- Mardanshahi, A.; Shokrieh, M.M.; Kazemirad, S. Identification of matrix cracking in cross-ply laminated composites using Lamb wave propagation. Compos. Struct. 2020, 235, 111790. [Google Scholar] [CrossRef]
- Zhu, F.; Pan, E.; Qian, Z. Waves in a generally anisotropic viscoelastic composite laminated bilayer: Impact of the imperfect interface from perfect to complete delamination. Int. J. Solids Struct. 2020, 202, 262–277. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic waves in solid media. Cambridge University Press 1999, 3, 24–25. [Google Scholar] [CrossRef]
- He, J.H. Generalized variational principles for buckling analysis of circular cylinders. Acta Mech. 2020, 231, 899–906. [Google Scholar] [CrossRef]
- He, J.H. Hamilton’s principle for dynamical elasticity. Appl. Math. Lett. 2017, 72, 65–69. [Google Scholar] [CrossRef]
- Al-Furjan, M.S.H.; Habibi, M.; won Jung, D.; Sadeghi, S.; Safarpour, H.; Tounsi, A.; Chen, G. A computational framework for propagated waves in a sandwich doubly curved nanocomposite panel. Eng. Comput. 2022, 38, 1679–1696. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method for autonomous ordinary differential systems. Appl. Math. Comput. 2000, 114, 115–123. [Google Scholar] [CrossRef]
- He, J.H.; El-Dib, Y.O. Homotopy perturbation method for Fangzhu oscillator. J. Math. Chem. 2020, 58, 2245–2253. [Google Scholar] [CrossRef]
- Anjum, N.; He, J.H. Homotopy perturbation method for N/MEMS oscillators. Math. Methods Appl. Sci. 2020, 1–15. [Google Scholar] [CrossRef]
- Debnath, L.; Bhatta, D. Integral Transforms and Their Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Rungger, I.; Droghetti, A.; Stamenova, M. Non-equilibrium Green’s Function Methods for Spin Transport and Dynamics. In Handbook of Materials Modeling: Methods: Theory and Modeling; Springer: Cham, Switzerland, 2020; pp. 957–983. [Google Scholar]
- Polyanin, A.D.; Zhurov, A.I. Separation of variables in PDEs using nonlinear transformations: Applications to reaction–diffusion type equations. Appl. Math. Lett. 2020, 100, 106055. [Google Scholar] [CrossRef]
- Ali, A. The Transform of Partial Differential Equations to Ordinary Differential Equations by Using Integral Transforms and Separation of Variables Methods; University of Gezira: Wad Medani, Sudan, 2017. [Google Scholar]
- Yilmaz, C.; Topal, S.; Ali, H.Q. Non-destructive determination of the stiffness matrix of a laminated composite structure with lamb wave. Compos. Struct. 2020, 237, 111956. [Google Scholar] [CrossRef]
- Ding, L.; Zhu, H.P.; Wu, L. Analysis of mechanical properties of laminated rubber bearings based on transfer matrix method. Compos. Struct. 2017, 159, 390–396. [Google Scholar] [CrossRef]
- Knopoff, L. A matrix method for elastic wave problems. Bull. Seismol. Soc. Am. 1964, 54, 431–438. [Google Scholar] [CrossRef]
- Gao, J.; Lyu, Y.; Zheng, M. Modeling guided wave propagation in multi-layered anisotropic composite laminates by state-vector formalism and the Legendre polynomials. Compos. Struct. 2019, 228, 111319. [Google Scholar] [CrossRef]
- Ogilvy, J.A. A model for the ultrasonic inspection of composite plates. Ultrasonics 1995, 33, 85–93. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Li, G. Reanalysis assisted metaheuristic optimization for free vibration problems of composite laminates. Compos. Struct. 2018, 206, 380–391. [Google Scholar] [CrossRef]
- Tuan, H.S.; Ponamgi, S.R. Excitation of Love Waves in a Thin Film Layer by a Line Source. IEEE Trans. Sonics Ultrason. 1972, 19, 9–14. [Google Scholar] [CrossRef]
- Hashimoto, K.; Yamaguchi, H. Excitation and propagation of shear-horizontal-type surface and bulk acoustic waves. IEEE Trans. Ultrason. Ferr. 2001, 48, 1181–1188. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.K.; Singh, S.; Kumari, R.; Ray, A. Impact of point source and mass loading sensitivity on the propagation of an SH wave in an imperfectly bonded FGPPM layered structure. Acta Mech. 2020, 231, 2603–2627. [Google Scholar] [CrossRef]
- Adachi, K.; Saiki, K.; Sato, H.; Ito, T. Ultrasonic frost suppression. Jpn. J. Appl. Phys. 2003, 42, 682–685. [Google Scholar] [CrossRef]
- Wang, Z. Recent progress on ultrasonic de-icing technique used for wind power generation, high-voltage transmission line and aircraft. Energy Build. 2017, 140, 42–49. [Google Scholar] [CrossRef]
- Palacios, J.; Smith, E.; Rose, J.; Royer, R. Instantaneous de-icing of freezer ice via ultrasonic actuation. AIAA J. 2011, 49, 1158–1167. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Chen, Z. Experimental study on instantaneously shedding frozen water droplets from cold vertical surface by ultrasonic vibration. Exp. Therm. Fluid Sci. 2014, 53, 17–25. [Google Scholar] [CrossRef]
- Tan, H.; Tao, T.; Xu, G. Experimental study on defrosting mechanism of intermittent ultrasonic resonance for a finned-tube evaporator. Exp. Therm. Fluid Sci. 2014, 52, 308–317. [Google Scholar] [CrossRef]
- Kalkowski, M.K.; Waters, T.P.; Rustighi, E. Delamination of surface accretions with structural waves: Piezo-actuation and power requirements. J. Intell. Mater. Syst. Struct. 2017, 28, 1454–1471. [Google Scholar] [CrossRef]
- Overmeyer, A.; Palacios, J.; Smith, E. Ultrasonic de-icing bondline design and rotor ice testing. AIAA J. 2013, 51, 2965–2976. [Google Scholar] [CrossRef]
- Budinger, M.; Pommier-Budinger, V.; Napias, G.; da Silva, A.C. Ultrasonic Ice Protection Systems: Analytical and Numerical Models for Architecture Tradeoff. J. Aircr. 2016, 53, 680–690. [Google Scholar] [CrossRef] [Green Version]
- Venna, S.V.; Lin, Y.J. Mechatronic development of self-actuating in-flight deicing structures. IEEE-ASME Trans. Mech. 2006, 11, 585–592. [Google Scholar] [CrossRef]
- Venna, S.V.; Lin, Y.J.; Botura, G. Piezoelectric transducer actuated leading edge de-icing with simultaneous shear and impulse forces. J. Aircr. 2007, 44, 509–515. [Google Scholar] [CrossRef]
- Zeng, J.; Song, B. Research on experiment and numerical simulation of ultrasonic de-icing for wind turbine blades. Renew. Energy 2017, 113, 706–712. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, Y.; Su, F.; Wang, Y. A light lithium niobate transducer for the ultrasonic de-icing of wind turbine blades. Renew. Energy 2016, 99, 1299–1305. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Lei, Y. An effect assessment and prediction method of ultrasonic de-icing for composite wind turbine blades. Renew. Energy 2018, 118, 1015–1023. [Google Scholar] [CrossRef]
- Habibi, H.; Cheng, L.; Zheng, H.; Kappatos, V.; Selcuk, C.; Gan, T.H. A dual de-icing system for wind turbine blades combining high-power ultrasonic guided waves and low-frequency forced vibrations. Renew. Energy 2015, 83, 859–870. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Xu, Y.; Huang, Q. Progress on ultrasonic guided waves de-icing techniques in improving aviation energy efficiency. Renew. Sust. Energy Rev. 2017, 79, 638–645. [Google Scholar] [CrossRef]
- Wang, D.; Tao, T.; Xu, G.; Luo, A.; Kang, S. Experimental study on frosting suppression for a finned-tube evaporator using ultrasonic vibration. Exp. Therm. Fluid Sci. 2012, 36, 1–11. [Google Scholar] [CrossRef]
- Tan, H.; Zhang, X.; Zhang, L. Ultrasonic influence mechanism of a cold surface frosting process and an optimised defrosting technique. Appl. Therm. Eng. 2019, 153, 113–127. [Google Scholar] [CrossRef]
- Guo, F.; Wu, J.H. Analytical solution and coupling resonance mechanism of interface delamination of composite laminates excited by ultrasonic shear horizontal waves. Compos. Struct. 2021, 276, 114583. [Google Scholar] [CrossRef]
- Guo, F.; Wu, J.H. Coupling resonance mechanism of interfacial stratification of sandwich plate structures excited by SH waves. J. Low Freq. Noise Vib. Act. Control 2021, 40, 1166–1193. [Google Scholar] [CrossRef]
- Guo, F.; Wu, J.H. Coupling resonance mechanism of interfacial fatigue stratification of adhesive and/or welding butt joint structures excited by horizontal shear waves. Int. J. Mod. Phys. B 2021, 35, 2150096. [Google Scholar] [CrossRef]
- Ramani, R.; Saparia, A.; Markna, J. Effect of Nanocoating (CuO Nanoparticles) on the Performance of Solar Evacuated Tube. J. Sustain. Mater. Process. Manag. 2022, 2, 64–71. [Google Scholar] [CrossRef]
- Gander, W.; Gautschi, W. Adaptive quadrature—Revisited. BIT Numer. Math. 2000, 40, 84–101. [Google Scholar] [CrossRef]
- Calvetti, D.; Golub, G.; Gragg, W. Computation of Gauss-Kronrod quadrature rules. Math. Comput. 2000, 69, 1035–1052. [Google Scholar] [CrossRef] [Green Version]
- Johnson, R.W. Algorithm 988: AMGKQ: An Efficient Implementation of Adaptive Multivariate Gauss-Kronrod Quadrature for Simultaneous Integrands in Octave/MATLAB. ACM Trans. Math. Softw. (TOMS) 2018, 44, 1–19. [Google Scholar] [CrossRef]
- Rahman, A.; Huang, H.; Ai, C. Fatigue performance of interface bonding between asphalt pavement layers using four-point shear test set-up. Int. J. Fatigue 2019, 121, 181–190. [Google Scholar] [CrossRef]

| Material | Young’s Modulus (GPa) | Poisson’s Ratio | Density (kg/m3) | Shear Modulus (GPa) | Shear Wave Velocity (m/s) |
|---|---|---|---|---|---|
| Frost | 7.759 | 0.343 | 800 | 2.661 | 1900 |
| Rime Ice | 8.759 | 0.337 | 900 | 3.276 | 1907 |
| Glaze Ice | 9.759 | 0.331 | 950 | 3.666 | 1964 |
| Aluminum | 69.4 | 0.337 | 2700 | 23.4 | 3140 |
| Titanium | 102 | 0.35 | 4600 | 37.778 | 2866 |
| Steel | 205.0 | 0.28 | 7850 | 80 | 3194 |
| Molybdenum | 297.3 | 0.297 | 10,200 | 114.3 | 3350 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, F.; Liu, L.; Yang, S.; Yin, Z.; Wu, J.H.; Zhang, Y.Y. Coupled Resonance Mechanism of Interface Stratification of Thin Coating Structures Excited by Horizontal Shear Waves. Coatings 2022, 12, 1509. https://doi.org/10.3390/coatings12101509
Guo F, Liu L, Yang S, Yin Z, Wu JH, Zhang YY. Coupled Resonance Mechanism of Interface Stratification of Thin Coating Structures Excited by Horizontal Shear Waves. Coatings. 2022; 12(10):1509. https://doi.org/10.3390/coatings12101509
Chicago/Turabian StyleGuo, Feng, Ling Liu, Senlin Yang, Zhifu Yin, Jiu Hui Wu, and Yong Yan Zhang. 2022. "Coupled Resonance Mechanism of Interface Stratification of Thin Coating Structures Excited by Horizontal Shear Waves" Coatings 12, no. 10: 1509. https://doi.org/10.3390/coatings12101509






