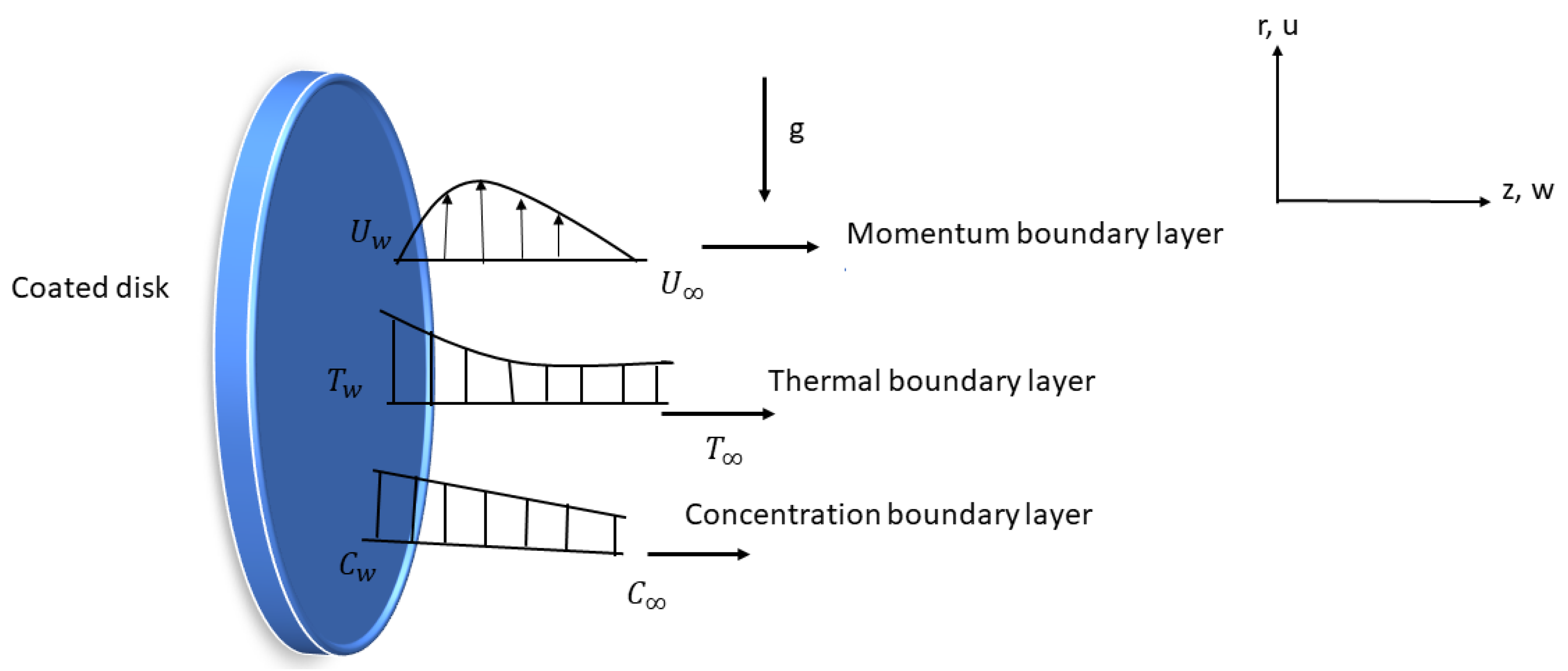
Buoyancy Effect on the Unsteady Diffusive Convective Flow of a Carreau Fluid Passed over a Coated Disk with Energy Loss

Abstract

The unsteady flow of a Carreau fluid over a coated disk under the simultaneous effects of a thermal and concentration field with buoyancy forces is reported. The time-dependent diffusive stream of a Carreau fluid over a conducting coated disk is carried out with energy loss. The time-dependent partial differential equations are first converted into a scheme of ordinary differential equations by the appropriate transformations and are then solved by shooting method. Significant results for speed, hotness and concentration profiles are revealed and deliberated by the graphical outcomes. The numerical values of skin friction suggest that the viscoelastic parameter of the Carreau fluid causes a reduction in the skin friction coefficient due to the coated surface, but the Nusselt and Sherwood numbers increase with the rise of the viscoelastic parameter of the Carreau fluid because of the coated surface. The present model is useful in the field of mechanical engineering to design a tesla turbine for the flow of viscous fluid.

1. Introduction

Thin liquid layers frequently develop on a solid surface or sheet during the coating process. It can be seen in thin-film, boundary-layer and slip flows. Due to the high demand of industry researchers worked on viscous flows over a coated surface under different situations; for instance, Benkeria et al. [1] have analyzed and classified the different types of coating flows and presented analytic solutions. The coating process has many applications in industrial fluid flow, especially in polymeric liquids [2]. Saini et al. [3] discussed an elastohydrodynamic thermal analysis of a couple stress fluid under a lubrication approach when the fluid is in contact with the roller. Chien et al. [4] presented the flow of liquid film between two rollers. A numerical solution was obtained and compared with experimental results. The Navier–Stokes equation in the presence of local acceleration presents the best way to explain flow over a coated surface and can be solved by common techniques, whereas for non-Newtonian fluid flow over a coated surface, Navier–Stokes equations with space and time variables are not adequate. Therefore, to study non-Newtonian fluid flow, Khan et al. [5] investigated the behavior of shear thinning and the thickening of a nanofluid over a radially stretching disk and observed that the heat transfer rate is significant to the boundary layer flow. Khashi’ie et al. [6] presented the axisymmetric steady flow of a hybrid nano fluid over a stretching/shrinking disk and found a similarity solution for the temperature and velocity field. Khashi’ie et al. [7] further considered the unsteady axisymmetric flow of nano fluid over a heated and radially stretching disk and found a dual solution for the control parameter. Ibrahim et al. [8] have computed the numerical solution of the time-dependent flow of viscous fluid over the stretching disk with heat and mass transfer and found that velocity decreases with the porosity parameter, and concentration decreases with the Schmidt number, while temperature increases with a high Prandtl number. Several studies on coated surfaces can be seen in [9,10,11,12,13,14,15] to obtain more understanding about coatings.

Khan et al. [16] presented non-similar solutions under slip conditions, and numerical results for the temperature-field and skin-friction coefficient were found by the RK method. Khan et al. [17] later presented a numerical solution by a shooting method for the boundary layer flow of radioactive Carreau fluid flow subject to thermophysical properties. Khan et al. [18] examined Carreau–Yasuda fluid flow over a conducting plate with zero mass flux and mixed-type boundary conditions. Hassan et al. [19] discussed the zero and high shear-rate viscosities for the momentum, thermal and concentration boundary layer and observed that the boundary layer depended on viscosity. Some other researchers investigated the convective flow of a Carreau fluid over an extending disk under a different situation. Few core investigations on the topic under consideration can be found in [20,21,22,23,24,25].

Since the mixed convective flow of a Carreau fluid under the buoyancy effect have a significant role in industry, researchers have focused their efforts on observing the effects of the Weissenberg number, Eckert number and buoyancy force. A dual solution of the chemically reactive flow of Carreau fluid over the shrinking surface under the effect of the buoyance force and Eckert number has been discussed by Hafeez et al. [26]. Hameed et al. [27] found the axisymmetric convective flow of a Carreau fluid over a stretching disk and found a decreasing effect of the Eckert number on temperature. Jamaluddin et al. [28] presented a BVP4c solution of a Cross fluid over a stretching and shrinking sheet, and a growing effect of Weissenberg number on the velocity and a decelerating effect of Weissenberg number on the temperature profile have been discussed. A few core investigations on the topic under consideration can be found in [29,30,31,32,33,34,35,36].

All of the above studies were limited to the momentum, energy and concentration equations for the flow of Carreau fluid under the effect of viscous dissipation or buoyancy effect. Still the buoyancy, time and viscous dissipation effects have not been incorporated by previous researchers due to temperature and concentration variance over coated disks.

The theme of the current investigation is to explore the unsteady diffusive convective flow of a Carreau fluid with the special effects of viscous dissipation and buoyancy forces over a coated disk. Mathematical modeling is made subject to the axisymmetric condition of the disk, and the governing equations are simplified with the lubrication approach in the axial direction of the disk. The similarity transformation and numerical methods are used to obtain the results of a nonlinear scheme of partial differential equations. The impacts of emerging parameters on the speed, hotness of the fluid and concentration profiles are shown through numerical results in the form of graphs. In the lubrication theory of the diffusive convective flow of a viscous fluid over the coated surface; the Nusselt number, Sherwood number and skin-friction coefficient are very significant, which is shown through the tables.

2. Method and Material

The incompressible unsteady diffusive convective flow of a Carreau fluid over a coated disk was considered under the effect of buoyancy force and viscous dissipation. The linear type of velocity on a disk ($U=\frac{cr}{t}$) is responsible for developing the axisymmetric thin-film flow of a Carreau fluid in a result of the coating process. The temperature of the conducting disk is $T_w$, and temperature of the fluid away from the surface is $T_{\infty }$; the concentration on the disk is assumed to be $C_w$, and the concentration of the fluid away from the disk is $C_{\infty }$. The modeling of the problem suggests the flow geometry in the rz-plane, which is shown in Figure 1.

For the axisymmetric flow, the following velocity function is chosen

$$\mathit{V}=u\left(t,r,z\right)e_r+w\left(t,r,z\right)e_z,$$

(1)

where $u$ and $w$ are the radial and axial velocity, respectively. The momentum, energy and concentration equations for the mixed diffusive flow of a Carreau fluid [37] are given as follows

$$div \mathit{V}=0,$$

(2)

$$\rho \left(\frac{\partial \mathit{V}}{\partial t}+\left(\mathit{V}.\mathbf{\nabla }\right)\mathit{V}\right)=div \mathbf{\tau }+\mathit{F},$$

(3)

where

$$\mathit{F}=\rho \mathit{g}\left\{{\beta }_T\left(T-T_{\infty }\right)+{\beta }_C\left(C-C_{\infty }\right)\right\},$$

(4)

$$\mathbf{\tau }={\eta }^{\ast }{\mathit{A}}_1-p\mathit{I}, {\mathit{A}}_{\mathit{1}}=\mathit{L}+{\mathit{L}}^{\mathit{T}}, L=grad\mathit{V},$$

(5)

$${\eta }^{\ast }={\eta }_{\infty }+\left({\eta }_0-{\eta }_{\infty }\right)\left[\frac{1}{1+{\left(\mathsf{\Gamma }\dot{\gamma }\right)}^n}\right], \rho C_p\left(\frac{\partial T}{\partial t}+\left(\mathit{V}.\mathbf{\nabla }\right)T\right)=\alpha {\mathbf{\nabla }}^{2}T+{\mu }^{\ast }trace\left({\mathit{A}}_{\mathit{1}}.\mathit{L}\right)$$

(6)

$$\frac{ \partial C}{\partial t}+\left(\mathit{V}.\mathbf{\nabla }\right)C=D\left({\mathbf{\nabla }}^{2}C\right)$$

(7)

The boundary and initial conditions for a linearly stretching conducting disk [38] are given as follows

$$u=U_w, w=0, T=T_w, C=C_w at z=0,$$

(8a)

$$u\to 0, T\to T_w, C\to C_{\infty }, \mathrm{as} z\to \infty$$

(8b)

$$u=0, w=0, T=0, C=0, at t=0,$$

(8c)

where $U_w=\frac{cr}{t}$ is the velocity on the coated surface, $\alpha$ is the thermal conductivity, ${\beta }_T$ is the thermal extension parameter, ${\beta }_C$ is the concentration extension parameter, ${\eta }^{\ast }$ is the Cross fluid viscosity, ${\eta }_{\infty }$ is the infinite shear-rate viscosity and is taken to be zero, ${\eta }_0$ is the zero shear-rate viscosity, $T_w$ and $C_w$ are the wall temperature and concentration, $T_{\infty }$ and $C_{\infty }$ are the ambient temperature and concentration of the fluid.

After using the following boundary layer approximation, Equations (2)–(8) take the form of Equations (9)–(13)

$$\begin{array}{c}w=o\left(\delta \right), r=o\left(1\right), u=o\left(1\right), z=o\left(\delta \right), C=o\left(1\right),\\ \mathsf{\nu }=o\left({\delta }^2\right) \mathsf{\Gamma }=o\left({\delta }^2\right), \mathrm{T}=o\left(1\right), t=o\left(1\right)\end{array}$$

$$\frac{ u}{r}+\frac{\partial u}{\partial r}=-\frac{\partial w}{\partial z}$$

(9)

$$\begin{array}{c}\frac{\partial u}{ \partial t}+u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}-\left\{g{\beta }_T\left(T-T_{\infty }\right)+g{\beta }_C\left(C-C_{\infty }\right)\right\}\\ =\upsilon \frac{\partial }{\partial z}\left[{\left\{1+{\mathsf{\Gamma }}^2{\left(\frac{\partial u}{\partial z}\right)}^n\right\}}^{-1}\frac{\partial u}{\partial z}\right],\end{array}$$

(10)

$$\frac{\partial T}{ \partial t}+u\frac{\partial \mathrm{T}}{\partial r}+w\frac{\partial \mathrm{T}}{\partial z}=\frac{k}{\rho c_p}\frac{{\partial }^{2}T}{\partial z^2}+\frac{\upsilon }{c_p}\left[\frac{{\left(\frac{\partial u}{\partial z}\right)}^2}{1+{\left(\mathsf{\Gamma }\left(\frac{\partial u}{\partial z}\right)\right)}^n}\right],$$

(11)

$$\frac{ \partial C}{\partial t}+u\frac{\partial C}{\partial r}+w\frac{\partial C}{\partial z}=D\frac{{\partial }^{2}C}{\partial z^2}.$$

(12)

The boundary and initial conditions are assumed as follows:

$$\mathrm{at} z=0 U=\frac{cr}{t},w=0,T=T_w, C=C_w$$

(13a)

$$as z\to \infty U\to 0, T\to T_w, C\to C_{\infty },$$

(13b)

$$\mathrm{at} t=0, u=0, w=0, T=0, C=0.$$

(13c)

For more simplification, we can use following similarity transformation and non-dimensional variables [38] as:

$$\eta =z\sqrt{\frac{c}{t\upsilon }}, \theta =\frac{T-T_{\infty }}{T_w-T_{\infty }}, u=\frac{cr}{t}{f}^{\prime }\left(\eta \right), w=-2\frac{\sqrt{c\upsilon }}{t}f\left(\eta \right), \varphi =\frac{C-C_{\infty }}{C_w-C_{\infty }}.$$

(14)

Using Equation (14) in Equations (9)–(13), the following system is obtained

$$\begin{array}{c}\left[2f{f}^{″}-{\left(f^{\prime }\right)}^2+\frac{1}{c}\left(f^{\prime }-\frac{\eta }{2}{f}^{″}\right)+\lambda \left(\theta +N_r\varphi \right)\right]{\left\{1+{\left(We{f}^{″}\right)}^n\right\}}^2\\ +\left\{1+\left(1-n\right){\left(We{f}^{″}\right)}^n\right\}{f}^{‴}=0,\end{array}$$

(15)

$$Pr{\theta }^{″}+2f{\theta }^{\prime }+\frac{\eta }{2c}{\theta }^{\prime }+\frac{Ec{\left(f^{″}\right)}^2}{\left(1+{\left(We{f}^{″}\right)}^n\right)}=0,$$

(16)

$${\varphi }^{″}+Sc\left(2f{\varphi }^{\prime }+\frac{\eta }{2c}{\varphi }^{\prime }\right)=0.$$

(17)

The above problem reduces into the boundary layer flow of the Navier–Stokes equation when $\lambda \mathrm{and} We\to 0$; furthermore, the effect of energy loss can be observed by the Eckert number for the Newtonian fluid, as mentioned in [39].

The relevant boundary conditions in reduced form are

$$f\left(0\right)=0, f^{\prime }\left(0\right)= \theta \left(0\right)= \varphi \left(0\right)=1,$$

(18a)

$$f^{\prime }\left(\infty \right), \theta \left(\infty \right), \varphi \left(\infty \right)\to 0$$

(18b)

where $We\left(=\Gamma cr\sqrt{\frac{c}{t\nu }}/t\right)$ is the Weissenberg number, $\lambda \left(=\frac{g{\beta }_T\left(T_w-T_{\infty }\right)r}{{\left(U_w\right)}^2}\right)$ is the buoyancy parameter, $N_r\left(=\frac{{\beta }_c\left(c_w-c_{\infty }\right)}{{\beta }_T\left(T_w-T_{\infty }\right)}\right)$ is the buoyancy ratio parameter, $Sc\left(=\upsilon /D\right)$ Schmidt number, $Ec\left(=\frac{U\left(r\right)}{T_{\infty }{C}_p}\right)$ is the Eckert number, and $Pr\left(=\frac{{\eta }_0{C}_p}{k}\right)$ is the Prandtl number.

The local skin-friction coefficient ${\mathit{C}}_f$ is important for its practical significance and is defined [39] as follows:

$${\mathit{C}}_f=\frac{{\left.{\tau }_{rz}\right|}_{z=0}}{\frac{1}{2}{U}_2\rho },$$

(19)

where

$${\left. {\tau }_{rz}\right|}_{z=0}={\left[{\eta }_0\frac{u_z}{{\left\{\mathsf{\Gamma }{u}_z\right\}}^n+1}\right]}_{z=0}.$$

(20)

The local skin-friction coefficient in non-dimensional form is

$$0.5\sqrt{Re}{C}_f=-\frac{f^{″}\left(0\right)}{1+{\left(We{f}^{″}\left(0\right)\right)}^n}.$$

(21)

The local Nusselt number [39] is defined as

$$Nu=\frac{r{q}_w}{k\left(T_w-T_{\infty }\right)},$$

(22)

where $q_w\left(=-{\left.k{T}_z\right|}_{z=0}\right)$ is the heat flux at the surface.

The non-dimensional Nusselt number is defined as

$$\frac{Nu}{\sqrt{\mathrm{Re}}}=-\theta \prime (0)$$

(23)

The local Sherwood number expression, which is the mass transfer rate [39], is expressible as

$$Sh=\frac{r{q}_c}{D\left(C_w-C_{\infty }\right)},$$

(24)

where $q_c\left(=-{\left.D{C}_z\right|}_{z=0}\right)$ is the mass flux at the surface, and the Sherwood number is written as

$$\frac{Sh}{\sqrt{\mathrm{Re}}}=-\varphi \prime (0)$$

(25)

The system of highly non-linear Equations (15)–(17) are solved by a numerical technique, the shooting method, which is an easy and efficient method of tackling the problem. The scheme of the shooting method is described as follows and is solved with the help of the software Matlab, which is more efficient than other software.

$$y_1=f, y_2=f^{\prime }, y_3=f″$$

(26)

$$y_3^{\prime }=f^{‴}=-\frac{{\left[1+{\left(We{y}_3\right)}^n\right]}^2\left[2y_1{y}_3-y_2^2+\frac{1}{c}\left(y_2-\frac{\eta }{2} y_3\right)+\lambda \left(y_4+N_r{y}_6\right)\right]}{\left[1+\left(1-n\right){\left(We{y}_3\right)}^n\right]}$$

(27)

$$y_4=\theta , y_5={\theta }^{\prime }$$

(28)

$$y_5^{\prime }={\theta }^{″}=-\frac{1}{Pr}\left[2y_1{y}_5+\frac{\eta }{2c}{y}_5+\frac{Ec{y}_3^2}{\left(1+{\left(We{y}_3\right)}^n\right)}\right]$$

(29)

$$y_6=\phi , y_7={\phi }^{\prime }$$

(30)

$$y_7^{\prime }={\phi }^{″}=-Sc\left(2y_1{y}_7+\frac{\eta }{2c}{y}_7\right)$$

(31)

With the intial condition

$$\begin{array}{c}{y}_1\left(0\right)=0, y_1^{\prime }\left(0\right)=1\\ y_4\left(0\right)=1, y_6\left(0\right)=1\end{array}$$

(32)

3. Results and Discussion

The mathematical analysis of the proposed problem is explained by the velocity, temperature and concentration profiles, which are computed with the help of the shooting method and the software “Matlab”. The flow behavior is discussed in the momentum, thermal and concentration boundary layer for Weissenberg number We (due to Carreau fluid parameter), buoyancy parameter $\lambda$ (due to temperature difference), buoyancy ratio parameter N_r (due to concentration difference), Schmidt number Sc (due to concentration boundary layer), Eckert number Ec (due to viscous dissipation term) and Prandtl number P_r (due to thermal boundary layer) through Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, and the values of the remaining parameters are chosen from the [37].

Figure 2 shows that the velocity boundary layer along the disk drops with the rising values of the fluid velocity parameter on the surface because the moving surface causes a reduction in the momentum boundary layer that controls the flow of a Carreau fluid in the boundary layer region near the disk. It is discernible from Figure 3 that the speed of the fluid along the surface increases with the rising values of the Weissenberg number in the boundary layer region because the Weissenberg number shows the shear thinning effects that weaken the resistive forces in the Carreau fluid stream. It can be seen in Figure 4 that the growing values of the buoyancy ratio parameter due to the concentration difference causes a reduction in the friction between the molecules that make the fluid thin, and the flow along the disk becomes fast in the velocity boundary layer region.

Figure 5 shows that the hotness of the Carreau fluid escalates with mounting values of the Eckert number because the energy loss due to kinetic energy relative to the enthalpy difference in the thermal boundary layer become high in the heat equation, which supports an increase in temperature. Since the thickness of the momentum and the thermal boundary layer can be controlled by the Prandtl number, to observe the effect of the Prandtl number on the temperature profile, Figure 6 is plotted. This graph shows that the growing values of the Prandtl number moderate the hotness of the Carreau fluid in the region of the thermal boundary layer. The chosen values of the Prandtl number shows that the fluid can freely move over a solid surface with high thermal conductivity. Figure 7 confirms that the hotness of a Carreau fluid falls as the Weissenberg number rises because the mentioned values of We (Weissenberg) specify that the viscous forces are dominant over the elastic forces. Therefore, the viscosity of the fluid helps to moderate the hotness in the thermal boundary layer near the surface of the coated disk due to the compactness of the molecules.

It is noticeable in Figure 8 that the concentration profile rises with the growing values of the velocity parameter on the coated disk. This figure shows that the fluid velocity on the disk helps the increase in the concentration boundary layer region because it causes fast movement and diffusion in the fluid. Figure 9 shows that the concentration field decays with the growing values of the Schmidt number because the simultaneous effects of momentum and mass diffusivity produce the concentration boundary layer. The indicated values of the Schmidt number show that the mass diffusion rate is dominant over the viscous diffusion rate, and, when this rate grows, the boundary layer due to concentration decays.

Table 1. Numerical results of local skin-friction, Nusselt and Sherwood numbers for $n=1; Ec=0.2; Pr=0.7; Sc=0.2; \lambda =0.1; Nr=1; c=5$.

$\mathit{W}\mathit{e}$	$\mathbf{0.5}\sqrt{\mathit{R}\mathit{e}}{\mathit{C}}_{\mathit{f}}$	$\frac{\mathit{N}\mathit{v}}{\sqrt{\mathit{R}\mathit{e}}}$=$\mathbf{-}{\mathit{\theta }}^{\mathbf{\prime }}\left(\mathbf{0}\right)$	$\frac{\mathit{S}\mathit{h}}{\sqrt{\mathit{R}\mathit{e}}}\mathbf{=}\mathbf{-}{\mathit{\phi }}^{\mathbf{\prime }}\left(\mathbf{0}\right)$
0.1	0.88008	0.58647	0.37169
0.3	0.79701	0.59361	0.3766
0.5	0.72481	0.60082	0.38182
0.7	0.66180	0.60799	0.38731
0.9	0.60660	0.61497	0.39302

shows that the skin friction decreases but the Nusselt and Sherwood numbers surge with the growing values of We, and the numerical results indicate that the viscoelastic parameter causes a reduction in the resistive force between the fluid layers and increases the heat transfer and diffusion rate near the surface due to the conducting and coated surfaces.

Table 2. Impact of $Pr$ on the Nusselt number for $We=0.2; n=2; Ec=0.2; sc=0.2; \lambda =0.1; Nr=1;c=5$.

$\mathit{P}\mathit{r}$	$\frac{\mathit{N}\mathit{v}\mathbf{ }}{\sqrt{\mathit{R}\mathit{e}}}\mathbf{ }$=$\mathbf{-}{\mathit{\theta }}^{\mathbf{\prime }}\left(\mathbf{0}\right)$
0.2	2.0853
0.4	1.4543
0.6	1.1674
0.8	0.99422
1.0	0.87521

demonstrates that the heat transfer rate on the surface of the coated disk drops with the growing values of Pr, since $Pr<1;$ therefore, the thermal boundary layer is thinner than the momentum boundary layer.

Table 3. Impact of $Sc$ on the Sherwood number for $We=0.2; n=2; Ec=0.2; Pr=0.7; \lambda =0.1; Nr=1; c=5$.

$\mathit{S}\mathit{c}$	$\frac{\mathit{S}\mathit{h}}{\sqrt{\mathit{R}\mathit{e}}}\mathbf{=}\mathbf{-}{\mathit{\phi }}^{\mathbf{\prime }}\left(\mathbf{0}\right)$
0.2	0.36651
0.4	0.53334
0.6	0.68433
0.8	0.81852
1.0	0.93893

confirms that the diffusion rate on the surface of the coated disk rises with the growing values of the Schmidt number, i.e., when the ratio of momentum to mass diffusivity increases, then the mass transfer coefficient boosts.

Table 4. Comparison of the values of $-f″\left(0\right)$ for a Newtonian fluid.

Exact [40]	Perturbation [40]	Approximate [40]	HAM [41]	Numerical [42]	Present
1.17372	1.17372	1.154701	1.17559	1.17373	1.1737

shows a good agreement between the present research and previous research conducted by [40,41,42] in the case of the forced convective flow of a Newtonian fluid when We = 0 and N_r = 0.

4. Conclusions

This study presents a mathematical analysis of the unsteady diffusive flow of a non-Newtonian (Carreau) fluid over a coated disk under the effect of buoyancy and thermal effects. A mathematical model of the complex problem is presented by a scheme of partial differential equations, which are reduced into a set of ordinary differential equations by suitable transformations. The shooting method is adopted to crack down on the problem, and results for speed, temperature and concentration field are calculated. The effects of emerging parameters are observed by the graphical results, which were plotted in the software Matlab. The numerical results for skin friction, the Nusselt number and the Sherwood number are presented for different values of the viscoelastic parameter We, Prandtl number Pr and the Schmidt number Sc. The crucial consequences are précised as follows:

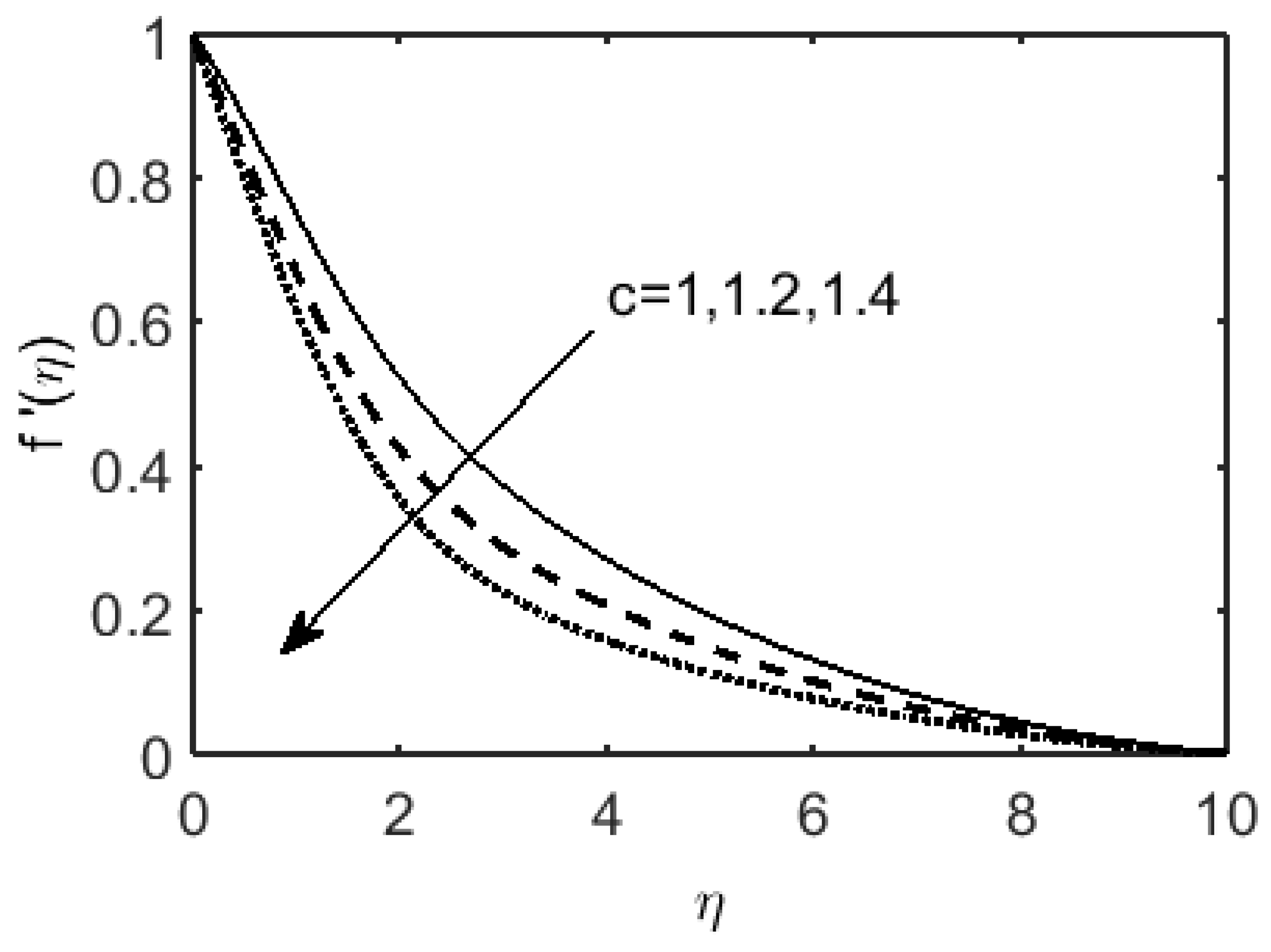
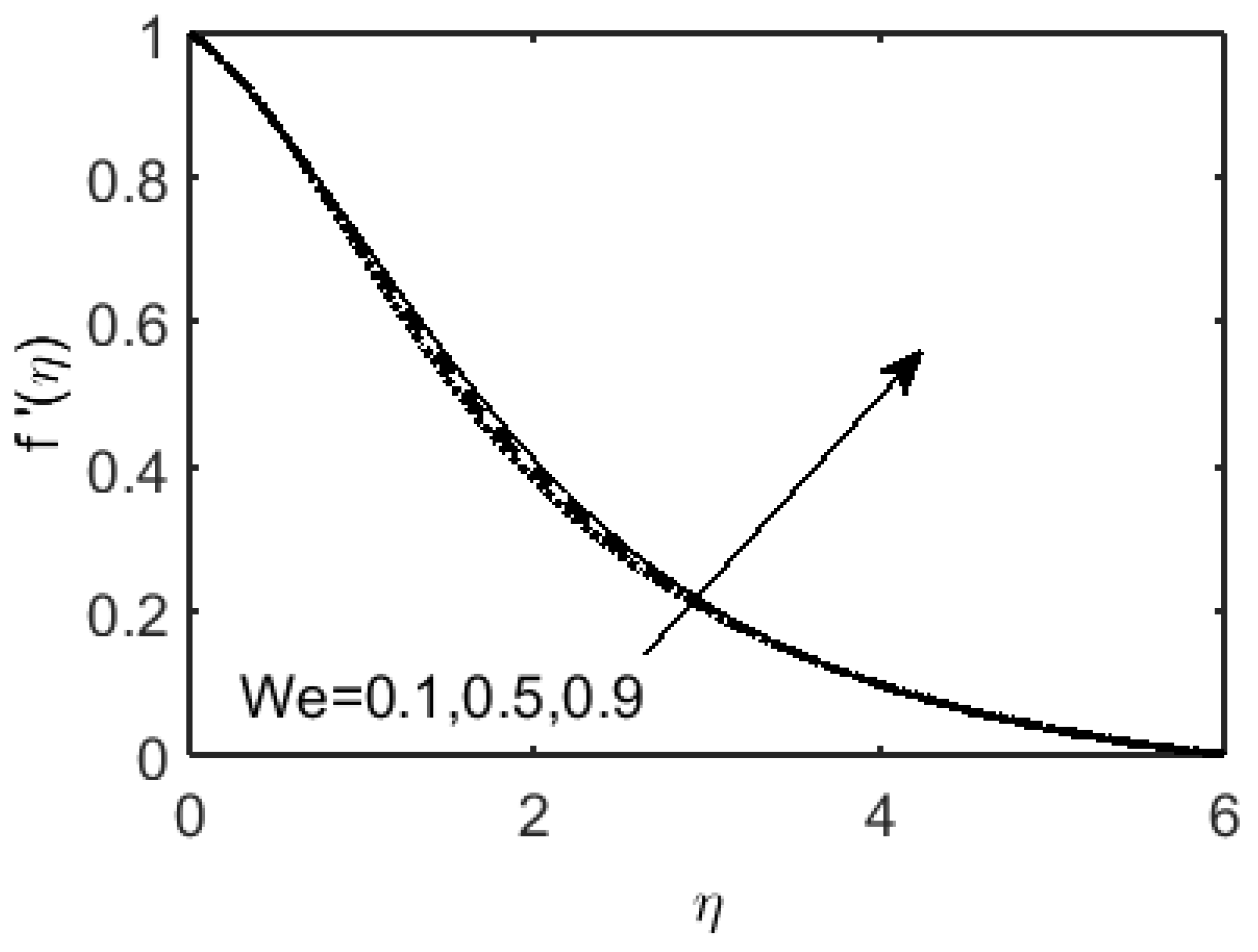
• The speed $c$ of the fluid on the surface helps to decelerate the momentum boundary layer of a Carreau fluid, whereas $We$ accelerates the boundary layer, and $Nr$ shows dual behavior on the momentum boundary layer.
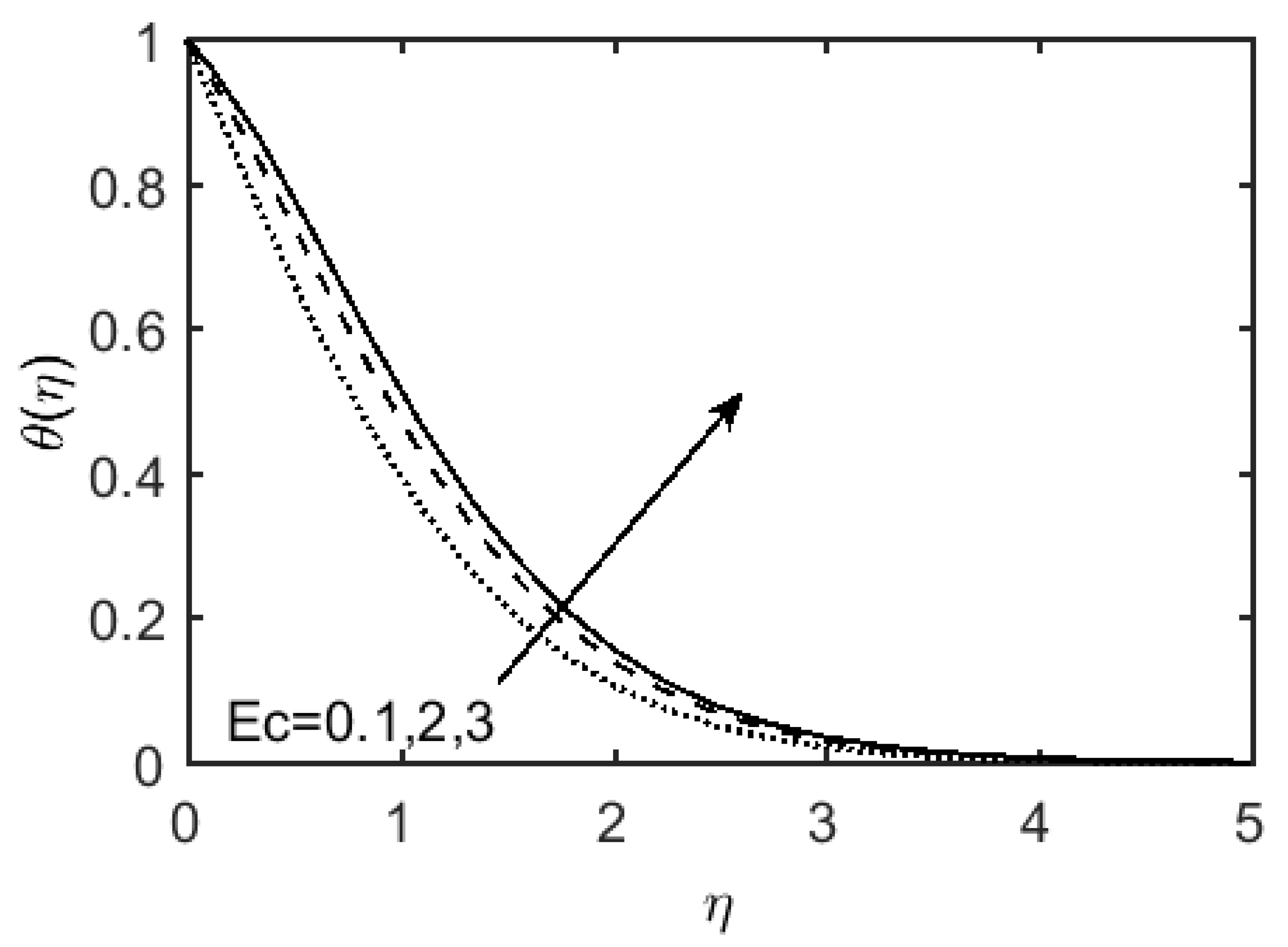
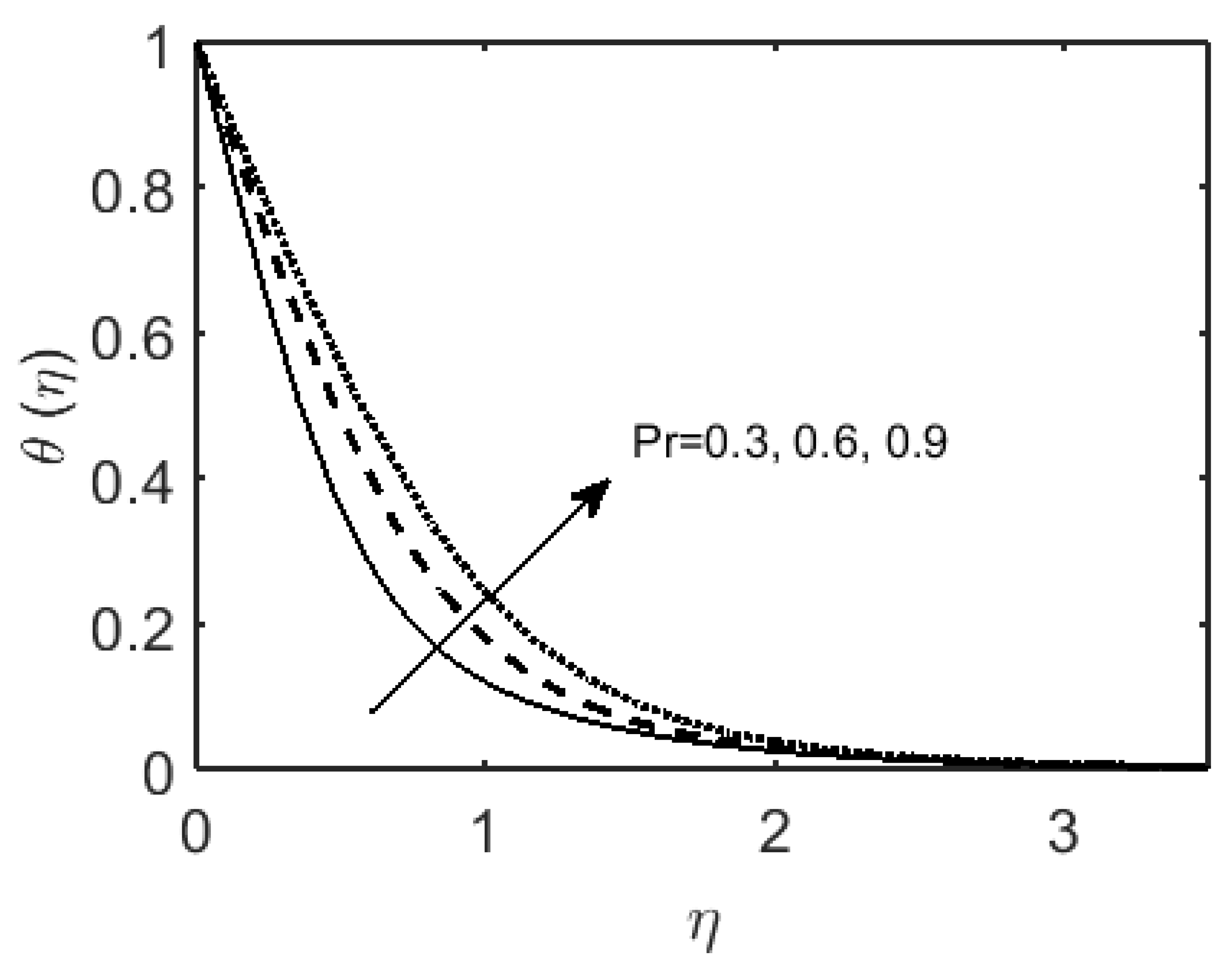
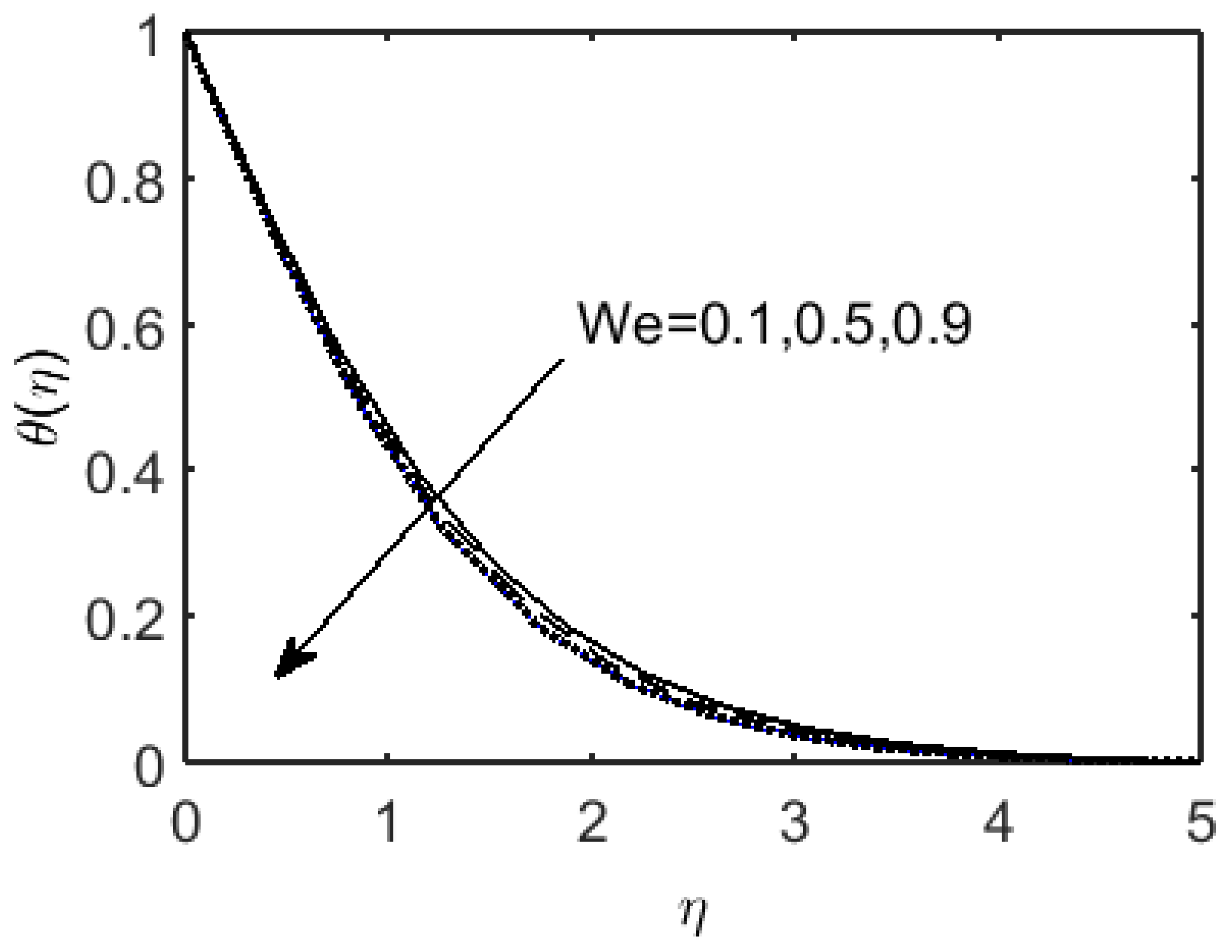
• The temperature of the fluid improves with $Pr$ and $Ec$, whereas it drops with $We$.
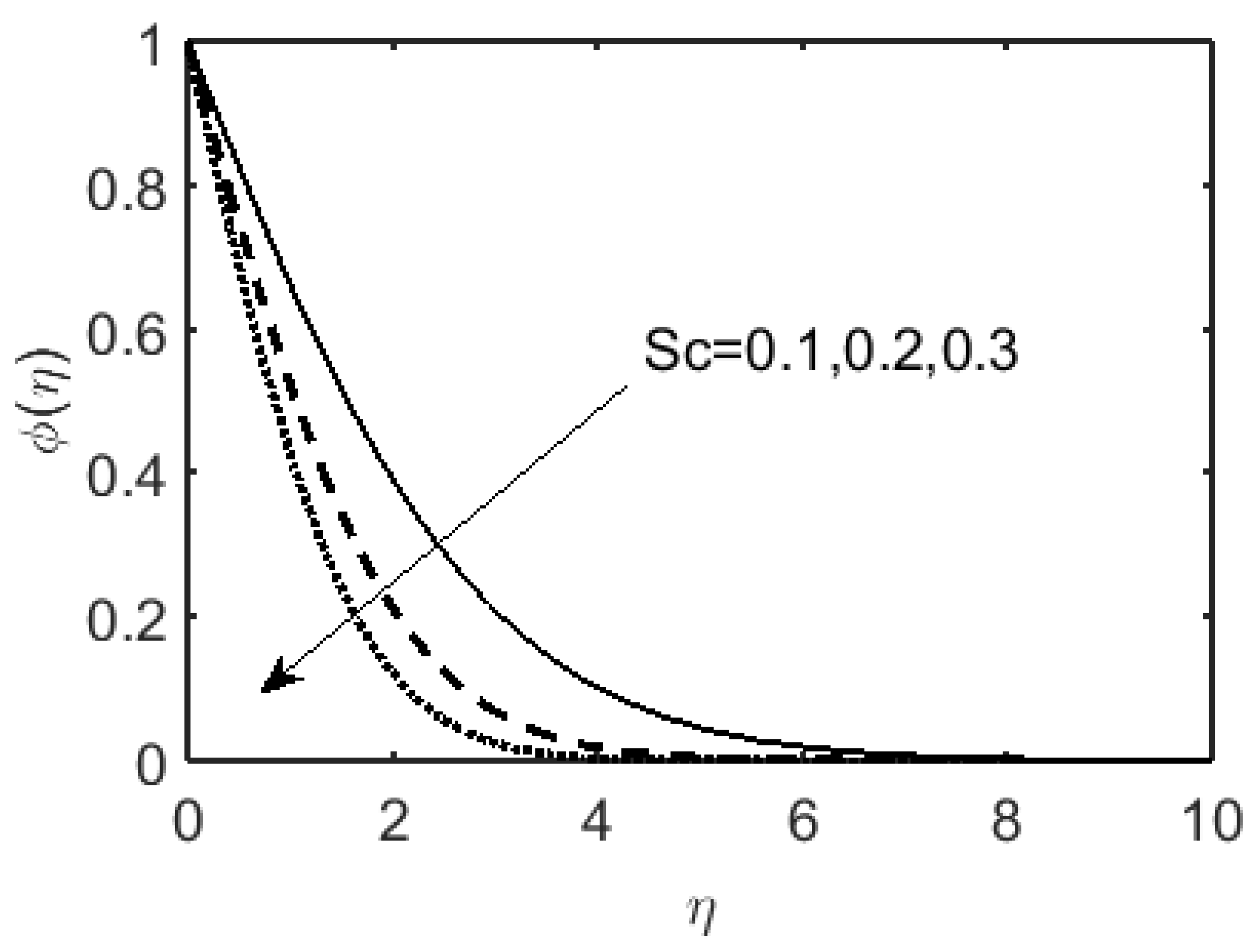
• The concentration of the fluid declines with $Sc$ and improves with fluid velocity on the coated surface $c$.
• The numerical values of the skin-friction coefficients show that the drag force on the coated surface of the disk drops with the rise in the viscoelastic fluid parameter $We.$
• The mathematical results of the Nusselt number indicates that the heat transfer rate on the conducting surface declines with the increase in $Pr.$
• The numerical values of the Sherwood number shows that the concentration rate on the coated surface surges with the rise in Sc.
• In the present study, authors have considered a linear type of velocity on a coated surface that can also be assumed to be nonlinear or exponential in future work.