Flow of Maxwell Fluid with Heat Transfer through Porous Medium with Thermophoresis Particle Deposition and Soret–Dufour Effects: Numerical Solution
Abstract
:1. Introduction
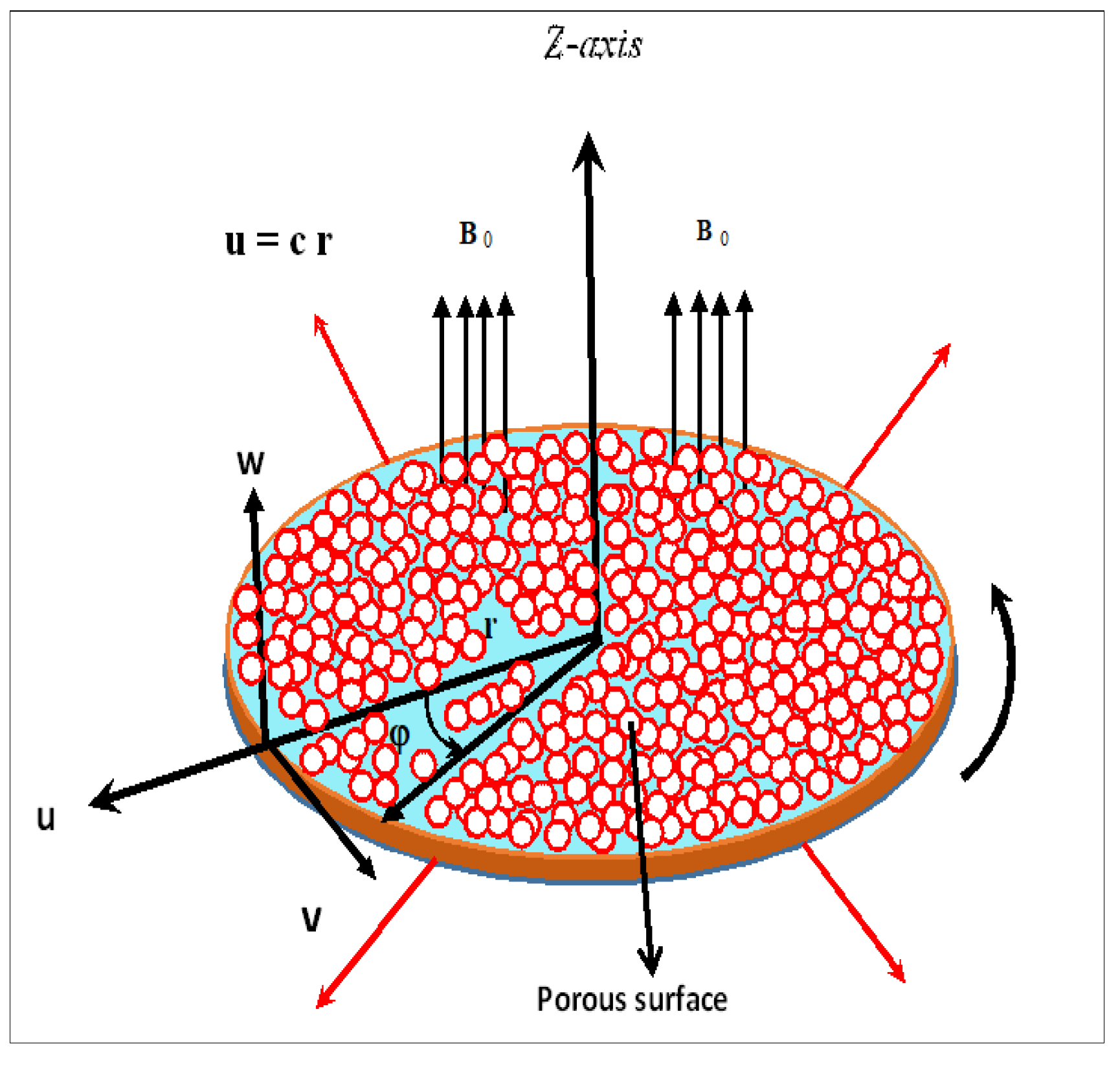
2. Formulation
| and |
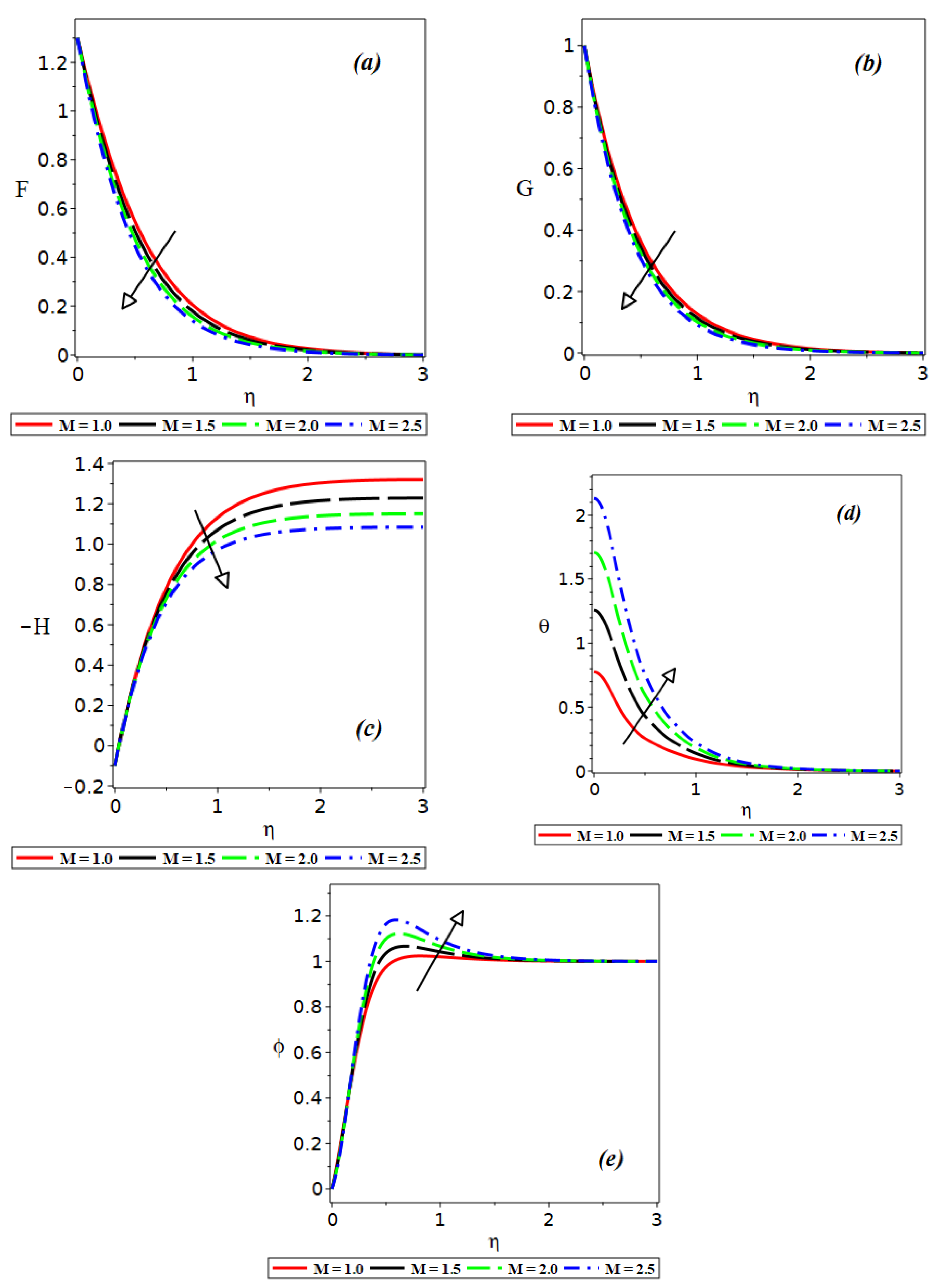
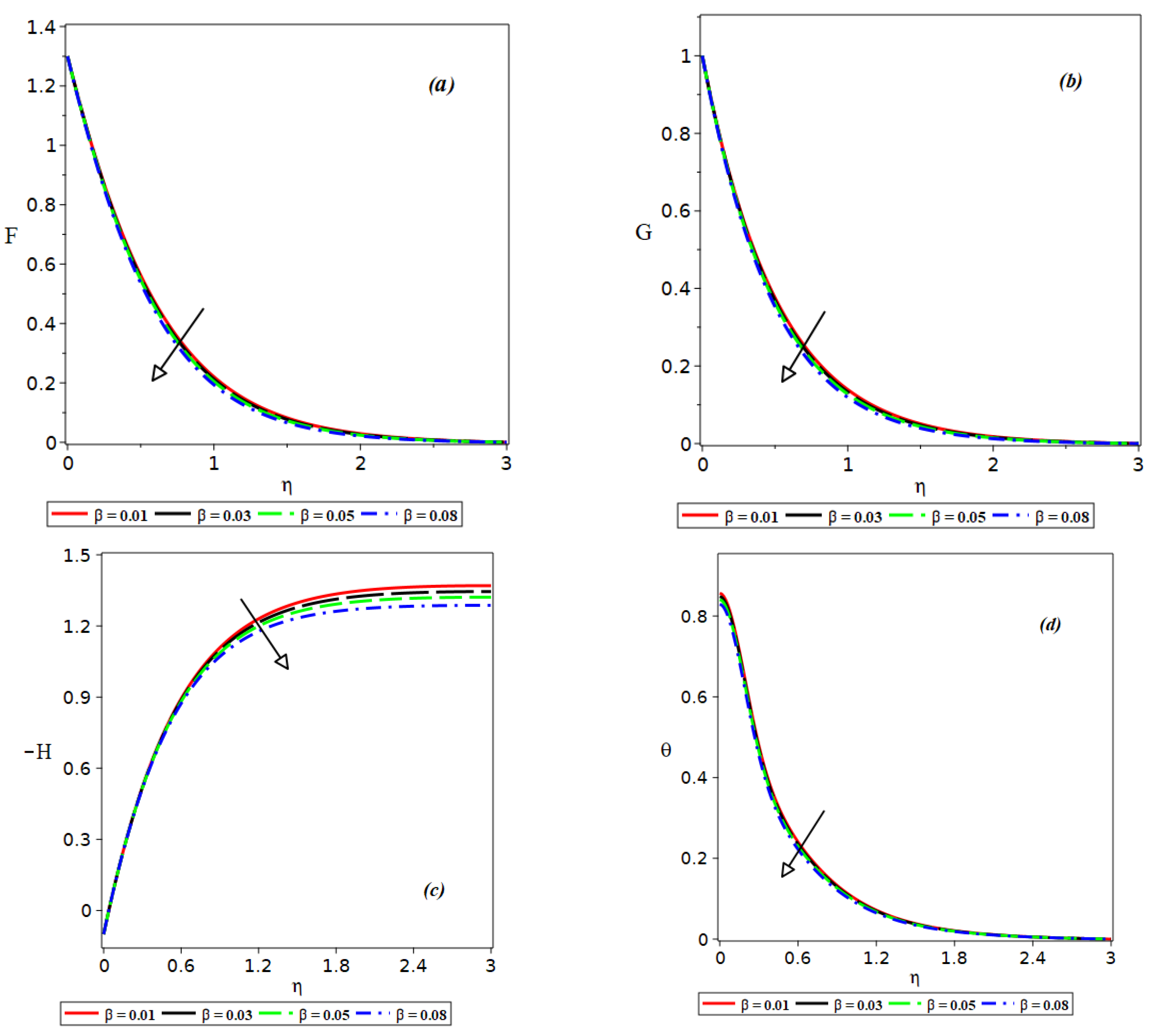
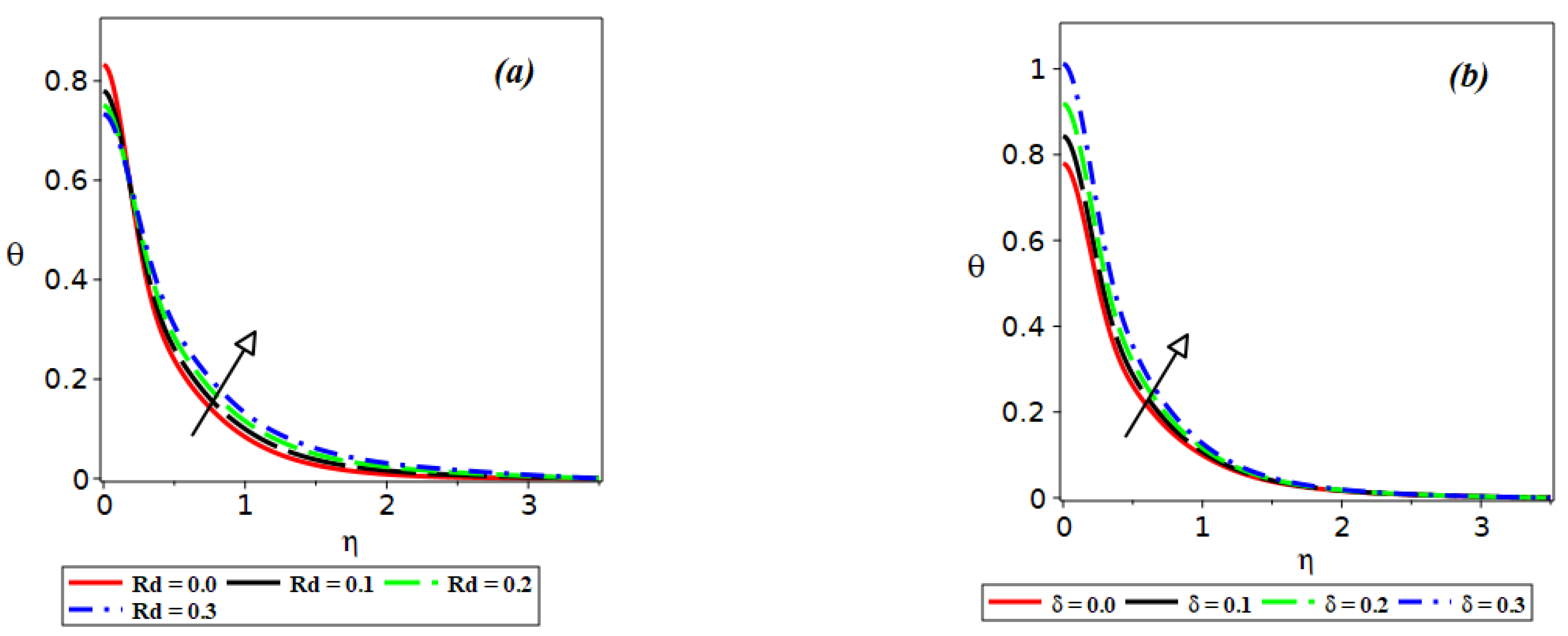
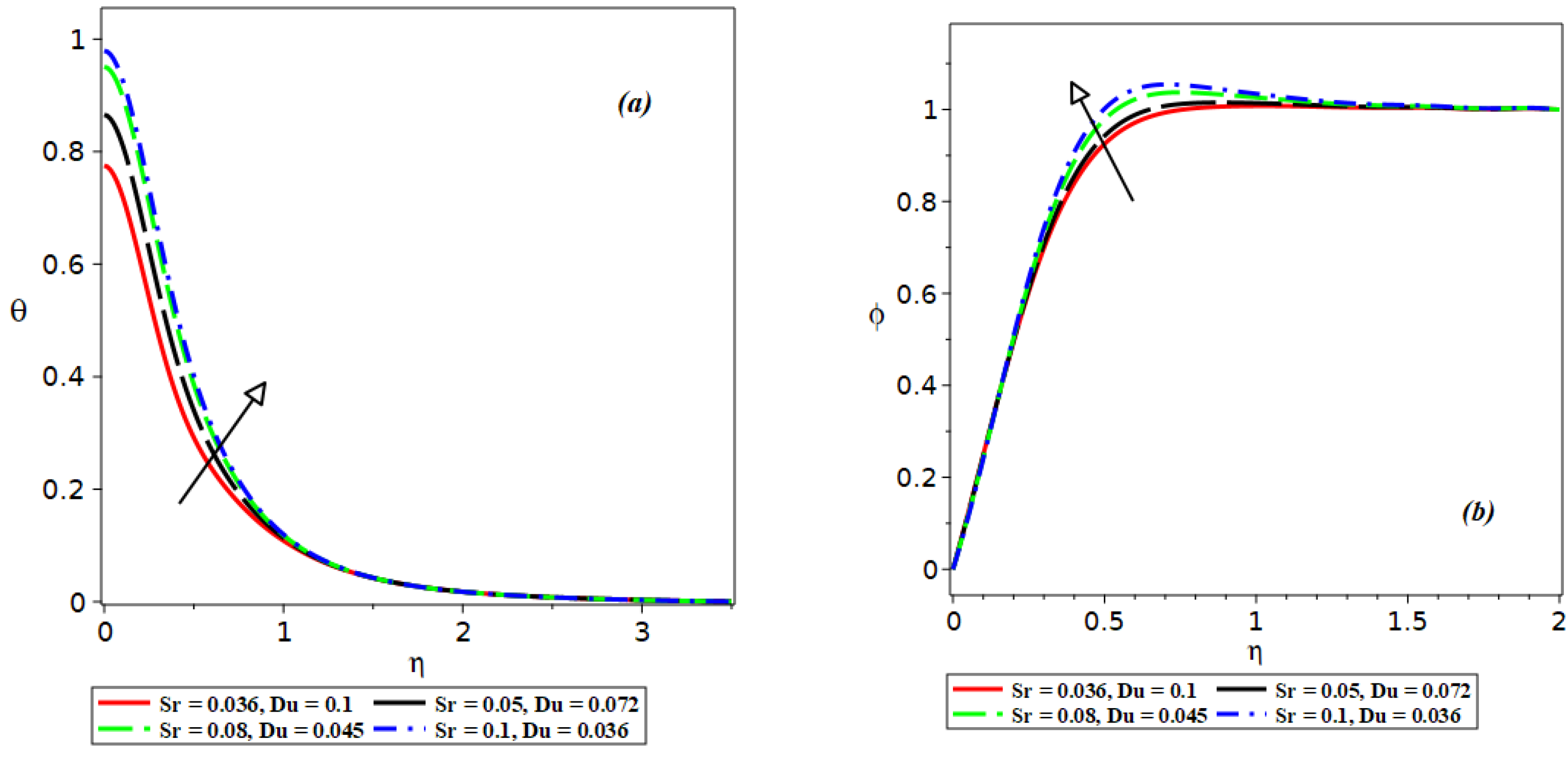
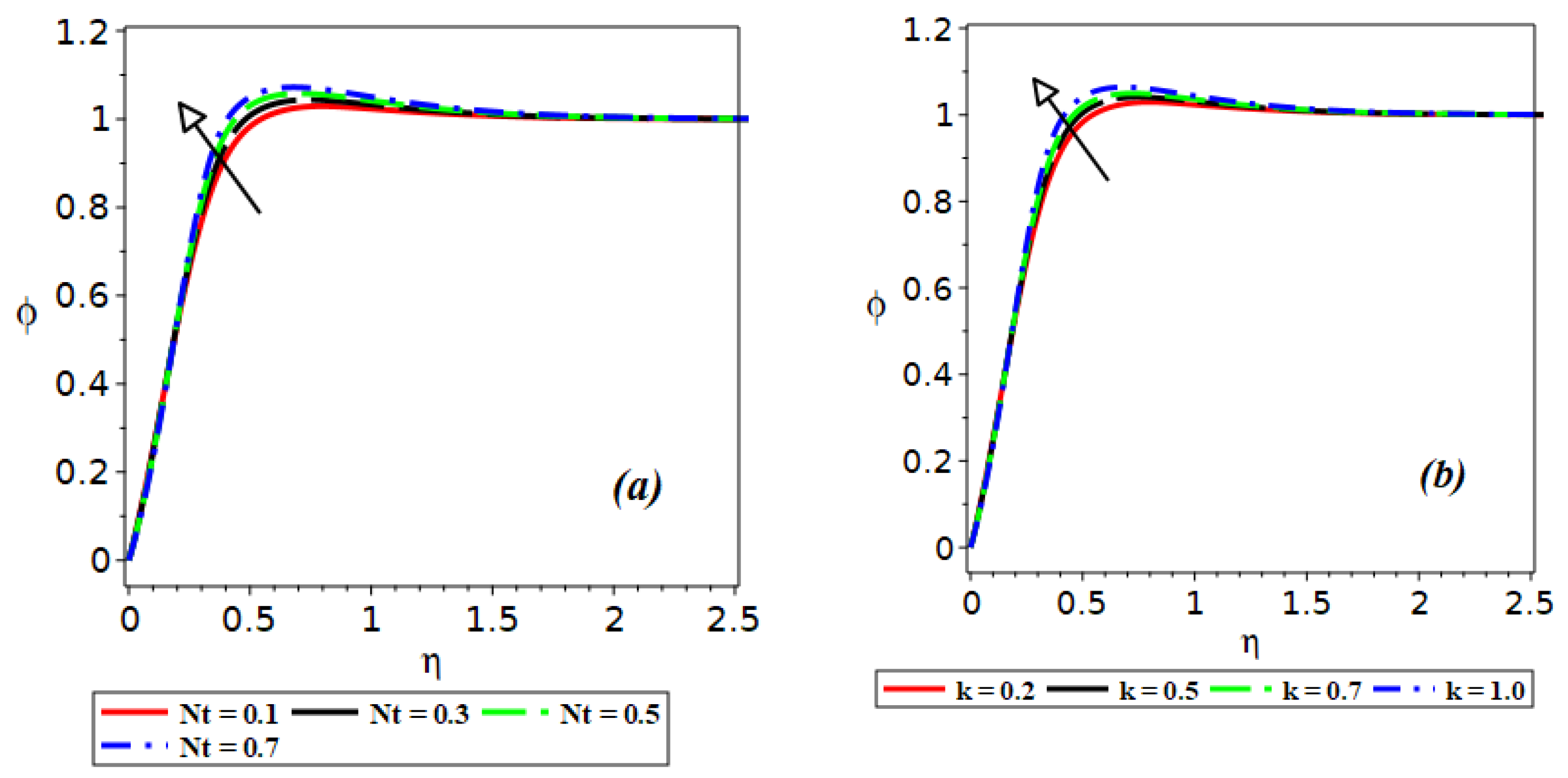
3. Results and Discussion
4. Conclusions
- The presence of a magnetic parameter impedes the movement of the liquid and enhances its temperature;
- Increasing the Soret number results in a significant increase in the mass concentration of the fluid;
- The solutal profile increases monotonically by increasing the values of the relative temperature difference parameter and the thermophoretic coefficient;
- The mass transportation in the Maxwell fluid seems to increase by increasing the values of the chemical reaction parameter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| cylindrical coordinate | |
| components of velocity | |
| fluid temperature | |
| convective fluid temperature | |
| convective heat transfer coefficient | |
| the electrical conductivity | |
| kinematic viscosity | |
| fluid concentration | |
| molecular diffusion coefficient | |
| thermal-diffusion ratio | |
| angular velocity rate | |
| stretching rate | |
| time relaxation | |
| mean spectral absorption coefficient | |
| magnetic field | |
| relaxation time parameter | |
| Prandtl number | |
| Biot number | |
| reaction parameter | |
| heat source/sink | |
| suction parameter | |
| Nusselt number | |
| dimensionless variable | |
| the radiative heat flux | |
| azimuthal velocity | |
| dimensionless temperature | |
| heat capacities ratio | |
| specific heat capacity | |
| ambient temperature | |
| wall concentration | |
| mass flux velocity | |
| dynamic viscosity | |
| fluid density | |
| ambient concentration | |
| permeability of medium | |
| reaction rate | |
| strength of magnetic field | |
| concentration susceptibility | |
| Stefan–Boltzmann constant | |
| thermal conductivity | |
| stretching parameter | |
| porosity parameter | |
| Schmidt number | |
| chemical reaction parameter | |
| radiation parameter | |
| temperature ratio parameter | |
| relative temperature difference parameter | |
| Sherwood number | |
| differentiation with respect to η | |
| radial velocity | |
| axial velocity | |
| dimensionless concentration |
References
- Khashi’ie, N.S.; Arifin, N.M.; Hafidzuddin, E.H.; Wahi, N. Dual stratified nanofluid flow past a permeable shrinking/stretching sheet using a non-Fourier energy model. Appl. Sci. 2019, 9, 2124. [Google Scholar] [CrossRef] [Green Version]
- Bakar, S.A.; Wahid, N.S.; Arifin, N.M.; Khashi’ie, N.S. The flow of hybrid nanofluid past a permeable shrinking sheet in a Darcy–Forchheimer porous medium with second-order velocity slip. Waves Random Complex Media 2022, 1–18. [Google Scholar] [CrossRef]
- Wahid, N.S.; Arifin, N.M.; Khashi’ie, N.S.; Pop, I.; Bachok, N.; Hafidzuddin, M.E.H. Hybrid Nanofluid Radiative Mixed Convection Stagnation Point Flow Past a Vertical Flat Plate with Dufour and Soret Effects. Mathematics 2022, 10, 2966. [Google Scholar] [CrossRef]
- Maxwell, J.C. On the dynamical theory of gases. Philos. Trans. R. Soc. Lond. 1867, 157, 49–88. [Google Scholar]
- Olsson, F.; Yström, J. Some properties of the upper convicted Maxwell model for viscoelastic fluid flow. J. Non-Newton. Fluid Mech. 1993, 48, 125–145. [Google Scholar] [CrossRef]
- Choi, J.J.; Rusak, Z.; Tichy, J.A. Maxwell fluid suction flow in a channel. J. Non-Newton. Fluid Mech. 1999, 85, 165–187. [Google Scholar] [CrossRef]
- Fetecau, C.; Fetecau, C. A new exact solution for the flow of a Maxwell fluid past an infinite plate. Int. J. Non Linear Mech. 2003, 38, 423–427. [Google Scholar] [CrossRef]
- Fetecau, C.; Fetecau, C. The Rayleigh Stokes problem for a fluid of Maxwellian type. Int. J. Non Linear Mech. 2003, 38, 603–607. [Google Scholar] [CrossRef]
- Mustafa, M. Cattaneo-Christov heat flux model for rotating flow and heat transfer of upper-convected Maxwell fluid. AIP Adv. 2015, 5, 047109. [Google Scholar] [CrossRef]
- Mabood, F.; Imtiaz, M.; Hayat, T.; Alsaedi, A. Unsteady convective boundary layer flow of Maxwell fluid with nonlinear thermal radiation: A numerical study. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 221–229. [Google Scholar] [CrossRef]
- Hosseinzadeh, K.; Gholinia, M.; Jafari, B.; Ghanbarpour, A.; Olfian, H.; Ganji, D.D. Nonlinear thermal radiation and chemical reaction effects on Maxwell fluid flow with convectively heated plate in a porous medium. Heat Transf.-Asian Res. 2019, 48, 744–759. [Google Scholar] [CrossRef]
- Ijaz, M.; Ayub, M. Nonlinear convective stratified flow of Maxwell nanofluid with activation energy. Heliyon 2019, 5, e01121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mabood, F.; Rauf, A.; Prasannakumara, B.C.; Izadi, M.; Shehzad, S.A. Impacts of Stefan blowing and mass convention on flow of Maxwell nanofluid of variable thermal conductivity about a rotating disk. Chin. J. Phys. 2021, 71, 260–272. [Google Scholar] [CrossRef]
- Devi, S.S.U.; Mabood, F. Entropy anatomization on Marangoni Maxwell fluid over a rotating disk with nonlinear radiative flux and Arrhenius activation energy. Int. Commun. Heat Mass Transf. 2020, 118, 104857. [Google Scholar] [CrossRef]
- Islam, S.; Dawar, A.; Shah, Z.; Tariq, A. Cattaneo–Christov theory for a time-dependent magnetohydrodynamic Maxwell fluid flow through a stretching cylinder. Adv. Mech. Eng. 2021, 13, 16878140211030152. [Google Scholar] [CrossRef]
- Riaz, M.B.; Awrejcewicz, J.; Rehman, A.U.; Abbas, M. Special functions-based solutions of unsteady convective flow of a MHD Maxwell fluid for ramped wall temperature and velocity with concentration. Adv. Differ. Equ. 2021, 2021, 500. [Google Scholar] [CrossRef]
- Riaz, M.B.; Rehman, A.U.; Awrejcewicz, J.; Akgül, A. Power Law Kernel Analysis of MHD Maxwell Fluid with Ramped Boundary Conditions: Transport Phenomena Solutions Based on Special Functions. Fractal Fract. 2021, 5, 248. [Google Scholar] [CrossRef]
- Hanif, H. A computational approach for boundary layer flow and heat transfer of fractional Maxwell fluid. Math. Comput. Simul. 2022, 191, 1–13. [Google Scholar] [CrossRef]
- Liu, Y.; Chi, X.; Xu, H.; Jiang, X. Fast method and convergence analysis for the magnetohydrodynamic flow and heat transfer of fractional Maxwell fluid. Appl. Math. Comput. 2022, 430, 127255. [Google Scholar] [CrossRef]
- Akyildiz, F.T.; Alshammari, F. A new analysis of Galerkin Legendre spectral methods for coupled hyperbolic/parabolic system arising in unsteady MHD flow of Maxwell fluid and numerical simulation. Appl. Numer. Math. 2022, 176, 83–103. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, J.; Bai, Y.; Wang, Q.; Sun, D.; Sun, X.; Lv, B. Numerical simulation of the fractional Maxwell fluid flow in locally narrow artery. Comput. Methods Biomech. Biomed. Eng. 2022, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Wang, X.; Zhang, Y. Unsteady oblique stagnation-point flow and heat transfer of fractional Maxwell fluid with convective derivative under modified pressure field. Comput. Math. Appl. 2022, 123, 13–25. [Google Scholar] [CrossRef]
- Samuel, D.J. Numerical Investigations of Thermal Radiation and Activation Energy Imparts on Chemically Reactive Maxwell Fluid Flow Over an Exothermal Stretching Sheet in a Porous Medium. Int. J. Appl. Comput. Math. 2022, 8, 148. [Google Scholar] [CrossRef]
- Samuel, D.J.; Olajuwon, B.I. Insight into the effects of thermal radiation and Ohmic heating on chemically reactive Maxwell fluid subject to Lorentz force and buoyancy force. J. Niger. Math. Soc. 2022, 41, 27–48. [Google Scholar]
- Hafeez, A.; Khan, M.; Ahmed, J. Stagnation point flow of radiative Oldroyd-B nanofluid over a rotating disk. Comput. Methods Programs Biomed. 2020, 199, 105342. [Google Scholar] [CrossRef] [PubMed]
- Batchelor, G.K.; Shen, C. Thermophoretic deposition of particles in gas flowing over cold surfaces. J. Colloid Interface Sci. 1985, 107, 21–37. [Google Scholar] [CrossRef] [Green Version]
- Talbot, L.; Cheng, R.K.; Schefer, R.W.; Willis, D.R. Thermophoresis of particles in a heated boundary layer. J. Fluid Mech. 1980, 101, 737–758. [Google Scholar] [CrossRef] [Green Version]
- Al Nuwairan, M.; Hafeez, A.; Khalid, A.; Syed, A. Heat generation/absorption effects on radiative stagnation point flow of Maxwell nanofluid by a rotating disk influenced by activation energy. Case Stud. Therm. Eng. 2022, 35, 102047. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Flow and heat transfer over a rotating porous disk in a nanofluid. Phys. B Condens. Matter 2011, 406, 1767–1772. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Nanofluid flow and heat transfer due to a rotating disk. Comput. Fluids 2014, 94, 139–146. [Google Scholar] [CrossRef]
| Bi | Sr | Du | Ec | ||
|---|---|---|---|---|---|
| 0.1 | 0.1 | 0.1 | 0.1 | 0.7 | 0.01516 |
| 0.2 | 0.04803 | ||||
| 0.3 | 0.06370 | ||||
| 0.1 | 0.3 | 0.04269 | |||
| 0.5 | 0.06705 | ||||
| 0.7 | 0.08869 | ||||
| 0.1 | 0.1 | 0.1 | 0.01516 | ||
| 0.15 | −0.02639 | ||||
| 0.2 | −0.25054 | ||||
| 0.1 | 01 | 0.1 | 0.1 | 0.01516 | |
| 0.11 | 0.01695 | ||||
| 0.12 | 0.01809 | ||||
| 0.1 | 0.12427 | ||||
| 0.3 | 0.09894 | ||||
| 0.5 | 0.06806 |
| 0.1 | 0.01 | 0.1 | 0.2 | 0.1 | −1.897503 |
| 0.2 | −1.894312 | ||||
| 0.3 | −1.891150 | ||||
| 0.1 | 0.02 | −1.837879 | |||
| 0.03 | −1.779653 | ||||
| 0.04 | −1.722789 | ||||
| 0.1 | 0.01 | 0.1 | −1.897504 | ||
| 0.15 | −1.349949 | ||||
| 0.2 | 0.205047 | ||||
| 0.1 | 0.01 | 0.1 | 0.3 | −1.864637 | |
| 0.5 | −1.792577 | ||||
| 0.7 | −1.714251 | ||||
| 0.1 | 0.01 | 0.1 | 0.7 | 0.2 | −1.836673 |
| 0.3 | −1.777058 | ||||
| 0.5 | −1.664599 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AL Nuwairan, M.; Hafeez, A.; Khalid, A.; Souayeh, B.; Alfadhli, N.; Alnaghmosh, A. Flow of Maxwell Fluid with Heat Transfer through Porous Medium with Thermophoresis Particle Deposition and Soret–Dufour Effects: Numerical Solution. Coatings 2022, 12, 1567. https://doi.org/10.3390/coatings12101567
AL Nuwairan M, Hafeez A, Khalid A, Souayeh B, Alfadhli N, Alnaghmosh A. Flow of Maxwell Fluid with Heat Transfer through Porous Medium with Thermophoresis Particle Deposition and Soret–Dufour Effects: Numerical Solution. Coatings. 2022; 12(10):1567. https://doi.org/10.3390/coatings12101567
Chicago/Turabian StyleAL Nuwairan, Muneerah, Abdul Hafeez, Asma Khalid, Basma Souayeh, Norah Alfadhli, and Aminh Alnaghmosh. 2022. "Flow of Maxwell Fluid with Heat Transfer through Porous Medium with Thermophoresis Particle Deposition and Soret–Dufour Effects: Numerical Solution" Coatings 12, no. 10: 1567. https://doi.org/10.3390/coatings12101567







