Heat Transfer Analysis of Unsteady MHD Carreau Fluid Flow over a Stretching/Shrinking Sheet
Abstract
:1. Introduction
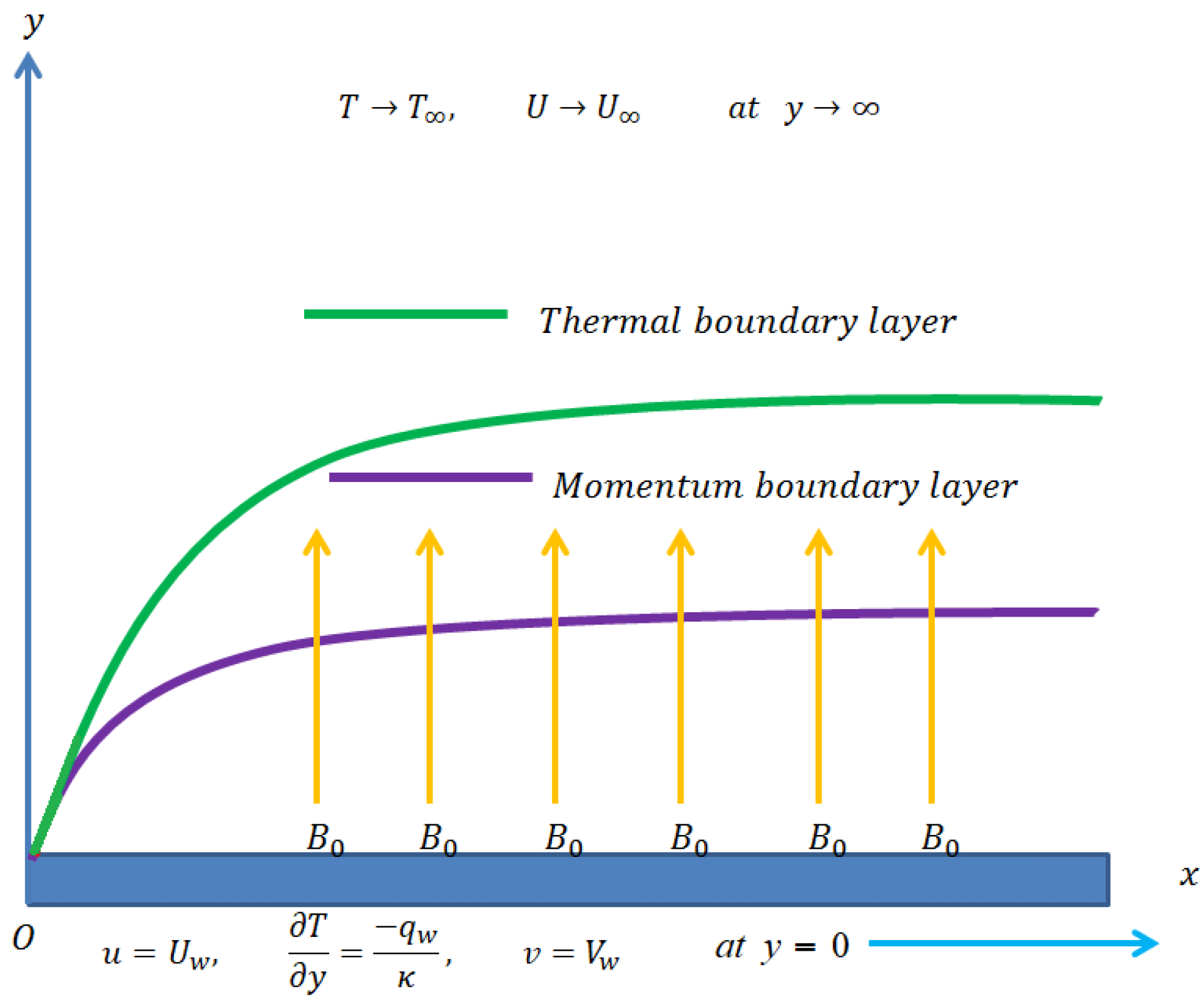
2. Problem Formulation
Quantities of Physical Interest
3. Homotopy Analysis Solution of the Problem
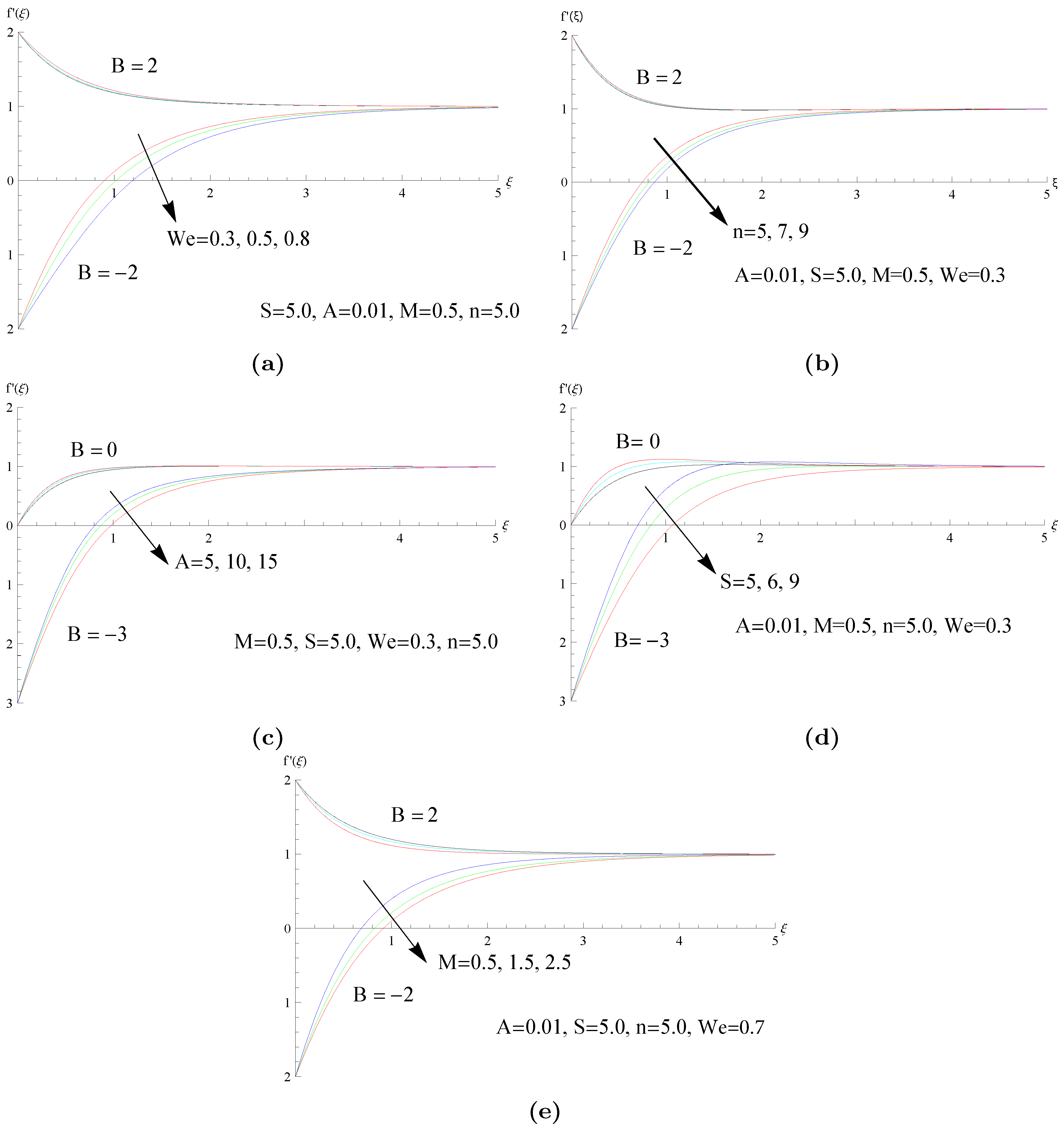
4. Analysis of Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| viscosity | kinematic viscosity | ||
| P | pressure | A | unsteadiness parameter |
| surface heat flux | Shear stress | ||
| The time constant | constant | ||
| fluid density | constants | ||
| components of velocity | thermal conductivity | ||
| spatial Cartesian coordinates | thermal diffusivity | ||
| Stretching surface velocity | magnetic parameter | ||
| n | Power law index | stream velocity | |
| stream function | skin friction coefficient | ||
| Electrical conductivity | Weissenberg number | ||
| suction/injection velocity | the free stream temperature | ||
| J | magnetic field | local Reynolds number | |
| similarity variable | Prandtl number | ||
| B | stretching/ shrinking parameter | T | Fluid temperature |
| local Nusselt number | S | Suction parameter |
References
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. J. AIChe 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Fur Angew. Math. Und Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- HRasheed, U.; L-Zubaidi, A.A.; Islam, S.; Saleem, S.; Khan, Z.; Khan, W. Effects of Joule Heating and Viscous Dissipation on Magnetohydrodynamic Boundary Layer Flow of Jeffrey Nanofluid Over a Vertically Stretching Cylinder. Coatings 2021, 11, 353. [Google Scholar] [CrossRef]
- Kalpana, G.; Saleem, S. Heat Transfer of Magnetohydrodynamic Stratified Dusty Fluid Flow through an Inclined Irregular Porous Channel. Nanomaterials 2022, 12, 3309. [Google Scholar] [CrossRef] [PubMed]
- Hamid, M.; Usman, M.; Khan, Z.H.; Ahmad, R.; Wang, W. Dual solutions and stability analysis of flow and heat transfer of Casson fluid over a stretching sheet. Phys. Lett. A 2019, 383, 2400–2408. [Google Scholar] [CrossRef]
- Ullah, I.; Rahim, M.T.; Khan, H.; Qayyum, M. Homotopy Analysis Solution for Magnetohydrodynamic Squeezing Flow in Porous Medium. Adv. Math. Phy. 2016, 2016, 3541512. [Google Scholar] [CrossRef]
- Kumar, R.N.; Jyothi, A.M.; Alhumade, H.; Gowda, R.J.P.; Alam, M.M.; Ahmad, I.; Gorji, M.R.; Prasannakumara, B.C. Impact of magnetic dipole on thermophoretic particle deposition in the flow of Maxwell fluid over a stretching sheet. J. Mol. Liq. 2021, 334, 116494. [Google Scholar] [CrossRef]
- Madhukesh, J.K.; Kumar, R.N.; Gowda, R.J.P.; Prasannakumara, B.C.; Ramesh, G.K.; Khan, M.I.; Khan, S.U.; Chu, Y. Numerical simulation of AA7072-AA7075/water-based hybrid nanofluid flow over a curved stretching sheet with Newtonian heating: A non-Fourier heat flux model approach. J. Mol. Liq. 2021, 335, 116103. [Google Scholar] [CrossRef]
- Wang, C.Y. Stagnation flow towards a shrinking sheet. Int. J. Non-Linear Mech. 2008, 43, 377–382. [Google Scholar] [CrossRef]
- Qayyum, M.; Khan, H.; Khan, O. Slip Analysis at fluid–solid interface in MHD squeezing flow of Casson fluid through porous medium. Results Phys. 2017, 7, 732–750. [Google Scholar] [CrossRef]
- Raza, J. Thermal radiation and slip effects on magnetohydrodynamic (MHD) stagnation point flow of Casson fluid over a convective stretching sheet. Propuls. Power Res. 2019, 8, 138–146. [Google Scholar] [CrossRef]
- Patel, M.; Timol, M.G. Magneto Hydrodynamic Orthogonal Stagnation Point Flow of a Power-Law Fluid Toward a Stretching Surface. Am. Comput. Math. 2011, 1, 129–133. [Google Scholar] [CrossRef] [Green Version]
- Ramesh, G.K.; Roopa, G.S.; Rauf, A.; Shehzad, S.A.; Abbasi, F.M. Time-dependent squeezing flow of Casson-micropolar nanofluid with injection/suction and slip effects. Int. Commun. Heat Mass Transf. 2021, 126, 105470. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–297. [Google Scholar] [CrossRef]
- Khan, M.; Malik, M.Y.; Salahuddin, T.; Khan, I. Numerical modeling of Carreau fluid due to variable thicked surface. Results Phys. 2017, 7, 2384–2390. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S.; Haq, R.U.; Ye, S. MHD stagnation point flow of Carreau fluid toward a permeable shrinking sheet: Dual solutions. Ain Shams Eng. J. 2014, 5, 1233–1239. [Google Scholar] [CrossRef] [Green Version]
- Raju, C.S.K.; Sandeep, N. Unsteady three-dimensional flow of Casson-Carreau fluids past a stretching surface. Alex. Eng. J. 2016, 55, 1115–1126. [Google Scholar] [CrossRef] [Green Version]
- Shabnam; Mei, S.; Khan, M.S. Numerical investigation of a squeezing flow between concentric cylinders under the variable magnetic field of intensity. Sci. Rep. 2022, 12, 9148. [Google Scholar]
- Ali, N.; Hayat, T. Peristaltic motion of a Carreau fluid in an asymmetric channel. Appl. Math. Comput. 2007, 193, 535–552. [Google Scholar] [CrossRef]
- Nazir, U.; Saleem, S.; Nawaz, M.; Sadiq, M.A.; Alderremy, A.A. Study of transport phenomenon in Carreau fluid using Cattaneo–Christov heat flux model with temperature dependent diffusion coefficients. Phys. A Stat. Mech. Its Appl. 2020, 554, 123921. [Google Scholar] [CrossRef]
- Nadeem, S.; Riaz, A.; Ellahi, R. Series solution of unsteady peristaltic flow of a Carreau fluid in eccentric cylinders. Ain. Shams. Eng. J. 2014, 5, 293–304. [Google Scholar] [CrossRef] [Green Version]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N. Three-Dimensional Hybrid Nanofluid Flow and Heat Transfer past a Permeable Stretching/Shrinking Sheet with Velocity Slip and Convective Condition, Chin. J. Phys. 2020, 66, 157–171. [Google Scholar] [CrossRef]
- Gopal, D.; Firdous, H.; Saleem, S.; Kishan, N. Impact of convective heat transfer and buoyancy on micropolar fluid flow through a porous shrinking sheet: An FEM approach. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 3974–3985. [Google Scholar]
- Bakar, S.A.; Arifin, N.M.; Khashi’ie, N.S.; Bachok, N. Hybrid Nanofluid Flow over a Permeable Shrinking Sheet Embedded in a Porous Medium with Radiation and Slip Impacts. Mathematics 2021, 9, 878. [Google Scholar] [CrossRef]
- Rohni, A.M.; Ahmad, S.; Pop, I. Flow and heat transfer over an unsteady shrinking sheet with suction in nanofluids. Int. J. Heat Mass Transfer. 2012, 55, 1888–1895. [Google Scholar]
- Warke, A.S.; Ramesh, K.; Mebarek-Oudina, F. Numerical investigation of the stagnation point flow of radiative magnetomicropolar liquid past a heated porous stretching sheet. J. Therm. Anal. Calorim. 2022, 147, 6901–6912. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.A.; Bazid, M.A.A. Heat transfer over an unsteady stretching surface. Heat Mass Transfer. 2004, 41, 1–4. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, W.A.; Abbas, S.Z. Impact of induced magnetic field on second-grade nanofluid flow past a convectively heated stretching sheet. Appl. Nanosci. 2020, 10, 3001–3009. [Google Scholar] [CrossRef]
- Khan, S.A.; Ali, B.; Eze, C.; Lau, K.T.; Ali, L.; Chen, J.; Zhao, J. Magnetic Dipole and Thermal Radiation Impacts on Stagnation Point Flow of Micropolar Based Nanofluids over a Vertically Stretching Sheet: Finite Element Approach. Processes 2021, 9, 1089. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I.; Nazar, R. Dusty hybrid nanofluid flow over a shrinking sheet with magnetic field effects. Int. J. Numer. Method H 2022, 32, 1067–1091. [Google Scholar] [CrossRef]
- Hassanien, I.A.; Al-arabi, T.H. Non-Darcy unsteady mixed convection flow near the stagnation point on a heated vertical surface embedded in a porous medium with thermal radiation and variable viscosity. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1366–1377. [Google Scholar] [CrossRef]
- Nandy, S.K.; Sidui, S.; Mahapatra, T.R. Unsteady MHD boundary-layer flow and heat transfer of nanofluid over a permeable shrinking sheet in the presence of thermal radiation. Alex. Eng. J. 2014, 53, 929–937. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Stability analysis of MHD hybrid nanofluid flow over a stretching/shrinking sheet with quadratic velocity. Alex. Eng. J. 2021, 60, 915–926. [Google Scholar] [CrossRef]
- Chu, Y.M.; Rehman, M.I.U.; Khan, M.I.; Nadeem, S.; Kadry, S.; Abdelmalek, Z.; Abbas, N. Transportation of heat and mass transport in hydromagnetic stagnation point flow of Carreau nanomaterial: Dual simulations through Runge-Kutta Fehlberg technique. Int. Commun. Heat Mass Transf. 2020, 118, 104858. [Google Scholar] [CrossRef]
- Ahmed, J.; Khan, M.; Ahmad, L. Stagnation point flow of Maxwell nanofluid over a permeable rotating disk with heat source/sink. J. Mol. Liq. 2019, 287, 110853. [Google Scholar] [CrossRef]
- Long, N.M.A.N.; Suali, M.; Ishak, A.; Bachok, N.; Arifm, N.M. Unsteady stagnation point flow and heat transfer over a stretching/shrinking sheet. J. Appl. Sci. 2011, 11, 3520–3524. [Google Scholar] [CrossRef] [Green Version]
- Jakeer, S.; Reddy, P.B.A. Entropy generation on EMHD stagnation point flow of hybrid nanofluid over a stretching sheet: Homotopy perturbation solution. Phys. Scr. 2020, 95, 125203. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Bakar, S.A.; Ishak, A. Stagnation-point flow of a hybrid nanoliquid over a non-isothermal stretching/shrinking sheet with characteristics of inertial and microstructure. Case Stud. Therm. Eng. 2021, 26, 101150. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Rostami, M.N.; Yousefi, M.; Dinarvand, S.; Pop, I.; Sheremet, M.A. Dual solutions for Casson hybrid nanofluid flow due to a stretching/shrinking sheet: A new combination of theoretical and experimental models. Chin. J. Phys. 2021, 71, 574–588. [Google Scholar] [CrossRef]
- Hayat, T.; Haider, F.; Alsaedi, A.; Ahmad, B. Entropy generation analysis of Carreau fluid with entire new concepts of modified Darcy’s law and variable characteristics. Int. Comm. Heat Mass Transf. 2021, 120, 105073. [Google Scholar] [CrossRef]
- Hussain, S.M.; Goud, B.S.; Madheshwaran, P.; Jamshed, W.; Pasha, A.A.; Safdar, R.; Arshad, M.; Ibrahim, R.W.; Ahmad, M.K. Effectiveness of Nonuniform Heat Generation (Sink) and Thermal Characterization of a Carreau Fluid Flowing across a Nonlinear Elongating Cylinder: A Numerical Study. ACS Omega 2022, 7, 25309–25320. [Google Scholar] [CrossRef] [PubMed]
- Abbas, T.; Rehman, S.; Shah, R.A.; Idrees, M.; Qayyum, M. Analysis of MHD Carreau fluid flow over a stretching permeable sheet with variable viscosity and thermal conductivity. Phys. A Stat. Mech. Appl. 2020, 551, 124225. [Google Scholar] [CrossRef]
- Raza, R.; Mabood, F.; Naz, R. Entropy analysis of non-linear radiative flow of Carreau liquid over curved stretching sheet. Int. Commun. Heat Mass Transf. 2020, 119, 104975. [Google Scholar] [CrossRef]
- Khan, M.; Azam, M. Unsteady heat and mass transfer mechanisms in MHD Carreau nanofluid flow. J. Mol. Liq. 2017, 225, 554–562. [Google Scholar] [CrossRef]
- Suali, M.; Long, N.M.A.N.; Arifin, N.M. Unsteady Stagnation Point Flow and Heat Transfer over a Stretching/Shrinking Sheet with Suction or Injection. J. Appl. Math. 2012, 12, 1–13. [Google Scholar] [CrossRef]

| Unsteady | Boundary | Stagnation | Suc./ | Stretch./ | HAM | |
|---|---|---|---|---|---|---|
| Layer | Point | Inj. | Shrink. | vs. BVP4C | ||
| Hayat et al. [41] | No | No | No | No | No | No |
| Hussain et al. [42] | No | No | No | No | Yes | No |
| Abbas et al. [43] | No | Yes | Yes | No | Yes | No |
| Raza et al. [44] | No | No | No | No | Yes | No |
| Present | Yes | Yes | Yes | Yes | Yes | Yes |
| B | n | S | A | M | |||
|---|---|---|---|---|---|---|---|
| 2.0 | 5.0 | ||||||
| 6.0 | |||||||
| 7.0 | |||||||
| −2.0 | 5.0 | ||||||
| 6.0 | |||||||
| 7.0 | |||||||
| 0.0 | 5.0 | 5.0 | |||||
| 5.5 | |||||||
| 6.0 | |||||||
| −3.0 | 5.0 | ||||||
| 5.5 | |||||||
| 6.0 | |||||||
| 0.0 | 0.5 | ||||||
| 1.0 | |||||||
| 1.5 | |||||||
| −3.0 | 0.5 | ||||||
| 1.0 | |||||||
| 1.5 | |||||||
| 2.0 | 0.01 | 5.0 | |||||
| 6.0 | − | ||||||
| 7.0 | − | ||||||
| −2.0 | 5.0 | ||||||
| 6.0 | |||||||
| 7.0 | |||||||
| 2.0 | 0.5 | − | |||||
| 1.4 | − | ||||||
| 1.8 | − | ||||||
| −2.0 | 0.5 | ||||||
| 1.4 | |||||||
| 1.8 |
| Analytical | Numerical | Analytical | Numerical | Analytical | Numerical | Analytical | Numerical | |
|---|---|---|---|---|---|---|---|---|
| 0.004504 | ||||||||
| 0.013513 | ||||||||
| 0.022527 | ||||||||
| 0.031531 | ||||||||
| 0.040540 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qayyum, M.; Abbas, T.; Afzal, S.; Saeed, S.T.; Akgül, A.; Inc, M.; Mahmoud, K.H.; Alsubaie, A.S. Heat Transfer Analysis of Unsteady MHD Carreau Fluid Flow over a Stretching/Shrinking Sheet. Coatings 2022, 12, 1661. https://doi.org/10.3390/coatings12111661
Qayyum M, Abbas T, Afzal S, Saeed ST, Akgül A, Inc M, Mahmoud KH, Alsubaie AS. Heat Transfer Analysis of Unsteady MHD Carreau Fluid Flow over a Stretching/Shrinking Sheet. Coatings. 2022; 12(11):1661. https://doi.org/10.3390/coatings12111661
Chicago/Turabian StyleQayyum, Mubashir, Tariq Abbas, Sidra Afzal, Syed Tauseef Saeed, Ali Akgül, Mustafa Inc, Khaled H. Mahmoud, and Abdullah Saad Alsubaie. 2022. "Heat Transfer Analysis of Unsteady MHD Carreau Fluid Flow over a Stretching/Shrinking Sheet" Coatings 12, no. 11: 1661. https://doi.org/10.3390/coatings12111661






