Numerical Simulation of Graphene Growth by Chemical Vapor Deposition Based on Tesla Valve Structure
Abstract
:1. Introduction
2. Thermodynamic Numerical Analysis of Graphene Prepared by the CVD Method
2.1. Principle of Chemical Reaction
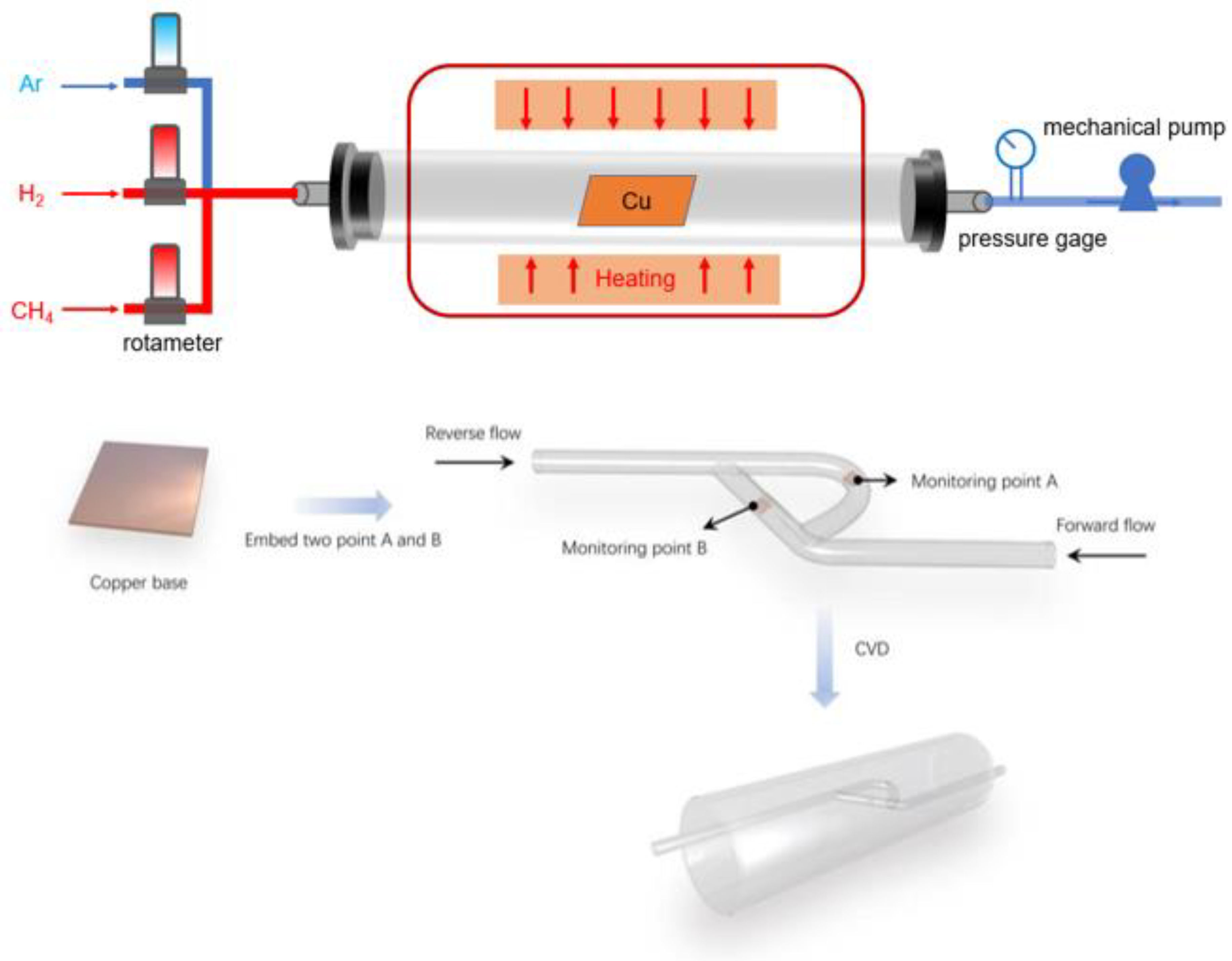
2.2. Reaction Geometry Model
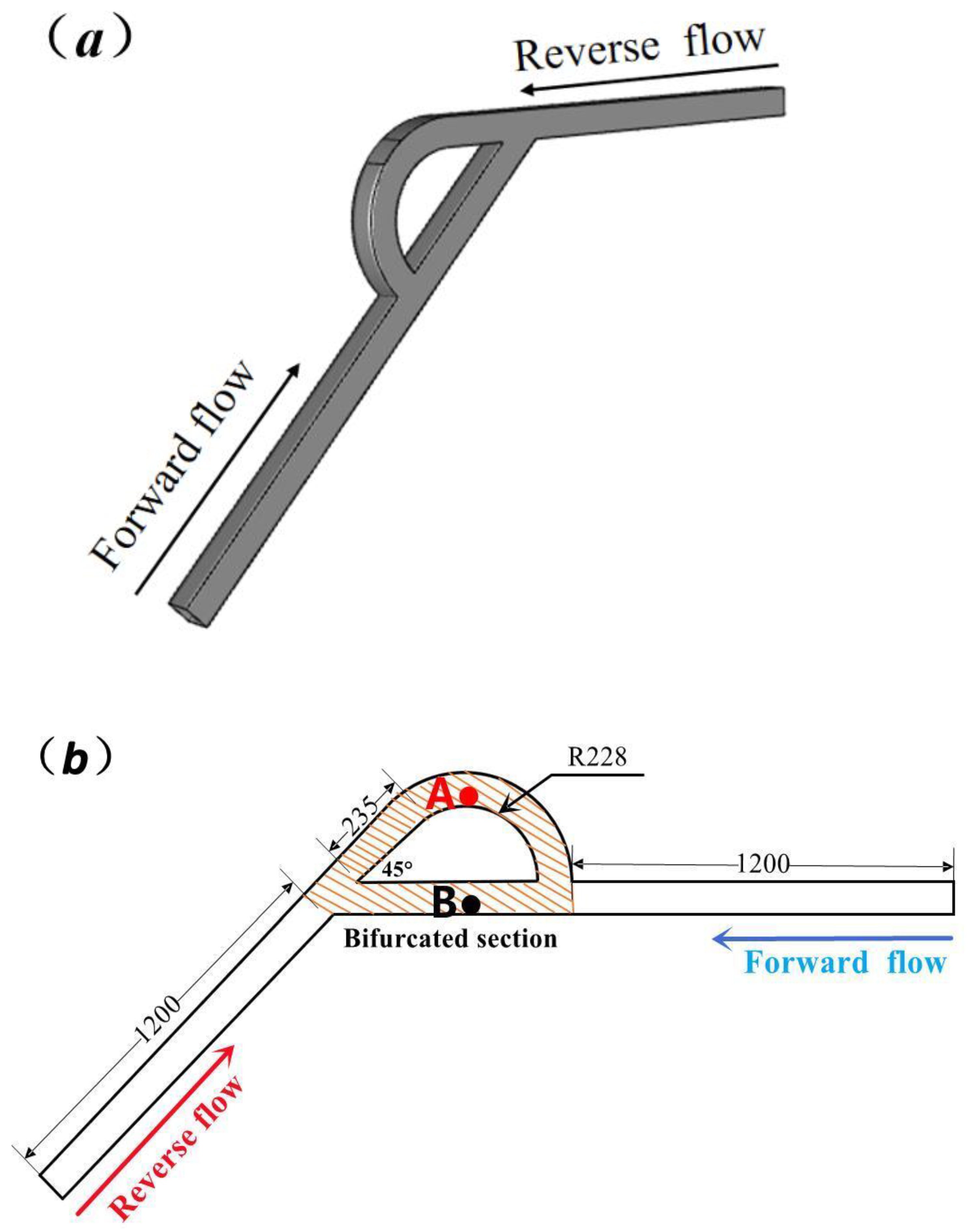
2.3. Simplified Numerical Model Based on T45-R Tesla Rice Structure
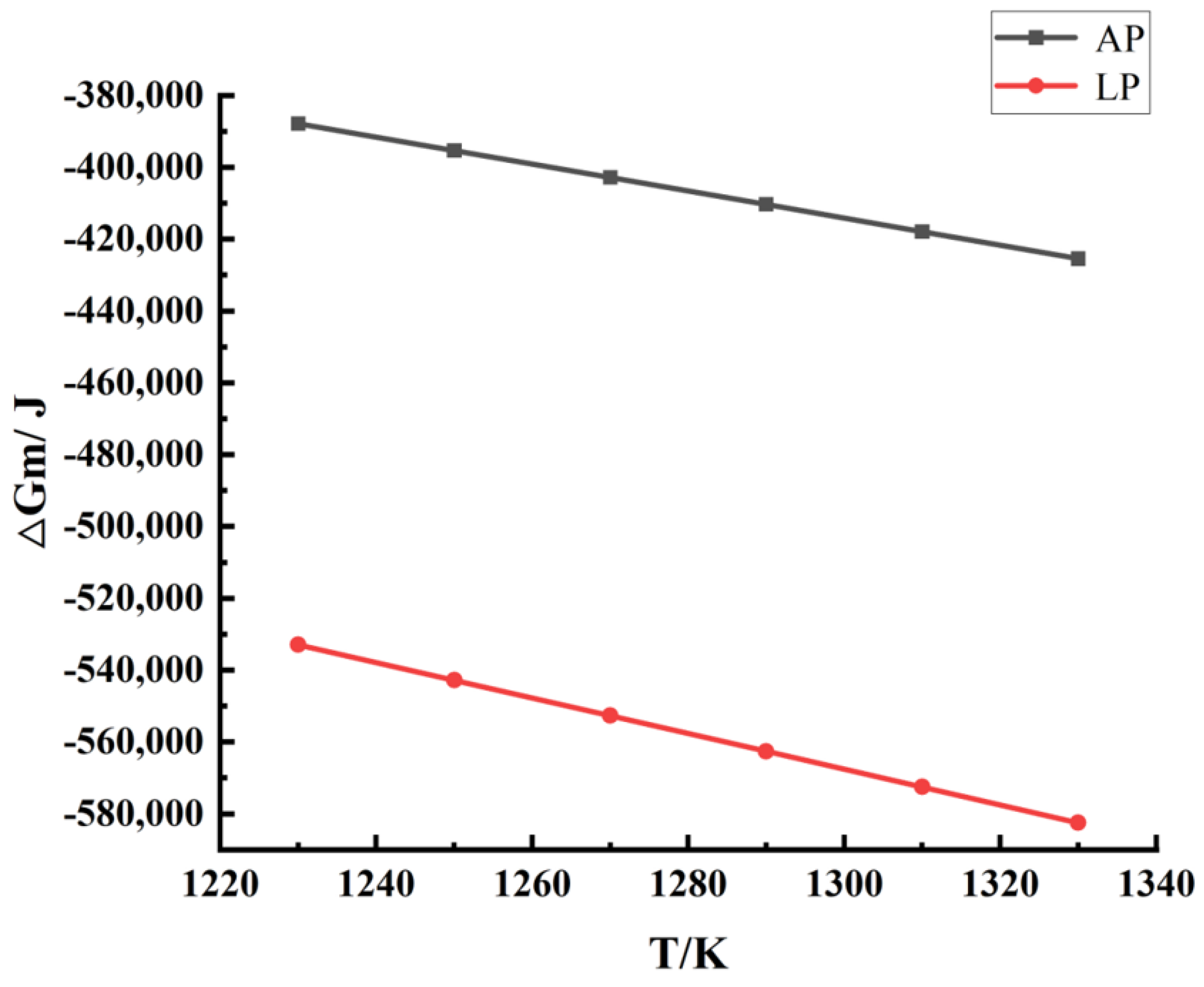
2.4. Thermodynamic Numerical Analysis
3. Numerical Model
3.1. Governing Equations
3.2. Forward Flow and Reverse Flow
3.3. Single Conductivity Parameter
3.4. Boundary Conditions and Parameter Settings
4. Results and Discussion
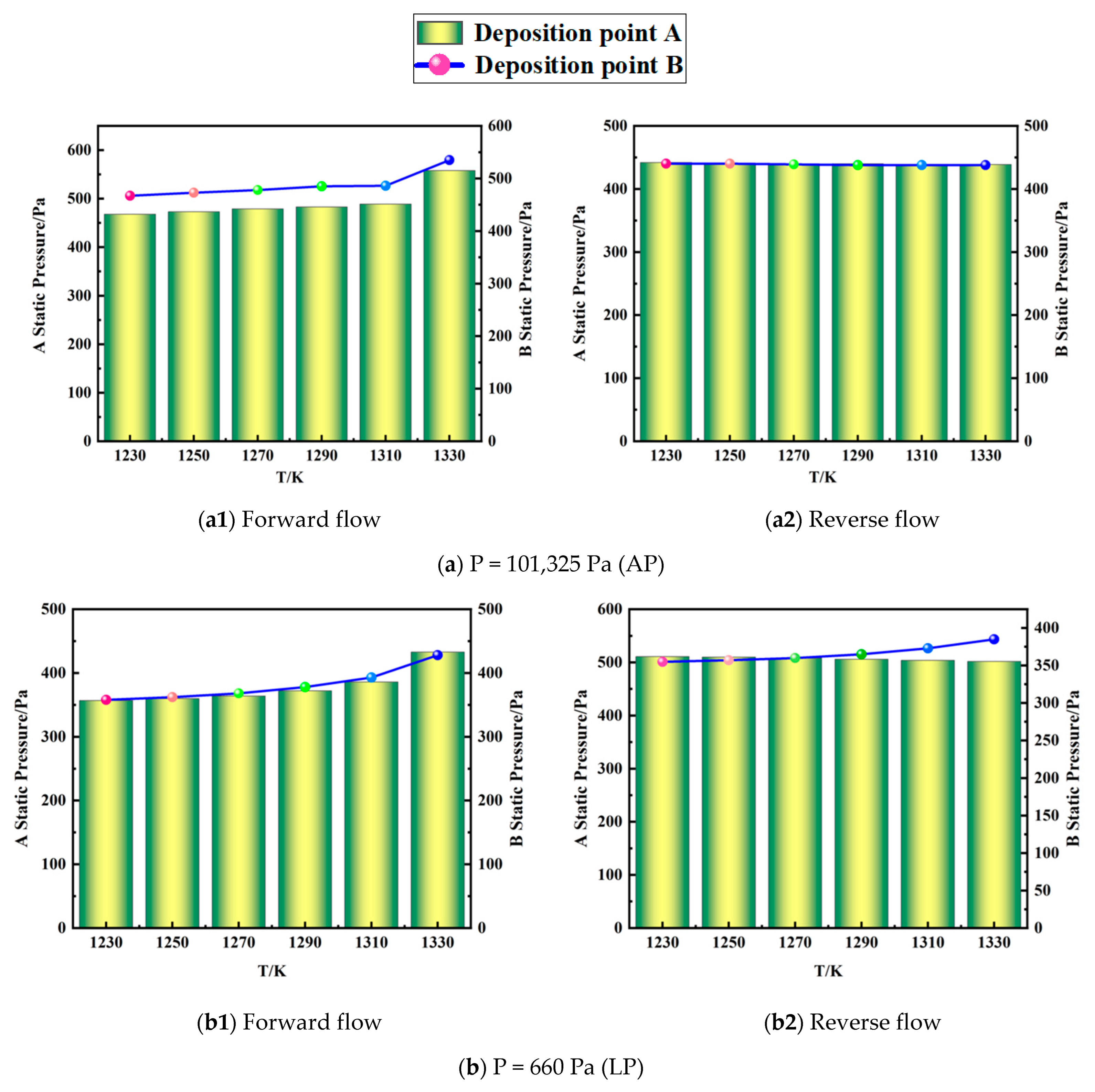
4.1. Effect of Pressure Field on Graphene Synthesis
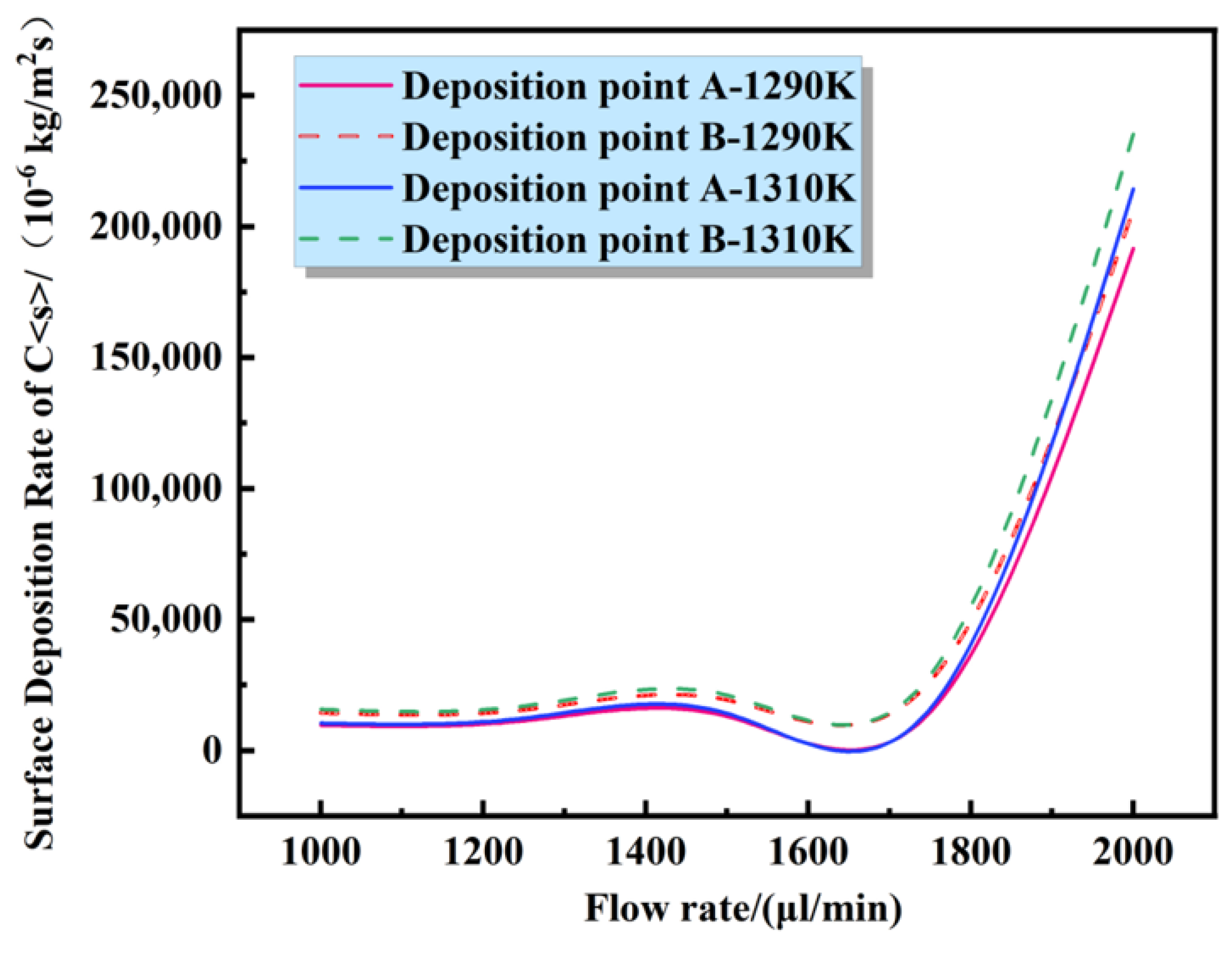
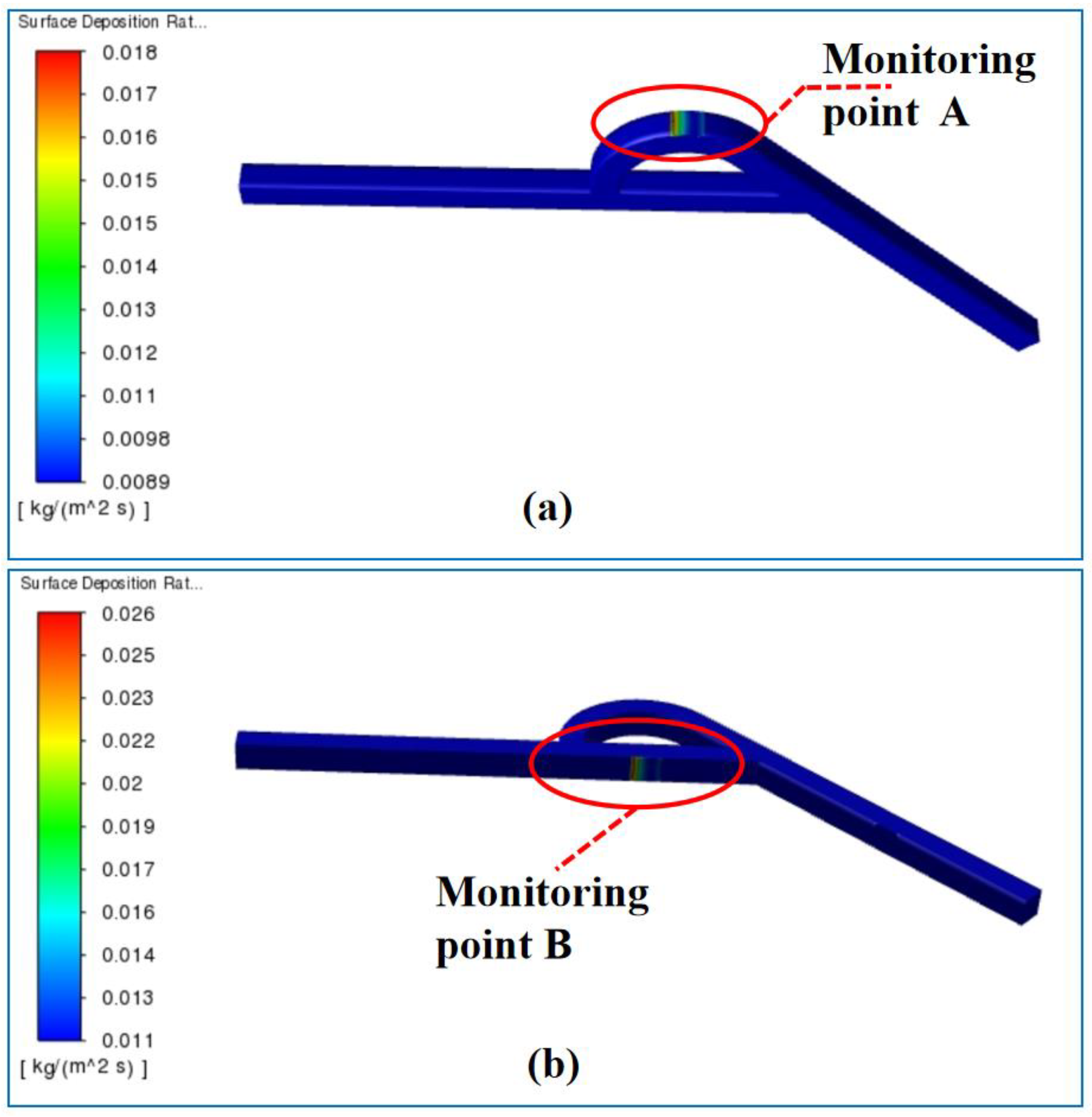
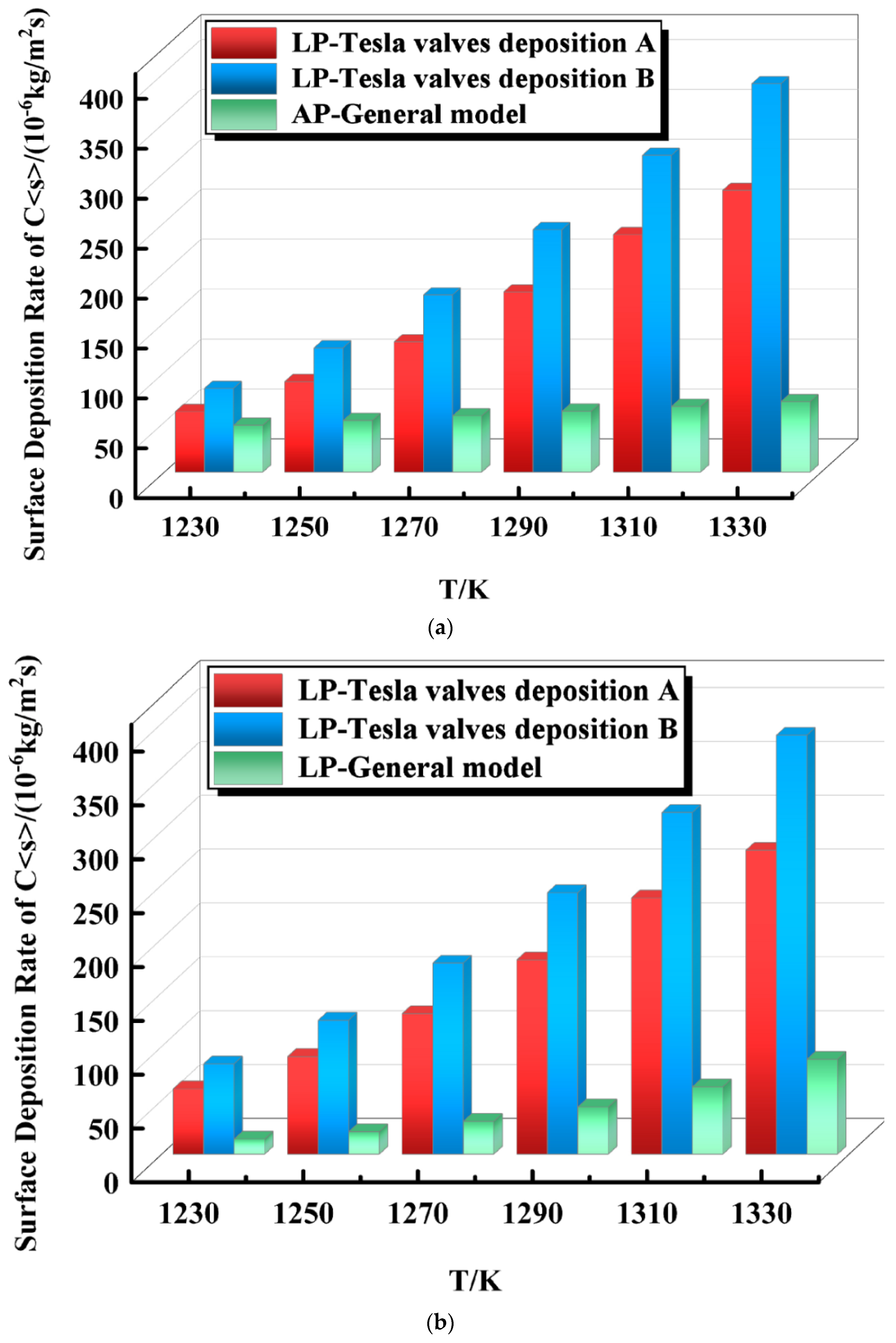
4.2. Effect of Temperature on the Surface Deposition Rate
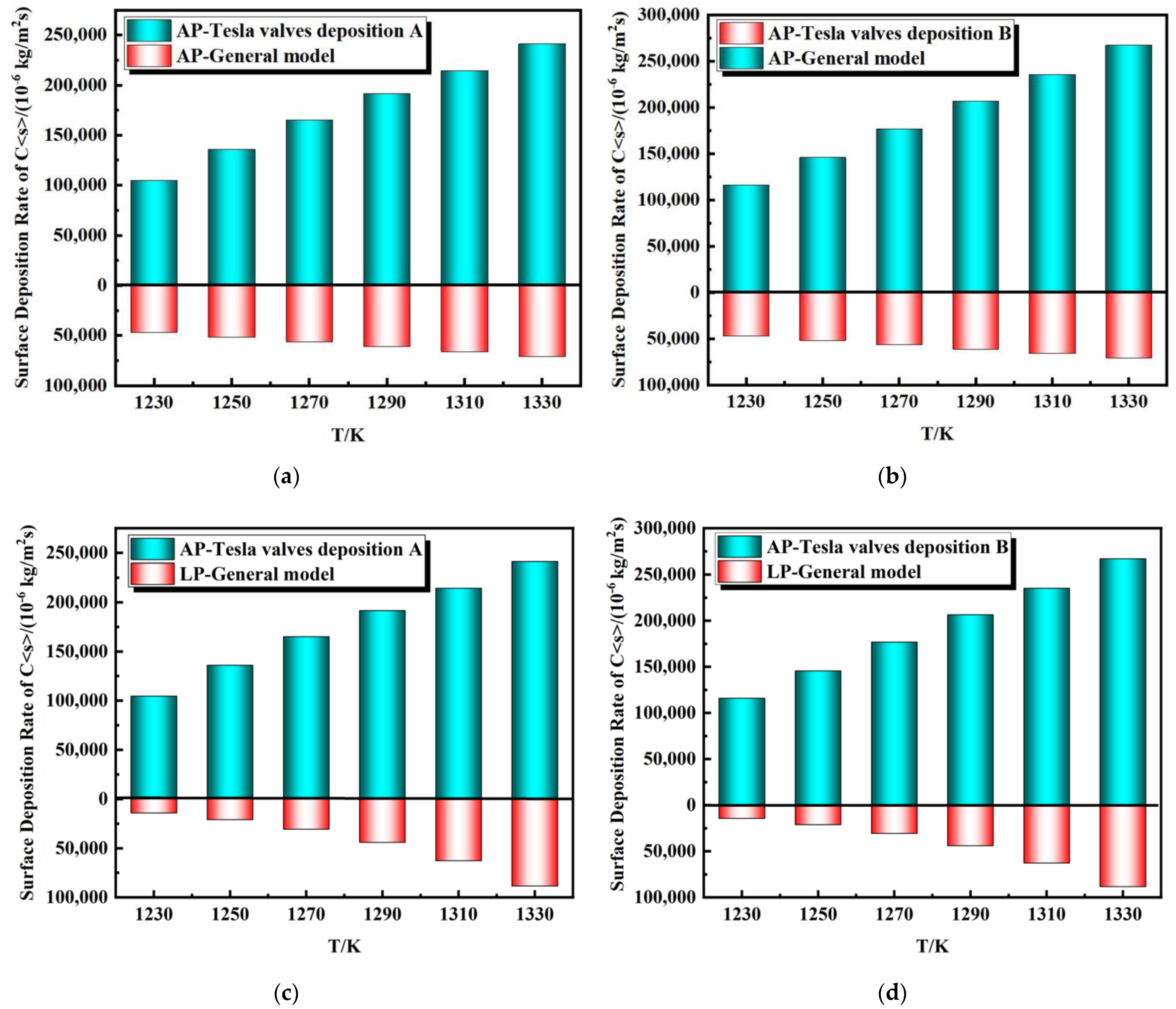
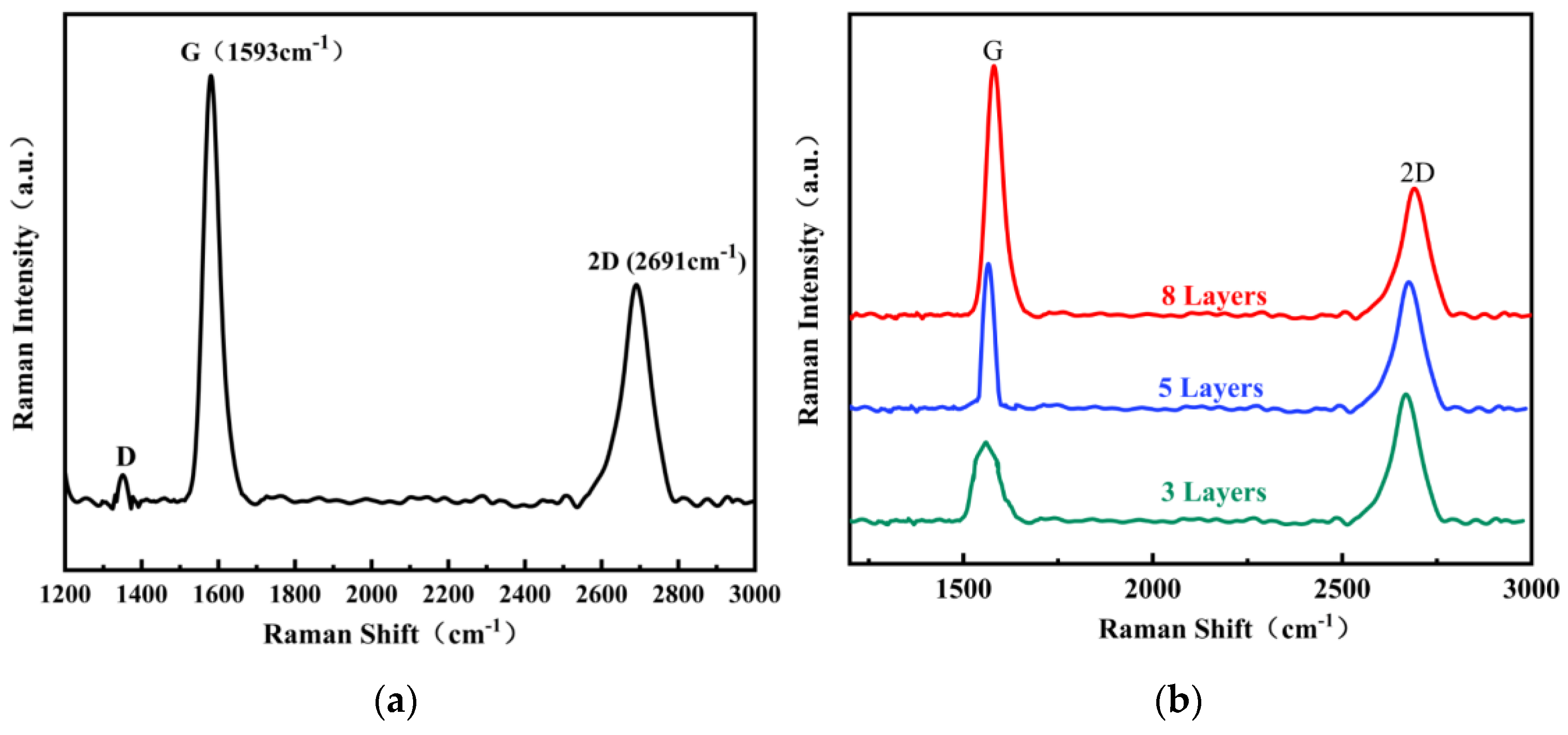
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Junge, P.; Greinacher, M.; Kober, D.; Stargardt, P.; Rupprecht, C. Metastable Phase Formation, Microstructure, and Dielectric Properties in Plasma-Sprayed Alumina Ceramic Coatings. Coatings 2022, 12, 1847. [Google Scholar] [CrossRef]
- Truong, T.Q.; Nguyen, N.T. Simulation and Optimization of Tesla Valves. In Proceedings of the Nanotech—Nanotechnology Conference and Trade Show, San Francisco, CA, USA, 23–28 February 2003; Volume 181, p. 178. [Google Scholar]
- Zhang, S.; Winoto, S.H.; Low, H.T. Performance Simulations of Tesla Microfluidic Valves. In Proceedings of the 2007 First International Conference on Integration and Commercialization of Micro and Nanosystems, Sanya, China, 10–13 January 2007. [Google Scholar] [CrossRef]
- Thompson, S.M.; Paudel, B.J.; Jamal, T.; Walters, D.K. Numerical Investigation of Multistaged Tesla Valves. J. Fluids Eng. 2014, 136, 081102. [Google Scholar] [CrossRef]
- Gan, L.; Sheng-Hong, H.; Zhenyu, L. Gas-Phase Dynamics in Graphene Growth by Chemical Vapour Deposition. Phys. Chem. Chem. Phys. 2015, 17, 22832–22836. [Google Scholar]
- Qian, J.-Y.; Chen, M.; Liu, X.; Jin, Z. A Numerical Investigation of the Flow of Nanofluids Through a Micro Tesla Valve. J. Zhejiang Univ. Sci. A 2019, 20, 50–60. [Google Scholar] [CrossRef]
- Bazilah, F.F.; Ismail, E.; Bakar, S.N.S.A.; Ismail, A.F.; Mohamed, M.A.; Din, M.F.M.; Illias, S.; Ani, M.H. The Role of Gas-Phase Dynamics in Interfacial Phenomena during Few-Layer Graphene Growth Through Atmospheric Pressure Chemical Vapour Deposition. Phys. Chem. Chem. Phys. 2020, 22, 3481–3489. [Google Scholar]
- Pan, M.; Wang, C.; Li, H.-F.; Xie, N.; Wu, P.; Wang, X.-D.; Zeng, Z.; Deng, S.; Dai, G.-P. Growth of U-shaped Graphene Domains on Copper Foil by Chemical Vapor Deposition. Materials 2019, 12, 1887. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stith, D. The Tesla Valve—A Fluidic Diode. Phys. Teach. 2019, 57, 201. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, Y.; Ren, Y.; Sang, Z. Effects of the Oxide Layer with Different Thicknesses on Copper Substrate on Depressing Graphene Nucleation by Low Pressure Chemical Vapor Deposition. J. Cryst. Growth 2020, 541, 125682. [Google Scholar] [CrossRef]
- Bale, C.W.; Bélisle, E.; Chartrand, P.; Decterov, S.A.; Eriksson, G.; Hack, K.; Jung, I.H.; Kang, Y.B.; Melançon, J.; Pelton, A.D. FactSage thermochemical software and databases—Recent developments. Calphad 2009, 33, 295–311. [Google Scholar] [CrossRef]
- Nie, Z.; Palghat, A. Ramachandran and Yanqing Hou. Optimization of effective parameters on Siemens reactor to achieve potential maximum deposition radius: An energy consumption analysis and numerical simulation. Int. J. Heat Mass Transf. 2018, 117, 1083–1098. [Google Scholar] [CrossRef]
- Al-Hilfi, S.H.; Derby, B.; Martin, P.A.; Whitehead, J.C. Chemical Vapour Deposition of Graphene on Copper-Nickel Alloys: The Simulation of a Thermodynamic and Kinetic Approach. Nanoscale 2020, 12, 15283–15294. [Google Scholar] [CrossRef] [PubMed]
- West, N. Tesla’s Valvular Conduit. Fluid Power J. 2013, 20, 18–19. [Google Scholar]
- Jan, R.; Shadi, A.; David, N. An Experimental Investigation of Flow Phenomena in a Multi-stage Micro Tesla Valve. J. Fluids Eng. 2021, 143, 111205. [Google Scholar]
- Fauzi, F.B.; Ismail, M.E.; Hanafi, A.; Bakar, S.N.S.A.; Mohamed, M.A.; Majlis, B.Y.; Din, M.F.M.; Abid, M.A.A.M. A critical review of the effects of fluid dynamics on graphene growth in atmospheric pressure chemical vapor deposition. J. Mater. Res. 2018, 33, 1088–1108. [Google Scholar] [CrossRef]
- Yunhao, B.; Huanguang, W. Numerical Study on Flow and Heat Transfer Characteristics of a Novel Tesla Valve with Improved Evaluation Method. Int. J. Heat Mass Transf. 2022, 187, 122540. [Google Scholar] [CrossRef]
- Mishra, P.; Verma, N. A CFD Study on a Vertical Chemical Vapor Deposition Reactor for Growing Carbon Nanofibers. Chem. Eng. Res. Des. 2012, 90, 2293–2301. [Google Scholar] [CrossRef]
- Machac, P.; Cichon, S.; Lapcak, L.; Fekete, L. Graphene Prepared by Chemical Vapour Deposition Process. Graphene Technol. 2020, 5, 9–17. [Google Scholar] [CrossRef]
- Goncharov, O.; Sapegina, I.; Faizullin, R.; Baldaev, L. Tantalum chemical vapour deposition on steel and tungsten substrates in the TaBr 5-Cd-He system. Surf. Coat Technol. 2019, 377, 124893. [Google Scholar] [CrossRef]
- Son, M.; Ham, M.H. Low-Temperature Synthesis of Graphene by Chemical Vapor Deposition and Its Applications. Flatchem 2017, 5, 40–49. [Google Scholar] [CrossRef]


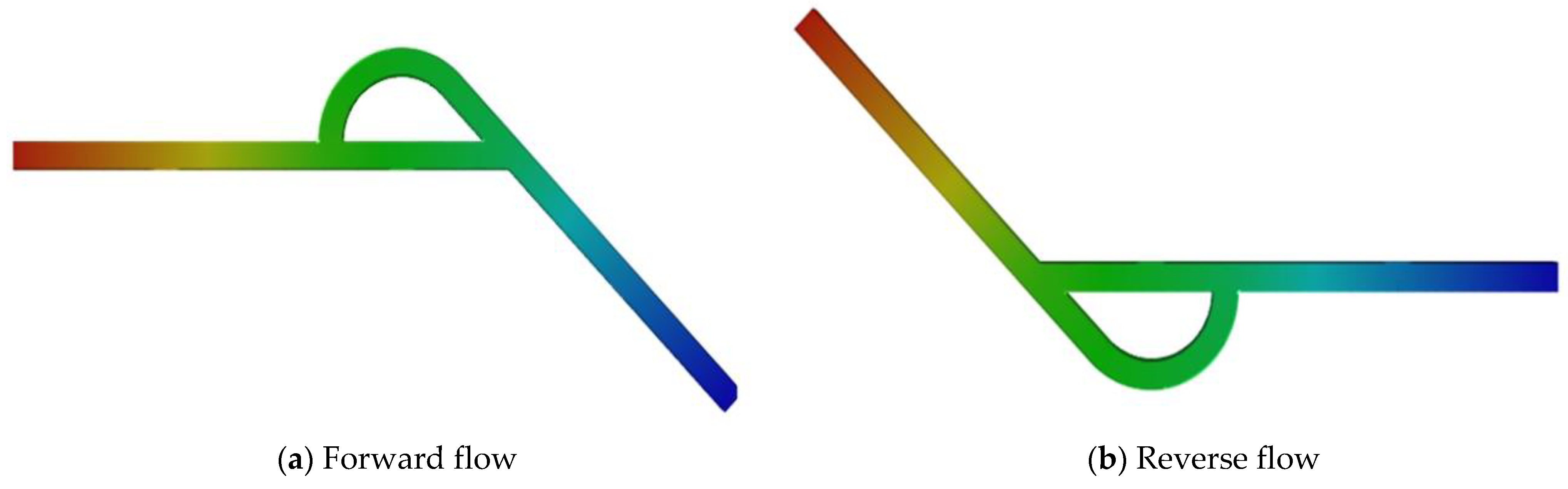





| Equation Name | Equations | No. |
|---|---|---|
| Continuity equation | (2) | |
| Momentum equation | (3) | |
| Energy equation | (4) | |
| Species equation | (5) |
| Physical Parameter | CH4 | H2 | Ar | C<S> |
|---|---|---|---|---|
| Density (kg/m3) | 0.6679 | 0.08189 | 1.6228 | 2000 |
| Cp (j/kg·k) | 2222 | 14,283 | 520.64 | 1220 |
| Thermal conductance (w/m·k) | 0.0332 | 0.1672 | 0.0158 | |
| Viscosity (kg/m·s) | 1.087 × 10−5 | 8.411 × 10−6 | 2.215 × 10−5 | |
| ΔHm (j/kmol) | −7.489518 × 107 | 0 | −3117.71 | −101.268 |
| ΔSm (j/kmol·k) | 186,040.1 | 130,579.1 | 154,719.3 | 5731.747 |
| Normal CVD Straight Pipe without Tesla Valve | |||||
|---|---|---|---|---|---|
| Number | T (K) | CH4 (mL/min) | H2 (mL/min) | Ar (mL/min) | Growth Time (s) |
| 1 | 1310 | 10 | 25 | 100 | 90, 180, 270 |
| Add the CVD Tube of the Tesla Valve | |||||
| Number | T (K) | CH4 (mL/min) | H2 (mL/min) | Ar (mL/min) | Growth Time(s) |
| 2 | 1310 | 1.6 | 3.9 | 15.5 | 90, 180, 270 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Yang, N.; Zhao, D.; Chen, F.; Yuan, X.; Kou, B.; Hou, Y.; Xie, G. Numerical Simulation of Graphene Growth by Chemical Vapor Deposition Based on Tesla Valve Structure. Coatings 2023, 13, 564. https://doi.org/10.3390/coatings13030564
Yang B, Yang N, Zhao D, Chen F, Yuan X, Kou B, Hou Y, Xie G. Numerical Simulation of Graphene Growth by Chemical Vapor Deposition Based on Tesla Valve Structure. Coatings. 2023; 13(3):564. https://doi.org/10.3390/coatings13030564
Chicago/Turabian StyleYang, Bo, Ni Yang, Dan Zhao, Fengyang Chen, Xingping Yuan, Bin Kou, Yanqing Hou, and Gang Xie. 2023. "Numerical Simulation of Graphene Growth by Chemical Vapor Deposition Based on Tesla Valve Structure" Coatings 13, no. 3: 564. https://doi.org/10.3390/coatings13030564
APA StyleYang, B., Yang, N., Zhao, D., Chen, F., Yuan, X., Kou, B., Hou, Y., & Xie, G. (2023). Numerical Simulation of Graphene Growth by Chemical Vapor Deposition Based on Tesla Valve Structure. Coatings, 13(3), 564. https://doi.org/10.3390/coatings13030564




