Model Development of Stress Intensity Factor on 7057T6 Aluminum Alloy Using Extended Finite Element Method
Abstract
:1. Introduction
2. Principle of Extended Finite Element Method
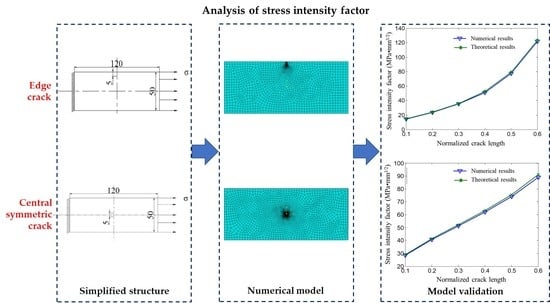
3. Prediction Model of Edge Crack Stress Intensity Factor
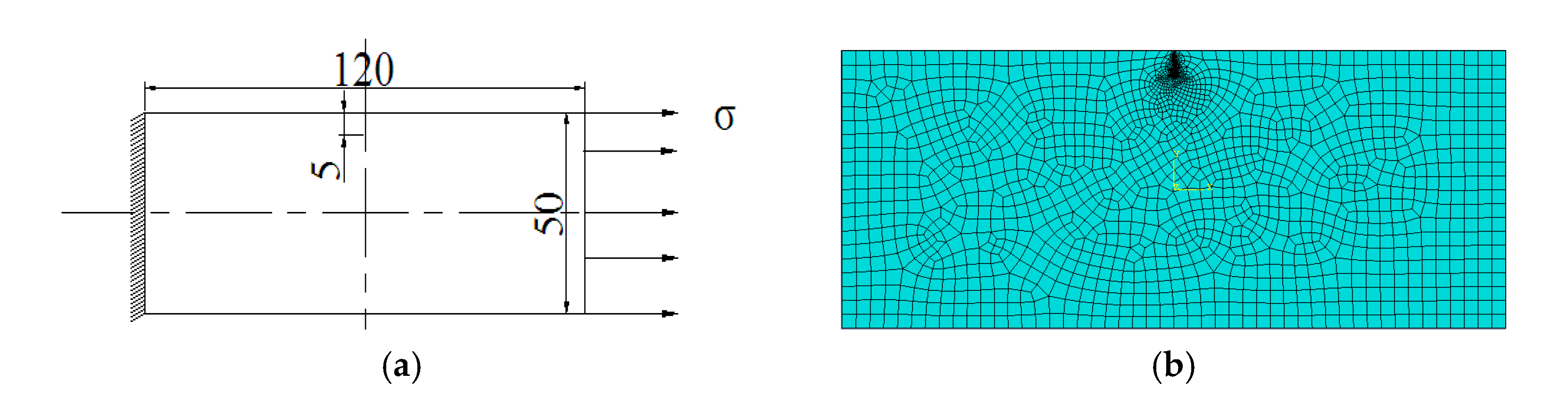
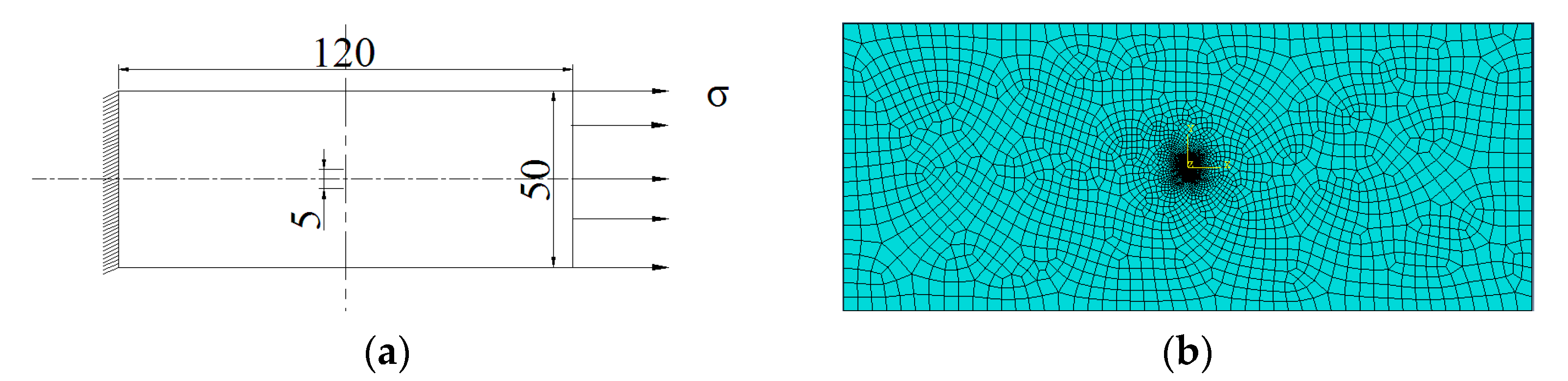
3.1. Development of Numerical Model for Crack Calculation
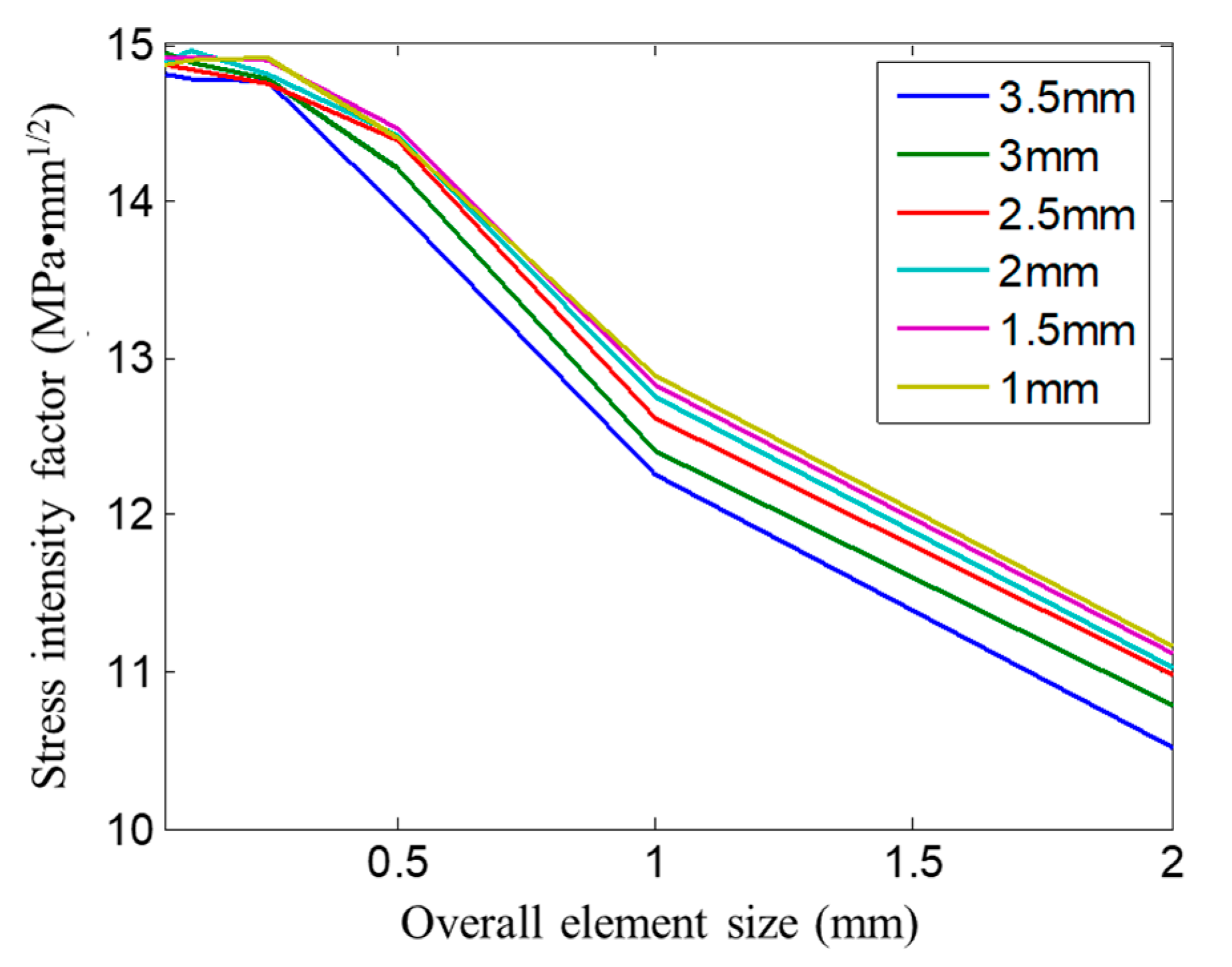
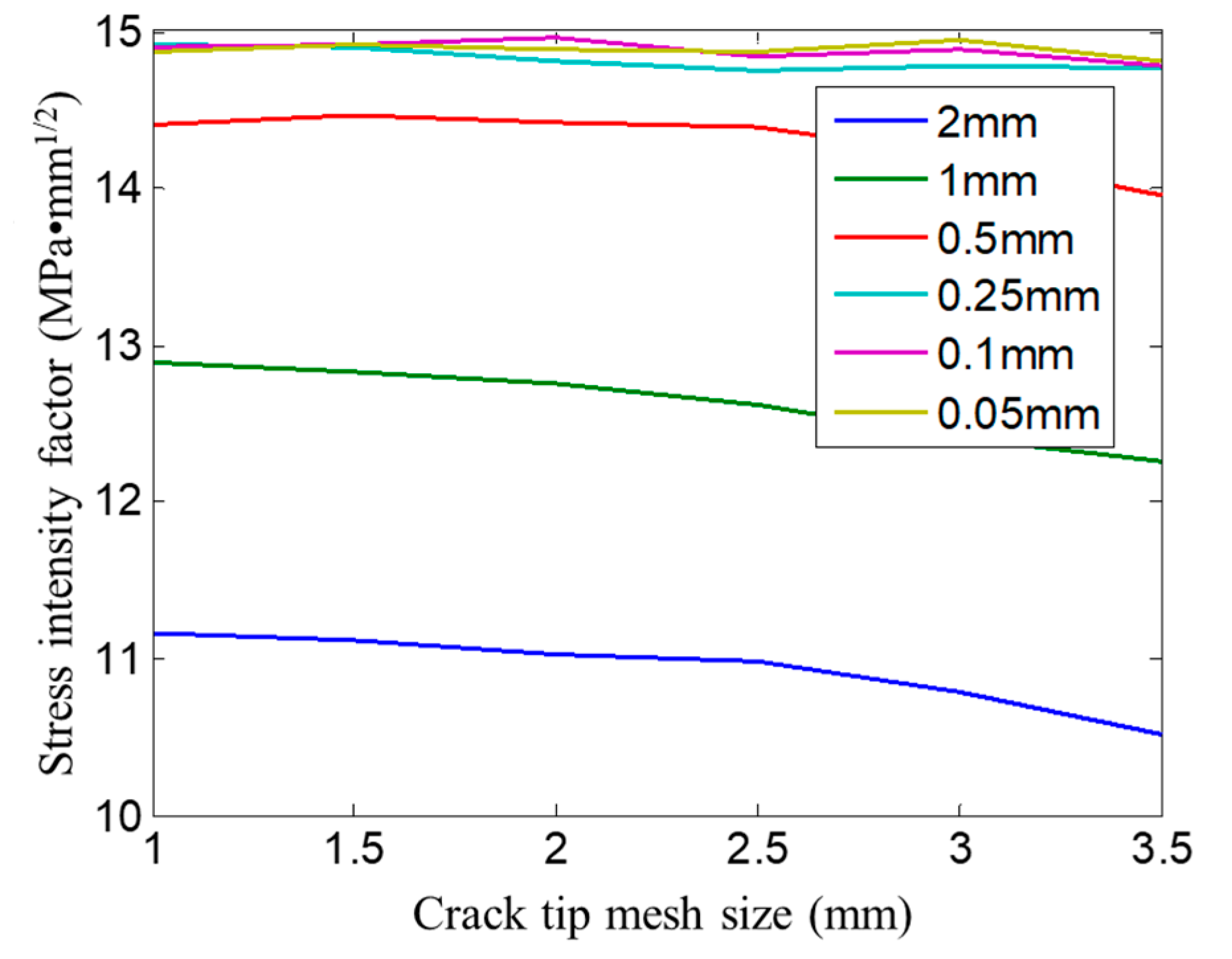
3.2. Effect of Crack Tip Mesh Size and Overall Element Size on Stress Intensity Factor
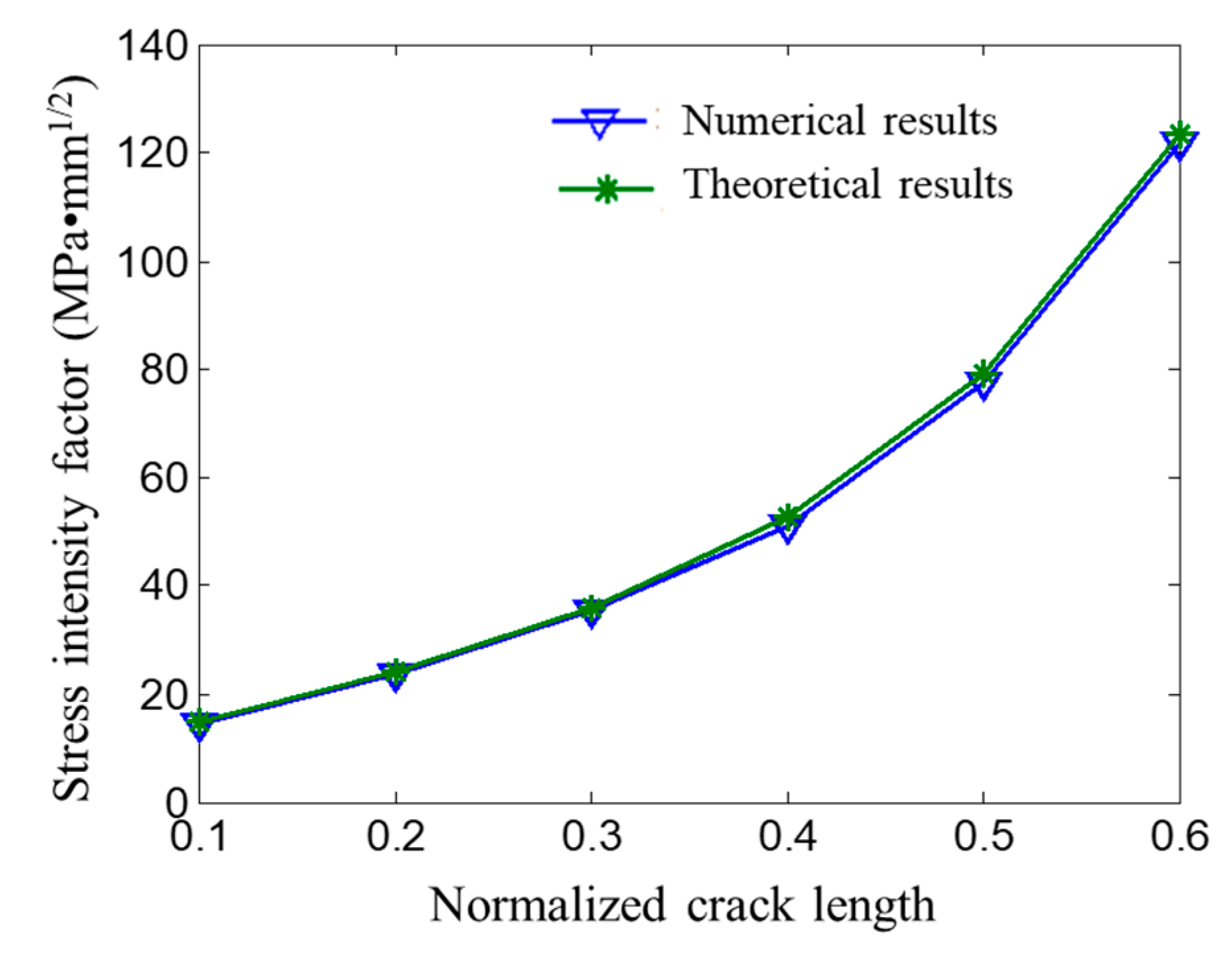
3.3. Stress Intensity Factor Calculation Results and Regression Model
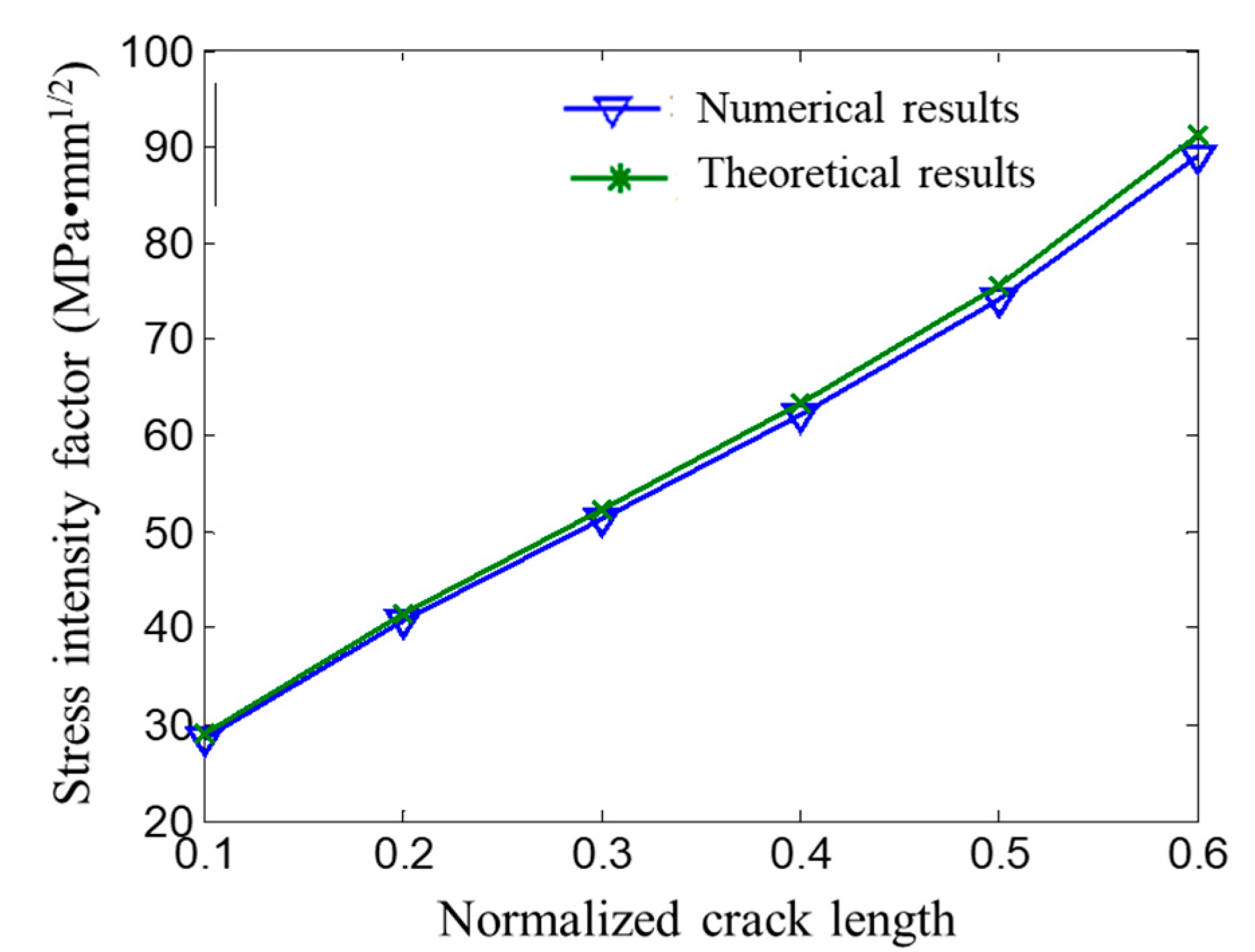
3.4. Model Validation
4. Prediction Model of Central Symmetric Crack Stress Intensity Factor
4.1. Development of Numerical Model for Crack Calculation
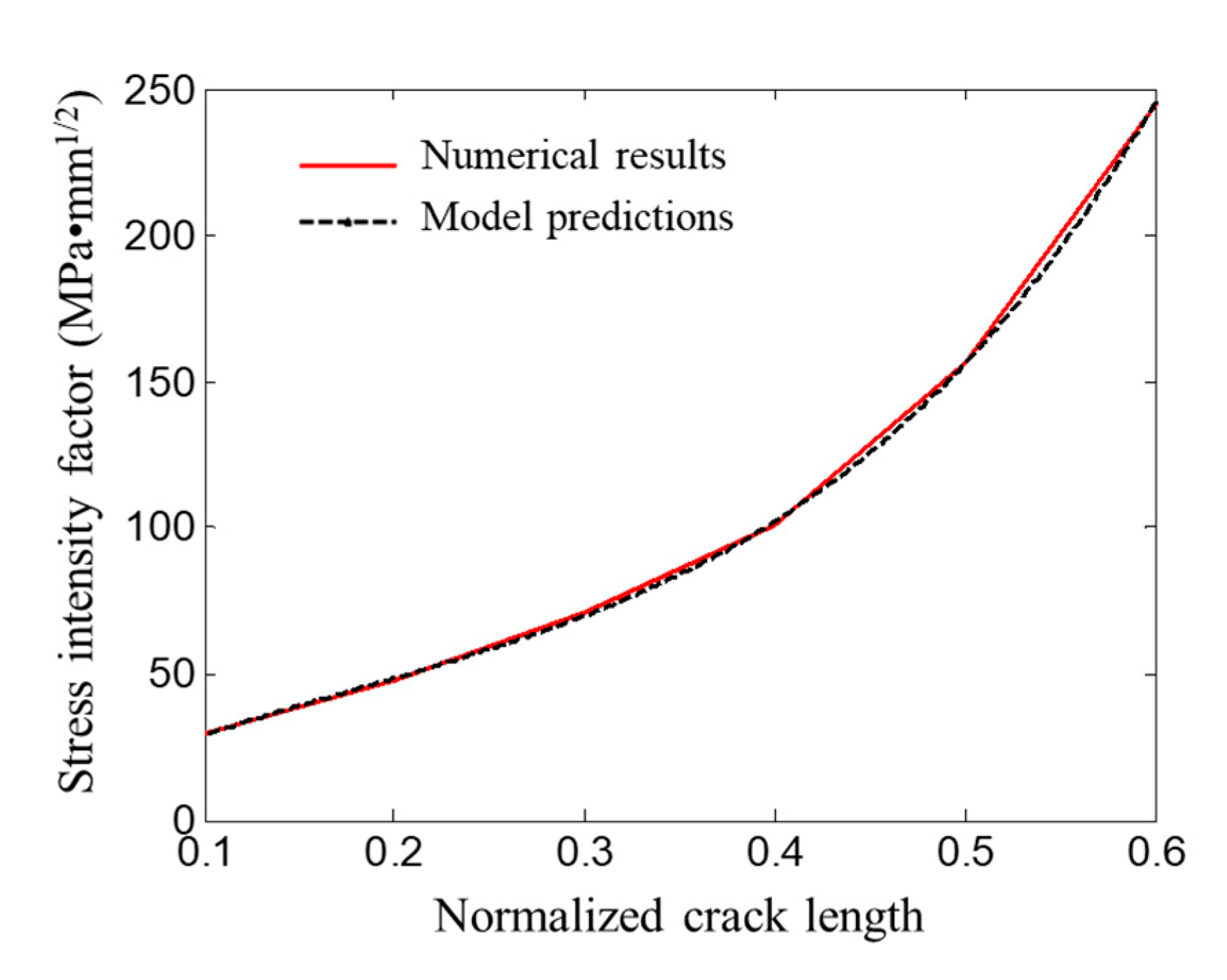
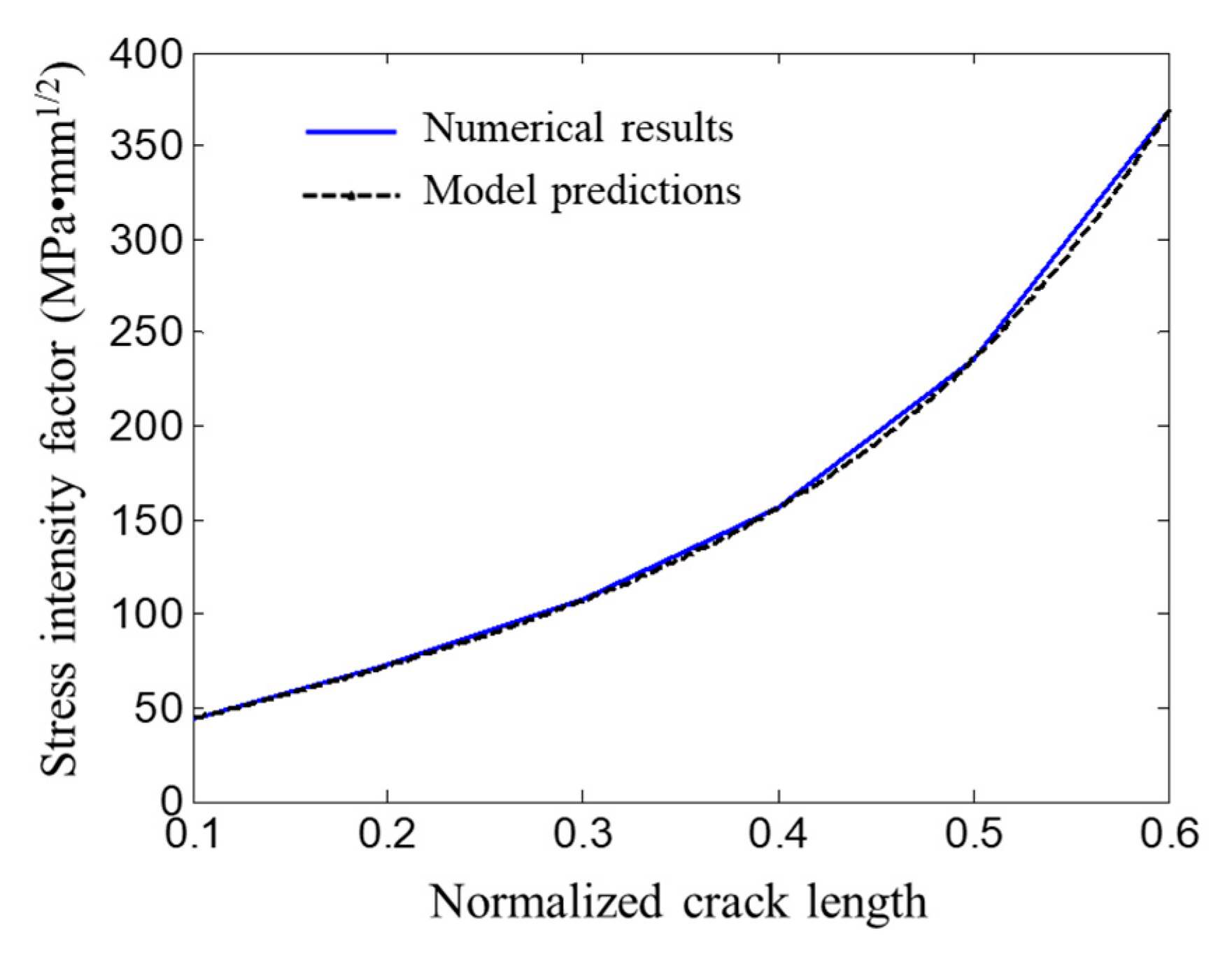
4.2. Calculation Results and Regression Model
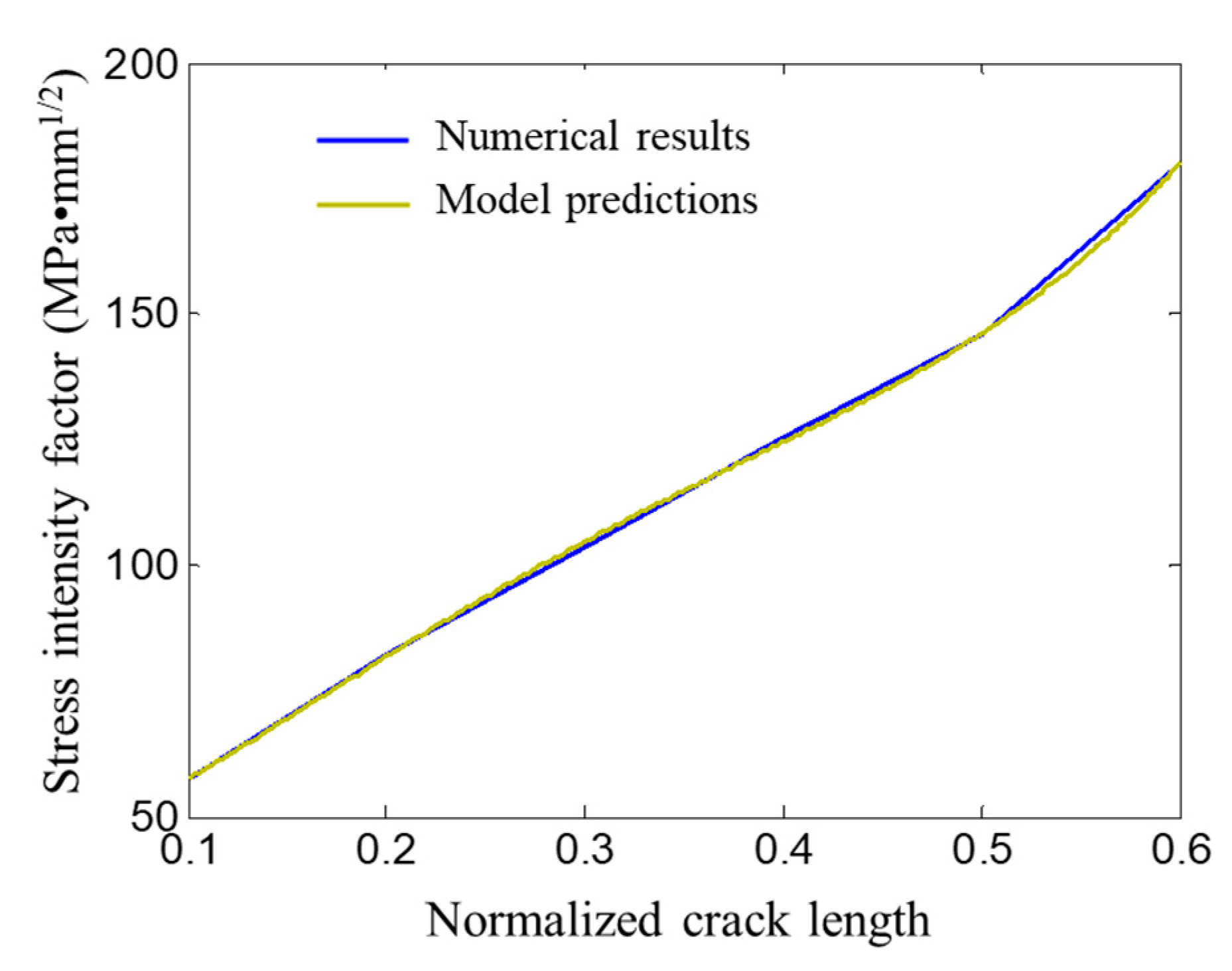
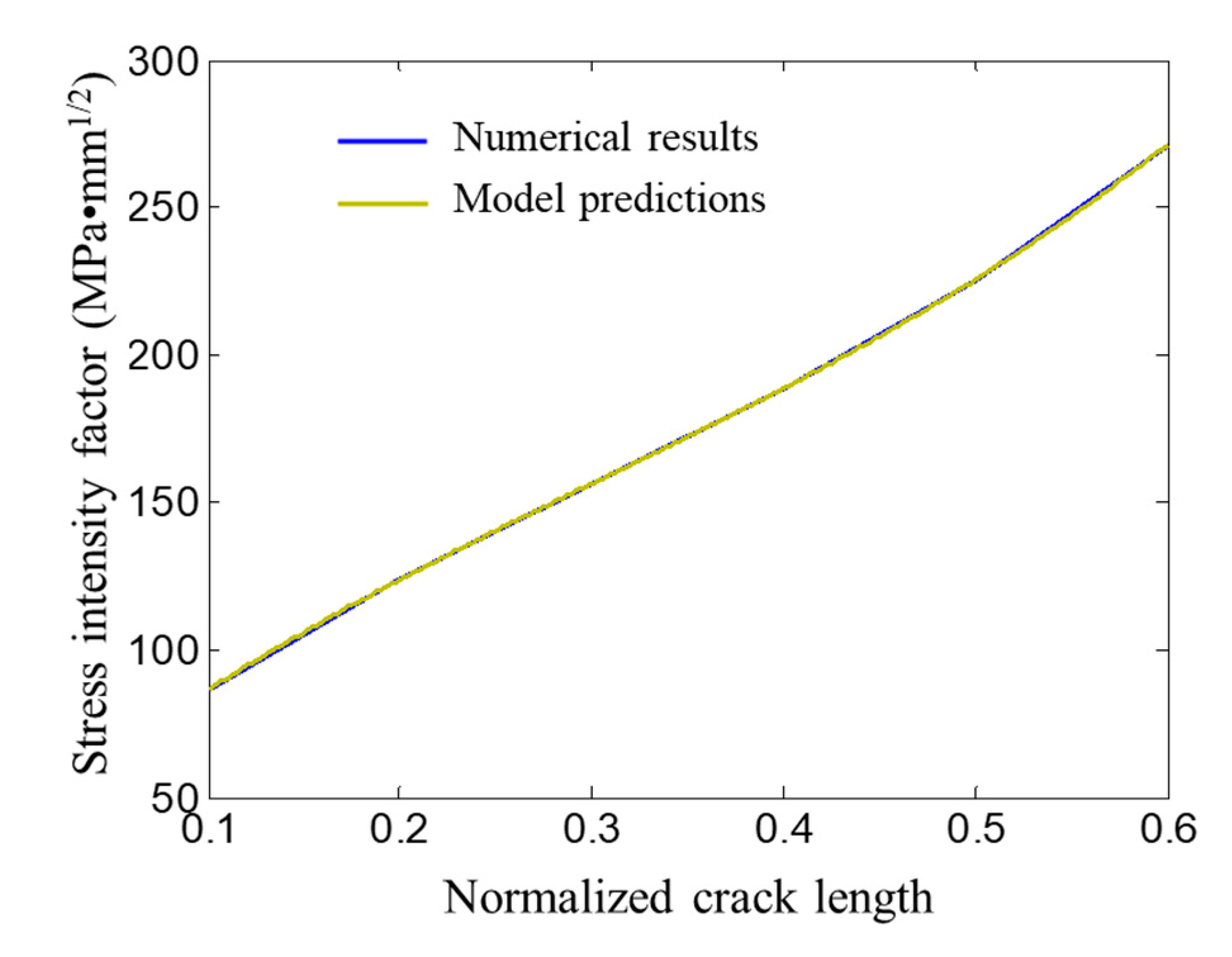
4.3. Model Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qi, H.; Qin, S.; Cheng, Z.; Zou, Y.; Cai, D.; Wen, D. DEM and experimental study on the ultrasonic vibration-assisted abrasive finishing of WC-8Co cemented carbide cutting edge. Powder Technol. 2021, 378, 716–723. [Google Scholar] [CrossRef]
- Charee, W.; Qi, H.; Saetang, V. Underwater laser micromachining of silicon in pressurized environment. Int. J. Adv. Manuf. Technol. 2022, 122, 3161–3169. [Google Scholar] [CrossRef]
- Lei, Y.; Wang, Z.; Qi, H. Strengthening Performance Optimization of Single Ball Impact Treatment by Evaluating Residual Stress. Materials 2022, 15, 3719. [Google Scholar] [CrossRef] [PubMed]
- Tangwarodomnukun, V.; Kringram, S.; Zhu, H.; Qi, H.; Rujisamphan, N. Fabrication of superhydrophobic surface on AISI316L stainless steel using a nanosecond pulse laser. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2022, 236, 680–693. [Google Scholar] [CrossRef]
- Ji, R.; Qi, Z.; Chen, J.; Zhang, L.; Lin, K.; Lu, S.; Li, Y. Numerical and Experimental Investigation on the Abrasive Flow Machining of Artificial Knee Joint Surface. Crystals 2023, 13, 430. [Google Scholar] [CrossRef]
- Xie, X.D.; Zhang, L.; Zhu, L.L.; Li, Y.B.; Hong, T.; Yang, W.B.; Shan, X.H. Sate of the art and perspectives on surface strengthening process and associated mechanisms by shot peening. Coatings 2023, 13, Submitted. [Google Scholar]
- Wu, B.; Li, D.R.; Zhou, Y.; Zhu, D.; Zhao, Y.P.; Z.K., Q.; Chen, B.; Wang, X.L.; Lin, Q. Construction of a calibration field of absolute gravity in a cave using the Cold Atom Gravimeter. Sensors 2023, 23, Submitted. [Google Scholar]
- Qi, H.; Xing, W.; Tan, W.; Lin, H.; Guo, H.J.; Chen, M.Z.; Tang, H.P. Effect of the sintering process on mechanical behaviors of Zirconia ceramics by NanoParticle Jetting. Ceram. Int. 2023, Submitted. [Google Scholar]
- Qian, H.; Chen, M.; Qi, Z.; Teng, Q.; Qi, H.; Zhang, L.; Shan, X. Review on Research and Development of Abrasive Scratching of Hard Brittle Materials and Its Underlying Mechanisms. Crystals 2023, 13, 428. [Google Scholar] [CrossRef]
- Qi, H.; Wen, D.; Lu, C.; Li, G. Numerical and experimental study on ultrasonic vibration-assisted micro-channelling of glasses using an abrasive slurry jet. Int. J. Mech. Sci. 2016, 110, 94–107. [Google Scholar] [CrossRef]
- Qi, H.; Wen, D.; Yuan, Q.; Zhang, L.; Chen, Z. Numerical investigation on particle impact erosion in ultrasonic-assisted abrasive slurry jet micro-machining of glasses. Powder Technol. 2017, 314, 627–634. [Google Scholar] [CrossRef]
- Li, H.N.; Yang, Y.; Zhao, Y.J.; Zhang, Z.; Zhu, W.; Wang, W.; Qi, H. On the periodicity of fixed-abrasive planetary lapping based on a generic model. J. Manuf. Process. 2019, 44, 271–287. [Google Scholar] [CrossRef]
- Elmhaia, O.; Belaasilia, Y.; Askour, O.; Braikat, B.; Damil, N. Numerical analysis of frictional contact between crack lips in the framework of Linear Elastic Fracture Mechanics by a mesh-free approach. Theor. Appl. Fract. Mech. 2023, 124, 103749. [Google Scholar] [CrossRef]
- Ongaro, G.; Bertani, R.; Galvanetto, U.; Pontefisso, A.; Zaccariotto, M. A multiscale peridynamic framework for modelling mechanical properties of polymer-based nanocomposites. Eng. Fract. Mech. 2022, 274, 108751. [Google Scholar] [CrossRef]
- Shojaei, A.; Hermann, A.; Cyron, C.J.; Seleson, P.; Silling, S.A. A hybrid meshfree discretization to improve the numerical performance of peridynamic models. Comput. Methods Appl. Mech. Eng. 2022, 391, 114544. [Google Scholar] [CrossRef]
- Shojaei, A.; Mudric, T.; Zaccariotto, M.; Galvanetto, U. A coupled meshless finite point/Peridynamic method for 2D dynamic fracture analysis. Int. J. Mech. Sci. 2016, 119, 419–431. [Google Scholar] [CrossRef]
- Ongaro, G.; Seleson, P.; Galvanetto, U.; Ni, T.; Zaccariotto, M. Overall equilibrium in the coupling of peridynamics and classical continuum mechanics. Comput. Methods Appl. Mech. Eng. 2021, 381, 113515. [Google Scholar] [CrossRef]
- Kamaya, M.; Sugamura, K.; Okada, H. Stress intensity factors of rectangular shape cracks for crack growth prediction. Int. J. Press. Vessel. Pip. 2023, 201, 104864. [Google Scholar] [CrossRef]
- Calvín, G.; Escalero, M.; Zabala, H.; Muñiz-Calvente, M. A new effective stress intensity factor approach to determine thickness-independent fatigue crack growth rate curves. Theor. Appl. Fract. Mech. 2022, 121, 103505. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Hu, C.; Ling, D.; Ren, X.; Gong, S.; Wang, L.; Huang, Z. An improved crack-tip element treatment for advanced FEMs. Theor. Appl. Fract. Mech. 2020, 108, 102587. [Google Scholar] [CrossRef]
- Melenk, J.M.; Babuška, I. The partition of unity finite element method: Basic theory and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 289–314. [Google Scholar] [CrossRef] [Green Version]
- Nakasone, Y.; Yoshimoto, S.; Stolarski, T.A. Chapter 3—Application of ANSYS to stress analysis. In Engineering Analysis with ANSYS Software; Nakasone, Y., Yoshimoto, S., Stolarski, T.A., Eds.; Butterworth-Heinemann: Oxford, UK, 2006; pp. 51–142. [Google Scholar]
- Wang, Y.Y.; Wang, Z.; Ni, P.C.; Wang, D.J.; Guo, S.H.; Chen, Z.Z. Experimental and numerical study on regulation of cutting temperature during the circular sawing of 45 steel. Coatings 2023, 13, Submitted. [Google Scholar]
- Yu, T.T. Numerical simulation of a body with cracks. Chin. J. Rock Mech. Eng. 2005, 24, 4434–4439. [Google Scholar]
- Suman, S.; Khan, M.K.; Pathak, M.; Singh, R.N. 3D simulation of hydride-assisted crack propagation in zircaloy-4 using XFEM. Int. J. Hydrogen Energy 2017, 42, 18668–18673. [Google Scholar] [CrossRef]
- Suman, S.; Khan, M.K.; Pathak, M.; Singh, R.N. Effects of Hydride on Crack Propagation in Zircaloy-4. Procedia Eng. 2017, 173, 1185–1190. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, I.V.; Mishra, B.K. A homogenized XFEM approach to simulate fatigue crack growth problems. Comput. Struct. 2015, 150, 1–22. [Google Scholar] [CrossRef]
- Maierhofer, J.; Pippan, R.; Gänser, H.P. Modified NASGRO equation for physically short cracks. Int. J. Fatigue 2014, 59, 200–207. [Google Scholar] [CrossRef] [Green Version]
- Ji, P.J.; Zhang, J.J.; Xie, X.D.; Ying, R.M.; Zhang, L. Review on Wear Characteristics of Artificial Hip Joint and Associated Physical Training. Front. Mater. 2023, 10. [Google Scholar]
- Kumar, M.; Singh, I.V.; Mishra, B.K. Fatigue crack growth simulations of plastically graded materials using XFEM and J-integral decomposition approach. Eng. Fract. Mech. 2019, 216, 106470. [Google Scholar] [CrossRef]
- Galić, I.; Čular, I.; Vučković, K.; Tonković, Z. Comparison of SIF solutions obtained by XFEM and conventional FEM for cracks in complex geometries like valve body. Procedia Struct. Integr. 2018, 13, 2109–2113. [Google Scholar] [CrossRef]
- Nasri, K.; Abbadi, M.; Zenasni, M.; Ghammouri, M.; Azari, Z. Double crack growth analysis in the presence of a bi-material interface using XFEM and FEM modelling. Eng. Fract. Mech. 2014, 132, 189–199. [Google Scholar] [CrossRef]
- Cruz, F.; Roehl, D.; Vargas, E.d.A. An XFEM implementation in Abaqus to model intersections between fractures in porous rocks. Comput. Geotech. 2019, 112, 135–146. [Google Scholar] [CrossRef]
- Qi, H.; Wang, Y.; Qi, Z.; Shi, L.; Fang, Z.; Zhang, L.; Riemer, O.; Karpuschewski, B. A Novel Grain-Based DEM Model for Evaluating Surface Integrity in Scratching of RB-SiC Ceramics. Materials 2022, 15, 8486. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Qin, S.; Fang, Z. Numerical Modeling and Experimental Study on the Material Removal Process Using Ultrasonic Vibration-Assisted Abrasive Water Jet. Front. Mater. 2022, 9. [Google Scholar] [CrossRef]




| Elastic Modulus, E (MPa) | Poisson Ratio, ν | Density, ρ (kg/m3) | Fracture Toughness, K (MPa•mm1/2) |
|---|---|---|---|
| 71,000 | 0.33 | 2740 | 917 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, H.; Yang, W.; Zhang, L.; Hong, T. Model Development of Stress Intensity Factor on 7057T6 Aluminum Alloy Using Extended Finite Element Method. Coatings 2023, 13, 581. https://doi.org/10.3390/coatings13030581
Yuan H, Yang W, Zhang L, Hong T. Model Development of Stress Intensity Factor on 7057T6 Aluminum Alloy Using Extended Finite Element Method. Coatings. 2023; 13(3):581. https://doi.org/10.3390/coatings13030581
Chicago/Turabian StyleYuan, Haiyang, Weibo Yang, Li Zhang, and Tao Hong. 2023. "Model Development of Stress Intensity Factor on 7057T6 Aluminum Alloy Using Extended Finite Element Method" Coatings 13, no. 3: 581. https://doi.org/10.3390/coatings13030581
APA StyleYuan, H., Yang, W., Zhang, L., & Hong, T. (2023). Model Development of Stress Intensity Factor on 7057T6 Aluminum Alloy Using Extended Finite Element Method. Coatings, 13(3), 581. https://doi.org/10.3390/coatings13030581