A Computational Study of Particle Mass Transport during Melting of NePCM in a Square Cavity with a Single Adiabatic Side
Abstract
1. Introduction
2. Mathematical Model
2.1. Initial and Boundary Conditions
2.2. Effective Thermo-Physical Properties
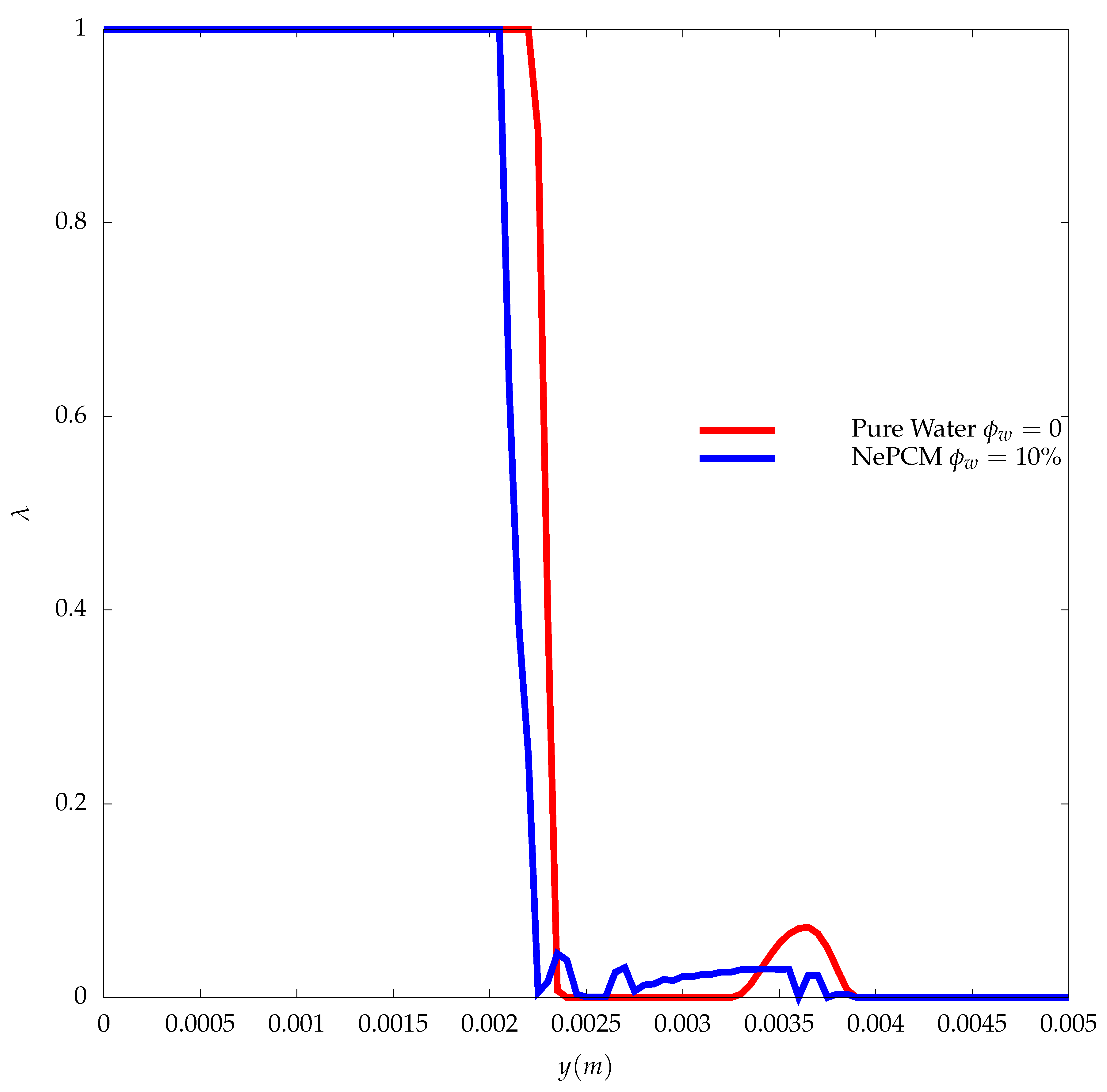
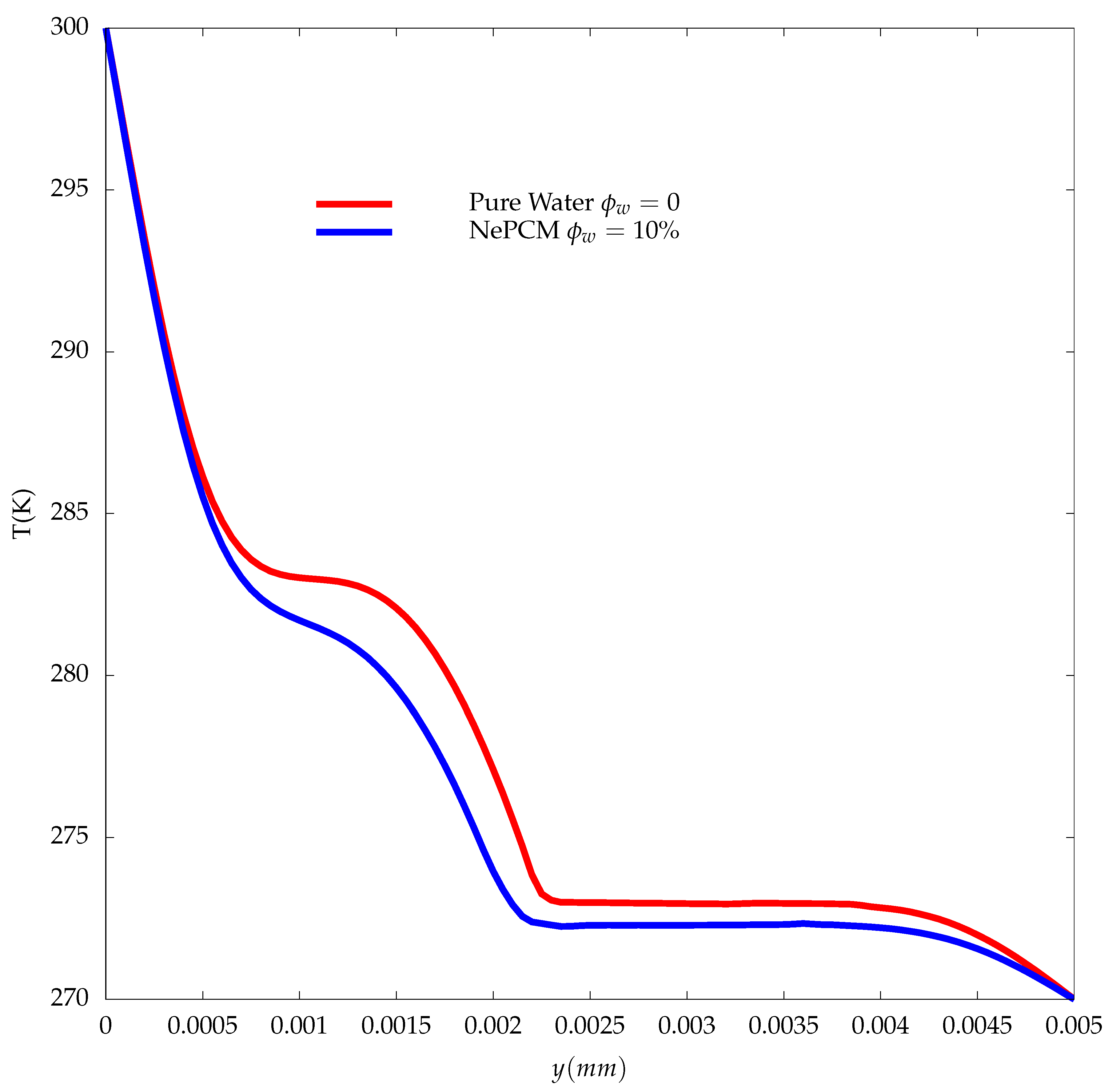
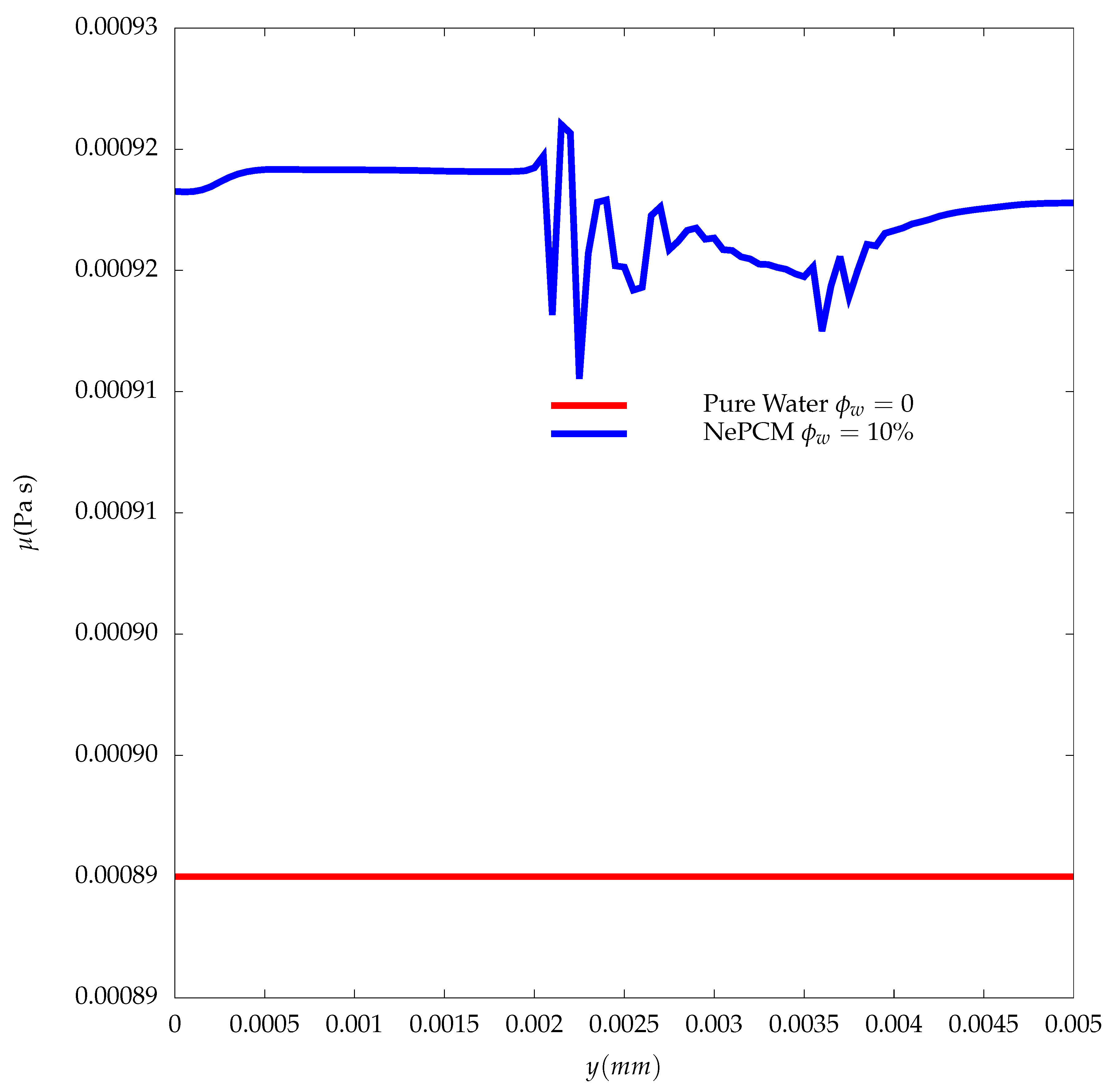
3. Results
4. Conclusions
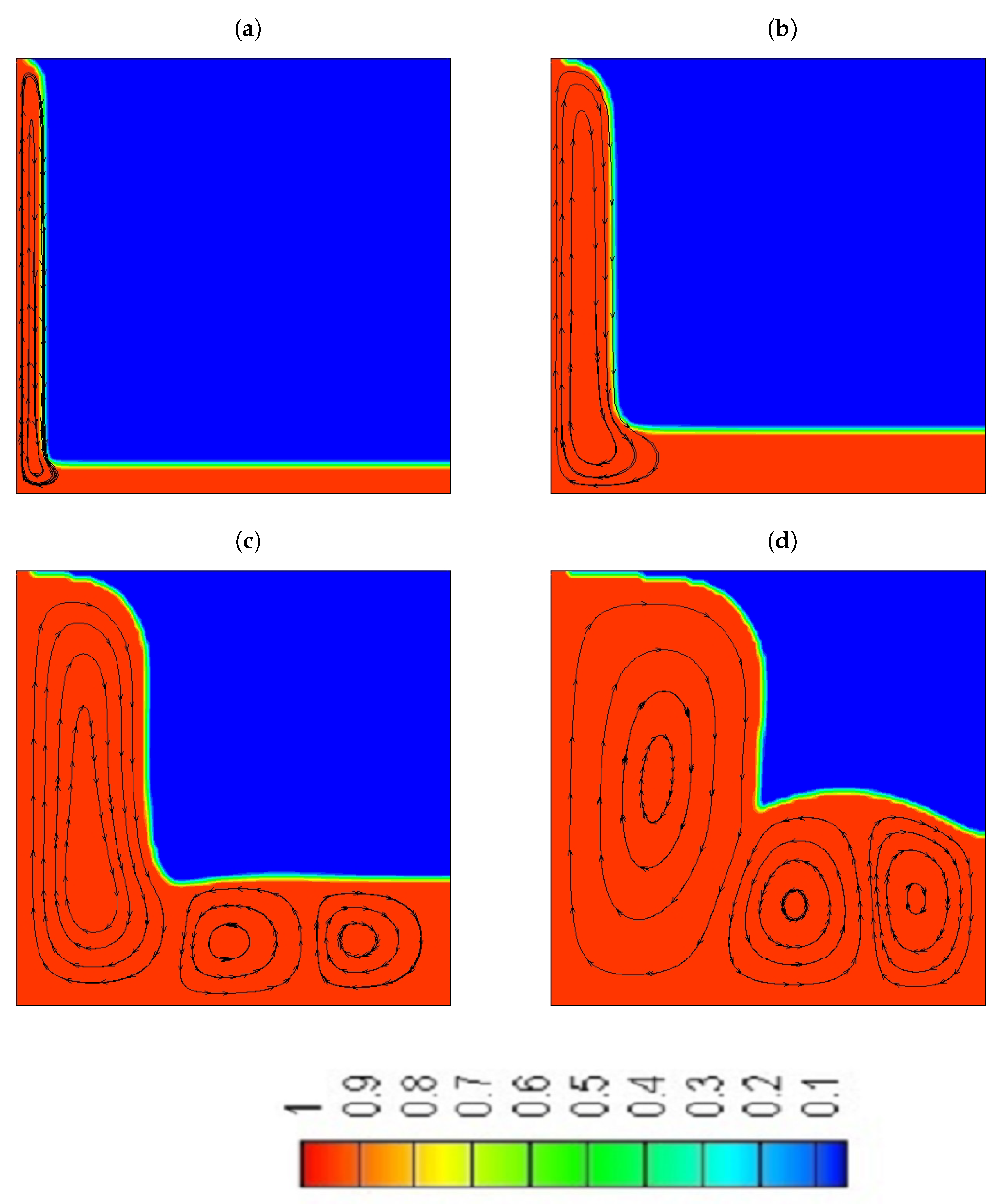
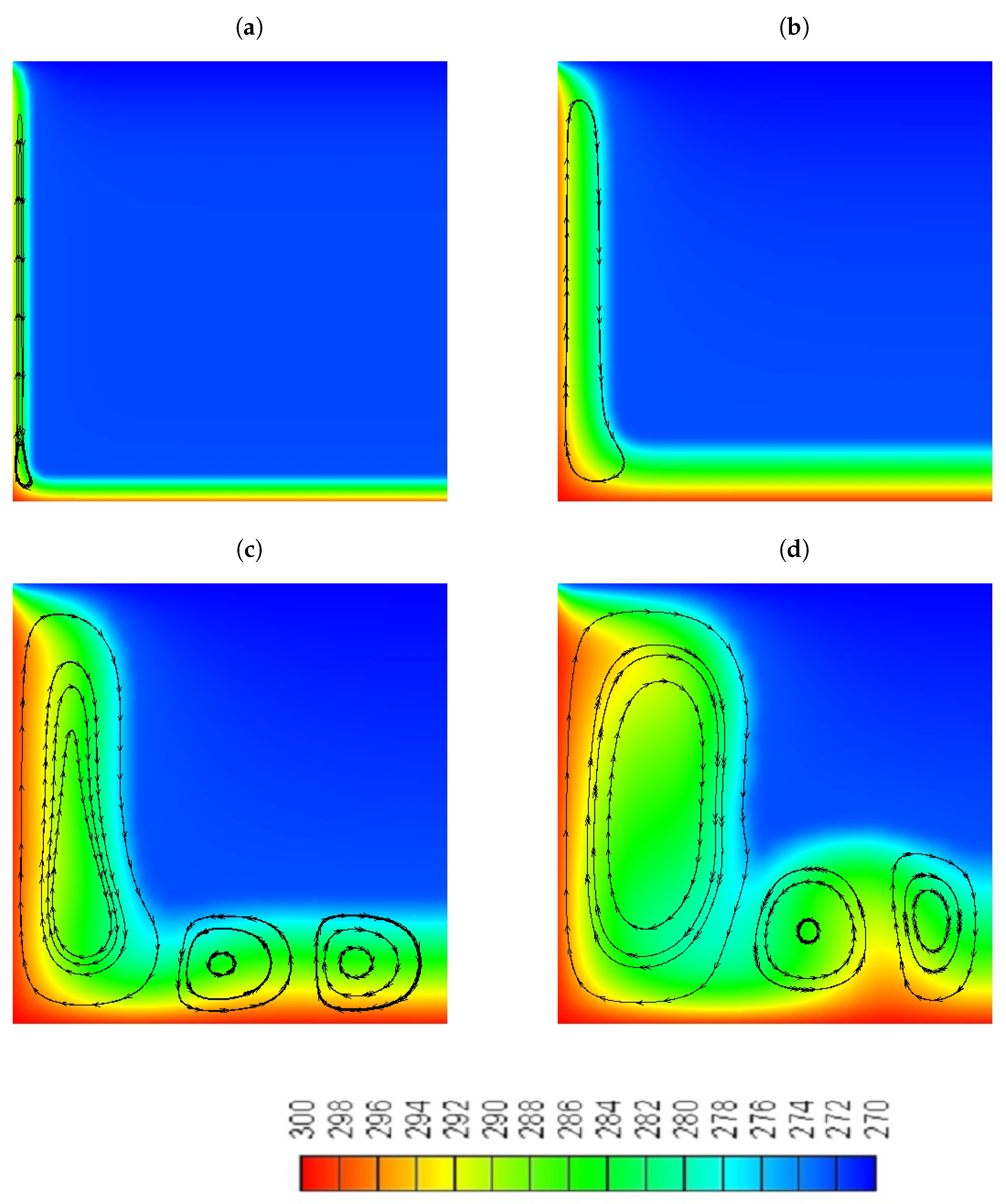
- For pure water and the NePCM, a large recirculating flow and two smaller counter-rotating cells are formed during the melting process.
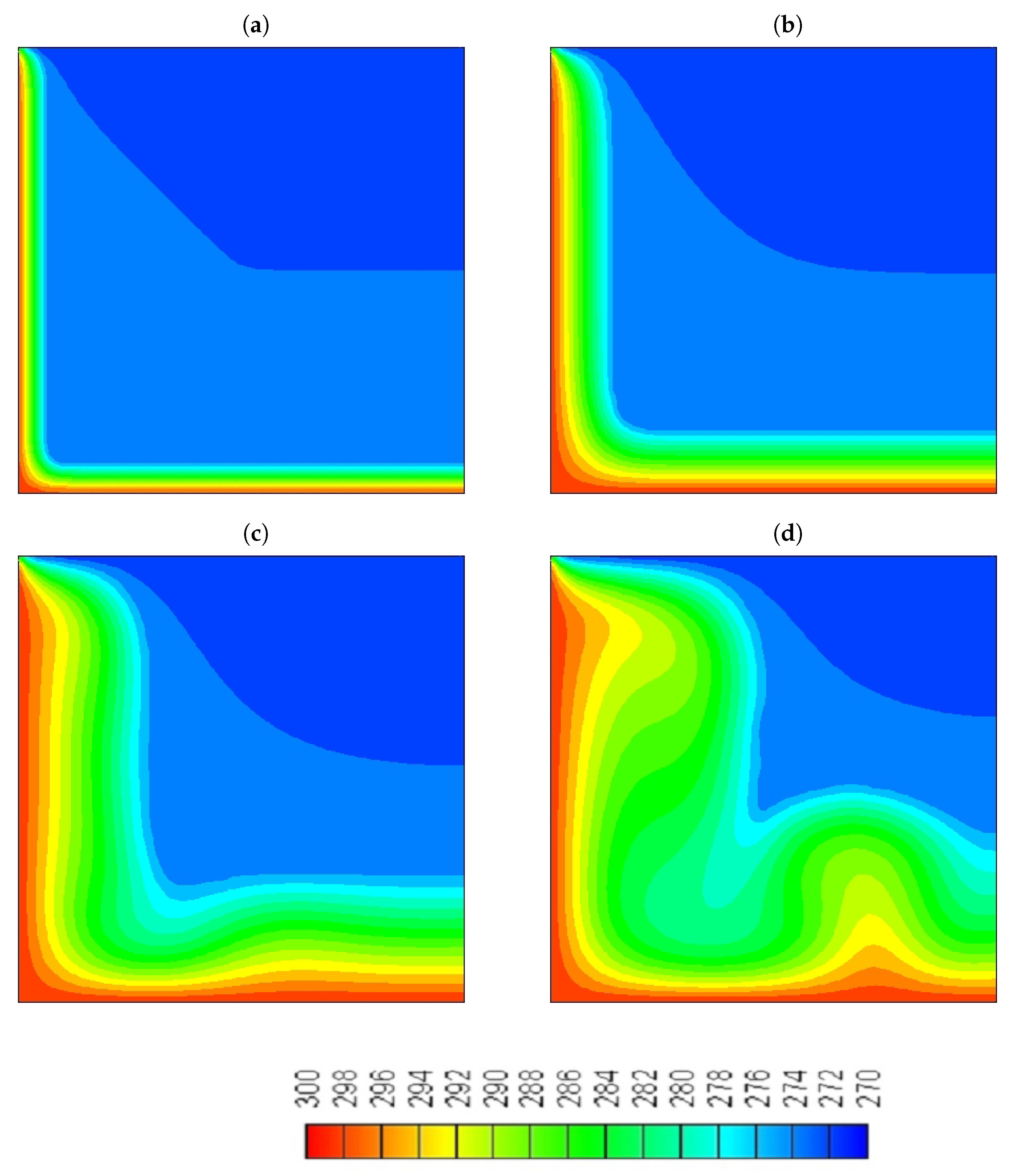
- At the early stages, where the heat transfer is controlled by conduction, both water and the NePCM are melting at the same rate, which shows that the increase in the thermal conductivity of the NePCM did not play a significant role in the enhancement of its performance.
- Adding particles reduces the intensity of the convection cells.
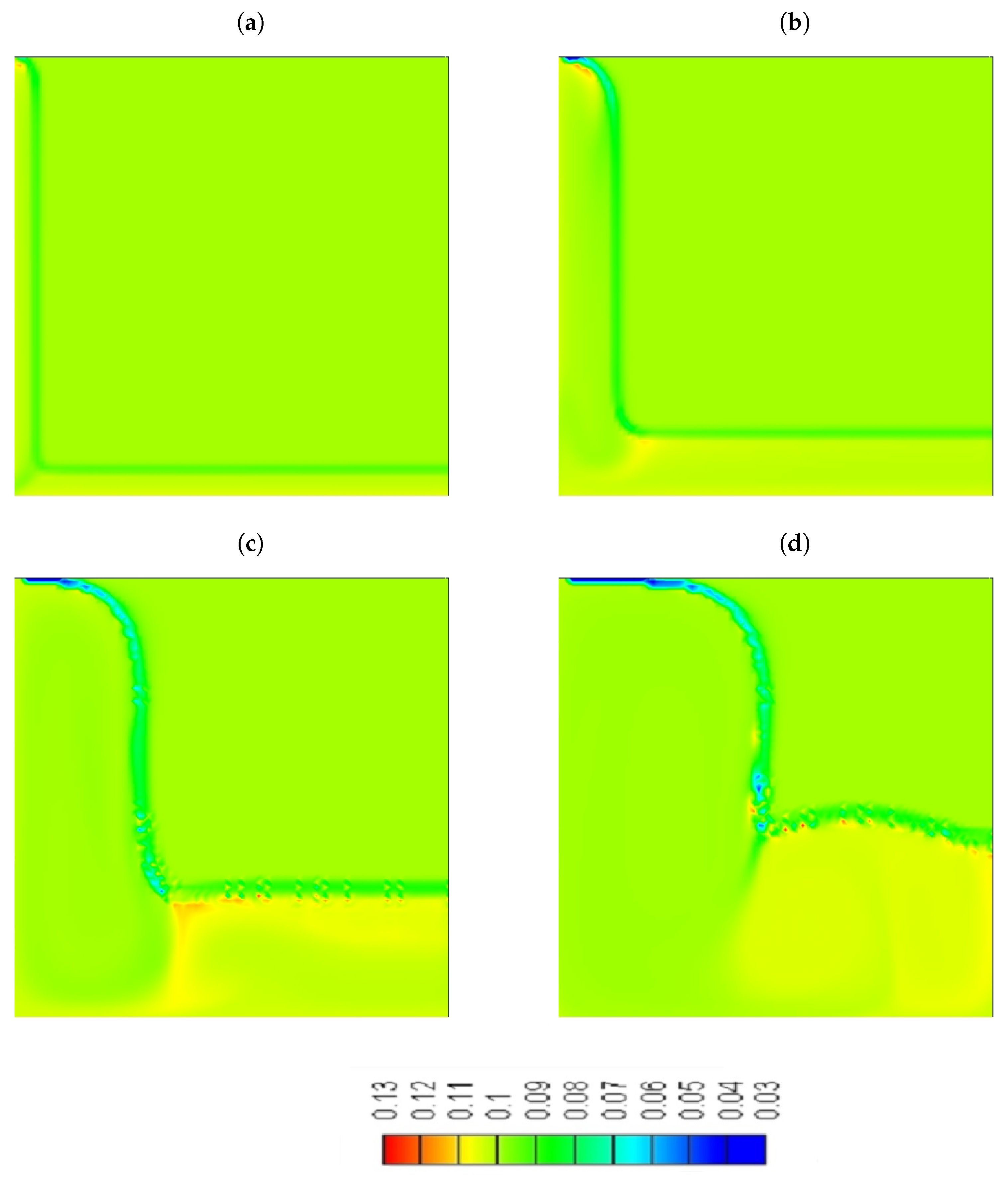
- A significant concentration of particles is located in the bottom side of the cavity.
- At the later stages of the melting process, when convection is the primary mechanism that controls the heat transfer, the NePCM will melt slower compared to the pure water as described by experiments.
- Although we were able to achieve a higher percentage increase in thermal conductivity (4%) compared to viscosity (3.37%) in the melting region of the NePCM, with the addition of particles with a mass fraction of = 10% still resulted in a deceleration of the solid-liquid interface.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| T | Temperature (K) |
| Velocity vector (m/s) | |
| Mass fraction of nanoparticels | |
| Liquid fraction | |
| Brownian Diffusion () | |
| Segregation coefficient | |
| p | Pressure (Pa) |
| Particle diameter (nm) | |
| Liquids temperature (K) | |
| Solidus temperature (K) | |
| Rayleigh number |
References
- Tol, R.S. The economic effects of climate change. J. Econ. Perspect. 2009, 23, 29–51. [Google Scholar] [CrossRef]
- Tao, Y.; He, Y.L. A review of phase change material and performance enhancement method for latent heat storage system. Renew. Sustain. Energy Rev. 2018, 93, 245–259. [Google Scholar] [CrossRef]
- Pássaro, J.; Rebola, A.; Coelho, L.; Conde, J.; Evangelakis, G.; Prouskas, C.; Papageorgiou, D.; Zisopoulou, A.; Lagaris, I. Effect of fins and nanoparticles in the discharge performance of PCM thermal storage system with a multi pass finned tube heat exchange. Appl. Therm. Eng. 2022, 212, 118569. [Google Scholar] [CrossRef]
- Wang, L.; Guo, L.; Ren, J.; Kong, X. Using of heat thermal storage of PCM and solar energy for distributed clean building heating: A multi-level scale-up research. Appl. Energy 2022, 321, 119345. [Google Scholar] [CrossRef]
- Izadi, M.; Hajjar, A.; Alshehri, H.M.; Saleem, A.; Galal, A.M. Analysis of applying fin for charging process of phase change material inside H-shaped thermal storage. Int. Commun. Heat Mass Transf. 2022, 139, 106421. [Google Scholar] [CrossRef]
- Patel, J.R.; Rathod, M.K.; Elavarasan, R.M.; Said, Z. Influence of longitudinal fin arrangement on the melting and solidification inside the triplex tube latent heat thermal storage system. J. Energy Storage 2022, 46, 103778. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Z.; Liu, G.; Yang, X.; Yan, J. Melting assessment on the effect of nonuniform Y-shaped fin upon solid–liquid phase change in a thermal storage tank. Appl. Energy 2022, 321, 119330. [Google Scholar] [CrossRef]
- Barthwal, M.; Rakshit, D. No fins attached? Numerical analysis of internal–external fins coupled PCM melting for solar applications. Appl. Therm. Eng. 2022, 215, 118911. [Google Scholar] [CrossRef]
- Li, Z.; Hu, N.; Tu, J.; Fan, L. Experimental investigation of heat storage and heat transfer rates during melting of nano-enhanced phase change materials (NEPCM) in a differentially-heated rectangular cavity. J. Therm. Sci. 2020, 29, 503–511. [Google Scholar] [CrossRef]
- Feng, Y.; Li, H.; Li, L.; Bu, L.; Wang, T. Numerical investigation on the melting of nanoparticle-enhanced phase change materials (NEPCM) in a bottom-heated rectangular cavity using lattice Boltzmann method. Int. J. Heat Mass Transf. 2015, 81, 415–425. [Google Scholar] [CrossRef]
- Han, Y.; Yang, Y.; Mallick, T.; Wen, C. Nanoparticles to Enhance Melting Performance of Phase Change Materials for Thermal Energy Storage. Nanomaterials 2022, 12, 1864. [Google Scholar] [CrossRef]
- Zhang, J.; Cao, Z.; Huang, S.; Huang, X.; Liang, K.; Yang, Y.; Zhang, H.; Tian, M.; Akrami, M.; Wen, C. Improving the melting performance of phase change materials using novel fins and nanoparticles in tubular energy storage systems. Appl. Energy 2022, 322, 119416. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, Z.; Zhou, Y.; Lu, B.; Zhang, Y. Numerical study using lattice Boltzmann method on melting and solidification of NEPCM placed inside a rectangular cavity with a new double-fin arrangement. Appl. Therm. Eng. 2023, 219, 119619. [Google Scholar] [CrossRef]
- Izadi, M.; Sheremet, M.; Hajjar, A.; Galal, A.M.; Mahariq, I.; Jarad, F.; Hamida, M.B.B. Numerical investigation of magneto-thermal-convection impact on phase change phenomenon of Nano-PCM within a hexagonal shaped thermal energy storage. Appl. Therm. Eng. 2023, 223, 119984. [Google Scholar] [CrossRef]
- Younis, O.; Abderrahmane, A.; Laidoudi, H.; Akkurt, N.; Fadhl, B.M.; Guedri, K. Buoyancy-driven flow and thermal activity of nano-enhanced phase change material in inversed U-shaped chamber. J. Energy Storage 2023, 61, 106705. [Google Scholar] [CrossRef]
- Faraji, H.; El Alami, M.; Arshad, A.; Faraji, M. Numerical simulation of the melting of a NePCM for cooling of electronic components. Therm. Sci. Eng. Prog. 2021, 21, 100766. [Google Scholar] [CrossRef]
- Zeng, Y.; Fan, L.W.; Xiao, Y.Q.; Yu, Z.T.; Cen, K.F. An experimental investigation of melting of nanoparticle-enhanced phase change materials (NePCMs) in a bottom-heated vertical cylindrical cavity. Int. J. Heat Mass Transf. 2013, 66, 111–117. [Google Scholar] [CrossRef]
- El Hasadi, Y.M.; Khodadadi, J. Numerical simulation of the effect of the size of suspensions on the solidification process of nanoparticle-enhanced phase change materials. J. Heat Transf. 2013, 135, 052901. [Google Scholar] [CrossRef]
- Beckermann, C.; Viskanta, R. Double-diffusive convection during dendritic solidification of a binary mixture. PhysicoChemical Hydrodyn. 1988, 10, 195–213. [Google Scholar]
- El Hasadi, Y.M.; Khodadadi, J. One-dimensional Stefan problem formulation for solidification of nanostructure-enhanced phase change materials (NePCM). Int. J. Heat Mass Transf. 2013, 67, 202–213. [Google Scholar] [CrossRef]
- EL Hasadi, Y.M.; Khodadadi, J. Numerical simulation of solidification of colloids inside a differentially heated cavity. J. Heat Transf. 2015, 137, 072301. [Google Scholar] [CrossRef]
- El Hasadi, Y.M.; Khodadadi, J. Numerical Simulation of Solidification of Colloidal Suspensions Inside a Differentially-Heated Cavity. In Proceedings of the ASME 2013 Heat Transfer Summer Conference collocated with the ASME 2013 7th International Conference on Energy Sustainability and the ASME 2013 11th International Conference on Fuel Cell Science, Engineering and Technology, Minneapolis, MN, USA, 14–19 July 2013; Volume 55485, p. V002T07A038. [Google Scholar]
- El Hasadi, Y.; Khodadadi, J.M. Numerical Simulation of Solidification of Nanoparticle-Enhanced Phase Change Materials (NEPCM) Considering Transport of Suspensions. In Proceedings of the TMNN-2010 International Symposium on Thermal and Materials Nanoscience and Nanotechnology, Antalya, Turkey, 29 May–3 June 2011. [Google Scholar]
- El Hasadi, Y.M. Numerical simulation of the melting process of nanostructured based colloidal suspensions phase change materials including the effect of the transport of the particles. J. Mol. Liq. 2019, 287, 110886. [Google Scholar] [CrossRef]
- Jegatheesan, M.; Bhattacharya, A. A model for predicting the effects of buoyancy driven convection on solidification of binary alloy with nanoparticles. Int. J. Heat Mass Transf. 2022, 182, 121916. [Google Scholar] [CrossRef]
- Patil, S.; Kataria, C.; Kumar, A.; Kumar, A. Effect of segregation and advection governed heterogeneous distribution of nanoparticles on NEPCM discharging behavior. J. Energy Storage 2023, 57, 106230. [Google Scholar] [CrossRef]
- Soni, V. Nanoadditive Particles segregation and mobility in phase change materials. Int. J. Heat Mass Transf. 2021, 165, 120676. [Google Scholar] [CrossRef]
- Voller, V.R.; Cross, M.; Markatos, N. An enthalpy method for convection/diffusion phase change. Int. J. Numer. Methods Eng. 1987, 24, 271–284. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Peppin, S.; Elliott, J.; Worster, M.G. Solidification of colloidal suspensions. J. Fluid Mech. 2006, 554, 147–166. [Google Scholar] [CrossRef]
- Wakao, N.; Kagei, S. Heat and Mass Transfer in Packed Beds; Taylor & Francis: Thames, UK, 1982; Volume 1. Available online: https://books.google.co.in/books?hl=zh-CN&lr=&id=Ya5hzOgC05wC&oi=fnd&pg=PR9&dq=Heat+and+Mass+Transfer+in+Packed+Beds&ots=73DN4U0GwS&sig=R0HNk3bRzE-Ti-ya8tt0VSblMJc&redir_esc=y#v=onepage&q=Heat%20and%20Mass%20Transfer%20in%20Packed%20Beds&f=false (accessed on 15 January 2023).
- El Hasadi, Y.M.; Crapper, M. Self-propelled nanofluids a path to a highly effective coolant. Appl. Therm. Eng. 2017, 127, 857–869. [Google Scholar] [CrossRef]
- El Hasadi, Y.M.; Crapper, M. Self-propelled nanofluids a coolant inspired from nature with enhanced thermal transport properties. J. Mol. Liq. 2020, 313, 113548. [Google Scholar] [CrossRef]
- Rappaz, M.; Dantzig, J.A. Solidification; EPFL Press: Lausanne, Switzerland, 2009. [Google Scholar]





| Water | Copper Nanoparticles | |
|---|---|---|
| Density | ||
| Viscosity | − | |
| Specific heat | ||
| Thermal conductivity | ||
| Thermal expansion coefficient | ||
| Heat of fusion | − |
| Transport Property | = 10% ( = 1.22%) |
|---|---|
| Thermal Conductivity | 6.23 |
| Density | 1.10 |
| Dynamic viscosity | 9.18 |
| Specific heat | 3.8 |
| Thermal expansion coefficient | 1.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Hasadi, Y.M.F. A Computational Study of Particle Mass Transport during Melting of NePCM in a Square Cavity with a Single Adiabatic Side. Coatings 2023, 13, 739. https://doi.org/10.3390/coatings13040739
El Hasadi YMF. A Computational Study of Particle Mass Transport during Melting of NePCM in a Square Cavity with a Single Adiabatic Side. Coatings. 2023; 13(4):739. https://doi.org/10.3390/coatings13040739
Chicago/Turabian StyleEl Hasadi, Yousef M. F. 2023. "A Computational Study of Particle Mass Transport during Melting of NePCM in a Square Cavity with a Single Adiabatic Side" Coatings 13, no. 4: 739. https://doi.org/10.3390/coatings13040739
APA StyleEl Hasadi, Y. M. F. (2023). A Computational Study of Particle Mass Transport during Melting of NePCM in a Square Cavity with a Single Adiabatic Side. Coatings, 13(4), 739. https://doi.org/10.3390/coatings13040739





