Owens–Wendt Characterization of Femtosecond-Laser-Textured Hydrophobic Aluminum Surfaces
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Texture Formation
2.2. Chemical Surface Treatment
2.3. Surface Characterization
2.4. Owens–Wendt Method
3. Results and Discussion
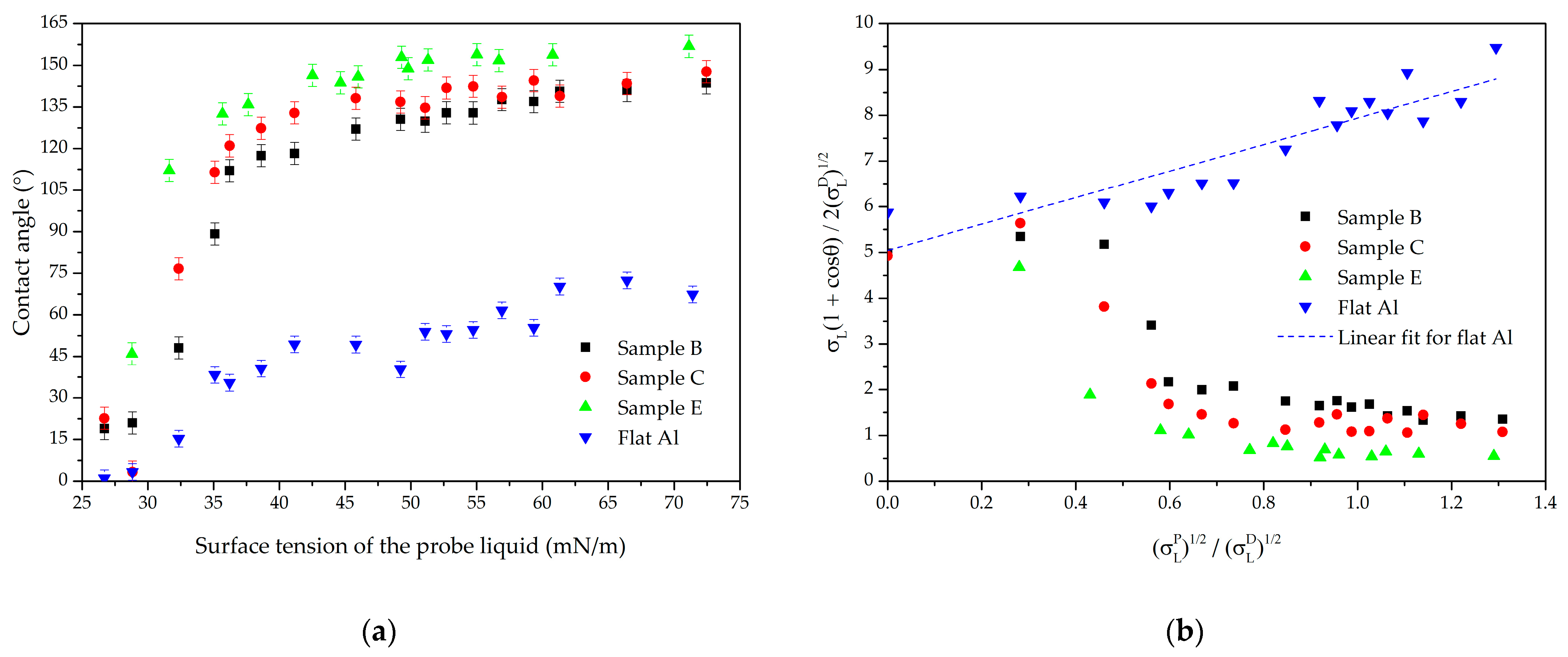
3.1. Owens–Wendt Plot on Micro- and Nanoscale Textures
3.2. Owens–Wendt Plots as a Tool for Comparing the Water Repellency of Microtextures
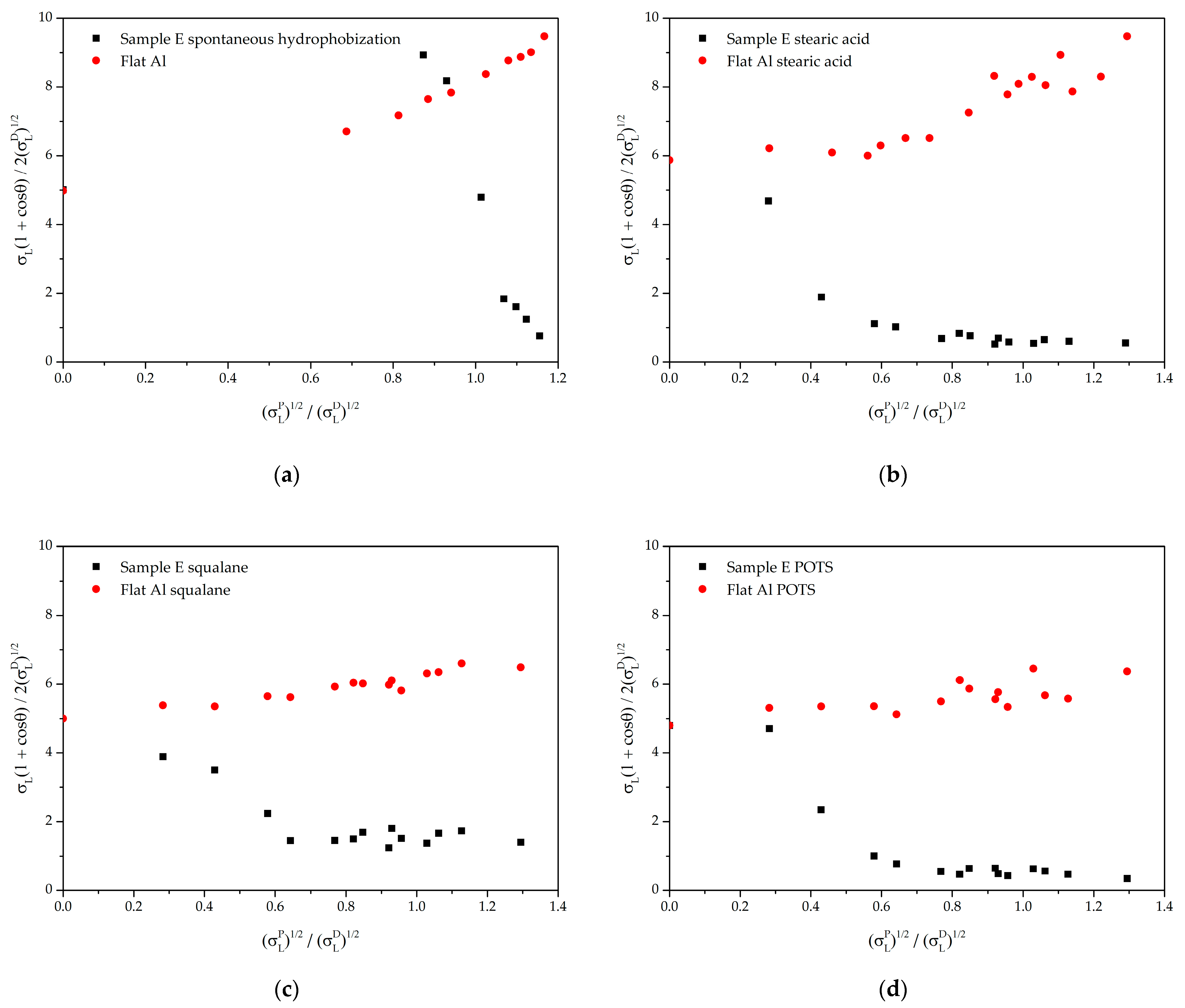
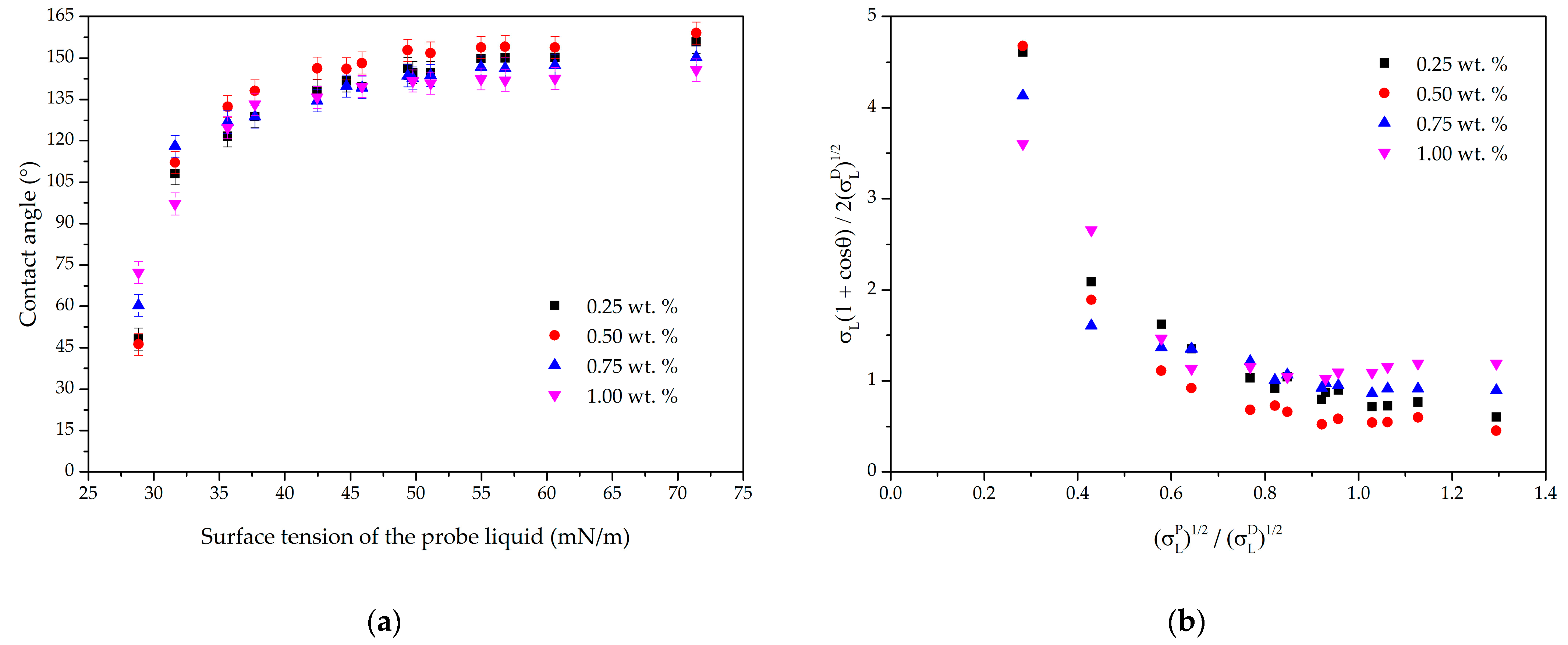
3.3. Characterization of the Effectiveness of Hydrophobic Agents in the Formation of Liquid-Repellent Properties of Textured Surfaces
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Si, Y.; Dong, Z.; Jiang, L. Bioinspired designs of superhydrophobic and superhydrophilic materials. ACS Cent. Sci. 2018, 4, 1102–1112. [Google Scholar] [CrossRef] [PubMed]
- Yong, J.; Yang, Q.; Guo, C.; Chen, F.; Hou, X. A review of femtosecond laser-structured superhydrophobic or underwater superoleophobic porous surfaces/materials for efficient oil/water separation. RSC Adv. 2019, 9, 12470–12495. [Google Scholar] [CrossRef]
- Long, J.; Fan, P.; Gong, D.; Jiang, D.; Zhang, H.; Li, L.; Zhong, M. Superhydrophobic surfaces fabricated by femtosecond laser with tunable water adhesion: From Lotus Leaf to Rose Petal. ACS Appl. Mater. Interfaces 2015, 7, 9858–9865. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Pan, L.; Fan, P.; Gong, D.; Jiang, D.; Zhang, H.; Li, L.; Zhong, M. Cassie-state stability of metallic superhydrophobic surfaces with various micro/nanostructures produced by a femtosecond laser. Langmuir 2016, 32, 1065–1072. [Google Scholar] [CrossRef] [PubMed]
- Myronyuk, O.; Dudko, V.; Baklan, D.; Melnyk, L. Study of structure influence on wear resistance of hierarchial superhydrophobic coatings. East.-Eur. J. Enterp. Technol. 2017, 3, 44–49. [Google Scholar] [CrossRef]
- Hooda, A.; Goyat, M.S.; Pandey, J.K.; Kumar, A.; Gupta, R. A review on Fundamentals, constraints and fabrication techniques of superhydrophobic coatings. Prog. Org. Coat. 2020, 142, 105557. [Google Scholar] [CrossRef]
- Somlyai-Sipos, L.; Baumli, P. Wettability of metals by water. Metals 2022, 12, 1274. [Google Scholar] [CrossRef]
- Milles, S.; Soldera, M.; Voisiat, B.; Lasagni, A.F. Fabrication of superhydrophobic and ice-repellent surfaces on pure aluminium using single and multiscaled periodic textures. Sci. Rep. 2019, 9, 13944. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, X.; Tian, Y. Insights into the wettability transition of nanosecond laser ablated surface under ambient air exposure. J. Colloid Interface Sci. 2019, 533, 268–277. [Google Scholar] [CrossRef]
- Yang, C.W.; Hao, P.F.; He, F. Effect of upper contact line on sliding behavior of water droplet on superhydrophobic surface. Sci. Bull. 2009, 54, 727–731. [Google Scholar] [CrossRef]
- Jin, M.; Xing, Q.; Chen, Z. A review: Natural superhydrophobic surfaces and applications. J. Biomater. Nanobiotechnol. 2020, 11, 110–149. [Google Scholar] [CrossRef]
- Law, K.-Y. Water–surface interactions and definitions for hydrophilicity, hydrophobicity and Superhydrophobicity. Pure Appl. Chem. 2015, 87, 759–765. [Google Scholar] [CrossRef]
- Kariper, İ.A. Low-cost, high-efficiency, new generation material for fog harvesting fumed silica-doped polypropylene. NPJ Clean Water 2021, 4, 24. [Google Scholar] [CrossRef]
- Majhy, B.; Iqbal, R.; Sen, A.K. Facile fabrication and mechanistic understanding of a transparent reversible superhydrophobic–superhydrophilic surface. Sci. Rep. 2018, 8, 18018. [Google Scholar] [CrossRef]
- Etzler, F.M. Determination of the surface free energy of Solids. Rev. Adhes. Adhes. 2013, 1, 3–45. [Google Scholar] [CrossRef]
- Fox, H.W.; Zisman, W.A. The spreading of liquids on low energy surfaces. I. Polytetrafluoroethylene. J. Colloid Sci. 1950, 5, 514–531. [Google Scholar] [CrossRef]
- Owens, D.K.; Wendt, R.C. Estimation of the surface free energy of polymers. J. Appl. Polym. Sci. 1969, 13, 1741–1747. [Google Scholar] [CrossRef]
- Mantel, M.; Wightman, J.P. Influence of the surface chemistry on the wettability of Stainless Steel. Surf. Interface Anal. 1994, 21, 595–605. [Google Scholar] [CrossRef]
- Becker, S.; Merz, R.; Hasse, H.; Kopnarski, M. Solvent cleaning and wettability of technical steel and titanium surfaces. Adsorp. Sci. Technol. 2016, 34, 261–274. [Google Scholar] [CrossRef]
- Wang, X.; Fu, C.; Zhang, C.; Qiu, Z.; Wang, B. A comprehensive review of wetting transition mechanism on the surfaces of microstructures from theory and testing methods. Materials 2022, 15, 4747. [Google Scholar] [CrossRef]
- Murakami, D.; Jinnai, H.; Takahara, A. Wetting transition from the cassie–baxter state to the Wenzel State on textured polymer surfaces. Langmuir 2014, 30, 2061–2067. [Google Scholar] [CrossRef] [PubMed]
- Fan, P.; Pan, R.; Zhong, M. Ultrafast laser enabling hierarchical structures for versatile superhydrophobicity with enhanced Cassie–Baxter stability and durability. Langmuir 2019, 35, 16693–16711. [Google Scholar] [CrossRef]
- Ai, Y.; Yu, L.; Huang, Y.; Liu, X. The investigation of molten pool dynamic behaviors during the “∞” shaped oscillating laser welding of aluminum alloy. Int. J. Therm. Sci. 2022, 173, 107350. [Google Scholar] [CrossRef]
- Ta, V.D.; Dunn, A.; Wasley, T.J.; Li, J.; Kay, R.W.; Stringer, J.; Smith, P.J.; Esenturk, E.; Connaughton, C.; Shephard, J.D. Laser textured superhydrophobic surfaces and their applications for homogeneous spot deposition. Appl. Surf. Sci. 2016, 365, 153–159. [Google Scholar] [CrossRef]
- Chun, D.-M.; Ngo, C.-V.; Lee, K.-M. Fast fabrication of superhydrophobic metallic surface using nanosecond laser texturing and low-temperature annealing. CIRP Ann. 2016, 65, 519–522. [Google Scholar] [CrossRef]
- Zhang, L.; Tan, Z.; Zhang, C.; Tang, J.; Yao, C.; You, X.; Hao, B. Research on metal corrosion resistant bioinspired special wetting surface based on laser texturing technology: A Review. Micromachines 2022, 13, 1431. [Google Scholar] [CrossRef]
- Manoharan, K.; Bhattacharya, S. Superhydrophobic Surfaces Review: Functional application, fabrication techniques and limitations. J. Micromanuf. 2019, 2, 59–78. [Google Scholar] [CrossRef]
- Rasouli, S.; Rezaei, N.; Hamedi, H.; Zendehboudi, S.; Duan, X. Superhydrophobic and superoleophilic membranes for oil-water separation application: A comprehensive review. Mater. Des. 2021, 204, 109599. [Google Scholar] [CrossRef]
- Parvate, S.; Dixit, P.; Chattopadhyay, S. Superhydrophobic surfaces: Insights from theory and experiment. J. Phys. Chem. B 2020, 124, 1323–1360. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Y.; Li, B.; Hu, T.; Yang, Y.; Li, L.; Zhang, J. Environmentally benign and durable superhydrophobic coatings based on SIO2 nanoparticles and silanes. J. Colloid Interface Sci. 2019, 542, 8–14. [Google Scholar] [CrossRef]
- Myronyuk, O.; Raks, V.A.; Baklan, D.; Vasyliev, G.; Vanagas, E.; Kurdil, N.; Sivolapov, P. Water repellent coatings with hierarchal structures obtained on anodized aluminum with femtosecond laser ablation. Appl. Nanosci. 2021, 12, 523–531. [Google Scholar] [CrossRef]
- Myronyuk, O.; Baklan, D.; Vasilyev, G.S.; Rodin, A.M.; Vanagas, E. Wetting patterns of liquid-repellent femtosecond laser textured aluminum surfaces. Coatings 2022, 12, 1852. [Google Scholar] [CrossRef]
- Yokoi, N.; Manabe, K.; Tenjimbayashi, M.; Shiratori, S. Optically transparent superhydrophobic surfaces with enhanced mechanical abrasion resistance enabled by mesh structure. ACS Appl. Mater. Interfaces 2015, 7, 4809–4816. [Google Scholar] [CrossRef] [PubMed]
- Çakır, M. Investigation of Coating Performance of UV-curable hybrid polymers containing 1H,1H,2H,2H-perfluorooctyltriethoxysilane coated on aluminum substrates. Coatings 2017, 7, 37. [Google Scholar] [CrossRef]
- Salazar-Hernández, C.; Salazar-Hernández, M.; Mendoza-Miranda, J.M.; Miranda-Avilés, R.; Elorza-Rodríguez, E.; Carrera-Rodríguez, R.; Puy-Alquiza, M.J. Organic modified silica obtained from DBTL polycondensation catalyst for anticorrosive coating. J. Solgel Sci. Technol. 2018, 87, 299–309. [Google Scholar] [CrossRef]
- Zhang, B.; Zeng, Y.; Wang, J.; Sun, Y.; Zhang, J.; Li, Y. Superamphiphobic aluminum alloy with low sliding angles and acid-alkali liquids repellency. Mater. Des. 2020, 188, 108479. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Korpacz, A.N.; Dufour, C.R.; Weiland, Z.J.; Lambert, C.R.; Timko, M.T. Binary liquid mixture contact-angle measurements for precise estimation of surface free energy. Langmuir 2019, 35, 12317–12325. [Google Scholar] [CrossRef]
- Kaelble, D.H. Dispersion-polar surface tension properties of organic solids. J. Adhes. 1970, 2, 66–81. [Google Scholar] [CrossRef]
- Park, I.W.; Ribe, J.M.; Fernandino, M.; Dorao, C.A. The Criterion of the Cassie–Baxter and Wenzel Wetting Modes and the Effect of Elastic Substrates on It. Adv. Mater. Interfaces 2023, 10, 2202439. [Google Scholar] [CrossRef]
- Drelich, J.; Marmur, A. Physics and applications of superhydrophobic and superhydrophilic surfaces and coatings. Surf. Innov. 2014, 2, 211–227. [Google Scholar] [CrossRef]
- Eriksson, M.; Swerin, A. Forces at superhydrophobic and superamphiphobic surfaces. Curr. Opin. Colloid Interface Sci. 2020, 47, 46–57. [Google Scholar] [CrossRef]
- Fang, R.; Zhang, X.; Zheng, J.; Pan, Z.; Yang, C.; Deng, L.; Li, R.; Lai, C.; Yan, W.; Maisotsenko, V.S.; et al. Super-wicking functionality of femtosecond laser textured aluminum at high temperatures. Nanomaterials 2021, 11, 2964. [Google Scholar] [CrossRef] [PubMed]
- Saito, M.; Yabe, A. Dispersion and polar force components of surface tension of oily soils. Text. Res. J. 1984, 54, 18–22. [Google Scholar] [CrossRef]
- Gros, A.T.; Feuge, R.O. Surface and interfacial tensions, viscosities, and other physical properties of some N-aliphatic acids and their methyl and ethyl esters. J. Am. Oil Chem. Soc. 1952, 29, 313–317. [Google Scholar] [CrossRef]
- Wei, S.; Liu, Y.; Kou, X.; Huang, S.; Chen, G.; Xu, L.; Tong, Q.; Zhu, F.; Xu, J.; Ouyang, G. Energy-efficient construction of thermally stable superhydrophobic nanoscale stacked lamellae based solid-phase microextraction coating for the determination of non-polar compounds. Anal. Chim. Acta 2019, 1092, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Lei, H.; Xiong, M.; Xiao, J.; Zheng, L.; Zhu, Y.; Li, X.; Zhuang, Q.; Han, Z. Fluorine-free low surface energy organic coating for anti-stain applications. Prog. Org. Coat. 2017, 103, 182–192. [Google Scholar] [CrossRef]
- Jiang, J.; Shen, Y.; Wang, Z.; Tao, J.; Liu, W.; Chen, H.; Liu, S.; Xie, X.; Zeng, C. Anti/de-icing performance of the one-step electrodeposited superhydrophobic surfaces: Role of surface polarity regulated by hydrocarbon radical length. J. Chem. Eng. 2022, 431, 133276. [Google Scholar] [CrossRef]
- Li, F.; Feng, G.; Yang, X.; Lu, C.; Ma, G.; Li, X.; Xue, W.; Sun, H. Tunable wettability pattern transfer photothermally achieved on zinc with microholes fabricated by femtosecond laser. Micromachines 2021, 12, 547. [Google Scholar] [CrossRef]
- Wang, R.; Kido, M.; Nakanishi, S.; Okabe, T. Adhesion of atmospheric micro-contaminants on SUS304 Steel and removal by UV illumination. Mater. Trans. 2009, 50, 1798–1804. [Google Scholar] [CrossRef]




| Sample | , % | |||
|---|---|---|---|---|
| M + OCTEO | 1.00 | 18.0 | 5.56 | 9.96 |
| N + OCTEO | 0.17 | 18.0 | 0.94 | 9.96 |
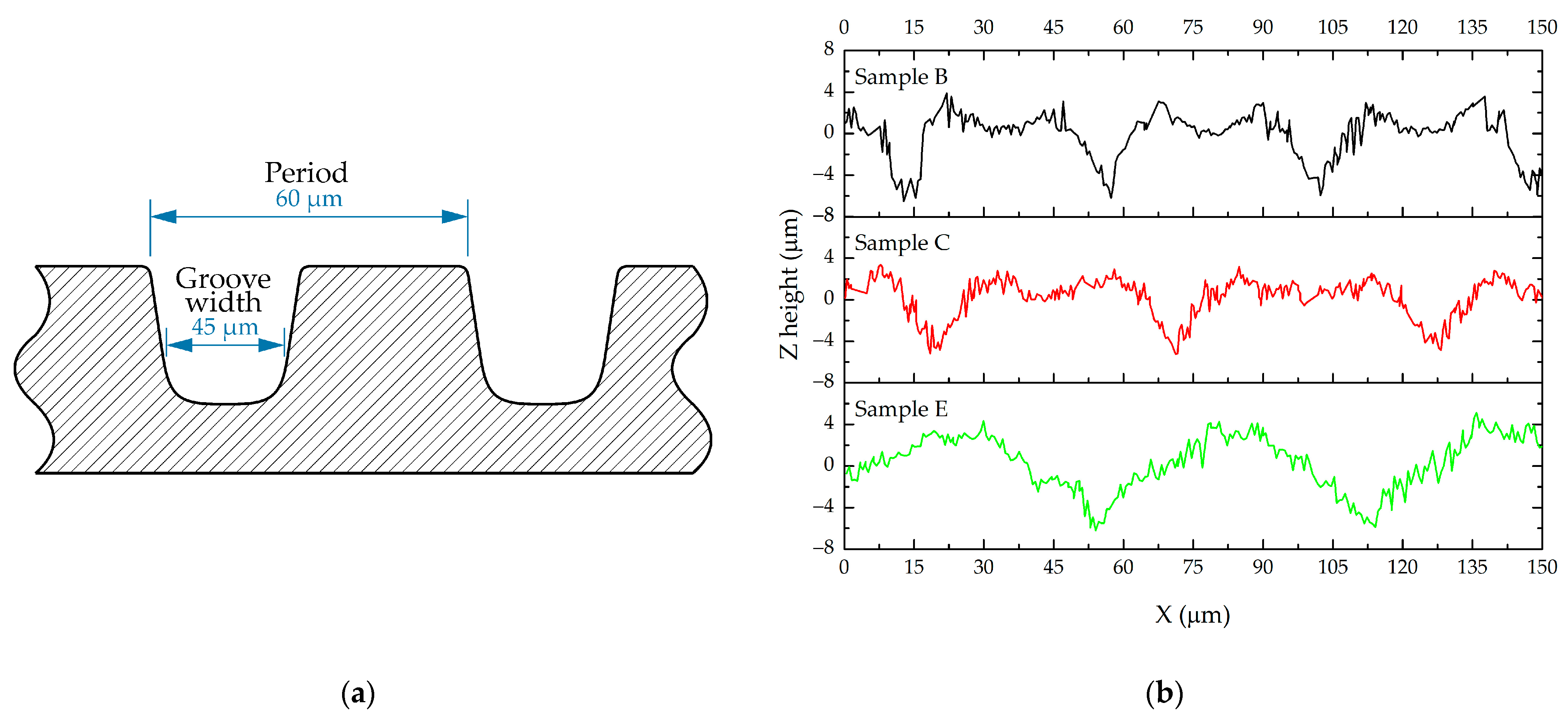
| Sample | Microtexture | |
|---|---|---|
| B | period 45 µm | groove width 20 µm |
| C | period 57 µm | groove width 20 µm |
| E | period 60 µm | groove width 45 µm |
| Sample (Figure) | , % | |||
|---|---|---|---|---|
| B + Stearic acid (Figure 5) | 1.82 | 25.3 | 7.19 | 9.3 |
| C + Stearic acid (Figure 5) | 1.16 | 25.3 | 4.58 | 9.3 |
| E + Stearic acid (Figure 5) | 0.24 | 25.3 | 0.94 | 9.3 |
| Area | C | O | Mg | Al |
|---|---|---|---|---|
| 1 | 11.40 | 8.04 | 3.41 | 77.15 |
| 2 | 13.32 | 38.90 | 6.04 | 41.74 |
| 3 | 10.12 | 6.58 | 3.22 | 80.08 |
| 4 | 14.93 | 28.27 | 4.52 | 52.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Myronyuk, O.; Baklan, D.; Rodin, A.M.; Vanagas, E.; Yong, Z. Owens–Wendt Characterization of Femtosecond-Laser-Textured Hydrophobic Aluminum Surfaces. Coatings 2023, 13, 1104. https://doi.org/10.3390/coatings13061104
Myronyuk O, Baklan D, Rodin AM, Vanagas E, Yong Z. Owens–Wendt Characterization of Femtosecond-Laser-Textured Hydrophobic Aluminum Surfaces. Coatings. 2023; 13(6):1104. https://doi.org/10.3390/coatings13061104
Chicago/Turabian StyleMyronyuk, Oleksiy, Denys Baklan, Aleksej M. Rodin, Egidijus Vanagas, and Zuo Yong. 2023. "Owens–Wendt Characterization of Femtosecond-Laser-Textured Hydrophobic Aluminum Surfaces" Coatings 13, no. 6: 1104. https://doi.org/10.3390/coatings13061104
APA StyleMyronyuk, O., Baklan, D., Rodin, A. M., Vanagas, E., & Yong, Z. (2023). Owens–Wendt Characterization of Femtosecond-Laser-Textured Hydrophobic Aluminum Surfaces. Coatings, 13(6), 1104. https://doi.org/10.3390/coatings13061104








