Next Article in Journal
Research on the Application of Domestic High-Modulus Carbon Fiber/Epoxy Composites to Solar Panels for Solar Arrays
Next Article in Special Issue
Characterization of CdS/CdTe Ultrathin-Film Solar Cells with Different CdS Thin-Film Thicknesses Obtained by RF Sputtering
Previous Article in Journal
Fluorine-Free Compound Water- and Oil-Repellent: Preparation and Its Application in Molded Pulp
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Coatings
Volume 13
Issue 7
10.3390/coatings13071258
coatings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Comparative Simulation Study of the Performance of Conventional and Inverted Hybrid Tin-Based Perovskite Solar Cells

by
Jack Arayro
,
Rabih Mezher
and
Hussein Sabbah
*
College of Engineering and Technology, American University of the Middle East, Egaila 54200, Kuwait
*
Author to whom correspondence should be addressed.
Coatings 2023, 13(7), 1258; https://doi.org/10.3390/coatings13071258
Submission received: 15 June 2023 / Revised: 4 July 2023 / Accepted: 13 July 2023 / Published: 17 July 2023
(This article belongs to the Special Issue Functional Layers in Thin Film Photovoltaics and Solar Energy)
Browse Figures
Versions Notes

Abstract

:
A hybrid tin-based (GA 0.2 FA 0.78 SnI 3 -1% EDAI 2 ) perovskite solar cell (PSC) with a p-i-n inverted structure has been reported to pass all the rigorous standard tests successfully and achieve a certified power conversion efficiency (PCE) of 8.3%. Our previous numerical study showed that this PCE could be considerably increased to 24.1% by engineering and controlling the interfaces of the cell. The aim of the current study is to compare the performance of a conventional n-i-p structure with its inverted p-i-n analog quantitatively, and demonstrate that, by improving the conventional structure, it can achieve a PCE score approximately equal to the inverted p-i-n structure. To that end, the absorber layer was chosen to be GA 0.2 FA 0.78 SnI 3 -1% EDAI 2 , while four ETL (electron transport layer) materials (TiO 2 , WS 2 , SnO 2 , and ZnOS), and four HTL (hole transport layer) materials (PEDOT:PSS, Cu 2 O, CuSCN, and CuI) were considered. Most used ETL/HTL combinations have been rigorously investigated with the aim of finding the ultimate configuration, providing the highest photovoltaic properties. Additionally, the effect of the layers’ thicknesses and their doping concentrations were inspected, and their impact on the photovoltaic properties of the PSC was investigated. The optimized structure with CuI (copper iodide) as the HTL and ZnOS (zinc oxysulphide) as the ETL scored a PCE of 24.1%, which is comparable to the value found with the inverted structure (26%). The current numerical simulation on GA 0.2 FA 0.78 SnI 3 -1% EDAI 2 could be considered as a milestone in its chances for commercial development.

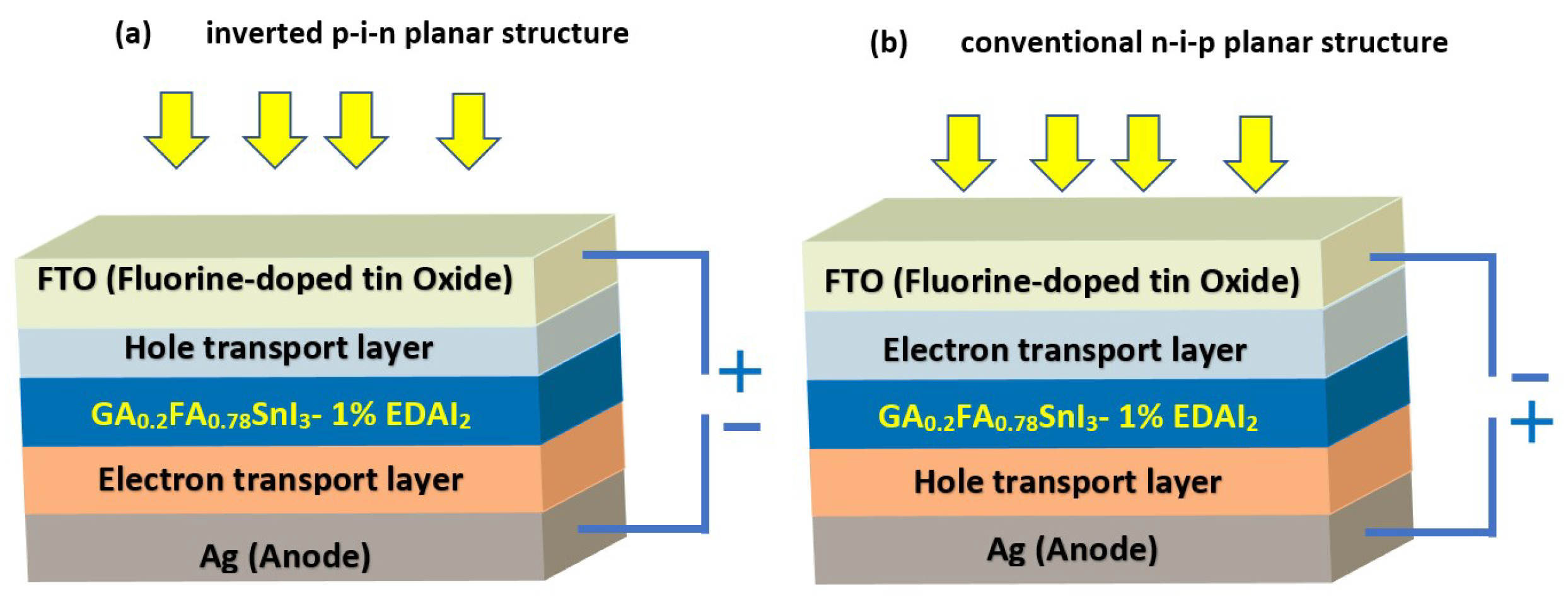
1. Introduction

Climate change and global warming have become serious threats to our planet. One of the major contributors to this environmental concern is the use of fossil fuels. Although alternative green sources of energy exist, such as solar cells, the limited efficiency of these sources prevents them from being globally employed. Extensive work has been carried out on enhancing the power conversion efficiency (PCE) of solar cells, in particular that of the organic–inorganic halide perovskite (OIHP) solar cells. Over the last decade, the PCE has increased from only 3% in 2009 to over 25% in 2019. This evolution suggested the perovskite solar cells as a promising candidate to compete with traditional silicon-based solar cells [1]. The latter rise in the PCE has been attributed to the high absorption coefficients [2,3], the low exciton binding energies [4], the long carrier diffusion lengths [5,6], the high carrier mobility, and the tunable bandgaps [7] of the solar cell materials.
Many generations of solar cells appeared, among them lead (Pb)-based perovskite solar cells (PSCs). Despite their superior properties, it has been found that the toxicity and carcinogenic nature of lead is a major drawback in the large-scale implementation of these cells [8]. To overcome this limitation, suitable alternatives of Pb-based perovskite absorbers have been explored such as tin (Sn) [9,10], bismuth (Bi) [11], germanium (Ge) [12], antimony (Sb) [13], and copper (Cu) [14]. Despite the existence of numerous articles on Pb-free perovskite solar cells, few of them discuss their toxicity and their environmental impacts [15,16,17]. To ensure safe applications, precautions against pollution must be considered at each stage: from fabrication to disposal or recycling of the devices. The toxicity of perovskite degradation products should also be considered, highlighting the need for in-depth knowledge before large-scale deployment of perovskite solar cell technologies. While Sn-based perovskites exhibit lower inherent toxicity, their environmental impact and potential risks should be considered. It is important to note that Sn-based perovskites are highly unstable, forming toxic byproducts in the presence of air and heat [15,16]. Both Pb-based and Sn-based perovskites have increased potential bio-availability, posing threats to human health and the environment [15,16,17,18]. Therefore, caution is advised when considering the environmental friendliness of Sn-based perovskites compared with Pb-based ones. Even though Sn-based perovskites constitute an excellent alternative to Pb-based ones, their performance is still lower than their Pb-based analogs. This is due to the poor stability of Sn-based PSCs in the presence of moisture [19], oxygen [20], light irradiation [21], thermal stresses [22], and defects in the perovskite film [23].
To address these inconveniences, extensive work on enhancing the performance of Sn-based PSCs all while maintaining their high stability was performed [24,25,26,27,28,29,30]. In particular, an experimental study by Jokar et al. [31] highlighted the presence of a highly stable perovskite. In their work, Jokar et al. [31] focused on incorporating a nonpolar organic cation (guanidinium (GA+)) into the formamidinium (FA+) tin triiodide perovskite (FASnI3) crystal structure in varied proportions. This incorporation happens in the presence of 1% ethylenediammonium diiodide (EDAI2). In the remainder of the paper, the obtained GA 0.2 FA 0.78 SnI 3 -1%EDAI2 is abbreviated as E1G20. Moreover, they concluded from their experimental work that the planar inverted structure with E1G20 recorded a PCE of 9.6% and exhibited high stability. This study is considered an incentive for this current work. Moreover, the structure of perovskite devices can be classified into conventional n-i-p and inverted p-i-n structures. In fact, when compared with their conventional counterparts, inverted structures are found to be more cost-effective, easier to manufacture, and highly compatible with large-area device fabrications [32]. In addition, the inverted structures provide a current density–voltage (J–V) hysteresis effect lower than that of the conventional structures [33,34,35]. Moreover, when their electron transport layer contains metal oxides, conventional perovskite solar cells are not convenient for flexible devices. This is mainly due to the rigidity of these ETL materials and the high temperature of processing necessary to obtain good electrical properties [36,37,38]. However, a major aspect behind the preference for conventional structures over inverted ones is the limited PCE of the latter category. Recent studies recorded PCE values of 22.8% for an inverted structure against 25.6% for a conventional one [33,39].
In a previous numerical study [40], it has been found that an adequate combination of electron transport layer (ETL) and hole transport layer (HTL) material can enhance the PCE to 26%. The current work aims to investigate the performance of a conventional n-i-p structure while comparing it with its inverted analog, previously studied by Jokar et al. [31]. Four HTLs (hole transport layers) and four other ETLs (electron transport layers) were combined and tested. Various device parameters were calculated using the solar cell capacitance simulator (SCAPS-1D) [41]. Then the thickness and the doping concentration of all three layers were investigated with the aim of finding the ultimate photovoltaic properties of the PSC. As a perspective, the results presented in this work can be extrapolated to reduce the manufacturing cost, time, and cycles spent to develop perovskite solar cells.

2. Materials and Methods

To perform a numerical study on the conventional n-i-p E1G20 structure, SCAPS-1D 3.8 was adopted as simulation software; it is a 1D simulator of photovoltaic cells, developed at the University of Gent, Ghent, Belgium [41]. SCAPS permits calculation and observation of various electrical characteristics of multi-layer solar cells. The most important parameters that SCAPS can evaluate are the PCE, hetero-junction energy band structure, current density, open circuit voltage (V o c ), short-circuit current density (J s c ), quantum efficiency (QE), current density, and fill factor (FF). These calculations are carried out by solving the Poisson equation, and the continuity equations of both charge carriers (the electron and the hole) within an adapted algorithm.
The considered solar cell is of the n-i-p configuration type, and is composed of a series of layers—FTO/ETL/E1G20/HTL/Ag (where FTO is chosen to be fluorine-doped tin oxide). The obtained sample is represented and compared with its inverted analog in Figure 1.
All simulations were conducted under a standard illumination of 1000 W/m 2 , at a temperature of 300 K, while the air mass was fixed to AM 1.5 G. The E1G20 absorber layer was confined between the ETL and HTL. The chosen front contact and back contact layers were FTO and silver (Ag), respectively, as shown in Figure 1.
The herein studied initial cell structure was obtained by inverting the sequence adopted by Jokar et al. interested in common materials [31]. In the current study, the ETL, absorber, and HTL materials were chosen to be C60 (fullerene), E1G20, and PEDOT:PSS (Poly(3,4-ethylenedioxythiophene)-poly(styrenesulfonate)), respectively. The optical and electrical properties of these materials are listed in Table 1 [31,42,43,44,45,46,47].
In order to validate the current simulation, an initial comparison of the J–V characteristics between results obtained by Jokar et al. [31] and those acquired using the SCAPS simulation was done.
In fact, this comparison showed in previous works [40] that the two experimental and simulated current density (J–V) curves were almost superimposed; which confirmed the robustness of the SCAPS simulation. As a result, the latter study leads to the following cell performance parameters:
  • Short-circuit current density J s c = 20.06 mA/cm 2 ;
  • Power conversion efficiency PCE = 7.99 % ;
  • Open-circuit voltage V o c = 0.55 V;
  • Fill factor FF = 71.64 % .
Furthermore, two studies were carried out for enhancing the performance of the PSC. The first study focuses on testing three other HTL materials: Cu 2 O (copper oxide), CuSCN (copper thiocyanate), and CuI (copper iodide). Then, these HTL materials are compared with the HTL of the initial reference structure (PEDOT:PSS). The parameters of these three HTL materials are included in Table 2.
In the current study, the second part deals with the investigation of four of the most commonly used ETL materials: TiO 2 (titanium dioxide), ZnOS (zinc oxysulphide), WS 2 (tungsten disulfide), and SnO 2 (tin oxide). Then, these ETL materials are compared with C60, the ETL used in the initial reference structure. The parameters of these four ETL materials are detailed in Table 3.
The defect densities of the HTL, absorber, and ETL, as well as the interfaces between them, are grouped in Table 4 [9,10,50,53,54,55,56,57,58,59,60].
Additionally, more studies were performed in this work on modifying different parameters; the latter ones being the thickness and doping concentration of the HTL, ETL, and absorber layers. The aim behind the modification of these parameters was to monitor their effect on the PSC with the aim of reaching the optimal cell structure.

3. Results and Discussion

This section is dedicated to the results obtained in this study. First, the ETL material was chosen to be C60 and different HTL materials were considered, with the aim of studying their impact on the PSC performance. Then, the optimal HTL material was chosen for further investigations. Second, the effect of ETL materials on solar cell performance was investigated. Finally, once the optimal ETL and HTL materials were identified, the impact of the absorber on the PSC properties was studied.

3.1. The HTL Material Impact on the Solar Cell Performance

The stability and the manufacturing cost are crucial for solar cells, and are directly related to the adequate choice of the HTL material. Moreover, properties such as carrier extraction and transportation, perovskite crystallization, and light harnessing are also governed by the HTL [61]. A general trend in the choice of HTL is to adopt organic materials. However, these materials are found to have weak stability originating from the difference in their morphology due to thermal conditions, hence leading to a variation in their properties. In addition, for organic HTL materials, the resistance is high, in particular when their thickness increases. The latter behavior has a negative impact on the performance of the cell [62]. To overcome these drawbacks, organic materials could be replaced by p-type inorganic materials.
Additionally, doping the HTL with particular additives is suggested as a solution to the low hole mobility and conductivity that organic HTL materials suffer from. However, these additives can accelerate the degradation of perovskite films and increase the manufacturing cost [63].
Moreover, previous studies highlighted the importance of the effect of HTL/E1G20 and E1G20/ETL interfaces on the PSC performance. More precisely, the recombination loss, which is more prominent at the E1G20/ETL interface, can reduce the voltage [64]. Thus, since the electron release and the recombination rates are directly influenced by the HTL and ETL properties, controlling the layers interface is crucial for determining the overall PSC performance [59,60,65]. Another important aspect that needs to be considered when choosing adequate HTL and ETL materials is the band alignment between the layers. The valence band offset (given by Equation (1)) can be used to evaluate the energy band alignment. Table 1 and Table 2 represent the values of VBO used in the current work.
V B O = χ H T L − χ E 1 G 20 + E g H T L − E g E 1 G 20
The obtained values of VBO of all studied HTL materials are shown in Table 5.
Figure 2 represent the J–V characteristics of the simulated inverted p-i-n structure and its comparison with its experimental analog, previously studied in [40] (red and blue curves, respectively), along with the curve of the n-i-p structure herein simulated (black curve).
Although they both have a similar V o c , it can be noticed that the conventional n-i-p structure exhibits an offset in the J s c when compared with the inverted p-i-n one. In fact, the J s c behavior is dominated by the bandgap of the ETL: the higher the bandgap is, the better is the J s c performance. In our case, the bandgap of ETL-C60 (1.7 eV) is lower than that of the HTL-PEDOT:PSS (2.2 eV) considered for the p-i-n structure. This low bandgap causes a high absorption of the light in the ETL prior to its arrival at the absorber layer. As a consequence, less light reaches the absorber, causing a decrease in the J s c .
To confirm this finding, the quantum efficiency was calculated for each tested HTL material with C60 as ETL, and is illustrated in Figure 3.
From Figure 3, for the inverted structure, a difference in the quantum efficiency behavior was attributed to the difference in HTL materials. It is worth mentioning, that the curve corresponding to Cu 2 O is overlapping with that of PEDOT:PSS. It is evident that only when the light wavelength exceeds 570 nm, all four HTLs exhibit identical quantum efficiency characteristics. However, at lower wavelengths, it becomes apparent that CuI and CuSCN, which possess higher transparency, display superior quantum efficiency. The similarity in the behavior of the CuI and CuSCN curves can be attributed to their identical bandgap energy. Both materials have a bandgap of 3.4 eV, leading to their parallel response.
Additionally, in Figure 4, representing the J–V characteristic of the PSC for each HTL material, it can be observed that the short-circuit current density (J s c ) of CuSCN and CuI reaches its highest value. This is primarily due to the large bandgap of these materials, which is advantageous for increased transparency to visible light in the HTL. When the bandgap of the HTL exceeds 2.9 eV, it exhibits enhanced transparency to visible light. Consequently, a greater amount of light can penetrate the perovskite layer and be absorbed, resulting in the generation of a higher number of electrons. On the other hand, in the case of the conventional structure, the choice of hole transport layer (HTL) material appears to have a minimal impact on the quantum efficiency (QE) and short-circuit current density (J s c ). This is because, in the case of the conventional PSC structure, light primarily enters the device through the electron transport layer (ETL), and the QE and J s c are mainly influenced by the bandgap of the ETL, rather than that of the HTL. The only parameter that significantly affects J s c in conventional perovskite solar cells is the conductivity of the HTL material. Higher conductivity of the HTL leads to higher J s c values. Therefore, the conventional structure with CuI as the HTL demonstrates the highest J s c , attributable to its superior conductivity. The major discrepancy in J s c between the simulated devices with the conventional structure and the inverted structure can be attributed to the use of C60 as the ETL in the conventional structure, through which the light enters. The bandgap of the ETL material in the conventional structure is relatively low (1.7 eV, resulting in more light being absorbed by the ETL and less light being absorbed by the perovskite layer. Consequently, fewer electrons are generated, leading to significantly lower J s c values in the conventional structure compared with the inverted one. Additionally, and for the same previously mentioned reason [40], it is noteworthy that PSCs having CuI as the HTL exhibit the highest V o c among all the tested solar cells with different HTL materials. This observation can be attributed to the presence of a negative valence band offset (VBO) at the HTL/absorber interface. This negative VBO leads to the formation of a barrier, promoting a more efficient electron–hole recombination process. Consequently, the V o c , as well as other performance metrics such as J s c , fill factor (FF), and power conversion efficiency (PCE), show a monotonic decrease. Conversely, when the VBO is positive and less than or equal to 0.3 eV (as is the case with CuI), excellent current–voltage (J–V) characteristics are obtained. The positive VBO facilitates a favorable charge transfer process, reducing electron–hole recombination and resulting in an improved J–V performance. Therefore, the utilization of CuI as the HTL material in PSCs proves beneficial, as it leads to the highest photovoltaic outputs and favorable J–V characteristics. These findings underscore the importance of the HTL material selection and its impact on the device’s performance. In summary, in the conventional structure, the HTL material has minimal influence on the QE and J s c , with the conductivity being the primary factor affecting J s c . The difference in J s c between the conventional and inverted structures is primarily due to the lower bandgap and higher light absorption of the ETL material in the conventional structure.

3.1.1. Impact of HTL Thickness

The thickness of the HTL was fixed on 100 nm in the previously presented results. It has been found that the HTL thickness could impact the PSC performance [61,66]. The HTL thickness should be carefully chosen: on the one hand, this layer needs to be thick enough to completely cover the absorber layer, and, on the other hand, it needs to be thin enough to reduce the recombination rate. In fact, the electron–hole recombination depends on the path length of charge carriers. Moreover, it has been found that the electric resistance of the device, directly influencing the resistance of the layer, can also play a major role in predicting the recombination rates. Therefore, it is very important to perform a study in order to determine the optimal HTL thickness.
Figure 5 describes the evolution of the parameters of the PSC (PCE, V o c , J s c , and FF) with respect to the thickness of HTL materials.
From Figure 5, it can be inferred that CuI exhibits a better PSC performance among the considered HTLs in the study. In addition to recording the best performance among the tested HTLs in this simulation study, CuI has been found to protect the HTL/perovskite interface from degradation, thereby improving the stability of the cell [67]. Furthermore, another study confirms that the PSCs with CuI exhibit good long-term stability in the ambient atmosphere, attributed to the hydrophobic nature of CuI as an HTL. These results highlight the potential of CuI, fabricated using a simple and low-temperature processing method presented here, as a promising low-cost alternative HTL material for the future development of efficient and stable inverted planar PSCs [68]. However, Figure 5 shows that the thickness of the HTL does not affect any of the photovoltaic properties. This behavior is due to the fact that the light is entering from the ETL side, hence the thickness of ETL material is expected to have more effect on the PSC photovoltaic properties.
In the previous study on the inverted structure [40], it was observed that the performance of the PSC decreased as the thickness of the hole transport layer (HTL) increased. This decrease was attributed to the reduction in conductivity of the Cu 2 O and PEDOT:PSS layers, as well as the increased light absorption by these HTL materials with lower bandgaps. However, in the current n-i-p structure, where light enters from the electron transport layer (ETL) side, the thickness of the HTL does not affect the light absorption by either the HTL or the perovskite layer. Consequently, it does not significantly impact the overall performance of the cell. Furthermore, it is worth noting that the J s c values for the most efficient PSC with the conventional structure are lower than those obtained for the least efficient and thicker PSC with the inverted structure. This indicates that the number of generated electrons in the conventional structure is already at its lowest. Therefore, increasing the thickness of the HTL and subsequently reducing its conductivity has little to no effect on the overall performance of the PSC. In conclusion, the impact of the HTL thickness on PSC performance differs between the inverted and conventional structures. While it plays a significant role in the inverted structure, it has minimal influence on the performance of the PSC with the current n-i-p structure.

3.1.2. Impact of HTL Doping Concentration

In the previous section, the focus was on identifying the adequate HTL material along with its suitable thickness. Moreover, it is also necessary to determine the equivalent acceptor doping concentration (N A ). A value of 1 × 10 18 cm − 3 was assigned to (N A ) in Section 3.1.1. In this part, the objective is to find the optimal value of N A for the CuI material.
Therefore, N A was changed from 10 14 to 10 20 cm − 3 , while studying its impact on the current density–voltage characteristics. The results of this study are plotted in Figure 6.
The doping concentration of an HTL material enhances its conductivity and therefore has a positive impact on the efficiency of the PSC. Figure 6 proves that the increasing of the doping concentration from 10 14 cm − 3 to 10 20 cm − 3 causes a rise of approximately 4 mA·cm − 2 in the J s c values due to an increase in the conductivity. Similarly, this also causes an increase in the PCE from 5.96 % to 7.81 % , mainly due to the decrease in the recombination rate. It is worth mentioning here that, in the previous study on the inverted structure [40], it was found that the doping concentration had a limited impact on the solar cell performance. This was attributed to the fact that the increase of the fill factor, caused by the increase of the HTL doping concentration, is limited to a certain upper value; this latter value is due to a saturation in the sheet resistance of the HTL. Moreover, this maximum can be due to a saturation in the conductivity of the HTL [69,70].
In the work herein, since this latter limit was not attained, a major effect of the HTL doping concentration was obtained. As a conclusion, an optimal HTL doping concentration of 10 19 cm − 3 was considered as a compromise between the fabrication cost and the enhanced PCE value of 7.27 % , slightly less than that obtained at 10 20 cm − 3 ( 7.81 % ).

3.2. The ETL Material Impact on the Solar Cell Performance

Choosing a proper HTL material is indeed important, but also the adequate selection of the ETL material is necessary.
In this section, four ETL materials (TiO 2 , WS 2 , SnO 2 , and ZnOS) and four HTL materials (PEDOT:PSS, Cu 2 O, CuSCN, and CuI) were considered with all possible combinations, while the doping concentration was maintained at 10 18 cm − 3 . The effect of the HTL/ETL combination on the J–V curve is schematized in Figure 7.
Figure 7 demonstrates that the photovoltaic device with CuI as the HTL outperforms the devices with other HTL materials. This trend is evident across all the graphs, where the green color consistently exhibits the highest value of the J s c . This outcome is further confirmed by the power PCE results shown in Figure 8. The discrepancy arises primarily from the superior conductivity of the devices with the CuI HTL, which leads to a larger J s c and thus an improved PCE. Notably, this disparity is even more pronounced when the devices are combined with SnO 2 and ZnOS as ETL materials. These two ETLs possess higher light transparency, resulting in an increased generation of electrons. Consequently, the difference in conductivity becomes more significant, indicating that the higher conductivity of the HTL correlates with a better J s c value.
In the previous work, where the structure was inverted [40], it was found that WS 2 induced a better performance than TiO 2 . In fact, they had close CBO values ( − 0.25 and −0.3 eV, respectively) and electron affinity ( − 3.95 and −4 eV, respectively). However, WS 2 had better permittivity, which ultimately caused a difference of 8.4 % in the PCE. In the current study on the conventional n-i-p structure, adopting SnO 2 and ZnOS as ETL materials led to the best performance, as can be seen in Figure 7 and Figure 8. More precisely, with ZnOs as the ETL, best performances are obtained, regardless of the HTL (highest J s c and V o c values). Although SnO 2 has better transparency to visible light since its bandgap is 3.6 eV, exceeding that of ZnOS of 2.83 eV; it appears that the counter impact of CBO and permittivity has more effect on the overall performance. Therefore, ZnOs is found to be the best ETL material in this study.
Ultimately, the HTL/ETL of CuI/ZnOS outperforms all other combinations, where the scored values are at their highest, with J s c = 19.5 mA·cm − 2 , V o c = 0.95 V, and PCE = 14.6%.
This latter finding is confirmed through the quantum efficiency represented in Figure 9, where the CuI HTL was selected and tested with all other ETLs.
From Figure 9, it can be noticed that WS 2 and C60 exhibit the lowest performance, due to their high light absorption (less light reaching the absorber layer). Moreover, ZnOs is found to overtake the other HTLs for the majority of the light spectrum [71].
As a conclusion to this part, for the remainder of the study, CuI and ZnOS were adopted as the HTL and ETL, respectively.

3.2.1. Impact of ETL Thickness

In the above sections, a thickness of 50 nm was adopted for all the conducted studies. In this part, the impact of the thickness of the ETL on the efficiency of the photovoltaic cell is explored.
Figure 10 shows the effect of the ETL ZnOS thickness on the J–V characteristics and the power conversion efficiency. According to the latter figure, while V o c remains constant, J s c and PCE slightly decrease with the thickness.
In fact, when the ETL thickness increases, more light will be absorbed and therefore less light will reach the absorber. According to [72], increasing the ETL thickness leads to larger pinholes forming, causing a deterioration in the J s c .
Also, when increasing the ETL thickness, the electron–hole recombination increases, resulting in a rise in the resistance, indicated by the decreasing of J s c . Consequently, this will cause a 0.6 % drop in the PCE. To complement the latter conclusion, the impact of the ZnOS ETL thickness on the PSC quantum efficiency was conducted; the obtained results are plotted in Figure 11.
At small wavelengths, light is susceptible to being absorbed by the ETL; therefore, its thickness will play a major role in determining the quantum efficiency. As shown in Figure 11, the higher the thickne isss, the lower is the quantum efficiency. Conversely, ETL materials are transparent to light of high wavelengths, regardless of thickness.
Thus, the optimal thickness for the ETL is found to be 20 nm, scoring the best photovoltaic properties.

3.2.2. Impact of ETL Doping Concentration

Although determining the adequate ETL material (ZnOS) as well as its optimal thickness (20 nm) are of high importance, the doping concentration (N D ) of the ETL material is also crucial. N D could impact both the J s c and the PCE. In all of the above sections, the ETL doping concentration was chosen to be N D = 1 × 10 17 cm − 3 for all the considered materials and thicknesses. In this section, the effect of the ZnOS doping concentration on the J s c and PCE is investigated.
Figure 12 depicts the effect of the doping concentration of the ETL ZnOS on the current density–voltage characteristics and the PCE of the PSC, where N D is varied from 1 × 10 14 to 1 × 10 20 cm − 3 .
The latter figure shows clearly that the increase of N D leads to a rise in the J–V characteristic, accompanied by a rise in the PCE, indicating an improvement in the PSC efficiency. Actually, an increase in the doping concentration of the ETL causes a rise in the electron conductivity and a drop in the resistivity of the ETL. Moreover, in a previous work carried out by Xu et al. [73], it was found that a high doping concentration of the ETL produces deep energy levels at the heterojunction interfaces, reducing the non-radiative recombination at the interface and enhancing the cell performance. Moreover, a large electric field is produced at high doping concentrations, effectively collecting the electrons and repelling the minority carriers away from the ETL/perovskite interface, thus diminishing interface recombination rates [73].
Figure 12 shows that the highest values of N D = 1 × 10 19 and N D = 1 × 10 20 cm − 3 generate the best performance (with respect to the PCE and J s c ). In addition, for these two doping concentrations, it can be noticed from the figure that the J–V curves are overlapped, and the PCE values are identical. Taking into consideration that a significant doping concentration of the ETL, of 1 × 10 20 cm − 3 and more, is complex in terms of fabrication [47], the optimal ETL doping concentration is proposed to be 1 × 10 19 cm − 3 .

3.3. The Absorber Impact on the Solar Cell Performance

In the study of PSC performance, in addition to the importance of ETL and HTL materials, the absorber also plays a major role [9,10,40]. In this section, the effect of the absorber thickness and its doping concentration on the photovoltaic properties are studied.

3.3.1. Effect of the Absorber Thickness

In PSC fabrication, a very high thickness of the absorber layer is avoided due to the increase in fabrication cost. However, the current density is found to be more enhanced in this condition. In addition, according to Bag et al., a thin absorber layer (of 200 nm) provides a low photogenerated current accompanied by a high charge extraction, causing a decrease in the recombination rate [69].
The study of the absorber layer thickness and its impact on the PSC photovoltaic outputs is performed in this section. The thickness of the absorber, GAFASnI 3 , is varied from 100 to 1200 nm while maintaining constant all the other parameters.
Figure 13 plots the impact of the absorber thickness on the quantum efficiency or QE (QE vs. wavelengths of the light), PCE, V o c , and J s c .
The behavior exhibited by the quantum efficiency (Figure 13a) suggests that the greater the thickness of the absorber is, the more the quantum efficiency is high. This trend is more obvious at low values of the thickness (from 100 to 600 nm) and diminished at higher thickness values (from 600 to 1000 nm). For clarity, in this figure, we limit the presentation of the curves to 1000 nm, and curves obtained for higher thicknesses are found to be overlapping with the latter one.
The previously described pattern is the same for PCE, V o c , and J s c , where the values are increasing at low absorber thicknesses (indicating an enhancement in light absorption), before reaching saturation at a thickness value of 600 nm. Therefore, for the remaining sections of the paper, a thickness of 600 nm for the absorber is considered.

3.3.2. Effect of the Absorber Doping Concentration

The acceptor doping concentration of the absorber can also play a major role in optimizing the performance of the PSC. In this section, the impact of the acceptor doping concentration (N A ) on the J–V curve and the PCE is studied by varying N A from 10 14 to 10 18 cm − 3 . Figure 14 shows the results of this study.
Figure 14 shows that, at the first stage, the increasing of the doping concentration from 10 14 to 10 17 cm − 3 induces a rise in the PCE and V o c . As the acceptor doping concentration increases, the Fermi energy level of the hole decreases, thus increasing V o c . Furthermore, as shown by Wei Liu et al. [74,75], doping the absorber layer can result in a decrease in trap-state density and an increase in carrier lifetime in the PSC, causing an additional rise in V o c . It is also important to note that high doping concentration rates lead to an increase in the built-in electric field, further separating the charge carriers, reducing charge recombination, and thereby improving the V o c and the efficiency of the solar cell.
At a later stage, Figure 14 shows that, when the N A value is 10 18 cm − 3 , an abrupt drop in all the previously mentioned parameters is obtained. A similar trend was found in a study carried out by Abdelaziz et al. [47]. In their study, it was found that the oxidation of Sn 2 + leads to an increase in the background carrier density. This, in turn, causes a decreasing in the V o c , according to Equation (2):
V o c = n V T l n 1 + I G I 0
where n is the diode ideality factor, V T the thermal voltage, I 0 the dark saturation current, and I G the light-generated current.
Moreover, when the doping concentration increases to values higher than 10 17 cm − 3 , the electric field at the absorber interface increases, which leads to a rise in the recombination rate and thus harms the performance of the PSC.
Thus, an N A = 10 17 cm − 3  is considered as the optimal value, providing maximum values for the V o c and PCE of 1.06 V and 24.1%, respectively.

4. Conclusions

In this study, a conventional n-i-p structure of the ETL/absorber/HTL sequence was simulated using SCAPS-1D software 3.8. The effective design of the interfaces between the ETL and the absorber from one side and between the absorber and the HTL from the other side is vital in improving the efficiency of the photovoltaic cell, just like the inverted structure. In the first stage, four HTL and four ETL materials were mutually selected and investigated while covering all 16 possible combinations. The studied absorber layer was the perovskite GA 0.2 FA 0.78 SnI 3 -1% EDAI 2 ; at a second stage the absorber parameters were explored. The first study revealed that the optimal HTL/ETL material combination is CuI/ZnOS. Moreover, while the thickness of the CuI (HTL) has no impact on the performance of the PSC, due to its position behind the absorber layer, it was found that the optimal performance is obtained when the ZnOS (ETL) thickness is at its minimum possible (20 nm), reducing the light attenuation to the maximum and allowing more light to reach the absorber layer. Furthermore, a doping concentration of 10 19 cm − 3  for both CuI and ZnOS was found to give the best photovoltaic properties. The second part of the study showed that a saturation performance was attained at an absorber thickness of 600 nmand a doping concentration of 10 17 cm − 3 . Ultimately, taking into consideration the aforementioned parameters for the ETL, absorber, and HTL, a PCE of 24.1% was registered, along with a V o c of 1.06 V.

Author Contributions

Conceptualization, H.S.; methodology, H.S.; software, H.S. and J.A.; validation, H.S., J.A. and R.M.; formal analysis, H.S., J.A. and R.M.; investigation, H.S.; resources, H.S.; data curation, H.S., J.A. and R.M.; writing—original draft preparation, H.S., J.A. and R.M.; writing—review and editing, H.S., J.A. and R.M.; visualization, H.S., J.A. and R.M.; supervision, H.S.; project administration, H.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The author would like to acknowledge Marc Burgelman (University of Gent) for providing the simulation software SCAPS 3.8.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
PSCperovskite solar cell
PCEpower conversion efficiency
E1G20GA 0.2 FA 0.78 SnI 3 -1% EDAI 2
HTL   hole transport layer
ETLelectron transport layer
V o c open circuit voltage
J s c short-circuit current density
QEquantum efficiency
FFfill factor
FTOFluorine-doped tin oxide
VBOvalence band offset
N A acceptor doping concentration
CBOconducting band offset
N D donor doping concentration

References

  1. Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef] [PubMed]
  2. Becker, M.; Klüner, T.; Wark, M. Formation of hybrid ABX 3 perovskite compounds for solar cell application: First-principles calculations of effective ionic radii and determination of tolerance factors. Dalton Trans. 2017, 46, 3500–3509. [Google Scholar] [CrossRef] [PubMed]
  3. Kim, H.S.; Lee, C.R.; Im, J.H.; Lee, K.B.; Moehl, T.; Marchioro, A.; Moon, S.J.; Humphry-Baker, R.; Yum, J.H.; Moser, J.E.; et al. Lead iodide perovskite sensitized all-solid-state submicron thin film mesoscopic solar cell with efficiency exceeding 9%. Sci. Rep. 2012, 2, 591. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Galkowski, K.; Mitioglu, A.; Miyata, A.; Plochocka, P.; Portugall, O.; Eperon, G.E.; Wang, J.T.W.; Stergiopoulos, T.; Stranks, S.D.; Snaith, H.J.; et al. Determination of the exciton binding energy and effective masses for methylammonium and formamidinium lead tri-halide perovskite semiconductors. Energy Environ. Sci. 2016, 9, 962–970. [Google Scholar] [CrossRef] [Green Version]
  5. Zhang, W.; Anaya, M.; Lozano, G.; Calvo, M.E.; Johnston, M.B.; Míguez, H.; Snaith, H.J. Highly efficient perovskite solar cells with tunable structural color. Nano Lett. 2015, 15, 1698–1702. [Google Scholar] [CrossRef] [Green Version]
  6. Gottesman, R.; Haltzi, E.; Gouda, L.; Tirosh, S.; Bouhadana, Y.; Zaban, A.; Mosconi, E.; De Angelis, F. Extremely slow photoconductivity response of CH3NH3PbI3 perovskites suggesting structural changes under working conditions. J. Phys. Chem. Lett. 2014, 5, 2662–2669. [Google Scholar] [CrossRef] [Green Version]
  7. Gao, W.; Ran, C.; Li, J.; Dong, H.; Jiao, B.; Zhang, L.; Lan, X.; Hou, X.; Wu, Z. Robust stability of efficient lead-free formamidinium tin iodide perovskite solar cells realized by structural regulation. J. Phys. Chem. Lett. 2018, 9, 6999–7006. [Google Scholar] [CrossRef] [Green Version]
  8. Konstantakou, M.; Stergiopoulos, T. A critical review on tin halide perovskite solar cells. J. Mater. Chem. A 2017, 5, 11518–11549. [Google Scholar] [CrossRef]
  9. Sabbah, H. Numerical Simulation of 30% Efficient Lead-Free Perovskite CsSnGeI3-Based Solar Cells. Materials 2022, 15, 3229. [Google Scholar] [CrossRef]
  10. Sabbah, H.; Arayro, J.; Mezher, R. Numerical Simulation and Optimization of Highly Stable and Efficient Lead-Free Perovskite FA1- xCsxSnI3-Based Solar Cells Using SCAPS. Materials 2022, 15, 4761. [Google Scholar] [CrossRef]
  11. Slavney, A.H.; Hu, T.; Lindenberg, A.M.; Karunadasa, H.I. A bismuth-halide double perovskite with long carrier recombination lifetime for photovoltaic applications. J. Am. Chem. Soc. 2016, 138, 2138–2141. [Google Scholar] [CrossRef] [PubMed]
  12. Stoumpos, C.C.; Frazer, L.; Clark, D.J.; Kim, Y.S.; Rhim, S.H.; Freeman, A.J.; Ketterson, J.B.; Jang, J.I.; Kanatzidis, M.G. Hybrid germanium iodide perovskite semiconductors: Active lone pairs, structural distortions, direct and indirect energy gaps, and strong nonlinear optical properties. J. Am. Chem. Soc. 2015, 137, 6804–6819. [Google Scholar] [CrossRef] [PubMed]
  13. Kour, R.; Arya, S.; Verma, S.; Gupta, J.; Bandhoria, P.; Bharti, V.; Datt, R.; Gupta, V. Potential substitutes for replacement of lead in perovskite solar cells: A review. Glob. Chall. 2019, 3, 1900050. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Zhang, Q.; Hao, F.; Li, J.; Zhou, Y.; Wei, Y.; Lin, H. Perovskite solar cells: Must lead be replaced—And can it be done? Sci. Technol. Adv. Mater. 2018, 19, 425–442. [Google Scholar] [CrossRef] [Green Version]
  15. Babayigit, A.; Duy Thanh, D.; Ethirajan, A.; Manca, J.; Muller, M.; Boyen, H.G.; Conings, B. Assessing the toxicity of Pb-and Sn-based perovskite solar cells in model organism Danio rerio. Sci. Rep. 2016, 6, 18721. [Google Scholar] [CrossRef] [PubMed]
  16. Babayigit, A.; Ethirajan, A.; Muller, M.; Conings, B. Toxicity of organometal halide perovskite solar cells. Nat. Mater. 2016, 15, 247–251. [Google Scholar] [CrossRef]
  17. Benmessaoud, I.R.; Mahul-Mellier, A.L.; Horváth, E.; Maco, B.; Spina, M.; Lashuel, H.A.; Forró, L. Health hazards of methylammonium lead iodide based perovskites: Cytotoxicity studies. Toxicol. Res. 2016, 5, 407–419. [Google Scholar] [CrossRef] [Green Version]
  18. Hailegnaw, B.; Kirmayer, S.; Edri, E.; Hodes, G.; Cahen, D. Rain on methylammonium lead iodide based perovskites: Possible environmental effects of perovskite solar cells. J. Phys. Chem. Lett. 2015, 6, 1543–1547. [Google Scholar] [CrossRef]
  19. Zhang, L.; Ju, M.G.; Liang, W. The effect of moisture on the structures and properties of lead halide perovskites: A first-principles theoretical investigation. Phys. Chem. Chem. Phys. 2016, 18, 23174–23183. [Google Scholar] [CrossRef]
  20. Yao, H.; Zhou, F.; Li, Z.; Ci, Z.; Ding, L.; Jin, Z. Strategies for improving the stability of tin-based perovskite (ASnX3) solar cells. Adv. Sci. 2020, 7, 1903540. [Google Scholar] [CrossRef] [Green Version]
  21. Zhang, Q.; Liu, S.; He, M.; Zheng, W.; Wan, Q.; Liu, M.; Liao, X.; Zhan, W.; Yuan, C.; Liu, J.; et al. Stable Lead-free Tin Halide Perovskite with Operational Stability > 1200 h by Suppressing Tin (II) Oxidation. Angew. Chem. Int. Ed. 2022, 134, e202205463. [Google Scholar]
  22. Ava, T.T.; Al Mamun, A.; Marsillac, S.; Namkoong, G. A review: Thermal stability of methylammonium lead halide based perovskite solar cells. Appl. Sci. 2019, 9, 188. [Google Scholar] [CrossRef] [Green Version]
  23. Niu, Q.; Zhang, L.; Xu, Y.; Yuan, C.; Qi, W.; Fu, S.; Ma, Y.; Zeng, W.; Xia, R.; Min, Y. Defect Passivation Using Trichloromelamine for Highly Efficient and Stable Perovskite Solar Cells. Polymers 2022, 14, 398. [Google Scholar] [CrossRef] [PubMed]
  24. Ke, W.; Stoumpos, C.C.; Spanopoulos, I.; Mao, L.; Chen, M.; Wasielewski, M.R.; Kanatzidis, M.G. Efficient lead-free solar cells based on hollow {en} MASnI3 perovskites. J. Am. Chem. Soc. 2017, 139, 14800–14806. [Google Scholar] [CrossRef]
  25. Shao, S.; Liu, J.; Portale, G.; Fang, H.H.; Blake, G.R.; Ten Brink, G.H.; Koster, L.J.A.; Loi, M.A. Highly reproducible Sn-based hybrid perovskite solar cells with 9% efficiency. Adv. Energy Mater. 2018, 8, 1702019. [Google Scholar] [CrossRef]
  26. Liao, Y.; Liu, H.; Zhou, W.; Yang, D.; Shang, Y.; Shi, Z.; Li, B.; Jiang, X.; Zhang, L.; Quan, L.N.; et al. Highly oriented low-dimensional tin halide perovskites with enhanced stability and photovoltaic performance. J. Am. Chem. Soc. 2017, 139, 6693–6699. [Google Scholar] [CrossRef]
  27. Lee, S.J.; Shin, S.S.; Kim, Y.C.; Kim, D.; Ahn, T.K.; Noh, J.H.; Seo, J.; Seok, S.I. Fabrication of efficient formamidinium tin iodide perovskite solar cells through SnF2—Pyrazine complex. J. Am. Chem. Soc. 2016, 138, 3974–3977. [Google Scholar] [CrossRef]
  28. Chen, K.; Wu, P.; Yang, W.; Su, R.; Luo, D.; Yang, X.; Tu, Y.; Zhu, R.; Gong, Q. Low-dimensional perovskite interlayer for highly efficient lead-free formamidinium tin iodide perovskite solar cells. Nano Energy 2018, 49, 411–418. [Google Scholar] [CrossRef]
  29. Tsai, C.M.; Mohanta, N.; Wang, C.Y.; Lin, Y.P.; Yang, Y.W.; Wang, C.L.; Hung, C.H.; Diau, E.W.G. Formation of Stable Tin Perovskites Co-crystallized with Three Halides for Carbon-Based Mesoscopic Lead-Free Perovskite Solar Cells. Angew. Chem. Int. Ed. 2017, 56, 13819–13823. [Google Scholar] [CrossRef]
  30. Wang, F.; Ma, J.; Xie, F.; Li, L.; Chen, J.; Fan, J.; Zhao, N. Organic Cation-Dependent Degradation Mechanism of Organotin Halide Perovskites. Adv. Funct. Mater. 2016, 26, 3417–3423. [Google Scholar] [CrossRef]
  31. Jokar, E.; Chien, C.H.; Tsai, C.M.; Fathi, A.; Diau, E.W.G. Robust tin-based perovskite solar cells with hybrid organic cations to attain efficiency approaching 10%. Adv. Mater. 2019, 31, 1804835. [Google Scholar] [CrossRef] [PubMed]
  32. Liu, T.; Chen, K.; Hu, Q.; Zhu, R.; Gong, Q. Inverted perovskite solar cells: Progresses and perspectives. Adv. Energy Mater. 2016, 6, 1600457. [Google Scholar] [CrossRef]
  33. Jeong, J.; Kim, M.; Seo, J.; Lu, H.; Ahlawat, P.; Mishra, A.; Yang, Y.; Hope, M.A.; Eickemeyer, F.T.; Kim, M.; et al. Pseudo-halide anion engineering for α-FAPbI3 perovskite solar cells. Nature 2021, 592, 381–385. [Google Scholar] [CrossRef]
  34. Liu, X.; Cheng, Y.; Liu, C.; Zhang, T.; Zhang, N.; Zhang, S.; Chen, J.; Xu, Q.; Ouyang, J.; Gong, H. 20.7% highly reproducible inverted planar perovskite solar cells with enhanced fill factor and eliminated hysteresis. Energy Environ. Sci. 2019, 12, 1622–1633. [Google Scholar] [CrossRef]
  35. Meng, L.; You, J.; Guo, T.F.; Yang, Y. Recent advances in the inverted planar structure of perovskite solar cells. Acc. Chem. Res. 2016, 49, 155–165. [Google Scholar] [CrossRef] [PubMed]
  36. Jeon, N.J.; Noh, J.H.; Yang, W.S.; Kim, Y.C.; Ryu, S.; Seo, J.; Seok, S.I. Compositional engineering of perovskite materials for high-performance solar cells. Nature 2015, 517, 476–480. [Google Scholar] [CrossRef]
  37. Yang, W.S.; Noh, J.H.; Jeon, N.J.; Kim, Y.C.; Ryu, S.; Seo, J.; Seok, S.I. High-performance photovoltaic perovskite layers fabricated through intramolecular exchange. Science 2015, 348, 1234–1237. [Google Scholar] [CrossRef]
  38. Yang, W.S.; Park, B.W.; Jung, E.H.; Jeon, N.J.; Kim, Y.C.; Lee, D.U.; Shin, S.S.; Seo, J.; Kim, E.K.; Noh, J.H.; et al. Iodide management in formamidinium-lead-halide–based perovskite layers for efficient solar cells. Science 2017, 356, 1376–1379. [Google Scholar] [CrossRef] [Green Version]
  39. Alsalloum, A.Y.; Turedi, B.; Almasabi, K.; Zheng, X.; Naphade, R.; Stranks, S.D.; Mohammed, O.F.; Bakr, O.M. 22.8%-Efficient single-crystal mixed-cation inverted perovskite solar cells with a near-optimal bandgap. Energy Environ. Sci. 2021, 14, 2263–2268. [Google Scholar] [CrossRef]
  40. Sabbah, H.; Arayro, J.; Mezher, R. Simulation and Investigation of 26% Efficient and Robust Inverted Planar Perovskite Solar Cells Based on GA0.2FA0.78SnI3-1% EDAI2 Films. Nanomaterials 2022, 12, 3885. [Google Scholar] [CrossRef]
  41. Burgelman, M.; Nollet, P.; Degrave, S. Modelling polycrystalline semiconductor solar cells. Thin Solid Film. 2000, 361, 527–532. [Google Scholar] [CrossRef]
  42. Liu, X.; Yan, K.; Tan, D.; Liang, X.; Zhang, H.; Huang, W. Solvent engineering improves efficiency of lead-free tin-based hybrid perovskite solar cells beyond 9%. ACS Energy Lett. 2018, 3, 2701–2707. [Google Scholar] [CrossRef]
  43. Gan, Y.; Bi, X.; Liu, Y.; Qin, B.; Li, Q.; Jiang, Q.; Mo, P. Numerical investigation energy conversion performance of tin-based perovskite solar cells using cell capacitance simulator. Energies 2020, 13, 5907. [Google Scholar] [CrossRef]
  44. Koh, T.M.; Krishnamoorthy, T.; Yantara, N.; Shi, C.; Leong, W.L.; Boix, P.P.; Grimsdale, A.C.; Mhaisalkar, S.G.; Mathews, N. Formamidinium tin-based perovskite with low E g for photovoltaic applications. J. Mater. Chem. A 2015, 3, 14996–15000. [Google Scholar] [CrossRef]
  45. Kim, C.; Huan, T.D.; Krishnan, S.; Ramprasad, R. A hybrid organic-inorganic perovskite dataset. Sci. Data 2017, 4, 170057. [Google Scholar] [CrossRef] [Green Version]
  46. Herz, L.M. Charge-carrier mobilities in metal halide perovskites: Fundamental mechanisms and limits. ACS Energy Lett. 2017, 2, 1539–1548. [Google Scholar] [CrossRef] [Green Version]
  47. Abdelaziz, S.; Zekry, A.; Shaker, A.; Abouelatta, M. Investigating the performance of formamidinium tin-based perovskite solar cell by SCAPS device simulation. Opt. Mater. 2020, 101, 109738. [Google Scholar] [CrossRef]
  48. Shasti, M.; Mortezaali, A. Numerical study of Cu2O, SrCu2O2, and CuAlO2 as hole-transport materials for application in perovskite solar cells. Phys. Status Solidi 2019, 216, 1900337. [Google Scholar] [CrossRef]
  49. Patel, P.K. Device simulation of highly efficient eco-friendly CH3NH3SnI3 perovskite solar cell. Sci. Rep. 2021, 11, 3082. [Google Scholar] [CrossRef]
  50. Singh, A.K.; Srivastava, S.; Mahapatra, A.; Baral, J.K.; Pradhan, B. Performance optimization of lead free-MASnI3 based solar cell with 27% efficiency by numerical simulation. Opt. Mater. 2021, 117, 111193. [Google Scholar] [CrossRef]
  51. Madhavan, V.E.; Zimmermann, I.; Baloch, A.A.; Manekkathodi, A.; Belaidi, A.; Tabet, N.; Nazeeruddin, M.K. CuSCN as hole transport material with 3D/2D perovskite solar cells. ACS Appl. Energy Mater. 2019, 3, 114–121. [Google Scholar] [CrossRef] [Green Version]
  52. Liu, J.; Zhang, Y.; Liu, C.; Peng, M.; Yu, A.; Kou, J.; Liu, W.; Zhai, J.; Liu, J. Piezo-phototronic effect enhanced UV photodetector based on CuI/ZnO double-shell grown on flexible copper microwire. Nanoscale Res. Lett. 2016, 11, 281. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  53. Du, H.J.; Wang, W.C.; Zhu, J.Z. Device simulation of lead-free CH3NH3SnI3 perovskite solar cells with high efficiency. Chin. Phys. B 2016, 25, 108802. [Google Scholar] [CrossRef]
  54. Stamate, M.D. On the dielectric properties of dc magnetron TiO2 thin films. Appl. Surf. Sci. 2003, 218, 318–323. [Google Scholar] [CrossRef]
  55. Sobayel, K.; Akhtaruzzaman, M.; Rahman, K.; Ferdaous, M.; Al-Mutairi, Z.A.; Alharbi, H.F.; Alharthi, N.H.; Karim, M.R.; Hasmady, S.; Amin, N. A comprehensive defect study of tungsten disulfide (WS2) as electron transport layer in perovskite solar cells by numerical simulation. Results Phys. 2019, 12, 1097–1103. [Google Scholar] [CrossRef]
  56. Zhang, Y.; Blom, P.W. Electron and hole transport in poly (fluorene-benzothiadiazole). Appl. Phys. Lett. 2011, 98, 143504. [Google Scholar] [CrossRef] [Green Version]
  57. Baena, J.P.C.; Steier, L.; Tress, W.; Saliba, M.; Neutzner, S.; Matsui, T.; Giordano, F.; Jacobsson, T.J.; Kandada, A.R.S.; Zakeeruddin, S.M.; et al. Highly efficient planar perovskite solar cells through band alignment engineering. Energy Environ. Sci. 2015, 8, 2928–2934. [Google Scholar] [CrossRef] [Green Version]
  58. Farahani, S.V.; Veal, T.; Mudd, J.; Scanlon, D.; Watson, G.; Bierwagen, O.; White, M.; Speck, J.; McConville, C. Valence-band density of states and surface electron accumulation in epitaxial SnO2 films. Phys. Rev. B 2014, 90, 155413. [Google Scholar] [CrossRef] [Green Version]
  59. Li, C.Z.; Chang, C.Y.; Zang, Y.; Ju, H.X.; Chueh, C.C.; Liang, P.W.; Cho, N.; Ginger, D.S.; Jen, A.K.Y. Suppressed charge recombination in inverted organic photovoltaics via enhanced charge extraction by using a conductive fullerene electron transport layer. Adv. Mater. 2014, 26, 6262–6267. [Google Scholar] [CrossRef]
  60. Zhou, H.; Chen, Q.; Li, G.; Luo, S.; Song, T.B.; Duan, H.S.; Hong, Z.; You, J.; Liu, Y.; Yang, Y. Interface engineering of highly efficient perovskite solar cells. Science 2014, 345, 542–546. [Google Scholar] [CrossRef] [PubMed]
  61. Arumugam, G.M.; Karunakaran, S.K.; Liu, C.; Zhang, C.; Guo, F.; Wu, S.; Mai, Y. Inorganic hole transport layers in inverted perovskite solar cells: A review. Nano Sel. 2021, 2, 1081–1116. [Google Scholar] [CrossRef]
  62. Roy, P.; Dongre, Y.; Tiwari, S.; Chaturvedi, D.; Khare, A. Impact of hole transport layer on the performance of all-inorganic tin (Sn) based perovskite solar cells. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Sanya, China, 12–14 November 2021; IOP Publishing: Bristol, UK, 2021; Volume 1120, p. 012016. [Google Scholar]
  63. Ke, W.; Priyanka, P.; Vegiraju, S.; Stoumpos, C.C.; Spanopoulos, I.; Soe, C.M.M.; Marks, T.J.; Chen, M.C.; Kanatzidis, M.G. Dopant-free tetrakis-triphenylamine hole transporting material for efficient tin-based perovskite solar cells. J. Am. Chem. Soc. 2018, 140, 388–393. [Google Scholar] [CrossRef] [PubMed]
  64. Ng, C.H.; Nishimura, K.; Ito, N.; Hamada, K.; Hirotani, D.; Wang, Z.; Yang, F.; Shen, Q.; Yoshino, K.; Minemoto, T.; et al. Role of GeI2 and SnF2 additives for SnGe perovskite solar cells. Nano Energy 2019, 58, 130–137. [Google Scholar] [CrossRef]
  65. Tan, H.; Jain, A.; Voznyy, O.; Lan, X.; García de Arquer, F.P.; Fan, J.Z.; Quintero-Bermudez, R.; Yuan, M.; Zhang, B.; Zhao, Y.; et al. Efficient and stable solution-processed planar perovskite solar cells via contact passivation. Science 2017, 355, 722–726. [Google Scholar] [CrossRef]
  66. Kim, G.W.; Shinde, D.V.; Park, T. Thickness of the hole transport layer in perovskite solar cells: Performance versus reproducibility. RSC Adv. 2015, 5, 99356–99360. [Google Scholar] [CrossRef]
  67. Srivastava, R.P.; Jung, H.S.; Khang, D.Y. Transfer-Printed Cuprous Iodide (CuI) Hole Transporting Layer for Low Temperature Processed Perovskite Solar Cells. Nanomaterials 2022, 12, 1467. [Google Scholar] [CrossRef] [PubMed]
  68. Wang, H.; Yu, Z.; Jiang, X.; Li, J.; Cai, B.; Yang, X.; Sun, L. Efficient and stable inverted planar perovskite solar cells employing CuI as hole-transporting layer prepared by solid—Gas transformation. Energy Technol. 2017, 5, 1836–1843. [Google Scholar] [CrossRef] [Green Version]
  69. Bag, A.; Radhakrishnan, R.; Nekovei, R.; Jeyakumar, R. Effect of absorber layer, hole transport layer thicknesses, and its doping density on the performance of perovskite solar cells by device simulation. Sol. Energy 2020, 196, 177–182. [Google Scholar] [CrossRef]
  70. Nguyen, W.H.; Bailie, C.D.; Unger, E.L.; McGehee, M.D. Enhancing the hole-conductivity of spiro-OMeTAD without oxygen or lithium salts by using spiro (TFSI)2 in perovskite and dye-sensitized solar cells. J. Am. Chem. Soc. 2014, 136, 10996–11001. [Google Scholar] [CrossRef]
  71. Warby, J.; Zu, F.; Zeiske, S.; Gutierrez-Partida, E.; Frohloff, L.; Kahmann, S.; Frohna, K.; Mosconi, E.; Radicchi, E.; Lang, F.; et al. Understanding performance limiting interfacial recombination in pin perovskite solar cells. Adv. Energy Mater. 2022, 12, 2103567. [Google Scholar] [CrossRef]
  72. Rai, N.; Rai, S.; Singh, P.K.; Lohia, P.; Dwivedi, D. Analysis of various ETL materials for an efficient perovskite solar cell by numerical simulation. J. Mater. Sci. Mater. Electron. 2020, 31, 16269–16280. [Google Scholar] [CrossRef]
  73. Xu, L.; Molaei Imenabadi, R.; Vandenberghe, W.G.; Hsu, J.W. Minimizing performance degradation induced by interfacial recombination in perovskite solar cells through tailoring of the transport layer electronic properties. APL Mater. 2018, 6, 036104. [Google Scholar] [CrossRef] [Green Version]
  74. Liu, W.; Liu, N.; Ji, S.; Hua, H.; Ma, Y.; Hu, R.; Zhang, J.; Chu, L.; Li, X.; Huang, W. Perfection of perovskite grain boundary passivation by rhodium incorporation for efficient and stable solar cells. Nano-Micro Lett. 2020, 12, 119. [Google Scholar] [CrossRef]
  75. Liu, W.; Feng, Y.; Li, L.; Ma, Y.; Hu, R.; Wu, X.; Chu, L.; Li, X.; Huang, W. Stable and Efficient Pb—Ni Binary Metal Perovskite Solar Cells. ACS Sustain. Chem. Eng. 2021, 9, 17112–17119. [Google Scholar] [CrossRef]
Coatings 13 01258 g001 550
Figure 1. Schematic diagram of E1G20-based PSC with: (a) an inverted structure and (b) a conventional structure.
Figure 1. Schematic diagram of E1G20-based PSC with: (a) an inverted structure and (b) a conventional structure.
Coatings 13 01258 g001
Coatings 13 01258 g002 550
Figure 2. Current density (J–V curve) obtained by simulation of inverted structure (in red), simulation of conventional structure (in black), and experimental results on inverted structure (in blue).
Figure 2. Current density (J–V curve) obtained by simulation of inverted structure (in red), simulation of conventional structure (in black), and experimental results on inverted structure (in blue).
Coatings 13 01258 g002
Coatings 13 01258 g003 550
Figure 3. Quantum efficiency for the PSCs with different HTL materials and C60 as ETL.
Figure 3. Quantum efficiency for the PSCs with different HTL materials and C60 as ETL.
Coatings 13 01258 g003
Coatings 13 01258 g004 550
Figure 4. Current density vs. voltage for the PSCs with fixed C60 as ETL and different HTL materials.
Figure 4. Current density vs. voltage for the PSCs with fixed C60 as ETL and different HTL materials.
Coatings 13 01258 g004
Coatings 13 01258 g005 550
Figure 5. Change in (a) PCE, (b) V o c , (c) J s c , and (d) FF vs. HTL thickness for four materials.
Figure 5. Change in (a) PCE, (b) V o c , (c) J s c , and (d) FF vs. HTL thickness for four materials.
Coatings 13 01258 g005
Coatings 13 01258 g006 550
Figure 6. Impact of the doping concentration of the HTL CuI on (a) the current density–voltage curve and (b) the PCE.
Figure 6. Impact of the doping concentration of the HTL CuI on (a) the current density–voltage curve and (b) the PCE.
Coatings 13 01258 g006
Coatings 13 01258 g007 550
Figure 7. Current density (J–V curve) for the PSC with different HTL and fixed ETL: (a) TiO 2 , (b) WS 2 , (c) SnO 2 , and (d) ZnOS.
Figure 7. Current density (J–V curve) for the PSC with different HTL and fixed ETL: (a) TiO 2 , (b) WS 2 , (c) SnO 2 , and (d) ZnOS.
Coatings 13 01258 g007
Coatings 13 01258 g008 550
Figure 8. Power conversion efficiency PCE for the PSC with different HTL and ETL materials.
Figure 8. Power conversion efficiency PCE for the PSC with different HTL and ETL materials.
Coatings 13 01258 g008
Coatings 13 01258 g009 550
Figure 9. Quantum efficiency for the four ETL materials and CuI as HTL.
Figure 9. Quantum efficiency for the four ETL materials and CuI as HTL.
Coatings 13 01258 g009
Coatings 13 01258 g010 550
Figure 10. Impact of the ETL ZnOS thickness on (a) the current density–voltage curve of the PSC and (b) the PCE.
Figure 10. Impact of the ETL ZnOS thickness on (a) the current density–voltage curve of the PSC and (b) the PCE.
Coatings 13 01258 g010
Coatings 13 01258 g011 550
Figure 11. Quantum efficiency for the PSCs with different ETL ZnOS thicknesses.
Figure 11. Quantum efficiency for the PSCs with different ETL ZnOS thicknesses.
Coatings 13 01258 g011
Coatings 13 01258 g012 550
Figure 12. Impact of the doping concentration of the ETL ZnOS on (a) the current density–voltage curve of the PSC and (b) the PCE.
Figure 12. Impact of the doping concentration of the ETL ZnOS on (a) the current density–voltage curve of the PSC and (b) the PCE.
Coatings 13 01258 g012
Coatings 13 01258 g013 550
Figure 13. Impact of the thickness of the absorber on (a) the quantum efficiency of the PSC, (b) PCE, (c) V o c , and (d) J s c .
Figure 13. Impact of the thickness of the absorber on (a) the quantum efficiency of the PSC, (b) PCE, (c) V o c , and (d) J s c .
Coatings 13 01258 g013
Coatings 13 01258 g014 550
Figure 14. Impact of the doping concentration of the absorber on (a) the current density curve of the PSC and (b) the PCE.
Figure 14. Impact of the doping concentration of the absorber on (a) the current density curve of the PSC and (b) the PCE.
Coatings 13 01258 g014
Table
Table 1. Optical and electrical properties adopted in the simulation of the GAFASnI 3 -based perovskite solar cell.
Table 1. Optical and electrical properties adopted in the simulation of the GAFASnI 3 -based perovskite solar cell.
ParametersE1G20 [31,44,45,46,47]PEDOT:PSS (HTL) [31,42,43]C60 (ETL) [31,42,43]
Thickness/μm0.350.10.05
Bandgap E g /eV1.52.21.7
Electron affinity χ /eV3.72.93.9
Dielectric permittivity8.22.34.2
CB effective density of states/cm − 3 1 × 10 18 2.2 × 10 18 8 × 10 19
VB effective density of states/cm − 3 1 × 10 18 2.8 × 10 18 1 × 10 20
Electron mobility/cm 2 /V·s22 2 × 10 − 4 0.08
Hole mobility/cm 2 /V·s Donor concentration N D /cm − 3 00 1 × 10 17
Acceptor concentration N A /cm − 3 1 × 10 17 1 × 10 18 0
Table
Table 2. Optical and electrical properties of the tested HTL materials.
Table 2. Optical and electrical properties of the tested HTL materials.
ParametersCu 2 O [48,49]CuSCN [50,51]CuI [50,52]
Thickness/μm0.10.10.1
Bandgap E g /eV2.1703.43.4
Electron affinity χ /eV3.21.92.1
Dielectric permittivity7.111010
CB effective density of states/cm − 3 2.02 × 10 17 2.2 × 10 18 1 × 10 18
VB effective density of states/cm − 3 1.1 × 10 19 1.8 × 10 19 1.8 × 10 19
Electron mobility/cm 2 /V·sHole mobility/cm 2 /V·s Donor concentration N D /cm − 3 000
Acceptor concentration N A /cm − 3 1 × 10 18 1 × 10 18 1 × 10 18
Table
Table 3. Electrical and optical properties of different ETL materials.
Table 3. Electrical and optical properties of different ETL materials.
ParametersTiO 2 [53,54]ZnOS [50]WS 2 [55,56]SnO 2 [57,58]
Thickness/μm0.050.050.050.05
Bandgap E g /eV3.262.831.803.60
Electron affinity χ /eV43.603.953.93
Dielectric permittivity32913.68
CB effective density of states/cm − 3 1 × 10 19 2.2 × 10 18 2.2 × 10 18 3.1 × 10 18
VB effective density of states/cm − 3 1 × 10 19 1.8 × 10 19 1.8 × 10 18 2.5 × 10 19
Electron mobility/cm 2 /V·s Hole mobility/cm 2 /V·s Donor concentration N D /cm − 3 1 × 10 17 1 × 10 17 1 × 10 17 1 × 10 17
Acceptor concentration N A /cm − 3 0000
Table
Table 4. Defect density values.
Table 4. Defect density values.
ParametersHTLETLE1G20HTL/E1G20E1G20/ETL
Defect TypeNeutralNeutralNeutralNeutralNeutral
Capture cross section for electrons σ n /cm − 2 1 × 10 − 15 1 × 10 − 15 1 × 10 − 15 1 × 10 − 18 1 × 10 − 15
Capture cross section for holes σ p /cm − 2 1 × 10 − 15 1 × 10 − 15 1 × 10 − 15 1 × 10 − 16 1 × 10 − 15
Energetic distributionSingleSingleGaussianSingleSingle
Energy level with respect to E v (above E v )/eV0.6500.650.60.60.6
Characteristic energy/eV0.10.10.10.10.1
Total density N t /cm − 3 1 × 10 15 1 × 10 15 1 × 10 15 1 × 10 12 1 × 10 12
Table
Table 5. VBO of the studied HTL materials.
Table 5. VBO of the studied HTL materials.
HTLVBO/eV
PEDOT:PSS (Reference cell)−0.1
Cu 2 O0.2
CuI0.3
CuSCN0.1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Arayro, J.; Mezher, R.; Sabbah, H. Comparative Simulation Study of the Performance of Conventional and Inverted Hybrid Tin-Based Perovskite Solar Cells. Coatings 2023, 13, 1258. https://doi.org/10.3390/coatings13071258

AMA Style

Arayro J, Mezher R, Sabbah H. Comparative Simulation Study of the Performance of Conventional and Inverted Hybrid Tin-Based Perovskite Solar Cells. Coatings. 2023; 13(7):1258. https://doi.org/10.3390/coatings13071258

Chicago/Turabian Style

Arayro, Jack, Rabih Mezher, and Hussein Sabbah. 2023. "Comparative Simulation Study of the Performance of Conventional and Inverted Hybrid Tin-Based Perovskite Solar Cells" Coatings 13, no. 7: 1258. https://doi.org/10.3390/coatings13071258

APA Style

Arayro, J., Mezher, R., & Sabbah, H. (2023). Comparative Simulation Study of the Performance of Conventional and Inverted Hybrid Tin-Based Perovskite Solar Cells. Coatings, 13(7), 1258. https://doi.org/10.3390/coatings13071258

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop