Studies on Protective Coatings for Molding Tools Applied in a Precision Glass Molding Process for a High Abbe Number Glass S-FPM3
Abstract
:1. Introduction
2. Materials and Methods
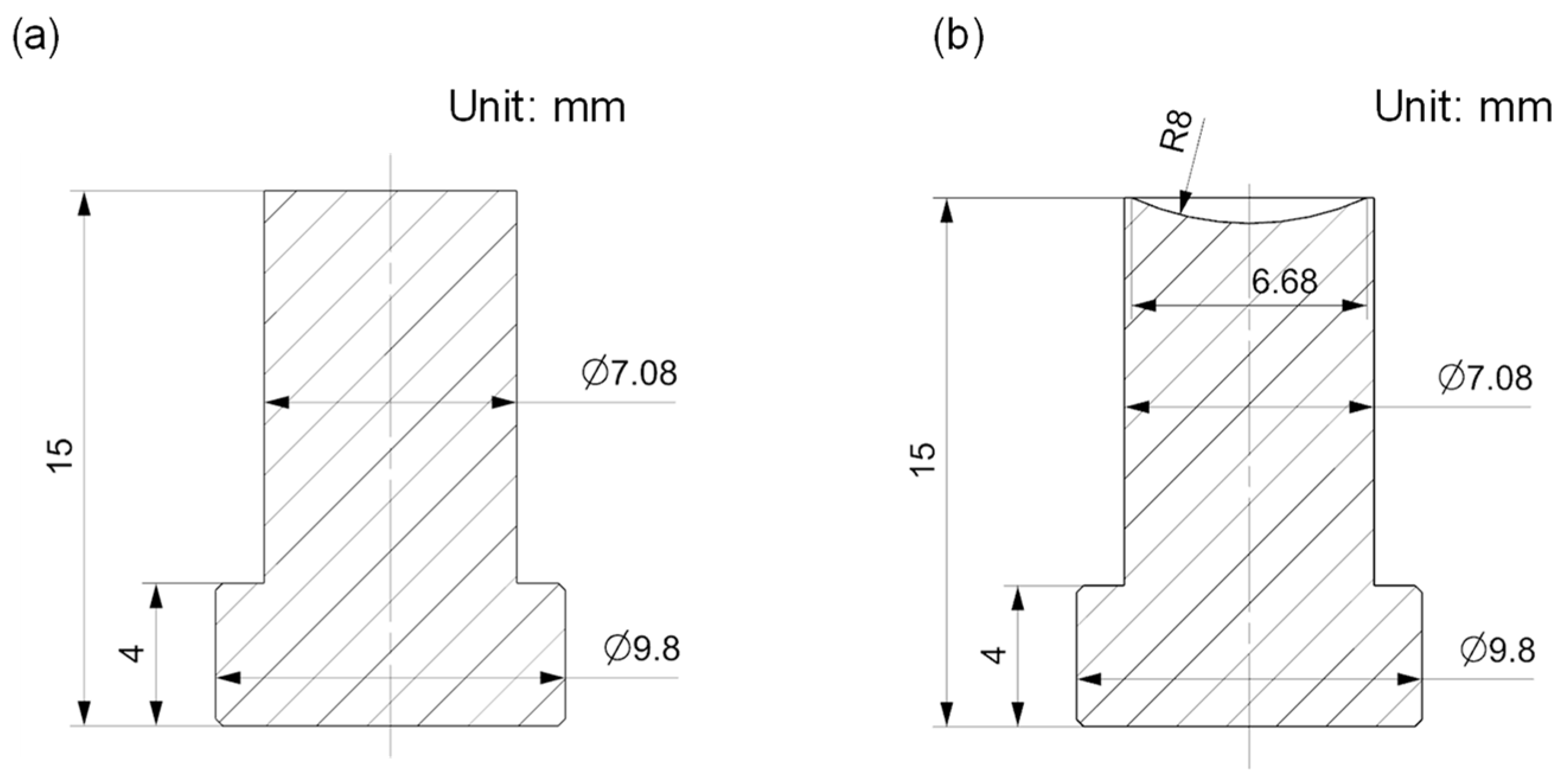
2.1. Sample Preparation
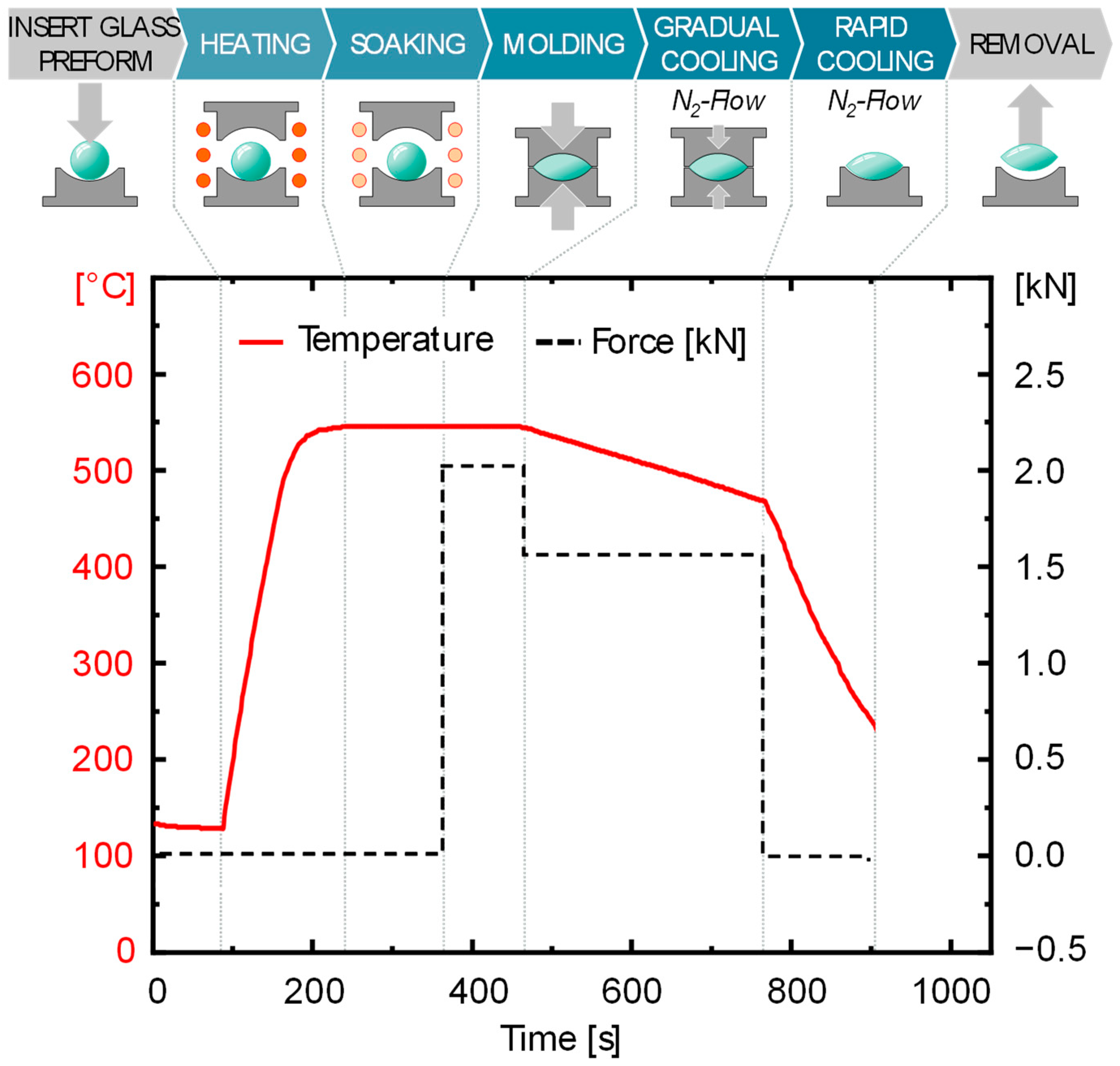
2.2. Molding Experiment
2.3. Specimen Characterization
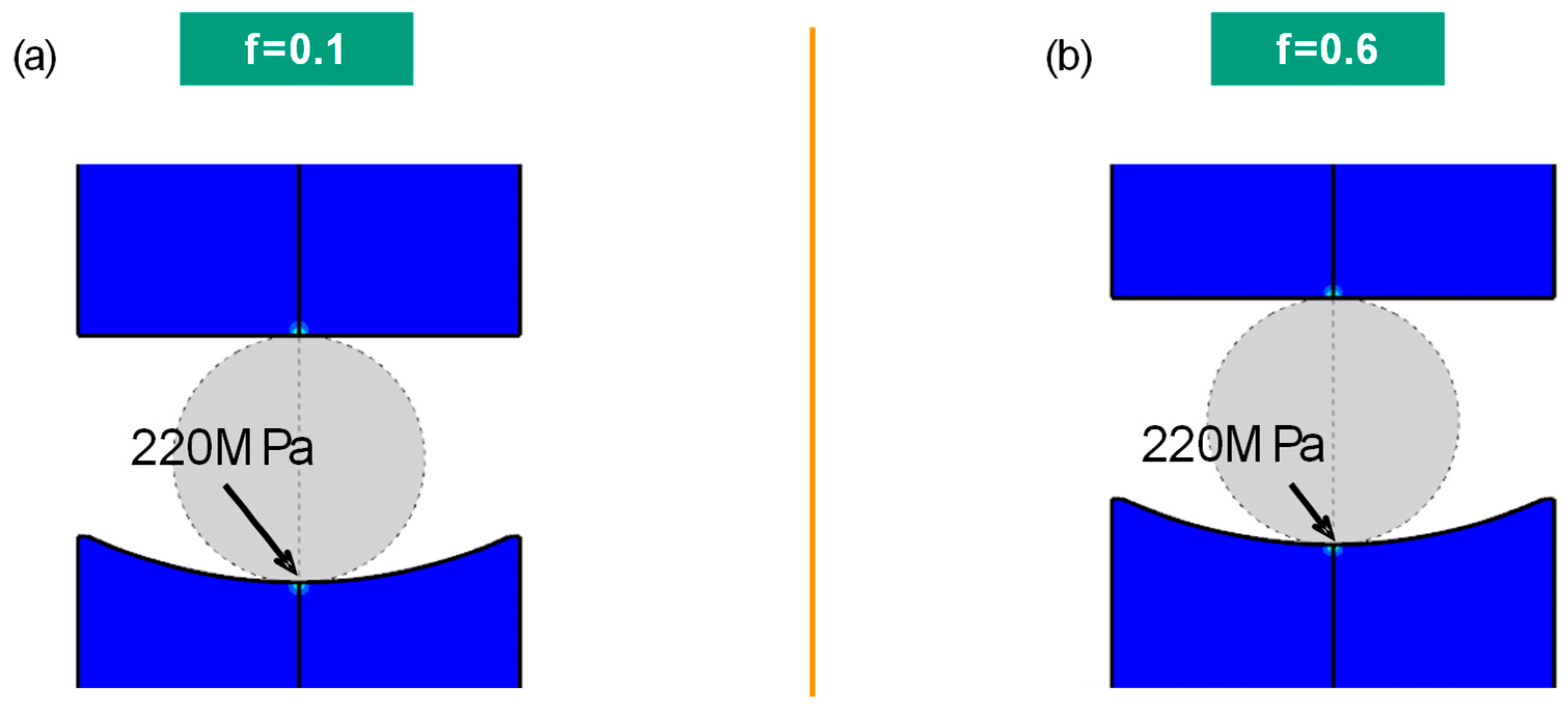
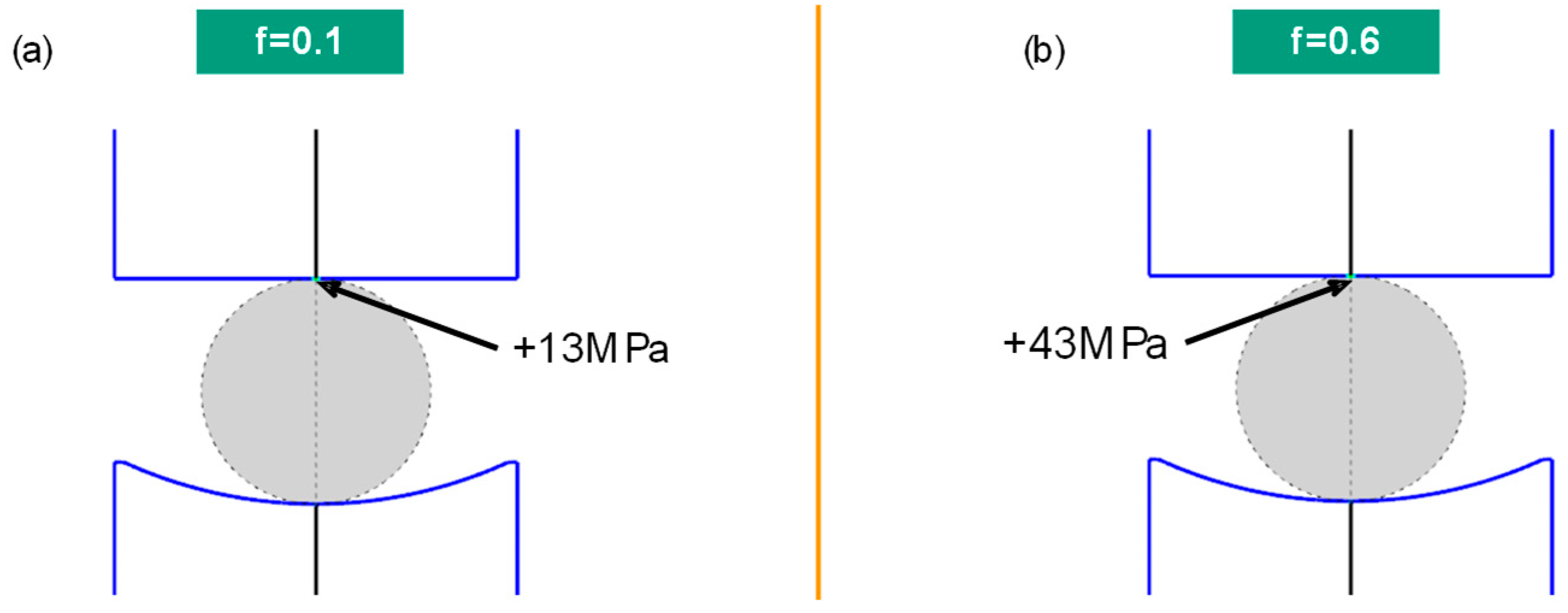
2.4. FEM Simulation
3. Results and Discussion
3.1. Initial Surface Conditions (Uncoated Molds)
3.2. Coated Surfaces (DLC/PtIr/CrAlN)
3.3. Degraded Coated Surfaces (DLC/PtIr/CrAlN)
3.4. FEM Analysis
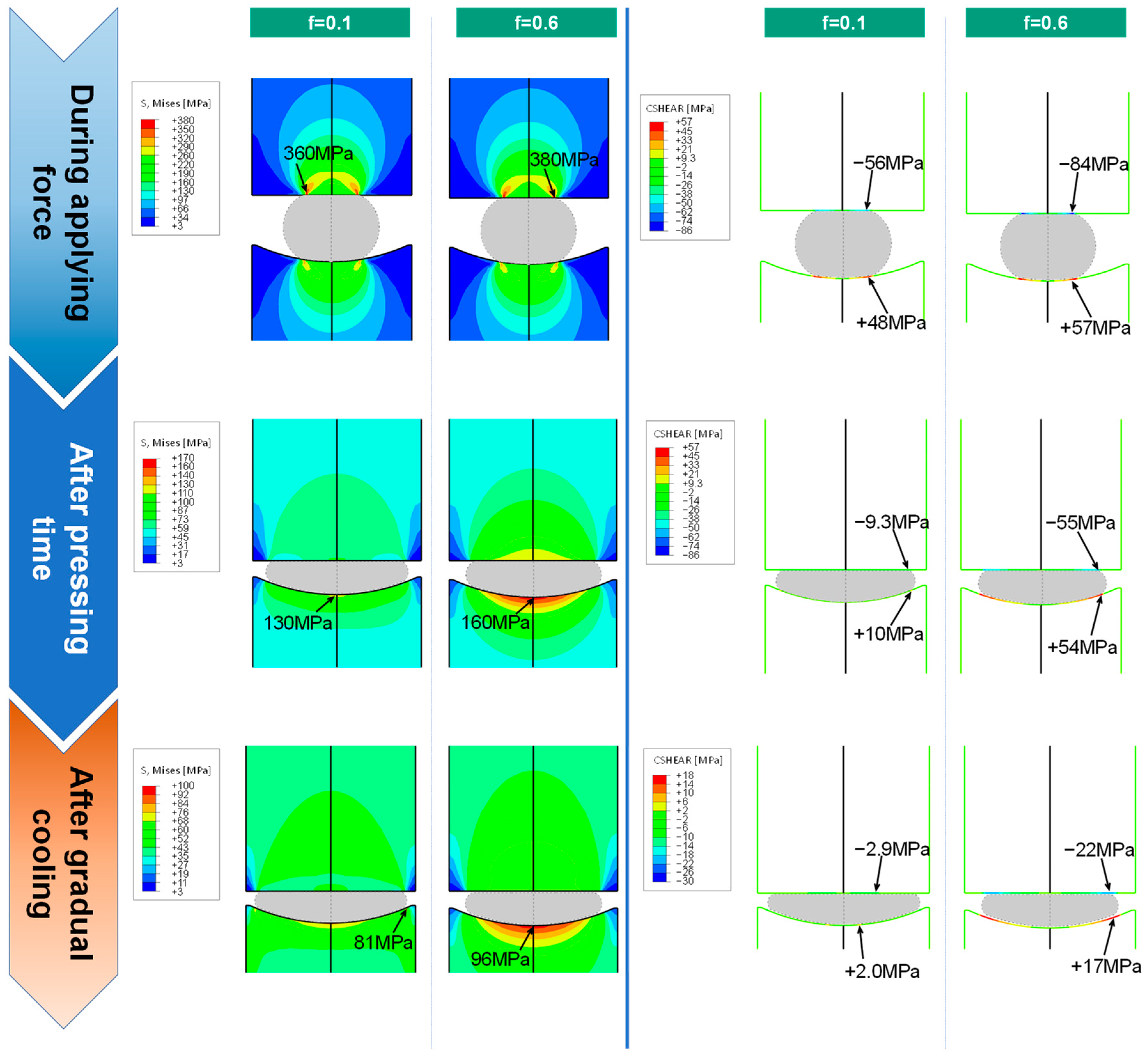
3.4.1. Stress Analysis at the First Contact between Molds and Glass
3.4.2. Stress Analysis in Molding and Gradual Cooling
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, P.; Tseng, Y.-C.; Tsai, C.-M. Wide field of view lens design with uniform image illumination in capsule endoscope system. Microsyst. Technol. 2021, 27, 1115–1122. [Google Scholar] [CrossRef]
- Hoy, C.L.; Ferhanoğlu, O.; Yildirim, M.; Piyawattanametha, W.; Ra, H.; Solgaard, O.; Ben-Yakar, A. Optical design and imaging performance testing of a 9.6-mm diameter femtosecond laser microsurgery probe. Opt. Express 2011, 19, 10536–10552. [Google Scholar] [CrossRef] [PubMed]
- Oh, J.-G.; Lee, D.-K.; Kim, Y.-G.; Lee, K.-H.; Park, Y.-S.; Jang, K.-H.; Kang, S.-G. A study on the optical parts for a semiconductor laser module. J. Korean Phys. Soc. 2014, 65, 1536–1541. [Google Scholar] [CrossRef]
- Park, K.-W.; Lee, J.U. A study for stray light distribution of mobile phone camera consisting of two aspheric lenses. Korean J. Opt. Photonic 2009, 20, 6–15. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, W. Precision glass molding: Toward an optimal fabrication of optical lenses. Front. Mech. Eng. 2017, 12, 3–17. [Google Scholar] [CrossRef]
- Maschmeyer, R.O.; Andrysick, C.A.; Geyer, T.W.; Meissner, H.E.; Parker, C.J.; Sanford, L.M. Precision molded-glass optics. Appl. Opt. 1983, 22, 2410–2412. [Google Scholar] [CrossRef]
- Yi, A.Y.; Jain, A. Compression molding of aspherical glass lenses—A combined experimental and numerical analysis. J. Am. Ceram. Soc. 2005, 88, 579–586. [Google Scholar] [CrossRef]
- Davis, J.R. ASM Specialty Handbook: Tool Materials; ASM International: Materials Park, OH, USA, 1995. [Google Scholar]
- Upadhyaya, G.S. Cemented Tungsten Carbides: Production, Properties and Testing; Noyes Publications: Westwood, NJ, USA, 1998. [Google Scholar]
- Guo, J. Corrective finishing of a micro-aspheric mold made of tungsten carbide to 50 nm accuracy. Appl. Opt. 2015, 54, 5764–5770. [Google Scholar] [CrossRef]
- Klocke, F.; Georgiadis, K.; Dambon, O.; Bouzakis, K.-D.; Gerardis, S.; Skordaris, G. A complete qualification methodology for coatings of precision glass molding tools. Proc. SPIE Opt. Manuf. Test. 2011, 9, 81260. [Google Scholar] [CrossRef]
- Ma, K.J.; Chien, H.H.; Chuan, W.H.; Chao, C.L.; Hwang, K.C. Design of protective coatings for glass lens molding. Key Eng. Mater. 2008, 364–366, 655–661. [Google Scholar] [CrossRef]
- Akhtar, A.; Ruan, H. Review on thin film coatings for precision glass molding. Surf. Interfaces 2022, 30, 101903. [Google Scholar] [CrossRef]
- Klocke, F.; Dambon, O.; Rohwerder, M.; Bernhardt, F.; Friedrichs, M.; Merzlikin, S.V. Model of coating wear degradation in precision glass molding. Int. J. Adv. Manuf. Technol. 2016, 87, 43–49. [Google Scholar] [CrossRef]
- Li, K.; Xu, G.; Huang, X.; Chen, Q.; Xie, Z.; Gong, F. Surface evolution analysis of CrxWyNz coatings on WC mold in glass molding process. Surf. Coat. Technol. 2020, 393, 125839. [Google Scholar] [CrossRef]
- Brand, J.; Gadow, R.; Killinger, A. Application of diamond-like carbon coatings on steel tools in the production of precision glass components. Surf. Coat. Technol. 2004, 180–181, 213–217. [Google Scholar] [CrossRef]
- Klocke, F.; Bouzakis, K.-D.; Georgiadis, K.; Gerardis, S.; Skordaris, G.; Pappa, M. Adhesive interlayers’ effect on the entire structure strength of glass molding tools’ Pt–Ir coatings by nano-tests determined. Surf. Coat. Technol. 2011, 206, 1867–1872. [Google Scholar] [CrossRef]
- Friedrichs, M.; Grunwald, T.; Bergs, T. Evaluation of mold materials for precision glass molding. Proc. Precis. Opt. Manuf. 2018, 11171, 111710B. [Google Scholar] [CrossRef]
- Lee, W.-Y.; Choi, J.-H. Application of Ta-C Coating on WC Mold to Molded Glass Lens. Tribol. Lubr. 2019, 35, 106–113. [Google Scholar] [CrossRef]
- Bernhardt, F.; Georgiadis, K.; Dolle, L.; Dambon, O.; Klocke, F. Development of a ta-C diamond-like carbon (DLC) coating by magnetron sputtering for use in precision glass molding. Mater. Werkst. 2013, 44, 661–666. [Google Scholar] [CrossRef]
- Robertson, J. Diamond-Like Amorphous Carbon. Mater. Sci. Eng. R. Rep. 2002, 37, 129–281. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, G.; You, K.; Fang, F. Study on α-Al2O3 anti-adhesion coating for molds in precision glass molding. Surf. Coat. Technol. 2020, 391, 125720. [Google Scholar] [CrossRef]
- Śliwa, A.; Mikuła, J.; Gołombek, K.; Tański, T.; Kwaśny, W.; Bonek, M.; Brytan, Z. Prediction of the properties of PVD/CVD coatings with the use of FEM analysis. Appl. Surf. Sci. 2016, 388, 281–287. [Google Scholar] [CrossRef]
- Wen, Z.; Zhang, X.; Yue, X.; Wang, X.; Zhang, C.; Yue, Z. FEM analysis of the stress response and failure mechanism of SiC-coated Cf/SiC composites during thermal shock. Ceram. Int. 2021, 47, 21996–22005. [Google Scholar] [CrossRef]
- Liu, G.; Vu, A.; Dambon, O.; Klocke, F. Glass Material Modeling and its Molding Behavior. MRS Adv. 2017, 2, 875–885. [Google Scholar] [CrossRef]
- Jankowiak, T.; Rusinek, A.; List, G.; Sutter, G.; Abed, F. Numerical analysis for optimizing the determination of dynamic friction coefficient. Trib. Inter. 2016, 95, 86–94. [Google Scholar] [CrossRef]
- Li, K.; Xu, G.; Wen, X.; Zhou, J.; Gong, F. High-temperature friction behavior of amorphous carbon coating in glass molding process. Friction 2021, 9, 1648–1659. [Google Scholar] [CrossRef]
- Bazrafshan, M.; de Rooij, M.B.; Schipper, D.J. The effect of adhesion and roughness on friction hysteresis loops. Int. J. Mech. Sci. 2019, 155, 9–18. [Google Scholar] [CrossRef]
- Tsai, K.M.; Hsieh, C.Y.; Lu, H.H. Sintering of binderless tungsten carbide. Ceram. Int. 2010, 36, 689–692. [Google Scholar] [CrossRef]
- Yin, L.; Spowage, A.C.; Ramesh, K.; Huang, H.; Pickering, J.P.; Vancoille, E.Y.J. Influence of microstructure on ultraprecision grinding of cemented carbides. Int. J. Mach. Tools Manuf. 2004, 44, 533–543. [Google Scholar] [CrossRef]
- Friedrichs, M.; Peng, Z.; Grunwald, T.; Rohwerder, M.; Gault, B.; Bergs, T. PtIr protective coating system for precision glass molding tools: Design, evaluation and mechanism of degradation. Surf. Coat. Technol. 2020, 385, 125378. [Google Scholar] [CrossRef]
- NJS Co., Ltd. SPS Center. Available online: http://www.njs-japan.co.jp/e_carbide.html (accessed on 9 June 2023).
- OHARA GmbH, S-FPM3_English_.pdf. Available online: https://www.ohara-gmbh.com/fileadmin/user_upload/export-data/pdf/product_datasheets/S-FPM3_English_.pdf (accessed on 9 June 2023).
- Teixeira, V. Residual stress and cracking in thin PVD coatings. Vacuum 2002, 64, 393–399. [Google Scholar] [CrossRef]
- Yang, J.; Odén, M.; Johansson-Jõesaar, M.P.; Llanes, L. Grinding Effects on Surface Integrity and Mechanical Strength of WC-Co emented Carbides. Procedia CIRP 2014, 13, 257–263. [Google Scholar] [CrossRef]
- Guo, B.; Zhao, Q. Wheel normal grinding of hard and brittle materials. Int. J. Adv. Manuf. Technol. 2015, 79, 873–880. [Google Scholar] [CrossRef]
- Dirks, A.G.; Wolters, R.A.M.; De Veirman, A.E.M. Columnar microstructures in magnetron-sputtered refractory metal thin films of tungsten, molybdenum and W-Ti-(N). Thin Solid Film. 1992, 208, 181–188. [Google Scholar] [CrossRef]
- Drnovšek, A.; Vo, H.T.; Figueiredo, M.R.; Kolozsvári, S.; Hosemann, P.; Franz, F. High temperature fracture toughness of single-layer CrAlN and CrAlSiN hard coatings. Surf. Coat. Technol. 2021, 409, 126909. [Google Scholar] [CrossRef]
- Peng, Z.; Rohwerder, M.; Choi, P.-P.; Gault, B.; Meiners, T.; Friedrichs, M.; Kreilkamp, H.; Klocke, F.; Raabe, D. Atomic diffusion induced degradation in bimetallic layer coated cemented tungsten carbide. Corros. Sci. 2017, 120, 1–13. [Google Scholar] [CrossRef]







| Material | Granularity (µm) | Density (g/cm3) | Hardness (HV) | Flexural Strength (MPa) | Compressive Strength (MPa) | Fracture Toughness KIC (MPa m0.5) | Coefficient of Thermal Expansion (10−6 K−1) | ||
|---|---|---|---|---|---|---|---|---|---|
| 400 °C | 600 °C | 800 °C | |||||||
| WC100 | <0.08 | 15.6 | 2700 | 1470 | 8120 | 5.6 | 4.8 | 4.9 | 5.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Friedrichs, M.; Jiang, C.; Wang, L.-A.; Dang, M.-Y.; Grunwald, T.; Bergs, T.; Li, Y.-L. Studies on Protective Coatings for Molding Tools Applied in a Precision Glass Molding Process for a High Abbe Number Glass S-FPM3. Coatings 2023, 13, 1438. https://doi.org/10.3390/coatings13081438
Chen C, Friedrichs M, Jiang C, Wang L-A, Dang M-Y, Grunwald T, Bergs T, Li Y-L. Studies on Protective Coatings for Molding Tools Applied in a Precision Glass Molding Process for a High Abbe Number Glass S-FPM3. Coatings. 2023; 13(8):1438. https://doi.org/10.3390/coatings13081438
Chicago/Turabian StyleChen, Chong, Marcel Friedrichs, Cheng Jiang, Li-Ang Wang, Ming-Yang Dang, Tim Grunwald, Thomas Bergs, and Yong-Liang Li. 2023. "Studies on Protective Coatings for Molding Tools Applied in a Precision Glass Molding Process for a High Abbe Number Glass S-FPM3" Coatings 13, no. 8: 1438. https://doi.org/10.3390/coatings13081438
APA StyleChen, C., Friedrichs, M., Jiang, C., Wang, L.-A., Dang, M.-Y., Grunwald, T., Bergs, T., & Li, Y.-L. (2023). Studies on Protective Coatings for Molding Tools Applied in a Precision Glass Molding Process for a High Abbe Number Glass S-FPM3. Coatings, 13(8), 1438. https://doi.org/10.3390/coatings13081438







