An Investigation of the Dynamic Curing Behavior and Micro-Mechanism of a Super-Tough Resin for Steel Bridge Pavements
Abstract
:1. Introduction
2. Objectives
3. Materials and Methods
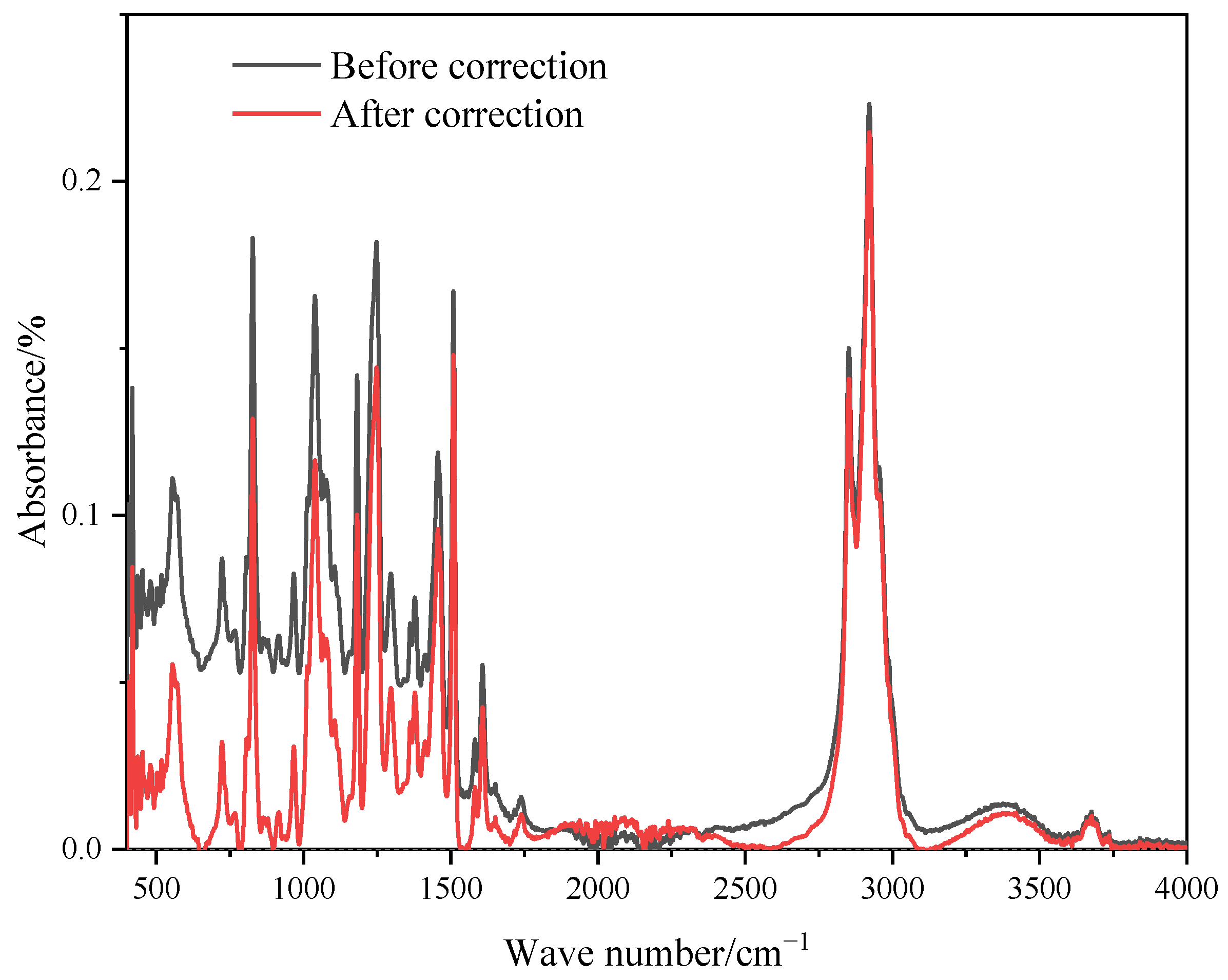
3.1. FTIR Test
3.2. Rheological Tests
3.2.1. Sample Preparation
3.2.2. Time Sweep Test
3.2.3. Linear Viscoelastic (LVE) Region Test
3.3. Weight Loss Monitoring
3.4. Experimental Schemes
4. Results and Discussion
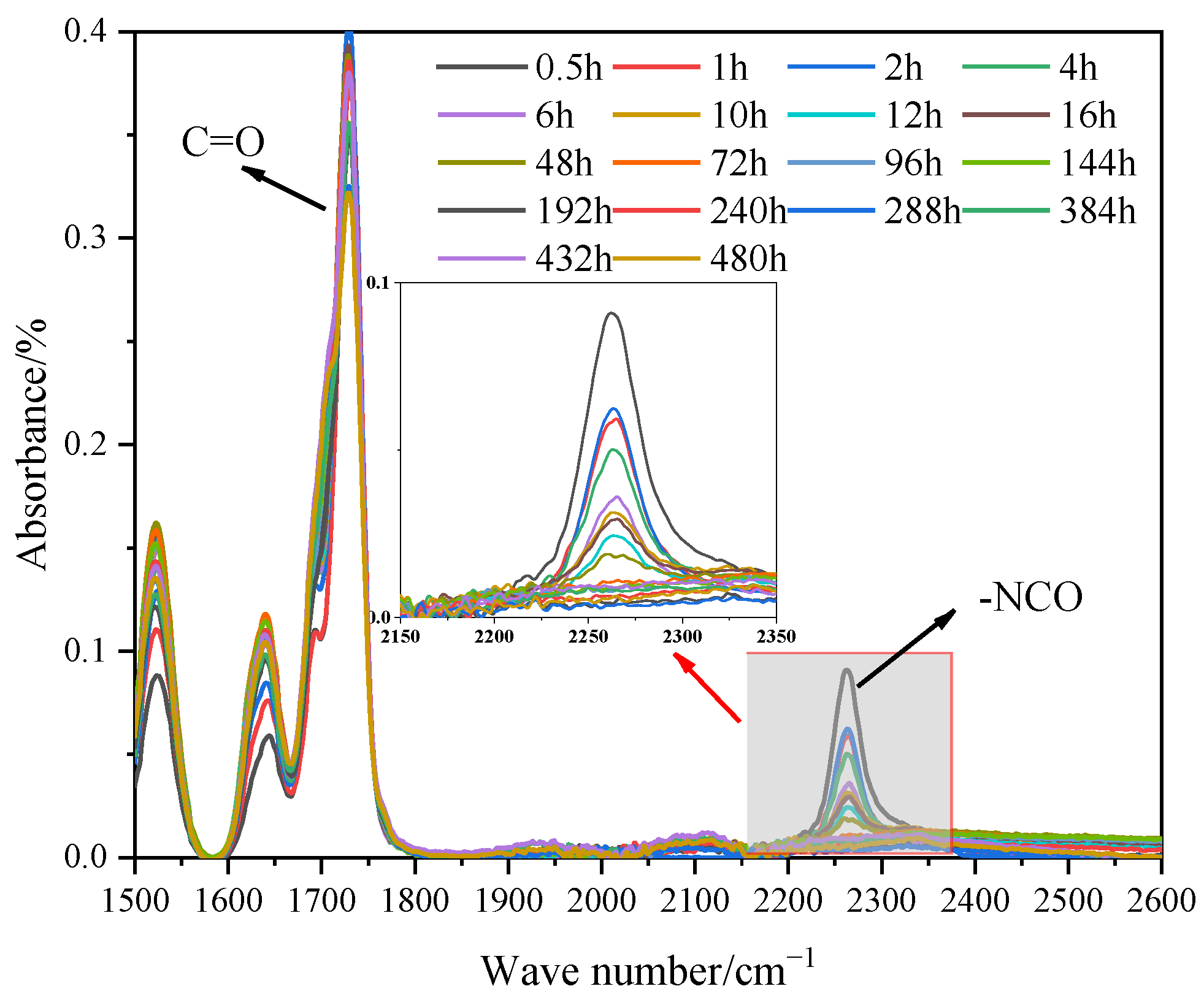
4.1. Results of FTIR Test
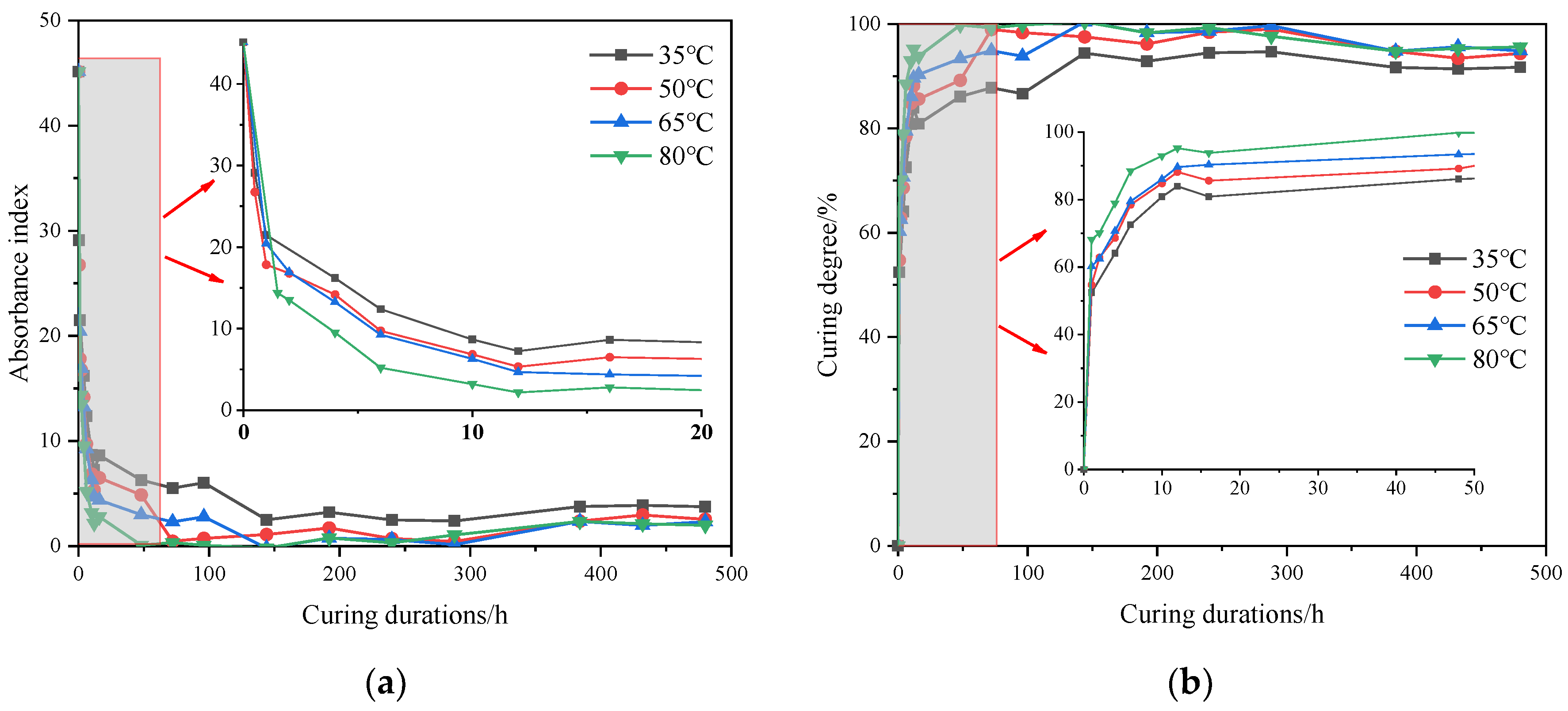
4.1.1. Curing Degree under Defined Curing Schemes
4.1.2. Curing Kinetics
4.2. Results of Time Sweep Test
4.3. Results of LVE Region Test
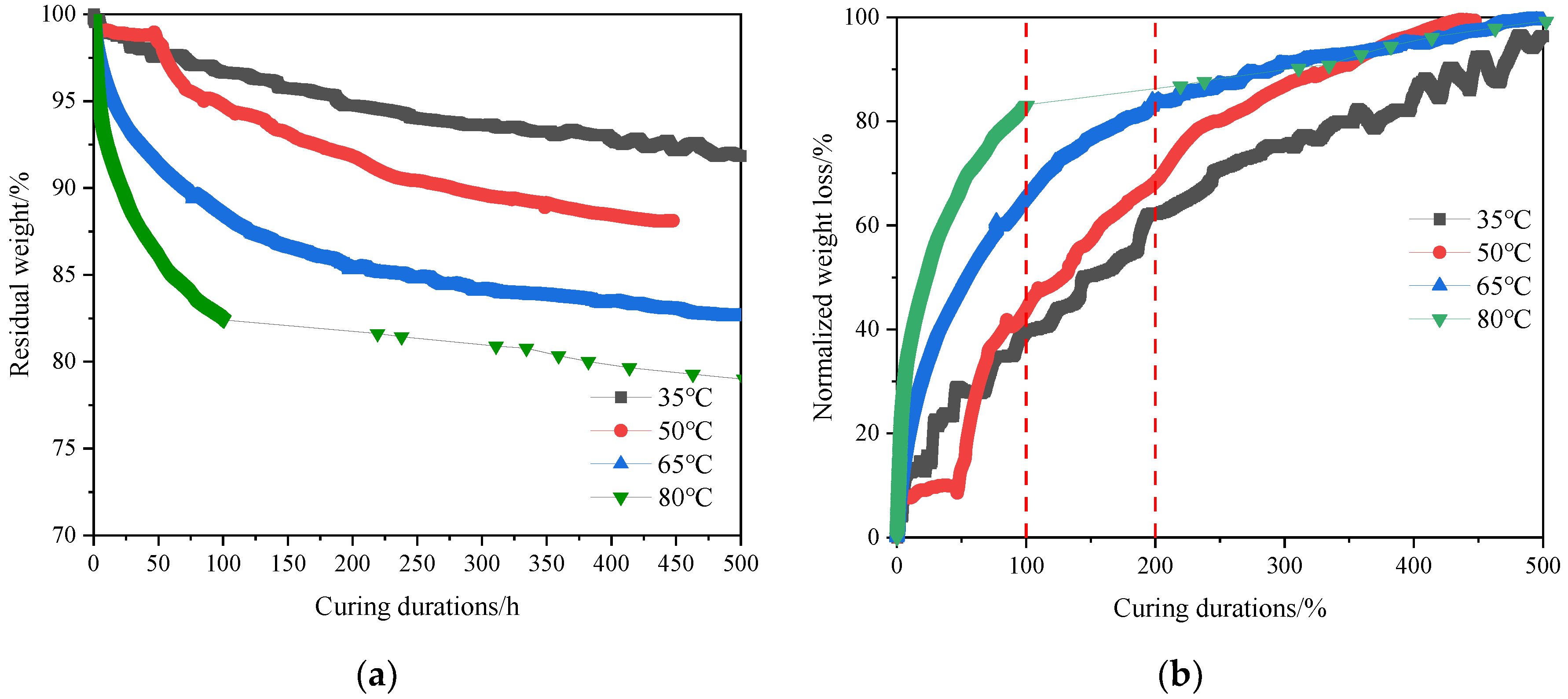
4.4. Weight Loss Monitoring
5. Conclusions
- (1)
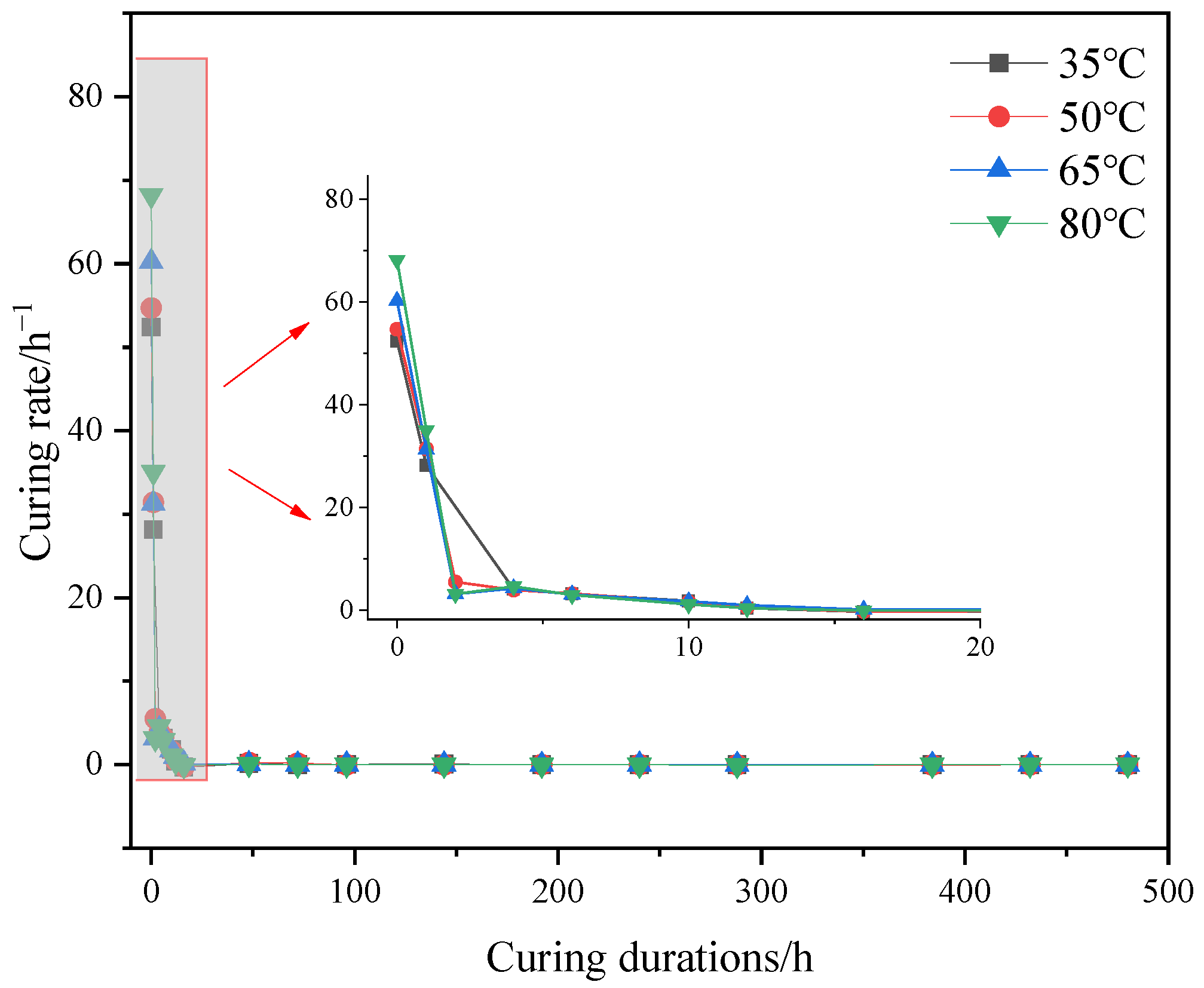
- The curing degrees increase significantly with the curing durations, particularly at the initial stage. Specifically, when cured for 10 h, the curing degrees increase remarkably at four curing temperatures, all exceeding 80%. When cured for 144 h, the curing degree reaches a plateau regardless of the curing temperature. Moreover, increased curing temperature can also increase the curing rate and ultimate curing degree.
- (2)
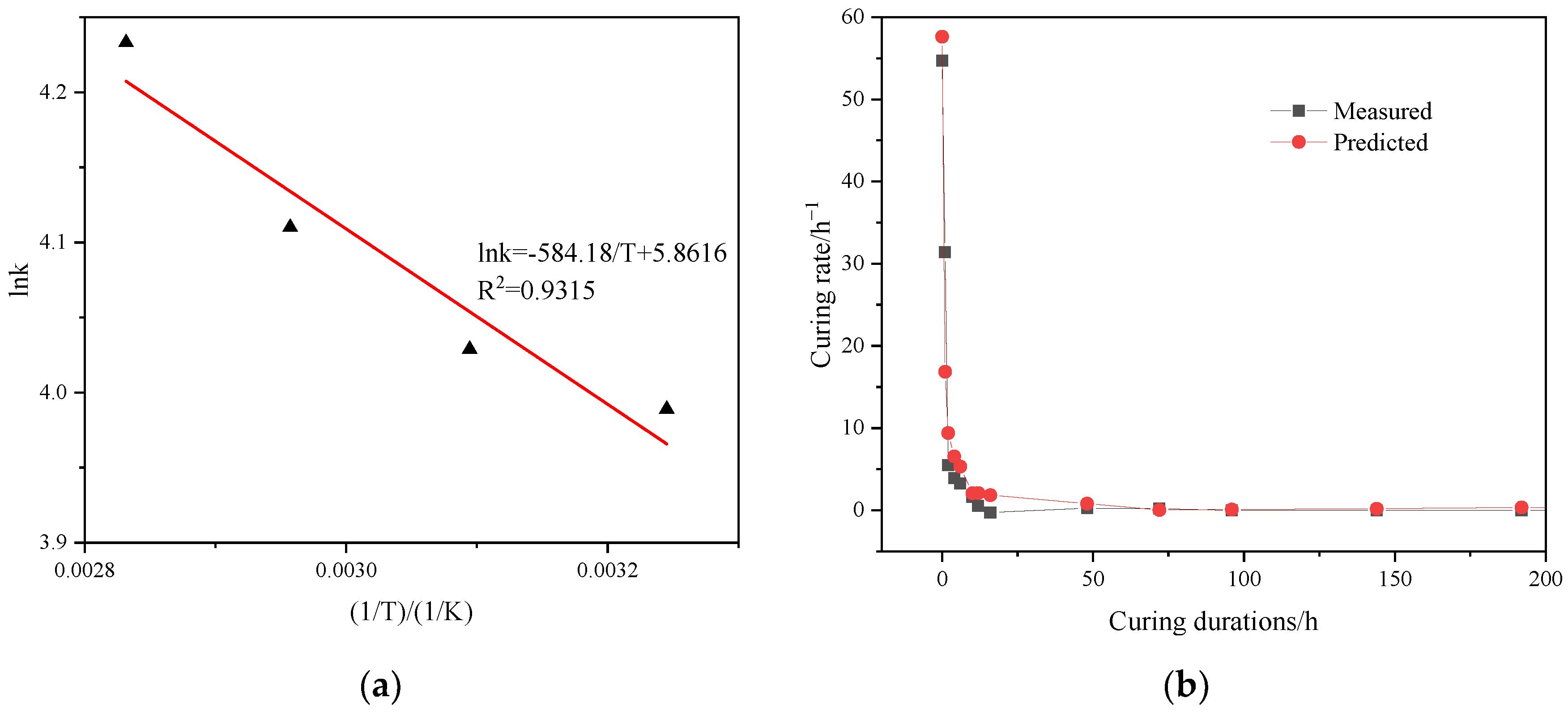
- The curing reaction of STR reaches the maximum rate at the beginning. Then, the reaction rate gradually levels off. Therefore, the curing reaction of STR is speculated to be the nth-order reaction. By fitting the test results, the nth-order curing kinetic model with an nth-order of 1.551 was established.
- (3)
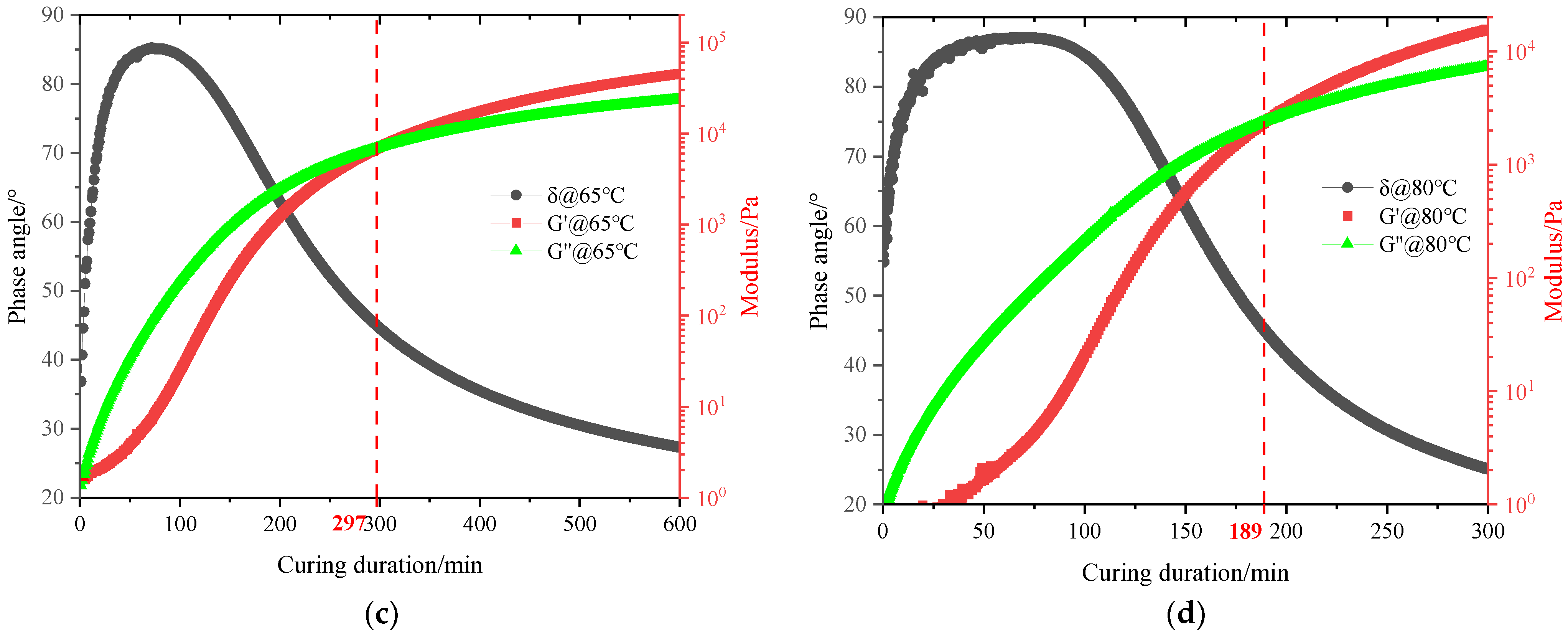
- With the increase in temperature from 35 to 80 °C, the gel point time decreases significantly from 480 to 189 min. However, the gel point curing degree does not present an obvious difference and concentrates around 75.73%.
- (4)
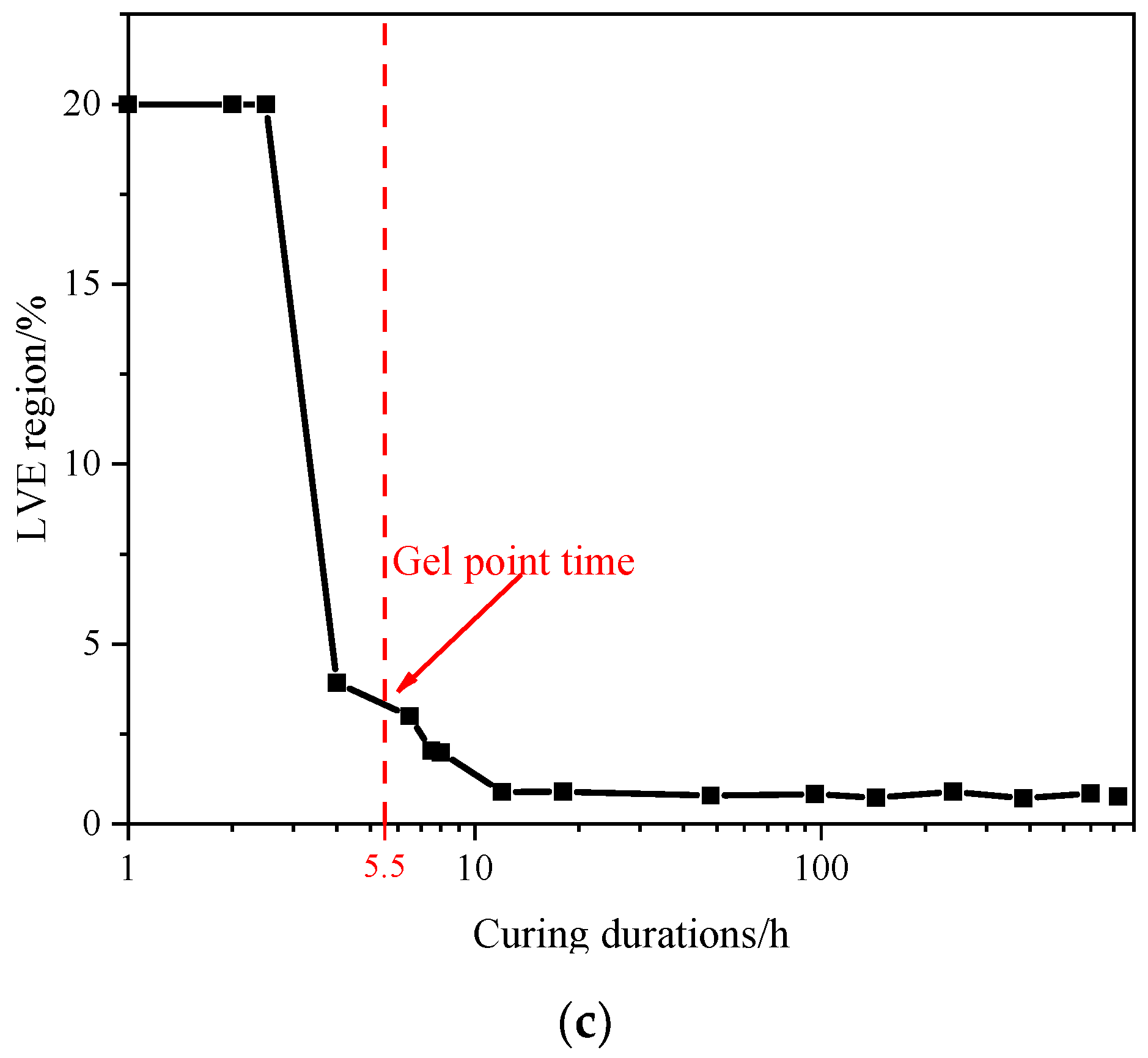
- The LVE region demonstrates an obvious decreasing trend, especially when the curing duration increases from 2.5 to 4 h. When cured at 50 °C for more than 10 h, a three-dimensional network is basically formed and the LVE region demonstrates a stable tendency concentrating around 1%.
- (5)
- Increased curing duration and temperature can boost the weight loss of reactants. After 400 h, the weight losses of specimens cured at 35 and 80 °C are about 8% and 20%, respectively. In addition, the initial weight loss occupies most of the total weight loss during the whole curing process. Finally, the Maxwell equation was proposed to predict the weight loss of STR with a specified curing scheme.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, Z.; Xiang, Z.; Li, J.; Huang, Y.; Ruan, S. Fatigue behavior of orthotropic bridge decks with two types of cutout geometry based on field monitoring and FEM analysis. Eng. Struct. 2020, 209, 109926. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, Z.; Tian, J.; Ni, F.; Gu, X. Long-Term In Situ Performance Evaluation of Epoxy Asphalt Concrete for Long-Span Steel Bridge Deck Pavement. Coatings 2023, 13, 545. [Google Scholar] [CrossRef]
- Jia, X.; Huang, B.; Chen, S.; Shi, D. Comparative investigation into field performance of steel bridge deck asphalt overlay systems. KSCE J. Civ. Eng. 2016, 20, 2755–2764. [Google Scholar] [CrossRef]
- Medani, T.O. Design Principles of Surfacings on Orthotropic Steel Bridge Decks. Ph.D. Thesis, Technische Universiteit Delft, Delft, The Netherlands, 2006. [Google Scholar]
- Farreras-Alcover, I.; Chryssanthopoulos, M.K.; Andersen, J.E. Data-based models for fatigue reliability of orthotropic steel bridge decks based on temperature, traffic and strain monitoring. Int. J. Fatigue 2017, 95, 104–119. [Google Scholar] [CrossRef]
- Xiang, Q.; Xiao, F. Applications of epoxy materials in pavement engineering. Constr. Build. Mater. 2020, 235, 117529. [Google Scholar] [CrossRef]
- Han, Y.; Ni, F.; Jiang, J.; Tian, J.; Zhang, Z.; Zhou, Z.; Dong, Q. Rheological investigation of a super-tough resin-based binder for steel bridge deck paving. Constr. Build. Mater. 2023, 384, 131441. [Google Scholar] [CrossRef]
- Han, Y.; Tian, J.; Ding, J.; Shu, L.; Ni, F. Evaluating the storage stability of SBR-modified asphalt binder containing polyphosphoric acid (PPA). Case Stud. Constr. Mater. 2022, 17, e01214. [Google Scholar] [CrossRef]
- Raisi, A.; Asefnejad, A.; Shahali, M.; Doozandeh, Z.; Kamyab Moghadas, B.; Saber-Samandari, S.; Khandan, A. A soft tissue fabricated using a freeze-drying technique with carboxymethyl chitosan and nanoparticles for promoting effects on wound healing. J. Nanoanalysis 2020, 7, 262–274. [Google Scholar] [CrossRef]
- Lesueur, D. Polymer modified bitumen emulsions (PMBEs). In Polymer Modified Bitumen; Elsevier: Amsterdam, The Netherlands, 2011; pp. 25–42. [Google Scholar]
- Li, X.; Li, J.; Wang, J.; Yuan, J.; Jiang, F.; Yu, X.; Xiao, F. Recent applications and developments of Polyurethane materials in pavement engineering. Constr. Build. Mater. 2021, 304, 124639. [Google Scholar] [CrossRef]
- Shundo, A.; Yamamoto, S.; Tanaka, K. Network formation and physical properties of epoxy resins for future practical applications. JACS Au 2022, 2, 1522–1542. [Google Scholar] [CrossRef]
- Cividanes, L.S.; Simonetti, E.A.; Moraes, M.B.; Fernandes, F.W.; Thim, G.P. Influence of carbon nanotubes on epoxy resin cure reaction using different techniques: A comprehensive review. Polym. Eng. Sci. 2014, 54, 2461–2469. [Google Scholar] [CrossRef]
- Xie, H.; Li, C.; Wang, Q. A critical review on performance and phase separation of thermosetting epoxy asphalt binders and bond coats. Constr. Build. Mater. 2022, 326, 126792. [Google Scholar] [CrossRef]
- Apostolidis, P.; Liu, X.; Kasbergen, C.; van de Ven, M.; Pipintakos, G.; Scarpas, A. Chemo-rheological study of hardening of epoxy modified bituminous binders with the finite element method. Transp. Res. Rec. 2018, 2672, 190–199. [Google Scholar] [CrossRef]
- Yu, L.; Chen, H.; Wang, H. Tracking and Analysis of Anti-slip Performance Evolutionary of Epoxy Asphalt Pavement on Steel Bridge Decks. J. Munic. Technol. 2022, 40, 29–34. [Google Scholar]
- Jamshidi, A.; White, G.; Kurumisawa, K. Functional and field performance of epoxy asphalt technology–state-of-the-art. Road Mater. Pavement Des. 2023, 24, 881–918. [Google Scholar] [CrossRef]
- Tian, J.; Luo, S.; Lu, Q.; Liu, S. Effects of epoxy resin content on properties of hot mixing epoxy asphalt binders. J. Mater. Civ. Eng. 2022, 34, 04022145. [Google Scholar] [CrossRef]
- Apostolidis, P.; Liu, X.; van de Ven, M.; Erkens, S.; Scarpas, T. Kinetic viscoelasticity of crosslinking epoxy asphalt. Transp. Res. Rec. 2019, 2673, 551–560. [Google Scholar] [CrossRef]
- Zhang, G. Study on Curing Deformation and Residual Stress of Variable Stiffness Composites. Ph.D. Thesis, Wuhan University of Technology, Wuhan, China, 2019. [Google Scholar]
- Gupta, A.M.; Macosko, C.W. Modeling strategy for systems with both stepwise and chainwise chemistry: Amine-epoxy networks with etherification. J. Polym. Sci. Part B Polym. Phys. 1990, 28, 2585–2606. [Google Scholar] [CrossRef]
- Wise, C.W.; Cook, W.D.; Goodwin, A.A. Chemico-diffusion kinetics of model epoxy-amine resins. Polymer 1997, 38, 3251–3261. [Google Scholar] [CrossRef]
- Lucio, B.; de la Fuente, J.L. Kinetic and thermodynamic analysis of the polymerization of polyurethanes by a rheological method. Thermochim. Acta 2016, 625, 28–35. [Google Scholar] [CrossRef]
- Boulkadid, M.K.; Touidjine, S.; Trache, D.; Belkhiri, S. Analytical methods for the assessment of curing kinetics of polyurethane binders for high-energy composites. Crit. Rev. Anal. Chem. 2022, 52, 1112–1121. [Google Scholar] [CrossRef] [PubMed]
- Apostolidis, P.; Liu, X.; Erkens, S.; Scarpas, T. Oxidative aging of epoxy asphalt. Int. J. Pavement Eng. 2022, 23, 1471–1481. [Google Scholar] [CrossRef]
- Huang, W.; Guo, W.; Wei, Y. Thermal effect on rheological properties of epoxy asphalt mixture and stress prediction for bridge deck paving. J. Mater. Civ. Eng. 2019, 31, 04019222. [Google Scholar] [CrossRef]
- Liu, M.; Hu, J.; Sun, J.; Li, Y.; Luo, S. Characterization of Roadway Epoxy Asphalt Binder with Different Epoxy Contents. J. Mater. Civ. Eng. 2023, 35, 04023144. [Google Scholar] [CrossRef]
- Sun, J.; Huang, W.; Lu, G.; Luo, S.; Li, Y. Investigation of the performance and micro-evolution mechanism of low-content thermosetting epoxy asphalt binder towards sustainable highway and bridge decks paving. J. Clean. Prod. 2023, 384, 135588. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, X.; Sun, Y.; Xu, W.; Pan, Y.; Xie, H.; Cheng, R. Flame retardancy, thermal, and mechanical properties of mixed flame retardant modified epoxy asphalt binders. Constr. Build. Mater. 2014, 68, 62–67. [Google Scholar] [CrossRef]
- Si, J.; Li, Y.; Yu, X. Curing behavior and mechanical properties of an eco-friendly cold-mixed epoxy asphalt. Mater. Struct. 2019, 52, 81. [Google Scholar] [CrossRef]
- Huang, W.; Guo, W.; Wei, Y. Prediction of Paving Performance for Epoxy Asphalt Mixture by Its Time- and Temperature-Dependent Properties. J. Mater. Civ. Eng. 2020, 32, 04020017. [Google Scholar] [CrossRef]
- Xu, J.; Ma, B.; Mao, W.; Wang, X. Strength characteristics and prediction of epoxy resin pavement mixture. Constr. Build. Mater. 2021, 283, 122682. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Q.; Wang, J.; Zhao, Z.; Jin, D. Physical and chemical evaluation of adhesion recovery property of aged high-viscosity asphalt based on specialized composite rejuvenators. J. Clean. Prod. 2023, 414, 137758. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Ma, S.; Luo, Y. Different catalytic systems on hydroxyl-terminated GAP and PET with poly-isocyanate: Curing kinetics study using dynamic in situ IR spectroscopy. Int. J. Polym. Anal. Charact. 2016, 21, 495–503. [Google Scholar] [CrossRef]
- Xu, L.; Li, C.; Ng, K.S. In-situ monitoring of urethane formation by FTIR and Raman spectroscopy. J. Phys. Chem. A 2000, 104, 3952–3957. [Google Scholar] [CrossRef]
- Cong, P.; Luo, W.; Xu, P.; Zhang, Y. Chemical and physical properties of hot mixing epoxy asphalt binders. Constr. Build. Mater. 2019, 198, 1–9. [Google Scholar] [CrossRef]
- Wekumbura, C.; Stastna, J.; Zanzotto, L. Destruction and recovery of internal structure in polymer-modified asphalts. J. Mater. Civ. Eng. 2007, 19, 227–232. [Google Scholar] [CrossRef]
- Jiang, J. Investigation of the Fatigue Property and Internal Structure of Asphalt Mixtures Based on Multiscale Methods. Ph.D. Thesis, Southeast University, Nanjing, China, 2019. [Google Scholar]
- Kincal, D.; Özkar, S. Kinetic study of the reaction between hydroxyl-terminated polybutadiene and isophorone diisocyanate in bulk by quantitative FTIR spectroscopy. J. Appl. Polym. Sci. 1997, 66, 1979–1983. [Google Scholar] [CrossRef]
- Martínez-Miranda, M.; García-Martínez, V.; Gude, M. Gel point determination of a thermoset prepreg by means of rheology. Polym. Test. 2019, 78, 105950. [Google Scholar] [CrossRef]
- Hu, H.; Li, S.; Wang, J.; Zu, L.; Cao, D.; Zhong, Y. Monitoring the gelation and effective chemical shrinkage of composite curing process with a novel FBG approach. Compos. Struct. 2017, 176, 187–194. [Google Scholar] [CrossRef]
- Shah, D.U.; Schubel, P.J. Evaluation of cure shrinkage measurement techniques for thermosetting resins. Polym. Test. 2010, 29, 629–639. [Google Scholar] [CrossRef]
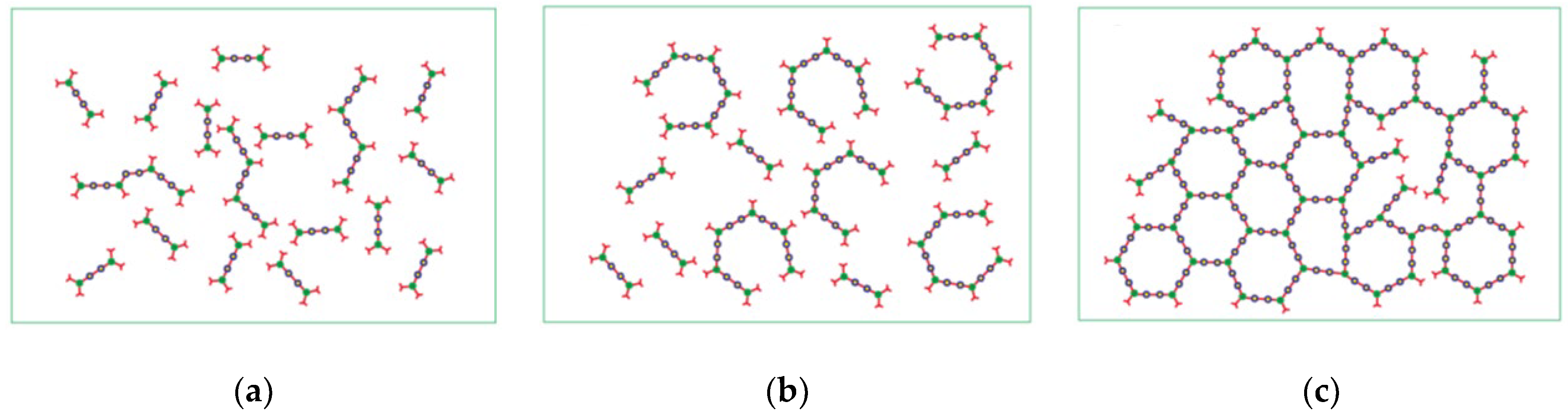




| Properties | Main Agent | Curing Agent |
|---|---|---|
| Results | Results | |
| Appearance | Clear liquid | Light yellow liquid |
| Brookfield Viscosity (23 °C, mPa·s) | 656 | 223 |
| Specific Gravity (23 °C, g/cm3) | 1.13 | 1.02 |
| Tests | Curing Schemes | Test Schemes | |||
|---|---|---|---|---|---|
| Curing Temperatures/°C | Curing Durations/h | Test Temperatures/°C | Strain/% | Frequency/Hz | |
| FTIR Test | 35, 50, 65, 80 | 0–480 | 25 | - | - |
| Weight Loss Test | 35, 50, 65, 80 | - | - | ||
| Time Sweep Test | 0–12 | 35, 50, 65, 80 | 1 | 1 | |
| LVE Test | 0–720 | 25 | 0.001–20/ 1 × 10−5–0.02 | 1.59 | |
| Parameters | 35 °C | 50 °C | 65 °C | 80 °C |
|---|---|---|---|---|
| k | 53.997 | 56.200 | 60.953 | 68.932 |
| n | 1.663 | 1.543 | 1.550 | 1.448 |
| Temperatures | 35 °C | 50 °C | 65 °C | 80 °C | Average |
|---|---|---|---|---|---|
| Gel Point Time/min | 480 | 330 | 297 | 189 | - |
| Gel Point Curing Degree/% | 76.69 | 76.01 | 75.06 | 75.164 | 75.73 |
| Temperatures/°C | A | B | C | R2 |
|---|---|---|---|---|
| 35 | 90.83 | 8.5 | 271.18 | 0.99 |
| 50 | 86.49 | 13.82 | 204.1 | 0.99 |
| 65 | 82.97 | 14.02 | 110.96 | 0.99 |
| 80 | 80.39 | 16.07 | 45.81 | 0.97 |
| Relationship between T and A, B, C | A = −0.23 × T + 98.53 R2 = 0.99 | B = 0.15 × T + 4.32 R2 = 0.84 | C = 452.89 − 5.13 × T R2 = 0.99 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Jiang, J.; Tian, J.; Zhang, Z.; Ni, F.; Zhang, S. An Investigation of the Dynamic Curing Behavior and Micro-Mechanism of a Super-Tough Resin for Steel Bridge Pavements. Coatings 2023, 13, 1567. https://doi.org/10.3390/coatings13091567
Han Y, Jiang J, Tian J, Zhang Z, Ni F, Zhang S. An Investigation of the Dynamic Curing Behavior and Micro-Mechanism of a Super-Tough Resin for Steel Bridge Pavements. Coatings. 2023; 13(9):1567. https://doi.org/10.3390/coatings13091567
Chicago/Turabian StyleHan, Yajin, Jiwang Jiang, Jiahao Tian, Zhu Zhang, Fujian Ni, and Sheng Zhang. 2023. "An Investigation of the Dynamic Curing Behavior and Micro-Mechanism of a Super-Tough Resin for Steel Bridge Pavements" Coatings 13, no. 9: 1567. https://doi.org/10.3390/coatings13091567
APA StyleHan, Y., Jiang, J., Tian, J., Zhang, Z., Ni, F., & Zhang, S. (2023). An Investigation of the Dynamic Curing Behavior and Micro-Mechanism of a Super-Tough Resin for Steel Bridge Pavements. Coatings, 13(9), 1567. https://doi.org/10.3390/coatings13091567







