Modelling the Impact of Graphene Coating of Different Thicknesses on Polyimide Substrate on the Secondary Electron Yield
Abstract
:1. Introduction
2. Materials and Methods
2.1. Electron Scattering Principle
2.1.1. Inelastic Scattering Properties
2.1.2. Elastic Scattering Properties
2.1.3. Electron–Phonon Interactions
2.2. Monte Carlo Simulation
2.3. Experimental Data
2.3.1. Material Preparation
2.3.2. Experimental Equipment
3. Results
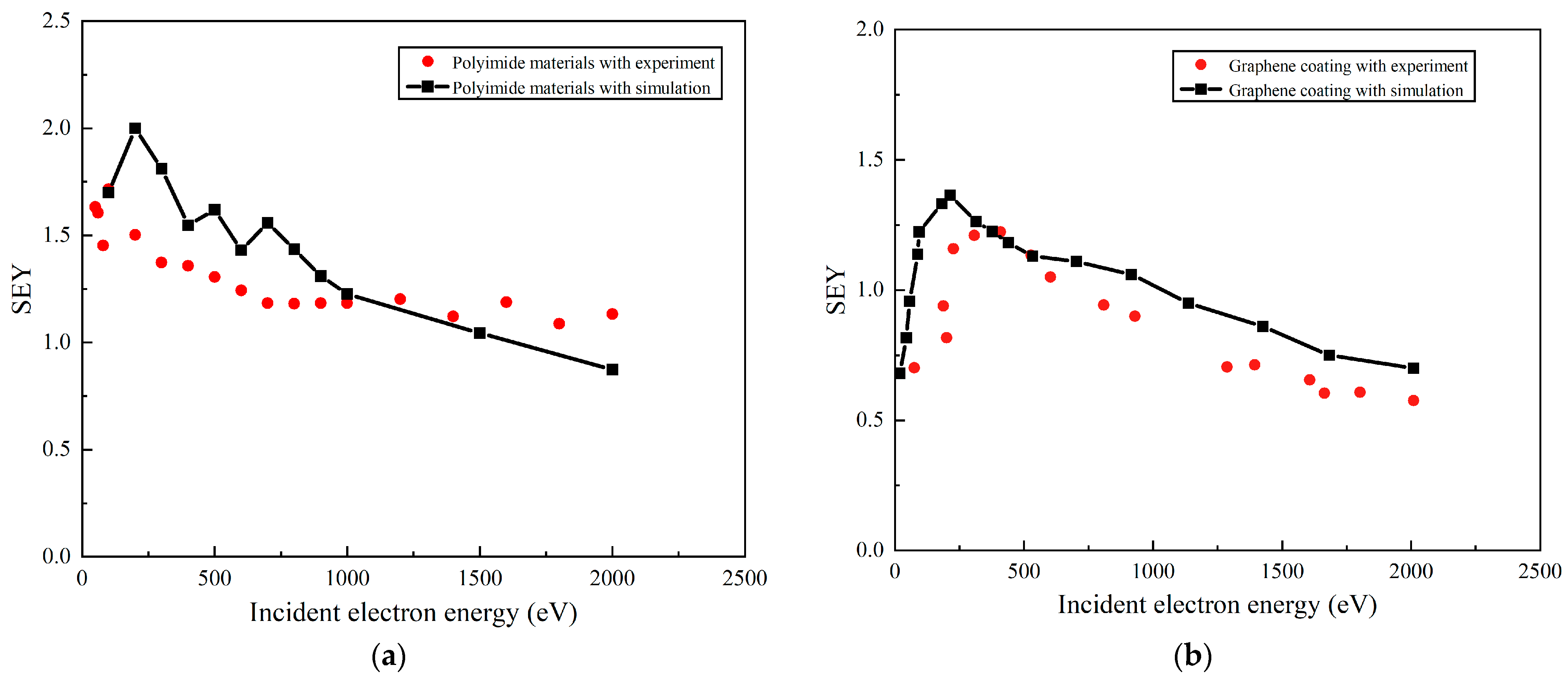
3.1. Graphene and Polyimide SEY Simulation and Experimental Analysis
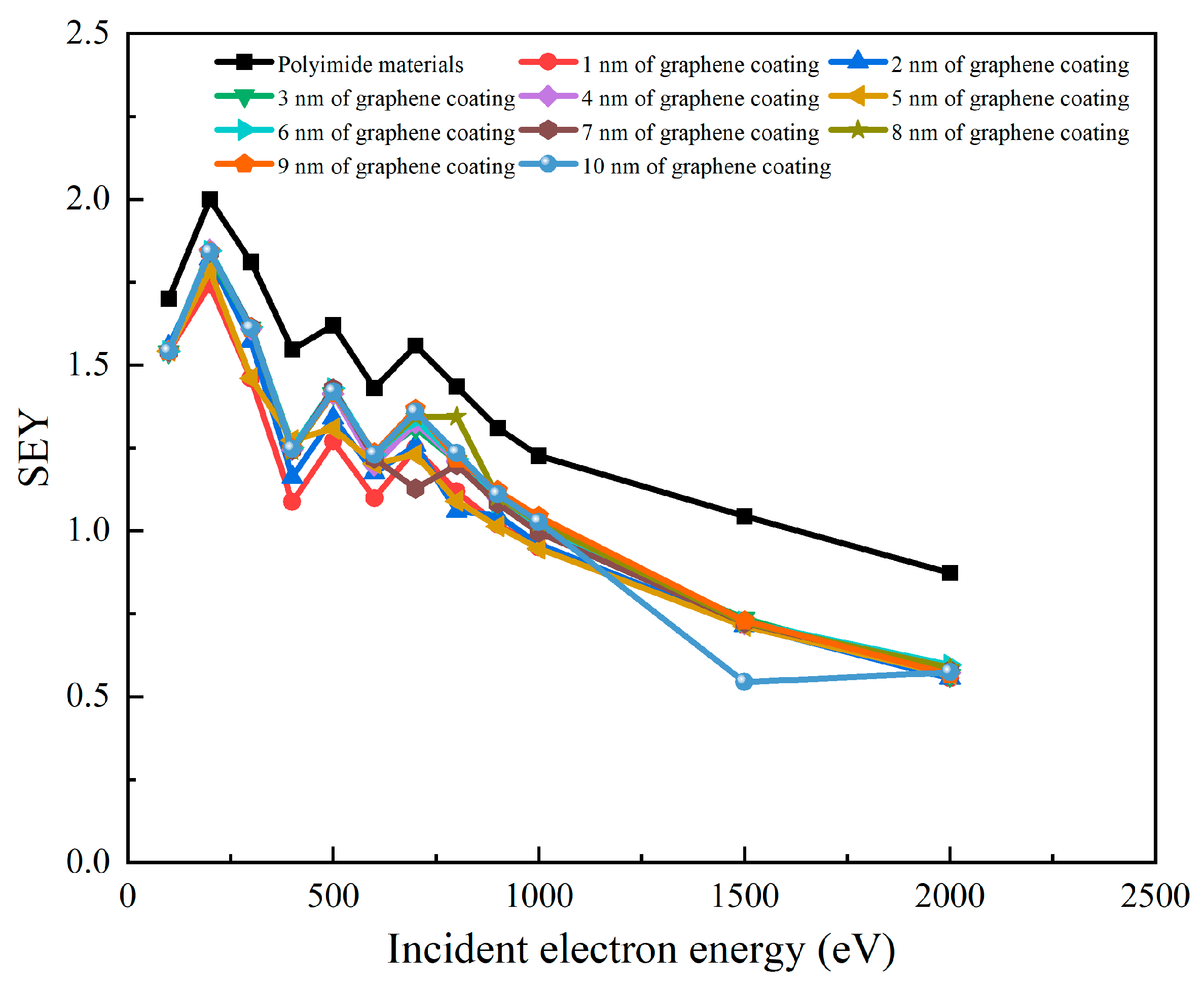
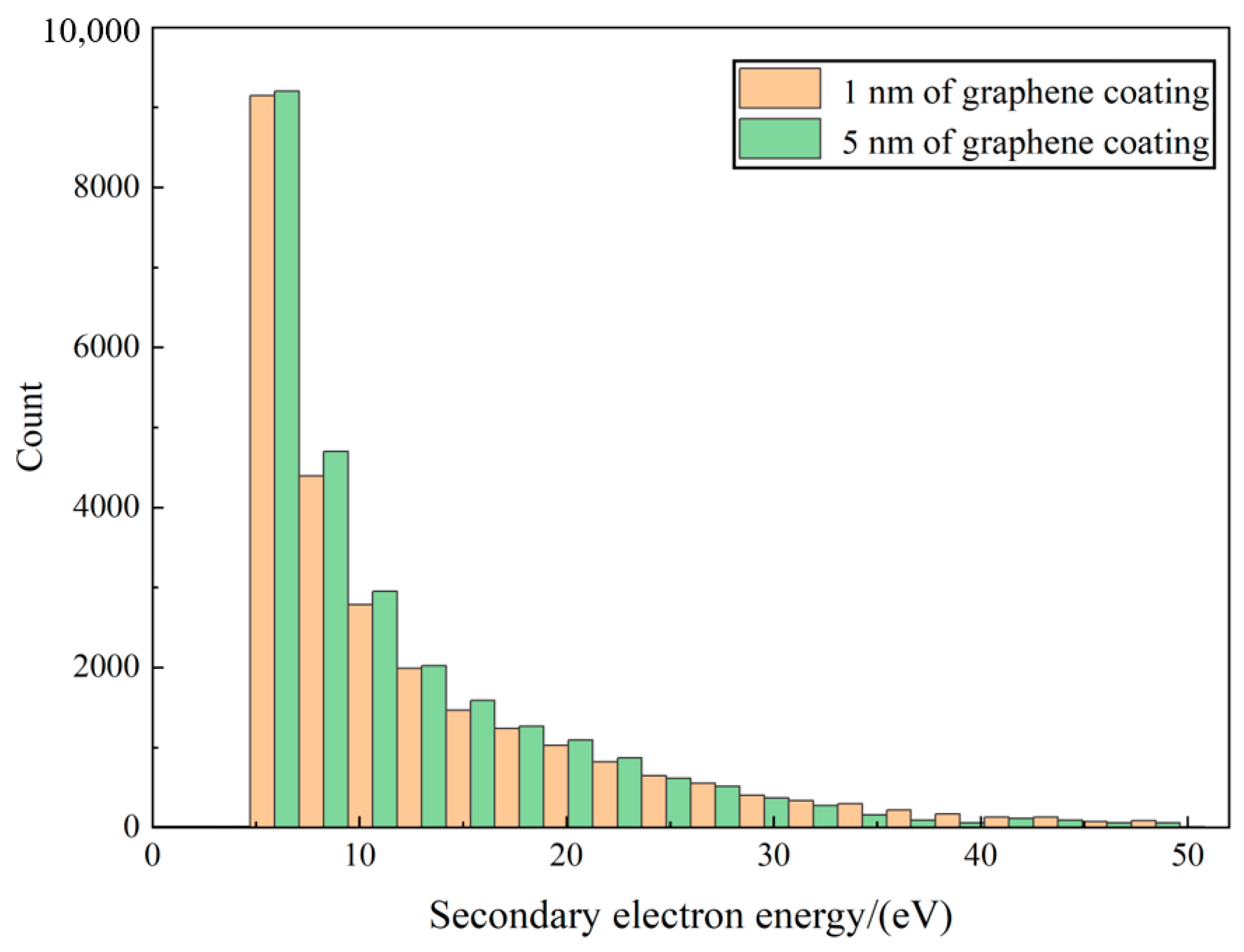
3.2. Effects of Different Thickness Graphene Coatings on SEY
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aguilera, L.; Montero, I.; Davila, M.E.; Ruiz, A.; Galan, L.; Nistor, V.; Raboso, D.; Palomares, J.; Soria, F. CuO nanowires for inhibiting secondary electron emission. J. Phys. D-Appl. Phys. 2013, 46, 165104. [Google Scholar] [CrossRef]
- Xie, A.; Guo, S.; Li, C.; Pei, Y. The measurement of secondary electron emission coefficient of MgO. J. Anhui University. Nat. Sci. 2006, 30, 61–64. [Google Scholar]
- Patino, M.; Raitses, Y.; Wirz, R. Secondary electron emission from plasma-generated nanostructured tungsten fuzz. Appl. Phys. 2016, 109, 201602. [Google Scholar] [CrossRef]
- Cao, W.; Wang, B.; Yang, Y.; Zhu, B.; Guo, J.; Xu, P.; Bai, X.; Qin, J.; Wang, C.; Zhu, J.; et al. Secondary electron emission characteristics of the Al2O3/MgO double-layer structure prepared by atomic layer deposition. Ceram. Int. 2021, 47, 9866–9872. [Google Scholar] [CrossRef]
- Cimino, R.; Commisso, M.; Grosso, D.; Demma, T.; Baglin, V.; Flammini, R.; Larciprete, R. Nature of the Decrease of the Secondary-Electron Yield by Electron Bombardment and its Energy Dependence. Phys. Rev. Lett. 2012, 109, 064801. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Song, B.; Yang, Y.; Huang, Y.; Zhou, R.; Cao, C.; Zhang, G.; Meng, N.; Zhao, S.; Ma, H. Study on Characteristics of Secondary Electron Emission for Spacecraft Surface Materials. Chin. J. Vac. Sci. Technol. 2021, 41, 770–774. [Google Scholar]
- Garcia-Valenzuela, A.; Muñoz-Piña, S.; Alcala, G.; Alvarez, R.; Lacroix, B.; Santos, A.; Cuevas-Maraver, J.; Rico, V.; Gago, R.; Vazquez, L.; et al. Growth of nanocolumnar thin films on patterned substrates at oblique angles. Plasma Process. Polym. 2019, 16, 1800135. [Google Scholar] [CrossRef]
- Li, Y.; Cui, W.-Z.; Wang, H.-G. Simulation investigation of multipactor in metal components for space application with an improved secondary emission model. Phys. Plasmas 2015, 22, 053108. [Google Scholar]
- Zhang, N.; Cao, M.; Cui, W.; Hu, T. Effect of rough surface morphology on secondary electron emission from metal surface. Jpn. J. Appl. Phys. 2017, 56, 075802. [Google Scholar] [CrossRef]
- Pivi, M.T.F.; Collet, G.; King, F.; Kirby, R.E.; Markiewicz, T.; Raubenheimer, T.O.; Seeman, J.; Le Pimpec, F. Experimental observations of in situ secondary electron yield reduction in the PEP-II particle accelerator beam line. Nucl. Inst. Methods Phys. Res. A 2010, 621, 47–56. [Google Scholar] [CrossRef]
- Krasnov, A.A. Molecular pumping properties of the LHC arc beam pipe and effective secondary electron emission from Cu surface with artificial roughness. Vacuum 2004, 73, 195–199. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Y.; Wang, S.; Fan, L.; Wei, W.; Fang, J.; Li, W.; Wang, Y. Study on the anisotropy of the secondary electron yield and resistance of the laser-etched copper. Appl. Surf. Sci. 2021, 564, 150419. [Google Scholar] [CrossRef]
- Valizadeh, R.; Malyshev, O.B.; Wang, S.; Zolotovskaya, S.; Gillespie, W.; Abdolvand, A. Low secondary electron yield engineered surface for electron cloud mitigation. Appl. Phys. Lett. 2014, 105, 231605. [Google Scholar] [CrossRef]
- Yamamoto, K.; Shibata, T.; Ogiwara, N.; Kinsho, M. Secondary electron emission yields from the J-PARC RCS vacuum components. Vacuum 2007, 81, 788–792. [Google Scholar] [CrossRef]
- Le Pimpec, F.; Kirby, R.; King, F.; Pivi, M. Properties of TiN and TiZrV thin film as a remedy against electron cloud. Nucl. Instrum. Methods Phys. Research. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2005, 551, 187–199. [Google Scholar] [CrossRef]
- Luo, J.; Tian, P.; Pan, C.; Robertson, A.; Warner, J.; Hill, E.; Briggs, G. Ultralow Secondary Electron Emission of Graphene. ACS Nano 2011, 5, 1047–1055. [Google Scholar] [CrossRef]
- Pisarra, M.; Riccardi, P.; Cupolillo, A.; Sindona, A.; Caputi, L. Studies of Electron Emission in the Interaction of Electrons with Graphene on Ni(111) Surface. Nanosci. Nanotechnol. Lett. 2012, 4, 1100–1103. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Wang, S.; Wei, W.; Ge, X.; Zhu, B.; Shao, J.; Wang, Y. Comparison of Carbon Thin Films with Low Secondary Electron Yield Deposited in Neon and Argon. Coatings 2020, 10, 884. [Google Scholar] [CrossRef]
- Alvarado, A.; Chang, H.; Nadvornick, W.; Ghoniem, N.; Marian, J. Monte Carlo raytracing method for calculating secondary electron emission from micro-architected surfaces. Appl. Surf. Sci. 2019, 478, 142–149. [Google Scholar] [CrossRef]
- Chang, T.; Zheng, J. Monte-Carlo simulation of secondary electron emission from solid metal. Acta Phys. Sin. 2012, 61, 241401. [Google Scholar] [CrossRef]
- Polak, M.P.; Morgan, D. MAST-SEY: MAterial Simulation Toolkit for Secondary Electron Yield. A monte carlo approach to secondary electron emission based on complex dielectric functions. Comput. Mater. Sci. 2021, 193, 110281. [Google Scholar] [CrossRef]
- Yasuda, M.; Nobuo, T.; Kawata, H. A Monte Carlo calculation of secondary electron emission from organic compounds. Jpn. J. Appl. Phys. Part 1-Regul. Pap. Brief Commun. Rev. Pap. 2004, 43, 4004–4008. [Google Scholar] [CrossRef]
- Pierron, J.; Inguimbert, C.; Belhaj, M.; Gineste, T.; Puech, J.; Raine, M. Electron emission yield for low energy electrons: Monte Carlo simulation and experimental comparison for Al, Ag, and Si. J. Appl. Phys. 2017, 121, 215107. [Google Scholar] [CrossRef]
- Brieda, L.; Pai, S.; Keidar, M. Kinetic Analysis of Electron Transport in a Cylindrical Hall Thruster. IEEE Trans. Plasma Sci. 2011, 39, 2946–2947. [Google Scholar] [CrossRef]
- Hollmann, E.; Doerner, R.; Nishijima, D.; Pigarov, A. Observation of reduction of secondary electron emission from helium ion impact due to plasma-generated nanostructured tungsten fuzz. J. Phys. D-Appl. Phys. 2017, 50, 445203. [Google Scholar] [CrossRef]
- Li, Y.; Yan, Y.; Lin, S.; Wang, H.; Liu, C. A fast single particle Monte-Carlo method of computing the breakdown threshold of multipactor in microwave device. Acta Phys. Sin. 2014, 63, 78–84. [Google Scholar]
- Liu, L.; Liu, D.; Wang, X.; Peng, K.; Yang, C. Implementation of secondary emission in three dimensional PIC numerical simulation. High Power Laser Part. Beams 2012, 24, 1980–1984. [Google Scholar]
- Balcon, N.; Payan, D.; Belhaj, M.; Tondu, T.; Inguimbert, V. Secondary Electron Emission on Space Materials: Evaluation of the Total Secondary Electron Yield From Surface Potential Measurements. IEEE Trans. Plasma Sci. 2012, 40, 282–290. [Google Scholar] [CrossRef]
- Ashley, J.C.; Anderson, V.E. Interaction of low-energy electrons with silicon dioxide. J. Electron Spectrosc. Relat. Phenom. 1981, 24, 127–148. [Google Scholar] [CrossRef]
- Ashley, J.C. Interaction of low-energy electrons with condensed matter: Stopping powers and inelastic mean free paths from optical data. J. Electron Spectrosc. Relat. Phenom. 1988, 46, 199–214. [Google Scholar] [CrossRef]
- Ashley, J.C. Energy-loss probabilities for electrons, positrons, and protons in condensed matter. J. Appl. Phys. 1991, 69, 674–678. [Google Scholar] [CrossRef]
- Nguyen, H.; Mankowski, J.; Dickens, J.; Neuber, A.; Joshi, R. Calculations of secondary electron yield of graphene coated copper for vacuum electronic applications. Aip Adv. 2018, 8, 015325. [Google Scholar] [CrossRef]
- Pivi, M.; King, F.; Kirby, R.; Raubenheimer, T.; Stupakov, G.; Le Pimpec, F. Sharp reduction of the secondary electron emission yield from grooved surfaces. J. Appl. Phys. 2008, 104, 104904. [Google Scholar] [CrossRef]
- Ran, M.; Jia, L.; Cheng, C.; Wu, Q. Temperature-variable raman scattering study on micromechanical properties of the carbon fiber reinforced polyimide composite film. Carbon 2019, 150, 555. [Google Scholar] [CrossRef]
- Ruzic, D.; Moore, R.; Mans, D.; Cohen, S. Secondary-electron yields of carbon-coated and polished stainless-steel. J. Vac. Sci. Technol. 1982, 20, 1313–1316. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Baglih, E.; Bagulyai, A.; Banerjee, S.; Barrand, G.; et al. Recent developments in Geant4. Nucl. Instrum. Methods Phys. Res. Sect. A 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Röpke, G.; Selchow, A.; Wierling, A.; Reinholz, H. Lindhard dielectric function in the relaxation-time approximation and generalized linear response theory. Phys. Lett. A 1999, 260, 365–369. [Google Scholar] [CrossRef]
- Xie, A.; Pei, Y.; Wang, R.; Sun, H. Discussion of the improving secondary electron emission coefficient. High Power Laser Part. Beams 2005, 17, 279–282. [Google Scholar]
- Ye, M.; He, Y.; Hu, S.; Wang, R.; Hu, T.; Yang, J.; Cui, W. Suppression of secondary electron yield by micro-porous array structure. J. Appl. Phys. 2013, 113, 074904. [Google Scholar] [CrossRef]
- Llacer, J.; Garwin, E.L. Electron-Phonon Interaction in Alkali Halides. I. The Transport of Secondary Electrons with Energies between 0.25 and 7.5 eV. J. Appl. Phys. 1969, 40, 2766–2775. [Google Scholar] [CrossRef]
- Gibaru, Q.; Inguimbert, C.; Caron, P.; Raine, M.; Lambert, D.; Puech, J. Geant4 physics processes for microdosimetry and secondary electron emission simulation: Extension of MicroElec to very low energies and 11 materials (C, Al, Si, Ti, Ni, Cu, Ge, Ag, W, Kapton and SiO2). Nucl. Instrum. Methods Phys. Res. Sect. B-Beam Interact. Mater. At. 2021, 487, 66–77. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, H.; Da, B.; Mao, S.; Ding, Z. Calculations of Energy-Loss Function for 26 Materials. Chin. J. Chem. Phys. 2016, 29, 663–667. [Google Scholar] [CrossRef]
- Da, B.; Shinotsuka, H.; Yoshikawa, H.; Ding, Z.; Tanuma, S. Extended Mermin Method for Calculating the Electron Inelastic Mean Free Path. Phys. Rev. Lett. 2014, 113, 063201. [Google Scholar] [CrossRef] [PubMed]
- Qi, X.; Ma, Y.; Liu, S.; Nie, X.; Zhang, T.; Wu, Y.; Peng, W.; Hu, G. Suppression of Secondary Electron Emissions on the Graphene-Coated Polyimide Materials Prepared by Chemical Vapor Deposition. Coatings 2023, 13, 1805. [Google Scholar] [CrossRef]
- Pinto, P.; Calatroni, S.; Neupert, H.; Letant-Delrieux, D.; Lucas, S. Carbon coatings with low secondary electron yield. Vacuum 2013, 98, 29–36. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Xu, Y.; Zhang, Y.; Zhang, B.; Wei, W. Secondary electron emission characteristics of graphene films with copper substrate. Chin. Phys. C 2016, 40, 117003. [Google Scholar] [CrossRef]
- Zhang, N.; Cao, M.; Cui, W.; Hu, T.; Wang, R.; Li, Y. Analytical model of secondary electron yield from metal surface with regular structures. Acta Phys. Sin. 2015, 64, 207901. [Google Scholar] [CrossRef]
- Inguimbert, C.; Gibaru, Q.; Caron, P.; Angelucci, M.; Spallino, L.; Cimino, R. Modelling the impact on the secondary electron yield of carbon layers of various thicknesses on copper substrate. Nucl. Instrum. Methods Phys. Res. Sect. B-Beam Interact. Mater. At. 2022, 526, 1–8. [Google Scholar] [CrossRef]
- Zhang, H.; Ge, Y.; Pan, P.; Du, Y.; Fu, H.; Yan, M.; Li, P.; Long, H.; Zhang, C.; Cai, J.; et al. Suppression of secondary electron emission on oxygen-free copper surface of reduced graphene oxide coatings prepared by electrophoretic deposition. Appl. Surf. Sci. 2022, 603, 154490. [Google Scholar] [CrossRef]
- Gibaru, Q.; Inguimbert, C.; Caron, P.; Belhaj, M.; Raine, M.; Lambert, D. Surface ionizing dose deposited by low energy electrons (10 eV–10 keV) in eleven monoatomic materials: Monte Carlo calculations and analytical expressions. Appl. Surf. Sci. 2022, 576, 151813. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, X.; Ma, Y.; Liu, S.; Nie, X.; Zhang, T.; Wu, Y.; Peng, W.; Hu, G. Modelling the Impact of Graphene Coating of Different Thicknesses on Polyimide Substrate on the Secondary Electron Yield. Coatings 2024, 14, 13. https://doi.org/10.3390/coatings14010013
Qi X, Ma Y, Liu S, Nie X, Zhang T, Wu Y, Peng W, Hu G. Modelling the Impact of Graphene Coating of Different Thicknesses on Polyimide Substrate on the Secondary Electron Yield. Coatings. 2024; 14(1):13. https://doi.org/10.3390/coatings14010013
Chicago/Turabian StyleQi, Xin, Yanzhao Ma, Sisheng Liu, Xiangyu Nie, Tao Zhang, Yong Wu, Weiping Peng, and Guoming Hu. 2024. "Modelling the Impact of Graphene Coating of Different Thicknesses on Polyimide Substrate on the Secondary Electron Yield" Coatings 14, no. 1: 13. https://doi.org/10.3390/coatings14010013
APA StyleQi, X., Ma, Y., Liu, S., Nie, X., Zhang, T., Wu, Y., Peng, W., & Hu, G. (2024). Modelling the Impact of Graphene Coating of Different Thicknesses on Polyimide Substrate on the Secondary Electron Yield. Coatings, 14(1), 13. https://doi.org/10.3390/coatings14010013




