Calcium Carbonate Deposition Model Supporting Multiple Operating Conditions Based on the Phase-Field Method for Free-Surface Flows
Abstract
:1. Introduction
2. Actual Tunnel Sampling
3. Laboratory Experiments
3.1. Monitoring Method
3.2. Experimental Data
4. Mathematical Model
4.1. Model and Basic Assumptions
4.2. Fluid Properties
4.3. Chemical Reactions and Mass Transfer
4.4. Boundary Movement Properties
4.5. Model Implementation Form
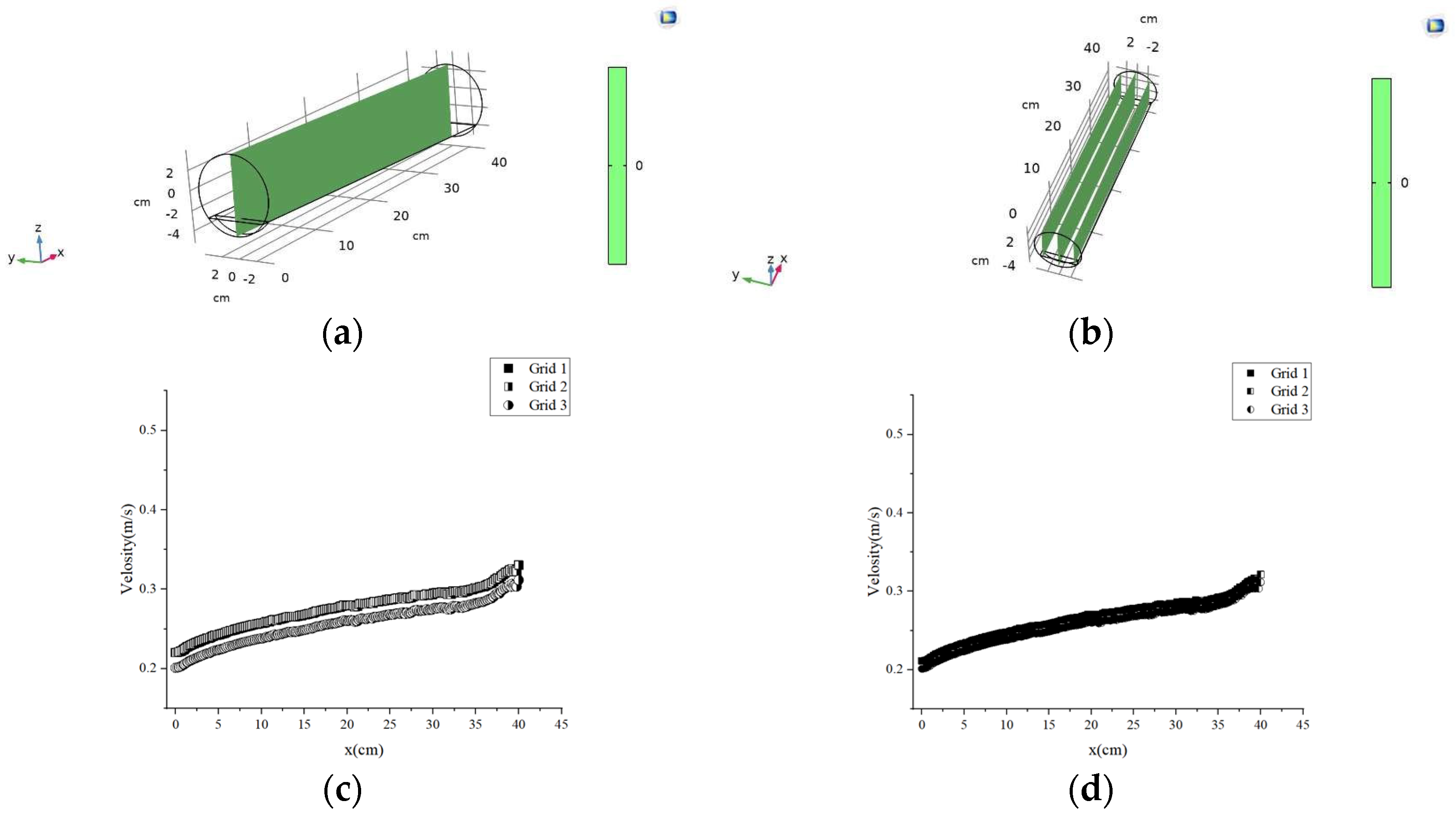
4.6. Grid Independence Verification
4.7. Simulation Conditions
4.8. Simulation Results
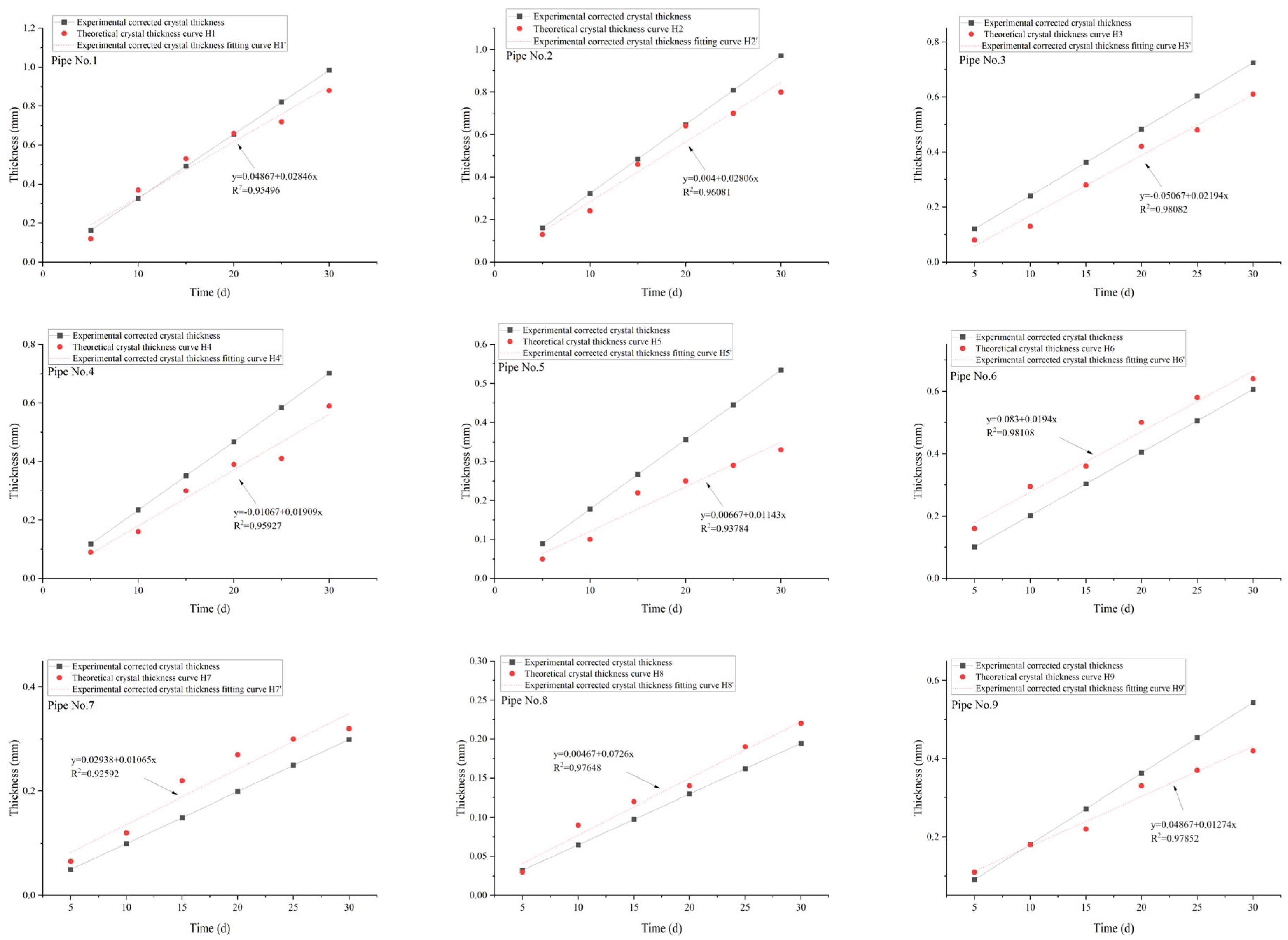
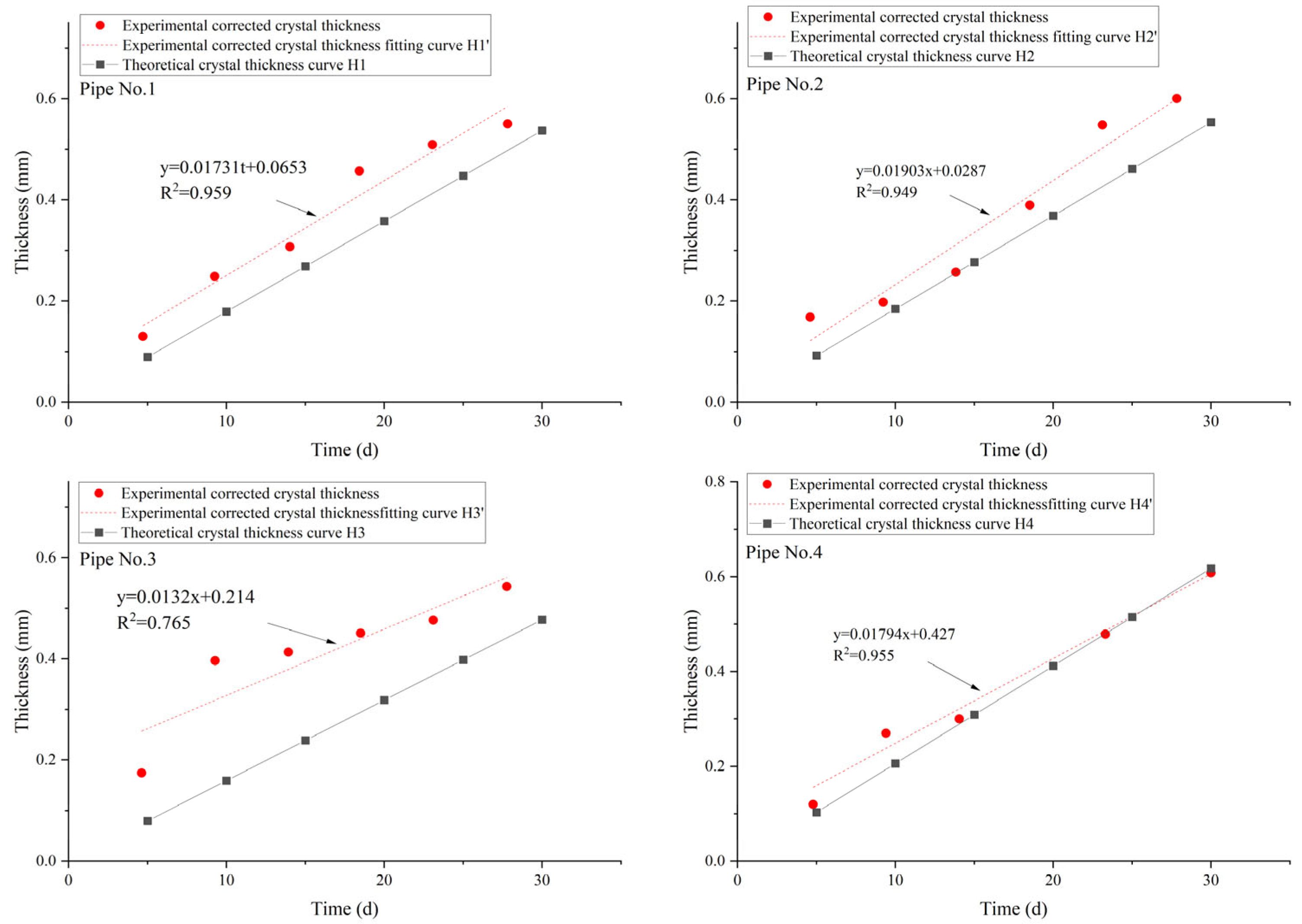
5. Data Comparison
6. Analysis
6.1. Hypothesis of Deviation in the Results
6.2. Calcium Carbonate on the Liquid Surface
6.3. Reasons for the Variation in Deposition Weight
6.4. Influence of Reynolds Number on the Situation
6.5. Impact of Local Obstructions
7. Discussion
8. Conclusions
- A two-phase flow model that is more in line with actual conditions was successfully developed, and it is capable of simulating variations in the liquid surface height with an error of approximately 20%. Additionally, the model can simulate flow velocity and concentration distributions under flow channel-blockage conditions. By utilizing the flow-field contours and concentration distributions, the deposition conditions can be better predicted.
- The deposition formula should be multiplied by a correction coefficient, which is related to the absolute roughness of the wall and the flow velocity.
- Through simulations using this model, we can visually analyze the impact of the flow velocity on the entire deposition process. Specifically, the flow velocity affects the overall deposition by influencing the mass-transfer coefficient, near-wall concentration, and erosion rate. With the aid of simulations, sedimentation research can gradually transition toward quantitative studies, allowing for the analysis of the effects of various parameters on the deposition process.
- Under the condition of non-pressurized, non-full pipe flow at the outlet, we observe that the deposition weight first increased and then decreased within a certain velocity range.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qian, Z.; Peng, H.; Lu, J.; Chen, G. Experimental study on chemical crystallization blockage of drainage pipes in limestone tunnels in southern China. Mod. Tunn. Technol. 2021, 58, 143–149. [Google Scholar]
- Lu, G.; Wang, P.; Yang, Y.; Mao, C.; Wu, Y.; Wu, J.; Dong, P.; Wu, J. Review of Research on Groundwater Seepage Induced Crystallization and Blockage Mechanism and Scale Inhibition Technology in the Tunnel Drainage System in Karst Areas. Mod. Tunn. Technol. 2021, 58, 11–20. [Google Scholar]
- Cui, Y.-J.; Lamas-Lopez, F.; Trinh, V.N.; Calon, N.; D’aguiar, S.C.; Dupla, J.-C.; Tang, A.M.; Canou, J.; Robinet, A. Investigation of interlayer soil behaviour by field monitoring. Transp. Geotech. 2014, 1, 91–105. [Google Scholar] [CrossRef]
- Jia, N.; Tassin, B.; Calon, N.; Deneele, D.; Koscielny, M.; Prévot, F. Scaling in railway infrastructural drainage devices: Site study. Innov. Infrastruct. Solut. 2016, 1, 42. [Google Scholar] [CrossRef]
- Chen, Y.; Cui, Y.; Barrett, A.G.; Chille, F.; Lassalle, S. Investigation of calcite precipitation in the drainage system of railway tunnels. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2019, 84, 45–55. [Google Scholar] [CrossRef]
- Wedenig, M.; Eichinger, S.; Boch, R.; Leis, A.; Wagner, H.; Dietzel, M. Understanding of tunnel drainage scale formation by in-situ monitoring. Tunn. Undergr. Space Technol. 2023, 131, 104853. [Google Scholar] [CrossRef]
- Wu, Z.; Cui, Y.; Barrett, A.G.; Moreno, M.M.; Deng, Y. Role of surrounding soils and pore water in calcium carbonate precipitation in railway tunnel drainage system. Transp. Geotech. 2019, 21, 100257. [Google Scholar] [CrossRef]
- Lun, M.; Yu, Z.; Hui, R. Study on Crystallization Mechanism & Prevention Measures of Non-Karst Tunnel Drainage System. China Munic. Eng. 2022, 5, 66–69, 124. [Google Scholar]
- Tang, Y.; Zhou, Z.; Wang, Y.; Zhang, J.; Tian, C.; Xue, B. Seasonal variations and sources of dripping CO, in karst caves: A case study of the Dafeng cave Guizhou Province. Carsologica Sin. 2021, 40, 521–530. [Google Scholar]
- Dietzel, M.; Rinder, T.; Leis, A.; Reichl, P.; Sellner, P.; Draschitz, C.; Plank, G.; Klammer, D.; Schöfer, H. Koralm Tunnel as a Case Study for Sinter Formation in Drainage Systems—Precipitation Mechanisms and Retaliatory Action. Geomech. Tunnelbau 2008, 1, 271–278. [Google Scholar] [CrossRef]
- Kun, X.; Jie, Z.; Xuefu, Z.; Chao, H.; Lin, S.; Li, S. Experimental Study on Crystallization Rule of Tunnel Drainpipe in Alkaline Environment. Tunn. Constr. 2019, 39, 207–212. [Google Scholar]
- Nie, C.; Rao, J.; Liu, J.; Li, Y.; Wang, S.; Xie, C. Study on the crystal composition and mechanism of tunnel drainage system. J. Henan Polytech. Univ. (Nat. Sci.) 2022, 41, 196–202. [Google Scholar]
- Eichinger, S.; Boch, R.; Leis, A.; Koraimann, G.; Grengg, C.; Domberger, G.; Nachtnebel, M.; Schwab, C.; Dietzel, M. Scale deposits in tunnel drainage systems—A study on fabrics and formation mechanisms. Sci. Total Environ. 2020, 718, 137140. [Google Scholar] [CrossRef] [PubMed]
- Dong, F.; Chen, Y.; Dai, Q.; Fei, Z.; Liu, M.; Jiang, Z.; Zhang, Q.; Li, B.; Baba, A.; O’Driscoll, M.; et al. Research progress on interfacial crystallization of travertine in secondary organic system. Carsologica Sin. 2021, 40, 34–43. [Google Scholar]
- Dong, F.; Chen, Y.; Dai, Q.; Fei, Z.; Liu, M.; Jiang, Z.; Zhang, Q.; Li, B.; Baba, A.; O’Driscoll, M.; et al. Preliminary study on nanometer growth process and regulatory mechanism of travertine nonclassical deposition-A case study of travertine in Jiuzhaigou valley and Huanglong region. Carsologica Sin. 2021, 40, 55–67. [Google Scholar]
- Chan, C.S.; Fakra, S.C.; Emerson, D.; Fleming, E.J.; Edwards, K.J. Lithotrophic iron-oxidizing bacteria produce organic stalks to control mineral growth: Implications for biosignature formation. ISME J. 2011, 5, 717–727. [Google Scholar] [CrossRef]
- Wei, L.; Guo, J.; Zhang, X.; Li, Y.; Huang, P. Study of electric field impact on crystallization in tunnel drainage pipes in hard water area. Adv. Civ. Eng. 2021, 2021, 1–17. [Google Scholar] [CrossRef]
- Nie, C.; Rao, J. Research on Fuzzy Evaluation Model for Crystal Blockage Risk in Tunnel Drainage System. China Water Transp. 2021, 21, 30–32. [Google Scholar]
- Plummer, L.N.; Wigley, T.M.; Parkhurst, D.L. The kinetics of calcite dissolution in CO2-water systems at 5 degrees to 60 degrees C and 0.0 to 1.0 atm CO2. Am. J. Sci. 1978, 278, 179–216. [Google Scholar] [CrossRef]
- Dreybrodt, W.; Buhmann, D. A mass transfer model for dissolution and precipitation of calcite from solutions in turbulent motion. Chem. Geol. 1991, 90, 107–122. [Google Scholar] [CrossRef]
- Mao, C.; Yang, Y.; Wu, J.; Dong, P.; Wu, J. Numerical simulation of crystal blockage in tunnel drainage pipe based ondynamic grid and level set. Carsologica Sin. 2023, 42, 245–256. [Google Scholar]
- Pääkkönen, T.M.; Riihimäki, M.; Simonson, C.J.; Muurinen, E.; Keiski, R.L. Crystallization fouling of CaCO3—Analysis of experimental thermal resistance and its uncertainty. Int. J. Heat Mass Transf. 2012, 55, 6927–6937. [Google Scholar] [CrossRef]
- Pääkkönen, T.M.; Ojaniemi, U.; Pättikangas, T.; Manninen, M.; Muurinen, E.; Keiski, R.L.; Simonson, C.J. CFD modelling of CaCO3 crystallization fouling on heat transfer surfaces. Int. J. Heat Mass Transf. 2016, 97, 618–630. [Google Scholar] [CrossRef]
- Hasan, B.O.; Nathan, G.J.; Ashman, P.J.; Craig, R.A.; Kelso, R.M. The effects of temperature and hydrodynamics on the crystallization fouling under cross flow conditions. Appl. Therm. Eng. 2012, 36, 210–218. [Google Scholar] [CrossRef]
- Nikoo, A.H.; Malayeri, M.R. Incorporation of surface energy properties into general crystallization fouling model for heat transfer surfaces. Chem. Eng. Sci. 2020, 215, 115461. [Google Scholar] [CrossRef]
- Duan, Z.; Cheng, C.; Tang, W. A mathematical model for predicting crystallization fouling in narrow rectangle channel incorporating crystal growth effect. Energy 2024, 291, 130399. [Google Scholar] [CrossRef]
- Coto, B.; Martos, C.; Peña, J.L.; Rodríguez, R.; Pastor, G. Effects in the solubility of CaCO3: Experimental study and model description. Fluid Phase Equilibria 2012, 324, 1–7. [Google Scholar] [CrossRef]
- Babuška, I.; Silva, R.S.; Actor, J. Break-off model for CaCO3 fouling in heat exchangers. Int. J. Heat Mass Transf. 2018, 116, 104–114. [Google Scholar] [CrossRef]
- Hissanaga, A.M.; Barbosa, J.R., Jr.; da Silva, A.K. Numerical analysis of inorganic fouling with multi-physics turbulent models. Appl. Therm. Eng. 2023, 220, 119624. [Google Scholar] [CrossRef]
- Mousavian, S.; Malayeri, M.R.; Fahiminia, F. Mathematical modeling of initial fouling rate of calcium Sulphate Dihydrate based on nucleation rate. Heat Mass Transf. 2020, 56, 2145–2158. [Google Scholar] [CrossRef]
- Xiong, C.; Chen, Y.; Ma, C. Prediction model of crystallization fouling of calcium carbonate in circulating cooling water. Int. J. Therm. Sci. 2023, 183, 107829. [Google Scholar] [CrossRef]
- Zhang, F.; Xiao, J.; Chen, X.D. Towards predictive modeling of crystallization fouling: A pseudo-dynamic approach. Food Bioprod. Process. 2015, 93, 188–196. [Google Scholar] [CrossRef]
- Shen, C.; Cirone, C.; Wang, X. A method for developing a prediction model of water-side fouling on enhanced tubes. Int. J. Heat Mass Transf. 2015, 85, 336–342. [Google Scholar] [CrossRef]
- Li, W.; Li, H.; Li, G.; Yao, S. Numerical and experimental analysis of composite fouling in corrugated plate heat exchangers. Int. J. Heat Mass Transf. 2013, 63, 351–360. [Google Scholar] [CrossRef]
- Jin, H.-Q.; Athreya, H.; Kalle, A.; Wang, S.; Nawaz, K. CFD modeling of crystallization fouling with CO2 desorption incorporated for a falling-film evaporator in thermal desalination. Desalination 2023, 553, 116456. [Google Scholar] [CrossRef]
- Mao, C.; Yang, Y.; Wu, J.; Dong, P.; Wu, J. Comparative study on hydrodynamic chemical reaction coupling simulation of crystallization blockage in karst pipelines. Carsologica Sin. 2023, 42, 245–256. [Google Scholar]
- Chen, Z.; Wang, Z.; Wu, W.; Xia, T.; Pan, E. A hybrid battery degradation model combining arrhenius equation and neural network for capacity prediction under time-varying operating conditions. Reliab. Eng. Syst. Saf. 2024, 252, 110471. [Google Scholar] [CrossRef]
- Brahim, F.; Augustin, W.; Bohnet, M. Numerical simulation of the fouling process. Int. J. Therm. Sci. 2003, 42, 323–334. [Google Scholar] [CrossRef]
- Wang, K.; Yang, W.; Shi, X.; Hou, H.; Zhao, Y. Study of Al by Phase Field Method_Mechanism of Cu rich phase precipitation in xCuMnNiFe high entropy alloy. Acta Phys. Sin. 2023, 72, 319–333. [Google Scholar]
- Fontes, E. Using COMSOL Multiphysics® Two Methods for Simulating a Free Liquid Surface. Available online: https://cn.comsol.com/blogs/two-methods-for-modeling-free-surfaces-in-comsol-multiphysics (accessed on 15 May 2024).
- Wang, Y.; Liu, Y.; Qi, C.; Zhou, T.; Ye, M.; Wang, T. Crystallization law of karst water in tunnel drainage system based on DBL theory. Open Phys. 2021, 19, 241–255. [Google Scholar] [CrossRef]
- Wei, X.; Liu, Y.; Shi, X.; Li, Y.; Ma, H.; Hou, B.; Shangguan, S.; Li, Z.; Niu, Y. Experimental research on brine crystallization mechanism in solution mining for salt cavern energy storage. J. Energy Storage 2022, 55, 105863. [Google Scholar] [CrossRef]

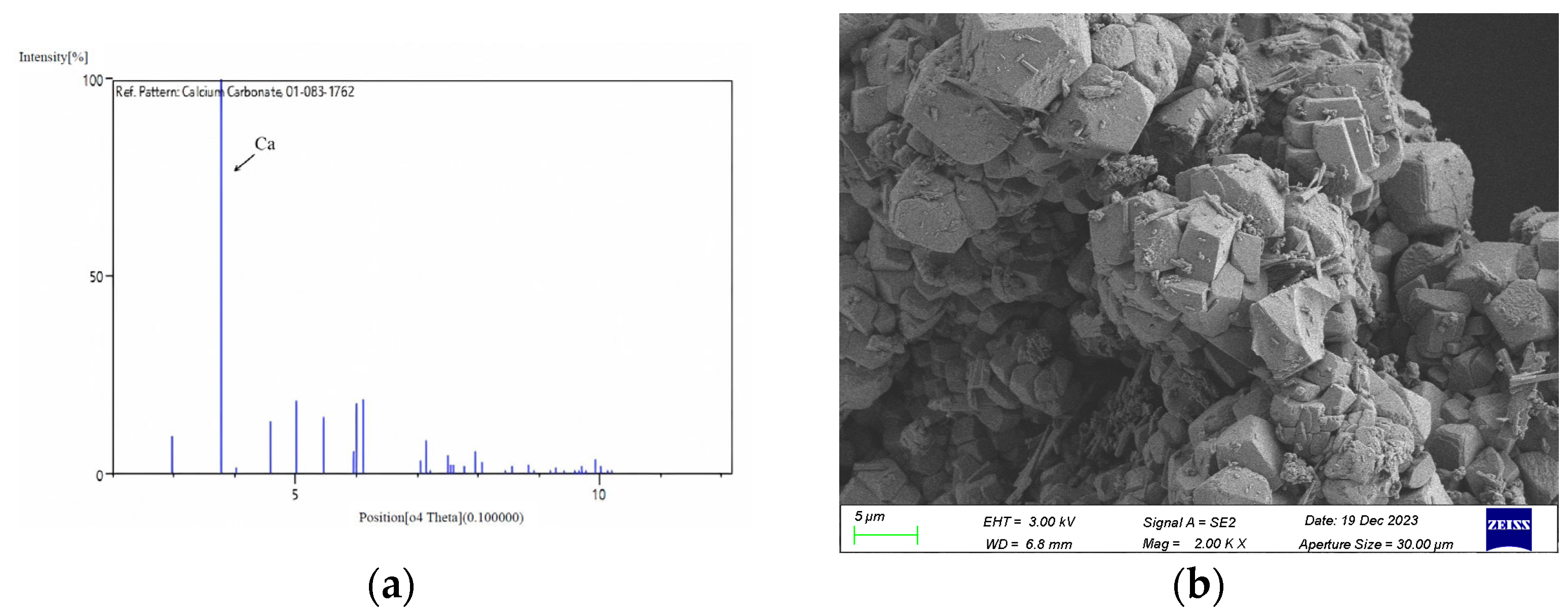
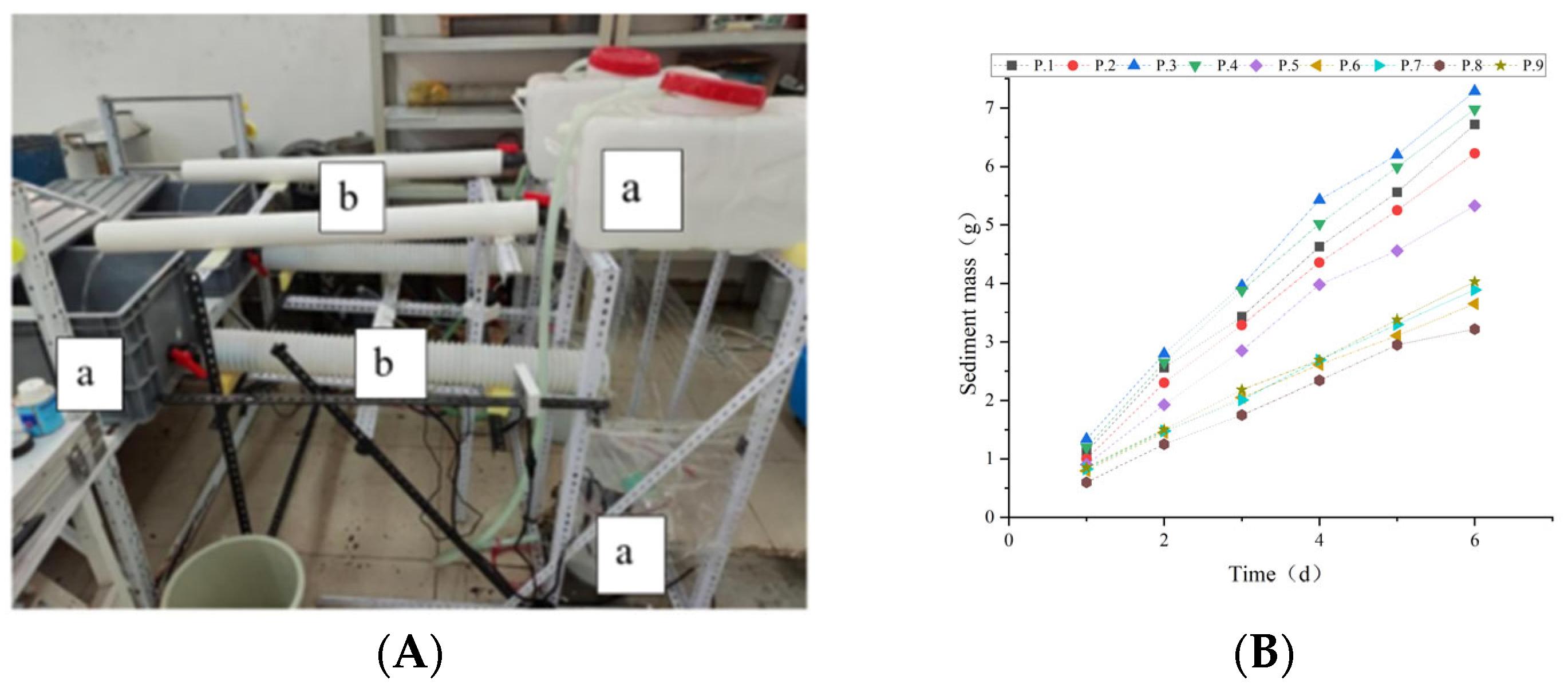

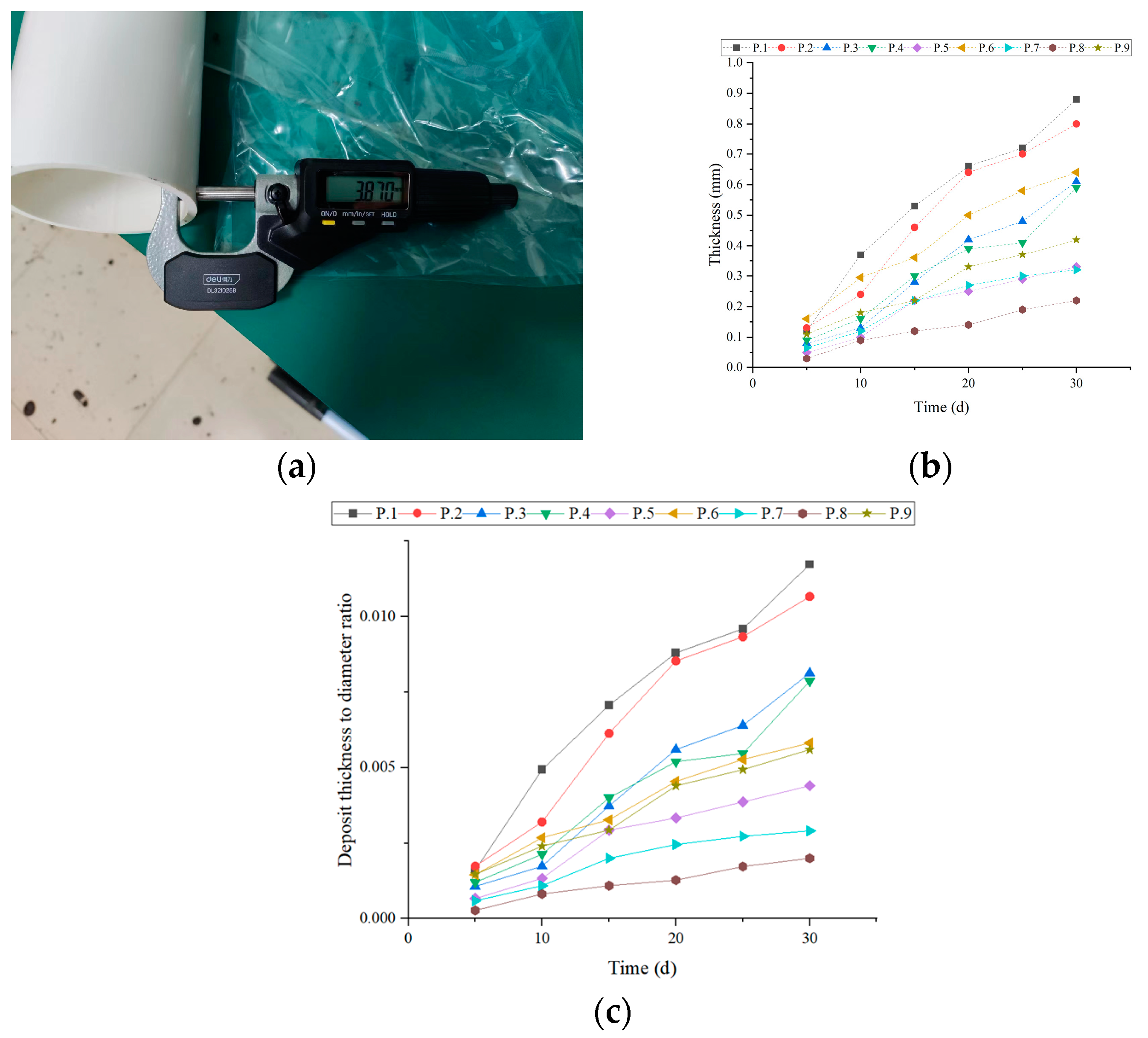


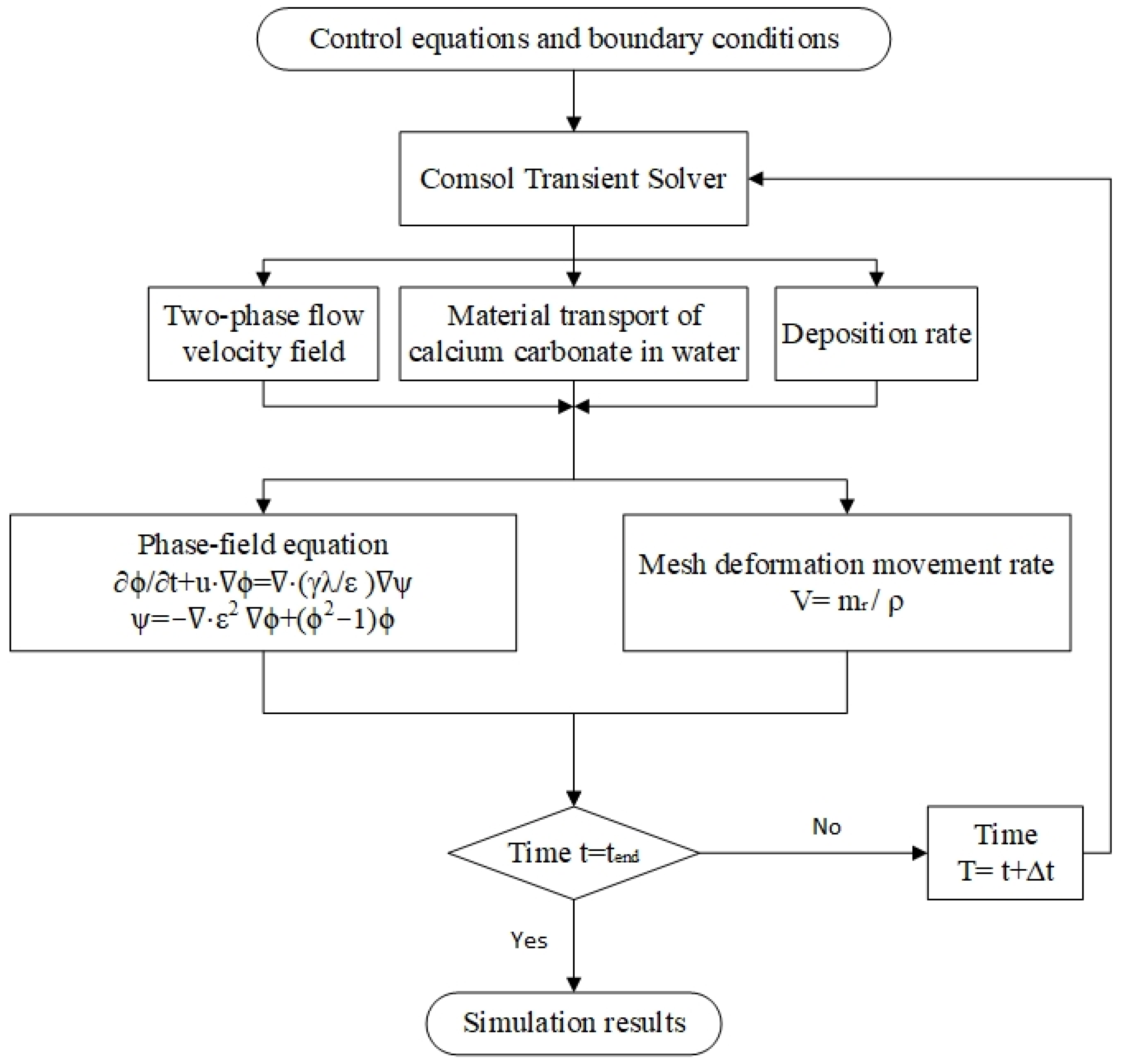


| Sample | Ca2+ (mg/L) | Mg2+ (mg/L) | Ba2+ (mg/L) | Na+ (mg/L) |
|---|---|---|---|---|
| a | 66.6316 | 9.3366 | 0.1119 | 1.0865 |
| b | 64.3725 | 9.3031 | 0.1061 | 0.7503 |
| c | 65.2342 | 9.2945 | 0.1124 | 0.9345 |
| Conditions | Liquid Level Height (mm) | Pipe Slope | Pipe Material Type and Diameter |
|---|---|---|---|
| 1 | 6.1 | 3% | Length: 1 m; pipe diameter: Ø75 mm; pipe material: PVC. |
| 2 | 6.1 | 4% | |
| 3 | 8.7 | 3% | |
| 4 | 9.0 | 4% | |
| 5 | 10.3 | 3% | |
| 6 | 7.1 | 3% | Length: 1 m; pipe diameter: Ø110 mm; pipe material: PVC. |
| 7 | 12.5 | 3% | Length: 1 m; pipe diameter: Ø110 mm; pipe material: HDPE double-wall corrugated pipe. |
| 8 | 12.4 | 4% | |
| 9 | 10.5 | 3% | Material: PVC smooth pipe; at the outlet, a sponge blockage with dimensions of 1 cm × 1.5 cm × 3 cm is used to obstruct the flow. |
| Pipe No. | Liquid Level Height (mm) | Pipe Slope | Inlet Velocity (m/s) | Absolute Roughness of Pipe Wall (μm) |
|---|---|---|---|---|
| 1 | 6.1 | 3% | 0.2205 | 2.03 |
| 2 | 6.1 | 4% | 0.2203 | 2.06 |
| 3 | 8.7 | 3% | 0.3680 | 2.04 |
| 4 | 9.0 | 4% | 0.3690 | 2.01 |
| 5 | 10.3 | 3% | 0.4106 | 2.07 |
| 6 | 7.1 | 3% | 0.4110 | 2.66 |
| 7 | 12.5 | 3% | 0.5328 | 2.71 |
| 8 | 12.4 | 4% | 0.5367 | 2.75 |
| 9 | 10.5 | 3% | 0.4123 | 2.05 |
| Pipe No. | Average Deposition Thickness from Experiments (mm/d) | Average Simulated Deposition Thickness (mm/d) | Relative Error (%) |
|---|---|---|---|
| 1 | 0.02933 | 0.03281 | 10.60 |
| 2 | 0.02667 | 0.03237 | 17.61 |
| 3 | 0.02033 | 0.02416 | 15.84 |
| 4 | 0.01967 | 0.02341 | 15.99 |
| 5 | 0.01100 | 0.01783 | 38.30 |
| 6 | 0.02133 | 0.02024 | 5.42 |
| 7 | 0.01067 | 0.00997 | 6.97 |
| 8 | 0.00733 | 0.00649 | 13.03 |
| Thickness of obstruction rear after experiment (mm) | Thickness of obstruction rear after simulation (mm) | ||
| 9 | 0.01400 | 0.01813 | 22.79 |
| Pipe No. | Average Deposition Thickness from Experiments (mm/d) | Average Simulated Deposition Thickness (mm/d) | Relative Error (%) |
|---|---|---|---|
| 1 | 0.0183 | 0.0179 | 2.53 |
| 2 | 0.0200 | 0.0184 | 7.79 |
| 3 | 0.0180 | 0.0159 | 12.04 |
| 4 | 0.0203 | 0.0206 | 1.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, J.; Chen, Z.; Feng, L.; Liang, C.; Li, J.; Huang, J. Calcium Carbonate Deposition Model Supporting Multiple Operating Conditions Based on the Phase-Field Method for Free-Surface Flows. Coatings 2024, 14, 1273. https://doi.org/10.3390/coatings14101273
Lv J, Chen Z, Feng L, Liang C, Li J, Huang J. Calcium Carbonate Deposition Model Supporting Multiple Operating Conditions Based on the Phase-Field Method for Free-Surface Flows. Coatings. 2024; 14(10):1273. https://doi.org/10.3390/coatings14101273
Chicago/Turabian StyleLv, Jianbing, Zuru Chen, Li Feng, Chen Liang, Jia Li, and Jingkai Huang. 2024. "Calcium Carbonate Deposition Model Supporting Multiple Operating Conditions Based on the Phase-Field Method for Free-Surface Flows" Coatings 14, no. 10: 1273. https://doi.org/10.3390/coatings14101273
APA StyleLv, J., Chen, Z., Feng, L., Liang, C., Li, J., & Huang, J. (2024). Calcium Carbonate Deposition Model Supporting Multiple Operating Conditions Based on the Phase-Field Method for Free-Surface Flows. Coatings, 14(10), 1273. https://doi.org/10.3390/coatings14101273






