Impact of Interfacial Transition Zone on Concrete Mechanical Properties: A Comparative Analysis of Multiphase Inclusion Theory and Numerical Simulations

Abstract

With the increasing implementation of sustainable development strategies, recycled concrete (RC) has garnered attention in research circles due to its substantial environmental and economic advantages. The presence and properties of various interface transition zones (ITZs) in RC play a vital role in its mechanical properties. This research uses a combination of multiphase inclusion theory and finite element numerical simulation to investigate and compare the impact of ITZs on concrete’s mechanical properties. The multiphase inclusion theory offers a theoretical framework for understanding ITZ behavior in concrete, categorizing it into new mortar, old mortar, new ITZ, old ITZ, and natural aggregate based on meso-structure. With simplified RC at the mesoscale, the study accurately predicts the mechanical properties of RC by adjusting the elastic modulus, Poisson’s ratio, and thickness of new and old ITZ models. Through finite element simulation and theoretical validation, the study achieves a minimal error of 6.24% in predicting the elastic modulus and 1.75% in predicting Poisson’s ratio. These results highlight the effectiveness of multiphase inclusion theory in capturing the meso-structure characteristics of RC and forecasting its macroscopic mechanical behavior while comprehensively considering the complexity of ITZs.

1. Introduction

Recycled concrete (RC) is an effective means of turning construction solid waste into treasure in modern society. It can not only save natural aggregates and protect the ecological environment of aggregate production areas, but also solve the problem of nowhere to stack waste concrete and environmental pollution caused by improper handling [1,2]. Current research has observed from a microscopic perspective that the composition of RC is complex and diverse [3]. At a microscopic level, we generally believe that recycled coarse aggregate concrete is a five-phase composite material composed of new mortar (NM), old mortar (OM), new interface transition zone (NITZ), old interface transition zone (OITZ), and natural aggregate (NA) [4]. In previous studies on ordinary concrete, the density and strength of ITZ were much lower than those of aggregates and mortar, and were generally considered as weak links in concrete [5]. Some scholars enhance the mechanical properties of ITZ in recycled concrete by adding fiber materials or nano-scale materials into RC [6,7,8], and it is beneficial to study the specific changes of ITZs in a cross-scale way. The interface situation of RC is more complex, and it is difficult to observe and analyze the impact of different ITZs on the overall mechanical properties of RC. Compared to macroscale mortar and aggregates, the typical ITZ thickness is only 10~100 μm [9,10,11]. Therefore, it is extremely necessary to study the influence of interfaces on the matrix through more effective means.

Researchers have attempted to observe the basic mechanical properties of ITZ at the macroscopic level through different experimental methods. Thomas et al. [12] concluded through uniaxial tensile tests that the tensile strength values of ITZ are discrete, and the measured strength is only 33% to 67% of the tensile strength of mortar. Qiu et al. [13] studied the effect of rough and smooth aggregates on the tensile strength of ITZ through splitting tests. However, due to the fact that most of the macroscopic studies on ITZ are conducted using mortar to make mortar joints, and no research is conducted on the combination of aggregates in mortar, this results in the experiment being affected by size. Therefore, the mechanical model refers to the model of recycled concrete used by Xiao et al. [14]. By simplifying RC into an observable form of regularly recycled aggregate combined with mortar, the non-uniform and nonlinear mechanical behavior that occurs in normal concrete tests can be avoided.

To investigate RC, a five-phase composite material with multi-inclusions and multi-interfaces, researchers propose the theory of multiphase inclusions. This approach examines the meso-mechanics of composite materials, seeking to define a quantitative link between the overall properties of composites and the composition of individual phases at a microscopic level. By integrating the mechanical characteristics of meso-structure morphology with macroscopic mechanical analysis, this theory bridges the gap between two scales [15]. The essence of using multiphase inclusion theory to predict the macroscopic equivalent mechanical properties of composite materials is to solve the equivalent problem of non-uniform inclusion homogenization. Scholars have currently applied the theory of multiphase inclusions to the study of the micromechanical properties of concrete, including the porosity, moisture content, and ITZ of concrete. Lin et al. [16] used the Mori–Tanaka method to describe the elastic properties of cement hydration products, simulated the effective elastic modulus of the cement slurry skeleton using a three-phase model, and finally applied the Mori–Tanaka model and porous medium theory again to calculate the drained and undrained elastic moduli of the cement slurry. Bai et al. [17] established a dual inclusion model based on the theory of equivalent inclusions and the Mori–Tanaka mean field, using two types of pores and cement mortar as equivalent matrices and coarse aggregates as hardened inclusions. Li et al. [18] preliminarily considered the influence of ITZ thickness on the overall mechanical properties and estimated the effective bulk modulus of three-phase concrete through two-phase composite materials and a four-phase sphere model.

However, currently, few researchers use inclusion theory to study RC and consider its different ITZs. The multiphase inclusion theory can address these gaps by providing a theoretical framework that incorporates the heterogeneity and multiphase nature of RC. It allows for a detailed analysis of the interactions between different phases, enabling more precise predictions of mechanical properties and enhancing our understanding of how ITZ characteristics influence the overall behavior of RC. This theoretical approach can also help to bridge the gap between macroscopic observations and microscopic interactions, providing insights that are difficult to obtain through empirical methods alone. Therefore, this study aims to use the multiphase inclusion theory method to analyze the impact of ITZs on the overall characteristics of RC in a mesoscale manner. A comparison was made between the theoretical results and numerical simulations to verify calculation errors, and study the influence of different types of ITZs in RC on the overall structural mechanical properties from the mesoscale to the macroscale.

2. Theoretical Model of Multiphase Inclusions

2.1. Theoretical Basis of Multiphase Inclusions

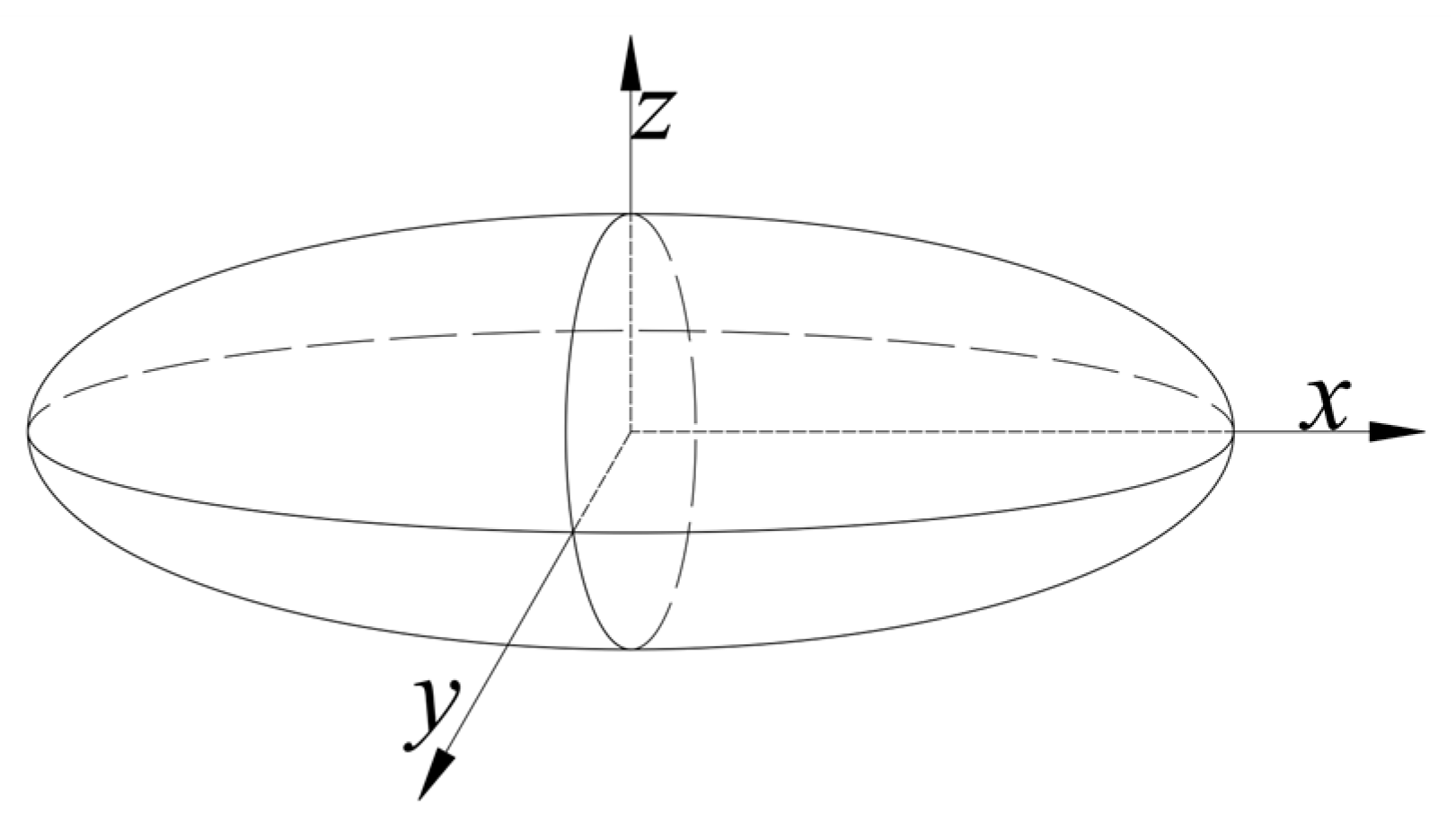
2.1.1. Eshelby’s Theory

Eshelby proposed that if a certain region within an isotropic elastic solid is retained, after removing the surrounding material, the region will spontaneously undergo a specified uniform deformation [19]. Due to the presence of surrounding materials, there will be stress fields both inside and outside the area. At this point, it is assumed that the elliptical region in an infinite medium has different mechanical parameters from the rest of the material, as shown in Figure 1 and Figure 2. The existence of this non-uniformity interferes with the uniform stress field applied at a long distance. This method for dealing with elastic isotropic inclusions embedded in an infinite elastic matrix is called the Eshelby method [20].

For ellipsoidal inclusions, as shown in Figure 1 ($a>b>c$),

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}\le 1$$

(1)

In the ellipsoidal region ${\mathit{\epsilon }}^{*}$, there is a set uniform intrinsic strain, and the total uniform strain can be expressed as a function of the intrinsic strain.

$$\mathit{\epsilon }=\mathit{S}:{\mathit{\epsilon }}^{*}$$

(2)

$${\mathit{\epsilon }}^{\ast }=\left\{\begin{array}{cc}{\mathit{\epsilon }}^{\ast }(x),& \forall x\in \mathrm{CA}\\ 0,& \forall x\in \mathrm{ITZ}\end{array}\right.$$

(3)

where $\mathit{S}$ is a fourth-order Eshelby tensor, which depends on the material properties and the shape of the inclusion (i.e., aspect ratio), represented by a 6th order matrix (specific expansion process can be found in reference [19]).

$$\mathit{S}=\left[\begin{array}{cccccc}{S}_{1111}& S_{1122}& S_{1133}& 0& 0& 0\\ S_{2211}& S_{2222}& S_{2233}& 0& 0& 0\\ S_{3311}& S_{3322}& S_{3333}& 0& 0& 0\\ 0& 0& 0& S_{1212}& 0& 0\\ 0& 0& 0& 0& S_{2323}& 0\\ 0& 0& 0& 0& 0& S_{1313}\end{array}\right]=\left[\begin{array}{cccccc}\frac{7-5\nu }{15\left(1-\nu \right)}& \frac{5\nu -1}{15\left(1-\nu \right)}& \frac{5\nu -1}{15\left(1-\nu \right)}& 0& 0& 0\\ \frac{5\nu -1}{15\left(1-\nu \right)}& \frac{7-5\nu }{15\left(1-\nu \right)}& \frac{5\nu -1}{15\left(1-\nu \right)}& 0& 0& 0\\ \frac{5\nu -1}{15\left(1-\nu \right)}& \frac{5\nu -1}{15\left(1-\nu \right)}& \frac{7-5\nu }{15\left(1-\nu \right)}& 0& 0& 0\\ 0& 0& 0& \frac{4-5\nu }{15\left(1-\nu \right)}& 0& 0\\ 0& 0& 0& 0& \frac{4-5\nu }{15\left(1-\nu \right)}& 0\\ 0& 0& 0& 0& 0& \frac{4-5\nu }{15\left(1-\nu \right)}\end{array}\right]$$

(4)

Similarly, the Eshelby tensor can be represented by the following identity.

$$8\pi (1-\nu )S_{ijkl}=\left(2\nu I_A+I_{AB}\right){\delta }_{ij}{\delta }_{kl}+\left[(1-\nu )\left(I_B+I_C\right)+I_{AC}\right]\left({\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk}\right)$$

(5)

where $\nu$ represents the Poisson’s ratio of the surrounding isotropic matrix,$A,B,C\in \left\{1,2,3\right\}$.

For ellipsoidal inclusions ($a>b>c$):

$$I_1=\frac{4\pi abc}{\left(a^2-b^2\right)\left(a^2-c^2\right)}F(\theta ,k)$$

(6)

$$I_3=\frac{4\pi abc}{\left(a^2-c^2\right)\left(a^2-c^2\right)}\left[\frac{b{\left(a^2-c^2\right)}^{1/2}}{ac}-E(\theta ,k)\right]$$

(7)

The elliptic integral is represented as,

$$F(\theta ,k)={\displaystyle {\int }_0^{\theta }\frac{dw}{{\left(1-k^2{\sin }^{2}w\right)}^{1/2}}}$$

(8)

$$E(\theta ,k)={\displaystyle {\int }_0^{\theta }{\left(1-k^2{\sin }^{2}w\right)}^{1/2}dw}$$

(9)

where $\theta =\sin \left[1-\left(c^2/a^2\right)\right]$, $k^2=(a^2-b^2)/(a^2-c^2)$.

The remaining functions satisfy the following equation,

$$I_1+I_2+I_3=4\pi$$

(10)

$$3I_{11}+I_{12}+I_{13}=\frac{4\pi }{a^2}$$

(11)

$$3a^2{I}_{11}+b^2{I}_{12}+c^2{I}_{13}=3I_1$$

(12)

$$I_{12}=\frac{I_2-I_1}{a^2-b^2}$$

(13)

From this, it can be concluded that the average internal and external Eshelby tensors of spherical inclusions ($a=b=c$) in an infinite domain are

$$S_{ijkl}^{I,\infty }=s_1^{I,\infty }{E}_{ijkl}^{(1)}+s_2^{I,\infty }{E}_{ijkl}^{(2)}$$

(14)

$$S_{ijkl}^{E,\infty }=s_1^{E,\infty }{E}_{ijkl}^{(1)}+s_2^{E,\infty }{E}_{ijkl}^{(2)}$$

(15)

$$s_1^{I,\infty }=\frac{1+\nu }{3(1-\nu )},\hspace{1em}{s}_2^{I,\infty }=\frac{2(4+5\nu )}{15(1-\nu )}$$

(16)

$$s_1^{E,\infty }=0,\hspace{1em}{s}_2^{E,\infty }=0$$

(17)

$$E_{ijkl}^{(1)}=\frac{1}{3}{\delta }_{ij}{\delta }_{kl},\hspace{1em}{E}_{ijkl}^{(2)}=\frac{1}{2}\left({\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk}\right)-\frac{1}{3}{\delta }_{ij}{\delta }_{kl}$$

(18)

where ${\delta }_{ij},{\delta }_{kl}$ is an isotropic unit tensor, and $S_{ijkl}^{I,\infty },S_{ijkl}^{E,\infty },E_{ijkl}^{(1)},E_{ijkl}^{(2)}$ adopts index representation.

This study found that the Eshelby tensor solution for spherical inclusions ($a=b=c$) in an infinite domain was found to be constant and size-independent. The infinite domain represents the presence of extremely low-content substances with similar dilutions in the inclusion phase, so the results directly applied to the case of finite domain inclusions are only close to [20]. Eshelby’s theory is fundamental in understanding the elastic behavior of inclusions within a composite material. The theory describes how an inclusion, embedded in an infinite elastic matrix, affects the surrounding stress and strain fields. By solving for the Eshelby tensor, which depends on the shape and material properties of the inclusion and the matrix, it is possible to predict the stress distribution within the inclusion and the matrix. In the context of recycled concrete, Eshelby’s theory helps model the ITZs as inclusions with distinct mechanical properties compared to the surrounding mortar and aggregate. This approach allows for the assessment of how different ITZs influence the overall mechanical properties of RC.

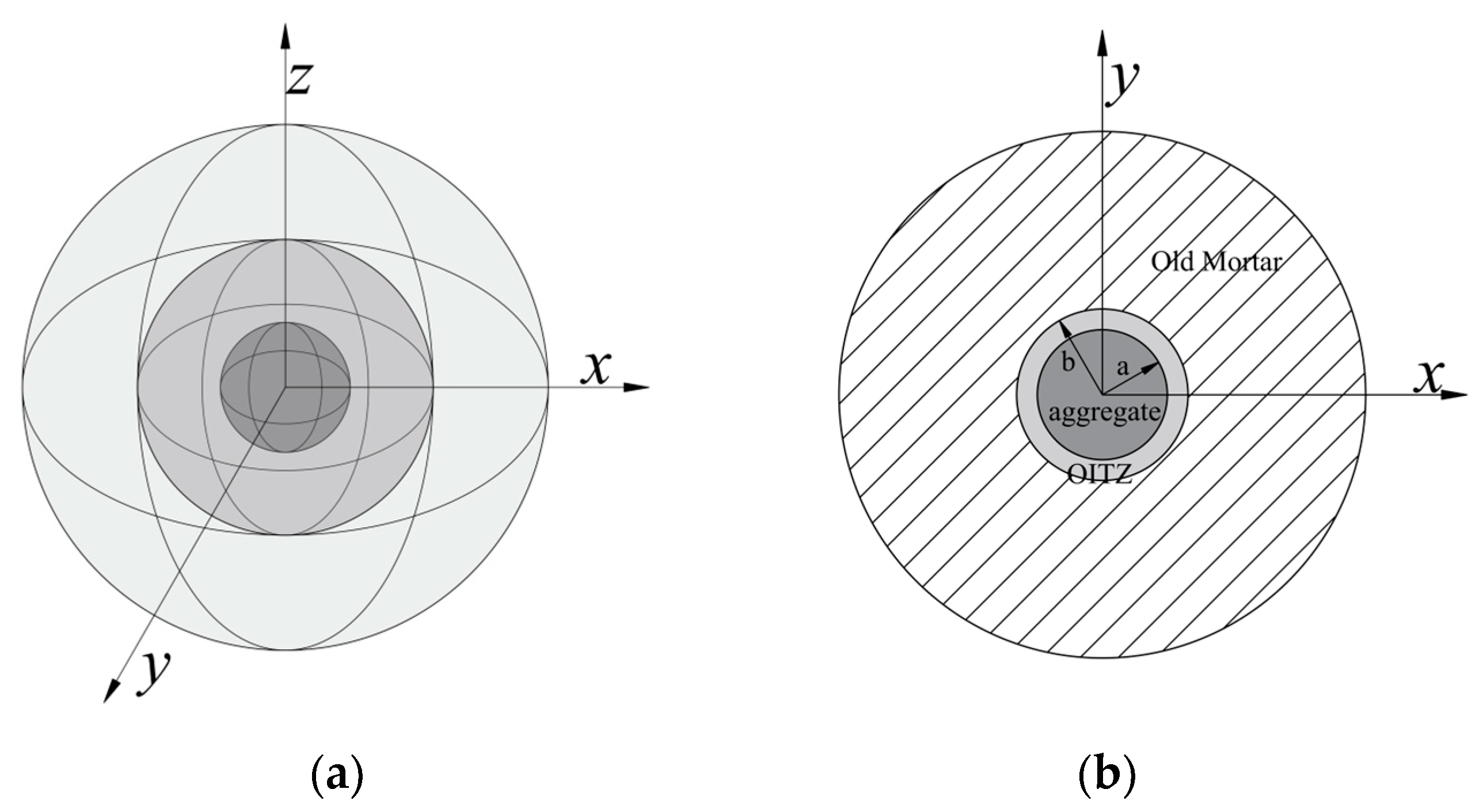
2.1.2. Three-Phase Sphere Model

ITZ is an indispensable part of the research on the mechanical properties of concrete, but its volume proportion is extremely small. If ITZ and the aggregates are regarded as matrix and inclusions, the prerequisite condition that the inclusion content envisioned by the inclusion theory is much smaller than that of the matrix itself will be destroyed. Therefore, these problems cannot be solved through the “Dilution method” anymore. When the observation is not limited to a simple combination of aggregates and ITZ, it is found that mortar as a large matrix envelops both. By referring to Christensen’s three-phase sphere model [21], this research combines OM, OITZ, and aggregate in the form of three-phase composites. It is assumed that the three-phase sphere does not interact with other parts of the matrix, as shown in Figure 3a, the mortar serves as the peripheral effective medium, the ITZ serves as the matrix as a uniform spherical shell, and the aggregate is considered as a spherical inclusion. All of them are isotropic homogeneous materials. To align with RC, we chose to do theoretical calculations using a two-dimensional model as shown in Figure 3b.

Where a is the radius of the aggregate, and b is the radius from the center to the outside of the matrix.

As shown in the figure, the two-dimensional circular domain has polar symmetry. Through studying Eshelby [19,20] and the three-phase sphere model [21], the circular domain has the following equilibrium equations:

Firstly, set some unknown constants as a₁, b₁, c₁, d₁, e₁, f₁, g₁, h₁.

Next, calculate the solutions of the elastic equilibrium equations for the following three regions.

In the uniform medium region outside ITZ, the calculation range is $r\ge b$,

$$u_{re}=\frac{b}{4{\mu }_0}\left[\frac{2r}{b}+(\eta +1)a_1\frac{b}{r}+b_1{\left(\frac{b}{r}\right)}^3\right]\cos 2\theta ,$$

(19)

$$u_{\theta e}=\frac{b}{4{\mu }_0}\left[\frac{-2r}{b}-(\eta -1)a_1\frac{b}{r}+b_1{\left(\frac{b}{r}\right)}^3\right]\sin 2\theta$$

(20)

In the internal area of ITZ, the calculation range is $a⩽r⩽b$,

$$u_{rm}=\frac{b}{4{\mu }_m}\left[c_1\left({\eta }_m-3\right){\left(\frac{r}{b}\right)}^3+d_1\frac{r}{b}+e_1\left({\eta }_m+1\right)\frac{\mathrm{b}}{2}\right.\left.+f_1{\left(\frac{b}{r}\right)}^3\right]\cos 2\theta$$

(21)

$$u_{\theta \mathrm{m}}=\frac{b}{4{\mu }_{\mathrm{m}}}\left[c_1\left({\eta }_{\mathrm{m}}+3\right){\left(\frac{r}{b}\right)}^3-d_1\frac{r}{b}-e_1\left({\eta }_{\mathrm{m}}-1\right)\frac{b}{r}\right.\left.+f_1{\left(\frac{b}{r}\right)}^3\right]\sin 2\theta$$

(22)

In the area of aggregate inclusions, the calculation range is $r\le a$,

$$u_{\mathrm{rf}}=\frac{b}{4{\mu }_{\mathrm{f}}}\left[g_1\left({\eta }_{\mathrm{f}}-3\right){\left(\frac{r}{b}\right)}^3+h_1\frac{r}{b}\right]\cos 2\theta$$

(23)

$$u_{\theta f}=\frac{b}{4{\mu }_{\mathrm{f}}}\left[g_1\left({\eta }_{\mathrm{f}}+3\right){\left(\frac{r}{b}\right)}^3-h_1\frac{r}{b}\right]\sin 2\theta$$

(24)

where, $\eta =(3-4v),\hspace{1em}{\eta }_m=\left(3-4v_m\right),\hspace{1em}{\eta }_{\mathrm{f}}=\left(3-4v_{\mathrm{f}}\right)$.

In the formula, $\mu , {\mu }_{\mathrm{m}}, {\mu }_{\mathrm{f}}$ represent the shear modulus of the homogeneous medium regions, ITZ, and aggregate, respectively, and $\nu , {\nu }_{\mathrm{m}}, {\nu }_{\mathrm{f}}$ represent the Poisson’s ratios of each phase.

When $r=a$, according to the displacement equilibrium condition,

$$h_1-d_1+4e_1{\left(\frac{b}{a}\right)}^2+3f_1{\left(\frac{b}{a}\right)}^4=0$$

(25)

$$g_1-c_1+e_1{\left(\frac{b}{a}\right)}^4+f_1{\left(\frac{b}{a}\right)}^6=0$$

(26)

According to the stress equilibrium conditions,

$$c_1\left[{\mu }_{\mathrm{f}}\left({\eta }_{\mathrm{m}}-3\right)-{\mu }_{\mathrm{m}}\left({\eta }_{\mathrm{f}}+3\right)\right]-e_1{\left(\frac{b}{a}\right)}^4\left[{\mu }_{\mathrm{f}}\left({\eta }_{\mathrm{m}}-1\right)-{\mu }_{\mathrm{m}}\left({\eta }_{\mathrm{f}}-1\right)\right]-d_1{\left(\frac{b}{a}\right)}^2\left({\mu }_{\mathrm{f}}-{\mu }_{\mathrm{m}}\right)+f_1{\left(\frac{b}{a}\right)}^6\left({\mu }_{\mathrm{f}}+{\mu }_{\mathrm{m}}{\eta }_{\mathrm{f}}\right)=0$$

(27)

$$c_1\left[{\mu }_{\mathrm{f}}\left({\eta }_{\mathrm{m}}-3\right)-{\mu }_{\mathrm{m}}\left({\eta }_{\mathrm{f}}-3\right)\right]+e_1{\left(\frac{b}{a}\right)}^4\left[{\mu }_{\mathrm{f}}\left({\eta }_{\mathrm{m}}+1\right)+{\mu }_{\mathrm{m}}\left({\eta }_{\mathrm{f}}+1\right)\right]+d_1{\left(\frac{b}{a}\right)}^2\left({\mu }_{\mathrm{f}}-{\mu }_{\mathrm{m}}\right)+f_1{\left(\frac{b}{a}\right)}^6\left({\mu }_{\mathrm{f}}+{\mu }_{\mathrm{m}}{\eta }_{\mathrm{f}}\right)=0$$

(28)

When $r=b$, according to the displacement balance condition,

$$2-4a_1-3b_1-d_1+4e_1+3f_1=0$$

(29)

$$2+2a_1+3b_1+6c_1-d_1-2e_1-3f_1=0$$

(30)

According to the stress equilibrium conditions,

$${\mu }_{\mathrm{m}}\left[-2-(\eta -1)a_1+b_1\right]-\mu \left[c_1\left({\eta }_{\mathrm{m}}+3\right)-d_1-f_1\left({\eta }_{\mathrm{m}}-1\right)+f_1\right]=0$$

(31)

$${\mu }_{\mathrm{m}}\left[2+(\eta +1)a_1+b_1\right]-\mu \left[c_1\left({\eta }_{\mathrm{m}}-3\right)+d_1+f_1\left({\eta }_{\mathrm{m}}+1\right)+f_1\right]=0$$

(32)

According to Eshelby’s theory, for a homogeneous medium containing inclusion, the strain energy is determined to be

$$U=U_0-\frac{1}{2}{{\displaystyle \int }}_L\left(T_{\mathrm{i}}^0{u}_{\mathrm{ie}}-T_{\mathrm{ie}}{u}_{\mathrm{i}}^0\right)dL$$

(33)

where $U_0$ is the strain energy of the homogeneous medium without inclusions, L is the surface of the inclusions, and the force and displacement in the medium without inclusions are $T_{\mathrm{i}}^0$ and $u_{\mathrm{i}}^0$. The force and displacement in the medium with inclusions are $T_{\mathrm{ie}}$ and $u_{\mathrm{ie}}$, respectively. Due to energy equivalence,

$$U=U_0$$

(34)

Assuming $dL=bd\theta ,\theta \in [0,2\pi ]$, it can be obtained that,

$${\int }_0^{2\pi }{\left[{\sigma }_r^0{u}_{re}+{\tau }_{r\theta }^0{u}_{\theta e}-{\sigma }_{re}{u}_r^0-{\tau }_{r\theta e}{u}_{\theta }^0\right]}_{r=b}bd\theta =0$$

(35)

In this formula,

$${\sigma }_r^0=\cos 2\theta ,\hspace{1em}{\tau }_{r\theta }^0=-\sin 2\theta$$

(36)

$$u_r^0=\frac{r}{2{\mu }_0}\cos 2\theta ,\hspace{1em}{u}_{\theta }^0=\frac{-r}{2{\mu }_0}\sin 2\theta$$

(37)

$${\sigma }_{re}=\left[1-2a_1{\left(\frac{b}{r}\right)}^2-\frac{3}{2}{b}_1{\left(\frac{b}{r}\right)}^4\right]\cos 2\theta$$

(38)

$${\tau }_{r\theta e}=-\left[1+a_1{\left(\frac{b}{r}\right)}^2+\frac{3}{2}{b}_1{\left(\frac{b}{r}\right)}^4\right]\sin 2\theta$$

(39)

Substituting Equations (19), (20), (37), (39) and (40) into Equation (36), it can be inferred that $\frac{0.5\pi a_1{b}^2(\eta +1)}{{\mu }_0}=0$, which leads to

$$a_1=0$$

(40)

Returning the result to the formula and omitting the complex simplification process, the control equation for the effective shear modulus can be obtained as follows:

$${\left({\mu }_0/{\mu }_{\mathrm{m}}\right)}^{2}A+\left({\mu }_0/{\mu }_{\mathrm{m}}\right)B+C=0$$

(41)

The volume fraction of aggregate inclusions is $c={(a/b)}^2$, in the equation,

$$A=3c{(1-c)}^2\left({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}-1\right)\left({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}+{\eta }_{\mathrm{f}}\right)+\left[{\mu }_{\mathrm{r}}/{\mu }_{\mathrm{m}}{\eta }_{\mathrm{m}}+{\eta }_{\mathrm{r}}{\eta }_m-\left({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}{\eta }_{\mathrm{m}}-{\eta }_{\mathrm{r}}\right)c^3\right]\times \left[{\eta }_{\mathrm{m}}c\left({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}-1\right)-\left({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}{\eta }_{\mathrm{m}}+1\right)\right]$$

(42)

$$\begin{array}{l}B=-6c{(1-c)}^2({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}-1)({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}+{\eta }_{\mathrm{f}})+\left[\left({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}\right){\eta }_{\mathrm{m}}+\left({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}-1\right)c+1\right]\left[\left({\eta }_{\mathrm{m}}-1\right)\left({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}+{\eta }_{\mathrm{f}}\right)-2c^3\left({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}{\eta }_{\mathrm{m}}-{\eta }_{\mathrm{f}}\right)\right]\\ +\left({\eta }_{\mathrm{m}}-1\right)c({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}-1)\left[{\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}{\eta }_{\mathrm{m}}+{\eta }_{\mathrm{f}}+\left({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}-1\right)c^3\right]\end{array}$$

(43)

$$C=3c{(1-c)}^2\left({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}-1\right)\left({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}+{\eta }_{\mathrm{f}}\right)+\left[\left({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}\right){\eta }_{\mathrm{m}}+\left({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}-1\right)c+1\right]\left[{\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}+{\eta }_{\mathrm{f}}+\left({\mu }_{\mathrm{f}}/{\mu }_{\mathrm{m}}{\eta }_{\mathrm{m}}-{\eta }_{\mathrm{f}}\right)c^3\right]$$

(44)

Based on the above conditions, the effective shear modulus $\mu$ of the three-phase sphere can be obtained. Assuming that the aggregate inclusions, ITZ layer, and mortar are connected in series, the total strain ${\epsilon }_0$ is the sum of the transverse strain ${\epsilon }_1$ of the cement slurry phase, ITZ layer ${\epsilon }_2$, and aggregate ${\epsilon }_3$. With the volume fractions $f_1$, $f_2$, and $f_3$ of each phase as weighting factors, it can be concluded that,

$${\epsilon }_0=f_1{\epsilon }_1+f_2{\epsilon }_2+f_3{\epsilon }_3$$

(45)

Assuming that each phase in concrete undergoes proportional strain in the axial direction, the effective Poisson’s ratio of the three-phase sphere is

$$v_0=f_{1}v+f_2{v}_{\mathrm{m}}+f_3{v}_{\mathrm{f}}$$

(46)

According to the conversion formula for elastic modulus, the effective elastic modulus of a three-phase sphere is

$$E_0=\frac{{\mu }_0}{2(1+{\nu }_0)}$$

(47)

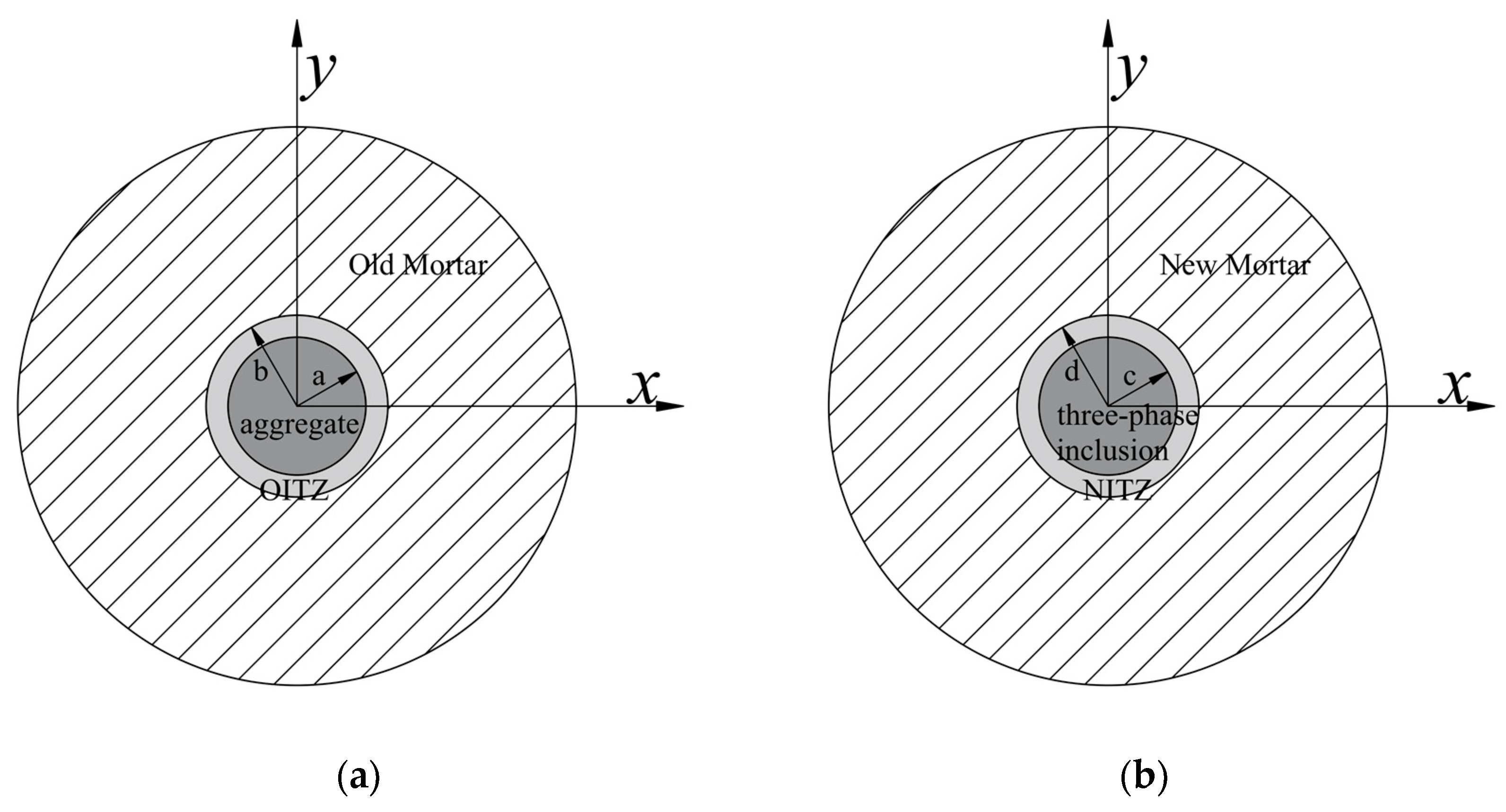
2.1.3. Superimposed Three-Phase Sphere and Mori–Tanaka Method

As mentioned earlier, we conducted a theoretical analysis of RC using multiphase inclusion theory. However, due to the more complex structure of RC, there will be an additional layer of OM outside of NA. The three-phase sphere model can be extended to the five-phase sphere model, where NA, OITZ, and OM are treated as new inclusions, NITZ between OM and NM is treated as a new matrix, and NM is treated as a homogeneous medium. According to the previous formula, inclusion is the recycled aggregate. This method can calculate the bulk modulus ${\mu }_{\mathrm{RA}}$ and Poisson’s ratio ${\nu }_{\mathrm{RA}}$ of recycled aggregate by using the shear module ${\mu }_{\mathrm{A}}$, ${\mu }_{\mathrm{OITZ}}$, ${\mu }_{\mathrm{OM}}$ and volume fractions $f_{\mathrm{A}}$, $f_{\mathrm{OITZ}}$, $f_{\mathrm{OM}}$ of NA, OITZ, and OM. We calculated the bulk modulus ${\mu }_{\mathrm{F}}$ and Poisson’s ratio ${\nu }_{\mathrm{F}}$ of the five-phase sphere based on the shear moduli ${\mu }_{\mathrm{RA}}$, ${\mu }_{\mathrm{NITZ}}$, ${\mu }_{\mathrm{NM}}$, and volume fractions $f_{\mathrm{A}}$, $f_{\mathrm{OITZ}}$, and $f_{\mathrm{OM}}$ of the recycled aggregates, NITZ, and NM in the five-phase sphere. The five-phase sphere obtained on this basis happens to be the new inclusion part, and the matrix surrounding it is a larger range of the new mortar. This type of problem can be solved through the Mori–Tanaka theory. Assuming that there is a perfect combination between components with general elastic anisotropy behavior, the particle phase is composed of elliptical particles with the same shape but different sizes, which can be aligned in space or have random directions. Firstly, the homogeneous boundary conditions for displacement and traction are defined as

$$\mathit{u}(S)={\mathit{\epsilon }}^0\mathit{x},{\mathit{\sigma }}_n(S)={\mathit{\sigma }}^0\mathit{n}$$

(48)

where $\mathit{u}$ and ${\mathit{\sigma }}_n$, respectively, represent displacement and external force vectors, S represents the outer surface of the composite material, ${\mathit{\epsilon }}^0$ and ${\mathit{\sigma }}^0$ represent constant strain and stress tensors, respectively, $\mathit{x}$ is the directional tensor, $\mathit{n}$ represents the external normal of surface S. This set of boundary conditions can be used to define the stiffness and flexibility tensors of effective composite media [22].

According to the above equation,

$$\overline{\mathit{\epsilon }}=v_1{\overline{\mathit{\epsilon }}}^{(1)}+v_2\left\{{\overline{\mathit{\epsilon }}}^{(2)}\right\}={\mathit{\epsilon }}^0$$

(49)

$$\overline{\mathit{\sigma }}=v_1{\overline{\mathit{\sigma }}}^{(1)}+v_2\left\{{\overline{\mathit{\sigma }}}^{(2)}\right\}={\mathit{\sigma }}^0$$

(50)

where ${\overline{\mathit{\epsilon }}}^{(2)}$ and ${\overline{\mathit{\sigma }}}^{(2)}$, respectively, represent the average strain and stress tensors related to the direction in typical single inclusions, while curly braces represent the average values of all possible directions. ${\overline{\mathit{\epsilon }}}^{(1)}$ and ${\overline{\mathit{\sigma }}}^{(1)}$ is the average quantity in the matrix, $v_i$ (I = 1, 2, where 1 represents the matrix and 2 represents the inclusion phase) represents the volume fraction, and $\overline{\mathit{\epsilon }}$ and $\overline{\mathit{\sigma }}$ represent the overall average strain and stress tensor, respectively.

The effective stiffness tensor ${\mathit{L}}^{\ast }$ and flexibility tensor ${\mathit{M}}^{\ast }$ are defined as

$$\overline{\mathit{\sigma }}={\mathit{L}}^{\ast }\overline{\mathit{\epsilon }},\overline{\mathit{\epsilon }}={\mathit{M}}^{\ast }\overline{\mathit{\sigma }}$$

(51)

$${\mathit{L}}^{\ast }={\mathit{L}}_1+v_2\left\{\left({\mathit{L}}_2-{\mathit{L}}_1\right)\mathit{A}\right\}$$

(52)

$${\mathit{M}}^{\ast }={\mathit{M}}_1+v_2\left\{\left({\mathit{M}}_2-{\mathit{M}}_1\right)\mathit{B}\right\}$$

(53)

where ${\mathit{L}}_i$ and ${\mathit{M}}_i$ (I = 1, 2) are the stiffness and flexibility tensors of each phase, respectively, and the direction-dependent tensor (also known as the “concentration factor” [22]), $\mathit{A}$ and $\mathit{B}$ are defined as

$${\overline{\mathit{\epsilon }}}^{(2)}=\mathit{A}{\mathit{\epsilon }}^0,{\overline{\mathit{\sigma }}}^{(2)}=\mathit{B}{\mathit{\sigma }}^0$$

(54)

Based on the Eshelby tensor solution in the previous text, similar results to the dilution approximation are obtained. The approximation is achieved by embedding a single particle in the entire matrix medium, because the strain field of the ellipsoidal inclusion embedded in the infinite domain is uniform after being processed by Equation (17). Therefore, in the dilution approximation, $\mathit{A}$ and $\mathit{B}$ are given by the following equation:

$${\mathit{A}}^{(\mathrm{dil})}=\mathit{T}\mathbf{,}{\mathit{B}}^{(\mathrm{dil})}=\mathit{W}$$

(55)

$$\mathit{T}={\left[\mathit{I}+\mathit{S}{\mathit{L}}_1^{-1}\left({\mathit{L}}_2-{\mathit{L}}_1\right)\right]}^{-1}$$

(56)

$$\mathit{W}={\mathit{L}}_2\mathit{T}{\mathit{M}}_1$$

(57)

where $\mathit{I}$ is a fourth-order unit tensor, $\mathit{S}$ represents a fourth-order Eshelby tensor. Under the same boundary conditions, the Mori–Tanaka method uses different approximation methods to handle $\mathit{A}$ and $\mathit{B}$. Firstly, the fourth-order direction-dependent tensors $\mathit{G}$ and $\mathit{H}$ are defined as follows:

$${\overline{\mathit{\epsilon }}}^{(2)}=\mathit{G}{\overline{\mathit{\epsilon }}}^{(1)},{\overline{\mathit{\sigma }}}^{(2)}=\mathit{H}{\overline{\mathit{\sigma }}}^{(1)}$$

(58)

Using the same method, use $\mathit{G}$ and $\mathit{H}$ to represent $\mathit{A}$ and $\mathit{B}$, respectively, as shown below,

$$\mathit{B}=\mathit{H}{\left[v_1\mathit{I}+v_2\left\{\mathit{H}\right\}\right]}^{-1}$$

(59)

$$\mathit{A}=\mathit{G}{\left[v_1\mathit{I}+v_2\left\{\mathit{G}\right\}\right]}^{-1}$$

(60)

By solving $\mathit{G}$ and $\mathit{H}$, ${\mathit{L}}^{\ast }$ and ${\mathit{M}}^{\ast }$ can be determined separately. Then, we approximate the setting,

$$\mathit{G}=\mathit{T},\mathit{H}=\mathit{W}$$

(61)

$${\overline{\mathit{\epsilon }}}^{(1)}={\mathit{\epsilon }}^0+{\tilde{\mathit{\epsilon }}}^{(1)},{\overline{\mathit{\epsilon }}}^{(2)}={\mathit{\epsilon }}^0+{\tilde{\mathit{\epsilon }}}^{(1)}+{\tilde{\mathit{\epsilon }}}^{(2)}$$

(62)

where ${\mathit{\epsilon }}^0$ is the constant strain at infinity, ${\tilde{\mathit{\epsilon }}}^{(1)}$ is the average perturbation strain in the matrix due to the presence of all inclusions, ${\tilde{\mathit{\epsilon }}}^{(2)}$ is the disturbance part of typical inclusions relative to the matrix. Based on the previous deduction,

$${\mathit{L}}_1\left({\mathit{\epsilon }}^0+{\tilde{\mathit{\epsilon }}}^{(1)}+{\tilde{\mathit{\epsilon }}}^{(2)}-{\mathit{\epsilon }}^{\ast }\right)={\mathit{L}}_2\left({\mathit{\epsilon }}^0+{\tilde{\mathit{\epsilon }}}^{(1)}+{\tilde{\mathit{\epsilon }}}^{(2)}\right)$$

(63)

$${\mathit{\epsilon }}^{\ast }={\mathit{S}}^{-1}{\tilde{\mathit{\epsilon }}}^{(2)}$$

(64)

The above formula covers the concepts of intrinsic strain and equivalent inclusion in Mori–Tanaka theory, and this method can accurately predict ${\mathit{L}}^{\ast }$ and ${\mathit{M}}^{\ast }$,

$${\mathit{L}}^{\ast }={\mathit{L}}_1+v_2\left\{\left({\mathit{L}}_2-{\mathit{L}}_1\right)T\right\}{\left[v_1\mathit{I}+v_2\left\{\mathit{T}\right\}\right]}^{-1}$$

(65)

$${\mathit{M}}^{\ast }={\mathit{M}}_1+v_2\left\{\left({\mathit{M}}_2-{\mathit{M}}_1\right)\mathit{W}\right\}{\left[v_1\mathit{I}+v_2\left\{\mathit{W}\right\}\right]}^{-1}$$

(66)

With the +direction of the Mori–Tanaka method, this study inserted the four-phase sphere model as an inclusion into the new mortar matrix, as illustrated in Figure 4b, and combined with Boucher’s [23] previous proof of the self-consistency of this method, only the material stiffness characteristics need to be considered. This method considers the new mortar and four-phase sphere as a two-phase composite material composed of a matrix with isotropic components and spherical inclusions. Therefore, the overall behavior of the material is isotropic and characterized by bulk modulus ${\kappa }_{\alpha }^{*}$ and shear modulus ${\mu }_{\alpha }^{*}$.

Firstly, simplify Equation (65) as follows:

$$\left({\kappa }_{\alpha }^{*}-{\kappa }_{\mathrm{NM}}\right)/\left({\kappa }_{\mathrm{F}}-{\kappa }_{\mathrm{NM}}\right)=f_{\mathrm{F}}\alpha {\left[\left(1-f_{\mathrm{F}}\right)+f_{\mathrm{F}}\alpha \right]}^{-1}$$

(67)

$$\left({\mu }_{\alpha }^{*}-{\mu }_{\mathrm{NM}}\right)/\left({\mu }_{\mathrm{F}}-{\mu }_{\mathrm{NM}}\right)=f_{\mathrm{F}}\beta {\left[\left(1-f_{\mathrm{F}}\right)+f_{\mathrm{F}}\beta \right]}^{-1}$$

(68)

where ${\kappa }_{\mathrm{F}}$ and ${\kappa }_{\mathrm{NM}}$ are the bulk moduli of the inclusion phase and matrix, ${\mu }_{\mathrm{F}}$ and ${\mu }_{\mathrm{NM}}$ are the shear moduli of the inclusion phase and matrix, $f_{\mathrm{F}}$ and $f_{\mathrm{NM}}$ are the volume fractions of the inclusion phase and matrix, respectively, and $\alpha$ and $\beta$ are the remaining scalars of the tensor $\mathit{T}$, given by the following equation [23]:

$$\alpha =\frac{1}{3}{T}_{rrpp},\beta =\frac{1}{5}\left(T_{rprp}-\frac{1}{3}{T}_{rrpp}\right)$$

(69)

The main factor affecting $\alpha$ and $\beta$ is the aspect ratio of ellipsoidal inclusions.

For spherical inclusions,

$${\alpha }_{\mathrm{s}1}=\frac{\left({\kappa }_{\mathrm{NM}}+\frac{4}{3}{\mu }_{\mathrm{NM}}\right)}{\left({\kappa }_{\mathrm{F}}+\frac{4}{3}{\mu }_{\mathrm{NM}}\right)},\hspace{1em}{\beta }_{\mathrm{s}1}=\frac{\left({\mu }_{\mathrm{NM}}+q_{\alpha }^{*}\right)}{\left({\mu }_{\mathrm{F}}+q_{\alpha }^{*}\right)}$$

(70)

$$q_{\alpha }^{*}={\mu }_{\mathrm{NM}}\left(9{\kappa }_{\mathrm{NM}}+8{\mu }_{\mathrm{NM}}\right)/6\left({\kappa }_{\mathrm{NM}}+2{\mu }_{\mathrm{NM}}\right)$$

(71)

Using these parameters, the bulk modulus and shear modulus of composite materials with spherical inclusions can be calculated using the following equation,

$$\left({\kappa }_{\alpha }^{*}-{\kappa }_{\mathrm{NM}}\right)/\left({\kappa }_{\mathrm{F}}-{\kappa }_{\mathrm{NM}}\right)=f_{\mathrm{F}}{\left\{1+f_{\mathrm{NM}}\left[\left(1/{\alpha }_{\mathrm{s}1}\right)-1\right]\right\}}^{-1}=f_{\mathrm{F}}{\left\{1+f_{\mathrm{NM}}\left[\left({\kappa }_{\mathrm{F}}-{\kappa }_{\mathrm{NM}}\right)/\left({\kappa }_{\mathrm{NM}}+\frac{4}{3}{\mu }_{\mathrm{NM}}\right)\right]\right\}}^{-1}$$

(72)

$$\left({\mu }_{\alpha }^{*}-{\mu }_{NM}\right)/\left({\mu }_{\mathrm{F}}-{\mu }_{\mathrm{NM}}\right)=f_{\mathrm{F}}{\left\{1+f_{\mathrm{NM}}\left[\left(1/{\beta }_{\mathrm{s}1}\right)-1\right]\right\}}^{-1}=f_{\mathrm{F}}{\left\{1+f_{\mathrm{NM}}\left[\left({\mu }_{\mathrm{F}}-{\mu }_{\mathrm{NM}}\right)/\left({\mu }_{\mathrm{NM}}+q_{\alpha }^{*}\right)\right]\right\}}^{-1}$$

(73)

According to the conversion formula, the elastic modulus $E_{\alpha }$ and Poisson’s ratio ${\nu }_{\alpha }$ of RC are obtained as

$${\nu }_{\alpha }=\frac{3{\kappa }_{\alpha }^{*}-2{\mu }_{\alpha }^{*}}{2(3{\kappa }_{\alpha }^{*}+{\mu }_{\alpha }^{*})}$$

(74)

$$E_{\alpha }=3{\kappa }_{\alpha }^{*}(1-2{\nu }_{\alpha })$$

(75)

2.2. Material Mechanical Performance Testing

To verify the theoretical results more accurately, mechanical performance tests were conducted. NA was cut into rectangular test blocks of 100 mm × 50 mm × 20 mm, and NM and OM boards of 100 mm × 50 mm × 20 mm were poured. The raw materials used for the mortar included P∙O.42.5 cement, tap water, and river sand, with a particle size of less than 2.36 mm. The mix ratio of old mortar in recycled aggregate is m_cement:m_water:m_sand = 1:0.55:3; the mix ratio of the new mortar is m_cement:m_water:m_sand = 1:0.42:3. The density of NA and mortars were tested separately in a completely dry state, and then the compressive strength, elastic modulus, and Poisson’s ratio of NA, OM, and NM were obtained with an electronic universal testing machine, as shown in

Table 1. Physical properties of various phase materials.

Material Type	Density (kg/m−3)	Elastic Modulus (GPa)	Compressive Strength (MPa)	Poisson’s Ratio
NA	2560	75.0	170.1	0.360
OM	2209	23.0	29.60	0.176
NM	2180	24.0	33.32	0.238
OITZ	1657	17.3	—	0.132
NITZ	1635	18	—	0.179

. According to reference [24], the mechanical properties of OITZ and NITZ were calculated proportionally.

2.3. Theoretical Calculation Example of RC

2.3.1. Simplified RC

In order to study the effect of old mortar attached to natural aggregates on the performance of RC, Xiao et al. [25,26,27] proposed the concept of model recycled concrete and conducted in-depth research on it. RC has been similarly simplified by regularizing the geometric shapes of NA and OM.

2.3.2. Theoretical Examples

This research adopts the model of RC as the research objective, and uses its experimental design for theoretical calculations. The model has a square area with a cross section of 100 mm × 100 mm, where NA is a circular surface with a diameter of 12 mm, as shown in Figure 5.

Due to the inconsistency in the ITZ between concrete and its aggregates poured in different mix proportions or curing environments, research on ITZ in macroscopic compression tests is often affected by the inability to accurately determine the ITZ range, making it difficult to define the impact of its mechanical properties on the overall performance. Therefore, after determining the material parameters required for theoretical research, researchers studied the mechanical properties of ITZ and its thickness on the mechanical properties of the RC model.

Due to the inconsistent effects of elastic modulus and Poisson’s ratio on mechanical properties in the calculation, these two parameters will be considered separately. This study takes the thickness of ITZ as a variable and theoretically assumes that ITZ is a uniform thin-walled shell, to study the effects of changing the value range of ITZ thickness from 0.05 mm to 0.15 mm on the elastic modulus and Poisson’s ratio of RC in the model.

Firstly, it is assumed that the different ITZ thicknesses of the two phases in the five-phase sphere are the same. According to the data in Figure 6, as the thickness of the new and old mortar ITZ changes simultaneously, the elastic modulus and Poisson’s ratio of ITZ are nonlinearly correlated with their overall mechanical properties. As shown in Figure 6a, although the ITZ Poisson’s ratio of both new and old mortar gradually increases with the increase of the reduction coefficient, the overall elastic modulus decreases under the synergistic effect of the five-phase sphere. This phenomenon reveals that the mechanical properties of RC do not solely rely on the so-called “strong matrix strong inclusion” bonding method, but should pay more attention to the fit between the matrix and inclusions. This suggests that when selecting concrete material combinations, researchers should look for materials with similar Poisson’s ratios to optimize the synergistic effect.

As shown in Figure 6b, although the influence of ITZ on the overall Poisson’s ratio is not linear, it also indicates that the influence of ITZ on the Poisson’s ratio is relatively small. In the calculation, the shear modulus and bulk modulus decrease simultaneously, so the Poisson’s ratio shows an upward trend under slight influence. However, it actually conforms to the research law, and there is not a direct correlation between the elastic modulus and Poisson’s ratio. The upward trend of Poisson’s ratio is precisely a manifestation of mesoscopic calculations. The main reason for this phenomenon is that theoretical research typically assumes that all materials are uniformly isotropic, and under external stress, the synergistic effect between different phases is not significantly affected. Unlike simply changing the Poisson’s ratio, Figure 6c,d show that the increase in elastic modulus has a significant impact on the overall mechanical properties of the concrete. In the initial stage, the improvement of the overall elastic modulus has a positive impact on material properties, which is consistent with general understanding. However, the increase in ITZ thickness also means that the volume proportion of ITZ in the material increases, which leads to a downward trend in the overall elastic modulus. This phenomenon emphasizes that when evaluating and designing composite materials such as RC, not only the physical properties of individual phases should be considered, but also the interactions and compatibility between the phases. Especially in the special region of ITZ, although it has a very small proportion in volume, the impact of changes in its physical properties on the overall material performance cannot be ignored.

The interface between different materials is inevitably different, and the thickness of the interface formed during pouring between NA and OM, and OM and NM may be affected as a result. In this study, only one of OITZ or NITZ is changed to analyze the influence of its thickness on the overall mechanical properties.

Figure 7a–d provide a detailed chart showing the individual changes in OITZ thickness when NITZ is determined to be 0.1 mm. Comparing Figure 7a–d, the information conveyed by the two figures is basically similar. From specific data analysis, when the elastic modulus decreases, the Poisson’s ratio still shows an upward trend, which is consistent with the data obtained earlier. Research has shown that there is no direct relationship between elastic modulus and Poisson’s ratio at this scale. The elastic modulus is gradually reduced as the thickness of ITZ increases, and then increases in another aspect due to the continuous increase of the reduction coefficient. This validates the crucial assumption of the geometric characteristics of ITZ in theoretical research. Under the condition of only adjusting the thickness of OITZ, the proportion of interface inclusions increases compared to when adjusting both ITZs simultaneously, and the discontinuity phenomenon is more significant. According to the theory of multiphase inclusions, this increased interface discontinuity has a negative impact on the overall mechanical properties of the material. Due to the weaker material properties in the interface region compared to the main material, an increase in interface thickness means an increase in the proportion of weak regions. The increase in thickness of a single interface leads to the phenomenon of stress concentration in this area, weakening the load-bearing capacity and deformation capacity of the structure, thereby causing a decline in the macroscopic mechanical properties. Especially when adjusting the OITZ separately, the discontinuity of the mesoscale becomes particularly evident, which causes the overall mechanical response of the material to be misaligned.

Figure 7e–h provide a detailed chart showing the individual changes in OITZ thickness when NITZ is determined to be 0.1 mm. As shown in the figure, the increase in Poisson’s ratio under different reduction rates has the same effect on the overall mechanical properties of the material as before, which is a decrease in elastic modulus and an increase in Poisson’s ratio. At the same time, it can be found that for a single change in Poisson’s ratio, the change in NITZ thickness only has a minimal impact on the overall elastic modulus and Poisson’s ratio, and is not as significant as the impact of OITZ on the overall structure, and there will be no significant fluctuations. In this research, it is generally believed that NITZ forms at the contact interface between new and old materials, which often have good structural integrity and fewer pores. Therefore, their interface transition zone is relatively new and their performance is more uniform. The material properties of NITZ, located between NM and recycled aggregate, are closer to that of new mortar as the main matrix material. The compatibility between NITZ and the main material is higher, and the stress distribution at the interface is more uniform, avoiding obvious stress concentration. Therefore, in terms of mechanical properties, the impact of NITZ on the overall material performance is relatively small. From Figure 7g,h, it can be seen that although there are similar numerical changes as before, the impact of changes in the overall elastic modulus of NITZ under different reduction rates on the overall elastic modulus and Poisson’s ratio is minimal. As the thickness increases, the increase in numerical elastic modulus and Poisson’s ratio is more significant within a very small range, indicating that when the material is relatively compatible, the overall mechanical properties of the material will be more stable.

3. Numerical Simulation

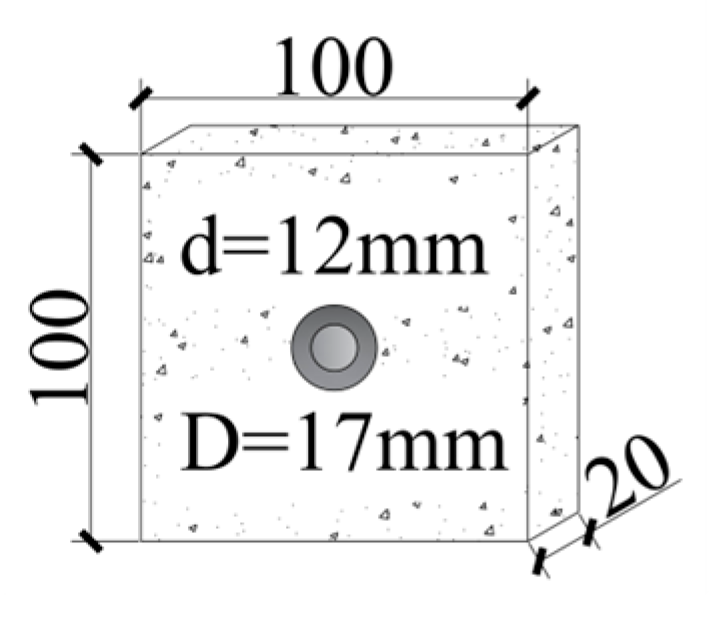
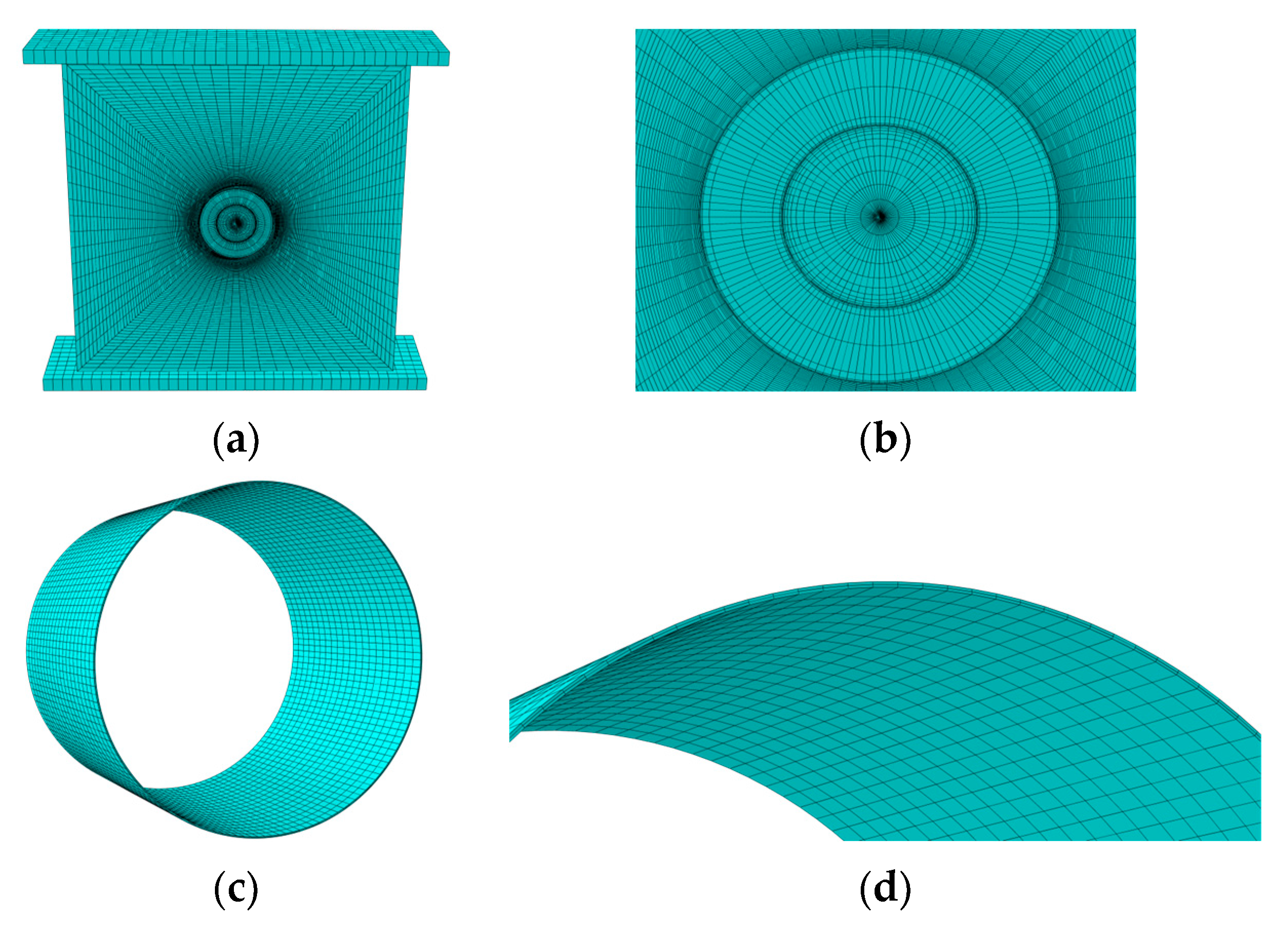
3.1. Model Establishment

A solid element model of RC plate components, measuring 20 mm × 100 mm × 100 mm, was established using finite element simulation software ABAQUS 2020. The interior comprised recycled aggregates and their corresponding ITZ, constituting five-phase materials, as shown in Figure 8. The NA radius was 6 mm, the OM layer thickness was 5 mm, and different ITZ regions were taken as 0.1 mm. To simulate the real compression test, this numerical study adds an upper loading steel plate and a lower bottom steel plate, and adds a small amount of friction force at the contact point of the loading plate to increase authenticity. The grid division form is shown in Figure 8. In order to grasp the local characteristics of the stress field and accurately calculate the maximum stress value, a denser grid is used in the stress concentration area of the aggregate, and a two-layer grid is used in ITZ to increase the calculation accuracy. In areas of low-stress concentration, sparser grids are employed to reduce the number of grids, and scaling factors are omitted from the calculations. As shown in

Table 2. Physical properties of various phase materials in ABAQUS.

Material Type	Elastic Modulus (GPa)	Poisson’s Ratio
NA	75.0	0.360
OM	23.0	0.176
NM	24.0	0.238
OITZ	17.3	0.132
NITZ	18	0.179

, the materials’ mechanical properties were all obtained from Section 1 for each phase material. The OITZ and NITZ material parameters are converted using the same reduction factor as previously mentioned. The pressure application method adopts the displacement loading method.

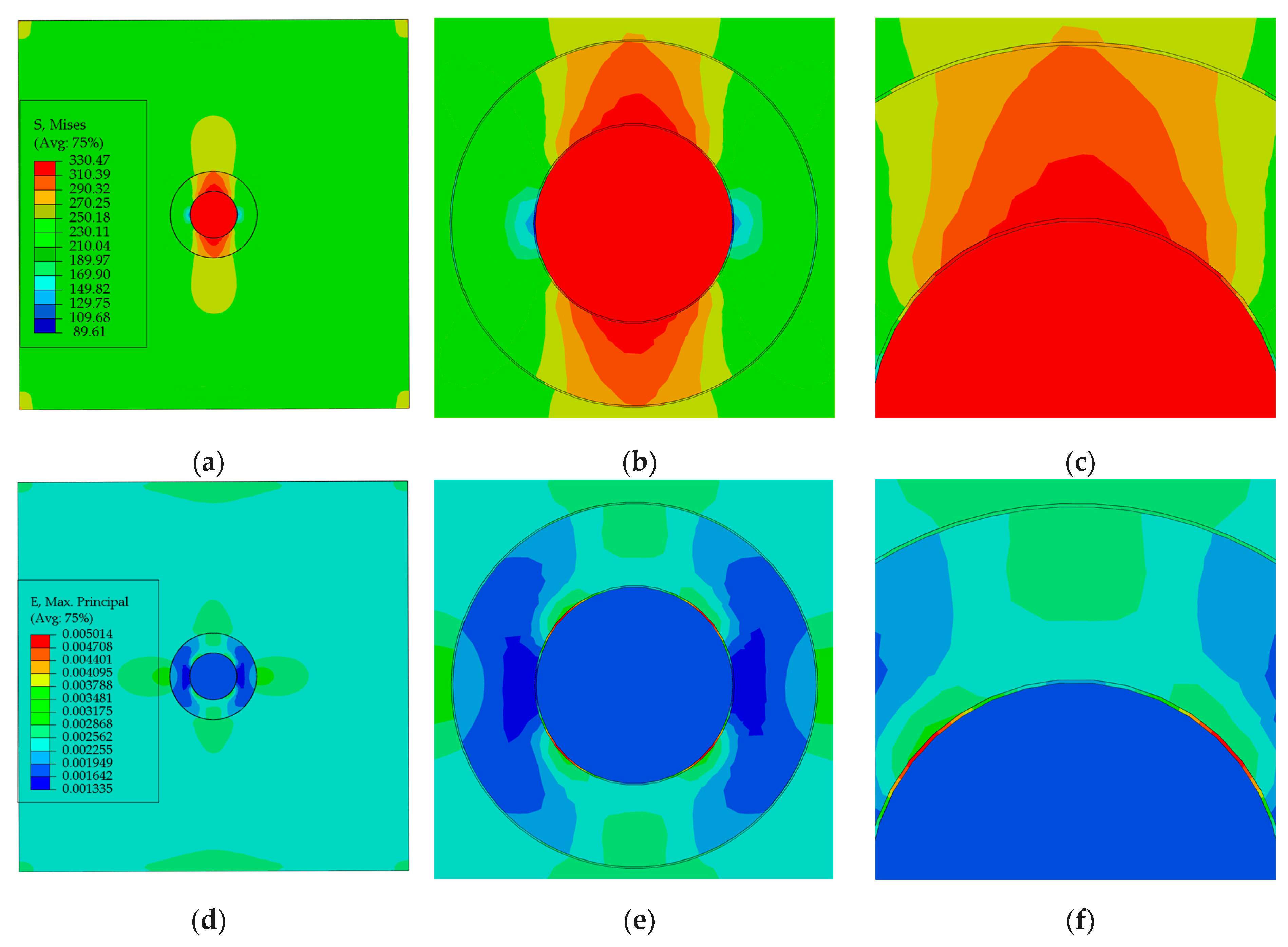
3.2. Stress Distribution Morphology and Analysis

By increasing the reduction rates of two different ITZs from 50% to 80% by 5%, the material properties were changed in terms of elastic modulus and Poisson’s ratio, respectively. A total of 14 sets of data were simulated and calculated. After finite element simulation displacement loading, due to the complete symmetry of all structures during modeling, the stress distribution morphology obtained through calculation presents an approximately completely symmetrical image, as shown in Figure 9, which is obtained at a reduction rate of 75%.

From the stress distribution morphology in Figure 9, it can be seen that, when the sample was subjected to a load, the stress was mainly concentrated near NA and spread vertically. The maximum stress passed through OITZ, and the larger stress also passed through OM and NITZ. This means that the stress is concentrated in the area with the worst mechanical performance. This area is highly likely to become the first position to be damaged, and initial failure will occur in the ITZ area where the yield point is first reached, and cracks will be generated along the vertical direction. By observing the strain distribution morphology, the areas with higher strain are mainly around the recycled aggregate and the compression area. Enlarge the recycled aggregate area, and the strain around OITZ is the highest, with the direction located at a 45° angle on the horizontal axis and symmetrically centered. Higher strains can cause the fragile OITZ to first damage during loading and cracks propagate along the area where they first appear.

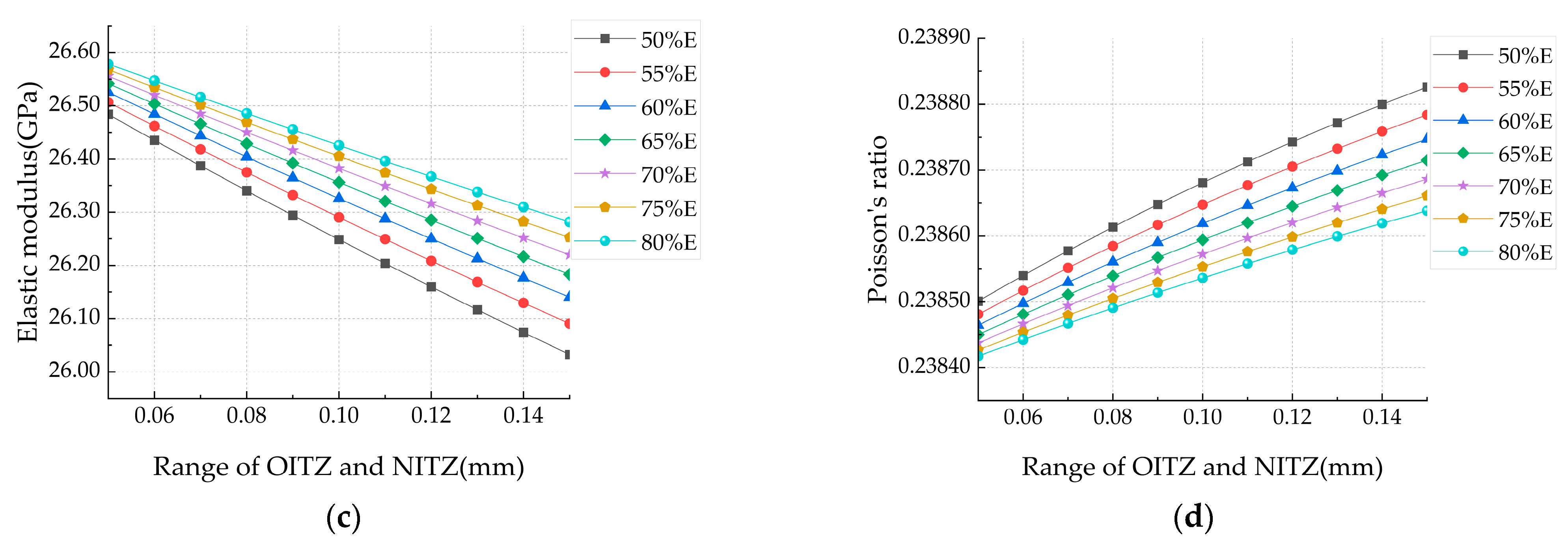
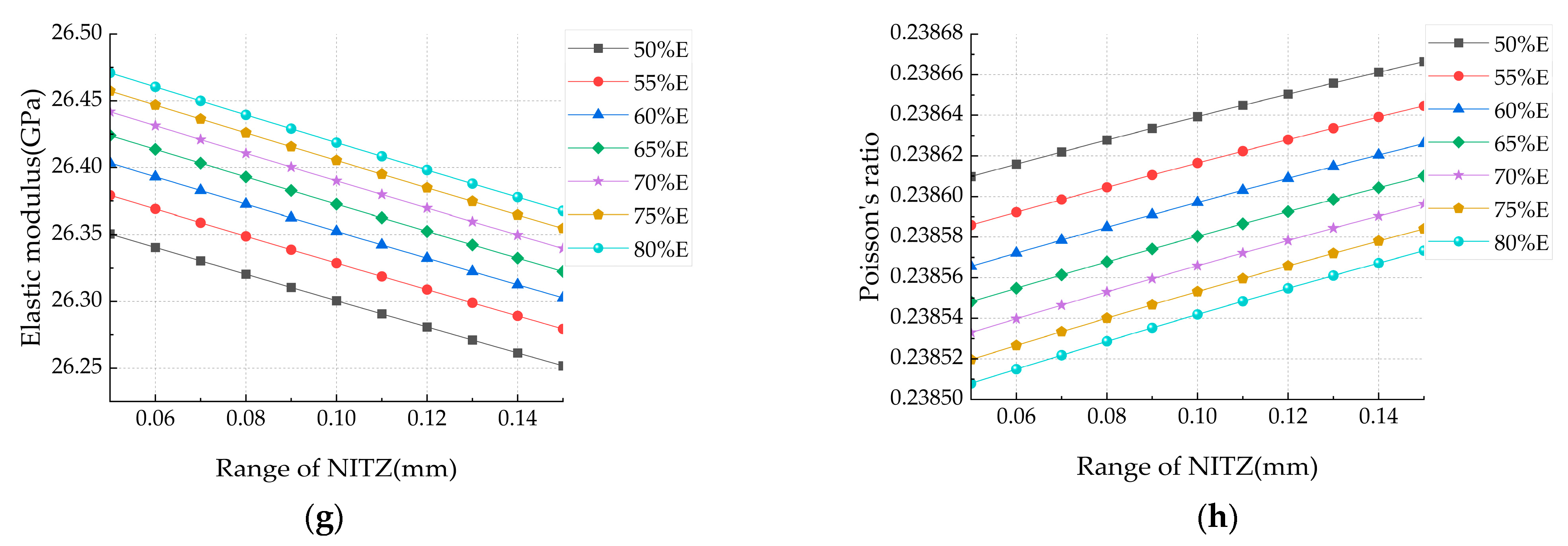
4. Discussion

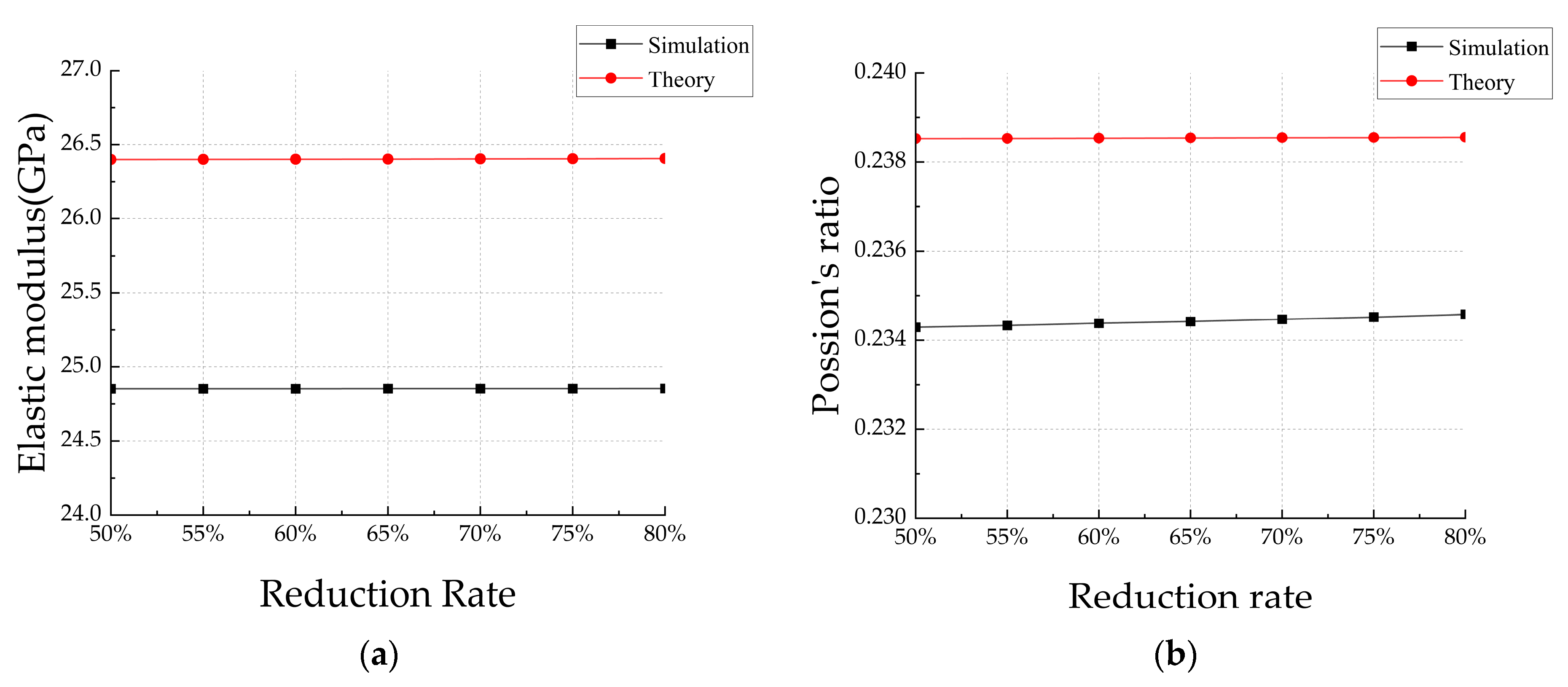
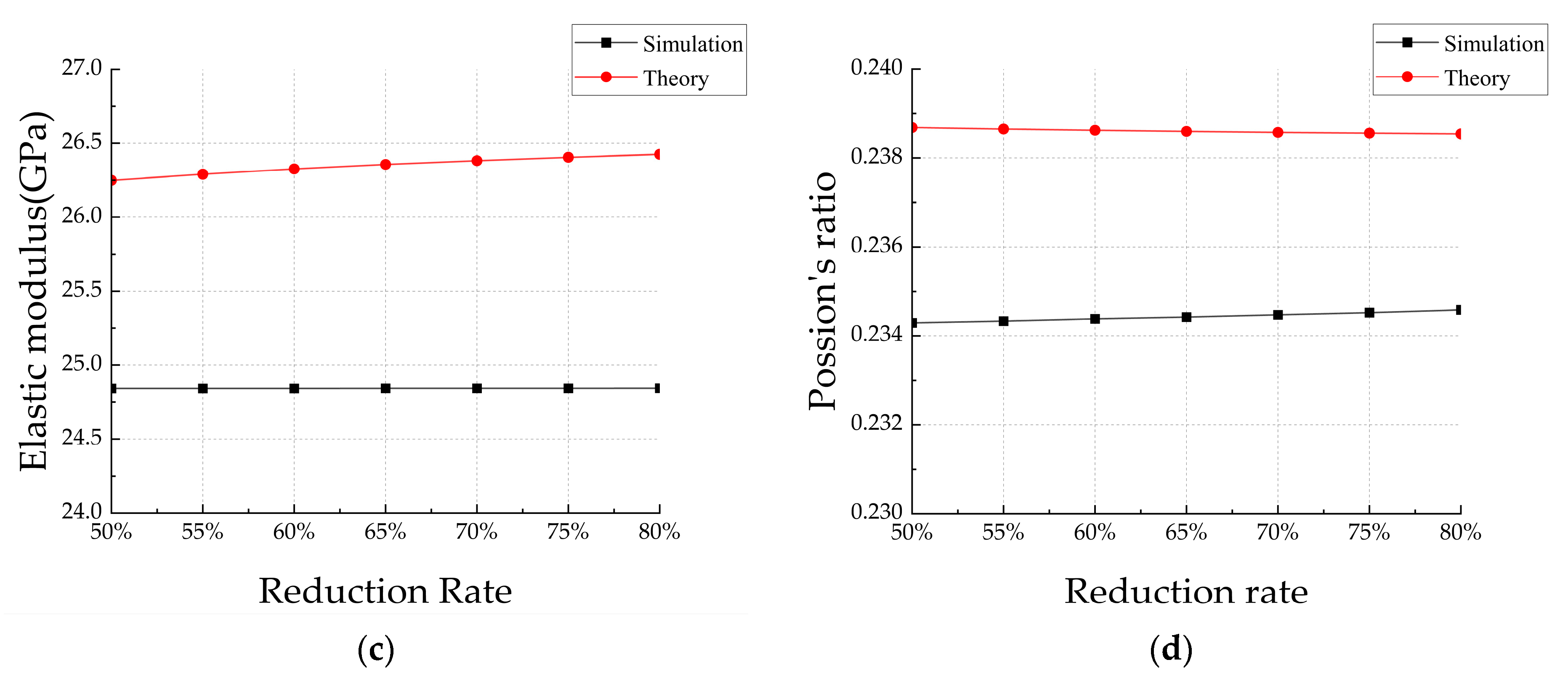
Comparison of Theoretical Analysis and Numerical Simulation Results

The focus of the research is whether the elastic modulus and Poisson’s ratio of RC can be effectively predicted through the theory of multiphase inclusions. The theoretical model considers the complex mesoscale of RC, especially the influence of different ITZ layers on the overall mechanical properties of the concrete. Theoretical calculations have shown that the predicted elastic modulus of RC is 26.4059 GPa and the predicted Poisson’s ratio is 0.2386. By comparison, the elastic modulus of RC obtained through finite element post processing is 24.8542 GPa, and the Poisson’s ratio is 0.2345, which is close to the theoretical prediction with errors of 6.24% and 1.75%, respectively. This indicates that the multiphase inclusion theory used can accurately predict the mechanical properties of RC, confirming the effectiveness of the theoretical model (

Table 3. Comparison between theoretical calculation and simulation results.

Result Type *	Elastic Modulus (GPa)	Poisson’s Ratio
RC theoretical results	26.4059	0.2386
RC simulation results	24.8542	0.2345
Absolute value of error rate (%)	6.24%	1.75%

* The ITZ thickness of the parameters in the table is 0.1 mm, and the reduction rate is 75%.

).

Although the error is indeed within a small range after calculation, it can be seen from Figure 10a–c that the trends of change in elastic modulus and Poisson’s ratio are relatively consistent. When the ITZ Poisson’s ratio is reduced, the error rate remains steady between 6% and 7%. Figure 10d is influenced by theoretical calculations, where minor variations in shear modulus and bulk modulus affect the trend of Poisson’s ratio changes. In fact, for the structure as a whole, minor fluctuations in Poisson’s ratio have a negligible impact on its mechanical properties. Additionally, it can be observed that the values calculated theoretically are always slightly higher than those obtained from numerical simulations, which may stem from inconsistencies in calculation accuracy, and the isotropic nature of materials in the finite element analysis. With displacement loading, the displacement between phases can generally achieve complete synergy. From the trend of the final prediction, the prediction results obtained by using the multiphase inclusion theory are more accurate than those obtained by using the finite element method in the elastic stage. During the elastic stage, the overall deformation trend of the specimen in the simulation is relatively stable. In the theory of multiphase inclusions, the weakening of the overall mechanical properties of ITZ is considered, as shown in Section 2. The theory accounts for the heterogeneity and complex interactions between different phases, including the ITZs, which are often challenging to model accurately through empirical methods alone.

5. Conclusions

This study examines the impact of ITZ on the mechanical behavior of RC. A comprehensive investigation using theoretical analysis and finite element simulation, focusing on the mechanical properties of RC with particular attention to the effects of different ITZs on the overall mechanical properties was conducted and the results are as follows:

(1)

This research is centered on the multiphase inclusion theory, which helps minimize errors stemming from simplified assumptions by utilizing precise theoretical calculations. RC is considered a multiphase composite material and details the interactions between different phases and their impacts on the overall properties of the material. The ITZ layer in the model plays a pivotal role in the mesoscale, significantly influencing the mechanical properties of the concrete. To accurately capture the characteristics of the recycled aggregate concrete, various mesoscale parameters are introduced, including different ITZ thicknesses and mechanical parameters, to predict the elastic modulus and Poisson’s ratio of RC. Based on the comparison of different ITZs in theory, it is suggested that the old mortar attached to RA should be removed as much as possible in practical application. In this way, the existence of OITZ is reduced to enhance the mechanical properties of RC.

(2)

Theoretical predictions are validated using the finite element method, maintaining consistency in parameters such as ITZ thickness. The results demonstrated that under identical conditions, the elastic modulus of RC is 26.4059 GPa, and the Poisson’s ratio is 0.2386. They closely align with those from the finite element simulation, which recorded an elastic modulus of 24.8542 GPa and a Poisson’s ratio of 0.2345, with errors controlled within 6.24% and 1.75%. This precision confirms the efficacy of multiphase inclusion theory in predicting the mechanical properties of composite materials and highlights the reliability of the inclusion theoretical model.

(3)

This study provides a scientific basis for the material design and performance optimization of RC, highlighting the significant value and application potential of theoretical research in the field of building materials. Future research will delve into the relationship between the mesoscale and macroscale properties of RC. By enhancing the theory of multiphase inclusions and improving the transition from microscale to macroscale analyses, we aim to extend this study beyond the elastic stage. The multiphase inclusion theory provides a detailed and accurate framework for predicting and optimizing the mechanical properties of recycled concrete. Although it has great potential for further computational research, it is clear that its updating requires complex models and hypotheses, as well as experimental verification of them. This approach will enable researchers to predict material strength and deepen the understanding of phase compatibility. Additionally, methods to enhance the strength of ITZ through the use of nanoscale materials continue to emerge in the future, and relying solely on microscopic experiments is not enough to fully demonstrate the macroscopic mechanical properties of materials, ongoing research on multiphase inclusion theory is expected to guide the selection of concrete materials and the optimization of ITZ layers in practical applications, enhancing the utilization efficiency of recycled materials in concrete.