Remaining Useful Life Prediction of Rolling Bearings Based on Deep Time–Frequency Synergistic Memory Neural Network
Abstract
1. Introduction
- Utilize the continuous wavelet transform to convert scalar vibration signals into 2D time–frequency feature maps.
- Automatically extract features from these time–frequency maps using a multi-layer convolutional neural network.
- Employ an improved inverted Transformer with a dynamic weighted attention mechanism to enhance the model’s performance by effectively capturing the global dependencies within the sequence data.
- Leverage a bidirectional long short-term memory (BiLSTM) network to capture the bidirectional dependencies of the time series, enabling the accurate prediction of the remaining lifespan of rolling bearings.
2. Methods
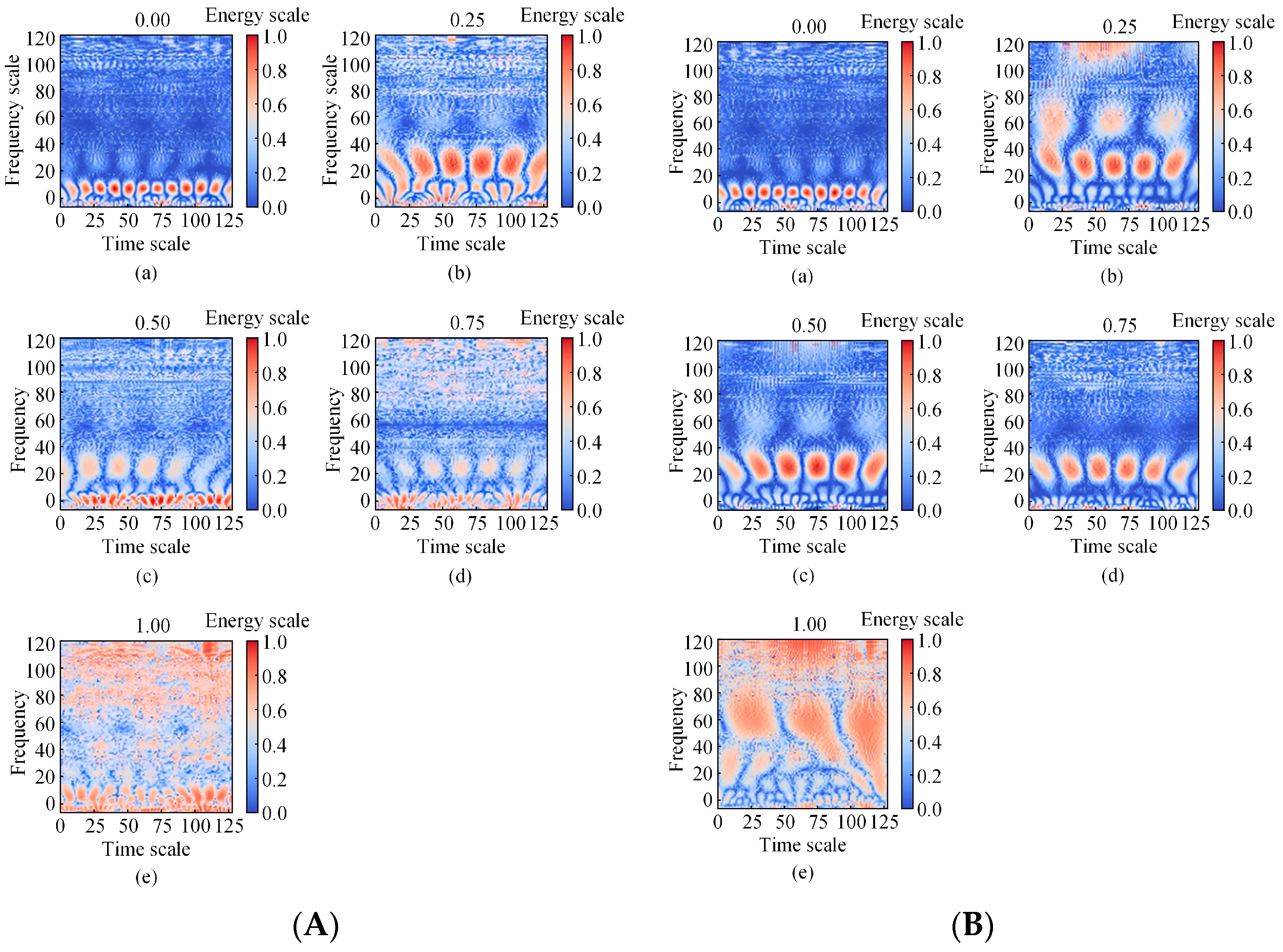
2.1. Continuous Wavelet Transform
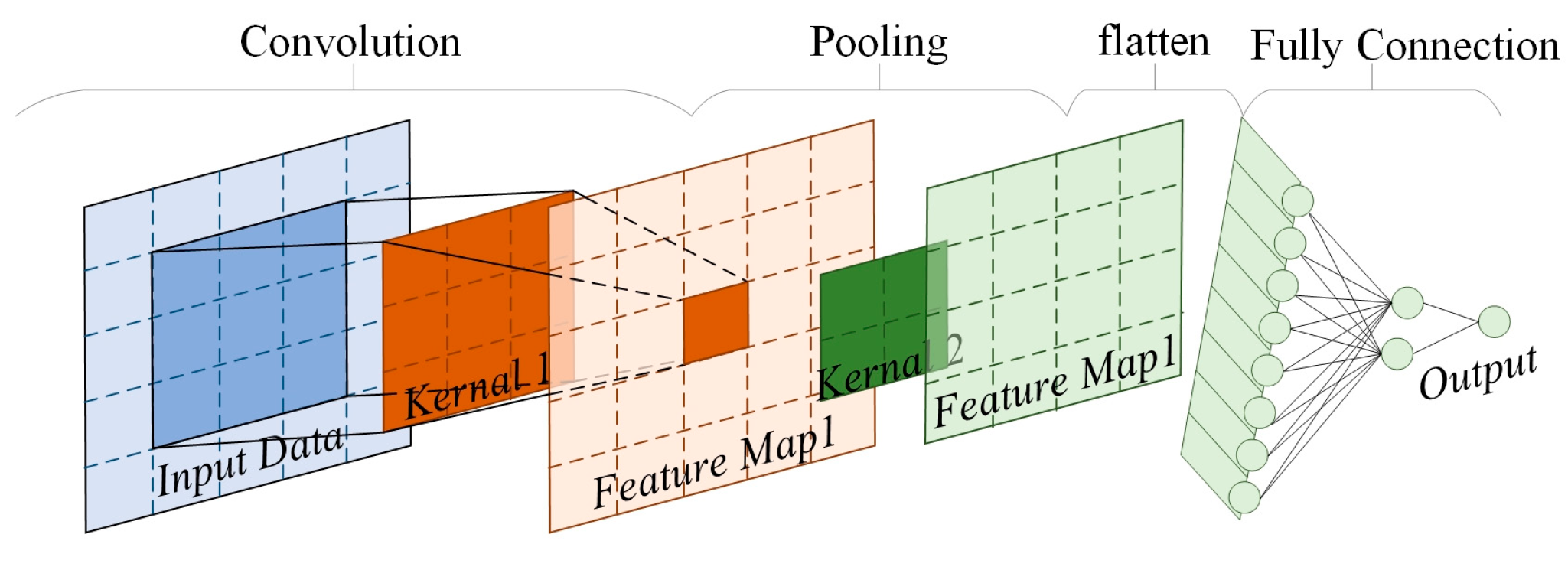
2.2. Convolutional Neural Network
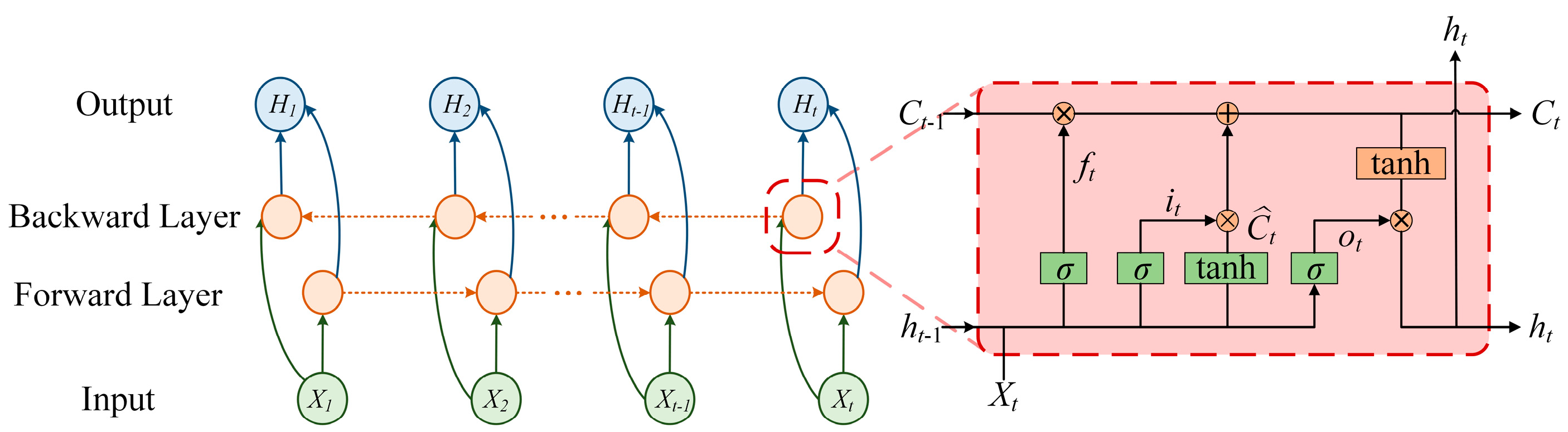
2.3. Bidirectional Long Short-Term Memory Network
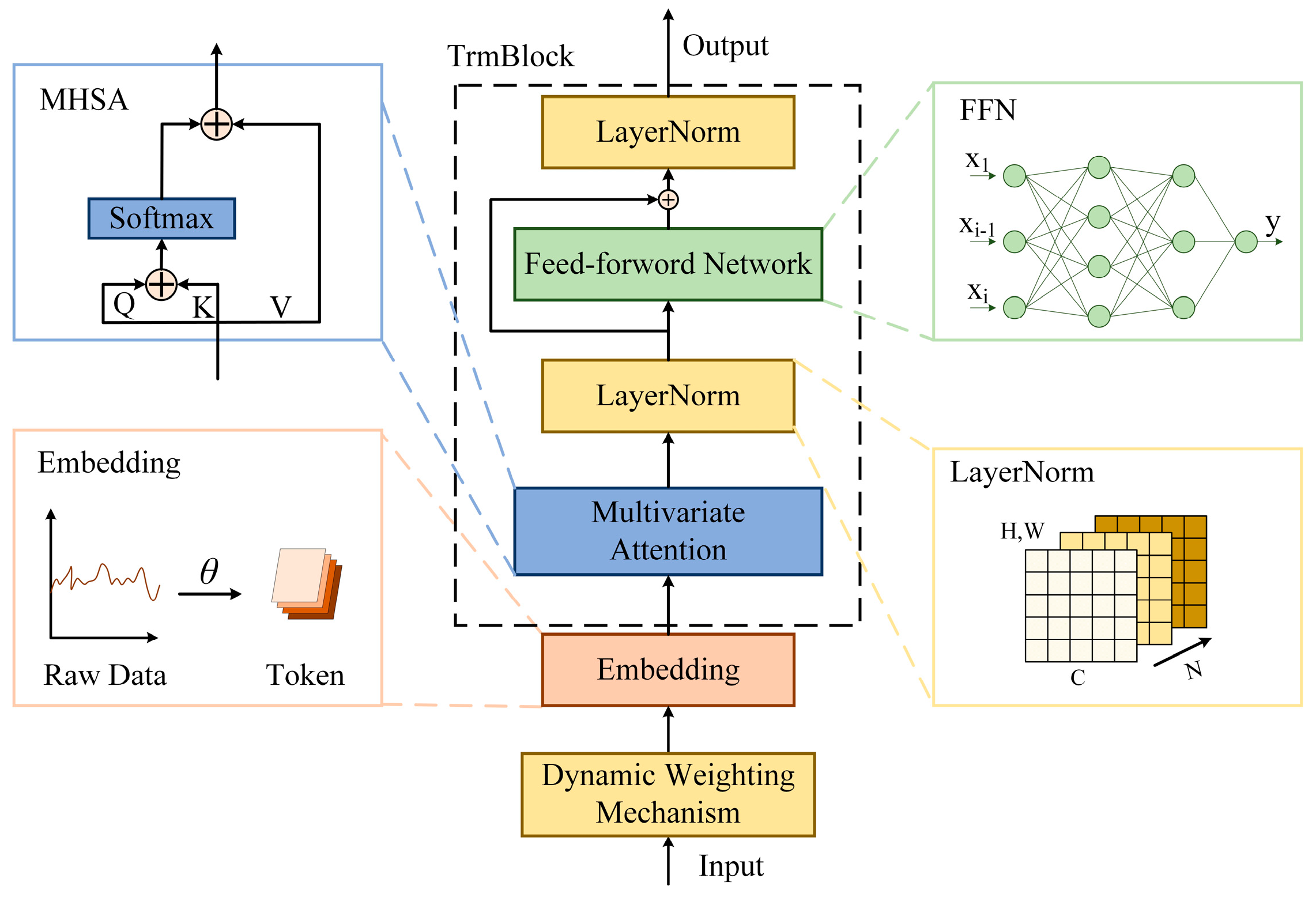
2.4. Optimized Inverted Transformer
2.4.1. Dynamic Weighting Mechanism
2.4.2. Multivariate Attention
2.4.3. Subsequent Module Design
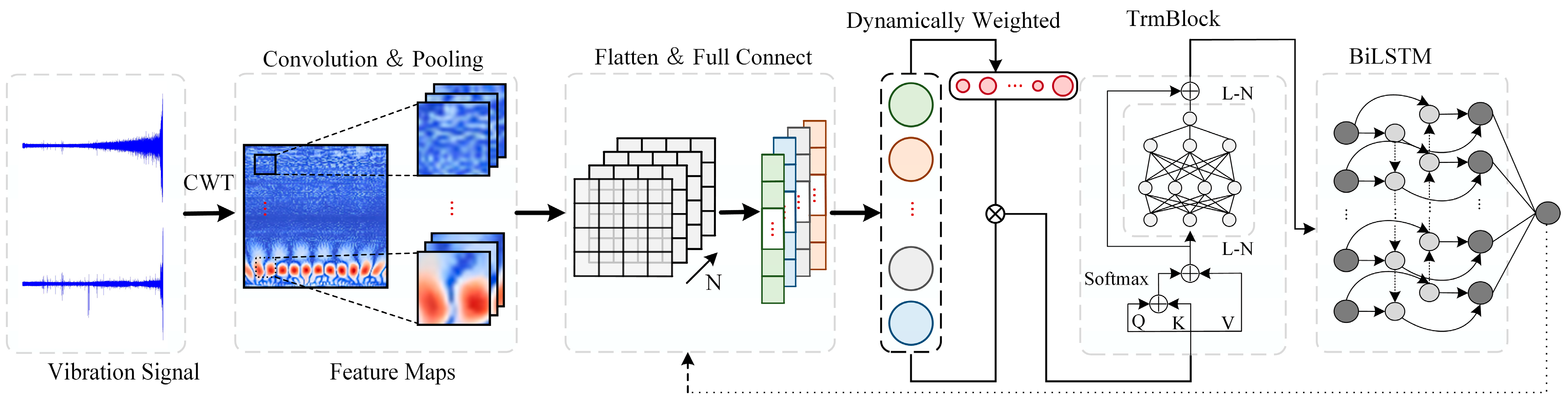
2.5. Model Composition
3. Simulation Case Verification
3.1. Test Data Presentation
3.2. Prediction Process
3.2.1. Data Preparation
3.2.2. Feature Engineering
3.2.3. Model Training
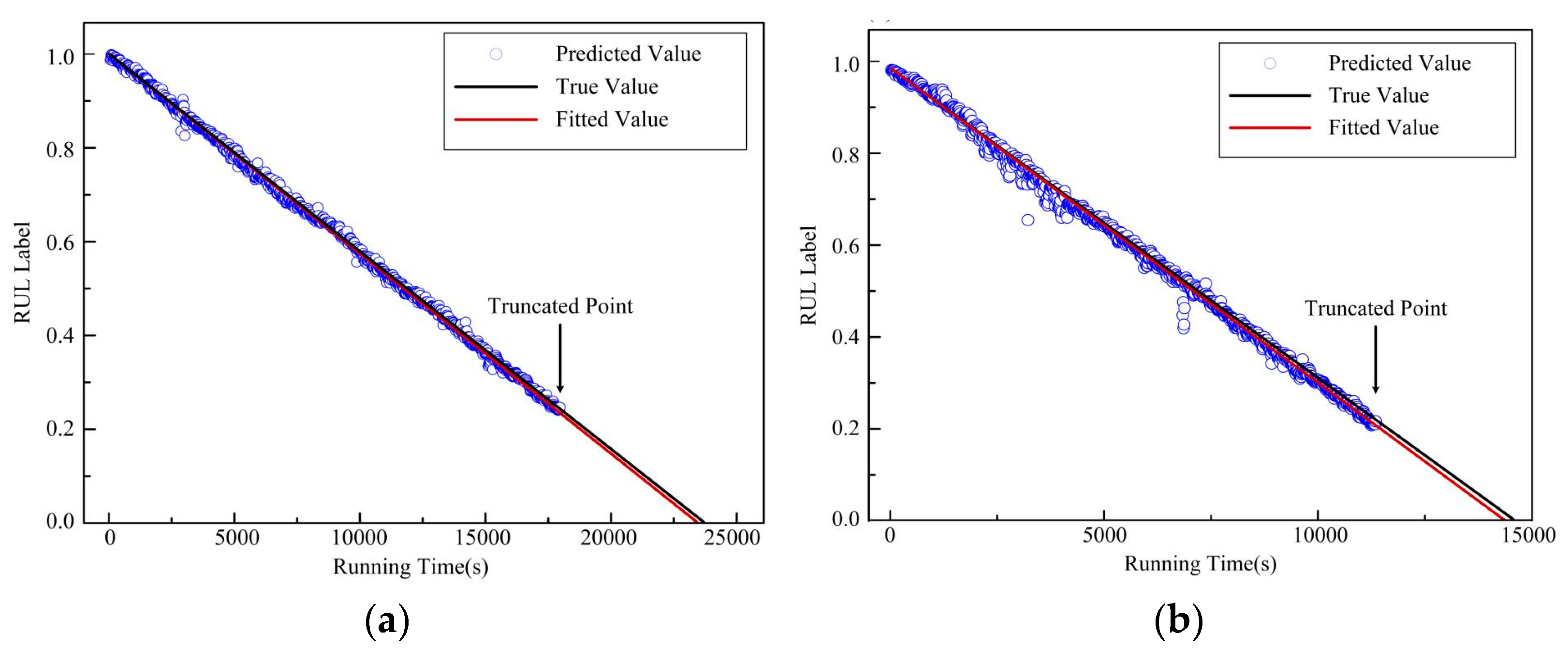
3.2.4. RUL Prediction
4. Results and Discussion
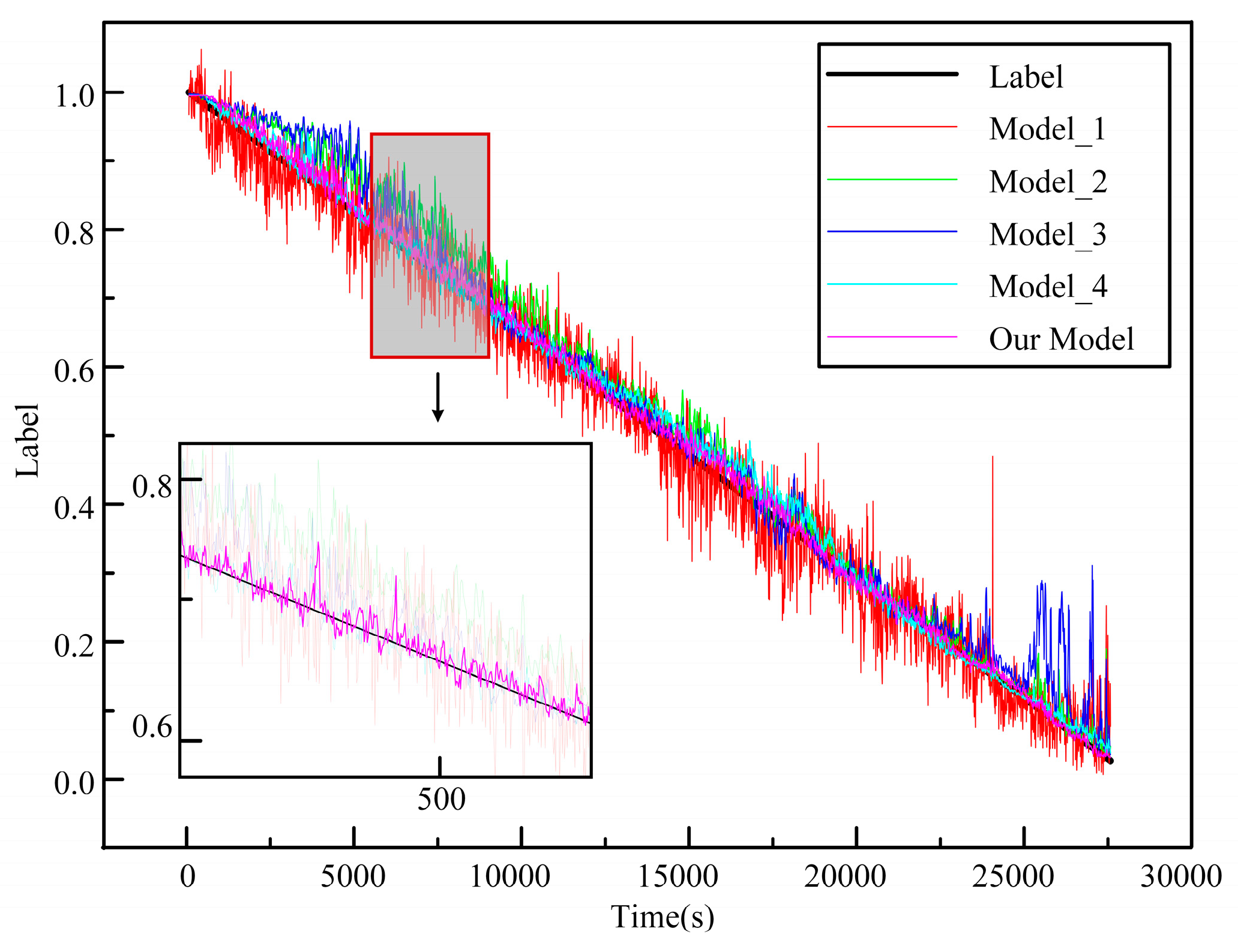
4.1. Evaluation of Model Early Prediction Ability
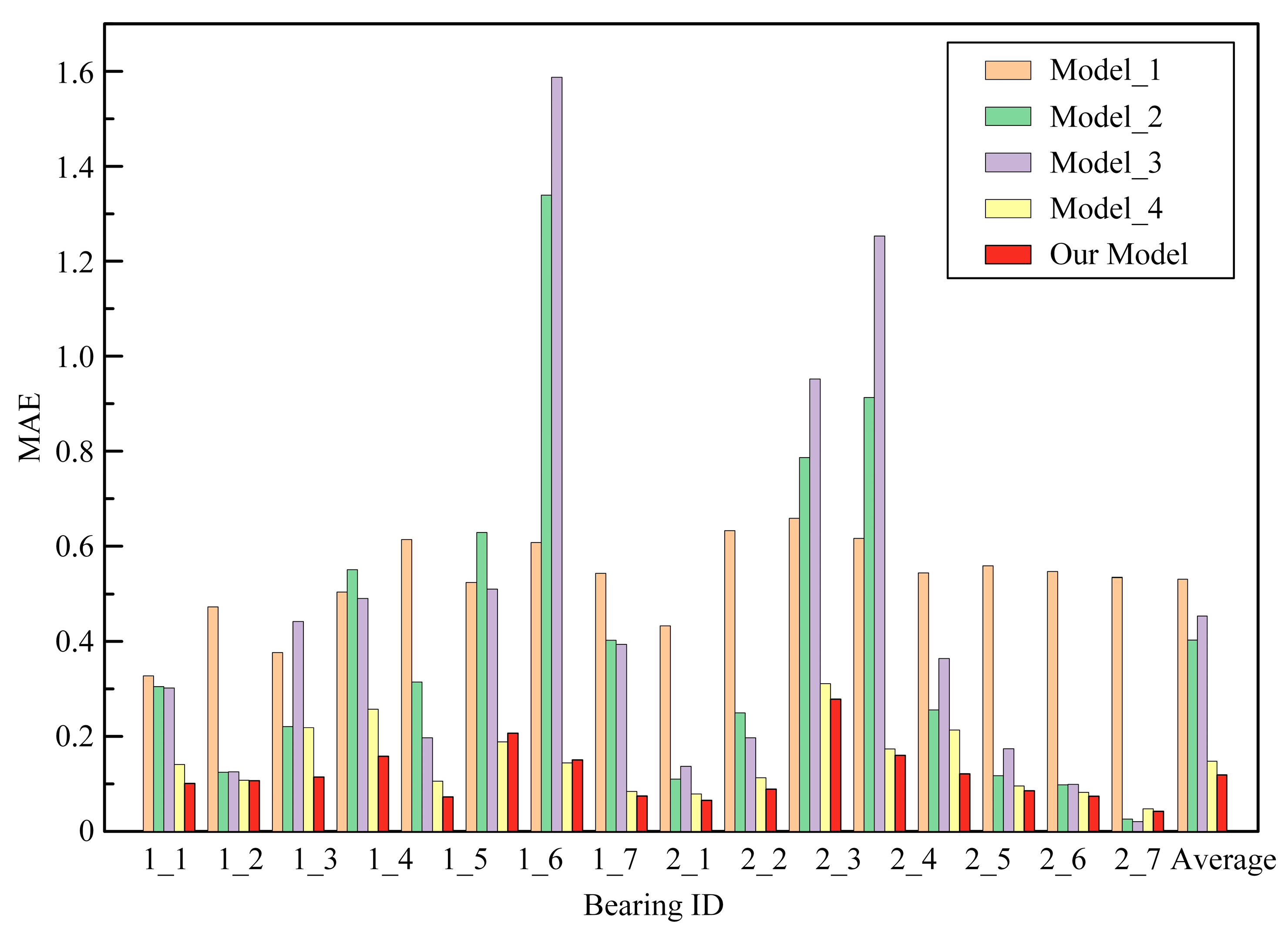
4.2. Comparative Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RUL | Remaining useful life |
| CWT | Continuous wavelet transform |
| CNN | Convolutional neural network |
| LSTM | Long short-term memory neural networks |
| BiLSTM | Bidirectional long short-term memory network |
| iTransformer | Inverted Transformer |
| FFN | Feed-forward network |
| DWM | Dynamic weighted mechanism |
| RNN | Recurrent neural network |
| MAE | Mean absolute error |
| MSE | Mean squared error |
| Er | Prediction error |
| WMA | Weighted moving average |
References
- Ma, M.; Zhang, X.; Tan, C.; Liu, P. Analysis of potential failure modes and failure mechanisms of aerospace components. Yanshan Univ. 2024, 38, 1–9. [Google Scholar] [CrossRef]
- Spreafico, C.; Russo, D.; Rizzi, C. A state-of-the-art review of FMEA/FMECA including patents. Comput. Sci. Rev. 2017, 25, 19–28. [Google Scholar] [CrossRef]
- Tandon, N.; Choudhury, A. A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings. Tribol. Int. 1999, 32, 469–480. [Google Scholar] [CrossRef]
- Zhe, N.; Yang, J.; Liu, W.; Chen, L. Application of KPCA and improved SVM in rolling bearing remaining life prediction. J. Mech. Eng. 2019, 43, 1–4+8. [Google Scholar] [CrossRef]
- Lei, Y.G.; Chen, W.; Li, N.P. Adaptive multi-core combined relevance vector machine prediction method and its application in remaining life prediction of mechanical equipment. Mech. Eng. 2016, 52, 87–93. [Google Scholar] [CrossRef]
- Zhang, M.; Yin, J.; Chen, W. Rolling bearing fault diagnosis based on time-frequency feature extraction and IBA-SVM. IEEE Access 2022, 10, 85641–85654. [Google Scholar] [CrossRef]
- Wang, X.; Han, Y.; Leung, V.C.M.; Niyato, D.; Yan, X.; Chen, X. Convergence of edge computing and deep learning: A comprehensive survey. IEEE Commun. Surv. Tutor. 2020, 22, 869–904. [Google Scholar] [CrossRef]
- Lu, B.; Liu, Z.; Wei, H.; Chen, L.; Zhang, H.; Li, X. A deep adversarial learning prognostics model for remaining useful life prediction of rolling bearings. IEEE Trans. Artif. Intell. 2021, 2, 329–340. [Google Scholar] [CrossRef]
- Ma, M.; Mao, Z. Deep-Convolution-Based LSTM Network for Remaining Useful Life Prediction. IEEE Trans. Ind. Informat. 2021, 17, 1658–1667. [Google Scholar] [CrossRef]
- Deng, L.F.; Li, W.; Yan, X.H. An intelligent hybrid deep learning model for rolling bearing remaining useful life prediction. Nondestruct. Test. Eval. 2024, 1, 1–28. [Google Scholar] [CrossRef]
- Xu, Z.F.; Jin, J.T.; Li, C. Fault diagnosis method of rolling bearings based on multi-scale convolutional neural networks. Vibration Shock 2021, 40, 212–220. [Google Scholar] [CrossRef]
- Meng, Z.; Dong, S.; Pan, X.; Wu, W.; He, K.; Liang, T.; Zhao, X. Fault diagnosis of rolling bearings based on improved convolutional neural networks. Comb. Mach. Autom. Process. Technol. 2020, 2, 79–83. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q. Deep learning-based remaining useful life estimation of bearings using multi-scale feature extraction. Reliab. Eng. Syst. Saf. 2019, 182, 208–218. [Google Scholar] [CrossRef]
- Akpudo, U.E.; Hur, J.W. A feature fusion-based prognostics approach for rolling element bearings. Mech. Sci. Technol. 2020, 34, 4025–4035. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Q.; Shu, Y.; Xiao, W.; Ma, W. Remaining useful life prediction for rolling bearings with a novel entropy-based health indicator and improved particle filter algorithm. IEEE Access 2023, 11, 3062–3079. [Google Scholar] [CrossRef]
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Lin, R.; Wang, H.; Xiong, M.; Hou, Z.; Che, C. Attention-based gate recurrent unit for remaining useful life prediction in prognostics. Appl. Soft Comput. 2023, 143, 110419. [Google Scholar] [CrossRef]
- Zhao, G.Q.; Jiang, P.; Lin, T.R. Intelligent rolling bearing remaining useful life prediction method based on CNN-BiLSTM network and attention mechanism. Mech. Electr. Eng. 2021, 38, 1253–1260. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, X.; Liu, S.; Yang, X.; Li, S. Rolling bearing residual useful life prediction model based on particle swarm optimization-optimized fusion of convolutional neural network and bidirectional long–short-term memory–multihead self-attention. J. Electron. 2024, 13, 2120. [Google Scholar] [CrossRef]
- Liu, C.Y.; Gryllias, K. Unsupervised domain adaptation based remaining useful life prediction of rolling element bearings. PHM Soc. Eur. Conf. 2020, 5, 10. [Google Scholar] [CrossRef]
- Li, P.; Liu, X.; Yang, Y. Remaining useful life prognostics of bearings based on a novel spatial graph-temporal convolution network. Sensors 2021, 21, 4217. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Xu, Z.; Zhao, S.; Zhao, J.; Fan, Y. Performance degradation prediction of rolling bearing based on temporal graph convolutional neural network. J. Mech. Sci. Technol. 2024, 38, 4019–4036. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, F.; Zhao, J.; Duan, Y.; Guo, X. Remaining useful life prediction of rolling bearing based on multi-domain mixed features and temporal convolutional networks. Appl. Sci. 2024, 14, 2354. [Google Scholar] [CrossRef]
- Zheng, G.; Li, Y.; Zhou, Z.; Yan, R. A remaining useful life prediction method of rolling bearings based on deep reinforcement learning. J. IEEE Internet Things 2024, 11, 22938–22949. [Google Scholar] [CrossRef]
- Morlet, J.; Arens, G.; Fourgeau, E.; Glard, D. Wave propagation and sampling theory; Part I, Complex signal and scattering in multilayered media. Geophysics 1982, 47, 203–221. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. ITRANSFORMER: Inverted transformers are effective for time series forecasting. arXiv 2023. [Google Scholar] [CrossRef]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Chebel-Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An experimental platform for bearings accelerated degradation tests. In Proceedings of the IEEE International Conference on Prognostics and Health Management, Denver, CO, USA, 18–21 June 2012. [Google Scholar]
- Chen, Y.; Peng, G.; Zhu, Z.; Li, S. A novel deep learning method based on attention mechanism for bearing remaining useful life prediction. Appl. Soft Comput. 2020, 86, 105919. [Google Scholar] [CrossRef]


| Algorithm of Model Steps |
|---|
| Input: T-F feature X ∈ ℝN×L×C×H×W |
| Output: RUL Tag Y ∈ ℝN×1 |
| 1. Reshape X to Xreshape ∈ ℝN×L×(C×H×W) |
| 2. Pass Xreshape through CNN Fcnn ← CNN_CWT_Encoder(Xreshape) |
| 3. Feed Fcnn into MLP to generate weights W = MLPθmlp(Fcnn), W ∈ ℝN×L |
| 4. Perform element-wise multiplication Fweighted ← Fcnn⊙W |
| 5. Reshape Fweighted to sequence format Fseq∈ℝN×L×128 |
| 6. Pass Fseq through Transformer Ftf ← TransformerEncoder(Fseq) |
| 7. Feed Ftf into bidirectional-LSTM Flstm ← BiLSTM(Ftf) |
| 8. Extract the final time step from Flstm and pass through FC Fout ← FC(Flstm[:, L−1, :]) |
| 9. Apply Sigmoid to Fout Y ← Sigmoid(Fout) |
| 10. Return Y |
| Conditions | C_1 | C_2 | C_3 |
|---|---|---|---|
| Speed (rpm) | 1800 | 1650 | 1500 |
| Force (N) | 4000 | 4200 | 5000 |
| Training set | Bearing 1_1 | Bearing 2_1 | Bearing 3_1 |
| Bearing 1_2 | Bearing 2_2 | Bearing 3_2 | |
| Validation set | Bearing 1_3 | Bearing 2_3 | Bearing 3_3 |
| Bearing 1_4 | Bearing 2_4 | ||
| Bearing 1_5 | Bearing 2_5 | ||
| Bearing 1_6 | Bearing 2_6 | ||
| Bearing 1_7 | Bearing 2_7 |
| Layer Type | Input Size (C, H, W) | Operation | Output Size (C, H, W) |
|---|---|---|---|
| Conv_1 | 2, 128, 128 | Kernel = 3 × 3; same padding | 16, 128, 128 |
| Maxpool_1 | 16, 128, 128 | Kernel = 2 × 2 | 16, 64, 64 |
| Conv_2 | 16, 64, 64 | Kernel = 3 × 3; same padding | 32, 64, 64 |
| Maxpool_2 | 32, 64, 64 | Kernel = 2 × 2 | 32, 32, 32 |
| Conv_3 | 32, 32, 32 | Kernel = 3 × 3; same padding | 64, 32, 32 |
| Maxpool_3 | 64, 32, 32 | Kernel = 2 × 2 | 64, 16, 16 |
| Conv_4 | 64, 16, 16 | Kernel = 3 × 3; same padding | 128, 16, 16 |
| Maxpool_4 | 128, 16, 16 | Kernel = 2 × 2 | 128, 8, 8 |
| Flatten | 128, 8, 8 | / | 8192 |
| Fc_1 | 8192 | Dropout = 0.5 | 256 |
| Fc_2 | 256 | Dropout = 0.2 | 128 |
| Bearing ID | Our Model (%) | CNN (%) | CNN-BiLSTM (%) | CNN-Attention [30] (%) |
|---|---|---|---|---|
| 1_3 | 0.92 | −2.18 | −0.87 | 7.62 |
| 1_4 | 1.88 | −4.07 | 4.50 | −157.71 |
| 1_5 | 0.20 | −7.69 | 0.21 | −72.57 |
| 1_6 | 0.69 | 4.15 | 6.06 | 0.93 |
| 1_7 | 1.51 | −6.94 | 45.42 | 85.99 |
| 2_3 | 0.20 | −5.51 | −1.22 | 81.24 |
| 2_4 | 4.49 | 9.20 | 17.86 | 9.04 |
| 2_5 | 1.51 | 6.11 | 29.58 | 28.19 |
| 2_6 | −0.69 | −4.08 | −0.15 | 24.92 |
| 2_7 | −3.41 | −5.12 | −3.88 | 19.06 |
| 1.55 | 5.50 | 10.98 | 40.67 |
| Bearing ID | Model_1 | Model_2 | Model_3 | Model_4 | Our Model |
|---|---|---|---|---|---|
| 1_1 | 0.9785 | 0.9823 | 0.975 | 0.9978 | 0.9979 |
| 1_2 | 0.9535 | 0.9969 | 0.9960 | 0.9978 | 0.9978 |
| 1_3 | 0.9707 | 0.9859 | 0.9581 | 0.9388 | 0.9964 |
| 1_4 | 0.9478 | 0.9074 | 0.9484 | 0.9506 | 0.9519 |
| 1_5 | 0.9141 | 0.9772 | 0.9919 | 0.9850 | 0.9982 |
| 1_6 | 0.9396 | 0.8937 | 0.9384 | 0.9430 | 0.9545 |
| 1_7 | 0.9168 | 0.5679 | 0.4501 | 0.9757 | 0.9914 |
| 2_1 | 0.9393 | 0.9209 | 0.9587 | 0.9989 | 0.9989 |
| 2_2 | 0.9633 | 0.9972 | 0.9862 | 0.9991 | 0.9991 |
| 2_3 | 0.9182 | 0.9836 | 0.9919 | 0.9310 | 0.9971 |
| 2_4 | 0.9075 | 0.8631 | 0.8132 | 0.9797 | 0.9310 |
| 0.9134 | 0.7974 | 0.6546 | 0.9905 | 0.9846 | |
| 0.9381 | 0.9852 | 0.9703 | 0.9387 | 0.9971 | |
| 0.9370 | 0.9966 | 0.9936 | 0.9978 | 0.9979 | |
| 0.9384 | 0.9182 | 0.9019 | 0.9732 | 0.9835 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, Q.; Wei, Q.; Wang, Y.; Liu, Y. Remaining Useful Life Prediction of Rolling Bearings Based on Deep Time–Frequency Synergistic Memory Neural Network. Coatings 2025, 15, 406. https://doi.org/10.3390/coatings15040406
Qu Q, Wei Q, Wang Y, Liu Y. Remaining Useful Life Prediction of Rolling Bearings Based on Deep Time–Frequency Synergistic Memory Neural Network. Coatings. 2025; 15(4):406. https://doi.org/10.3390/coatings15040406
Chicago/Turabian StyleQu, Qiaoqiao, Qiang Wei, Yufeng Wang, and Yuming Liu. 2025. "Remaining Useful Life Prediction of Rolling Bearings Based on Deep Time–Frequency Synergistic Memory Neural Network" Coatings 15, no. 4: 406. https://doi.org/10.3390/coatings15040406
APA StyleQu, Q., Wei, Q., Wang, Y., & Liu, Y. (2025). Remaining Useful Life Prediction of Rolling Bearings Based on Deep Time–Frequency Synergistic Memory Neural Network. Coatings, 15(4), 406. https://doi.org/10.3390/coatings15040406







