Numerical Examination of Particle and Substrate Oxide Layer Failure and Porosity Formation in Coatings Deposited Using Liquid Cold Spray
Abstract
1. Introduction
2. Numerical Methodology
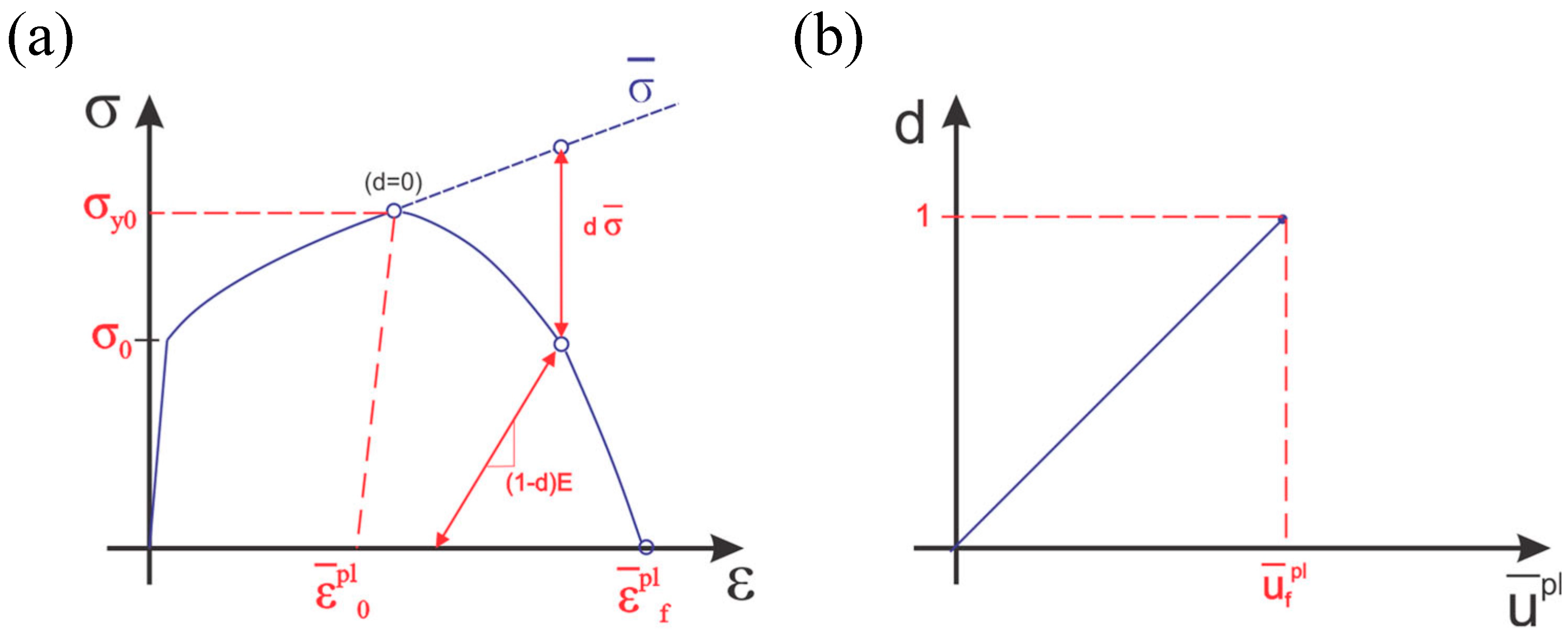
2.1. Mie–Grüneisen Equation of State and Johnson–Cook Plasticity Model
2.2. Johnson–Cook Damage Model
2.3. Finite Element Method
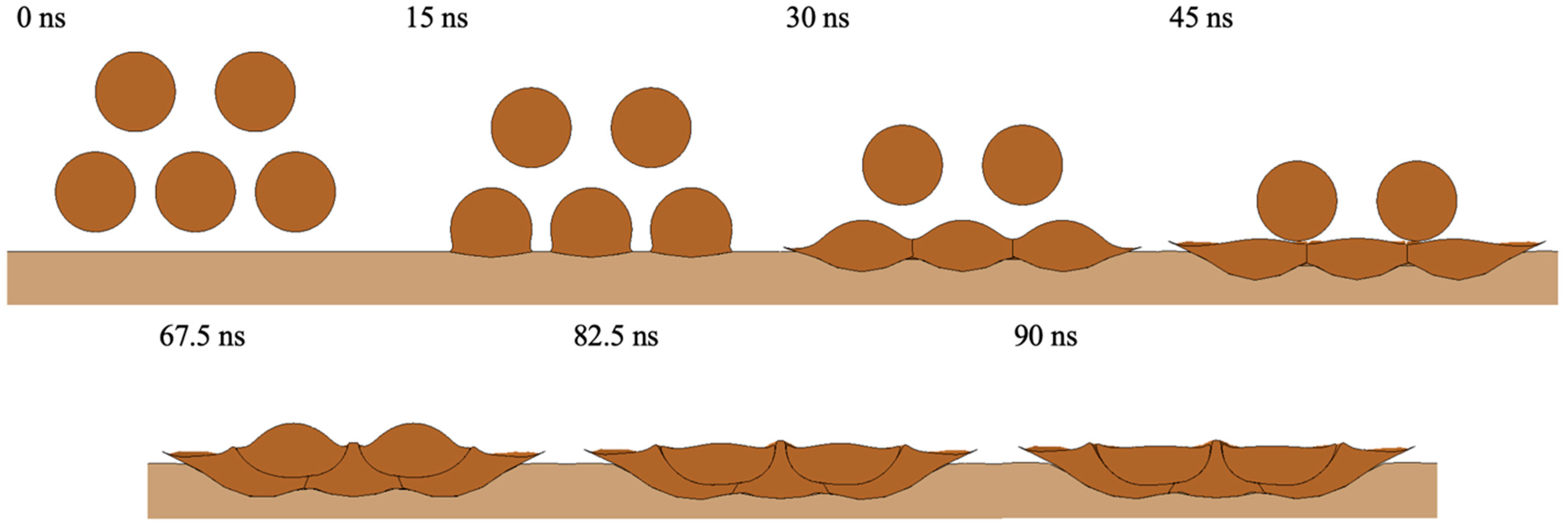
3. Results and Discussion
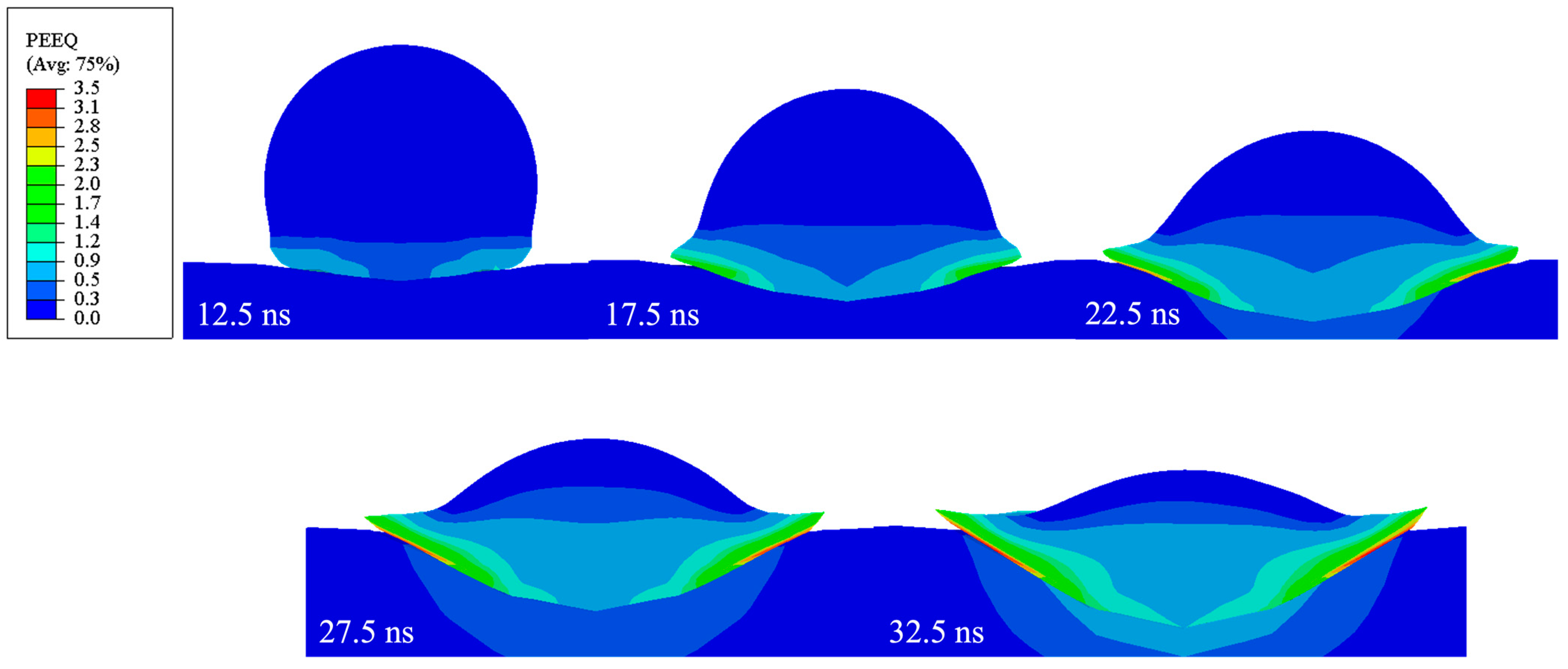
3.1. Oxide Layer Behavior
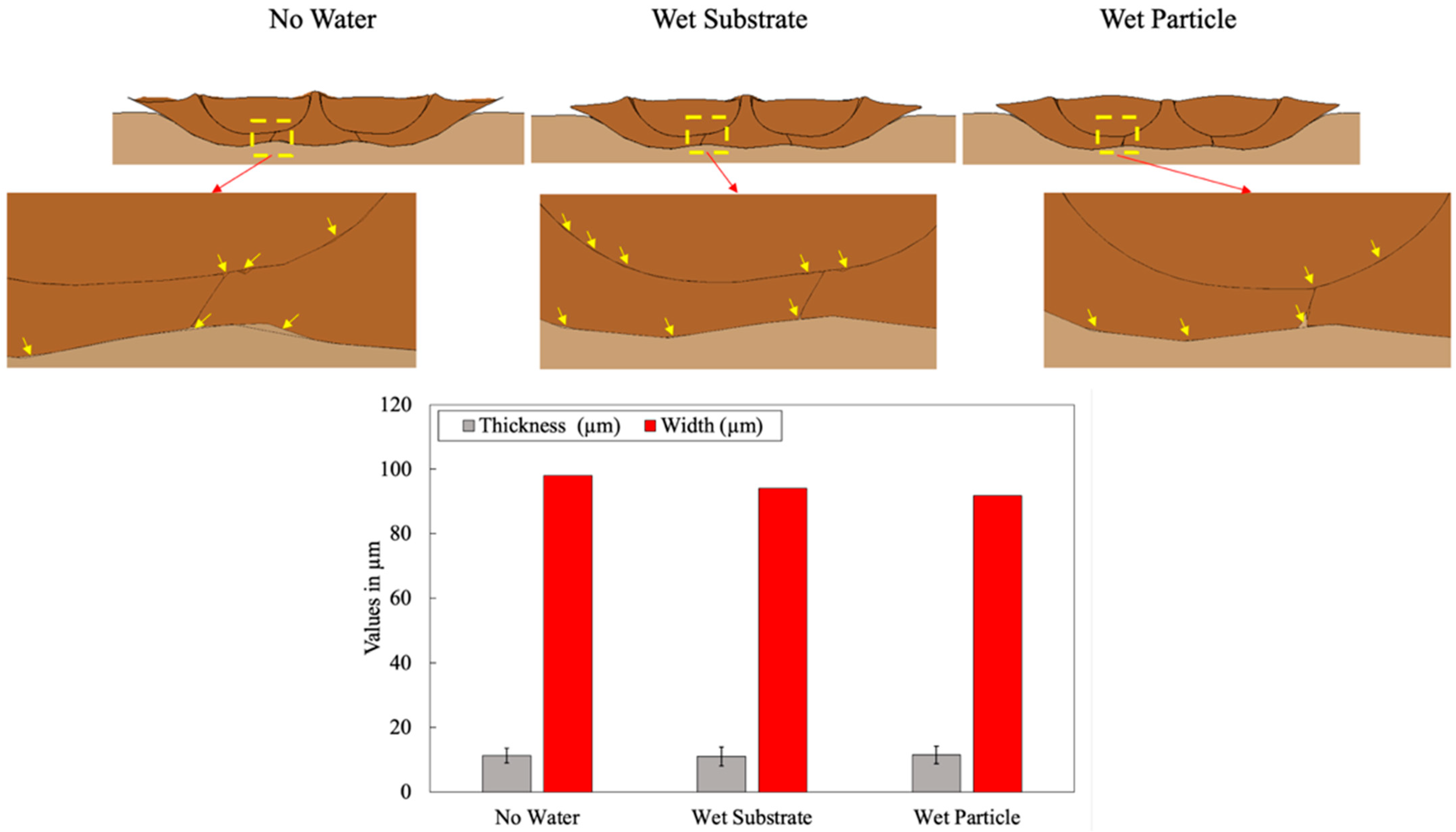
3.1.1. Oxide Layer Failure in LCS
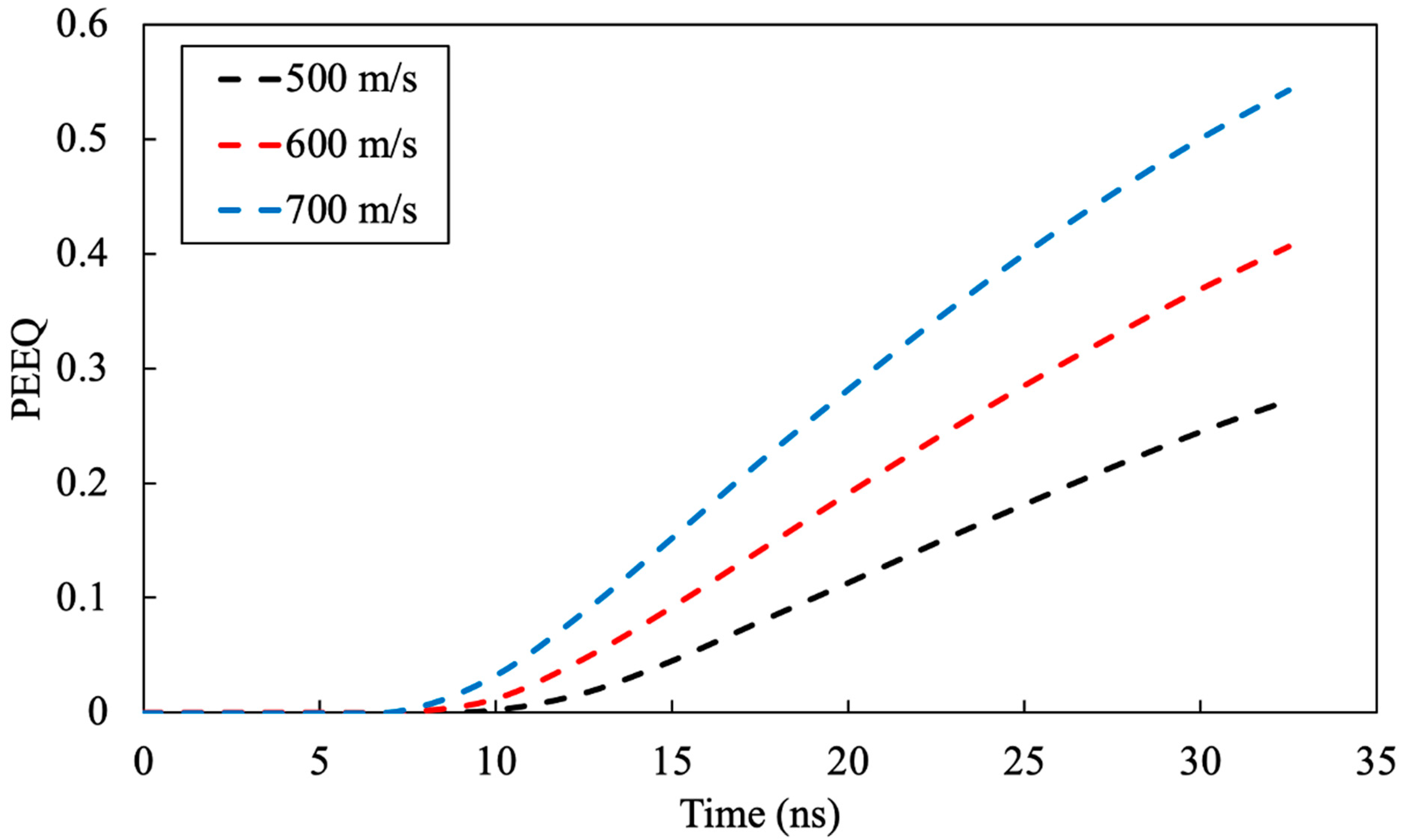
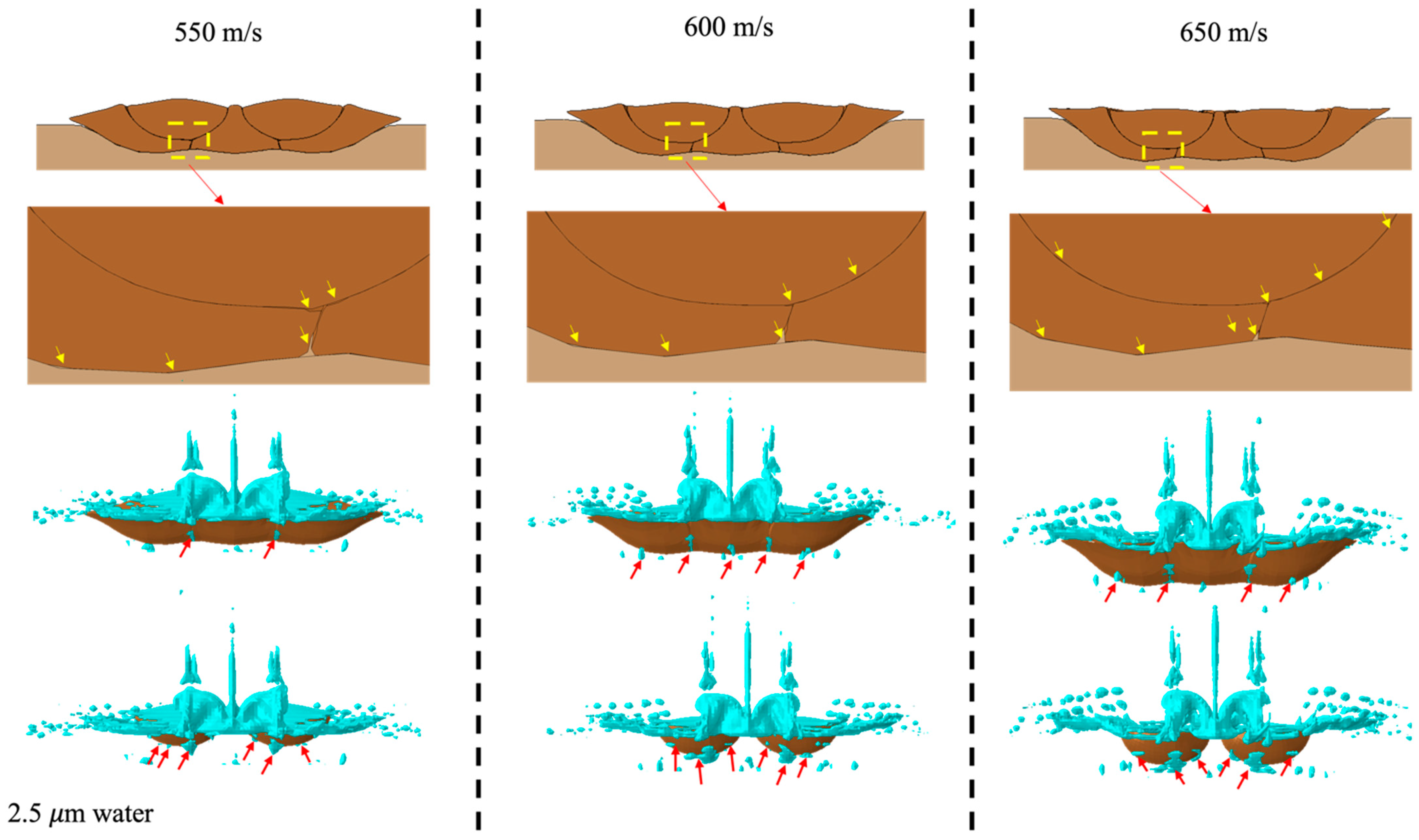
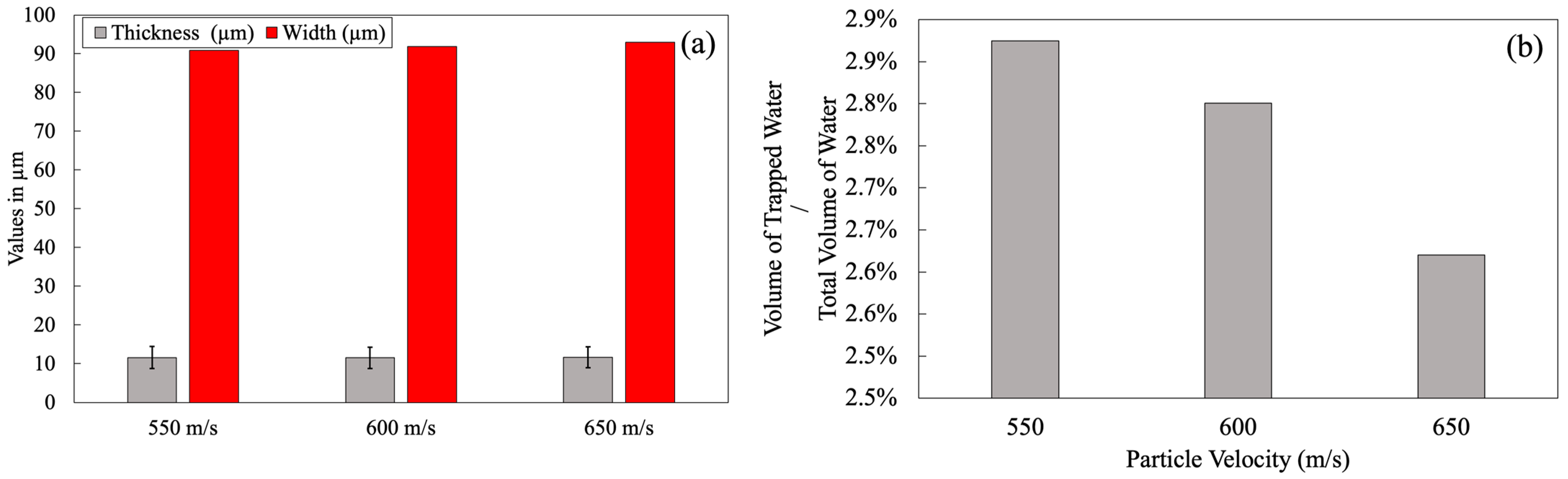
3.1.2. Particle Velocity Effect
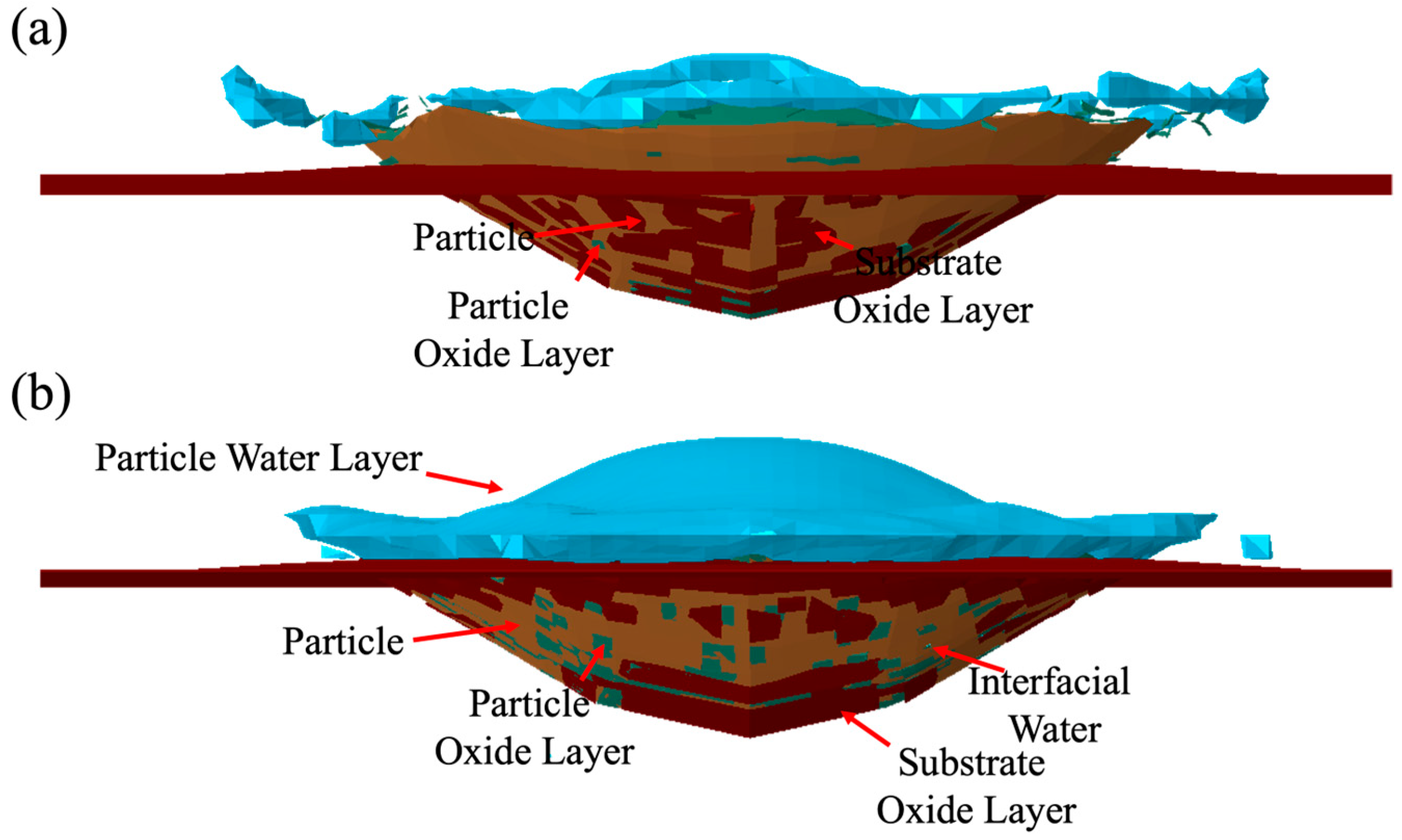
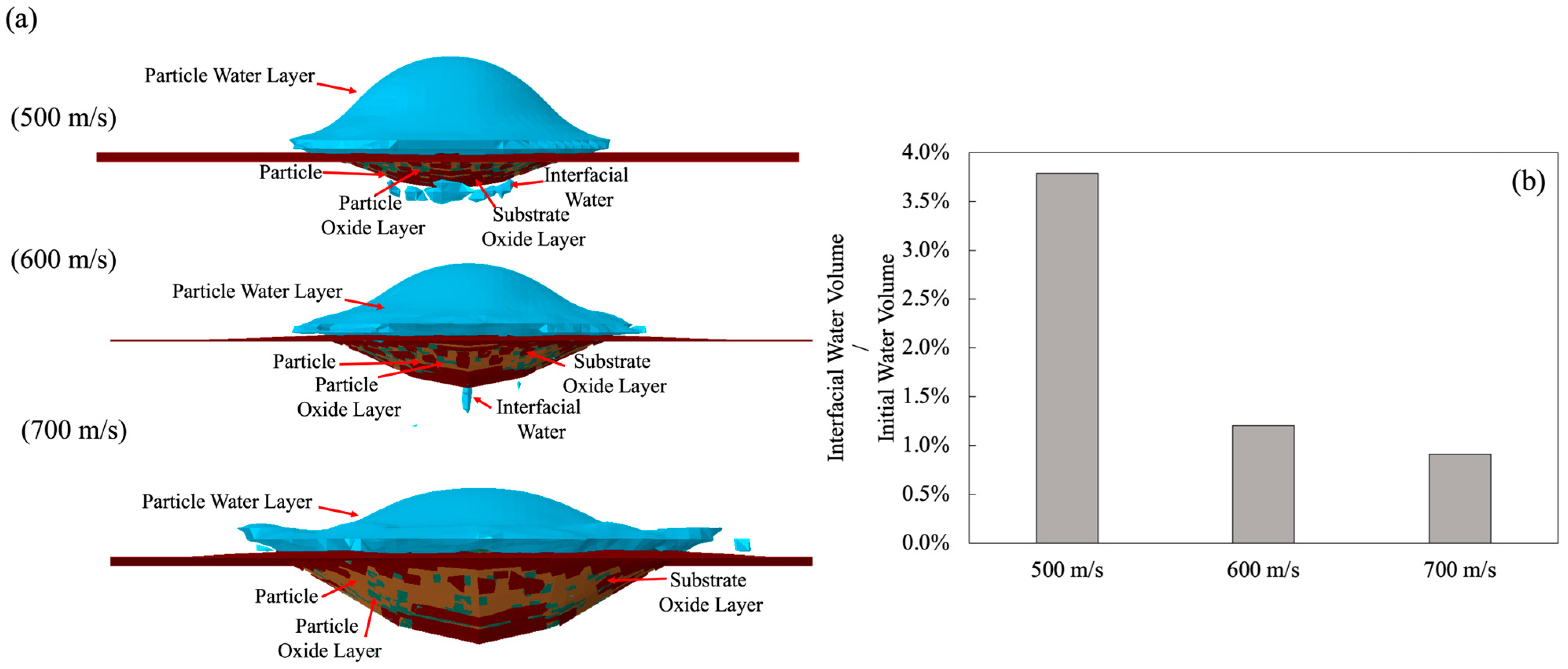
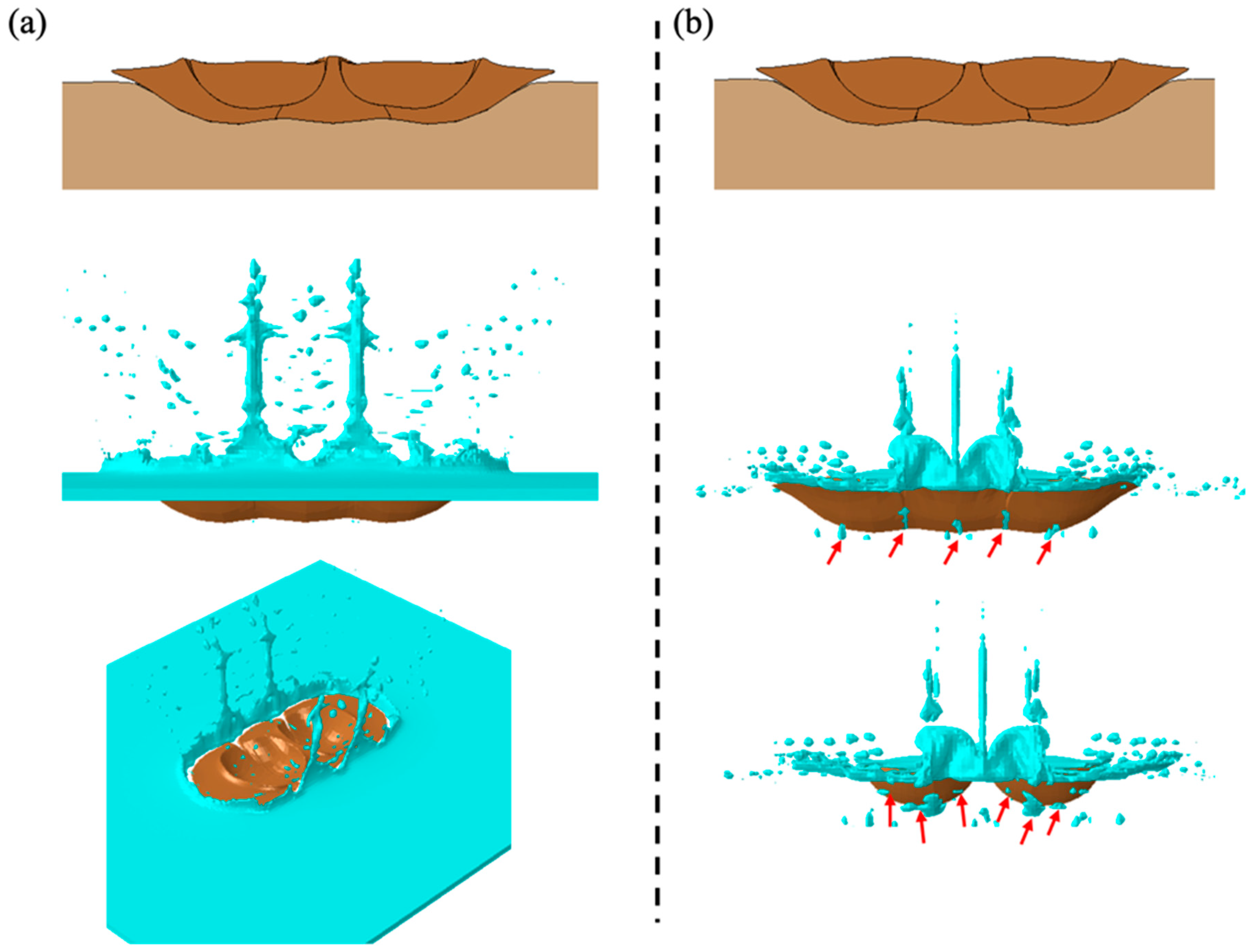
3.2. Porosity Level Formation
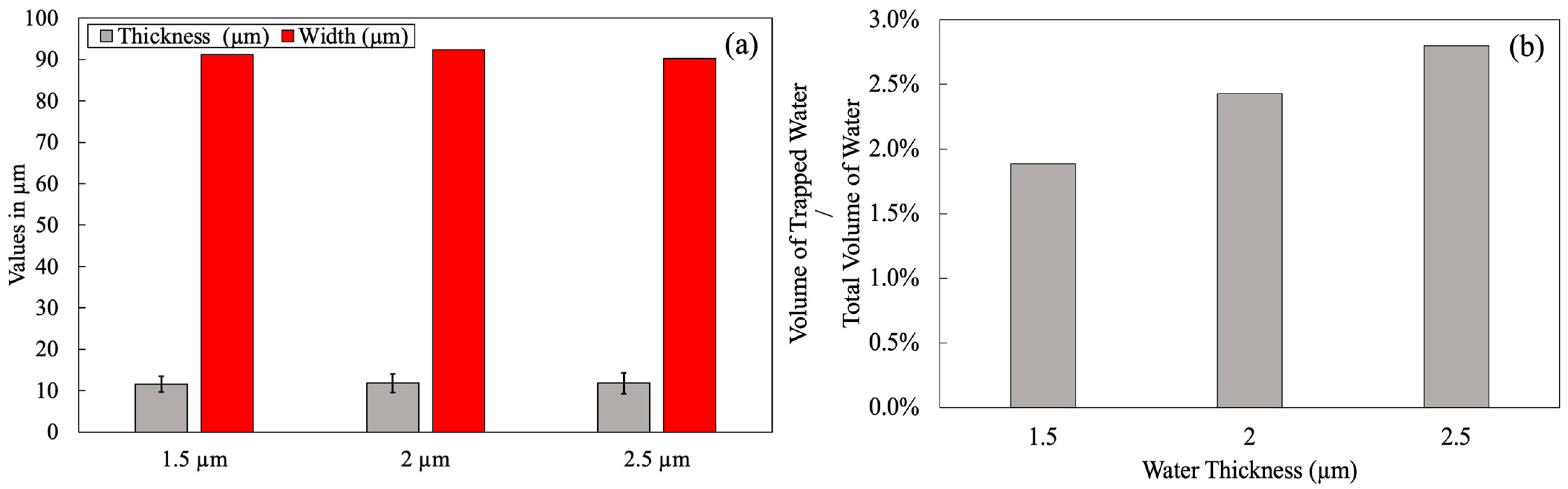
3.2.1. Water Effect on Porosity Formation
3.2.2. Particle Velocity Effect
3.2.3. Particle Velocity Effect
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CS | Cold spray |
| LCS | Liquid cold spray |
| CEL | Coupled Eulerian–Lagrangian |
| EoS | Equation of state |
| CFD | Computational fluid dynamics |
| PEEQ | Equivalent plastic strain |
| NSERC | Natural Sciences and Engineering Research Council of Canada |
Appendix A
Appendix A.1. Methodology for Systematic Study of Mesh Size Effect
| Wet Particle | Wet Substrate | |||||
|---|---|---|---|---|---|---|
| Condition Name | Eulerian Element Size (µm) | Water Element Size (µm) | Condition Name | Eulerian Element Size (µm) | Water Element Size (µm) | |
| Change in Water Element Size | EL15_W01 | 1.5 | 0.1 | EL15_W1 | 1.5 | 1 |
| EL15_W03 | 1.5 | 0.3 | EL15_W15 | 1.5 | 1.5 | |
| EL15_W06 | 1.5 | 0.6 | EL15_W2 | 1.5 | 2 | |
| EL15_W09 | 1.5 | 0.9 | EL15_W25 | 1.5 | 2.5 | |
| EL15_W12 | 1.5 | 1.2 | EL15_W3 | 1.5 | 3 | |
| EL15_W15 | 1.5 | 1.5 | EL15_W35 | 1.5 | 3.5 | |
| Change in Water Element Size | EL1_W03 | 1 | 0.3 | EL1_W2 | 1 | 2 |
| EL12_W03 | 1.2 | 0.3 | EL12_W2 | 1.2 | 2 | |
| EL15_W03 | 1.5 | 0.3 | EL15_W2 | 1.5 | 2 | |
| EL2_W03 | 2 | 0.3 | EL2_W2 | 2 | 2 | |
| EL25_W03 | 2.5 | 0.3 | EL25_W2 | 2.5 | 2 | |
| EL3_W03 | 3 | 0.3 | EL3_W2 | 3 | 2 | |
Appendix A.2. Results and Discussion of Systematic Analysis of Element Size

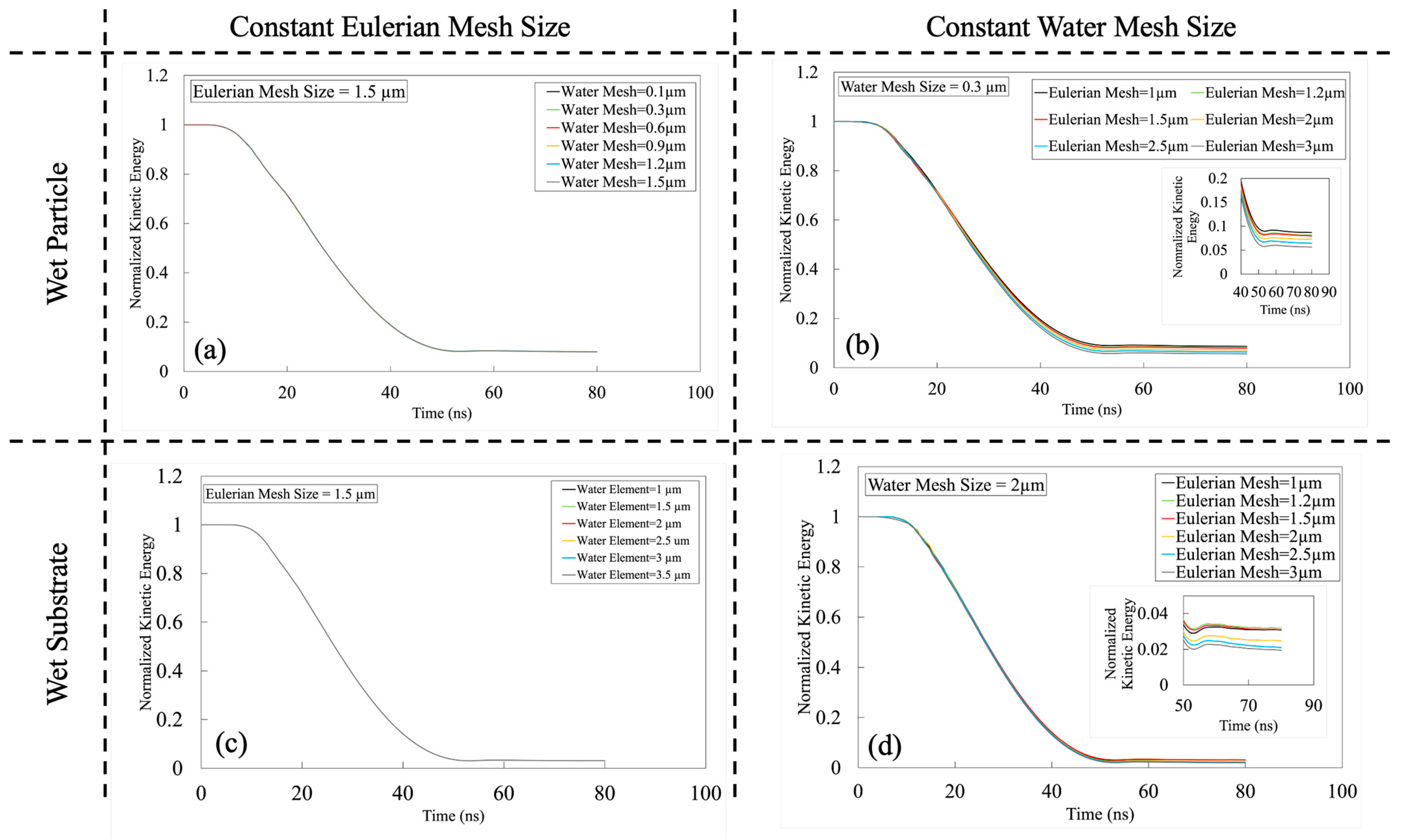



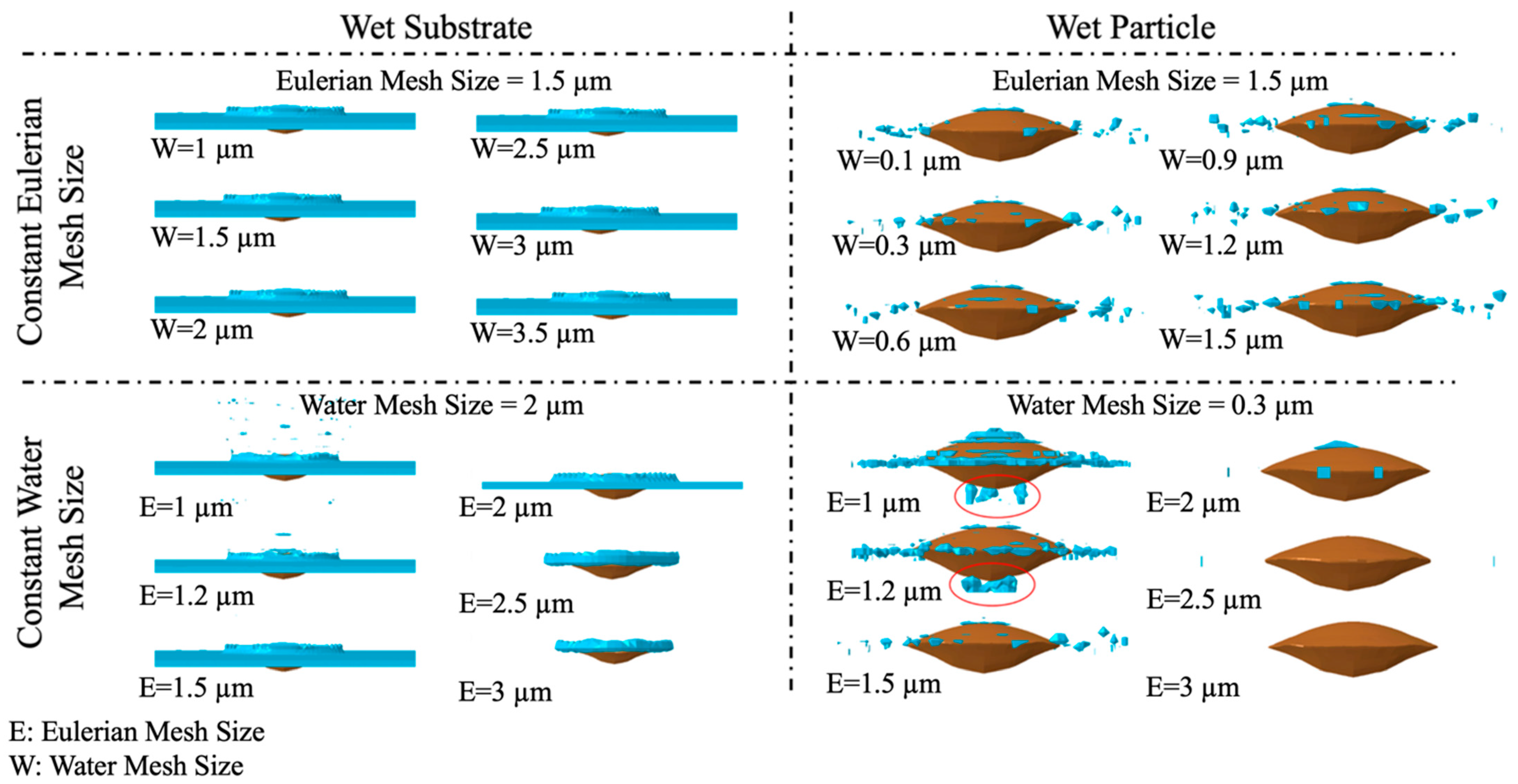

References
- Yan, X.; Huang, C.; Chen, C.; Bolot, R.; Dembinski, L.; Huang, R.; Ma, W.; Liao, H.; Liu, M. Additive Manufacturing of WC Reinforced Maraging Steel 300 Composites by Cold Spray and Selective Laser Melting. Surf. Coat. Technol. 2019, 371, 161–171. [Google Scholar] [CrossRef]
- Khodabakhshi, F.; Marzbanrad, B.; Jahed, H.; Gerlich, A.P. Interfacial Bonding Mechanisms between Aluminum and Titanium during Cold Gas Spraying Followed by Friction-Stir Modification. Appl. Surf. Sci. 2018, 462, 739–752. [Google Scholar] [CrossRef]
- Goldbaum, D.; Shockley, J.M.; Chromik, R.R.; Rezaeian, A.; Yue, S.; Legoux, J.; Irissou, E. The Effect of Deposition Conditions on Adhesion Strength of Ti and Ti6Al4V Cold Spray Splats. J. Therm. Spray Technol. 2012, 21, 288–303. [Google Scholar] [CrossRef]
- Bagherifard, S.; Monti, S.; Zuccoli, M.V.; Riccio, M.; Kondas, J.; Guagliano, M. Cold Spray Deposition for Additive Manufacturing of Freeform Structural Components Compared to Selective Laser Melting. Mater. Sci. Eng. A 2018, 721, 339–350. [Google Scholar] [CrossRef]
- Chen, C.; Xie, Y.; Yan, X.; Yin, S.; Fukanuma, H.; Huang, R.; Zhao, R.; Wang, J.; Ren, Z.; Liu, M.; et al. Effect of Hot Isostatic Pressing (HIP) on Microstructure and Mechanical Properties of Ti6Al4V Alloy Fabricated by Cold Spray Additive Manufacturing. Addit. Manuf. 2019, 27, 595–605. [Google Scholar] [CrossRef]
- Fauchais, P.L.; Heberlein, J.V.R.; Boulos, M.I. Thermal Spray Fundamentals from Powder to Parts, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Rahmati, S.; Jodoin, B. Physically Based Finite Element Modeling Method to Predict Metallic Bonding in Cold Spray. J. Therm. Spray Technol. 2020, 29, 611–629. [Google Scholar] [CrossRef]
- Xie, Y.; Yin, S.; Chen, C.; Planche, M.; Liao, H.; Lupoi, R. New Insights into the Coating/Substrate Interfacial Bonding Mechanism in Cold Spray. Scr. Mater. 2016, 125, 1–4. [Google Scholar] [CrossRef]
- Li, W.; Liao, H.; Li, C.; Bang, H.; Coddet, C. Numerical Simulation of Deformation Behavior of Al Particles Impacting on Al Substrate and Effect of Substrate Oxide Films on Interfacial Bonding in Cold Spraying. Appl. Surf. Sci. 2007, 253, 5084–5091. [Google Scholar] [CrossRef]
- Schmidt, T.; Gartner, F.; Assadi, H.; Kreye, H. Development of a Generalized Parameter Window for Cold Spray Deposition. Acta Mater. 2006, 54, 729–742. [Google Scholar] [CrossRef]
- Hassani-Gangaraj, M.; Veysset, D.; Champagne, V.K.; Nelson, K.A.; Schuh, C.A. Adiabatic Shear Instability is not Necessary for Adhesion in Cold Spray. Acta Mater. 2018, 158, 430–439. [Google Scholar] [CrossRef]
- Huang, R.; Ma, W.; Fukanuma, H. Development of Ultra-Strong Adhesive Strength Coatings Using Cold Spray. Surf. Coat. Technol. 2014, 258, 832–841. [Google Scholar] [CrossRef]
- Tiamiyu, A.A.; Chen, X.; Pang, E.L.; Sun, Y.; Lienhard, J.; LeBeau, J.M.; Nelson, K.A.; Schuh, C.A. Oxide Layer Delamination: An Energy Dissipation Mechanism During High-Velocity Microparticle Impacts. Appl. Surf. Sci. 2022, 574, 151673. [Google Scholar] [CrossRef]
- Xie, Y.; Planche, M.; Raoelison, R.; Liao, H.; Suo, X.; Herve, P. Effect of Substrate Preheating on Adhesive Strength of SS 316L Cold Spray Coatings. J. Therm. Spray Technol. 2016, 25, 123–130. [Google Scholar] [CrossRef]
- Almeida, C.M.; Prioli, R.; Ponce, F.A. Effect of native oxide mechanical deformation on InP nanoindentation. J. Appl. Phys. 2008, 104, 113509. [Google Scholar] [CrossRef]
- Zhang, C.; Kalia, R.K.; Nakano, A.; Vashishta, P.; Branicio, P.S. Deformation mechanisms and damage in α-alumina under hypervelocity impact loading. J. Appl. Phys. 2008, 103, 083508. [Google Scholar] [CrossRef]
- Khoei, A.R.; Khorrami, M.S. Mechanical properties of graphene oxide: A molecular dynamics study. Fuller. Nanotub. Carbon Nanostructures 2016, 24, 594–603. [Google Scholar] [CrossRef]
- Rahmati, S.; Veiga, R.G.A.; Zuniga, A.; Jodoin, B. A Numerical Approach to Study the Oxide Layer Effect on Adhesion in Cold Spray. J. Therm. Spray Technol. 2021, 30, 1777–1791. [Google Scholar] [CrossRef]
- Khamsepour, P.; Moreau, C.; Dolatabadi, A. Effect of Particle and Substrate Pre-Heating on the Oxide Layer and Material Jet Formation in Solid-state Spray Deposition: A Numerical Study. J. Therm. Spray Technol. 2023, 32, 1153–1166. [Google Scholar] [CrossRef]
- Ren, B.; Song, J. Effect of Particle Oxidation, Size and Material on Deformation, Bonding and Deposition During Cold Spray: A Peridynamic Investigation. arXiv 2024, arXiv:2403.01311. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Z.; Wang, B.; Cai, Y. Effect of Plastic Deformation of Particle and Substrate on Metallurgical Bonding During Cold Spray. Mater. Lett. 2024, 373, 137157. [Google Scholar] [CrossRef]
- Vandadi, M.; Bond, T.; Asumadu, T.K.; Klenam, D.; Rahbar, N.; Soboyejo, W. Effect of Nanoscale Surface Oxide Layer on the Cold Spray of Commercially Pure Titanium and Ti-6Al-4V Powders. Comput. Mater. Sci. 2025, 246, 113454. [Google Scholar] [CrossRef]
- Ren, B.; Song, J. Peridynamics Simulation of Microparticle Impact: Deformation, Jetting, and the Influence of Surface Oxide Layer. Surf. Coat. Technol. 2024, 493, 131257. [Google Scholar] [CrossRef]
- Xie, J.; Nelias, D.; Berre, H.W.; Ogawa, K.; Ichikawa, Y. Simulation of the Cold Spray Particle Deposition Process. J. Tribol. 2015, 137, 041101. [Google Scholar] [CrossRef]
- Khamsepour, P.; Moreau, C.; Dolatabadi, A. Numerical Simulation of the Effect of Particle and Substrate Pre-Heating on Porosity Level and Residual Stress of As-Sprayed Ti6Al4V Components. J. Therm. Spray Technol. 2021, 31, 70–83. [Google Scholar] [CrossRef]
- Khamsepour, P.; Oberste-Berghaus, J.; Aghasibeig, M.; Moreau, C.; Dolatabadi, A. The Effect of Spraying Parameters of the Inner-Diameter High-Velocity Air–Fuel (ID-HVAF) Torch on Characteristics of Ti-6Al-4V In-Flight Particles and Coatings Formed at Short Spraying Distances. J. Therm. Spray Technol. 2023, 32, 568–585. [Google Scholar] [CrossRef]
- Oberste-Berghaus, J.; Aghasibeig, M.; Burgess, A.; Khamsepour, P.; Moreau, C.; Dolatabadi, A. Exploring Miniaturized HVOF Systems for the Deposition of Ti-6Al-4V. J. Therm. Spray Technol. 2023, 32, 760–772. [Google Scholar] [CrossRef]
- Xie, J. Simulation of Cold Spray Particle Deposition Process. Ph.D. Thesis, L’institut National des Sciences Appliquées de Lyon, Villeurbanne, France, 2014. [Google Scholar]
- Suhonen, T.; Varis, T.; Torrell, S.M.; Guilemany, J.M. Residual Stress Development in Cold Sprayed Al, Cu, and Ti Coatings. Acta Mater. 2013, 61, 6329–6337. [Google Scholar] [CrossRef]
- Khamsepour, P.; Akbarnozari, A.; Garmeh, S.; Moreau, C.; Dolatabadi, A. The Effect of Water Layer Covering Substrate Surface on the Deformation of the Impacting Particle Deposited by Liquid Cold Spray. In Proceedings of the Canadian Society for Mechanical Engineering International Congress, Edmonton, AB, Canada, 5–8 June 2022. [Google Scholar] [CrossRef]
- Khamsepour, P.; Akbarnozari, A.; Garmeh, S.; Moreau, C.; Dolatabadi, A. The Effect of Water Film Surrounding the Deposited Particle on Bonding Area: A Numerical Study. J. Therm. Spray Technol. 2023, 32, p877–p892. [Google Scholar] [CrossRef]
- Butler, T. Liquid Accelerated Cold Spray; Cold Spray Action Team (CSAT): Worcester, MA, USA, 2011. [Google Scholar]
- Butler, T. Liquid Accelerated Cold Spray; Cold Spray Action Team (CSAT): Worcester, MA, USA, 2012. [Google Scholar]
- Akbarnozari, A.; Garmeh, S.; Attouil, F.B.; Dolatabadi, A.; Desaulniers, S.; Pouliot, L.; Moreau, C. Recent Advance in Liquid Cold Spray (LCS). In Proceedings of the North American Cold Spray Conference 2022, New Orleans, LA, USA, 13–14 September 2022. [Google Scholar]
- Liu, Y.; Li, C.X.; Huang, X.F.; Ma, K.; Luo, X.T.; Li, C.J. Effect of Water Environment on Particle Deposition of Underwater Cold Spray. Appl. Surf. Sci. 2020, 506, 144542. [Google Scholar] [CrossRef]
- Meng, Y.; Saito, H.; Bernard, C.; Ichikawa, Y.; Ogawa, K. Parametric Study to Repair Leaks in Water Pipe Using the Low-Pressure Cold Spray Technique. J. Therm. Spray Technol. 2022, 31, 2560–2576. [Google Scholar] [CrossRef]
- Rahmati, S.; Ghaei, A. The Use of Particle/Substrate Material Models in Simulation of Cold-Gas Dynamic-Spray Process. J. Therm. Spray Technol. 2014, 23, 530–540. [Google Scholar] [CrossRef]
- Dassault Systemes. ABAQUS Analysis User’s Manuel, 6.11 ed.; Simulia: Providence, RI, USA, 2011. [Google Scholar]
- Wang, X.; Shi, J. Validation of Johnson-Cook Plasticity and Damage Model Using Impact Experiment. Int. J. Impact Eng. 2013, 60, 67–75. [Google Scholar] [CrossRef]
- Banerjee, A.; Dhar, S.; Acharyya, S.; Datta, D.; Nayak, N. Determination of Johnson Cook Material and Failure Model Constants and Numerical Modelling of Charpy Impact Test of Armour Steel. Mater. Sci. Eng. A 2015, 640, 200–209. [Google Scholar] [CrossRef]
- Pereira, L.M.; Rahmati, S.; Zuniga, A.; Jodoin, B.; Veiga, R.G.A. Atomistic Study of Metallurgical Bonding upon the High Velocity Impact of Fcc Core-Shell Particles. Comput. Mater. Sci. 2021, 186, 110045. [Google Scholar] [CrossRef]
- Nishimura, K.; Kalia, R.K.; Nakano, A.; Vashishta, P. Nanoindentation hardness anisotropy of alumina crystal: A molecular dynamics study. Appl. Phys. Lett. 2008, 92, 161904. [Google Scholar] [CrossRef]
- Cai, M.B.; Li, X.P.; Rahman, M. Study of the temperature and stress in nanoscale ductile mode cutting of silicon using molecular dynamics simulation. J. Mater. Process. Technol. 2007, 192, 607–612. [Google Scholar] [CrossRef]
- Bubar, S.F.; Vermilyea, D.A. Deformation of anodic oxide films. J. Electrochem. Soc. 1966, 113, 892. [Google Scholar] [CrossRef]
- Propp, M.; Young, L. Adhesion, Ductility, and Fracture of Anodic Oxide Films on Tantalum. J. Electrochem. Soc. 1979, 126, 624. [Google Scholar] [CrossRef]
- Assadi, H.; Schmidt, T.; Richter, H.; Kliemann, J.-O.; Binder, K.; Gärtner, F.; Klassen, T.; Kreye, H. On Parameter Selection in Cold Spraying. J. Therm. Spray Technol. 2011, 20, 1161–1176. [Google Scholar] [CrossRef]
- Kim, K.; Li, W.; Guo, X. Detection of Oxygen at the Interface and Its Effect on Strain, Stress, and Temperature at the Interface between Cold Sprayed Aluminum and Steel Substrate. Appl. Surf. Sci. 2015, 357, 1720–1726. [Google Scholar] [CrossRef]
- JSchreiber, M.; Smid, I.; Eden, T.J.; Koudela, K.; Cote, D.; Champagne, V. Cold Spray Particle Impact Simulation Using the Preston-Tonks-Wallace Plasticity Model. Finite Elem. Anal. Des. 2021, 191, 103557. [Google Scholar] [CrossRef]
- MacDoland, D.; Fernandez, R.; Delloro, F.; Jodoin, B. Cold Spraying of Armstrong Process Titanium Powder for Additive Manufacturing. J. Therm. Spray Technol. 2017, 26, 598–609. [Google Scholar] [CrossRef]

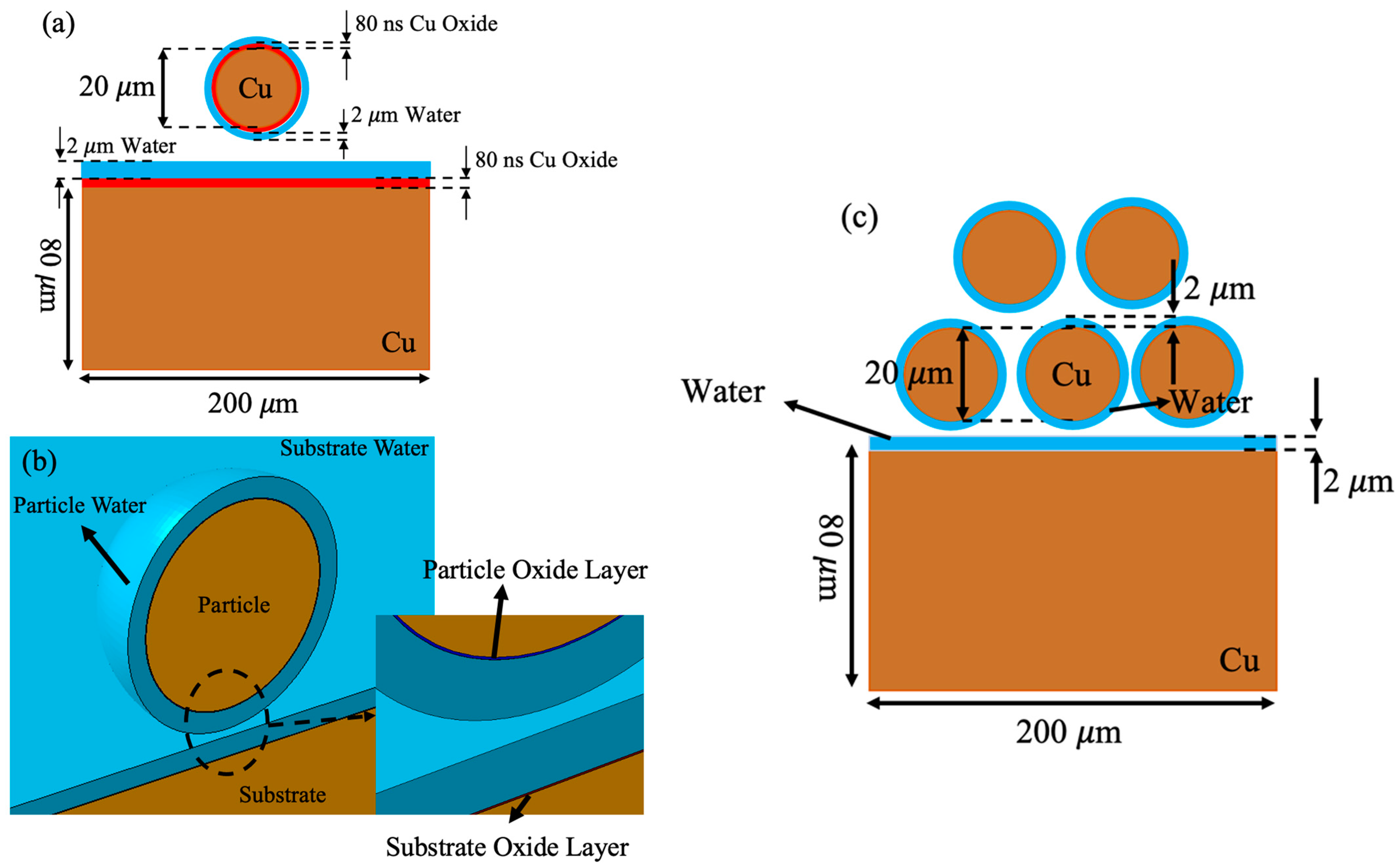



| Copper | Water | ||
|---|---|---|---|
| Property | Value | Property | Value |
| Thermal Conductivity | 386 W/m.K | Thermal Conductivity | 0.598 W/m.K |
| Specific Heat | 383 J/Kg.K | Specific Heat | 4.186 J/Kg.K |
| Density | 8930 Kg/m3 | Density | 985 Kg/m3 |
| Shear Modulus | 45 GPa | Speed of Sound | 1490 m/s |
| Melting Point | 1356 K | Viscosity | 1 mPa-s |
| Grüneisen’s Constant | 1.99 | ||
| Speed of Sound | 3933 m/s | ||
| Hugoniot Slope | 1.5 | ||
| A | 90 MPa | ||
| B | 292 MPa | ||
| C | 0.025 | ||
| m | 1.09 | ||
| n | 0.31 | ||
| Reference Strain Rate | 1/s | ||
| Transition Temperature | 298 K | ||
| Name of the Condition | Particle Velocity (m/s) | Particle Temperature (K) | Substrate Temperature (K) | Water Layer Thickness (µm) | Water Temperature (K) |
|---|---|---|---|---|---|
| VP1 | 500 | 298 | 298 | 2 | 298 |
| VP2 | 600 | 298 | 298 | 2 | 298 |
| VP3 | 650 | 298 | 298 | 2 | 298 |
| VP4 | 600 | 298 | 298 | 1.5 | 298 |
| VP5 | 600 | 298 | 298 | 2 | 298 |
| VP6 | 600 | 298 | 298 | 2.5 | 298 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khamsepour, P.; Akbarnozari, A.; MacDonald, D.; Pouliot, L.; Moreau, C.; Dolatabadi, A. Numerical Examination of Particle and Substrate Oxide Layer Failure and Porosity Formation in Coatings Deposited Using Liquid Cold Spray. Coatings 2025, 15, 405. https://doi.org/10.3390/coatings15040405
Khamsepour P, Akbarnozari A, MacDonald D, Pouliot L, Moreau C, Dolatabadi A. Numerical Examination of Particle and Substrate Oxide Layer Failure and Porosity Formation in Coatings Deposited Using Liquid Cold Spray. Coatings. 2025; 15(4):405. https://doi.org/10.3390/coatings15040405
Chicago/Turabian StyleKhamsepour, Peyman, Ali Akbarnozari, Daniel MacDonald, Luc Pouliot, Christian Moreau, and Ali Dolatabadi. 2025. "Numerical Examination of Particle and Substrate Oxide Layer Failure and Porosity Formation in Coatings Deposited Using Liquid Cold Spray" Coatings 15, no. 4: 405. https://doi.org/10.3390/coatings15040405
APA StyleKhamsepour, P., Akbarnozari, A., MacDonald, D., Pouliot, L., Moreau, C., & Dolatabadi, A. (2025). Numerical Examination of Particle and Substrate Oxide Layer Failure and Porosity Formation in Coatings Deposited Using Liquid Cold Spray. Coatings, 15(4), 405. https://doi.org/10.3390/coatings15040405







