Techniques for Modelling and Optimizing the Mechanical Properties of Natural Fiber Composites: A Review
Abstract
:1. Introduction
2. Natural Fiber Composites
Mechanical Properties of Natural Fiber Composites
3. Modelling and Optimization of Mechanical Properties of Natural Fiber Composites
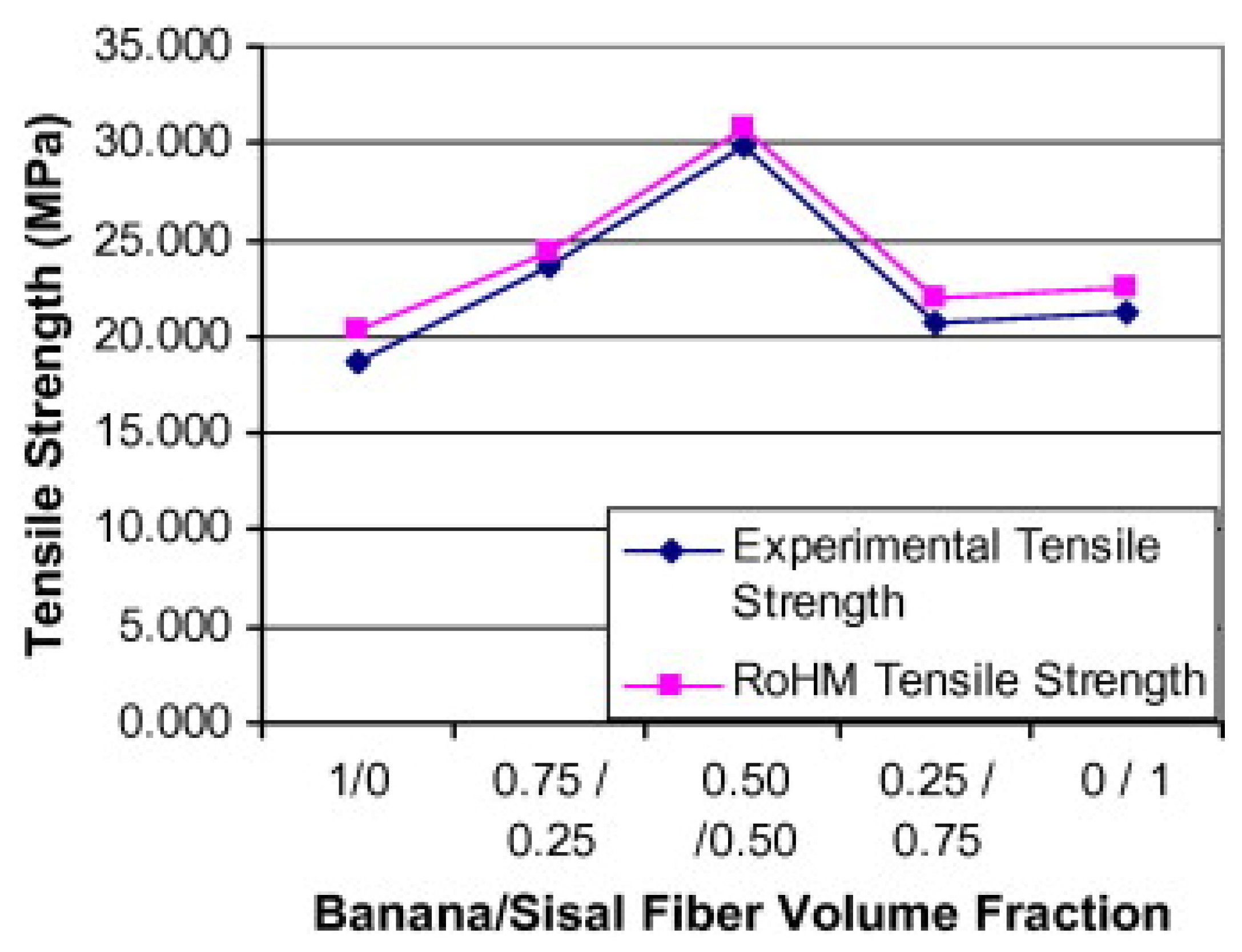
3.1. Rule of Mixture/Rule of Hybrid Mixture
3.2. Halpin–Tsai Model
3.3. Hirsch Model
3.4. Modified Bowyer and Bader’s Model
3.5. Continuum Theory
3.6. Finite Element Analysis
3.7. Artificial Intelligence
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| A Measure of fiber geometry, fiber distribution and fiber loading conditions | |
| ANFIS | Adaptive neuro-fuzzy inference system |
| ANN | Artificial neural networks |
| CDM | Continuum damage mechanics |
| AI | Artificial Intelligence |
| FEA | Finite Element analysis |
| GEP | Gene expression programming |
| GP | Genetic programming |
| KNN | K-Nearest Neighbor |
| ML | Machine Learning |
| NFC | Natural fiber composite |
| NN | Neural networks |
| PLA | Poly(lactic acid) |
| PP | Polypropylene |
| RoM | Rule of mixture |
| RoHM | Rule of hybrid mixture |
| SVM | Support Vector Machines |
| UP | Unsaturated Polyester |
List of Symbols Used
| Symbol | Description |
| Overall material strain | |
| Single fiber strain | |
| Elasticity of hybrid composite | |
| Vc | Relative hybrid volume |
| Vt | Overall reinforcement volume fraction |
| Vf | Volume fraction of fiber |
| Ec | Elasticity of composite material |
| Tm | Tensile strength of matrix material |
| Tc | Tensile strength of composite material |
| Em | Elasticity of matrix material |
| Tf | Tensile strength of fiber |
| K | Einstein coefficient |
| A | Measure of fiber geometry, fiber distribution and fiber loading conditions |
| Ef | Elasticity of fiber |
| Fiber/matrix ratio | |
| Vm | Volume fraction of matrix |
| x | Variable which gives the load transfer between the matrix and fiber |
| Helmholtz free energy | |
| Modified right Cauchy-Green deformation tensor | |
| Molar concentration of water molecules | |
| J | Volume ratio of the fiber |
| Material parameter | |
| Mechanical energy caused by deformation | |
| Chemical energy by water diffusion |
References
- Kerni, L.; Singh, S.; Patnaik, A.; Kumar, N. A review on natural fiber reinforced composites. Mater. Today: Proc. 2020, 28, 1616–1621. [Google Scholar] [CrossRef]
- Mochane, M.J.; Mokhena, T.C.; Mokhothu, T.H.; Mtibe, A.; Sadiku, E.R.; Ray, S.S.; Ibrahim, I.D.; Daramola, O.O. Recent progress on natural fiber hybrid composites for advanced applications: A review. Express Polym. Lett. 2019, 13, 159–198. [Google Scholar] [CrossRef]
- Ramu, P.; Kumar, C.J.; Palanikumar, K. Mechanical Characteristics and Terminological Behavior Study on Natural Fiber Nano reinforced Polymer Composite—A Review. Mater. Today Proc. 2019, 16, 1287–1296. [Google Scholar] [CrossRef]
- Otto, G.P.; Moisés, M.P.; Carvalho, G.; Rinaldi, A.W.; Garcia, J.C.; Radovanovic, E.; Fávaro, S.L. Mechanical properties of a polyurethane hybrid composite with natural lignocellulosic fibers. Compos. Part B Eng. 2017, 110, 459–465. [Google Scholar] [CrossRef]
- Ude, A.U.; Eshkoor, R.A.; Azhari, C.H. Crashworthy characteristics of axial quasi-statically compressed Bombyx mori composite cylindrical tubes: Experimental. Fibers Polym. 2017, 18, 1594–1601. [Google Scholar] [CrossRef]
- Ude, A.U.; Azhari, C.H. Lateral crashworthiness response of bombyx mori fibre/glass–fibre/epoxy hybrid composite cylindrical tubes-experimental. AIMS Mater. Sci. 2019, 6, 1227–1239. [Google Scholar] [CrossRef]
- Mulenga, T.K.; Ude, A.; Vivekanandhan, C. Concise review on the mechanical characteristics of hybrid natural fibres with filler content. AIMS Mater. Sci. 2020, 7, 650–664. [Google Scholar] [CrossRef]
- Thakur, V.K.; Voicu, S.I. Recent advances in cellulose and chitosan based membranes for water purification: A concise review. Carbohydr. Polym. 2016, 146, 148–165. [Google Scholar] [CrossRef]
- Singha, A.S.; Thakur, V.K. Fabrication and Characterization of H. sabdariffa Fiber-Reinforced Green Polymer Composites. Polym. Technol. Eng. 2009, 48, 482–487. [Google Scholar] [CrossRef]
- Motaleb, K.Z.M.A.; Milašius, R.; Ahad, A. Influence of Gamma Radiation on Mechanical Properties of Jute Fabric-Reinforced Polymer Composites. Fibers 2020, 8, 58. [Google Scholar] [CrossRef]
- Trache, D.; Thakur, V.K.; Boukherroub, R. Cellulose Nanocrystals/Graphene Hybrids—A Promising New Class of Materials for Advanced Applications. Nanomaterials 2020, 10, 1523. [Google Scholar] [CrossRef] [PubMed]
- Thakur, V.K.; Thakur, M.K.; Gupta, R.K. Review: Raw Natural Fiber–Based Polymer Composites. Int. J. Polym. Anal. Charact. 2014, 19, 256–271. [Google Scholar] [CrossRef]
- Węcławski, B.T.; Fan, M.; Hui, D. Compressive behaviour of natural fibre composite. Compos. Part B Eng. 2014, 67, 183–191. [Google Scholar] [CrossRef]
- Senthilkumar, K.; Saba, N.; Rajini, N.; Chandrasekar, M.; Jawaid, M.; Siengchin, S.; Alotman, O.Y. Mechanical properties evaluation of sisal fibre reinforced polymer composites: A review. Constr. Build. Mater. 2018, 174, 713–729. [Google Scholar] [CrossRef]
- Shireesha, Y.; Suresh, B.V.; Bahubalendruni, M.R.; Nandipati, G. Experimental Investigation on Mechanical Properties ofBi-Directional Hybrid Natural Fibre Composite (HNFC). Mater. Today Proc. 2019, 18, 165–174. [Google Scholar] [CrossRef]
- Tisserat, B.; Montesdeoca, N.; Boddu, V.M. Accelerated Thermal Aging of Bio-Based Composite Wood Panels. Fibers 2020, 8, 32. [Google Scholar] [CrossRef]
- Bambach, M.R. Direct Comparison of the Structural Compression Characteristics of Natural and Synthetic Fiber-Epoxy Composites: Flax, Jute, Hemp, Glass and Carbon Fibers. Fibers 2020, 8, 62. [Google Scholar] [CrossRef]
- Parbin, S.; Waghmare, N.K.; Singh, S.K.; Khan, S. Mechanical properties of natural fiber reinforced epoxy composites: A review. Procedia Comput. Sci. 2019, 152, 375–379. [Google Scholar] [CrossRef]
- Eshkoor, R.A.; Ude, A.U.; Sulong, A.B.; Zulkifli, R.; Ariffin, A.K.; Azhari, C.H. Energy absorption and load carrying capability of woven natural silk epoxy–triggered composite tubes. Compos. Part B Eng. 2015, 77, 10–18. [Google Scholar] [CrossRef]
- Trache, D.; Thakur, V.K. Nanocellulose and Nanocarbons Based Hybrid Materials: Synthesis, Characterization and Applications. Nanomaterials 2020, 10, 1800. [Google Scholar] [CrossRef]
- Ates, B.; Koytepe, S.; Ulu, A.; Gurses, C.; Thakur, V.K. Chemistry, Structures, and Advanced Applications of Nanocomposites from Biorenewable Resources. Chem. Rev. 2020, 120, 9304–9362. [Google Scholar] [CrossRef] [PubMed]
- Hariprasad, K.; Ravichandran, K.; Jayaseelan, V.; Muthuramalingam, T. Acoustic and mechanical characterisation of polypropylene composites reinforced by natural fibres for automotive applications. J. Mater. Res. Technol. 2020, 9, 14029–14035. [Google Scholar] [CrossRef]
- Khan, S.M.; Malik, S.A.; Gull, N.; Saleemi, S.; Islam, A.; Butt, M.T.Z. Fabrication and modelling of the macro-mechanical properties of cross-ply laminated fibre-reinforced polymer composites using artificial neural network. Adv. Compos. Mater. 2019, 28, 409–423. [Google Scholar] [CrossRef]
- Nwobi-Okoye, C.C.; Uzochukwu, C.U. RSM and ANN modeling for production of Al 6351/ egg shell reinforced composite: Multi objective optimization using genetic algorithm. Mater. Today Commun. 2020, 22, 100674. [Google Scholar] [CrossRef]
- Singha, A.S.; Thakur, V.K. Synthesis, Characterisation and Analysis of Hibiscus Sabdariffa Fibre Reinforced Polymer Matrix Based Composites. Polym. Polym. Compos. 2009, 17, 189–194. [Google Scholar] [CrossRef]
- Manral, A.R.S.; Gariya, N.; Bansal, G.; Singh, H.P.; Rawat, A. Computational stress analysis of Chicken Feather Fibre (CFF) with Epoxy-Resin matrix composite material. Mater. Today Proc. 2020, 26, 2805–2810. [Google Scholar] [CrossRef]
- Nwobi-Okoye, C.C.; Ochieze, B.Q.; Okiy, S. Multi-objective optimization and modeling of age hardening process using ANN, ANFIS and genetic algorithm: Results from aluminum alloy A356/cow horn particulate composite. J. Mater. Res. Technol. 2019, 8, 3054–3075. [Google Scholar] [CrossRef]
- Li, M.; Pu, Y.; Thomas, V.M.; Yoo, C.G.; Ozcan, S.; Deng, Y.; Nelson, K.; Ragauskas, A.J. Recent advancements of plant-based natural fiber–reinforced composites and their applications. Compos. Part B Eng. 2020, 200, 108254. [Google Scholar] [CrossRef]
- Balasubramanian, K.; Rajeswari, N.; Vaidheeswaran, K. Analysis of mechanical properties of natural fibre composites by experimental with FEA. Mater. Today Proc. 2020, 28, 1149–1153. [Google Scholar] [CrossRef]
- Saini, M.K.; Bagha, A.K.; Kumar, S.; Bahl, S. Finite element analysis for predicting the vibration characteristics of natural fiber reinforced epoxy composites. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Behzad, T.; Sain, M. Finite element modeling of polymer curing in natural fiber reinforced composites. Compos. Sci. Technol. 2007, 67, 1666–1673. [Google Scholar] [CrossRef]
- Pujari, S.; Ramakrishna, A.; Padal, K.B. Prediction of Swelling Behaviour of Jute and Banana Fiber Composites by using ANN and Regression Analysis. Mater. Today Proc. 2017, 4, 8548–8557. [Google Scholar] [CrossRef]
- Summerscales, J.; Virk, A.S.; Hall, W. Enhanced rules-of-mixture for natural fibre reinforced polymer matrix (NFRP) composites (comment on Lau et al. in volume 136). Compos. Part B Eng. 2019, 160, 167–169. [Google Scholar] [CrossRef] [Green Version]
- Summerscales, J.; Virk, A.S.; Hall, W. Fibre area correction factors (FACF) for the extended rules-of-mixtures for natural fibre reinforced composites. Mater. Today Proc. 2020, 31, S318–S320. [Google Scholar] [CrossRef]
- Velmurugan, V.; Kumar, D.D.; Thanikaikarasan, S. Experimental evaluation of mechanical properties of natural fibre reinforced polymer composites. Mater. Today Proc. 2020, 16, 167. [Google Scholar] [CrossRef]
- Chokshi, S.; Gohil, P.P.; Lalakiya, A.; Patel, P.; Parmar, A. Tensile strength prediction of natural fiber and natural fiber yarn: Strain rate variation upshot. Mater. Today Proc. 2020, 27, 1218–1223. [Google Scholar] [CrossRef]
- Kumar, S.; Prasad, L.; Kumar, S.; Patel, V.K. Physico-mechanical and Taguchi-designed sliding wear properties of Himalayan agave fiber reinforced polyester composite. J. Mater. Res. Technol. 2019, 8, 3662–3671. [Google Scholar] [CrossRef]
- Potluri, R.; Diwakar, V.; Venkatesh, K.; Reddy, B.S. Analytical Model Application for Prediction of Mechanical Properties of Natural Fiber Reinforced Composites. Mater. Today Proc. 2018, 5, 5809–5818. [Google Scholar] [CrossRef]
- Tian, F.; Zhong, Z. Modeling of load responses for natural fiber reinforced composites under water absorption. Compos. Part A Appl. Sci. Manuf. 2019, 125, 105564. [Google Scholar] [CrossRef]
- Wu, T.; Yao, W.; Xu, C.; Li, P. A natural frequency degradation model for very high cycle fatigue of woven fiber reinforced composite. Int. J. Fatigue 2020, 134, 105398. [Google Scholar] [CrossRef]
- Xiong, X.; Hua, L.; Miao, M.; Shen, S.Z.; Li, X.; Wan, X.; Guo, W. Multi-scale constitutive modeling of natural fiber fabric reinforced composites. Compos. Part A Appl. Sci. Manuf. 2018, 115, 383–396. [Google Scholar] [CrossRef]
- Blanchard, J.M.F.A.; Mutlu, U.; Sobey, A.J.; Blake, J.I.R. Modelling the different mechanical response and increased stresses exhibited by structures made from natural fibre composites. Compos. Struct. 2019, 215, 402–410. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Zuo, Q.; Lin, T.; Anuar, N.I.S.; Salleh, K.M.; Gan, S.; Yousfani, S.H.S.; Zuo, H.; Zakaria, S. Predicting thermal conductivity and mechanical property of bamboo fibers/polypropylene nonwovens reinforced composites based on regression analysis. Int. Commun. Heat Mass Transf. 2020, 118, 104895. [Google Scholar] [CrossRef]
- Venkateshwaran, N.; Elayaperumal, A.; Sathiya, G.K. Prediction of tensile properties of hybrid-natural fiber composites. Compos. Part B Eng. 2012, 43, 793–796. [Google Scholar] [CrossRef]
- Wang, K.F.; Wang, B.L. A mechanical degradation model for bidirectional natural fiber reinforced composites under hydrothermal ageing and applying in buckling and vibration analysis. Compos. Struct. 2018, 206, 594–600. [Google Scholar] [CrossRef]
- Omrani, E.; Menezes, P.L.; Rohatgi, P.K. State of the art on tribological behavior of polymer matrix composites reinforced with natural fibers in the green materials world. Eng. Sci. Technol. Int. J. 2016, 19, 717–736. [Google Scholar] [CrossRef] [Green Version]
- Pappu, A.; Thakur, V.K. Towards sustainable micro and nano composites from fly ash and natural fibers for multifunctional applications. Vacuum 2017, 146, 375–385. [Google Scholar] [CrossRef] [Green Version]
- Jeyapragash, R.; Srinivasan, V.; Sathiyamurthy, S. Mechanical properties of natural fiber/particulate reinforced epoxy composites—A review of the literature. Mater. Today Proc. 2020, 22, 1223–1227. [Google Scholar] [CrossRef]
- Vijayakumar, S.; Palanikumar, K. Mechanical Property Evaluation of Hybrid Reinforced Epoxy Composite. Mater. Today Proc. 2019, 16, 430–438. [Google Scholar] [CrossRef]
- Dhanola, A.; Bisht, A.S.; Kumar, A.; Kumar, A. Influence of natural fillers on physico-mechanical properties of luffa cylindrica/ polyester composites. Mater. Today Proc. 2018, 5, 17021–17029. [Google Scholar] [CrossRef]
- Islam, M.S.; Hasbullah, N.A.B.; Hasan, M.; Talib, Z.A.; Jawaid, M.; Haafiz, M.K.M. Physical, mechanical and biodegradable properties of kenaf/coir hybrid fiber reinforced polymer nanocomposites. Mater. Today Commun. 2015, 4, 69–76. [Google Scholar] [CrossRef]
- Pickering, K.L.; Efendy, M.G.A.; Le, T.M. A review of recent developments in natural fibre composites and their mechanical performance. Compos. Part A Appl. Sci. Manuf. 2016, 83, 98–112. [Google Scholar] [CrossRef] [Green Version]
- Cavalcanti, D.K.K.; Banea, M.D.; Neto, J.S.S.; Lima, R.A.A.; Da Silva, L.; Carbas, R.J.C. Mechanical characterization of intralaminar natural fibre-reinforced hybrid composites. Compos. Part B Eng. 2019, 175, 107149. [Google Scholar] [CrossRef]
- Subasinghe, A.; Das, R.; Bhattacharyya, D. Study of thermal, flammability and mechanical properties of intumescent flame retardant PP/kenaf nanocomposites. Int. J. Smart Nano Mater. 2016, 7, 202–220. [Google Scholar] [CrossRef] [Green Version]
- Chollakup, R.; Smitthipong, W.; Kongtud, W.; Tantatherdtam, R. Polyethylene green composites reinforced with cellulose fibers (coir and palm fibers): Effect of fiber surface treatment and fiber content. J. Adhes. Sci. Technol. 2013, 27, 1290–1300. [Google Scholar] [CrossRef]
- Pappu, A.; Pickering, K.L.; Thakur, V.K. Manufacturing and characterization of sustainable hybrid composites using sisal and hemp fibres as reinforcement of poly (lactic acid) via injection moulding. Ind. Crop. Prod. 2019, 137, 260–269. [Google Scholar] [CrossRef]
- Saw, S.K.; Akhtar, K.; Yadav, N.; Singh, A.K. Hybrid Composites Made from Jute/Coir Fibers: Water Absorption, Thickness Swelling, Density, Morphology, and Mechanical Properties. J. Nat. Fibers 2014, 11, 39–53. [Google Scholar] [CrossRef]
- Boopalan, M.; Niranjanaa, M.; Umapathy, M.J. Study on the mechanical properties and thermal properties of jute and banana fiber reinforced epoxy hybrid composites. Compos. Part B Eng. 2013, 51, 54–57. [Google Scholar] [CrossRef]
- Vassilopoulos, A.P.; Georgopoulos, E.F. Computational intelligence methods for the fatigue life modeling of composite materials. In Fatigue Life Prediction of Composites and Composite Structures; Woodhead Publishing: Cambridge, UK, 2020; pp. 349–383. [Google Scholar]
- Kashyap, S.; Nath, D.; Das, D. Characterization, weathering and modeling of natural fibre based composites. Mater. Today Proc. 2020, 26, 963–971. [Google Scholar] [CrossRef]
- Venkateshwaran, N.; Elayaperumal, A. Modeling and evaluation of tensile properties of randomly oriented banana/epoxy composite. J. Reinf. Plast. Compos. 2011, 30, 1957–1967. [Google Scholar] [CrossRef]
- Krishnan, K.A.; Anjana, R.; George, K. Effect of alkali-resistant glass fiber on polypropylene/polystyrene blends: Modeling and characterization. Polym. Compos. 2014, 37, 398–406. [Google Scholar] [CrossRef]
- Arrakhiz, F.Z.; Hamou, K.B.; Erchiqui, F.; Hammiche, D.; Kaddami, H. Development and characterization of hybrid composite laminate based on luffa and glass fibers. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Pan, Y.; Zhong, Z. Relative humidity and temperature dependence of mechanical degradation of natural fiber composites. Sci. China Ser. G Physics, Mech. Astron. 2016, 59, 664603. [Google Scholar] [CrossRef]
- Tian, F.; Zhong, Z.; Pan, Y. Modeling of natural fiber reinforced composites under hygrothermal ageing. Compos. Struct. 2018, 200, 144–152. [Google Scholar] [CrossRef]
- Karakoti, A.; Tripathy, P.; Kar, V.R.; Jayakrishnan, K.; Rajesh, M.; Manikandan, M. Finite element modeling of natural fiber-based hybrid composites. In Modelling of Damage Processes in Biocomposites, Fibre-Reinforced Composites and Hybrid Composites; Woodhead Publishing: Cambridge, UK, 2019; pp. 1–18. [Google Scholar]
- Kern, W.T.; Kim, W.; Argento, A.; Lee, E.C.; Mielewski, D.F. Finite element analysis and microscopy of natural fiber composites containing microcellular voids. Mater. Des. 2016, 106, 285–294. [Google Scholar] [CrossRef] [Green Version]
- Sowmya, C.; Ramesh, V.; Karibasavaraja, D. An Experimental Investigation of New Hybrid Composite Material using Hemp and Jute Fibres and Its Mechanical Properties through Finite Element Method. Mater. Today Proc. 2018, 5, 13309–13320. [Google Scholar] [CrossRef]
- Ang, J.Y.; Majid, M.A.; Nor, A.M.; Yaacob, S.; Ridzuan, M.J.M. First-ply failure prediction of glass/epoxy composite pipes using an artificial neural network model. Compos. Struct. 2018, 200, 579–588. [Google Scholar] [CrossRef]
- Raschka, S.; Mirjalili, V. Python Machine Learning: Machine Learning and Deep Learning with Python, Scikit-Learn, and TensorFlow 2, 3rd ed.; Packt Publishing, Limited: Birmingham, UK, 2019; ISBN 9781789955750. [Google Scholar]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. In IEEE Transactions on Systems, Man, and Cybernetics; IEEE: Piscataway, NJ, USA, 1985; pp. 116–132. [Google Scholar] [CrossRef]







| Cellulose Materials | Application Industries | Example: Application Areas |
|---|---|---|
| Hemp, Oil palm, Wood, Flax, Rice husk, Bagasse, Sisal, Stalk, Coconut, Bamboo | Construction/Civil |
|
| Flax, Coir, Hemp, Jute, Sisal, Kenaf | Automobile |
|
| Kenaf, Flax, Sisal | Aerospace |
|
| Hemp, Cellulose | Electronics |
|
| Nanoclay, Rice husk, Ramie | Packaging |
|
| Lignin nanoparticles, Hydroxyapatite (HA)/collagen alginate, Xyloglucan, | Biomedical |
|
| Flax | Sports |
|
| Hemp, Kenaf, Cotton, Coir, Ramie, Coconut, Bamboo | Household |
|
| Fiber | Matrix | Tensile Strength (MPa) | Stiffness (GPa) | Flexural Strength (MPa) | Flexural Modulus (GPa) | Reference |
|---|---|---|---|---|---|---|
| Banana | Epoxy | 46 | 8 | - | - | [1] |
| Sisal | Epoxy | 212 | 6 | 320 | 27 | [51] |
| Oil Palm | PP | 53 | 2 | 80 | 3 | [52] |
| Jute | PP | 74 | 11 | 112 | 12 | [53] |
| Coir | Epoxy | 225 | 6 | - | - | [52] |
| Kenaf | PLA | 223 | 23 | 259 | 22 | [54] |
| Coir | PP | 17 | 2.3 | 27.4 | 1.8 | [55] |
| Hemp | Epoxy | 165 | 17 | 180 | 9 | [52] |
| Sisal/Hemp | PLA | 60.23 | 6.1 | 79.76 | 6.04 | [56] |
| Flax | UP | 147 | 14 | 198 | 17 | [52] |
| Jute/Banana | Epoxy | 18.96 | 0.724 | 59.84 | 9.170 | [57] |
| Jute/Sisal | Epoxy | 74.78 | 6.76 | - | - | [58] |
| Hemp | PP | 52 | 4 | 86 | 4 | [53] |
| Flax | Epoxy | 160 | 15 | 190 | 18 | [52] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mulenga, T.K.; Ude, A.U.; Vivekanandhan, C. Techniques for Modelling and Optimizing the Mechanical Properties of Natural Fiber Composites: A Review. Fibers 2021, 9, 6. https://doi.org/10.3390/fib9010006
Mulenga TK, Ude AU, Vivekanandhan C. Techniques for Modelling and Optimizing the Mechanical Properties of Natural Fiber Composites: A Review. Fibers. 2021; 9(1):6. https://doi.org/10.3390/fib9010006
Chicago/Turabian StyleMulenga, Timothy K., Albert U. Ude, and Chinnasamy Vivekanandhan. 2021. "Techniques for Modelling and Optimizing the Mechanical Properties of Natural Fiber Composites: A Review" Fibers 9, no. 1: 6. https://doi.org/10.3390/fib9010006
APA StyleMulenga, T. K., Ude, A. U., & Vivekanandhan, C. (2021). Techniques for Modelling and Optimizing the Mechanical Properties of Natural Fiber Composites: A Review. Fibers, 9(1), 6. https://doi.org/10.3390/fib9010006







