The Significance of Cross-Sectional Shape Accuracy and Non-Linear Elasticity on the Numerical Modelling of Cerebral Veins under Tensile Loading
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
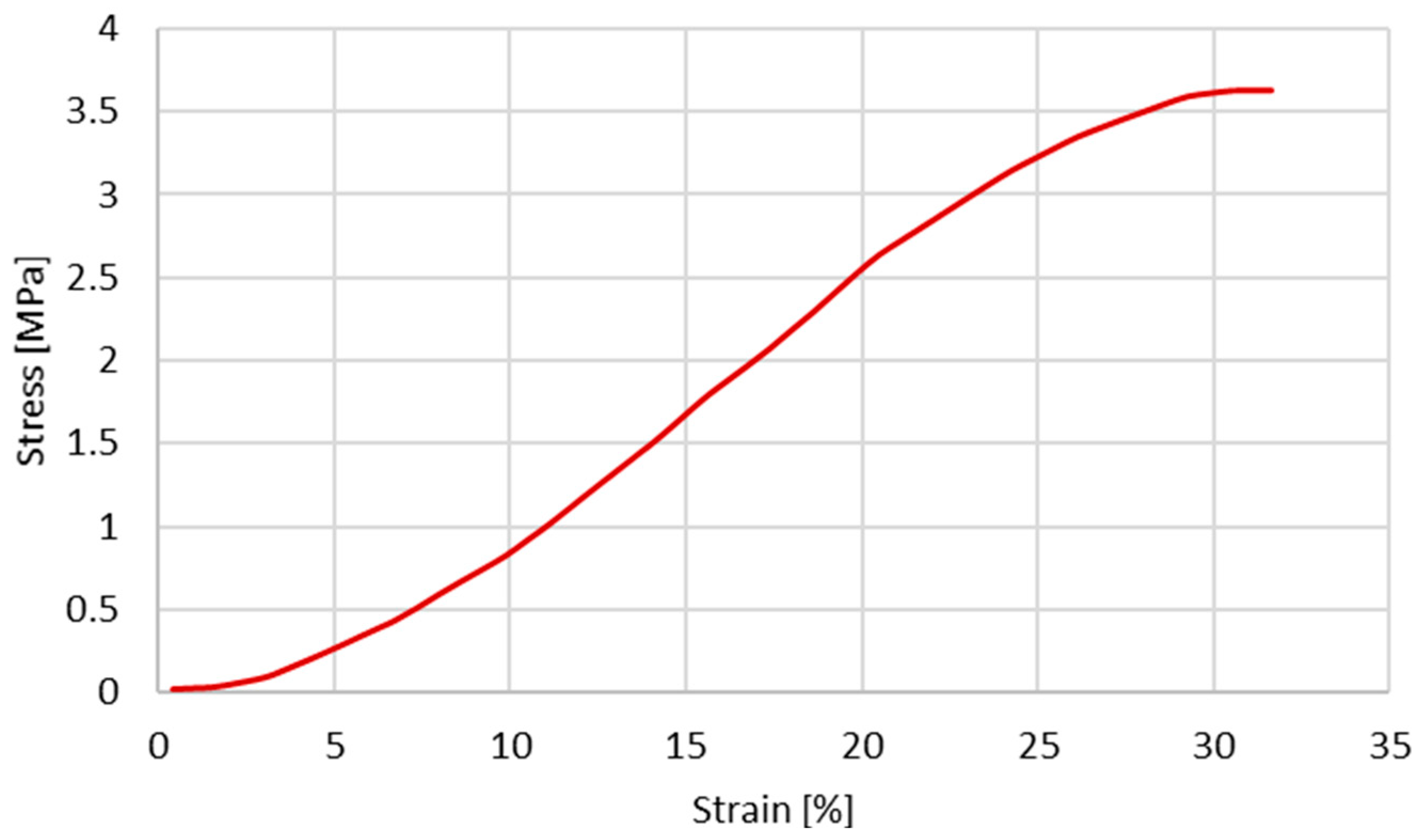
2.1. FE Modelling and BV Tensile Testing in Monea et al. [24]
2.2. Constitutive Modelling—Hyperelasticity
3. Results
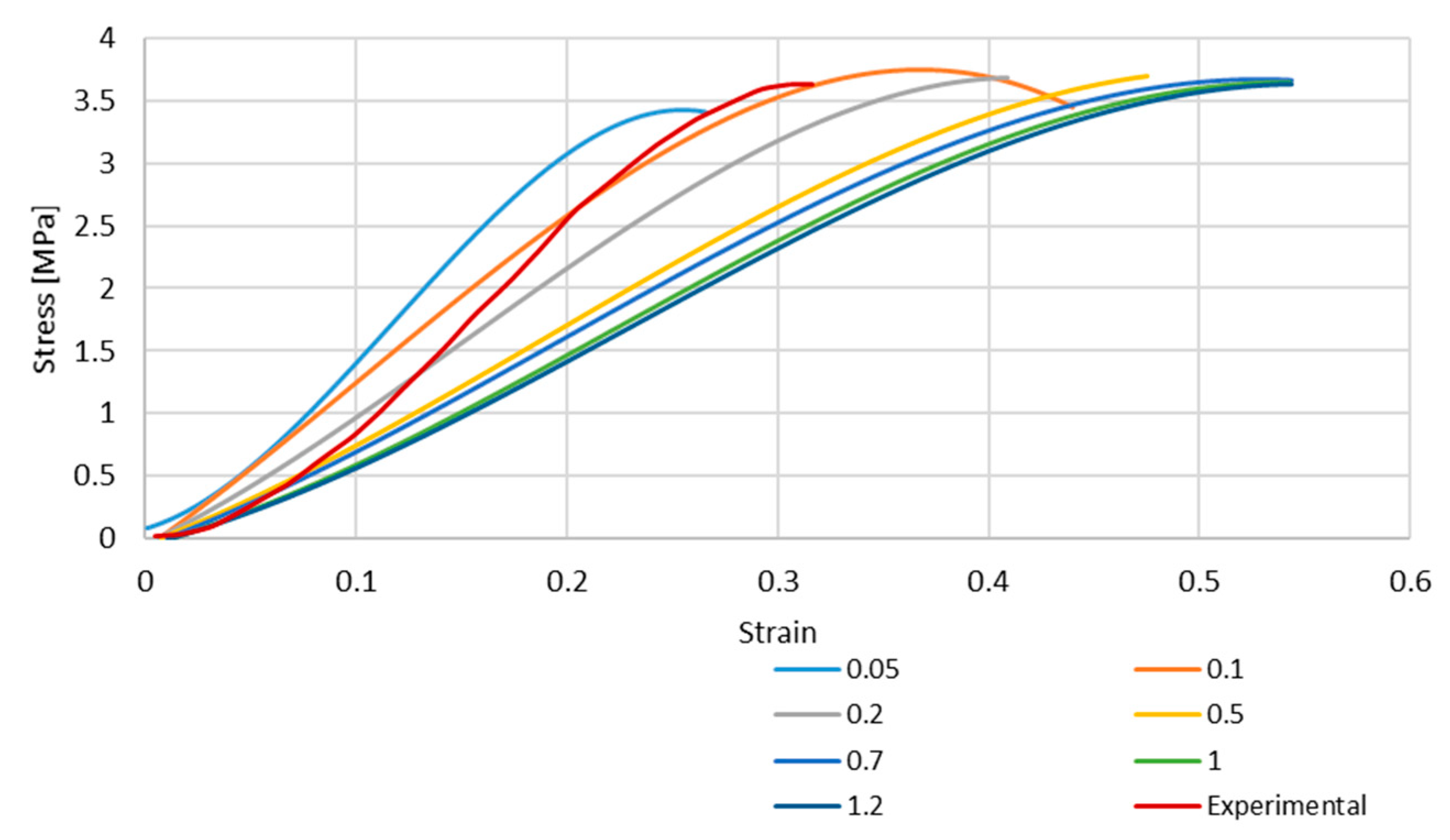
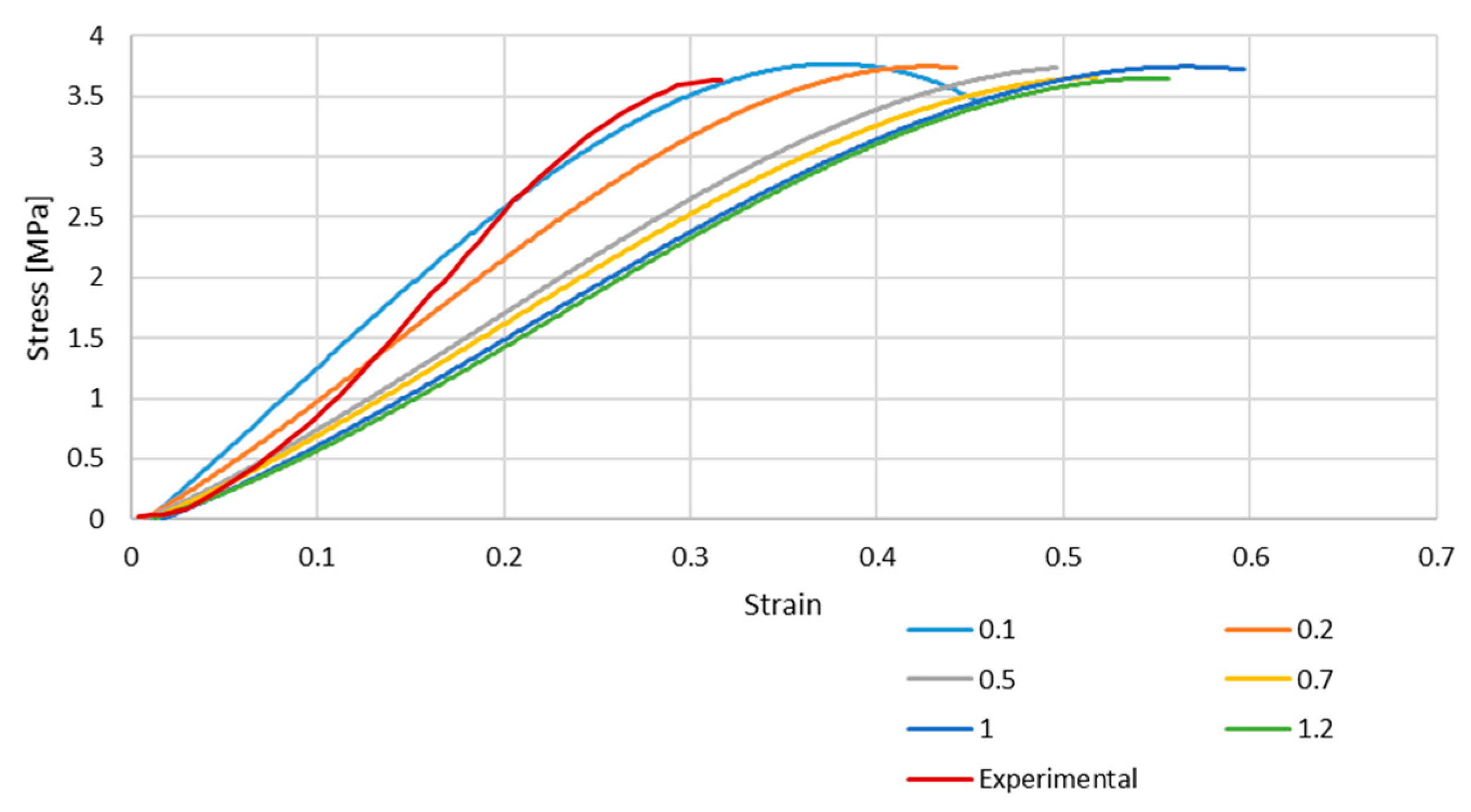
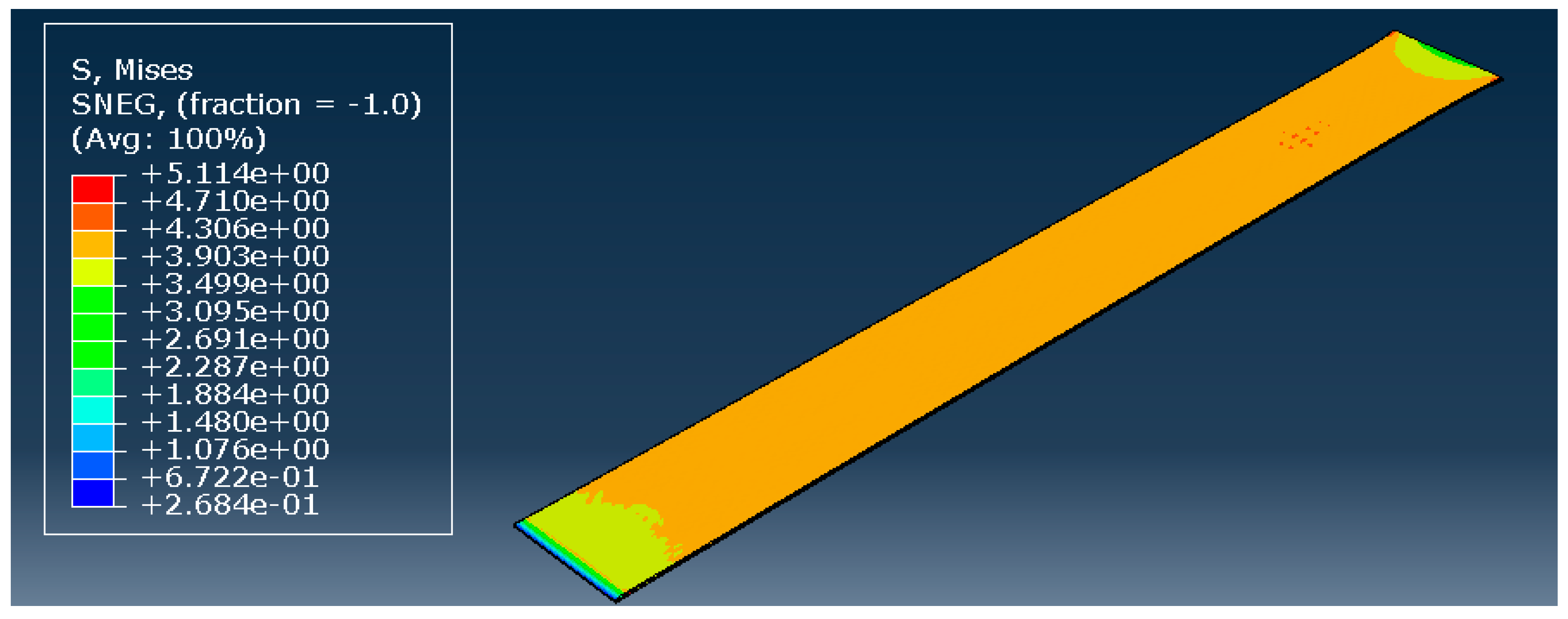
3.1. The Influence of the Geometrical Shape of the Cross-Section
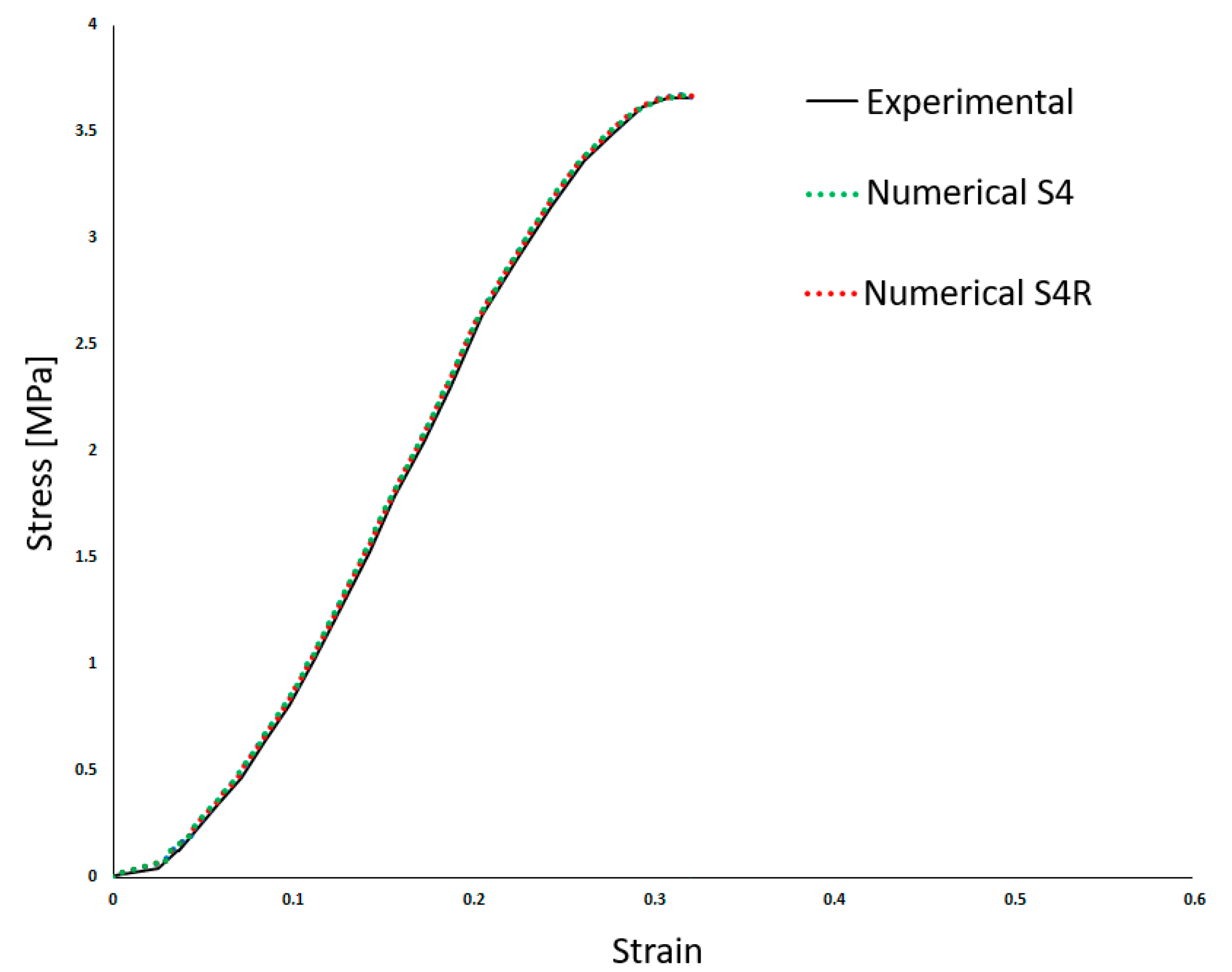
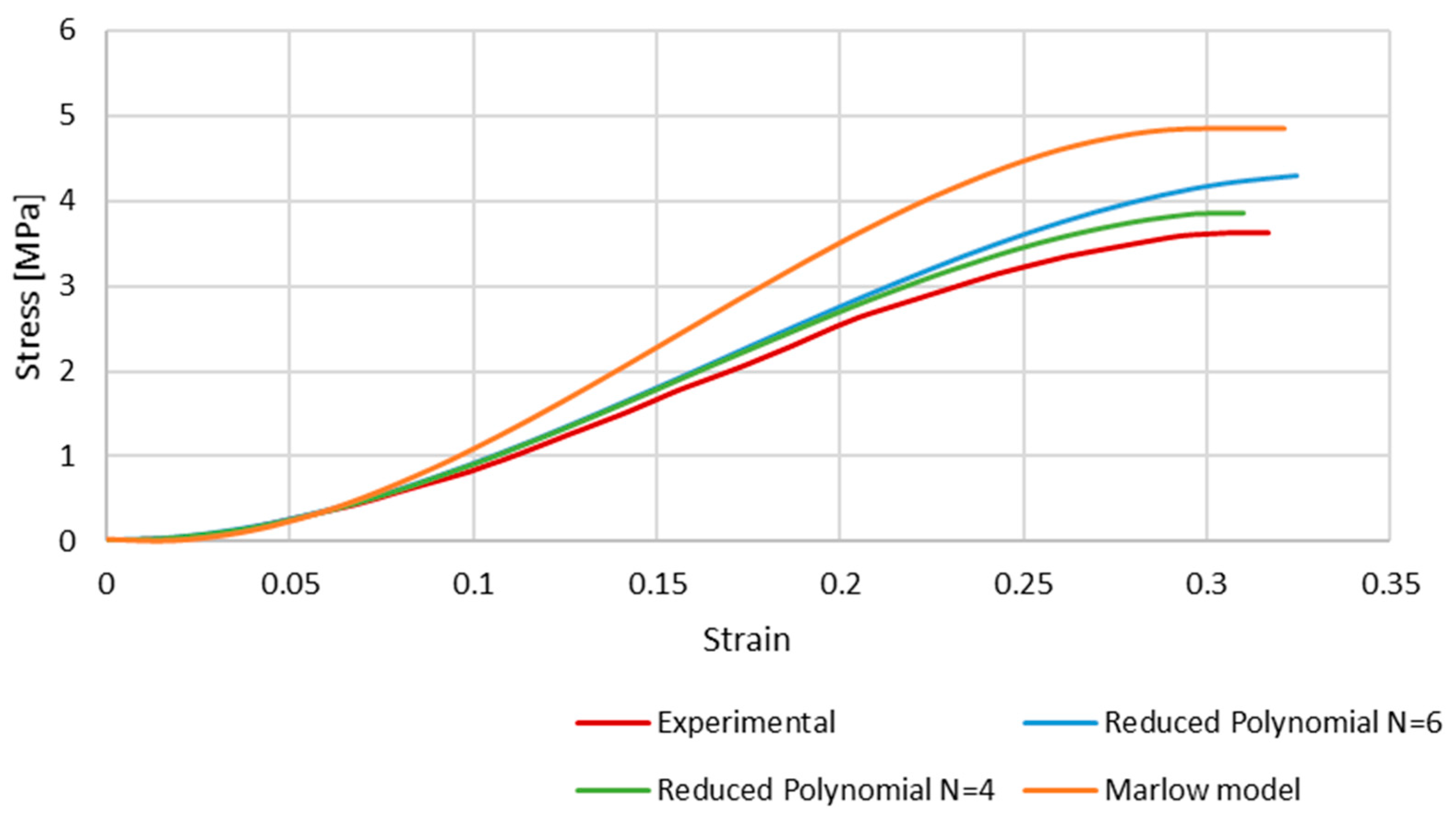
3.2. Hyperelastic Material Model Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- James, S.L.; Bannick, M.S.; Montjoy-Venning, W.C.; Lucchesi, L.R.; Dandona, L.; Dandona, R.; Hawley, C.; Hay, S.I.; Jakovljevic, M.; Khalil, I.; et al. Global, Regional, and National Burden of Traumatic Brain Injury and Spinal Cord Injury, 1990–2016: A Systematic Analysis for the Global Burden of Disease Study 2016. Lancet Neurol. 2019, 18, 56–87. [Google Scholar] [CrossRef] [PubMed]
- Dewan, M.C.; Rattani, A.; Gupta, S.; Baticulon, R.E.; Hung, Y.C.; Punchak, M.; Agrawal, A.; Adeleye, A.O.; Shrime, M.G.; Rubiano, A.M.; et al. Estimating the Global Incidence of Traumatic Brain Injury. J. Neurosurg. 2018, 130, 1080–1097. [Google Scholar] [CrossRef] [PubMed]
- Traumatic Brain Injury: Epidemiology, Classification, and Pathophysiology—UpToDate. Available online: https://www.uptodate.com/contents/traumatic-brain-injury-epidemiology-classification-and-pathophysiology/print (accessed on 17 August 2023).
- Bartels, R.H.M.A.; Meijer, F.J.A.; van der Hoeven, H.; Edwards, M.; Prokop, M. Midline Shift in Relation to Thickness of Traumatic Acute Subdural Hematoma Predicts Mortality. BMC Neurol. 2015, 15, 220. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Song, S.W.; Choe, W.J.; Cho, J.; Moon, C.T.; Koh, Y.-C. Risk Stratification in Patients with Severe Traumatic Acute Subdural Hematoma. Nerve 2017, 3, 50–57. [Google Scholar] [CrossRef][Green Version]
- AbdelFatah, M.A.R. Prognosis of Acute Subdural Hematoma Greater than 10 Mm in Thickness in Head Injury Patients with an Extension or No Motor Response to Pain after Resuscitation. Egypt. J. Neurosurg. 2019, 34, 9. [Google Scholar] [CrossRef]
- Hufnagle, J.J.; Tadi, P. Neuroanatomy, Brain Veins. In StatPearls; StatPearls Publishing: Tampa, FL, USA, 2021. [Google Scholar]
- Letchuman, V.; Donohoe, C. Neuroanatomy, Superior Sagittal Sinus. In Study Guide; StatPearls Publishing: Treasure Island, FL, USA, 2022. [Google Scholar]
- Brockmann, C.; Kunze, S.; Scharf, J. Computed Tomographic Angiography of the Superior Sagittal Sinus and Bridging Veins. Surg. Radiol. Anat. 2011, 33, 129–134. [Google Scholar] [CrossRef] [PubMed]
- Pang, Q.; Lu, X.; Gregersen, H.; Von Oettingen, G.; Astrup, J. Biomechanical Properties of Porcine Cerebral Bridging Veins with Reference to the Zero-Stress State. J. Vasc. Res. 2001, 38, 83–90. [Google Scholar] [CrossRef]
- Camasão, D.B.; Mantovani, D. The Mechanical Characterization of Blood Vessels and Their Substitutes in the Continuous Quest for Physiological-Relevant Performances. A Critical Review. Mater. Today Bio 2021, 10, 100106. [Google Scholar] [CrossRef]
- Hardy, C.H.; Marcal, P.V. Elastic Analysis of a Skull. J. Appl. Mech. Trans. ASME 1973, 40, 838–842. [Google Scholar] [CrossRef]
- Shugar, T.A. Transient Structural Response of the Linear Skull-Brain System. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 1975. [Google Scholar] [CrossRef]
- Chan, H.S. Mathematical Model for Closed Head Impact. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 1974. [Google Scholar] [CrossRef]
- Khalil, T.B.; Hubbard, R.P. Parametric Study of Head Response by Finite Element Modeling. J. Biomech. 1977, 10, 119–132. [Google Scholar] [CrossRef]
- Oka, K.; Rhoton, A.L.; Barry, M.; Rodriguez, R. Microsurgical Anatomy of the Superficial Veins of the Cerebrum. Neurosurgery 1985, 17, 711–748. [Google Scholar] [CrossRef] [PubMed]
- Ratajczak, M.; Ptak, M.; Chybowski, L.; Gawdzińska, K.; Bedziński, R. Material and Structural Modeling Aspects of Brain Tissue Deformation under Dynamic Loads. Materials 2019, 12, 271. [Google Scholar] [CrossRef] [PubMed]
- Takhounts, E.G.; Ridella, S.A.; Hasija, V.; Tannous, R.E.; Campbell, J.Q.; Malone, D.; Danelson, K.; Stitzel, J.; Rowson, S.; Duma, S.; et al. Investigation of Traumatic Brain Injuries Using the Next Generation of Simulated Injury Monitor (SIMon) Finite Element Head Model. Stapp Car Crash J. 2008, 52, 403. [Google Scholar]
- Migueis, G.F.J.; Fernandes, F.A.O.; Ptak, M.; Ratajczak, M.; Alves de Sousa, R.J. Detection of Bridging Veins Rupture and Subdural Haematoma Onset Using a Finite Element Head Model. Clin. Biomech. 2019, 63, 104–111. [Google Scholar] [CrossRef] [PubMed]
- Costa, J.M.C.; Fernandes, F.A.O.; Alves de Sousa, R.J. Prediction of Subdural Haematoma Based on a Detailed Numerical Model of the Cerebral Bridging Veins. J. Mech. Behav. Biomed. Mater. 2020, 111, 103976. [Google Scholar] [CrossRef]
- Kapeliotis, M.; Musigazi, G.U.; Famaey, N.; Depreitere, B.; Kleiven, S.; Sloten, J. Vander the Sensitivity to Inter-Subject Variability of the Bridging Vein Entry Angles for Prediction of Acute Subdural Hematoma. J. Biomech. 2019, 92, 6–10. [Google Scholar] [CrossRef]
- Cui, Z.Y.; Famaey, N.; Depreitere, B.; Ivens, J.; Kleiven, S.; Vander Sloten, J. On the Assessment of Bridging Vein Rupture Associated Acute Subdural Hematoma through Finite Element Analysis. Comput. Methods Biomech. Biomed. Engin. 2017, 20, 530–539. [Google Scholar] [CrossRef]
- Depreitere, B.; Van Lierde, C.; Vander Sloten, J.; Van Audekercke, R.; Van Der Perre, G.; Plets, C.; Goffin, J. Mechanics of Acute Subdural Hematomas Resulting from Bridging Vein Rupture. J. Neurosurg. 2006, 104, 950–956. [Google Scholar] [CrossRef]
- Monea, A.G.; Baeck, K.; Verbeken, E.; Verpoest, I.; Vander Sloten, J.; Goffin, J.; Depreitere, B. The Biomechanical Behaviour of the Bridging Vein–Superior Sagittal Sinus Complex with Implications for the Mechanopathology of Acute Subdural Haematoma. J. Mech. Behav. Biomed. Mater. 2014, 32, 155–165. [Google Scholar] [CrossRef]
- Famaey, N.; Ying Cui, Z.; Umuhire Musigazi, G.; Ivens, J.; Depreitere, B.; Verbeken, E.; Vander Sloten, J. Structural and Mechanical Characterisation of Bridging Veins: A Review. J. Mech. Behav. Biomed. Mater. 2015, 41, 222–240. [Google Scholar] [CrossRef]
- Sánchez-Molina, D.; García-Vilana, S.; Llumà, J.; Galtés, I.; Velázquez-Ameijide, J.; Rebollo-Soria, M.C.; Arregui-Dalmases, C. Mechanical Behavior of Blood Vessels: Elastic and Viscoelastic Contributions. Biology 2021, 10, 831. [Google Scholar] [CrossRef] [PubMed]
- García-Vilana, S.; Sánchez-Molina, D.; Llumà, J.; Galtés, I.; Velázquez-Ameijide, J.; Rebollo-Soria, M.C.; Arregui-Dalmases, C. Viscoelastic Characterization of Parasagittal Bridging Veins and Implications for Traumatic Brain Injury: A Pilot Study. Bioengineering 2021, 8, 145. [Google Scholar] [CrossRef] [PubMed]
- Pasquesi, S.A.; Margulies, S.S. Measurement and Finite Element Model Validation of Immature Porcine Brain-Skull Displacement during Rapid Sagittal Head Rotations. Front. Bioeng. Biotechnol. 2018, 6, 317719. [Google Scholar] [CrossRef] [PubMed]
- Pasquesi, S.A.; Seidi, M.; Hajiaghamemar, M.; Margulies, S.S. Predictions of Neonatal Porcine Bridging Vein Rupture and Extra-Axial Hemorrhage during Rapid Head Rotations. J. Mech. Behav. Biomed. Mater. 2020, 106, 103740. [Google Scholar] [CrossRef] [PubMed]
- García-Vilana, S.; Sánchez-Molina, D. Age Effects on the Mechanical Behavior of Human Cerebral Bridging Veins. Clin. Biomech. 2022, 100, 105792. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Ji, S. Cerebral Vascular Strains in Dynamic Head Impact Using an Upgraded Model with Brain Material Property Heterogeneity. J. Mech. Behav. Biomed. Mater. 2022, 126, 104967. [Google Scholar] [CrossRef]
- Subramaniam, D.R.; Unnikrishnan, G.; Sundaramurthy, A.; Rubio, J.E.; Kote, V.B.; Reifman, J. The Importance of Modeling the Human Cerebral Vasculature in Blunt Trauma. Biomed. Eng. Online 2021, 20, 11. [Google Scholar] [CrossRef]
- Quantifying Biovariability in Position and Diameter of Bridging Veins to Improve Acute Subdural Hematoma Prediction in FE Head Models. Available online: http://www.ircobi.org/wordpress/downloads/irc21/pdf-files/2141.pdf (accessed on 15 October 2023).
- Large Deformation Isotropic Elasticity—On the Correlation of Theory and Experiment for Incompressible Rubberlike Solids. Proc. R. Soc. Lond. A Math. Phys. Sci. 1972, 326, 565–584. [CrossRef]
- Arruda, E.M.; Boyce, M.C. A Three-Dimensional Constitutive Model for the Large Stretch Behavior of Rubber Elastic Materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Boyce, M.C.; Arruda, E.M. Constitutive Models of Rubber Elasticity: A Review. Rubber Chem. Technol. 2000, 73, 504–523. [Google Scholar] [CrossRef]
- Melly, S.K.; Liu, L.; Liu, Y.; Leng, J. A Review on Material Models for Isotropic Hyperelasticity. Int. J. Mech. Syst. Dyn. 2021, 1, 71–88. [Google Scholar] [CrossRef]
- ABAQUS Version 6.6 Documentation. Available online: https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/index.html (accessed on 4 September 2022).

| Ømax SSS opening (mm) | Ømin BV (mm) | dmean (mm) | h (mm) |
| 4.99 ± 1.86 | 1.88 ± 0.83 | 3.42 ± 1.18 | 0.044 ± 0.017 |
| ρ (kg/m3) | E (MPa) | ν |
| 1130 | 25.72 | 0.45 |
| Fracture Strain | Stress Triaxiality | Strain Rate [s−1] | Displacement at Fracture |
| 0.31875 | 0.33 | 135.86 | 0.05 |
| C10 (MPa) | C20 (MPa) | C30 (MPa) | C40 (MPa) | D1 [MPa−1] |
| 0.507231065 | 21.4170360 | −92.7419760 | 142.420876 | 0.203947043 |
| C10 (MPa) | C20 (MPa) | C30 (MPa) | C40 (MPa) | C50 (MPa) | C60 (MPa) | D1 [MPa−1] |
| 0.464417032 | 29.4654136 | −278.559124 | 1660.99772 | −5202.69082 | 6384.20622 | 0.222748669 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernandes, F.A.O.; Silveira, C.I.C. The Significance of Cross-Sectional Shape Accuracy and Non-Linear Elasticity on the Numerical Modelling of Cerebral Veins under Tensile Loading. Biology 2024, 13, 16. https://doi.org/10.3390/biology13010016
Fernandes FAO, Silveira CIC. The Significance of Cross-Sectional Shape Accuracy and Non-Linear Elasticity on the Numerical Modelling of Cerebral Veins under Tensile Loading. Biology. 2024; 13(1):16. https://doi.org/10.3390/biology13010016
Chicago/Turabian StyleFernandes, Fábio A. O., and Clara I. C. Silveira. 2024. "The Significance of Cross-Sectional Shape Accuracy and Non-Linear Elasticity on the Numerical Modelling of Cerebral Veins under Tensile Loading" Biology 13, no. 1: 16. https://doi.org/10.3390/biology13010016
APA StyleFernandes, F. A. O., & Silveira, C. I. C. (2024). The Significance of Cross-Sectional Shape Accuracy and Non-Linear Elasticity on the Numerical Modelling of Cerebral Veins under Tensile Loading. Biology, 13(1), 16. https://doi.org/10.3390/biology13010016








