Performance Evaluation and Influencing Factors of Scientific Communication in Research Institutions
Abstract
:1. Introduction
- Firstly, we introduce a comprehensive and objective evaluation framework tailored to research institutions. The research institutions discussed in this paper only include those in the field of natural sciences whose main work is scientific research. This framework incorporates a scientific communication performance evaluation index system and utilizes the two-stage DEA method to assess efficiency. This approach ensures a rigorous and unbiased assessment of scientific communication performance, considering the unique characteristics of research institutions.
- Secondly, our study employs advanced analytical techniques, including K-means clustering and the Tobit Model, to delve deeper into the similarities and differences among research institutions. This analysis reveals critical patterns and identifies the influencing factors that impact scientific communication efficiency. These insights provide a deeper understanding of the factors that drive performance variations across institutions.
- Lastly, based on our evaluation and analysis findings, we offer practical recommendations tailored to enhance the scientific communication performance of research institutions. These recommendations aim to guide institutions in leveraging their strengths, addressing weaknesses, and capitalizing on opportunities for improvement. By implementing these recommendations, institutions can foster a more robust scientific communication ecosystem, leading to enhanced research outcomes and a more significant impact.
2. Literature Review
2.1. Scientific Communication
2.2. Efficiency Evaluation
2.3. Scientific Communication Evaluation
3. Method
3.1. Two-Stage DEA
3.2. Tobit Regression
4. Results and Discussions
4.1. Indicator System
4.2. Descriptive Statistics of Indicators
4.3. Two-Stage Efficiency
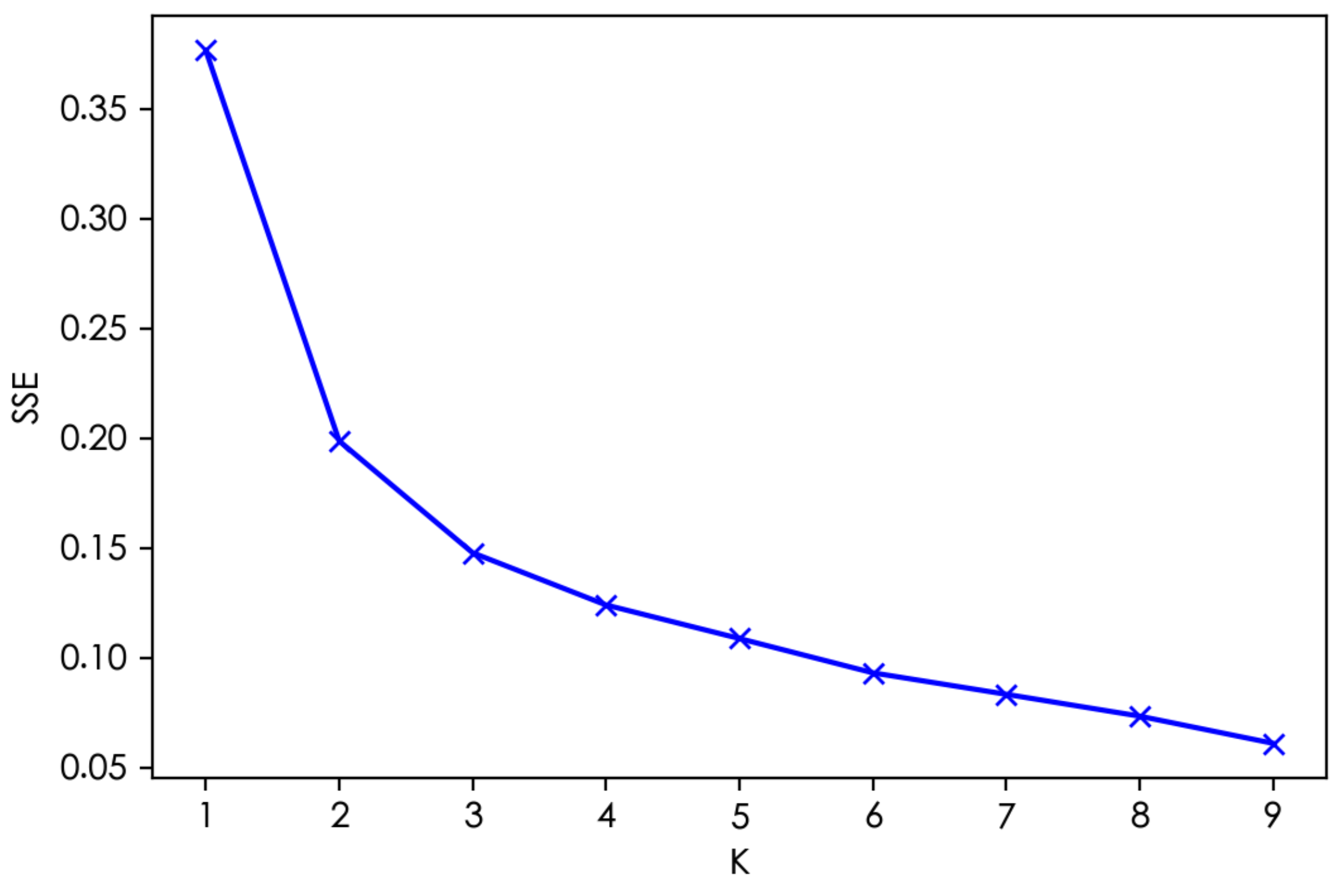
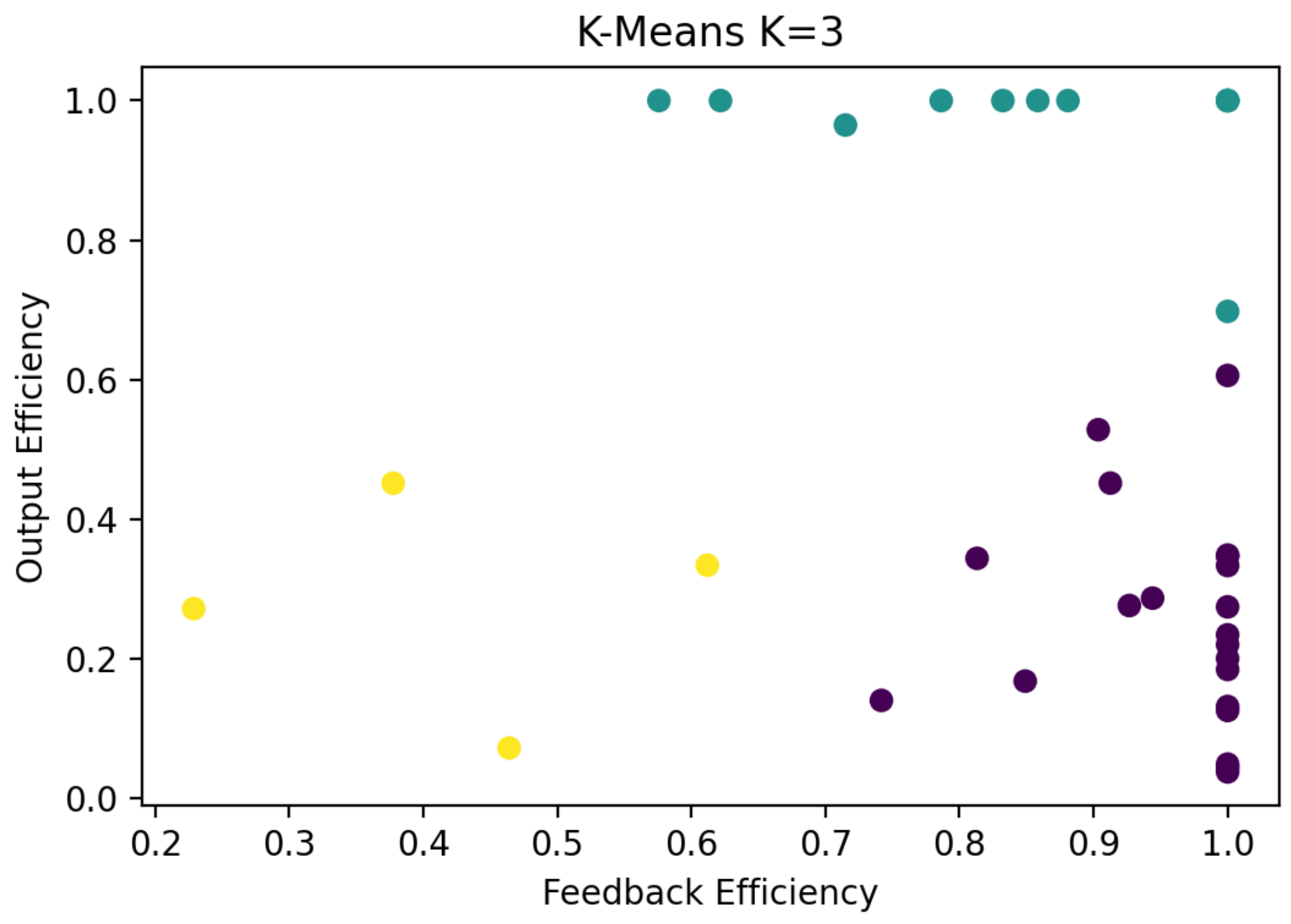
4.4. Cluster Analysis
4.5. Influence Factor Analysis
4.6. Discussions
- 1.
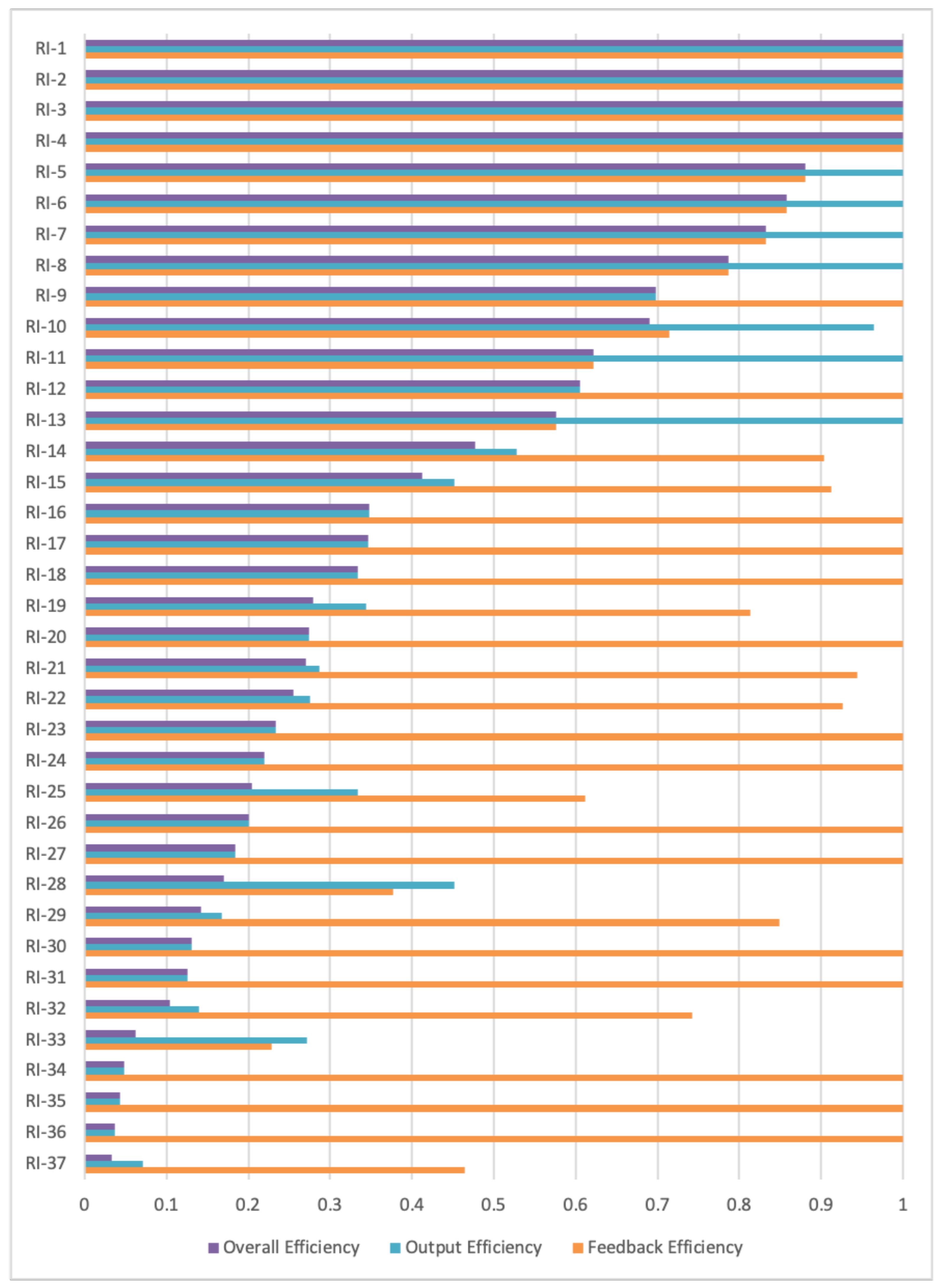
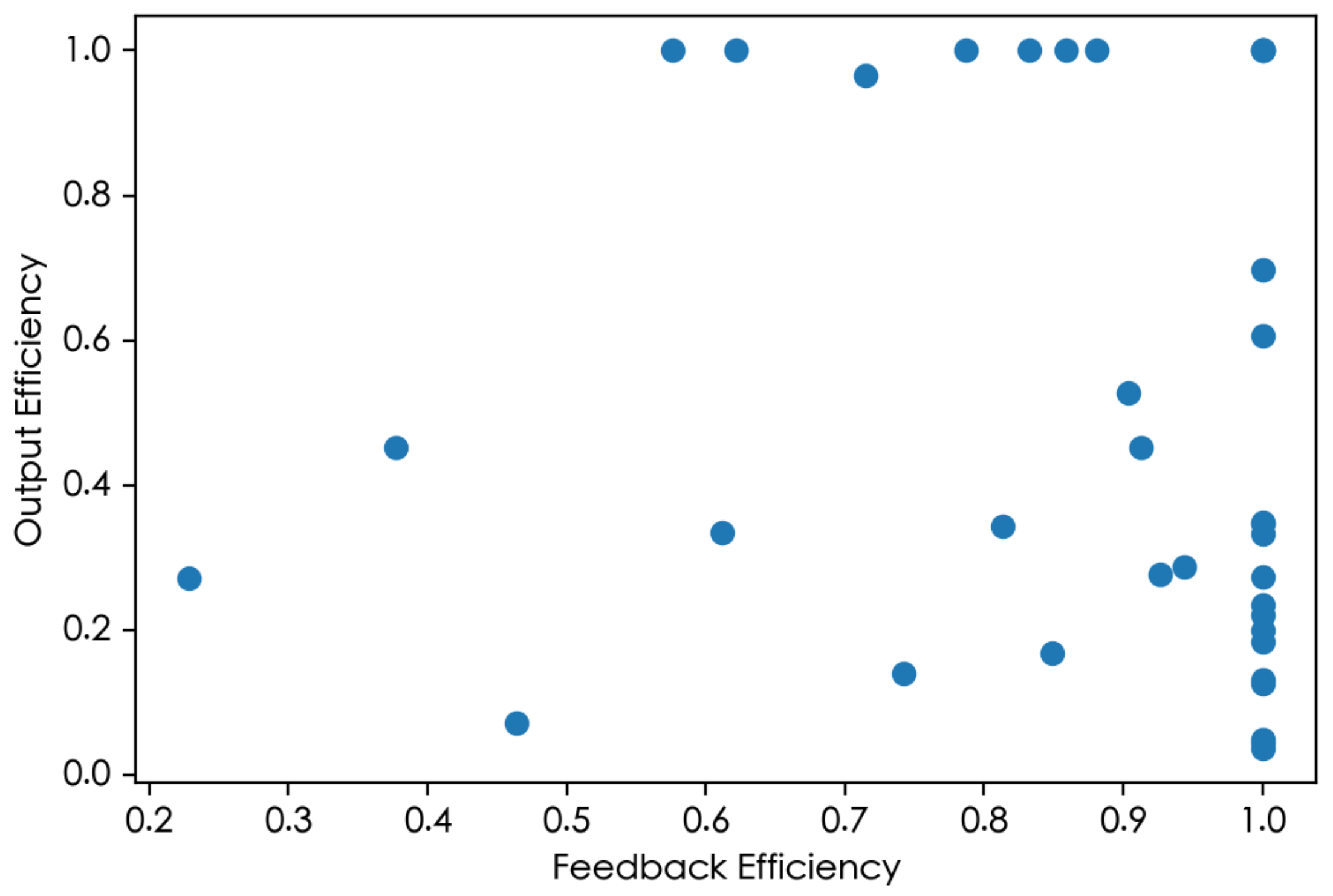
- Enhancing content output efficiency: For research institutions that exhibit high feedback efficiency but relatively low output efficiency, such as the purple institutions identified in Table 5, the low output efficiency may be attributed to factors such as inefficient work processes, resource constraints, or a lack of focused content production strategies. To address this issue, it is advisable to prioritize the optimization of their workflows. This optimization should aim to streamline processes, allocate resources more effectively, and establish clear content production goals. By doing so, not only will the volume of scientific communication output increase, but the maintenance of content quality will also be ensured. A thorough analysis of existing workflows is crucial in identifying and eliminating any bottlenecks or obstacles, thereby enabling a smoother and more efficient production process for scientific content.
- 2.
- Improving content quality: Institutions like RI-11 and RI-13 in Figure 2, which demonstrate low feedback efficiency despite high output efficiency, may be facing challenges in terms of content relevance, target audience engagement, or the quality of their communication channels. This could be due to a lack of focus on content quality, limited interaction with stakeholders, or ineffective dissemination strategies. To enhance their overall effectiveness, it is strongly recommended that these institutions focus on strengthening content quality control. This should involve conducting deeper research, enhancing the originality and practicality of their findings, and refining the way they present and disseminate their content to better engage their target audience. By doing so, they can create more influential, high-quality scientific communication content that not only establishes their academic credibility, but also fosters meaningful interactions and feedback loops.
- 3.
- Leveraging technology and tools: Nowadays, the significance of online social networks in information dissemination cannot be overstated [26]. Our evaluation indicators system, encompassing both traditional and online media, reflects this reality. However, merely acknowledging their importance is insufficient. Research institutions must actively harness modern technology and digital tools to revolutionize scientific communication. We propose a multifaceted approach: firstly, leveraging social media platforms to engage directly with target audiences, disseminating research findings in real-time and fostering meaningful discussions; secondly, developing comprehensive online resources, such as repositories and interactive visualizations, to enhance both the accessibility and usability of scientific information; and finally, creating interactive websites that incorporate feedback loops from users, allowing institutions to gather insights, refine communication strategies, and ultimately broaden their impact. By embracing these strategies, research institutions can optimize their communication processes as well as significantly enhance the visibility and influence of their scientific work. Certainly, while pursuing these improvements, it is imperative to maintain the rigorousness and professionalism inherent to research institutions, ensuring the uncompromised scientific integrity of their work while maintaining an appropriate level of interaction.
- 4.
- Balancing efficiency and investments in personnel and funding: Our analysis in Section 4.5 reveals correlations between the number of formal employees, total expenditure and the efficiency of scientific communication. Research institutions must strike a delicate balance between efficiently utilizing existing funds and optimizing their personnel investments. By prioritizing both the effective use of funds and the deployment of a capable workforce, research institutions can achieve improvements in scientific communication efficiency.
- 5.
- Regular evaluation and adjustment: As time goes by, the way science is disseminated is also changing, and inappropriate evaluation methods can have adverse effects on science dissemination [4]. Therefore, institutions should establish a comprehensive monitoring and evaluation mechanism that regularly assesses the efficiency of their communication efforts. This includes quantitative and qualitative measures to gauge the reach, engagement, and overall impact of their scientific messages. Based on these evaluations, strategic adjustments and workflow optimizations must be made to align with current trends and best practices. By continuously evaluating and adapting their approaches, research institutions can maximize the impact of their scientific communication, ensuring that their work is recognized and valued, and contributes to the advancement of knowledge and science.
- 6.
- Awareness of data bias: In this study, we used data such as reading volume in the second stage to evaluate the quality of scientific communication content, which may lead to some biases. The reading volume of scientific communication content is not only related to the quality of the content, but also to the theme of the communication content. The related content of hot topics will lead to wider dissemination and reading. In addition, feedback indicators are collected at the end of the year, which can lead to poor feedback data on scientific communication content released at the end of the year.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Burns, T.W.; O’Connor, D.J.; Stocklmayer, S.M. Science communication: A contemporary definition. Public Underst. Sci. 2003, 12, 183–202. [Google Scholar] [CrossRef]
- Nosek, B.A.; Bar-Anan, Y. Scientific utopia: I. Opening scientific communication. Psychol. Inq. 2012, 23, 217–243. [Google Scholar] [CrossRef]
- Fischhoff, B. Evaluating science communication. Proc. Natl. Acad. Sci. USA 2019, 116, 7670–7675. [Google Scholar] [CrossRef] [PubMed]
- Scheufele, D.A. Science communication as political communication. Proc. Natl. Acad. Sci. USA 2014, 111, 13585–13592. [Google Scholar] [CrossRef]
- Saaty, R.W. The analytic hierarchy process—What it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Julong, D. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Hwang, C.L.; Yoon, K.; Hwang, C.L.; Yoon, K. Methods for multiple attribute decision making. In Multiple Attribute Decision Making: Methods and Applications a State-of-the-Art Survey; Springer: Berlin/Heidelberg, Germany, 1981; pp. 58–191. [Google Scholar]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Song, M.; Wang, R.; Zeng, X. Water resources utilization efficiency and influence factors under environmental restrictions. J. Clean. Prod. 2018, 184, 611–621. [Google Scholar] [CrossRef]
- Seiford, L.M.; Zhu, J. Profitability and marketability of the top 55 US commercial banks. Manag. Sci. 1999, 45, 1270–1288. [Google Scholar] [CrossRef]
- Kao, C.; Hwang, S.N. Efficiency decomposition in two-stage data envelopment analysis: An application to non-life insurance companies in Taiwan. Eur. J. Oper. Res. 2008, 185, 418–429. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Liang, L.; Xie, J. DEA models for extended two-stage network structures. Omega 2012, 40, 611–618. [Google Scholar] [CrossRef]
- Kao, C. Efficiency decomposition in network data envelopment analysis: A relational model. Eur. J. Oper. Res. 2009, 192, 949–962. [Google Scholar] [CrossRef]
- Zhou, F.; Si, D.; Hai, P.; Ma, P.; Pratap, S. Spatial-temporal evolution and driving factors of regional green development: An empirical study in Yellow River Basin. Systems 2023, 11, 109. [Google Scholar] [CrossRef]
- Welbourne, D.J.; Grant, W.J. Science communication on YouTube: Factors that affect channel and video popularity. Public Underst. Sci. 2016, 25, 706–718. [Google Scholar] [CrossRef] [PubMed]
- Mou, Y.; Lin, C.A. Communicating food safety via the social media: The role of knowledge and emotions on risk perception and prevention. Sci. Commun. 2014, 36, 593–616. [Google Scholar] [CrossRef]
- Liang, X.; Su, L.Y.F.; Yeo, S.K.; Scheufele, D.A.; Brossard, D.; Xenos, M.; Nealey, P.; Corley, E.A. Building Buzz: (Scientists) Communicating Science in New Media Environments. J. Mass Commun. Q. 2014, 91, 772–791. [Google Scholar] [CrossRef]
- Jensen, E. Evaluating impact and quality of experience in the 21st century: Using technology to narrow the gap between science communication research and practice. JCOM J. Sci. Commun. 2015, 14, 1–9. [Google Scholar] [CrossRef]
- Olesk, A.; Renser, B.; Bell, L.; Fornetti, A.; Franks, S.; Mannino, I.; Roche, J.; Schmidt, A.L.; Schofield, B.; Villa, R.; et al. Quality indicators for science communication: Results from a collaborative concept mapping exercise. J. Sci. Commun. 2021, 20, A06. [Google Scholar] [CrossRef]
- Liang, L.; Cook, W.D.; Zhu, J. DEA models for two-stage processes: Game approach and efficiency decomposition. Nav. Res. Logist. (NRL) 2008, 55, 643–653. [Google Scholar] [CrossRef]
- Tobin, J. Estimation of relationships for limited dependent variables. Econom. J. Econom. Soc. 1958, 26, 24–36. [Google Scholar] [CrossRef]
- Kenny, L.W.; Lee, L.F.; Maddala, G.; Trost, R.P. Returns to college education: An investigation of self-selection bias based on the project talent data. Int. Econ. Rev. 1979, 20, 775–789. [Google Scholar] [CrossRef]
- Kodinariya, T.M.; Makwana, P.R. Review on determining number of Cluster in K-Means Clustering. Int. J. 2013, 1, 90–95. [Google Scholar]
- Wu, J.; Wu, J. Cluster analysis and K-means clustering: An introduction. In Advances in K-Means Clustering: A Data Mining Thinking; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–16. [Google Scholar]
- Guille, A.; Hacid, H.; Favre, C.; Zighed, D.A. Information diffusion in online social networks: A survey. ACM Sigmod Rec. 2013, 42, 17–28. [Google Scholar] [CrossRef]

| First-Level Indicators | Second-Level Indicators |
|---|---|
| Personnel Investment | Number of Personnel Engaged in Scientific Communication |
| Proportion of Total Employees | |
| Funding Investment | Funding for Scientific Communication |
| The Proportion of Self Raised Funds |
| First-Level Indicators | Second-Level Indicators | Third-Level Indicators |
|---|---|---|
| News Promotion | News Media Coverage | Number of Reports in Traditional Media |
| Number of Reports in New Media | ||
| Online Promotion | Website Operation | Number of Reports in Wechat |
| Wechat Operation | Number of Reports in RI Websites |
| First-Level Indicators | Second-Level Indicators | Third-Level Indicators |
|---|---|---|
| News Promotion | News Quality | The Score for Traditional Media Coverage |
| The Score for New Media Coverage | ||
| Online Promotion | Website Operation | Page Clicks |
| Wechat Operation | Article Reading Volume |
| Minimum | Maximum | Mean | Standard Deviation | |
|---|---|---|---|---|
| Number of Personnel Engaged in Scientific Communication | 0 | 17 | 2.58 | 3.68 |
| Proportion of Total Employees | 0 | 109.09 | 3.52 | 17.87 |
| Funding for Scientific Communication | 0 | 100.57 | 16.26 | 23.04 |
| The Proportion of Self Raised Funds | 0 | 100 | 55.18 | 47.57 |
| Traditional Media Coverage | 41 | 1191 | 269.59 | 259.28 |
| New Media Coverage | 8 | 654 | 141.14 | 144.78 |
| Number of Information Releases | 35 | 2381 | 621.45 | 507.58 |
| WeChat Information Releases | 0 | 400 | 123.11 | 94.28 |
| The Score for Traditional Media Coverage | 335 | 17,095 | 3740.14 | 3904.56 |
| The Score for New Media Coverage | 80 | 6540 | 1411.35 | 1447.8 |
| Page clicks | 1 | 11,350 | 1544.58 | 2150.19 |
| Article reading volume | 0 | 265 | 23.27 | 46 |
| Research Institutions | |
|---|---|
| Purple | RI-12, RI-14∼RI-24, RI-26, RI-27, RI-29∼RI-32, RI-34∼RI-36 |
| Green | RI-1∼RI-11, RI-13 |
| Yellow | RI-25, RI-28, RI-33, RI-37 |
| Output Efficiency | Feedback Efficiency | Overall Efficiency | |
|---|---|---|---|
| Constant | 0.217 *** | 0.419 *** | 0.087 |
| 0.506 | −0.479 * | −0.301 | |
| −0.383 | 0.572 * | 0.381 | |
| −0.014 | 0.566 *** | 0.134 | |
| 0.836 *** | 0.438 *** | −0.4810 *** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Liu, C.; Fan, S.; He, Z. Performance Evaluation and Influencing Factors of Scientific Communication in Research Institutions. Systems 2024, 12, 192. https://doi.org/10.3390/systems12060192
Zhu W, Liu C, Fan S, He Z. Performance Evaluation and Influencing Factors of Scientific Communication in Research Institutions. Systems. 2024; 12(6):192. https://doi.org/10.3390/systems12060192
Chicago/Turabian StyleZhu, Weiwei, Chengwen Liu, Sisi Fan, and Zhou He. 2024. "Performance Evaluation and Influencing Factors of Scientific Communication in Research Institutions" Systems 12, no. 6: 192. https://doi.org/10.3390/systems12060192
APA StyleZhu, W., Liu, C., Fan, S., & He, Z. (2024). Performance Evaluation and Influencing Factors of Scientific Communication in Research Institutions. Systems, 12(6), 192. https://doi.org/10.3390/systems12060192







