Integrating Trade-In Strategies for Optimal Pre-Positioning Decisions in Relief Supply-Chain Systems
Abstract
:1. Introduction
- In the relief supply-chain system, what is the optimal decision for pre-positioning relief supplies under a trade-in strategy?
- How does the profit function of suppliers of relief supplies change with different decisions?
- What are the conditions for achieving coordination between procurement organizations and suppliers in the relief supply chain?
- How do certain characteristics of relief supplies, such as urgency and storability, impact the optimal decision and the overall relief supply-chain system?
2. Literature Review
2.1. Optimal Decision-Making in Relief Supply Chains
2.2. Emergency Supply Pre-Positioning Optimization
2.3. Relief Supply-Chain Coordination
3. Model Description and Assumption
3.1. Methodology
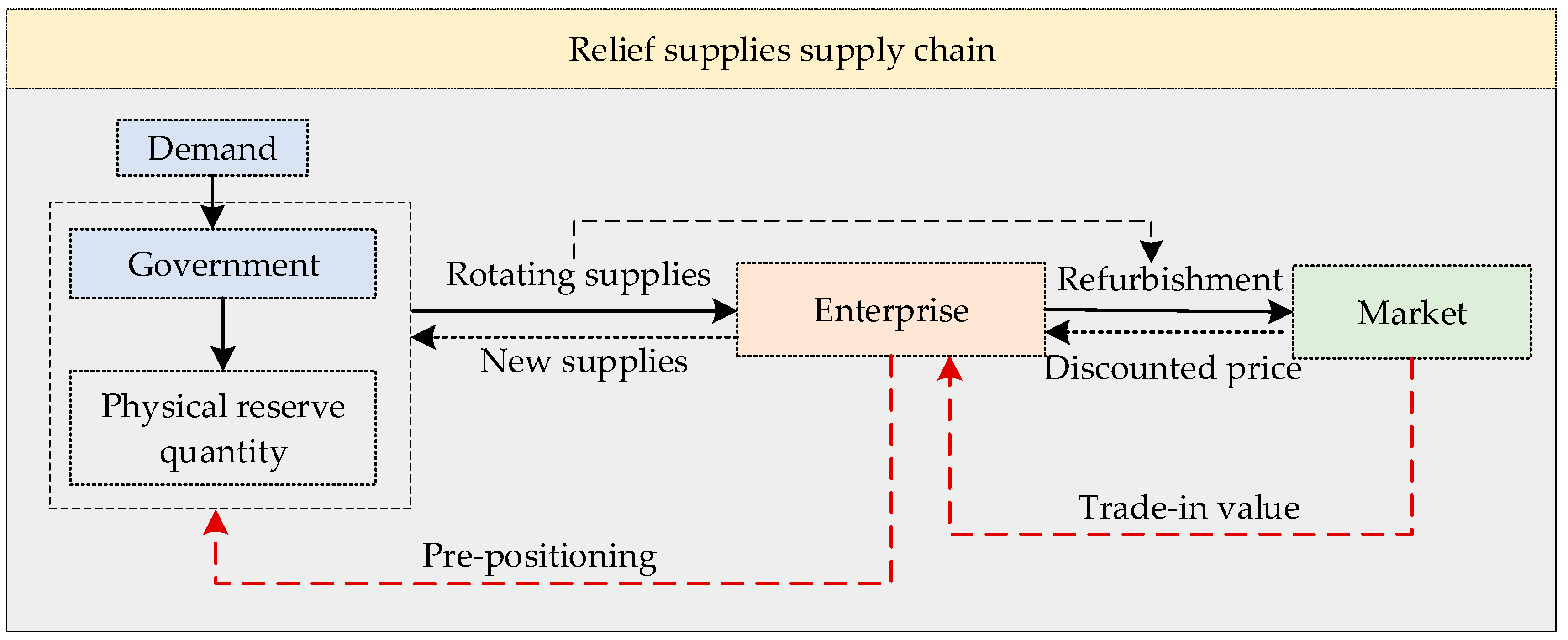
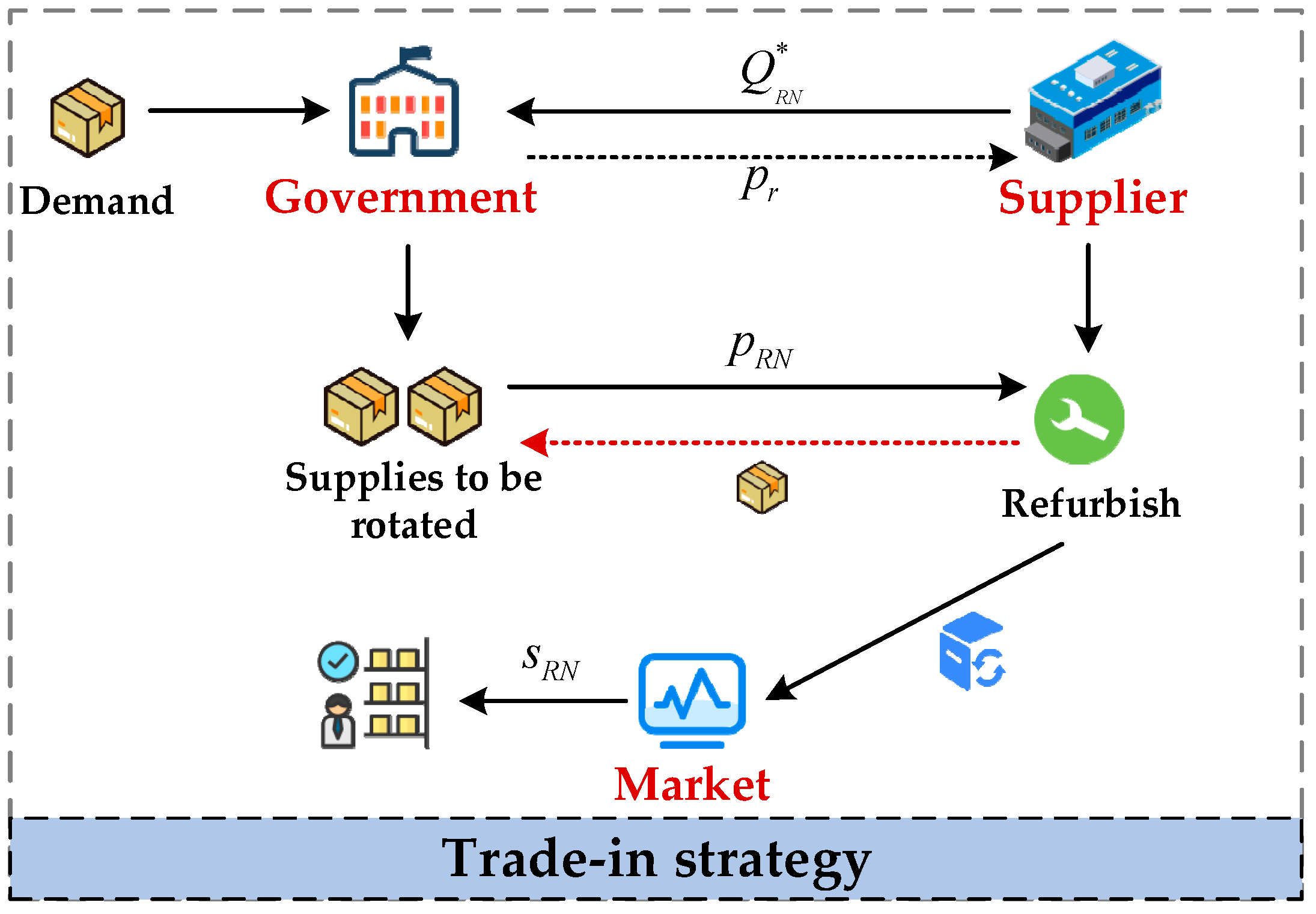
3.2. Problem Description
3.3. Decision Sequence
- The government first sets the supplies rotation cycle , the emergency parameter of the supplies is , and the parameter of the ease of storing is ;
- Upon the arrival of the single-cycle stockpile period, the government needs to rotate and renew a certain amount of relief supplies in the physical stockpile. Firstly, when there are no disasters during the reserve period, and firms are capable of refurbishing and accepting new replacements, the government can choose the “trade-in” model for the rotation of supplies;
- Subject to the government’s willingness to “trade-in” some of the supplies, enterprises receive the supplies and then provide the government with brand-new supplies at a price . Enterprises can recondition these recovered goods and reintroduce them to the market at a more favorable price;
- When there is a disaster event within the stockpile cycle , the rotation of supplies varies with the change of demand, mainly in the following scenarios:
- (1)
- If , that is, the demand for relief supplies is less than the government’s physical reserves. In this case, the “trade-in” mode is similar to the no-disaster scenario, but the base number of materials that need to be replaced is .
- (2)
- When , the remaining supplies need to be purchased from the spot. With reference to the decision problem and process described above, Figure 2 illustrates the logical structure of the model.
3.4. Assumption
- In combination with previous research [1,14,69,70], the government’s expected cost function covers not only reserve costs but also social welfare costs. For example, deprivation costs are considered in the urgency parameter. The urgency parameter also encompasses other considerations such as the number of suppliers, supply speed, daily consumption rate, general/specific applicability, and per capita daily demand. Therefore, parameter is a comprehensive metric ranging from 0 to 1, with deprivation cost being one of its factors. Specifically, it measures the cost that disaster victims are willing to bear due to the absence of the commodity by the third day after the disaster, as the initial three days post-disaster are considered an emergency relief period in emergency management;
- In the physical pre-positioning procurement phase, which consists of the Government (the purchaser of relief supplies) and enterprises (the suppliers of relief supplies), a single-cycle procurement contract is signed between the two parties. There are two main parties in the rotation of supplies: the Government and the suppliers who have the capacity to recover and refurbish the supplies. The purpose of the contract is for the government and enterprises to prearrange the implementation of the “trade-in” strategy during the procurement of relief supplies. This is formalized through the contract, serving as a tool for implementing the “trade-in” strategy;
- The logic requires that the sales price of the refurbished supplies brought back to the market after the “trade-in” is lower than the market purchase price of the supplies, that is, , ;
- Considering the introduction of the “trade-in” strategy, the cost incurred by the government for self-rotation, denoted as , needs to be greater than for the “trade-in” strategy to be viable. Therefore, .
4. Optimal Pre-Positioning Decision Model for Relief Supplies Based on Trade-In Strategy
4.1. Decision-Making Model for Purchasers (Government) under the Trade-In Strategy
4.1.1. Government Cost Function in the Absence of Disasters
4.1.2. Government Cost Function in the Event of a Disaster
- When , meaning the demand for emergency supplies is less than the government’s physical stock , the government’s cost function is expressed as follows:
- When , meaning the government’s physical stock is insufficient to meet the demand for emergency supplies , additional supplies need to be purchased on the spot. The order of purchase prioritizes contracted businesses; if they cannot meet the demand, purchases are made on the open market. The resulting loss cost arises because the fixed supply channels (own reserves and contracted businesses) cannot satisfy the demand. The government’s cost expression at this point is the following:
4.2. Profit Function for Suppliers (Enterprise) under the Trade-In Strategy
4.2.1. Enterprise Profit Function in the Absence of Disasters
4.2.2. Enterprise Profit Function in the Event of a Disaster
- When , meaning that the demand for emergency supplies is less than the government’s physical reserve , the profit expression for enterprises is as follows:
- 2.
- When , meaning that the government’s physical stock is insufficient to meet the relief supplies demand , additional supplies need to be purchased from the spot market without any trade-in transactions. Under these circumstances, the profit expression for enterprises is as follows:
4.3. Supply-Chain Coordination Model
5. Numerical Examples
5.1. Parameter Setting
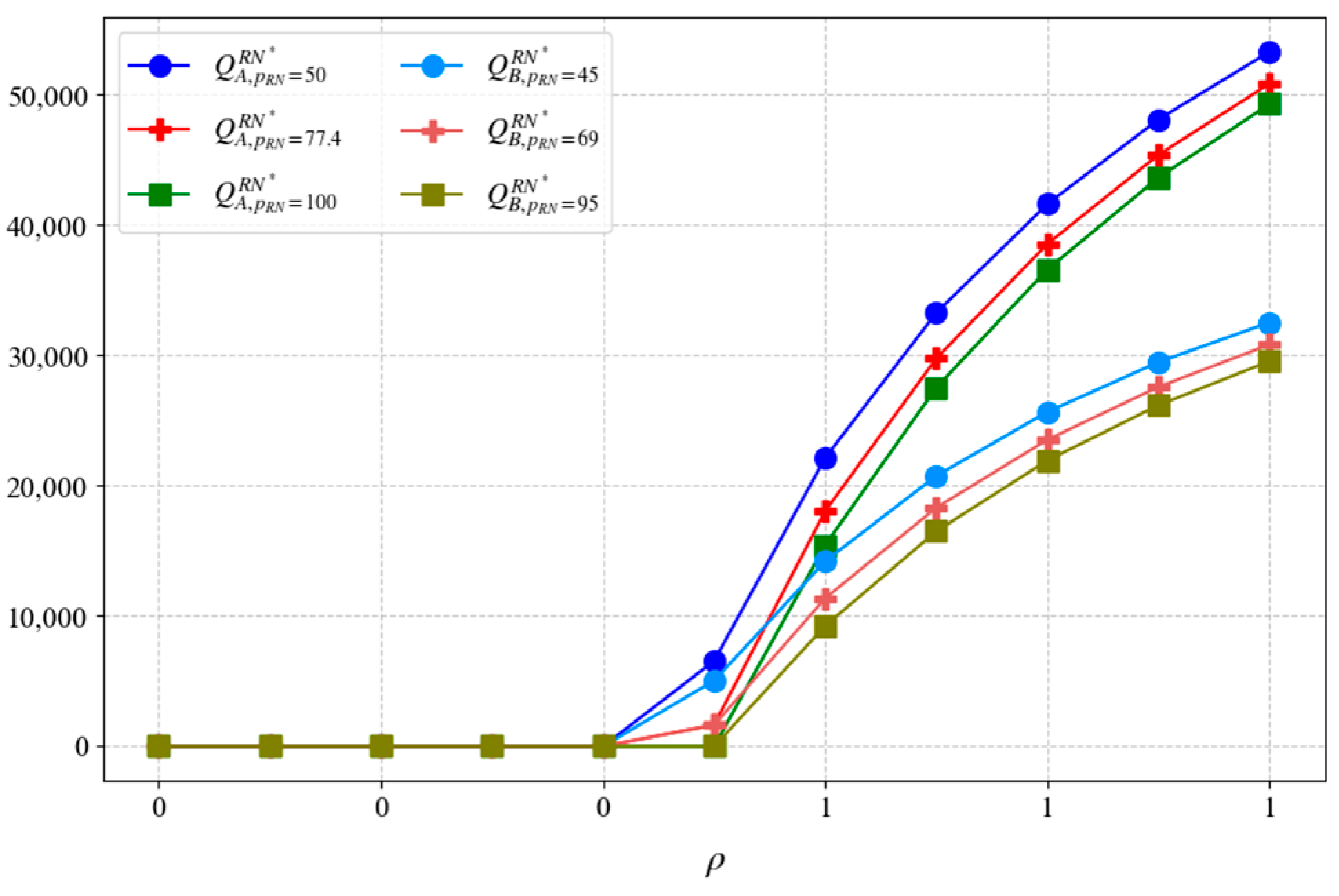
5.2. Optimal Decision-Making and Sensitivity Analysis
6. Discussion and Implications
6.1. Discussion
6.2. Implications
7. Conclusions and Limitation
7.1. Conclusions
7.2. Limitations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Patra, T.D.P.; Jha, J.K. Bidirectional option contract for prepositioning of relief supplies under demand uncertainty. Comput. Ind. Eng. 2022, 163, 107861. [Google Scholar] [CrossRef]
- Hu, Z.; Tian, J.; Feng, G. A relief supplies purchasing model based on a put option contract. Comput. Ind. Eng. 2019, 127, 253–262. [Google Scholar] [CrossRef]
- Ai, Y.-F.; Tian, J.; Feng, G.-Z. Pre-positioning and procurement strategy for relief supplies with the critical raw material participation. Comput. Ind. Eng. 2024, 187, 109780. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, J.; Feng, G. Pre-positioning strategies for relief supplies in a relief supply chain. J. Oper. Res. Soc. 2022, 73, 1457–1473. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.; Liang, L.; Huang, Z. Service outsourcing and disaster response methods in a relief supply chain. Ann. Oper. Res. 2016, 240, 471–487. [Google Scholar] [CrossRef]
- Hu, S.; Ma, Z.-J.; Sheu, J.-B. Optimal prices and trade-in rebates for successive-generation products with strategic consumers and limited trade-in duration. Transp. Res. Part E-Logist. Transp. Rev. 2019, 124, 92–107. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhou, S.X. Trade-in for Cash or for Upgrade? Dynamic Pricing with Customer Choice. Prod. Oper. Manag. 2020, 29, 856–881. [Google Scholar] [CrossRef]
- Tang, F.; Ma, Z.-J.; Dai, Y.; Choi, T.-M. Upstream or Downstream: Who Should Provide Trade-in Services in Dyadic Supply Chains? Decis. Sci. 2021, 52, 1071–1108. [Google Scholar] [CrossRef]
- Tang, F.; Dai, Y.; Ma, Z.-J. Optimal joint trade-in rebate strategies in a retailer-led supply chain. Manag. Decis. Econ. 2023, 44, 399–415. [Google Scholar] [CrossRef]
- Shi, P.; Chen, X. Analysis on trade-in strategy of manufacturers competing with informal recycling enterprises. Environ. Sci. Pollut. Res. 2023, 30, 66274–66290. [Google Scholar] [CrossRef]
- Feng, L.; Li, Y.; Fan, C. Optimization of pricing and quality choice with the coexistence of secondary market and trade-in program. Ann. Oper. Res. 2020. [Google Scholar] [CrossRef]
- Li, W.; Tian, L. Optimizing prices in trade-in strategies for vehicle retailers. Expert Syst. Appl. 2024, 238, 122004. [Google Scholar] [CrossRef]
- Natarajarathinam, M.; Capar, I.; Narayanan, A. Managing supply chains in times of crisis: A review of literature and insights. Int. J. Phys. Distrib. Logist. Manag. 2009, 39, 535–573. [Google Scholar] [CrossRef]
- Balcik, B.; Ak, D. Supplier Selection for Framework Agreements in Humanitarian Relief. Prod. Oper. Manag. 2014, 23, 1028–1041. [Google Scholar] [CrossRef]
- Cankaya, E.; Ekici, A.; Ozener, O.O. Humanitarian relief supplies distribution: An application of inventory routing problem. Ann. Oper. Res. 2019, 283, 119–141. [Google Scholar] [CrossRef]
- Day, J.M.; Melnyk, S.A.; Larson, P.D.; Davis, E.W.; Whybark, D.C. Humanitarian and Disaster Relief Supply Chains: A Matter of Life and Death. J. Supply Chain Manag. 2012, 48, 21–36. [Google Scholar] [CrossRef]
- Gossler, T.; Wakolbinger, T.; Burkart, C. Outsourcing in humanitarian logistics—Status quo and future directions. Int. J. Phys. Distrib. Logist. Manag. 2020, 50, 403–438. [Google Scholar] [CrossRef]
- Upadhyay, A.; Mukhuty, S.; Kumari, S.; Garza-Reyes, J.A.; Shukla, V. A review of lean and agile management in humanitarian supply chains: Analysing the pre-disaster and post-disaster phases and future directions. Prod. Plan. Control 2022, 33, 641–654. [Google Scholar] [CrossRef]
- Wang, D.; Yang, K.; Yang, L.; Dong, J. Two-stage distributionally robust optimization for disaster relief logistics under option contract and demand ambiguity. Transp. Res. Part E-Logist. Transp. Rev. 2023, 170, 103025. [Google Scholar] [CrossRef]
- Fan, Y.; Shao, J.; Wang, X.; Liang, L. Contract design between relief organisations and private-sector vendors: A humanitarian logistics framework. Transp. Res. Part E-Logist. Transp. Rev. 2024, 182, 103395. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Jia, H.M. An intuitionistic fuzzy grey-Markov method with application to demand forecasting for emergency supplies during major epidemics. Grey Syst.-Theory Appl. 2024, 14, 185–208. [Google Scholar] [CrossRef]
- Taskin, S.; Lodree, E.J. A Bayesian decision model with hurricane forecast updates for emergency supplies inventory management. J. Oper. Res. Soc. 2011, 62, 1098–1108. [Google Scholar] [CrossRef]
- Zhang, L.; Tian, J.; Fung, R.Y.K.; Dang, C.Y. Materials procurement and reserves policies for humanitarian logistics with recycling and replenishment mechanisms. Comput. Ind. Eng. 2019, 127, 709–721. [Google Scholar] [CrossRef]
- Yadavalli, V.S.S.; Sundar, D.K.; Udayabaskaran, S. Two substitutable perishable product disaster inventory systems. Ann. Oper. Res. 2015, 233, 517–534. [Google Scholar] [CrossRef]
- Rezaei-Malek, M.; Tavakkoli-Moghaddam, R.; Zahiri, B.; Bozorgi-Amiri, A. An interactive approach for designing a robust disaster relief logistics network with perishable commodities. Comput. Ind. Eng. 2016, 94, 201–215. [Google Scholar] [CrossRef]
- Zhou, Q.S.; Olsen, T.L. Rotating the medical supplies for emergency response: A simulation based approach. Int. J. Prod. Econ. 2018, 196, 1–11. [Google Scholar] [CrossRef]
- Meng, Q.C.; Guo, Y.; Zhao, P.X.; Lu, T.X.; Wan, X.L.; Rong, X.X.; Pan, W. Optimization and simulation for airport emergency inventory with replacement. Int. J. Simul. Model. 2017, 16, 133–144. [Google Scholar] [CrossRef] [PubMed]
- Arani, H.V.; Rabbani, M.; Rafiei, H. A revenue-sharing option contract toward coordination of supply chains. Int. J. Prod. Econ. 2016, 178, 42–56. [Google Scholar] [CrossRef]
- Charles, A.; Lauras, M.; Van Wassenhove, L.N.; Dupont, L. Designing an efficient humanitarian supply network. J. Oper. Manag. 2016, 47–48, 58–70. [Google Scholar] [CrossRef]
- Roh, S.Y.; Shin, Y.; Seo, Y.J. The Pre-positioned Warehouse Location Selection for International Humanitarian Relief Logistics. Asian J. Shipp. Logist. 2018, 34, 297–307. [Google Scholar] [CrossRef]
- Roh, S.; Pettit, S.; Harris, I.; Beresford, A. The pre-positioning of warehouses at regional and local levels for a humanitarian relief organisation. Int. J. Prod. Econ. 2015, 170, 616–628. [Google Scholar] [CrossRef]
- Chen, J.X.; Liang, L.; Yao, D.Q. Pre-positioning of relief inventories: A multi-product newsvendor approach. Int. J. Prod. Res. 2018, 56, 6294–6313. [Google Scholar] [CrossRef]
- Duran, S.; Gutierrez, M.A.; Keskinocak, P. Pre-Positioning of Emergency Items for CARE International. Interfaces 2011, 41, 223–237. [Google Scholar] [CrossRef]
- Sotelo-Salas, C.; Monardes-Concha, C.A.; Pérez-Galarce, F.; Santa González, R. A multi-objective optimization model for planning emergency shelters after a tsunami. Socio-Econ. Plan. Sci. 2024, 93, 101909. [Google Scholar] [CrossRef]
- Rawls, C.G.; Turnquist, M.A. Pre-positioning planning for emergency response with service quality constraints. OR Spectr. 2011, 33, 481–498. [Google Scholar] [CrossRef]
- Aslan, E.; Çelik, M. Pre-positioning of relief items under road/facility vulnerability with concurrent restoration and relief transportation. IISE Trans. 2019, 51, 847–868. [Google Scholar] [CrossRef]
- Hu, S.L.; Hu, Q.M.; Tao, S.; Dong, Z.S. A multi-stage stochastic programming approach for pre-positioning of relief supplies considering returns. Socio-Econ. Plan. Sci. 2023, 88, 101617. [Google Scholar] [CrossRef]
- Torabi, S.A.; Shokr, I.; Tofighi, S.; Heydari, J. Integrated relief pre-positioning and procurement planning in humanitarian supply chains. Transp. Res. Part E-Logist. Transp. Rev. 2018, 113, 123–146. [Google Scholar] [CrossRef]
- Ni, W.J.; Shu, J.; Song, M. Location and Emergency Inventory Pre-Positioning for Disaster Response Operations: Min-Max Robust Model and a Case Study of Yushu Earthquake. Prod. Oper. Manag. 2018, 27, 160–183. [Google Scholar] [CrossRef]
- Che, A.; Li, J.; Chu, F.; Chu, C.B. Optimizing emergency supply pre-positioning for disaster relief: A two-stage distributionally robust approach. Comput. Oper. Res. 2024, 166, 106607. [Google Scholar] [CrossRef]
- Yang, M.; Liu, Y.K.; Yang, G.Q. Multi-period dynamic distributionally robust pre-positioning of emergency supplies under demand uncertainty. Appl. Math. Model. 2021, 89, 1433–1458. [Google Scholar] [CrossRef]
- Rezaei-Malek, M.; Tavakkoli-Moghaddam, R.; Cheikhrouhou, N.; Taheri-Moghaddam, A. An approximation approach to a trade-off among efficiency, efficacy, and balance for relief pre-positioning in disaster management. Transp. Res. Part E-Logist. Transp. Rev. 2016, 93, 485–509. [Google Scholar] [CrossRef]
- Arnette, A.N.; Zobel, C.W. A Risk-Based Approach to Improving Disaster Relief Asset Pre-Positioning. Prod. Oper. Manag. 2019, 28, 457–478. [Google Scholar] [CrossRef]
- Wang, J.; Cai, J.P.; Yue, X.H.; Suresh, N.C. Pre-positioning and real-time disaster response operations: Optimization with mobile phone location data. Transp. Res. Part E-Logist. Transp. Rev. 2021, 150, 102344. [Google Scholar] [CrossRef]
- Kouvelis, P.; Zhao, W.H. Who Should Finance the Supply Chain? Impact of Credit Ratings on Supply Chain Decisions. MSom-Manuf. Serv. Oper. Manag. 2018, 20, 19–35. [Google Scholar] [CrossRef]
- Ergun, Ö.; Gui, L.; Heier Stamm, J.L.; Keskinocak, P.; Swann, J. Improving Humanitarian Operations through Technology-Enabled Collaboration. Prod. Oper. Manag. 2014, 23, 1002–1014. [Google Scholar] [CrossRef]
- Cai, J.H.; Zhong, M.; Shang, J.F.; Huang, W.L. Coordinating VMI supply chain under yield uncertainty: Option contract, subsidy contract, and replenishment tactic. Int. J. Prod. Econ. 2017, 185, 196–210. [Google Scholar] [CrossRef]
- Wang, X.H.; Li, F.; Liang, L.; Huang, Z.M.; Ashley, A. Pre-purchasing with option contract and coordination in a relief supply chain. Int. J. Prod. Econ. 2015, 167, 170–176. [Google Scholar] [CrossRef]
- Xue, K.L.; Li, Y.J.; Zhen, X.P.; Wang, W. Managing the supply disruption risk: Option contract or order commitment contract? Ann. Oper. Res. 2020, 291, 985–1026. [Google Scholar] [CrossRef]
- Wang, X.H.; Fan, Y.; Liang, L.; De Vries, H.; Van Wassenhove, L.N. Augmenting Fixed Framework Agreements in Humanitarian Logistics with a Bonus Contract. Prod. Oper. Manag. 2019, 28, 1921–1938. [Google Scholar] [CrossRef]
- Noham, R.; Tzur, M. Design and incentive decisions to increase cooperation in humanitarian relief networks. Iise Trans. 2020, 52, 1297–1311. [Google Scholar] [CrossRef]
- Cai, J.H.; Hu, X.Q.; Han, Y.; Cheng, H.F.; Huang, W.L. Supply chain coordination with an option contract under vendor-managed inventory. Int. Trans. Oper. Res. 2016, 23, 1163–1183. [Google Scholar] [CrossRef]
- Elçi, Ö.; Noyan, N. A chance-constrained two-stage stochastic programming model for humanitarian relief network design. Transp. Res. Part B-Methodol. 2018, 108, 55–83. [Google Scholar] [CrossRef]
- Nosoohi, I.; Nookabadi, A.S. Outsource planning through option contracts with demand and cost uncertainty. Eur. J. Oper. Res. 2016, 250, 131–142. [Google Scholar] [CrossRef]
- Doganoglu, T.; Inceoglu, F. Buyback contracts to solve upstream opportunism. Eur. J. Oper. Res. 2020, 287, 875–884. [Google Scholar] [CrossRef]
- Kremer, M.; Van Wassenhove, L.N. Willingness to Pay for Shifting Inventory Risk: The Role of Contractual Form. Prod. Oper. Manag. 2014, 23, 239–252. [Google Scholar] [CrossRef]
- Nikkhoo, F.; Bozorgi-Amiri, A.; Heydari, J. Coordination of relief items procurement in humanitarian logistic based on quantity flexibility contract. Int. J. Disaster Risk Reduct. 2018, 31, 331–340. [Google Scholar] [CrossRef]
- Aghajani, M.; Torabi, S.A.; Heydari, J. A novel option contract integrated with supplier selection and inventory prepositioning for humanitarian relief supply chains. Socio-Econ. Plan. Sci. 2020, 71. [Google Scholar] [CrossRef]
- Qin, Y.H.; Shao, Y.F.; Gu, B. Buyback contract coordination in supply chain with fairness concern under demand updating. Enterp. Inf. Syst. 2021, 15, 725–748. [Google Scholar] [CrossRef]
- Zhao, X.; Xia, X.H.; Yu, G.D. Buyback contract of reverse supply chains with different risk attitudes under fuzzy demands. J. Intell. Fuzzy Syst. 2018, 34, 47–56. [Google Scholar] [CrossRef]
- Vafaeinejad, K.; Sajadieh, M.S. Trade-in price and base warranty length: A heuristic algorithm for concurrent optimization. Comput. Ind. Eng. 2022, 171, 108504. [Google Scholar] [CrossRef]
- Tang, F.; Dai, Y.; Ma, Z.-J.; Choi, T.-M. Trade-in operations under retail competition: Effects of brand loyalty. Eur. J. Oper. Res. 2023, 310, 397–414. [Google Scholar] [CrossRef]
- Li, Y.; Wang, K.; Xu, F.; Fan, C. Management of trade-in modes by recycling platforms based on consumer heterogeneity. Transp. Res. Part E-Logist. Transp. Rev. 2022, 162, 102721. [Google Scholar] [CrossRef]
- Xiao, L.; Wang, X.J.; Chin, K.S. Trade-in strategies in retail channel and dual-channel closed-loop supply chain with remanufacturing. Transp. Res. Part E-Logist. Transp. Rev. 2020, 136, 101898. [Google Scholar] [CrossRef]
- Feng, L.P.; Li, Y.J.; Xu, F.C.; Deng, Q.Z. Optimal pricing and trade-in policies in a dual-channel supply chain when considering market segmentation. Int. J. Prod. Res. 2019, 57, 2828–2846. [Google Scholar] [CrossRef]
- Xiao, L.; Chen, Z.S.; Govindan, K.; Skibniewski, M.J. Effects of Online Consumer Reviews on a Dual-Channel Closed-Loop Supply Chain With Trade-In. IEEE Trans. Eng. Manag. 2024, 71, 2168–2183. [Google Scholar] [CrossRef]
- Dowty, R.A.; Wallace, W.A. Implications of organizational culture for supply chain disruption and restoration. Int. J. Prod. Econ. 2010, 126, 57–65. [Google Scholar] [CrossRef]
- Boroumand, A.; Nojavan, M.; Mohammaditabar, D.; Ghaemi, R. Competitive Relief Supply Chain under the Uncertain Conditions. Discret. Dyn. Nat. Soc. 2023, 2023, 3352255. [Google Scholar] [CrossRef]
- Shokr, I.; Jolai, F.; Bozorgi-Amiri, A. A collaborative humanitarian relief chain design for disaster response. Comput. Ind. Eng. 2022, 172, 108643. [Google Scholar] [CrossRef]
- Zhu, R.; Chen, X.L.; Dasgupta, S. Can trade-ins hurt you? Exploring the effect of a trade-in on consumers’ willingness to pay for a new product. J. Mark. Res. 2008, 45, 159–170. [Google Scholar] [CrossRef]
- Cao, K.Y.; Xu, X.Y.; Bian, Y.W.; Sun, Y.H. Optimal trade-in strategy of business-to-consumer platform with dual-format retailing model. Omega-Int. J. Manag. Sci. 2019, 82, 181–192. [Google Scholar] [CrossRef]



| Notation | Definition |
|---|---|
| Randomized requirements for relief supplies. Following a specific probability distribution, defining as the maximum, is its inverse function. | |
| Emergency level parameters, the initial range is [0, 1], with 0 indicating not urgent and 1 indicating very urgent. | |
| . | |
| Reserve difficulty parameter, the initial range is [0, 1], 0 means easy to reserve, 1 means very difficult to reserve. | |
| : adjusted unit loss costs, weighted for reserve difficulty. | |
| Probability of a disaster occurring during the agreement cycle. | |
| Regular procurement prices for emergency supplies. | |
| Unit cost of production of relief supplies in an enterprise. | |
| Cost of spot purchases of relief supplies for post-disaster units. | |
| , the trade-in price is adjusted solely on the basis of the degree of wear and tear of the supplies. | |
| Government trade-in prices to enterprises. | |
| Cost of refurbishing and disposing of recycled relief supplies. | |
| The re-sale price of the refurbished relief supplies. | |
| Government’s willingness to “trade-in”. | |
| The residual value of supplies not subjected to rotation through the “trade-in” process. | |
| Decision variable | |
| The pre-positioning quantity of physical relief supplies by the government. | |
| Parameters | Supply Names | Parameters | Supply Names | ||
|---|---|---|---|---|---|
| Pharmaceuticals (Packs) | Life Jackets (Pieces) | Pharmaceuticals (Packs) | Life Jackets (Pieces) | ||
| Basic Parameters | |||||
| X~U (0, 100,000) | X~U (0, 60,000) | 29.394 | 8.304 | ||
| 0.9871 | 0.7231 | 0.5 | 0.5 | ||
| 100 | 100 | 258 | 169 | ||
| 98.71 | 72.31 | 178 | 119 | ||
| 0.5101 | 0.7924 | 588 | 398 | ||
| 60 | 40 | ||||
| Parameters related to trade-in strategy | |||||
| 0.645 | 0.566 | 189 | 109 | ||
| 15 | 6 | 208 | 119 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, Y.; Hou, H.; Yang, J.; Ren, Y.; Yang, J. Integrating Trade-In Strategies for Optimal Pre-Positioning Decisions in Relief Supply-Chain Systems. Systems 2024, 12, 216. https://doi.org/10.3390/systems12060216
Ju Y, Hou H, Yang J, Ren Y, Yang J. Integrating Trade-In Strategies for Optimal Pre-Positioning Decisions in Relief Supply-Chain Systems. Systems. 2024; 12(6):216. https://doi.org/10.3390/systems12060216
Chicago/Turabian StyleJu, Yingjie, Hanping Hou, Jianliang Yang, Yuheng Ren, and Jimei Yang. 2024. "Integrating Trade-In Strategies for Optimal Pre-Positioning Decisions in Relief Supply-Chain Systems" Systems 12, no. 6: 216. https://doi.org/10.3390/systems12060216
APA StyleJu, Y., Hou, H., Yang, J., Ren, Y., & Yang, J. (2024). Integrating Trade-In Strategies for Optimal Pre-Positioning Decisions in Relief Supply-Chain Systems. Systems, 12(6), 216. https://doi.org/10.3390/systems12060216






