Towards Assessing the Economic Sustainability of Reconfigurable Modularization in Semi-Automatic Assembly Systems: A System Dynamics Perspective
Abstract
:1. Introduction
2. Theoretical Background
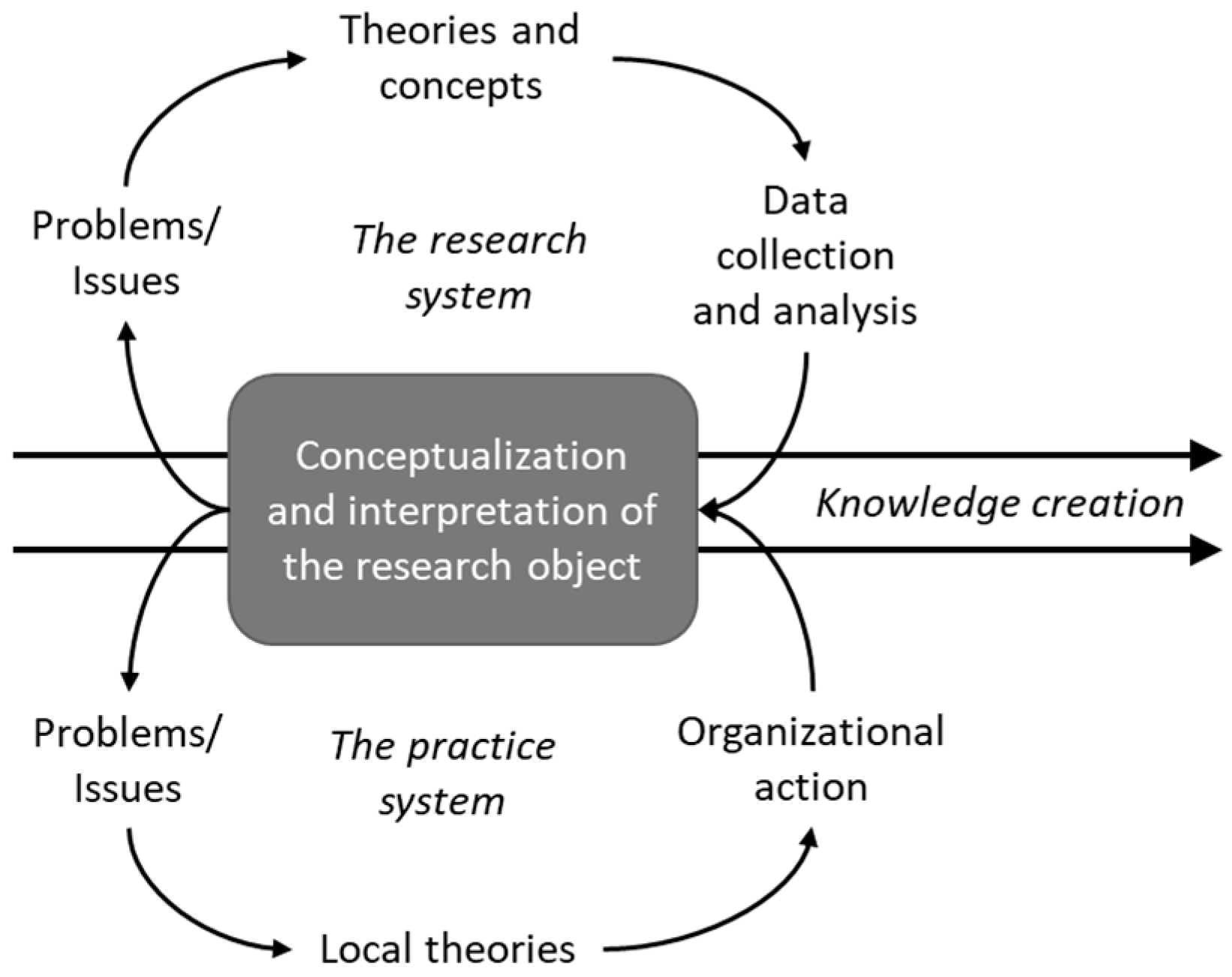
3. Research Method and Model Building
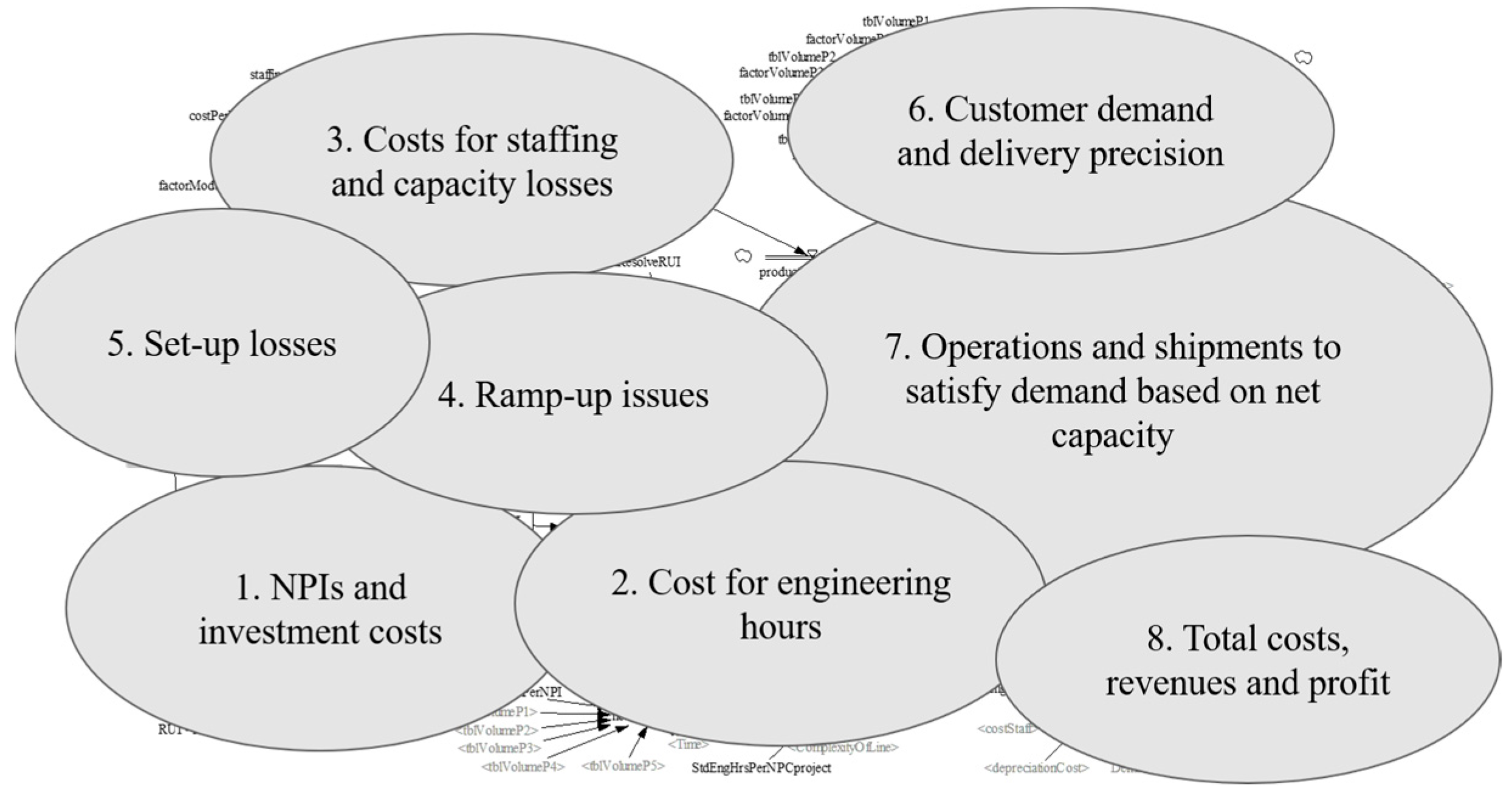
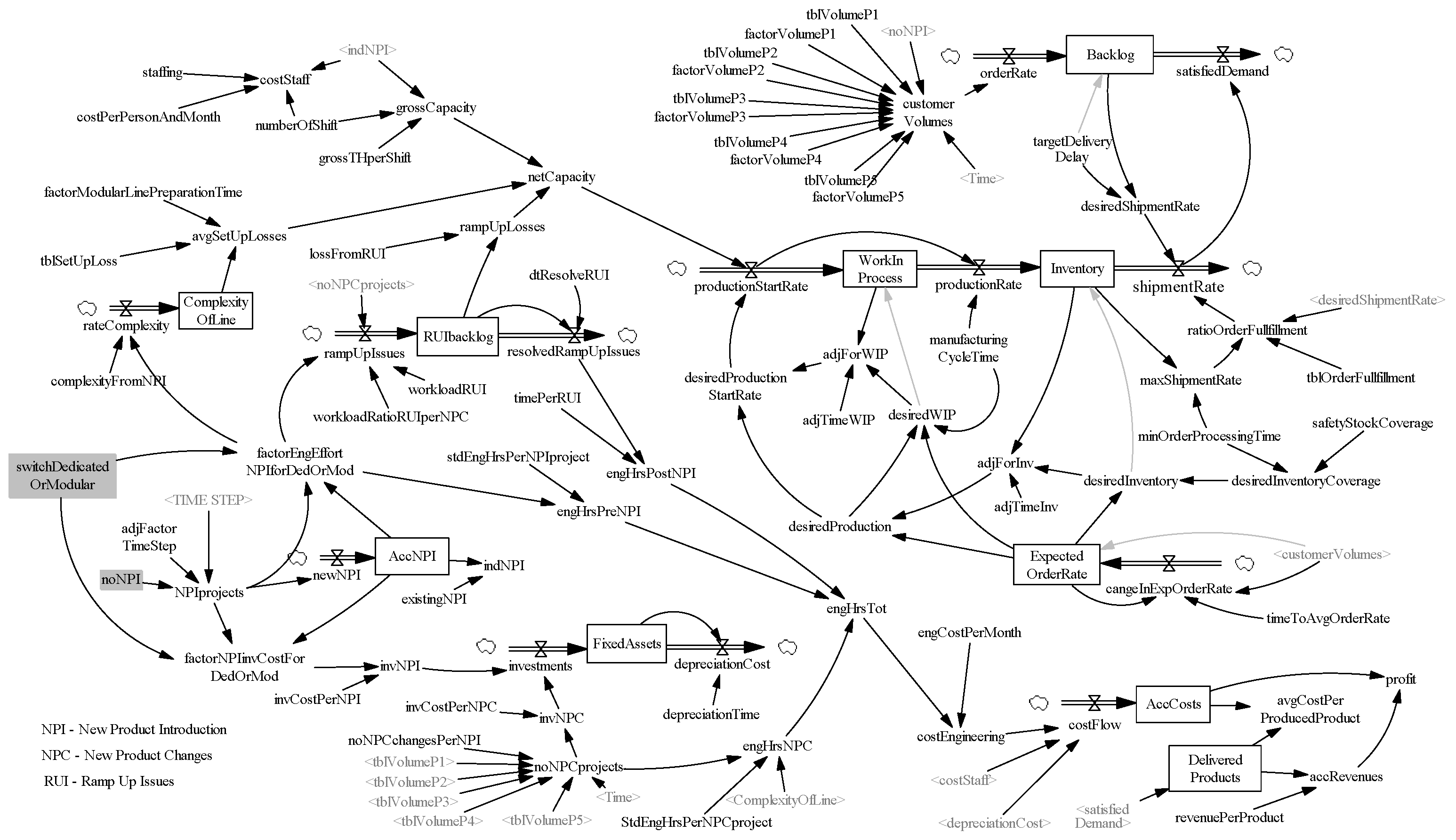
4. Model Description
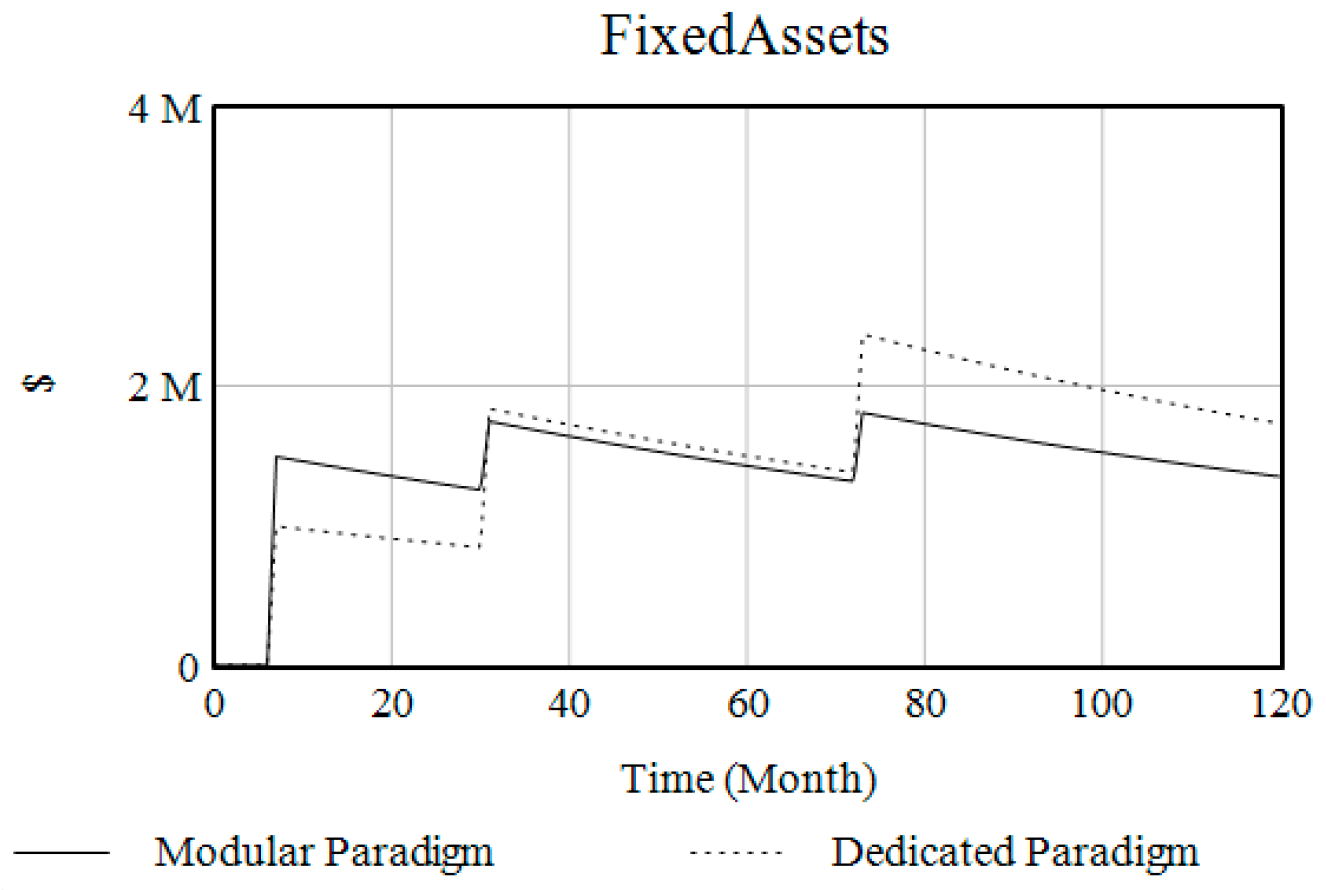
5. Experiments
6. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Variable name | Expression | Unit |
| AccCosts | INTEG (costFlow, 0) | $ |
| AccNPI | INTEG (newNPI, 0) | NPI |
| accRevenues | DeliveredProducts*revenuePerProduct | $ |
| adjFactorTimeStep | 8 | Dmnl |
| adjForInv | (desiredInventory-Inventory)/adjTimeInv | Pcs/Month |
| adjForWIP | (desiredWIP-WorkInProcess)/adjTimeWIP | Pcs/Month |
| adjTimeInv | 4 | Month |
| adjTimeWIP | 0.5 | Month |
| avgCostPerProducedProduct | AccCosts/DeliveredProducts | $/Pcs |
| avgSetUpLosses= tblSetUpLoss | (MAX(ComplexityOfLine/factorModularLinePreparationTime, 1)) | Dmnl |
| Backlog | INTEG (orderRate-satisfiedDemand, orderRate * targetDeliveryDelay) | Pcs |
| cangeInExpOrderRate | (customerVolumes-ExpectedOrderRate)/timeToAvgOrderRate | (Pcs/Month)/Month |
| complexityFromNPI | 1 | Dmnl/NPI |
| ComplexityOfLine | INTEG (rateComplexity, 0) | Dmnl |
| costEngineering | engCostPerMonth*engHrsTot | $/Month |
| costFlow | depreciationCost + costStaff + costEngineering | $/Month |
| costPerPersonAndMonth | 4600 | $/Person/Month |
| costStaff | indNPI*staffing*numberOfShift * costPerPersonAndMonth | $/Month |
| customerVolumes= | IF THEN ELSE(noNPI=1, tblVolumeP1(Time) * factorVolumeP1, IF THEN ELSE( noNPI=2, tblVolumeP1(Time) * factorVolumeP1 + tblVolumeP2(Time) * factorVolumeP2, IF THEN ELSE(noNPI=3, tblVolumeP1(Time) * factorVolumeP1 + tblVolumeP2(Time) * factorVolumeP2 + tblVolumeP3(Time), IF THEN ELSE(noNPI=4, tblVolumeP1(Time) * factorVolumeP1 + tblVolumeP2(Time) * factorVolumeP2 + tblVolumeP3(Time) * factorVolumeP3 + factorVolumeP4 * tblVolumeP4(Time), tblVolumeP1(Time)* factorVolumeP1 + tblVolumeP2(Time)* factorVolumeP2 + tblVolumeP3(Time) * factorVolumeP3 + factorVolumeP4 * tblVolumeP4(Time) + factorVolumeP5 * tblVolumeP5(Time))))) | Pcs/Month |
| DeliveredProducts | INTEG (satisfiedDemand, 1) | Pcs |
| depreciationCost | FixedAssets/depreciationTime | $/Month |
| depreciationTime | 120 | Month |
| desiredInventory | desiredInventoryCoverage * ExpectedOrderRate | Pcs |
| desiredInventoryCoverage | minOrderProcessingTime + safetyStockCoverage | Month |
| desiredProduction | MAX(0, ExpectedOrderRate + adjForInv) | Pcs/Month |
| desiredProductionStartRate | MAX(0,desiredProduction + adjForWIP) | Pcs/Month |
| desiredShipmentRate | Backlog/targetDeliveryDelay | Pcs/Month |
| desiredWIP | (desiredProduction + ExpectedOrderRate) * manufacturingCycleTime | Pcs |
| dtResolveRUI | 0.5 | Month |
| engCostPerMonth | 100 | $/WorkHrs |
| engHrsNPC | StdEngHrsPerNPCproject * ComplexityOfLine * noNPCprojects | WorkHrs/Month |
| engHrsPostNPI | timePerRUI*resolvedRampUpIssues | WorkHrs/Month |
| engHrsPreNPI | factorEngEffortNPIforDedOrMod * stdEngHrsPerNPIproject | WorkHrs/Month |
| engHrsTot | engHrsPreNPI + engHrsNPC + engHrsPostNPI | WorkHrs/Month |
| existingNPI | 1 | NPI |
| ExpectedOrderRate | INTEG (cangeInExpOrderRate, customerVolumes) | Pcs/Month |
| factorEngEffortNPIforDedOrMod | IF THEN ELSE(switchDedicatedOrModular = 0, IF THEN ELSE(AccNPI >= 1, 2, 1) * NPIprojects, IF THEN ELSE(AccNPI >= 1, 0.5, 2) * NPIprojects) | NPI/Month |
| factorModularLinePreparationTime | 2 | Dmnl |
| factorNPIinvCostForDedOrMod | IF THEN ELSE(switchDedicatedOrModular = 0, 1, IF THEN ELSE(AccNPI>=1, 0.5, 1.5)) * NPIprojects | NPI/Month |
| factorVolumeP1 | 1 | Dmnl |
| factorVolumeP2 | 1 | Dmnl |
| factorVolumeP3 | 1 | Dmnl |
| factorVolumeP4 | 1 | Dmnl |
| factorVolumeP5 | 1 | Dmnl |
| FINAL TIME | 120 | Month |
| FixedAssets | INTEG (investments - depreciationCost, 0) | $ |
| grossCapacity | indNPI*numberOfShift * grossTHperShift | Pcs/Month |
| grossTHperShift | 12*40*4.1 | Pcs/Month/shift |
| indNPI | MIN(AccNPI, existingNPI)/existingNPI | Dmnl |
| INITIAL TIME | 0 | Month |
| invCostPerNPC | 40000 | $/NPC |
| invCostPerNPI | 1e+06 | $/NPI |
| Inventory | INTEG (productionRate-shipmentRate, desiredInventory) | Pcs |
| investments | invNPC+invNPI | $/Month |
| invNPC | noNPCprojects*invCostPerNPC | $/Month |
| invNPI | invCostPerNPI * factorNPIinvCostForDedOrMod | $/Month |
| lossFromRUI | 1 | Dmnl/RUI |
| manufacturingCycleTime | 2 | Month |
| maxShipmentRate | MAX(0, Inventory/minOrderProcessingTime) | Pcs/Month |
| minOrderProcessingTime | 0.5 | Month |
| netCapacity | grossCapacity*rampUpLosses* avgSetUpLosses | Pcs/Month |
| newNPI | NPIprojects | NPI/Month |
| noNPCchangesPerNPI | 4/12 | NPC/Month |
| noNPCprojects= | (IF THEN ELSE(tblVolumeP1(Time)>1, noNPCchangesPerNPI, 0)+ IF THEN ELSE( tblVolumeP2(Time)>1, noNPCchangesPerNPI, 0)+ IF THEN ELSE(tblVolumeP3(Time)>1, noNPCchangesPerNPI, 0)+ IF THEN ELSE(tblVolumeP4(Time)>1, noNPCchangesPerNPI, 0)+ IF THEN ELSE(tblVolumeP5(Time)>1, noNPCchangesPerNPI, 0))/12 | NPC/Month |
| noNPI | 2 | NPI |
| NPIprojects | IF THEN ELSE(noNPI=1, PULSE(6, TIME STEP*adjFactorTimeStep), IF THEN ELSE(noNPI=2, PULSE(6, TIME STEP * adjFactorTimeStep) + PULSE((28), TIME STEP * adjFactorTimeStep), IF THEN ELSE(noNPI=3, PULSE(6, TIME STEP * adjFactorTimeStep) + PULSE((28), TIME STEP * adjFactorTimeStep) + PULSE((28+22), TIME STEP * adjFactorTimeStep), IF THEN ELSE(noNPI=4, PULSE(6, TIME STEP * adjFactorTimeStep) + PULSE((28), TIME STEP * adjFactorTimeStep) + PULSE((28+22), TIME STEP * adjFactorTimeStep) + PULSE((28+22+22), TIME STEP * adjFactorTimeStep), IF THEN ELSE(noNPI=5, PULSE(6, TIME STEP * adjFactorTimeStep) + PULSE((28), TIME STEP * adjFactorTimeStep) + PULSE((28+22), TIME STEP * adjFactorTimeStep) + PULSE((28+22+22), TIME STEP * adjFactorTimeStep) + PULSE((28+22+22+22), TIME STEP * adjFactorTimeStep), 0))))) | NPI/Month |
| numberOfShift | 1 | shifts |
| orderRate | customerVolumes | Pcs/Month |
| productionRate | MAX(0, DELAY3(productionStartRate, manufacturingCycleTime)) | Pcs/Month [0,?] |
| productionStartRate | MIN(netCapacity, desiredProductionStartRate) | Pcs/Month |
| profit | accRevenues-AccCosts | $ |
| rampUpIssues | factorEngEffortNPIforDedOrMod * workloadRUI + noNPCprojects/workloadRatioRUIperNPC | RUI/Month |
| rampUpLosses | 1 - MIN(1, lossFromRUI*RUIbacklog) | Dmnl |
| rateComplexity | factorEngEffortNPIforDedOrMod * complexityFromNPI | Dmnl/Month |
| ratioOrderFullfillment | IF THEN ELSE(maxShipmentRate/desiredShipmentRate > 1, 1, tblOrderFullfillment(maxShipmentRate/desiredShipmentRate)) | Dmnl |
| resolvedRampUpIssues | RUIbacklog/dtResolveRUI | RUI/Month |
| revenuePerProduct | 40 | $/Pcs |
| RUIbacklog | INTEG (rampUpIssues-resolvedRampUpIssues, 1) | RUI |
| safetyStockCoverage | 0.5 | Month |
| satisfiedDemand | shipmentRate | Pcs/Month |
| SAVEPER | TIME STEP | Month [0,?] |
| shipmentRate | desiredShipmentRate * ratioOrderFullfillment | Pcs/Month |
| staffing | 3 | persons/shift |
| StdEngHrsPerNPCproject | 172 | WorkHrs/NPC |
| stdEngHrsPerNPIproject | 6*172 | WorkHrs/NPI |
| switchDedicatedOrModular | 0 | Dmnl |
| targetDeliveryDelay | 1 | Month |
| tblOrderFullfillment | ([(0,0)-(20,1)],(0,0),(0.2,0.2),(0.4,0.4), (0.6,0.58), (0.8,0.73), (1,0.85), (1.2,0.93),(1.4,0.97), (1.6,0.99), (1.8,1), (10,1),(20,1)) | Dmnl |
| tblSetUpLoss | ([(0,0)-(10,2)],(0.5,1),(1,1),(1.5,0.93), (1.93,0.9), (2.5,0.88), (3.5,0.85), (6,0.8), (10,0.75)) | Dmnl |
| tblVolumeP1 | ([(0,0)-(120,2000)],(0,1),(6,1),(9,200), (18,1050), (21,1313.53),(24,1500),(28,1580),(32,1518),(35,1399), (39,1062),(48,1),(120,1)) | Pcs/Month |
| tblVolumeP2 | ([(0,0)-(120,2000)],(0,1),(28,0),(33,145), (39,640), (42,1062),(46,1392),(51,1531), (55,1531), (60,1419), (65,1108),(75,171),(80,1),(120,1)) | Pcs/Month |
| tblVolumeP3 | ([(0,0)-(120,2000)], (0,1), (50,0), (54,105), (66,1082), (69,1366), (74,1504), (79,1518), (83,1425), (87,1188), (94,534), (102,1), (120,1)) | Pcs/Month |
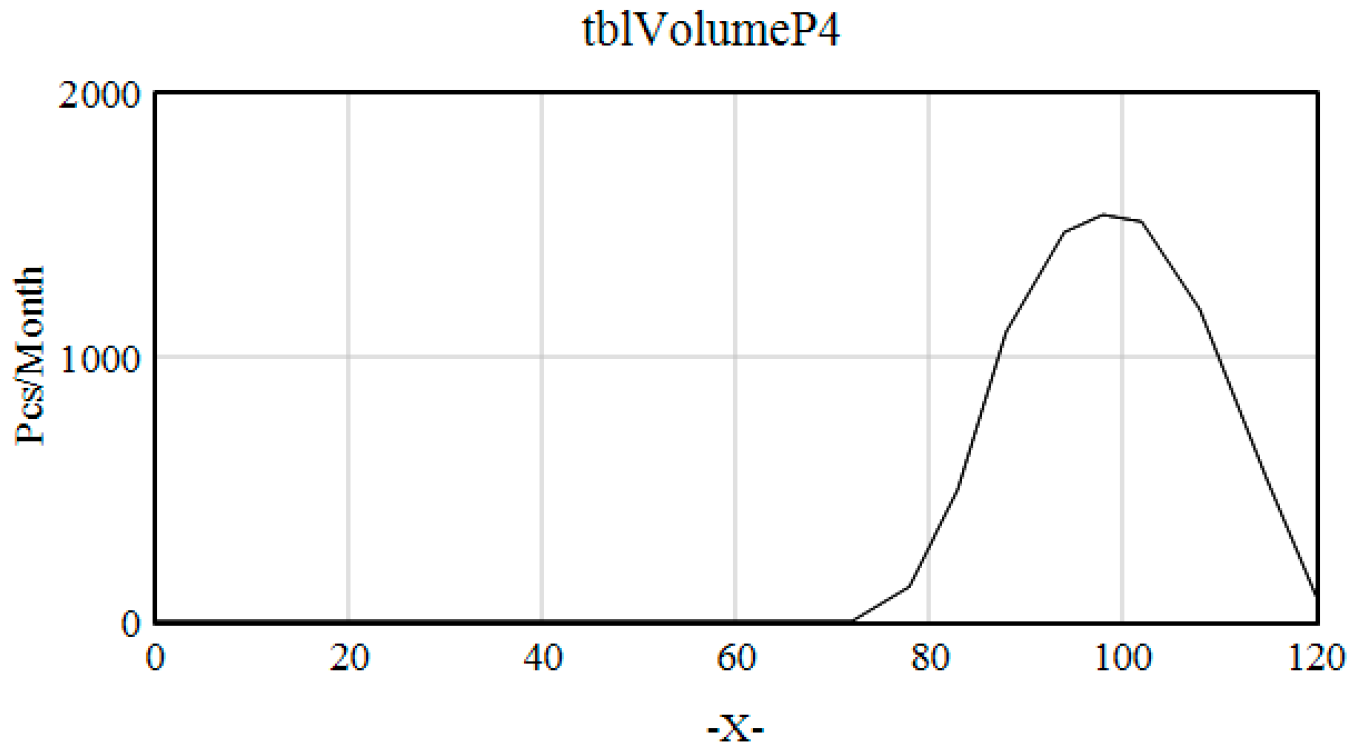
| tblVolumeP4 | ([(0,0)-(120,2000)],(0,1),(72,1),(78,132), (83,501), (88,1095),(94,1471),(98,1537), (102,1511), (108,1181), (115,534),(120,100)) | Pcs/Month |
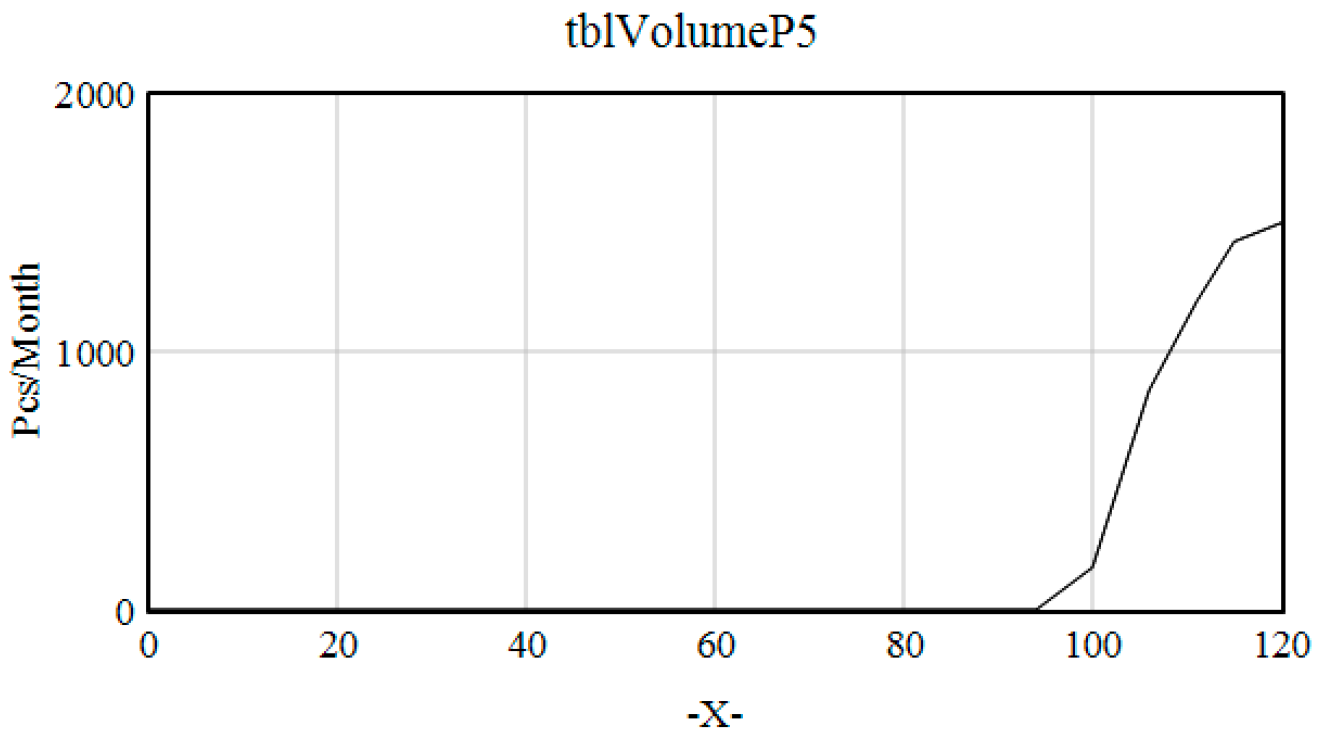
| tblVolumeP5 | ([(0,1)-(120,2000)],(0,1),(94,1),(100,165), (106,851), (111,1194),(115,1425),(120,1498)) | Pcs/Month |
| TIME STEP | 0.125 | Month [0,?] |
| timePerRUI | 40 | WorkHrs/RUI |
| timeToAvgOrderRate | 1 | Month |
| WorkInProcess | INTEG (productionStartRate - productionRate, desiredWIP) | Pcs |
| workloadRatioRUIperNPC | 50 | NPC/RUI |
| workloadRUI | 10 | RUI/NPI |
References
- Fogliatto, F.S.; Da Silveira, G.J.C.; Borenstein, D. The mass customization decade: An updated review of the literature. Int. J. Prod. Econ. 2012, 138, 14–25. [Google Scholar] [CrossRef]
- Dombrowski, U.; Ebentreich, D.; Krenkel, P. Impact Analyses of Lean Production Systems. Procedia CIRP 2016, 57, 607–612. [Google Scholar] [CrossRef]
- Zikopoulos, C. On the effect of upgradable products design on circular economy. Int. J. Prod. Econ. 2022, 254, 108629. [Google Scholar] [CrossRef]
- Vielhaber, M.; Stoffels, P. Product development vs. Production development. Procedia CIRP 2014, 21, 252–257. [Google Scholar] [CrossRef]
- Dogea, R.; Stolt, R. Identifying Challenges Related to Industry 4.0 in Five Manufacturing Companies. Procedia Manuf. 2021, 55, 328–334. [Google Scholar] [CrossRef]
- Yang, J.; Son, Y.H.; Lee, D.; Do Noh, S. Digital Twin-Based Integrated Assessment of Flexible and Reconfigurable Automotive Part Production Lines. Machines 2022, 10, 75. [Google Scholar] [CrossRef]
- Barrera-Diaz, C.A.; Nourmohammadi, A.; Smedberg, H.; Aslam, T.; Ng, A.H.C. An Enhanced Simulation-Based Multi-Objective Optimization Approach with Knowledge Discovery for Reconfigurable Manufacturing Systems. Mathematics 2023, 11, 1527. [Google Scholar] [CrossRef]
- Goienetxea Uriarte, A.; Ng, A.H.C.; Urenda Moris, M. Bringing together Lean and simulation: A comprehensive review. Int. J. Prod. Res. 2020, 58, 87–117. [Google Scholar] [CrossRef]
- Anderson, E.G.; Lim, S.Y.; Joglekar, N. Are more frequent releases always better? Dynamics of pivoting, scaling, and the minimum viable product. In Proceedings of the Annual Hawaii International Conference on System Sciences, Waikoloa Village, HI, USA, 4–7 January 2017; pp. 5849–5858. [Google Scholar] [CrossRef]
- Landahl, J.; Jiao, R.J.; Madrid, J.; Söderberg, R.; Johannesson, H. Dynamic platform modeling for concurrent product-production reconfiguration. Concurr. Eng. Res. Appl. 2021, 29, 102–123. [Google Scholar] [CrossRef]
- ElMaraghy, H. Changeable and Reconfigurable Manufacturing Systems; Springer: London, UK, 2009. [Google Scholar]
- Skärin, F.; Rösiö, C.; Andersen, A.L. Towards Circular Production Systems: Outlining the Concept, Challenges and Future Research Directions. In Advances in System-Integrated Intelligence, Proceedings of the 6th International Conference on System-Integrated Intelligence (SysInt 2022), Genova, Italy, 7–9 September 2022; Lecture Notes in Networks and Systems; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2023; Volume 546, pp. 616–625. [Google Scholar]
- Boldt, S.; Rösiö, C.; Linnéusson, G. Mapping Production Capabilities: Proposing Support Towards Changeable Production. In Production Processes and Product Evolution in the Age of Disruption, Proceedings of the 9th Changeable, Agile, Reconfigurable and Virtual Production Conference (CARV 2023) and the 11th World Mass Customization & Personalization Conference (MCPC 2023), Bologna, Italy, 20–23 June 2023; Galizia, F.G., Bortolini, M., Eds.; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Helbig, T.; Hoos, J.; Westkaämper, E. A Method for Estimating and Evaluating Life Cycle Costs of Decentralized Component-based Automation Solutions. Procedia CIRP 2014, 17, 332–337. [Google Scholar] [CrossRef]
- Andersen, A.L.; Brunoe, T.D.; Bockholt, M.T.; Napoleone, A.; Hemdrup Kristensen, J.; Colli, M.; Vejrum Wæhrens, B.; Nielsen, K. Changeable Closed-Loop Manufacturing Systems: Challenges in Product Take-Back and Evaluation of Reconfigurable Solutions. Int. J. Prod. Res. 2023, 61, 839–858. [Google Scholar] [CrossRef]
- Skärin, F.; Abdelmageed, M.E.; Linnéusson, G.; Rösiö, C. Supporting Manufacturing Investment Decisions in New Product Introductions through Line Balancing Techniques. In Advances in Transdisciplinary Engineering, Proceedings of the 10th Swedish Production Symposium (SPS 2022), Skövde, Sweden, 26–29 April 2022; IOS Press BV: Amsterdam, The Netherlands, 2022; Volume 21, pp. 89–100. [Google Scholar]
- Sterman, J.D. Business Dynamics: Systems Thinking and Modeling for a Complex World; Irwin McGraw-Hill: Boston, MA, USA, 2000. [Google Scholar]
- Warren, K. Improving strategic management with the fundamental principles of system dynamics. Syst. Dyn. Rev. 2005, 21, 329–350. [Google Scholar] [CrossRef]
- Linnéusson, G.; Ng, A.H.C.; Aslam, T. Towards strategic development of maintenance and its effects on production performance by using system dynamics in the automotive industry. Int. J. Prod. Econ. 2018, 200, 151–169. [Google Scholar] [CrossRef]
- Koufteros, X.; Lu, G.; Peters, R.C.; Lai, K.H.; Wong, C.W.Y.; Cheng, T.C.E. Product development practices, manufacturing practices, and performance: A mediational perspective. Int. J. Prod. Econ. 2014, 156, 83–97. [Google Scholar] [CrossRef]
- Zhang, L.L. A literature review on multitype platforming and framework for future research. Int. J. Prod. Econ. 2015, 168, 1–12. [Google Scholar] [CrossRef]
- Robertson, D.; Ulrich, K. Planning for Product Platforms. Sloan Manag. Rev. 1998, 39, 19–31. [Google Scholar]
- Meyer, M.H.; Lehnerd, A.P. The Power of Product Platforms: Building Value and Cost Leadership; The Free Press: New York, NY, USA, 1997. [Google Scholar]
- Sorensen, D.G.H.; ElMaraghy, H.A.; Brunoe, T.D.; Nielsen, K. Classification coding of production systems for identification of platform candidates. CIRP J. Manuf. Sci. Technol. 2020, 28, 144–156. [Google Scholar] [CrossRef]
- Michaelis, M.T.; Johannesson, H. From Dedicated to Platform-Based Co-Development of Products and Manufacturing Systems. In Proceedings of the 4th International Conference on Changeable, Agile, Reconfigurable and Virtual Production, Montreal, QC, Canada, 2–5 October 2011; pp. 197–202. [Google Scholar] [CrossRef]
- Boldt, C.S.; Linnéusson, G.; Rösiö, C. Exploring the concept of production platforms—A literature review. Procedia CIRP 2021, 104, 158–163. [Google Scholar] [CrossRef]
- ElMaraghy, H.A.; Abbas, M. Products-manufacturing systems Co-platforming. CIRP Ann. Manuf. Technol. 2015, 64, 407–410. [Google Scholar] [CrossRef]
- Sorensen, D.G.H.; Bossen, J.; Bejlegaard, M.; Brunoe, T.D.; Nielsen, K. Production Platform Development through the Four Loops of Concern. In Customization 4.0; Hankammer, S., Nielsen, K., Piller, F., Schuh, G., Wang, N., Eds.; Springer: Cham, Switzerland, 2018; pp. 479–493. [Google Scholar] [CrossRef]
- Brunoe, T.D.; Andersen, A.L.; Sorensen, D.G.H.; Nielsen, K.; Bejlegaard, M. Integrated product-process modeling for platform-based co-development. Int. J. Prod. Res. 2020, 58, 6185–6201. [Google Scholar] [CrossRef]
- Andersen, A.L.; Brunoe, T.D.; Nielsen, K.; Rösiö, C. Towards a generic design method for reconfigurable manufacturing systems: Analysis and synthesis of current design methods and evaluation of supportive tools. J. Manuf. Syst. 2017, 42, 179–195. [Google Scholar] [CrossRef]
- Andersen, A.L.; Rösiö, C. Investigating the Transition towards Changeability through Platform-based Co-development of Products and Manufacturing Systems. Procedia Manuf. 2019, 28, 114–120. [Google Scholar] [CrossRef]
- Dashchenko, A.I. Reconfigurable Manufacturing Systems and Transformable Factories; Springer: Berlin, Germany, 2006. [Google Scholar] [CrossRef]
- Singh, P.P.; Madan, J.; Singh, S. Economically Sustainable Configuration Selection in Reconfigurable Manufacturing System. In Sustainable Development through Engineering Innovations; Singh, H., Cheema, P.P.S., Garg, P., Eds.; Lecture Notes in Civil Engineering 113; Springer Nature: Singapore, 2021; pp. 457–466. [Google Scholar] [CrossRef]
- Amjad, M.S.; McCleeary, D.; Nagaraj, S.; Diaz-Elsayed, N. Integrating Carbon Credits with Life Cycle Costing for Economic Sustainability in SMEs. Procedia CIRP 2023, 116, 672–677. [Google Scholar] [CrossRef]
- Ellström, E. Knowledge Creation through Interactive Research: A Learning Perspective, Linköping. 2007. Available online: https://www.ltu.se/cms_fs/1.24923!/per-erik%20ellstr%C3%B6m.pdf (accessed on 20 September 2023).
- Ørngreen, E.L.; Levinsen, R.T. Workshops as a Research Methodology. Electron. J. e-Learn. 2017, 15, 70–81. [Google Scholar]
- Slack, N.; Brandon-Jones, A.; Johnston, R. Operations Management, 8th ed.; Pearson: Halow, UK, 2016. [Google Scholar]

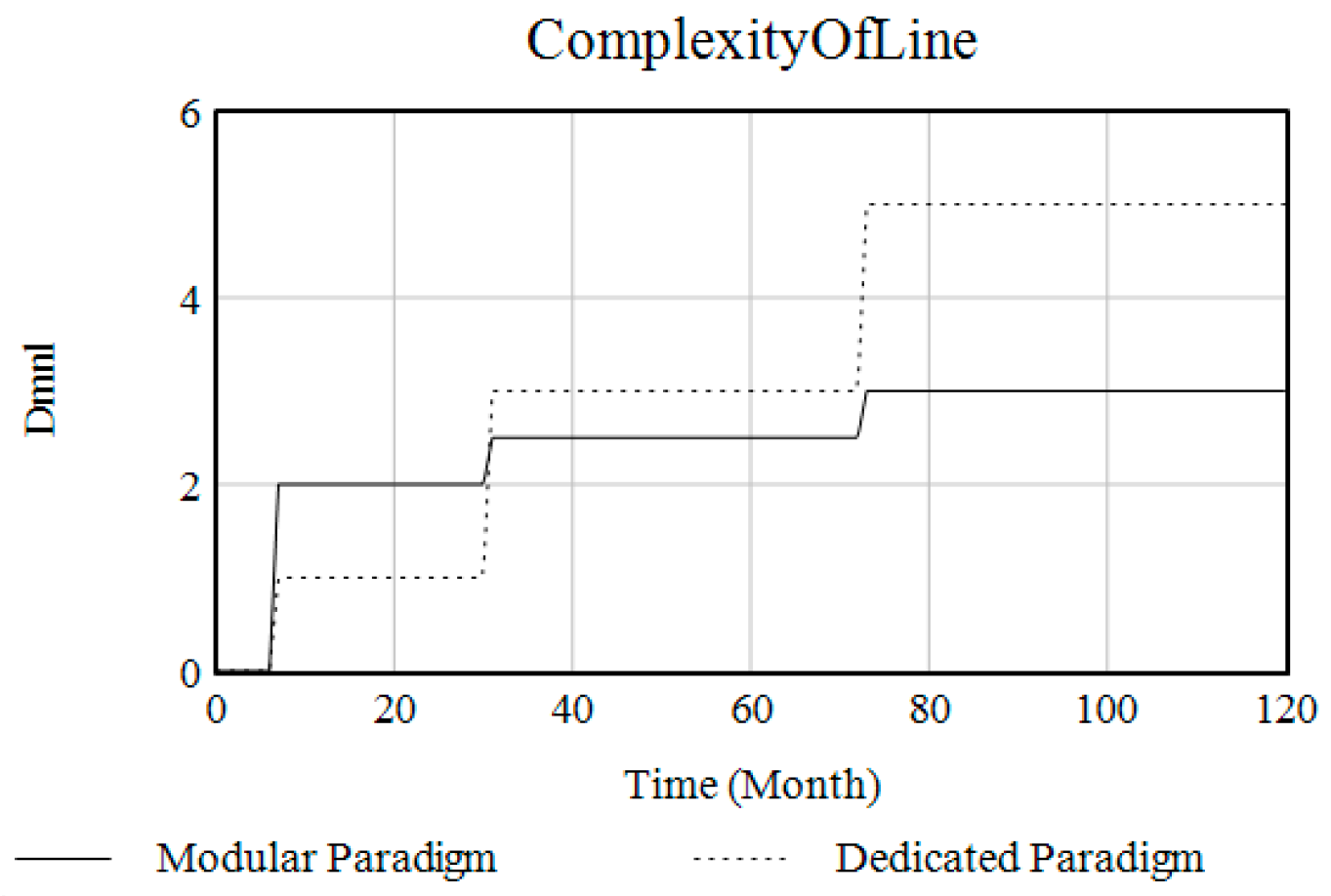
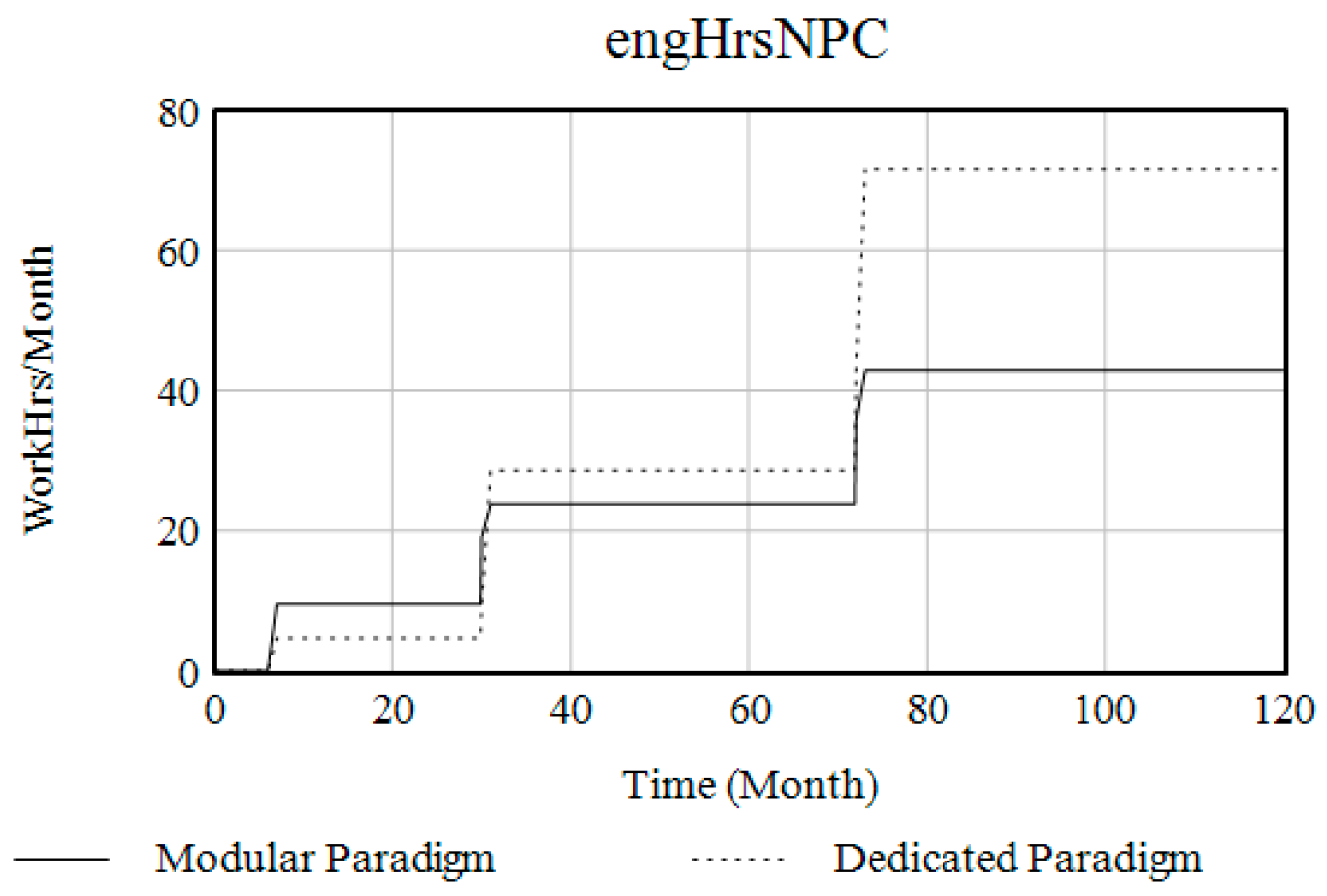
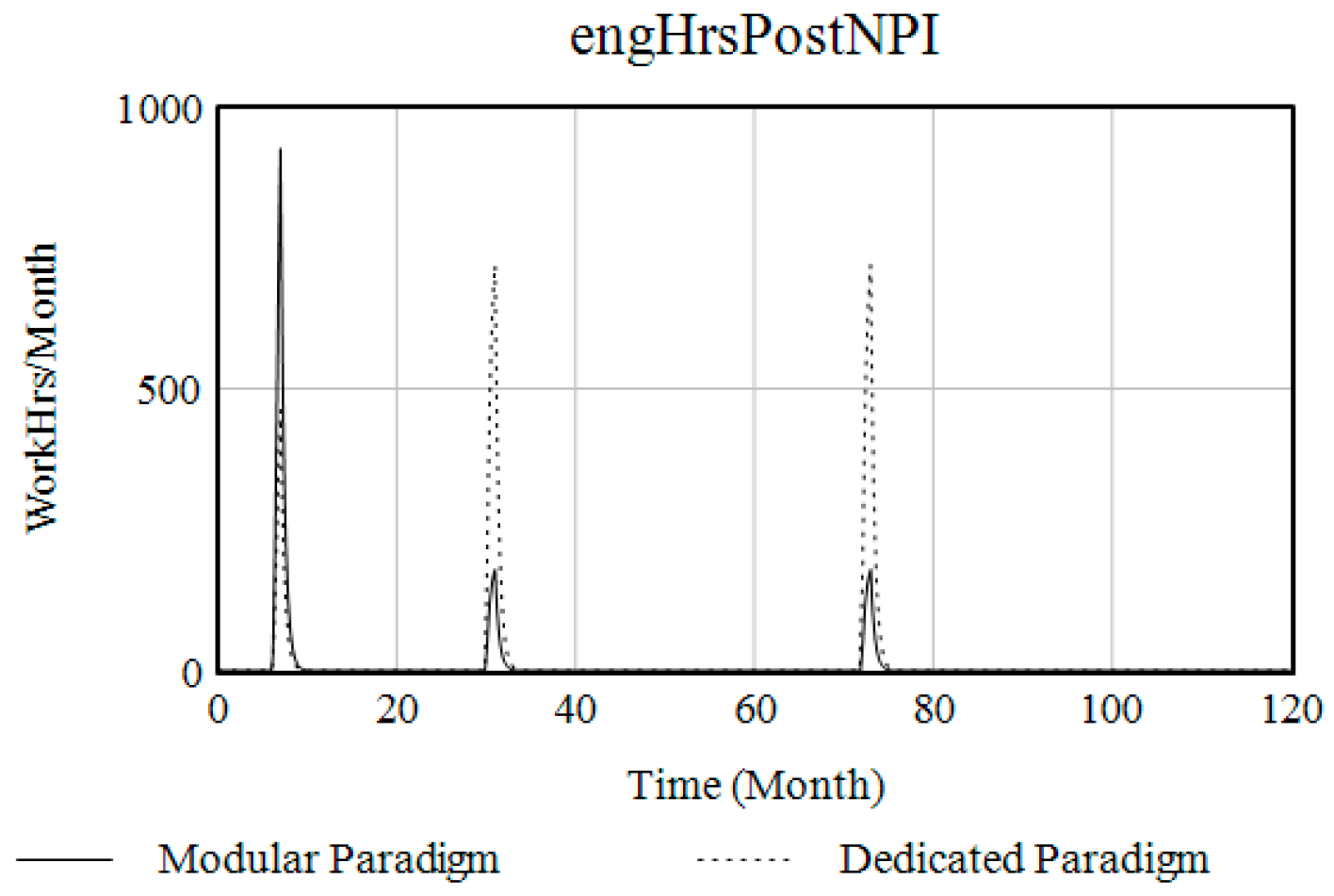

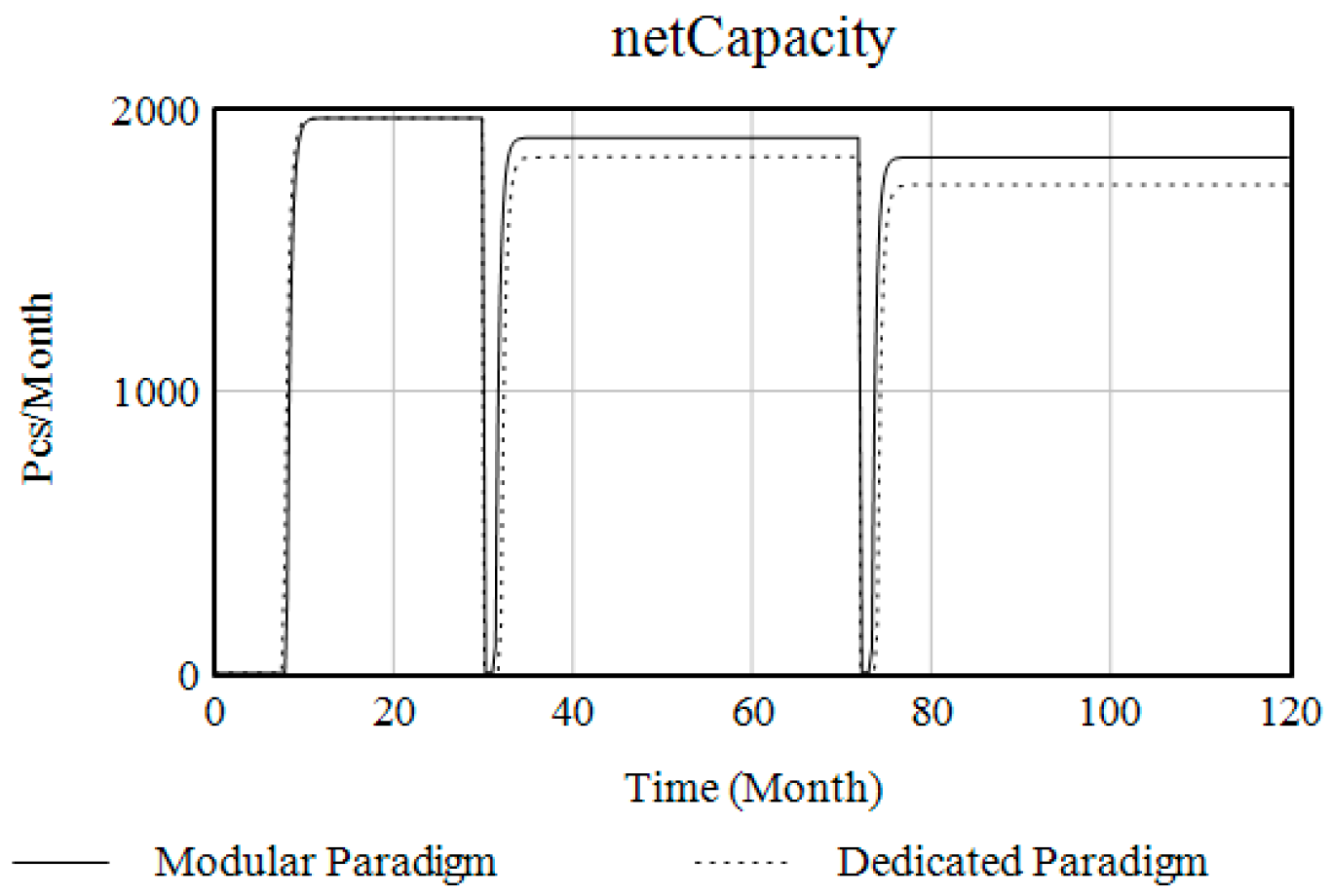

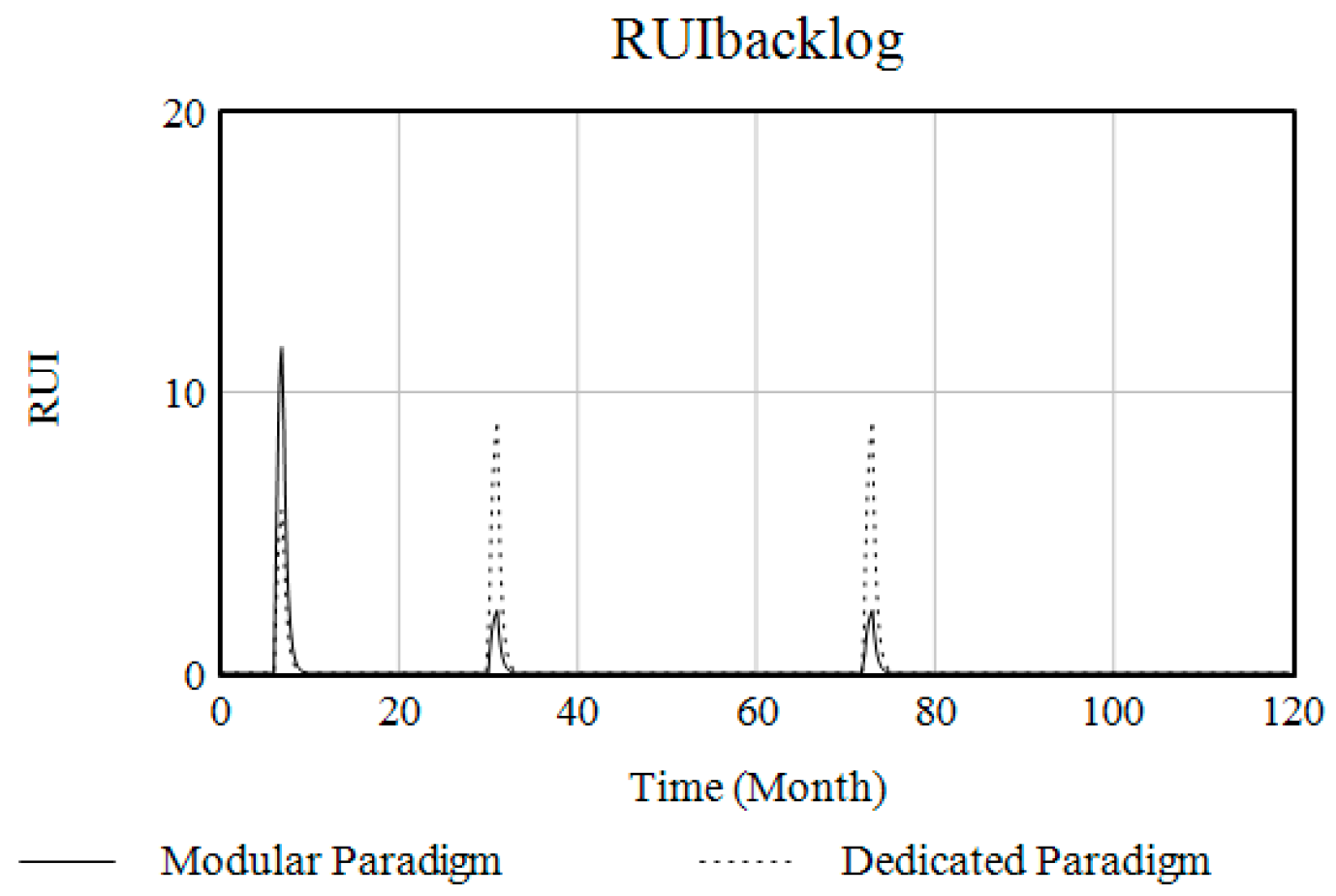
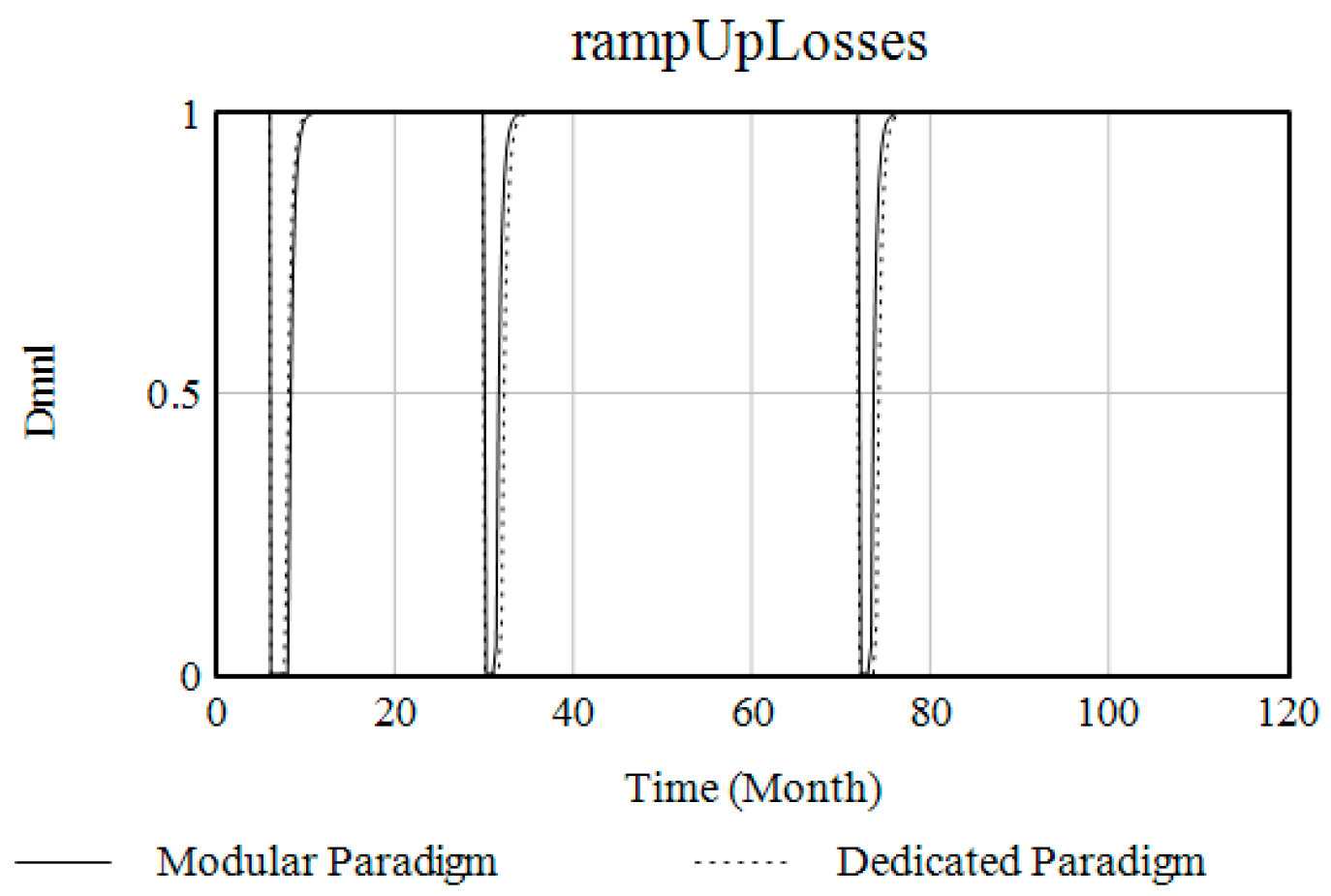
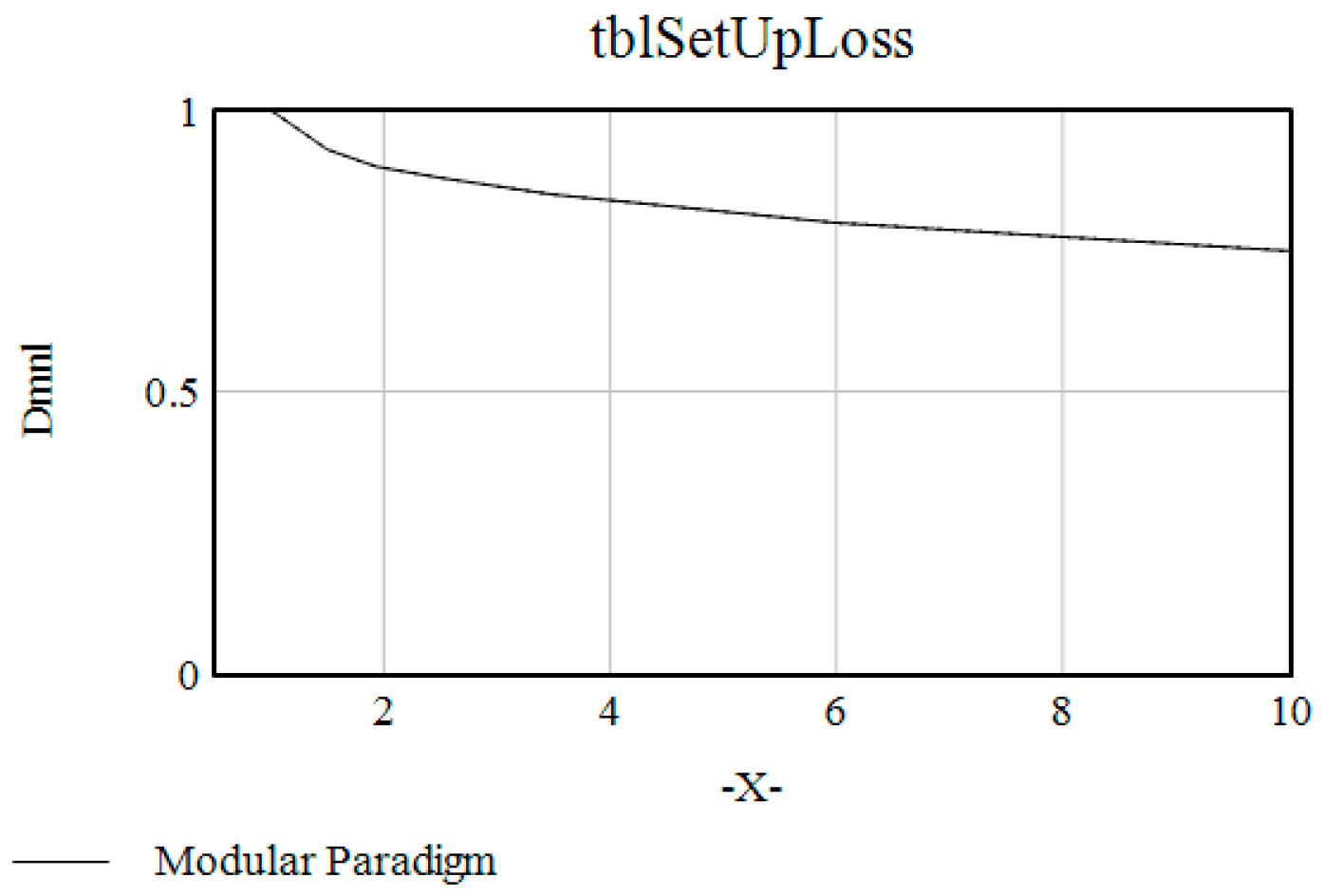
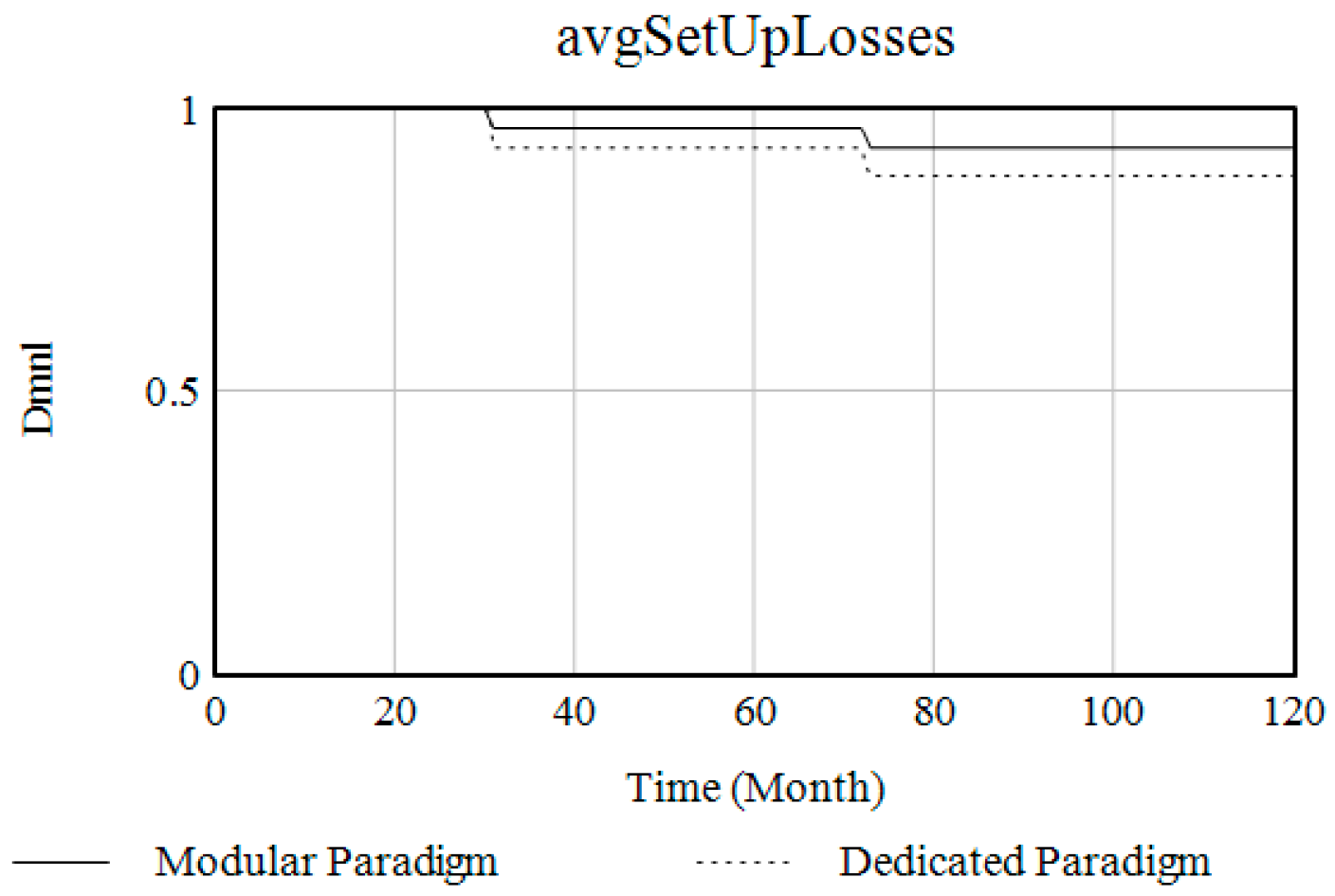


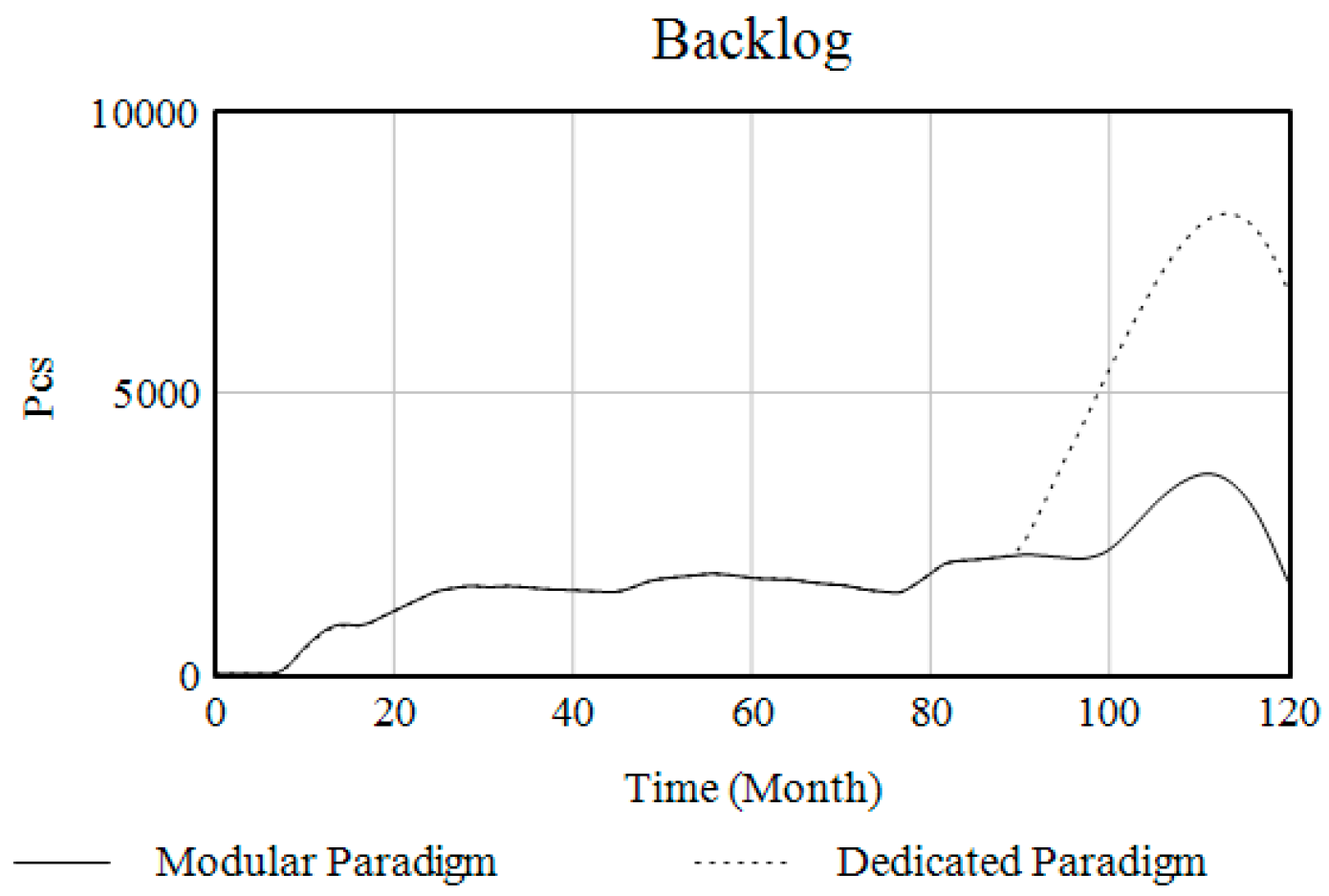


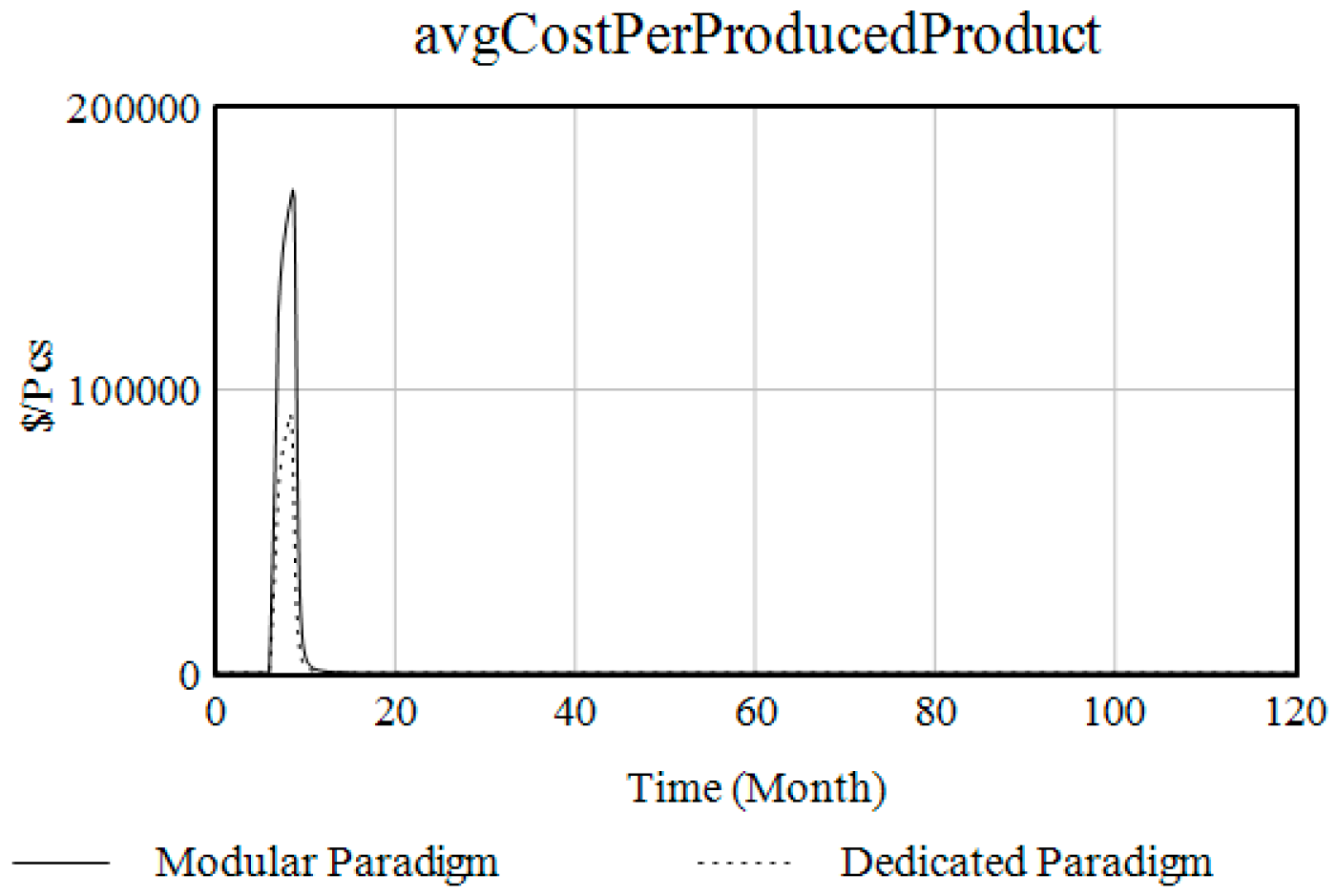
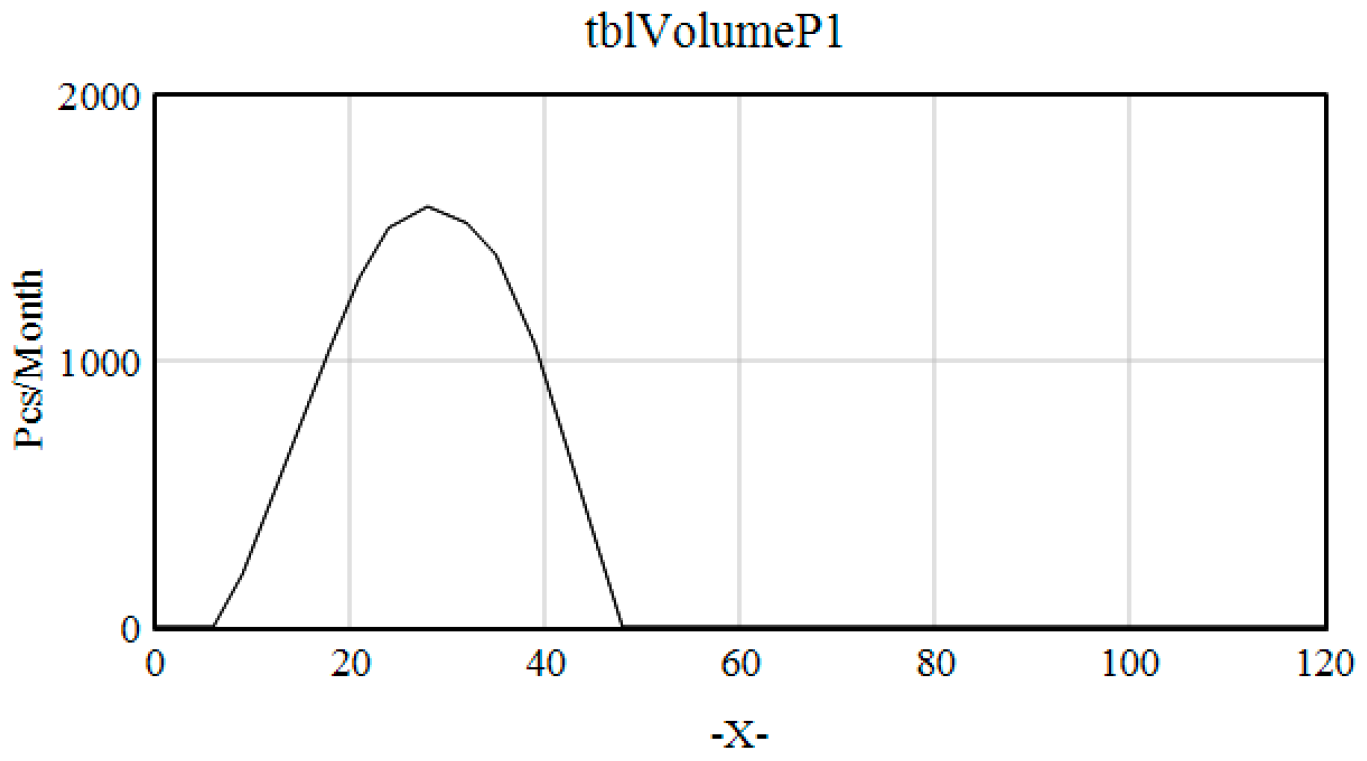
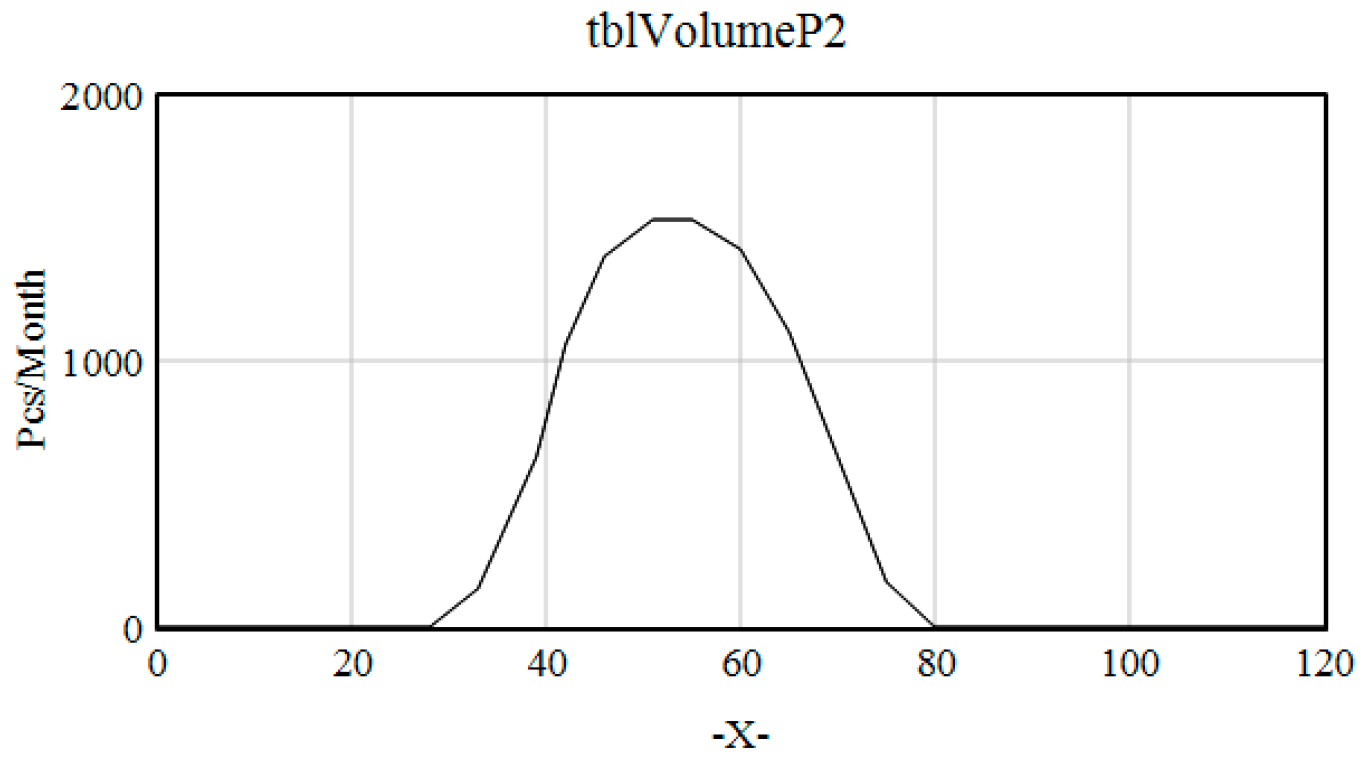


| Project | Dedicated Paradigm | Modular Paradigm |
|---|---|---|
| P1 NPI | 1 × n (hours) | 2 × n (hours) |
| P2 NPI | 2 × n (hours) | 0.5 × n (hours) |
| P3 NPI | 2 × n (hours) | 0.5 × n (hours) |
| Simulation | Input Variables | NPI/NPC | Uncertainty Ranges | |
|---|---|---|---|---|
| name | noNPI | tblVolumePη | introduced at | min/max |
| 1 NPI | 1 | P1 | Month 6 | 0.5/1.5 |
| 2 NPI | 2 | P1+P2 | Month 28 | 0.5/1.5 |
| 3 NPI | 3 | P1+…+P3 | Month 50 | 0.5/1.5 |
| 4 NPI | 4 | P1+…+P4 | Month 72 | 0.5/1.5 |
| 5 NPI | 5 | P1+…+P5 | Month 94 | 0.5/1.5 |
| Simulation Name | Comparison of Simulated Results | Comparison of Uncertainty Risk |
|---|---|---|
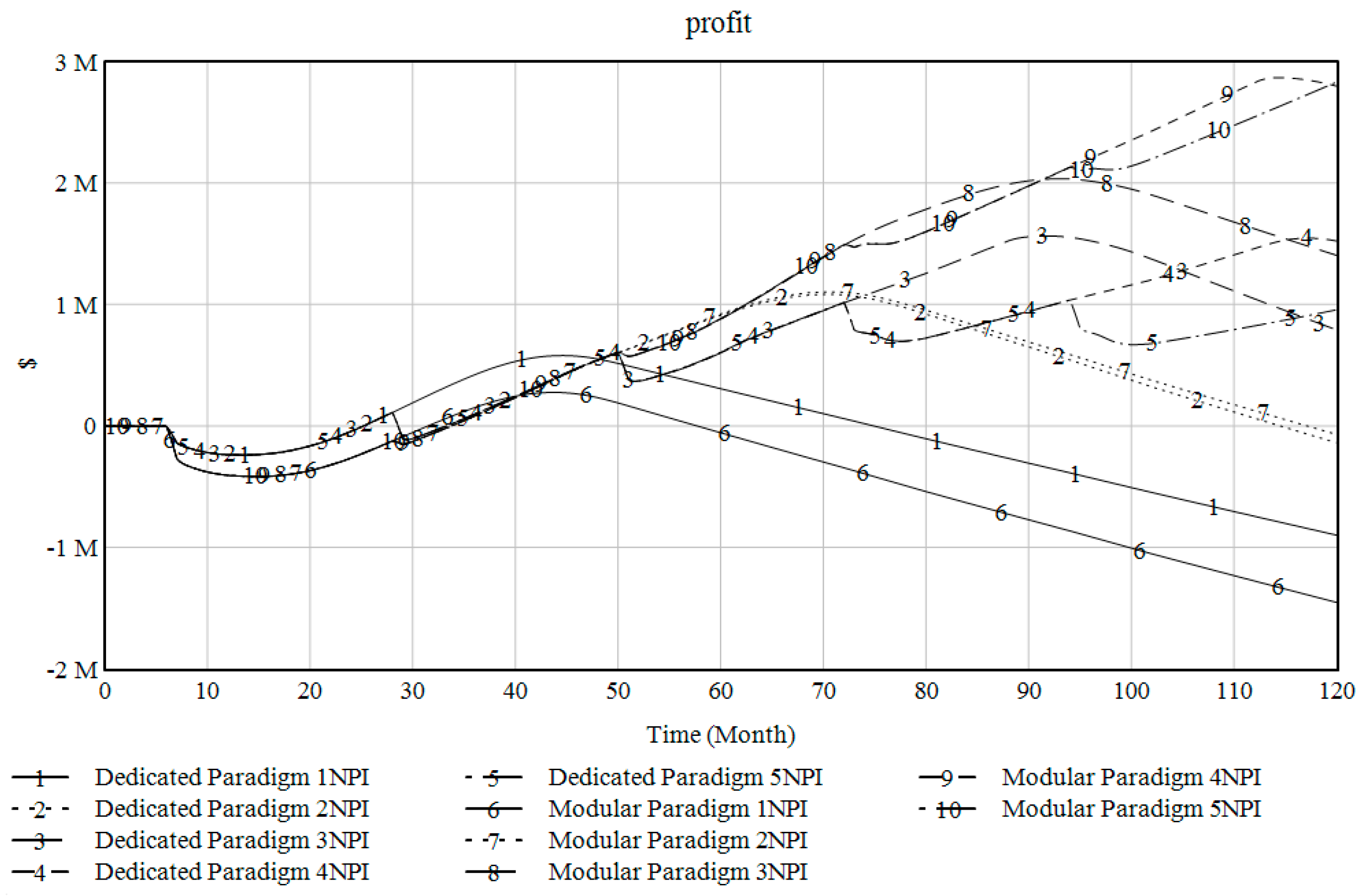
| 1 NPI | The dedicated paradigm reaches break even first. | Low uncertainty during the 1st NPI as expected, even if the dedicated approach presents a bit wider range of uncertainty at Month 28. |
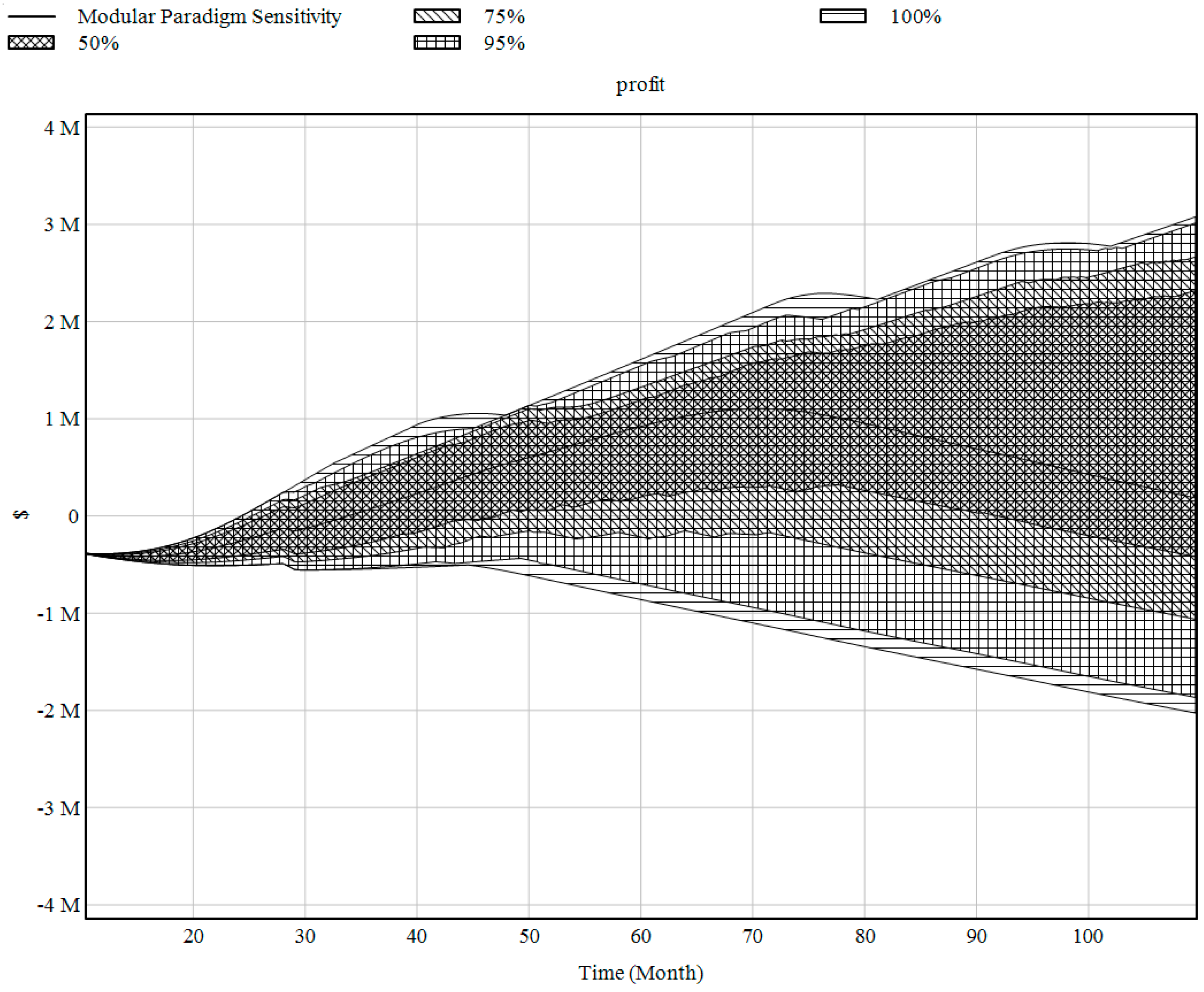
| 2 NPI | During the 2nd NPI, all scenarios follow a similar pattern. | The uncertainty analysis depicts a similar potential for the 50% variance to the normal value, while the dedicated approach would be more beneficial if having higher production volumes. * |
| 3 NPI | At the 3rd NPI, the modular paradigm indicates a small advantage. | Both paradigms have similar risks, even if the dedicated seems safer at lower volumes. Looking at the 50% range the modular approach follows a higher performing behavior. |
| 4 NPI | At the 4th NPI, the modular approach indicates nearly twice the profit. | For the first time, the modular approach indicates higher profit potentials yet also a wider range for the 50%. * |
| 5 NPI | At the 5th NPI, the modular approach indicates nearly three times the profit. | The indicated potential of higher profit is attached to selecting the modular paradigm. * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Linnéusson, G.; Boldt, S. Towards Assessing the Economic Sustainability of Reconfigurable Modularization in Semi-Automatic Assembly Systems: A System Dynamics Perspective. Systems 2024, 12, 218. https://doi.org/10.3390/systems12060218
Linnéusson G, Boldt S. Towards Assessing the Economic Sustainability of Reconfigurable Modularization in Semi-Automatic Assembly Systems: A System Dynamics Perspective. Systems. 2024; 12(6):218. https://doi.org/10.3390/systems12060218
Chicago/Turabian StyleLinnéusson, Gary, and Simon Boldt. 2024. "Towards Assessing the Economic Sustainability of Reconfigurable Modularization in Semi-Automatic Assembly Systems: A System Dynamics Perspective" Systems 12, no. 6: 218. https://doi.org/10.3390/systems12060218
APA StyleLinnéusson, G., & Boldt, S. (2024). Towards Assessing the Economic Sustainability of Reconfigurable Modularization in Semi-Automatic Assembly Systems: A System Dynamics Perspective. Systems, 12(6), 218. https://doi.org/10.3390/systems12060218











