An Evolutionary Game Study of Collaborative Innovation across the Whole Industry Chain of Rural E-Commerce under Digital Empowerment

Abstract

With the profound integration of digital technology and traditional agriculture, the whole industry chain of rural e-commerce, as an advanced system, is reshaping the production, sales, and management models of agriculture and is emerging as a new catalyst for the advancement of digital agriculture through significant innovation. This paper focuses on the digital empowerment attributes and strategic attributes of the whole industrial chain of rural e-commerce, and evolutionary game models under market mechanisms and regulations are constructed. It examines the influence of various elements, such as the digital technology empowerment coefficient, on collaborative innovation within the whole industry chain of rural e-commerce. Using case simulations, this paper discusses the role of government regulation and intervention when market mechanisms are inadequate. The study reveals that factors such as the digital technology empowerment coefficient, technology absorptive capacity, and the amount of technology and information stored in collaborative innovation positively influence the whole industry chain. Potential risk losses and free-rider gains have negative effects on the evolution of the system toward collaborative innovation. When market mechanisms are inadequate, a combination of operational cost subsidies and incentive measures can yield more effective policy synergy, with the incentive impact of cost subsidies being particularly notable. The strategic application of enterprise-liquidated damage and government penalties will aid in regulating and directing corporate behavior. The findings of this research not only offer a new microlevel explanation for understanding the decision-making mechanism behind collaborative innovation in the whole industrial chain of rural e-commerce but also serve as a reference for government policy formulation to ensure the stability of the whole rural e-commerce industry chain.

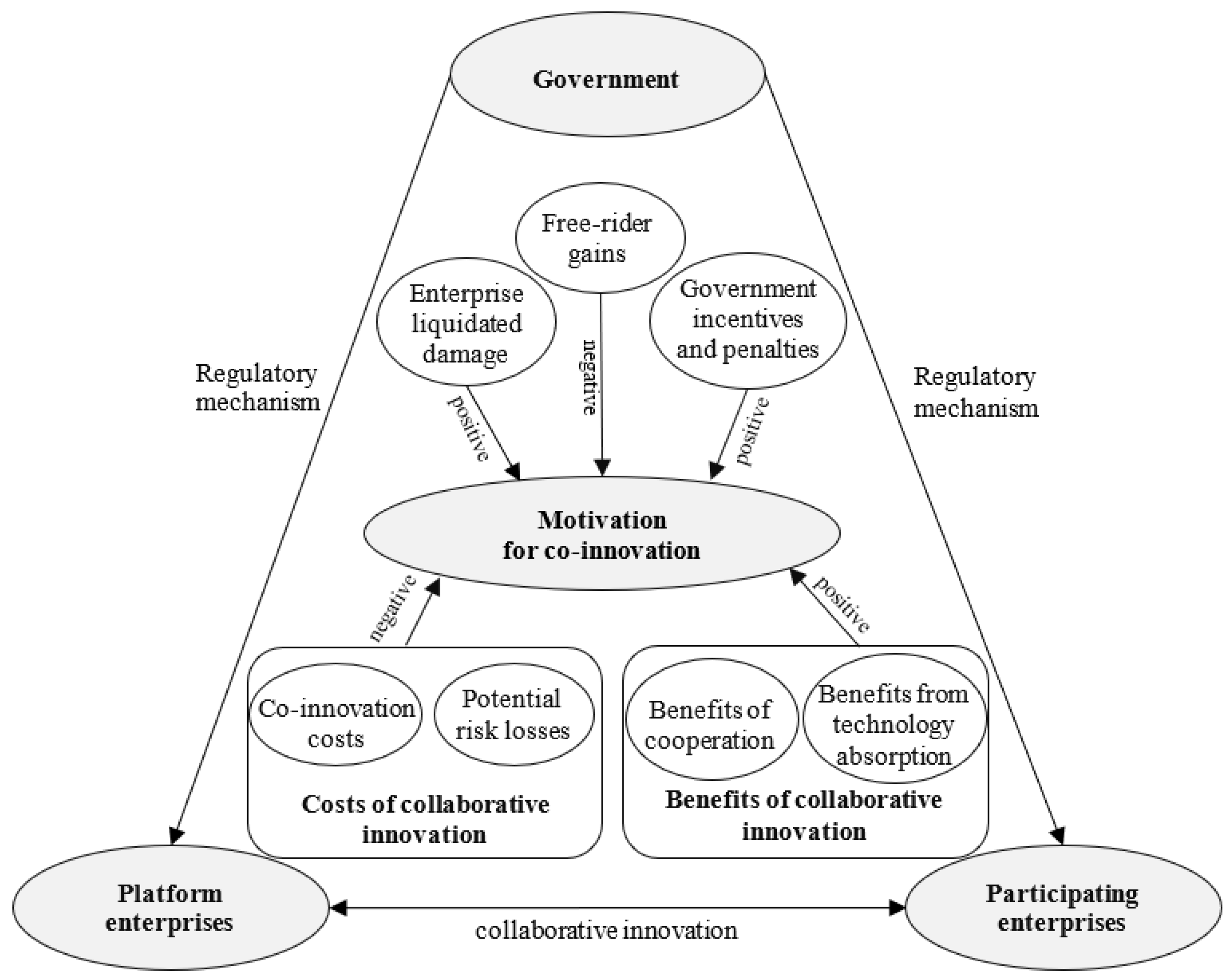
1. Introduction

As a fundamental industry linked to the national economy and the livelihood of the populace, agriculture is experiencing essential transformations due to digital technology. The impact of digital agriculture is widening, reshaping the economic framework, and redrawing global competitive boundaries [1,2]. Rural e-commerce can be fully integrated with various aspects of agricultural production, operation, management, and service, particularly breaking the traditional linear supply chain through industrial chain integration and establishing a new ecosystem centered around consumer and customer needs [3,4]. Enterprises such as Amazon, Jingdong (JD), Pinduoduo (PDD), and eBay are actively pursuing online sales of agricultural products, facilitating the transformation and upgrading of the industrial chain with the aid of Internet and big data technologies, closely cooperating with all segments of the industrial chain, and aiming to achieve precise supply–demand matching and reduce production missteps through collaborative innovation [5]. Platform enterprises are the core of the collaborative innovation of the rural e-commerce industry chain under digital empowerment, cooperating in depth with other participating enterprises in the chain to jointly promote e-commerce innovation [6,7]. Nevertheless, the whole industry chain model faces challenges such as an unbalanced distribution of synergy benefits among enterprises, asymmetric information, leakage of core digital technologies, or “free-riding” behavior [8,9], which often results in “blocked chains”, “broken chains”, and “missing chain” issues, adversely affecting the smooth operation and collaborative innovation effects of the whole chain [10,11]. At present, we do not have a clear understanding of the evolution law of collaborative innovation behavior decision-making among enterprises in the whole industrial chain of rural e-commerce under digital empowerment. Moreover, the strategic nature of collaborative innovation in the whole industrial chain of rural e-commerce underscores the significant role of the government [4,12]. Effective government intervention can increase the level of trust and cooperation enthusiasm between partners, significantly improving the overall synergy efficiency of the system [13]. Therefore, what is the evolution law of collaborative innovation behavior decision making among enterprises in the whole industrial chain of rural e-commerce under digital empowerment? To address market failure effectively in the whole industrial chain of rural e-commerce, how should we formulate and implement corresponding regulation strategies? This realistic problem needs to be studied urgently at present.

The collaborative innovation of the whole industry chain offers a new analytical perspective for research in the field of rural e-commerce. However, as a nascent business model, the whole industry chain of rural e-commerce is still in its developmental infancy, and corresponding academic research is just beginning. Research on the collaboration of the rural e-commerce industry chain has focused mainly on the integration and restructuring of the rural e-commerce industry chain and efficiency improvement. (1) The restructuring and construction of the rural e-commerce industry chain have been pivotal areas of focus in recent studies, with an emphasis on the crucial role of multiagent collaboration. Bai [14] analyzed the developmental pathways and mechanisms of rural e-commerce from the perspective of a sustainable development ecosystem, highlighting the significance of multiagent collaboration in the restructuring of industrial chains. Zhang et al. [15] described in detail the mobility and interaction between the platform and participating enterprises in the rural e-commerce industry chain through a case study, which provides support for understanding the upgrading of the industry chain. Prajapati et al. [16] further expanded the theoretical framework of rural e-commerce industrial chain collaboration and introduced the concept of a sustainable supply chain. Zeng et al.’s case study revealed that in the process of promoting industrial clusters and success, it is very important for enterprises and other multi-stakeholders to work together to build a supporting ecosystem conducive to the prosperity of rural e-commerce [17]. (2) Additionally, enhancing the efficiency of the rural e-commerce industry chain has been another focal point, with scholars concentrating more on technological changes and innovative modes. Zhu et al. [18] proposed strategies to increase the efficiency of the industrial chain from the perspective of geographical and spatial planning, such as optimizing resource allocation and strengthening cooperation between entities. Karine [19] suggested a traceability system for agricultural products based on blockchain technology, highlighting the significance of this technology for the development of agricultural e-commerce. The most recent study by Du [20] delves deeper into the impact of technological advancements on improving the efficiency of the rural e-commerce industry chain, emphasizing a collaborative strategy involving digital intelligence.

In summary, although the literature recognizes that the restructuring and efficiency improvement of the rural e-commerce industry chain require multiagent collaborative support and innovation, fully revealing the dynamic behavior evolution logic of micro-integration subjects in the rural e-commerce industry chain by scholars, who rely primarily on theoretical analysis, case studies, or questionnaires, is difficult. From the above discussion, we can see that there is an interactive relationship between platform enterprises and other participating enterprises in the rural e-commerce industry chain, and this interactive relationship changes with the passage of time in practice. The dynamic interaction among populations should be simulated by replicator dynamics [21]. Evolutionary game theory, as an effective analytical tool, can reflect this dynamic interaction well. However, there is currently a scarcity of studies in the literature that apply this theory to the analysis of the rural e-commerce industrial chain. Furthermore, the whole industrial chain of rural e-commerce has the characteristics of digital empowerment [15,22,23]. The game relationship of collaborative innovation among enterprises is affected not only by the information flow and technology quantity brought by digital empowerment but also by factors such as the digital technology empowerment coefficient and technology absorption capacity. Potential market risks such as copying, imitating, and stealing core technologies in cooperation [24] should also be fully considered when establishing the evolution model. Nevertheless, these factors have not yet been integrated into a unified framework for evolutionary research in the existing literature. Moreover, the primary goal of studying the influencing factors of collaborative innovation is to clarify how the government should implement targeted regulatory measures to guide the coordinated and stable development of the whole industry chain of rural e-commerce when the market mechanism fails [25]. Although the literature has proven its positive role in promoting the collaborative innovation of the new energy automobile industry chain [26], takeaway garbage recycling industry chain [27], green dairy industry chain [28], and cold chain [29], there are no studies in the literature discussing how to effectively optimize the regulatory mechanism when the market operation mechanism of the whole rural e-commerce industry chain fails under digital empowerment.

To bridge these research gaps, in this paper, according to the digital empowerment characteristics and policy-oriented characteristics of the whole industrial chain of rural e-commerce, an evolutionary game model of “platform enterprise-participating enterprises” under market mechanisms and regulations is constructed. This study aims to address the following questions:

RQ1. What is the evolutionary game model of collaborative innovation in the rural e-commerce industry chain under digital empowerment?

RQ2. How will the strategic choices of platform enterprises and participating enterprises be affected when factors such as the digital technology enabling coefficient and technology absorption capacity change?

RQ3. When there is market failure, that is, when the game between platform enterprises and participating enterprises fails to achieve collaborative innovation, how should we design and implement accurate and effective control measures?

To solve the above problems, this paper discusses the coevolution law of platform enterprises and participating enterprises in the whole industrial chain of rural e-commerce under market mechanisms and regulations, explores key factors influencing collaborative innovation among enterprises, and explains the necessity of government regulation and appropriate intervention. Compared with other similar studies, the potential contributions of this paper are as follows: First, considering the digital empowerment characteristics of the whole industrial chain of rural e-commerce, an evolutionary game model of “platform enterprises-participating enterprises” under both pure market mechanisms and government regulation is constructed. It serves as a theoretical model reference for understanding the collaborative behaviors within the rural e-commerce industry chain. Second, on the basis of the theoretical verification of various influencing factors, such as the digital technology empowerment coefficient, it simulates the effects of various cost–benefit ratios, potential risk losses, free-rider gains, and other factors on the collaborative innovation behaviors of enterprises by adjusting the relative proportions of the parameters, thereby revealing the dynamic evolution law of strategy choice between platform enterprises and participating enterprises and offering strategic insights for the cooperation and competition among industry chain enterprises. Third, this paper focuses on how to facilitate the collaborative innovation of the whole rural e-commerce industry chain through specific government regulatory mechanisms when market mechanisms fail, offering significant practical insights for government policy formulation to ensure the stability of the whole rural e-commerce industry chain.

The structure of the remainder of the paper is as follows: Section 2 introduces the model assumptions and develops decision models. Section 3 provides a case and performs numerical simulations. Section 4 is the discussion section. Section 5 presents the research conclusions and implications.

2. Basic Assumptions and Model Construction

2.1. Model Assumptions

The operation mechanism of the whole industrial chain of rural e-commerce under digital empowerment is reflected mainly in the process whereby core platform enterprises and other participating enterprises realize integration, innovation, and value creation through digital technology application and information sharing [30,31]. In the practice of the whole industrial chain of rural e-commerce, platform enterprises, as the core of the whole industrial chain, effectively integrate and allocate the resources of other participating enterprises in the chain through advanced digital technology to provide key support for the whole industrial chain. While other participating enterprises in the chain have different functions, they all have certain complementarity and dependence on platform enterprises. They need to share resources with the platform to realize their own [14,15,30]. Given the pivotal role that platform enterprises play and the common characteristic shared by participating enterprises, this paper investigates the collaborative evolution process between core platform enterprises and other participating enterprises. Each player has two strategic choices: “collaborative innovation” or “non-collaborative innovation”. “Collaborative innovation” means that platform enterprises and participating enterprises realize value increases through information sharing and technological innovation on the basis of common goals and interests. In contrast, “non-collaborative innovation” means that both parties maintain only superficial cooperation, lack a strong willingness to share information and technology, and may have the psychology of “free riders”.

If both sides of the game choose “collaborative innovation”, then in addition to the initial net benefits, there can also be collaborative innovation benefits and benefits from technology absorption. On the one hand, platform enterprises and participating enterprises rely on digital technology empowerment to accurately capture and efficiently integrate market information to jointly establish an information base to obtain collaborative innovation benefits. This benefit depends on the digital technology empowerment coefficient and the amount of information established through collaborative innovation [15,30]. On the other hand, in the long run, with the improvement of the technical capabilities of both parties, there can be benefits from technology absorption, but the size of the benefits depends on their respective technology absorption capacity and the amount of technology stored [32,33]. However, in terms of cost, both parties should not only bear the direct input cost of collaborative innovation but also face potential risks and losses, such as copying, imitating, and stealing key technologies or information [8,24].

As key players in collaborative innovation, the strategic choices of platform enterprises and participating enterprises influence each other. Enterprises make strategic selections on the basis of profitability. However, if hitchhiking occurs, different actors may adopt inconsistent behavioral strategies. This misalignment can lead to difficulties in realizing collaborative innovation, wasting technology and data resources, and ultimately affecting the stability of the whole industry chain’s collaborative innovation. In the case of market failure, the government, as a crucial supporter of the whole industry chain, addresses these market failures by subsidizing operating costs, implementing reward and penalty mechanisms for oversight, and guiding all participants in the industry chain to unite and fully use digital technology for efficient collaborative development [34]. Figure 1 shows the game relationship.

2.1.1. Modeling Assumptions under the Market Mechanism

Assumption 1:

Game players. In the rural e-commerce industry chain collaborative innovation game under the market mechanism, two types of game subjects exist: core platform enterprises and other participating enterprises. Both parties exhibit bounded rationality and face information asymmetry, implying that confirming whether their behavioral choices directly lead to maximized effects is challenging. Conversely, through iterative strategic adjustments and continuous learning, they ultimately achieve an equilibrium strategy to maximize their respective interests.

Assumption 2:

Game strategies. Platform enterprises and participating enterprises can determine their involvement in collaborative innovation on the basis of their interests and needs. The strategy sets of both parties comprise options for co-innovation and non-co-innovation. Assuming that the probability of platform enterprises choosing “co-innovation” is $x$, the probability of choosing “non-co-innovation” is $1-x$. The probability that a participating firm chooses “co-innovation” is $y$, the probability of choosing “non-co-innovation” is $1-y$, and $x,y\in [0,1]$ are functions of time $t$.

Assumption 3:

Initial net benefits. Regardless of the strategies chosen by the platform enterprise and the participating enterprises, each has its own initial net benefits derived from independent operations. Assuming that the initial net benefit of the platform enterprises of the game before gameplay is ${\mathrm{R}}_1$, the initial net benefit of the participating enterprises is ${\mathrm{R}}_2$.

Assumption 4:

Cooperation benefits. If platform enterprises and participating enterprises choose “co-innovation” in their cooperation, they will share collaborative innovation benefits and benefits from technology absorption. The benefits of collaborative innovation are recorded as $\theta \mathrm{H}$, in which the digital technology empowerment coefficient $\theta$ is used to evaluate the degree to which digital technology enhances the ability of information capture, integration, and utilization in the process of collaborative innovation [30]. It reflects how digital technology can improve the collaborative efficiency between platform enterprises and participating enterprises, accelerate information sharing, optimize resource allocation, and finally, transform it into collaborative innovation benefits. The amount of information established by $H$ for collaborative innovation is an important index for measuring the richness of information resources [15,30]. The synergistic benefit will be divided between the two parties on the basis of a particular percentage. The number of platform enterprises will be $\lambda$, with an allocation factor for participating enterprises of  $1-\lambda$ and $\lambda \in [0,1]$. In the long term, collaborative innovation between both sides will lead to sustained technological benefits, as enterprises enhance their absorptive and recreational capacities [32,33]. It is assumed that the technology generated through collaborative innovation is $T$, the absorptive capacity coefficient of the platform enterprise is ${\alpha }_1$, and the absorptive capacity coefficient of participating enterprises is ${\alpha }_2$, where ${\alpha }_1,{\alpha }_2\in [0,1]$.

Assumption 5:

Cost parameters. Both sides of the game should consider synergy costs and risk costs when choosing strategies. When the decision-making body opts for co-innovation, it must bear the co-innovation cost; that is, the collaborative innovation cost of platform enterprises is $C_1$, and the cost of collaborative innovation of participating enterprises is $C_2$. In addition, there is a risk cost associated with core technology exchange or information sharing during collaborative innovation [8,24]. This risk involves the possibility of partners copying, imitating, or stealing crucial core technologies or data resources, which can pose a significant hindrance to active cooperation between the two parties. The risk cost of platform enterprises is $e_1{D}_1$, the risk cost of participating enterprises is $e_2{D}_2$, of which $D_1$ and $D_2$ are potential losses, $e_1$ and $e_2$ are the risk factor, and $e_1,e_2\in [0,1]$.

Assumption 6:

Free-rider benefits and liquid damage. If one party chooses “co-innovation” and the other chooses “non-co-innovation”, the non-participating party may “hitchhike” in an attempt to indirectly benefit from the efforts or resources of the other party without directly participating in substantive cooperation [35]. That is, the free-riding benefits $S_1$ of platform enterprises are the free-riding benefits $S_2$ of participating enterprises. However, free-riding behavior violates the principle of cooperation, and the non-participating party needs to pay liquidated damages $K$ to bear the liability for breach of contract.

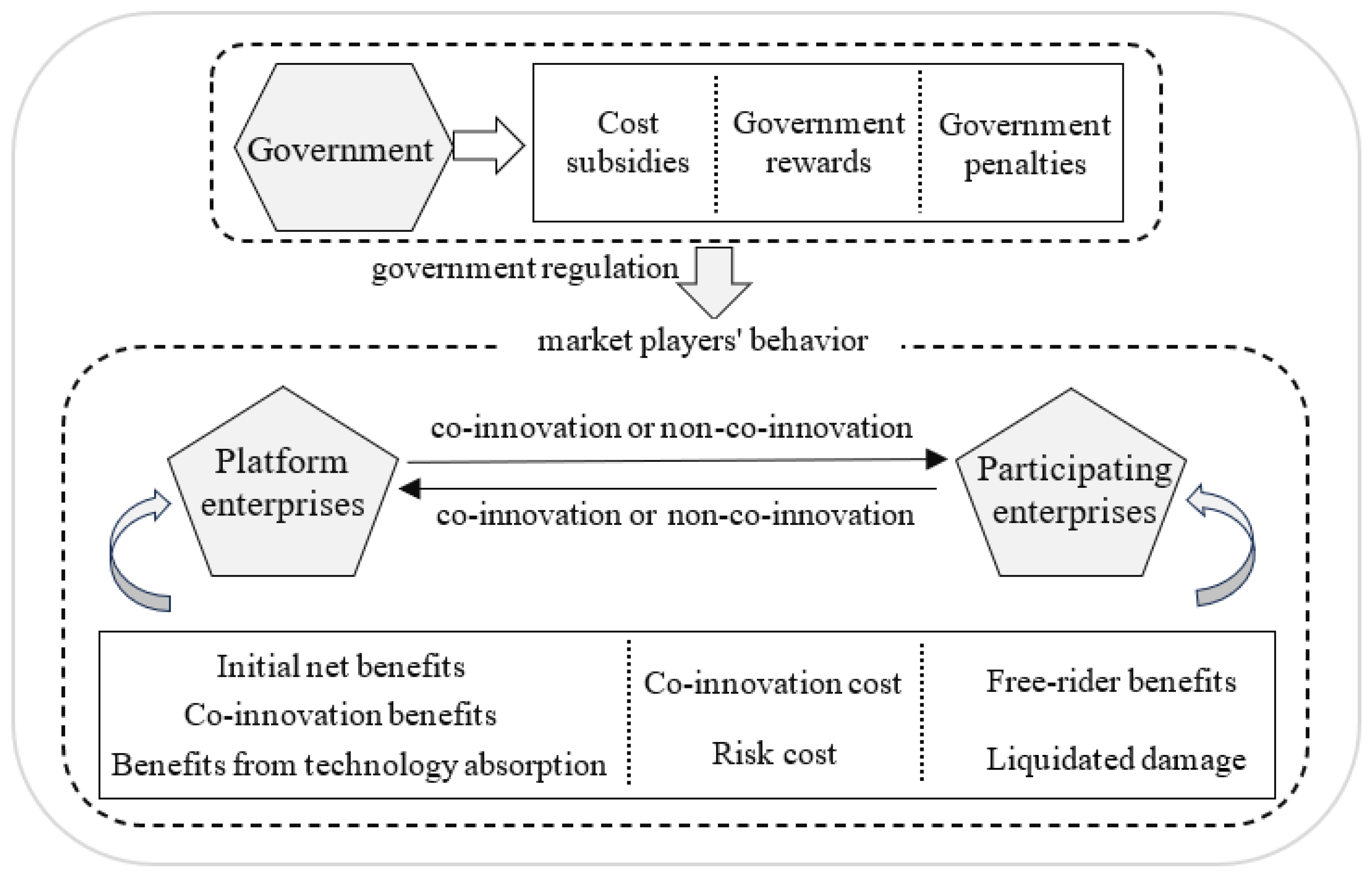
2.1.2. Modeling Assumptions under Government Regulation

By integrating the “government regulation” parameter into the market mechanism evolution game model, we developed the “platform enterprise-participating enterprises” evolution game model under government regulation. This study aimed to examine the government’s role in the rural e-commerce industry chain innovation process and explore suitable and effective regulatory measures by the government.

Assumption 7:

Government regulatory parameters. There are three main measures to promote collaborative innovation of the industrial chain in the practice of building the whole industrial chain of rural e-commerce: First, operating cost subsidies. The government provides subsidies to enterprises engaging in collaborative innovation to encourage their active participation [3,36], the operating cost subsidy of platform enterprises is $\beta C_1$, and the operating cost subsidy of participating enterprises is  $\beta C_2$, where $\beta$ is the cost subsidy strength and $C_1,C_2$ is the collaborative innovation cost. The second is the government reward. The government promotes rural e-commerce’s active role in various aspects of social impact within e-commerce, including consumption assistance, employment generation, brand certification, and standardization construction, through collaborative innovation across the whole industry chain [4,12,37]. The government will directly reward enterprises that meet the reward standards, $\gamma G$, $\gamma$ is the incentive strength factor, and $G$ is a base for government incentives. Third, government fines are needed. To ensure fair competition among enterprises, the government imposes penalties on those not engaging in collaborative innovation, such as those involved in false advertising, intellectual property rights infringement, and price fraud $\delta \mathrm{F}$, where $\delta$ is the strength of government regulation.

The symbols and meanings of the above parameters are shown in

Table 1. Description of parameters.

Parameter Symbols	Description	Parameter Symbols	Description
$x$	The probability of platform enterprises participating in collaborative innovation	$y$	The probability of participating enterprises engaging in co-innovation
${\mathrm{R}}_1$	The initial net benefits to platform enterprises before gaming	${\mathrm{R}}_2$	The initial net benefits to participating enterprises before gaming
$\theta$	The digital technology empowerment coefficient	$H$	The amount of information generated by collaborative innovation
$\lambda$	Coefficients for the distribution of benefits from co-innovation among platform enterprises and participating enterprises	$T$	The amount of technology generated by co-innovation
${\alpha }_1$	Technology absorptive capacity coefficients for platform enterprises	${\alpha }_2$	Technology absorptive capacity coefficients of participating enterprises
$C_1$	Input costs for platform enterprises to participate in collaborative innovation	$C_2$	Input costs for participating enterprises to engage in co-innovation
$S_1$	Platform enterprises’ “free-rider” benefits	$S_2$	“Free-rider” benefits for participating enterprises
$D_1$	Potentially risky losses for platform enterprises	$D_2$	Potentially risky losses of participating enterprises
$e_1$	Risk factor for platform enterprises	$e_2$	Risk factor for participating enterprises
$K$	Liquidated damages for non-participants	$\gamma$	Intensity of government incentives
$\mathrm{G}$	Government incentive base	$\delta$	Government regulatory efforts
$F$	Government fines	$\beta$	Government cost subsidization efforts

.

2.2. Collaborative Decision-Making Mechanism of the Whole Industry Chain under the Market Mechanism

2.2.1. Model Construction

On the basis of Assumptions 1–6, the payment matrix for the whole industry chain collaborative innovation game under the market mechanism is derived, as illustrated in

Table 2. Payment matrix for both sides of the game under the market mechanism.

		Participating Enterprises
		Co-Innovation ($y$)	Non-Co-Innovation ($1-y$)
Platform enterprises	Co-innovation ($x$)	$\begin{array}{l}{\mathrm{R}}_1+\lambda \theta H+{\alpha }_1\mathrm{T}-C_1-e_1{D}_1,\\ {\mathrm{R}}_2+(1-\lambda )\theta H+{\alpha }_2\mathrm{T}-C_2-e_2{D}_2\end{array}$	$\begin{array}{l}{\mathrm{R}}_1-C_1-e_1{D}_1+K,\\ {\mathrm{R}}_2+S_2-K\end{array}$
	Non-co-innovation ($1-x$)	$\begin{array}{l}{\mathrm{R}}_1+S_1-K,\\ {\mathrm{R}}_2-C_2-e_2{D}_2+K\end{array}$	${\mathrm{R}}_1,{\mathrm{R}}_2$

.

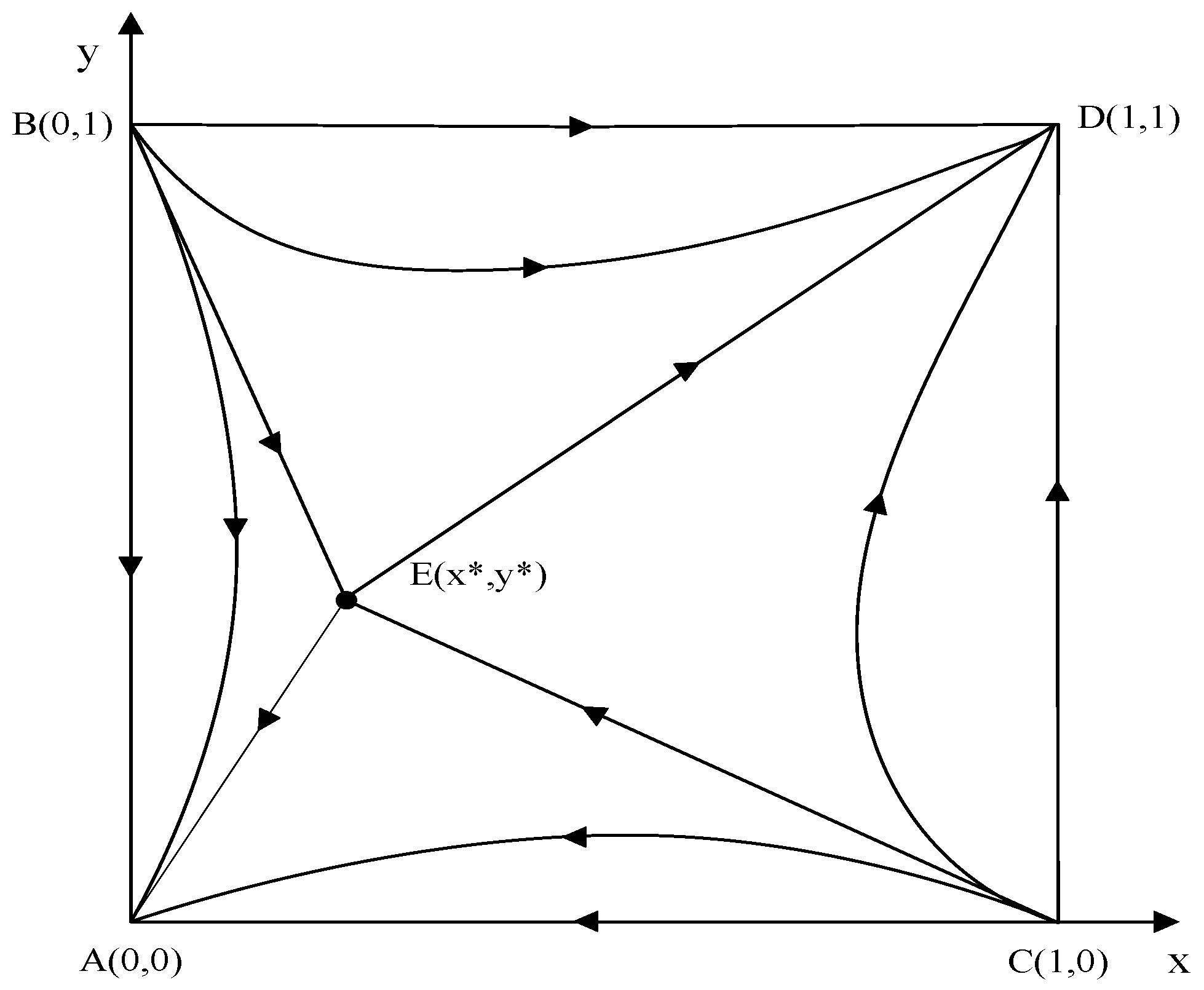
2.2.2. Model Analysis

The expected benefits of platform enterprises that choose “co-innovation” ${\mathrm{U}}_{11}$, “non-co-innovation” ${\mathrm{U}}_{12}$, and the average returns ${\mathrm{U}}_1$ are as follows.

$$\begin{array}{l}{\mathrm{U}}_{11}=y({\mathrm{R}}_1+\lambda \theta H+{\alpha }_1\mathrm{T}-C_1-e_1{D}_1)+(1-y)({\mathrm{R}}_1-C_1-e_1{D}_1+K)=y\lambda \theta H+y{\alpha }_1\mathrm{T}\\ +{\mathrm{R}}_1-C_1-e_1{D}_1+(1-y)K\end{array}$$

(1)

$${\mathrm{U}}_{12}=y({\mathrm{R}}_1+S_1-K)+(1-y){\mathrm{R}}_1={\mathrm{R}}_1+y{S}_1-yK$$

(2)

$${\mathrm{U}}_1=x{\mathrm{U}}_{11}+(1-x){\mathrm{U}}_{12}=xy(\lambda \theta H+{\alpha }_{1}T-S_1)-x(C_1+e_1{D}_1)+R_1+y{S}_1$$

(3)

The equation for the replication dynamics of the platform enterprises is as follows:

$$F(x)={\displaystyle \frac{dx}{dt}}=x(U_{11}-U_1)=x(1-x)(y\theta H\lambda +y{\alpha }_{1}T-C_1-y{S}_1-e_1{D}_1+K)$$

(4)

Similarly, the expected benefits of participating enterprises that choose “co-innovation” ${\mathrm{U}}_{21}$, “non-co-innovation” ${\mathrm{U}}_{22}$, and the average returns ${\mathrm{U}}_2$ are as follows.

$$\begin{array}{l}{\mathrm{U}}_{21}=x[{\mathrm{R}}_2+(1-\lambda )\theta H+{\alpha }_2\mathrm{T}-C_2-e_2{D}_2]+(1-x)({\mathrm{R}}_2-C_2-e_2{D}_2+K)\\ =x(1-\lambda )\theta H+x{\alpha }_2{\mathrm{T}+\mathrm{R}}_2-C_2-e_2{D}_2+(1-x)K\end{array}$$

(5)

$${\mathrm{U}}_{22}=x({\mathrm{R}}_2+S_2-K)+(1-x){\mathrm{R}}_2=x(S_2-K)+{\mathrm{R}}_2$$

(6)

$${\mathrm{U}}_2=y{U}_{21}+(1-y)U_{22}=xy[(1-\lambda )\theta H+{\alpha }_{2}T-S_2]-x(S_2+K)+R_2-y(e_2{D}_2+C_2-K)$$

(7)

The equation for the replication dynamics of the participating enterprises is as follows:

$$F(y)={\displaystyle \frac{dy}{dt}}=y(U_{21}-U_1)=y(1-y)[\mathrm{x}(1-\lambda )\theta H+x{\alpha }_{2}T-C_2-x{S}_2-e_2{D}_2+K]$$

(8)

Linking Equations (4) and (8) yields a two-dimensional replication of the dynamics of the platform and participating enterprises $L_1$:

$$\left\{\begin{array}{c}F(x)=x(1-x)(y\theta H\lambda +y{\alpha }_{1}T-C_1-y{S}_1-e_1{D}_1+K)\\ F(y)=y(1-y)[x(1-\lambda )\theta H+x{\alpha }_{2}T-C_2-x{S}_2-e_2{D}_2+K]\end{array}\right.$$

(9)

When $F(x)=F(y)=0$ is in the region of $\left\{\left.(x,y)\right|0\le x\le 1,0\le y\le 1\right\}$, there are five local equilibrium points, namely: $A(0,0)$, $\mathrm{B}(0,1)$, $C(1,0)$, $\mathrm{D}(1,1)$, and $\mathrm{E}(\mathrm{x}*,\mathrm{y}*)$, of which $x*={\displaystyle \frac{C_2+e_2{D}_2-K}{(1-\lambda )\theta H+{\alpha }_{2}T-S_2}}$ and $y*={\displaystyle \frac{C_1+e_1{D}_1-K}{\lambda \theta H+{\alpha }_{1}T-S_1}}$. Continuing to solve the partial derivatives of $F(x)$ and $F(y)$ about $x$ and $y$, we obtain the Jacobian matrix of the replica dynamical system $L$:

$$J=\left[\begin{array}{cc}(1-2x)(y\lambda \theta H+y{\alpha }_{1}T-C_1-y{S}_1-e_1{D}_1+K)& x(1-x)(\lambda \theta H+{\alpha }_{1}T-S_1)\\ y(1-y)\left[(1-\lambda )\theta H+{\alpha }_{2}T-S_2\right]& (1-2y)[x(1-\lambda )\theta H+x{\alpha }_{2}T-C_2-x{S}_2-e_2{D}_2+K]\end{array}\right]$$

According to Friedman [38], when the determinant of the Jacobian matrix $Det(J)>0$ and the traces $\mathrm{T}\mathrm{r}(J)<0$, the local equilibrium point is the evolutionary stability strategy (ESS). Five local equilibrium points $Det(J)$ and $\mathrm{T}\mathrm{r}(J)$ are shown in

Table 3. Local equilibrium at the points of market mechanism for $Det(J)$ and $\mathrm{Tr}(J)$.

Equilibrium	$\mathit{D}\mathit{e}\mathit{t}(\mathit{J})$	$\mathbf{T}\mathbf{r}(\mathit{J})$
$A(0,0)$	$\left(C_1+e_1{D}_1-K\right)\times \left(C_2+e_2{D}_2-K\right)$	$2K-C_1-C_2-e_1{D}_1-e_2{D}_2$
$\mathrm{B}(0,1)$	$\left(C_2+e_2{D}_2-K\right)\times \left(\lambda \theta H+{\alpha }_{1}T+K-S_1-C_1-e_1{D}_1\right)$	$C_2+e_2{D}_2-C_1-S_1-e_1{D}_1+{\alpha }_{1}T+\lambda \theta H$
$C(1,0)$	$-\left(C_1+e_1{D}_1-K\right)\times \left(C_2+e_2{D}_2-K-\theta H+\lambda \theta H-{\alpha }_{2}T+S_2\right)$	$C_1+e_1{D}_1+\theta H-\lambda \theta H-C_2-S_2-e_2{D}_2+{\alpha }_{2}T$
$\mathrm{D}(1,1)$	$\begin{array}{l}-\left(K-C_1-S_1-e_1{D}_1+{\alpha }_{1}T+\lambda \theta H\right)\\ \times \left(C_2-\theta H-K+S_2+e_2{D}_2-{\alpha }_{2}T+\lambda \theta H\right)\end{array}$	$\begin{array}{l}{C}_1-\theta H-2K+C_2+S_1+S_2+e_1{D}_1\\ +e_2{D}_2-{\alpha }_{1}T-{\alpha }_{2}T\end{array}$
$\mathrm{E}(\mathrm{x}*,\mathrm{y}*)$	$-{\mathrm{A}}_1{\mathrm{A}}_2$	0

Note: ${\mathrm{A}}_1={\displaystyle \frac{C_2+e_2{D}_2-K}{(1-\lambda )\theta H+{\alpha }_{2}T-S_2}}\times \left[1-{\displaystyle \frac{C_2+e_2{D}_2-K}{(1-\lambda )\theta H+{\alpha }_{2}T-S_2}}\right]\times \left(\lambda \theta H+{\alpha }_{1}T-S_1\right)$, ${\mathrm{A}}_2={\displaystyle \frac{C_1+e_1{D}_1-K}{\lambda \theta H+{\alpha }_{1}T-S_1}}\times \left(1-{\displaystyle \frac{C_1+e_1{D}_1-K}{\lambda \theta H+{\alpha }_{1}T-S_1}}\right)\times \left[(1-\lambda )\theta H+{\alpha }_{2}T-S_2\right]$.

.

In the plane $R=\left\{\left.(x,y)\right|0\le x,y\le 1\right\}$, we discuss the stability of the local equilibrium point, when $0\le C_2+e_2{D}_2-K\le (1-\lambda )\theta H+{\alpha }_{2}T-S_2$ and $0\le C_1+e_1{D}_1-K\le \lambda \theta H+{\alpha }_{1}T-S_1$. The stability results of the five local equilibrium points are shown in

Table 4. Stability analysis of local equilibrium points under the market mechanism.

Equilibrium	$\mathit{D}\mathit{e}\mathit{t}(\mathit{J})$	$\mathbf{T}\mathbf{r}(\mathit{J})$	Results
$A(0,0)$	+	−	ESS
$\mathrm{B}(0,1)$	+	+	Unstable point
$C(1,0)$	+	+	Unstable point
$\mathrm{D}(1,1)$	+	−	ESS
$\mathrm{E}(\mathrm{x}*,\mathrm{y}*)$	−	0	Saddle point

.

As shown in Table 4, $A(0,0)$ and $D(1,1)$ are evolutionary stabilization strategies for the whole industry chain of rural e-commerce under the market mechanism, $B(0,1)$ and $C(1,0)$ are unstable points, and $E(x*,y*)$ is the saddle point. The phase diagram of the evolutionary game is shown in Figure 2.

Figure 2 illustrates that the final evolution state of the strategy portfolio for both platform enterprises and participating enterprises is contingent upon the initial state $x$, $y$. The dashed line BEC in Figure 1 partitions the value of the regional ABDC into two segments, ABEC and BECD. When the initial state falls within the lower-left region of the dashed line ABEC, the strategy combination converges to point $A(0,0)$, indicating that both platform enterprises and participating enterprises are moving toward the strategy of “non-co-innovation”. Conversely, when the initial state is situated in the upper-right area of the dashed line BECD, the strategy combination converges to point $\mathrm{D}(1,1)$, signifying that both sides of the game opt for the “co-innovation” strategy. The movement of the saddle point $\mathrm{E}(x*,y*)$ can adjust the relative sizes of the two regions, thereby influencing the evolution direction of the strategy combination. The areas of ABEC and BECD are recorded as ${\mathrm{S}}_{\mathrm{ABEC}}$ and ${\mathrm{S}}_{BECD}$, and the following can be obtained:

$${\mathrm{S}}_{BECD}=1-{\displaystyle \frac{X*+Y*}{2}}=1-{\displaystyle \frac{C_2+e_2{D}_2-K}{2\left[(1-\lambda )\theta H+{\alpha }_{2}T-S_2\right]}}-{\displaystyle \frac{C_1+e_1{D}_1-K}{2(\lambda \theta H+{\alpha }_{1}T-S_1)}}$$

(10)

The main factors that impact ${\mathrm{S}}_{BECD}$ are analyzed, and the following propositions are made.

Proposition 1:

Under the market mechanism, the probability that both platform enterprises and participating enterprises choose a “co-innovation” strategy increases with decreasing costs of co-innovation $C_1$ and $C_2$.

Proof. 

Solving for the first-order partial derivative of Equation (10) with respect to $C_1$, we yield ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial {\mathrm{C}}_1}}=-{\displaystyle \frac{1}{2(\lambda \theta H+{\alpha }_{1}T-S_1)}}$, because $R=\left\{\left.(x,y)\right|0\le x,y\le 1\right\}$; therefore, ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial {\mathrm{C}}_1}}<0$. The same reasoning can be used to obtain that ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial {\mathrm{C}}_2}}<0$. Therefore, the higher the cost of collaborative innovation, the less advantageous it becomes for both sides of the game to opt for the “co-innovation” strategy. □

Given that the majority of platform enterprises and participating enterprises in the whole rural e-commerce industry chain are in the stage of formation or development, and their cost recovery cycle is longer, elevated costs will directly weaken the net income of the project and inhibit the enthusiasm and willingness of both parties to choose collaborative innovation strategies.

Proposition 2:

Under the market mechanism, the probability that both platform enterprises and participating enterprises choose a “co-innovation” strategy increases with the digital technology empowerment coefficient $\theta$ and the amount of information established by collaborative innovation $H$.

Proof. 

Solving for the first-order partial derivative of Equation (10) with respect to $\theta$, we yield ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial \theta }}={\displaystyle \frac{(C_2+e_2{D}_2-K)(1-\lambda )H}{2{\left[(1-\lambda )\theta H+{\alpha }_{2}T-S_2\right]}^2}}+{\displaystyle \frac{(C_1+e_1{D}_1-K)\lambda H}{2(\lambda \theta H+{\alpha }_{1}T-S_1)}}>0$, and in the same way,${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial H}}>0$. Therefore, ${\mathrm{S}}_{BECD}$ is the increasing function of $\theta$ and $H$. As $\theta$ and $H$ increase, both sides of the game tend to choose the “co-innovation” strategy. □

On the one hand, a higher digital technology empowerment coefficient promotes the rapid capture, accurate integration, and efficient use of information, which means that the synergy efficiency between platform enterprises and participating enterprises is greater. On the other hand, a significant increase in the amount of information enables enterprises to capture richer market information in collaborative innovation [30]. Therefore, the higher the income coefficient of collaborative innovation is, the greater the amount of information generated by collaborative innovation, and enterprises are more inclined to opt for cooperative innovation.

Proposition 3:

Under the market mechanism, the probability that both enterprises choose the “co-innovation” strategy increases with the amount of technology generated by the co-innovation $T$ and the increase in their own technology absorptive capacity factors ${\alpha }_1$ and ${\alpha }_2$.

Proof. 

Solving for the first-order partial derivative of Equation (10) with respect to ${\alpha }_1$, we yield ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial {\alpha }_1}}={\displaystyle \frac{(C_1+e_1{D}_1-K)T}{2(\lambda \theta H+{\alpha }_{1}T-S_1{)}^2}}>0$; the same reasoning can be used to ascertain that ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial {\alpha }_2}}>0$ and ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial T}}>0$. Therefore, ${\mathrm{S}}_{BECD}$ is a monotonically increasing function of ${\alpha }_1$, ${\alpha }_2$, and $T$. When ${\alpha }_1$, ${\alpha }_2$, and $T$ increase, both parties tend to choose the “co-innovation” strategy. □

Platform enterprises and participating enterprises improve the overall technical level of the whole industrial chain they jointly build through collaborative innovation, while a strong technology absorption capacity accelerates technology absorption and transformation [32,33] and then enhances their respective technological benefits, so the possibility of both parties choosing collaborative innovation strategies increases.

Proposition 4:

Under the market mechanism, the impact of the coefficient of distribution of benefits from co-innovation $\lambda$ on the final decision choices of both sides in the game depends on specific conditions.

Proof. 

Solving for the first-order partial derivative of Equation (10) with respect to $\lambda$, we obtain ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial \lambda }}=-{\displaystyle \frac{(C_2+e_2{D}_2-K)\theta H}{2{\left[(1-\lambda )\theta H+{\alpha }_{2}T-S_2\right]}^2}}+{\displaystyle \frac{(C_1+e_1{D}_1-K)\theta H}{2(\lambda \theta H+{\alpha }_{1}T-S_1{)}^2}}$; as seen, the size of ${\mathrm{S}}_{BECD}$ and the coefficient of distribution of benefits from co-innovation $\lambda$ are not monotonic relationships. When ${\displaystyle \frac{C_1+e_1{D}_1-K}{C_2+e_2{D}_2-K}}>{\displaystyle \frac{(\lambda \theta H+{\alpha }_{1}T-S_1{)}^2}{{\left[(1-\lambda )\theta H+{\alpha }_{2}T-S_2\right]}^2}}$ and ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial \lambda }}>0$, ${\mathrm{S}}_{BECD}$ is a monotonically increasing function of $\lambda$. As $\lambda$ increases, both sides of the game tend to choose the “co-innovation” strategy. Conversely, when ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial \lambda }}<0$, as $\lambda$ increases, the probability of both sides in the game evolving in the “non-co-innovation” direction increases. □

Therefore, the ultimate evolution result of the system depends on specific conditions. It is influenced by many factors, including the fairness of distribution, the negotiation ability of both sides of the game and the market position. Therefore, it is necessary to fully consider these factors to ensure the rationality and acceptability of the distribution scheme when formulating the collaborative innovation income distribution scheme.

Proposition 5:

Under the market mechanism, a decrease in the risk factors  $e_1$ and  $e_2$  and potential losses  $D_1$  and   $D_2$  will increase the probability that both players will choose the “co-innovation” strategy.

Proof. 

Solving for the first-order partial derivative of Equation (10) with respect to $e_1$, we obtain ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial {\mathrm{e}}_1}}=-{\displaystyle \frac{D_1}{2(\lambda \theta H+{\alpha }_{1}T-S_1)}}<0$; the same reasoning can be used to determine that ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial e_2}}<0$, ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial {\mathrm{D}}_1}}<0$, and ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial {\mathrm{D}}_2}}<0$. Therefore, ${\mathrm{S}}_{BECD}$ is the monotonically decreasing function of $e_1$, $e_2$, $D_1$, and $D_2$. As $e_1$, $e_2$, $D_1$, and $D_2$ decrease, ${\mathrm{S}}_{BECD}$ increases, and both sides of the game tend to choose the “co-innovation” strategy. □

With the decrease in the risk coefficient and potential loss of the game, the uncertainty of cooperation between the two parties is significantly reduced. This risk mitigation enhances the confidence of both parties in collaborative innovation projects and alleviates cooperation concerns. Therefore, platform enterprises and participating enterprises are more likely to choose the strategy of “collaborative innovation”.

Proposition 6:

Under market-based mechanisms, the smaller the free-rider gains  $S_1$ and  $S_2$  are for the platform and participating firms, the greater the probability that both sides of the game will choose collaborative innovation.

Proof. 

Solving for the first-order partial derivative of Equation (10) with respect to $S_1$, we obtain ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial S_1}}=-{\displaystyle \frac{(C_1+e_1{D}_1-K)}{2(\lambda \theta H+{\alpha }_{1}T-S_1{)}^2}}<0$; the same reasoning can be used to determine that ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}}{\partial S_2}}<0$. Therefore, ${\mathrm{S}}_{BECD}$ is the monotonically decreasing function of $S_1$ and $S_2$. When $S_1$ and $S_2$ decrease, ${\mathrm{S}}_{BECD}$ increases, and both parties tend to choose the “co-innovation” strategy. □

In the context of limited rationality and information asymmetry, both platform enterprises and participating enterprises expect other parties to adopt a collaborative innovation strategy and obtain free-riding benefits. Nevertheless, as the other party’s free-riding benefits escalate, the fairness imbalance between the two parties intensifies. Over numerous iterations, this imbalance may reach a critical threshold, potentially resulting in a “non-co-innovation” dilemma. In contrast, if free-rider income is lower, it will help maintain a sense of fairness in cooperation and encourage both parties to choose “collaborative innovation”.

2.3. Collaborative Decision-Making Mechanism of the Whole Industry Chain under Government Regulation

2.3.1. Model Construction

Combined with Assumption 7, the payment matrix for the whole industry chain collaborative innovation game under government regulation is derived, as depicted in

Table 5. Payment matrix for both sides of the game under government regulation.

		Participating Enterprises
		Co-Innovation ($y$)	Non-Co-Innovation ($1-y$)
Platform enterprises	Co-innovation ($x$)	$\begin{array}{l}{\mathrm{R}}_1+\lambda \theta H+{\alpha }_1\mathrm{T}-C_1-e_1{\mathrm{D}}_1+\beta {\mathrm{C}}_1+\gamma \mathrm{G},\\ {\mathrm{R}}_2+(1-\lambda )\theta H+{\alpha }_2\mathrm{T}-C_2-e_2{\mathrm{D}}_2+\beta {\mathrm{C}}_2+\gamma \mathrm{G}\end{array}$	$\begin{array}{l}{\mathrm{R}}_1-C_1-e_1{\mathrm{D}}_1+K+\beta C_1,\\ {\mathrm{R}}_2+S_2-K-\delta F\end{array}$
	Non-co-innovation ($1-x$)	$\begin{array}{l}{\mathrm{R}}_1+S_1-K-\delta F,\\ {\mathrm{R}}_2-C_2-e_2{D}_2+K+\beta C_2\end{array}$	${\mathrm{R}}_1,{\mathrm{R}}_2$

.

2.3.2. Model Analysis

Similar to the model solution under the market mechanism, the equation for the replication dynamics of platform enterprises is as follows:

$$F(x)={\displaystyle \frac{dx}{dt}}=x(1-x)(y\theta H\lambda +y{\alpha }_{1}T-C_1-y{S}_1-e_1{D}_1+K+\beta C_1+y\gamma G+y\delta F)$$

(11)

The equation for the replication dynamics of the participating enterprises is as follows:

$$F(y)={\displaystyle \frac{dy}{dt}}=y(1-y)[x(1-\lambda )\theta H+x{\alpha }_{2}T-C_2-x{S}_2-e_2{D}_2+K+\beta C_2+x\gamma G+x\delta F]$$

(12)

Combining Equations (11) and (12) leads to a two-dimensional replication of the dynamic system of the platform enterprises and the participating enterprises as follows:

$$\left\{\begin{array}{c}F(x)=x(1-x)(y\theta H\lambda +y{\alpha }_{1}T-C_1-y{S}_1-e_1{D}_1+K+\beta C_1+y\gamma G+y\delta F)\\ F(y)=y(1-y)[x(1-\lambda )\theta H+x{\alpha }_{2}T-C_2-x{S}_2-e_2{D}_2+K+\beta C_2+x\gamma G+x\delta F]\end{array}\right.$$

(13)

When $F(x)=F(y)=0$, in the region of $\left\{\left.(x,y)\right|0\le x\le 1,0\le y\le 1\right\}$, there are five local equilibrium points, namely: $A(0,0)$, $\mathrm{B}(0,1)$, $C(1,0)$, $\mathrm{D}(1,1)$, and $\mathrm{E}(\mathrm{x}*,\mathrm{y}*)$, of which $\mathrm{x}*={\displaystyle \frac{C_2+e_2{D}_2-K-\beta C_2}{(1-\lambda )\theta H+{\alpha }_{2}T-S_2+\delta F+\gamma G}}$ and $\mathrm{y}*={\displaystyle \frac{C_1+e_1{D}_1-K-\beta C_1}{\lambda \theta H+{\alpha }_{1}T-S_1+\delta F+\gamma G}}$. Continuing with the solution of the partial derivatives of $F(x)$ and $F(y)$ about $x$ and $y$, we obtain the Jacobian matrix of the replica dynamical system L:

$$J=\left[\begin{array}{cc}\begin{array}{l}(1-2x)(y\theta H\lambda +y{\alpha }_{1}T-C_1-y{S}_1\\ -e_1{D}_1+K+\beta C_1+y\gamma G+y\delta F)\end{array}& \begin{array}{cc}& x(1-x)(\lambda \theta H+{\alpha }_{1}T-S_1+\gamma G+\delta F)\end{array}\\ y(1-y)\left[(1-\lambda )\theta H+{\alpha }_{2}T-S_2+\gamma G+\delta F\right]& \begin{array}{cc}& \begin{array}{l}(1-2y)[x(1-\lambda )\theta H+x{\alpha }_{2}T-C_2-x{S}_2\\ -e_2{D}_2+K+\beta C_2+x\gamma G+x\delta F]\end{array}\end{array}\end{array}\right]$$

(14)

According to Friedman [38], the stability of the local equilibrium point on the plane $R=\left\{\left.(x,y)\right|0\le x,y\le 1\right\}$ is discussed, so that $0\le \mathrm{x}*={\displaystyle \frac{C_2+e_2{D}_2-K-\beta C_2}{(1-\lambda )\theta H+{\alpha }_{2}T-S_2+\delta F+\gamma G}}\le 1$ and $0\le \mathrm{y}*={\displaystyle \frac{C_1+e_1{D}_1-K-\beta C_1}{\lambda \theta H+{\alpha }_{1}T-S_1+\delta F+\gamma G}}\le 1$. That is, the combined input cost and potential loss associated with collaborative innovation surpass the total government cost subsidy and the penalties imposed on non-participants, whereas the total revenue exceeds the disparity between the free-riding income and the government fines. The stability outcomes for the five partial equilibria are outlined in

Table 6. Stability analysis of local equilibrium points under government regulation.

Equilibrium	$\mathit{D}\mathit{e}\mathit{t}(\mathit{J})$	$\mathbf{T}\mathbf{r}(\mathit{J})$	Results
$A(0,0)$	+	−	ESS
$\mathrm{B}(0,1)$	+	+	Unstable point
$C(1,0)$	+	+	Unstable point
$\mathrm{D}(1,1)$	+	−	ESS
$\mathrm{E}(\mathrm{x}*,\mathrm{y}*)$	−	0	Saddle point

.

As shown in Table 6, the stability analysis results of the local equilibrium point under government regulation are the same as those under the market mechanism, so the evolutionary phase diagram is the same as that in Figure 2, and the final evolutionary results of the system depend on ${\mathrm{S}}_{\mathrm{ABEC}}$ and ${\mathrm{S}}_{BECD}$. The larger the relative size of ${\mathrm{S}}_{BECD}$ is, the greater the probability of evolution of the system toward $\mathrm{D}(1,1)$.

$${\mathrm{S}}_{BECD}^{\prime }=1-{\displaystyle \frac{\mathrm{X}*+\mathrm{Y}*}{2}}=1-{\displaystyle \frac{C_2+e_2{D}_2-K-\beta C_2}{2\left[(1-\lambda )\theta H+{\alpha }_{2}T-S_2+\delta F+\gamma G\right]}}-{\displaystyle \frac{C_1+e_1{D}_1-K-\beta C_1}{2\left[\lambda \theta H+{\alpha }_{1}T-S_1+\delta F+\gamma G\right]}}$$

(15)

Proposition 7:

Under government regulation, the greater the operating cost subsidies  $\beta$, intensity of government incentives$\gamma$, and incentive base  $G$  are, the greater the probability that the two sides of the game will choose collaborative innovation.

Proof. 

Solving for the first-order partial derivative of Equation (15) with respect to $\beta$, we obtain ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}^{\prime }}{\partial \beta }}={\displaystyle \frac{C_2}{2\left[(1-\lambda )\theta H+{\alpha }_{2}T-S_2+\delta F+\gamma G\right]}}+{\displaystyle \frac{C_1}{2\left[\lambda \theta H+{\alpha }_{1}T-S_1+\delta F+\gamma G\right]}}>0$, and so, ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}^{\prime }}{\partial \gamma }}>0$ and ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}^{\prime }}{\partial \mathrm{G}}}>0$. Therefore, ${\mathrm{S}}_{BECD}^{\prime }$ is a monotonically decreasing function of $\beta$, $\gamma$, and $G$. As the cost subsidy and incentives given by the government increase, both sides of the game tend to choose the “co-innovation” strategy. □

Cost is a key factor in the business decision making of enterprises. By providing operating cost subsidies, the economic burden of enterprises is directly reduced [37]. In addition, when enterprises are rewarded for their positive social effects, a positive economic incentive is formed, which stimulates the enthusiasm of both sides of the game to participate in collaborative innovation.

Proposition 8:

Under government regulation, as the intensity of government regulation  $\delta$ and the severity of penalties  $F$  increase, the likelihood of both sides of the game selecting “co-innovation” increases.

Proof. 

Solving for the first-order partial derivative of Equation (15) with respect to $\delta$, we yield ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}^{\prime }}{\partial \delta }}={\displaystyle \frac{(C_2+e_2{D}_2-K-\beta C_2)\mathrm{F}}{2{\left[(1-\lambda )\theta H+{\alpha }_{2}T-S_2+\delta F+\gamma G\right]}^2}}+{\displaystyle \frac{(C_1+e_1{D}_1-K-\beta C_1)\mathrm{F}}{2{\left[\lambda \theta H+{\alpha }_{1}T-S_1+\delta F+\gamma G\right]}^2}}>0$, and similarly, ${\displaystyle \frac{\partial {\mathrm{S}}_{BECD}^{\prime }}{\partial \mathrm{F}}}>0$. Therefore ${\mathrm{S}}_{BECD}^{\prime }$ is the monotonically decreasing function of $\delta$ and $F$.□

As government regulation and penalties intensify, both sides of the game gravitate toward adopting the “co-innovation” strategy. Strengthening supervision and punishment significantly increases the cost of corporate default. In the face of high costs, platform enterprises and participating enterprises are more inclined to choose collaborative innovation to avoid risk and pursue stable cooperation.

3. Case Analysis and Numerical Simulation

This paper conducts a numerical simulation analysis via the Smart Cloud Warehouse Project in Caoxian Shandong Province, China, as a case study. The rural e-commerce project is located in the industrial park of China’s e-commerce demonstration base. As a landmark project for a park’s digital transformation, it integrates the most advanced modern information technologies, including the Internet of Things, big data, and cloud computing. Through collaborative innovation between the core platform and other enterprises within the industry chain, the platform automatically connects to supplier shops. Upon the sale of each product, the core platform automatically captures the order, facilitating the seamless operation of the entire chain, encompassing shipment, delivery, and after-sales services.

The cost–benefit ratio (BCR) is the core basis for the decision making of both platform enterprises and chain-participating enterprises [39]. Therefore, five different BCRs are set up in this paper to simulate the influence of BCR changes on the system evolution results. The parameter assignment in

Table 7. Parameter assignments for the five game scenarios.

	${\mathit{C}}_1$	${\mathit{C}}_2$	$\mathit{H}$	$\mathit{\theta }$	$\mathit{\lambda }$	$\mathit{T}$	${\mathit{\alpha }}_1$	${\mathit{\alpha }}_2$	Cost–Benefit Ratio (BCR)
Scenario 1	3	2.2	10	1	0.5	10	1	0.6	0.2
Scenario 2	4.5	3.3	10	1	0.5	10	1	0.6	0.3
Scenario 3	6	4.4	10	1	0.5	10	1	0.6	0.4
Scenario 4	7.5	5.5	10	1	0.5	10	1	0.6	0.5
Scenario 5	9	6.6	10	1	0.5	10	1	0.6	0.6

follows the following principles: (1) It is in line with the actual operation and cost–benefit characteristics of the smart cloud warehouse project in Cao County, Shandong Province and ensures that the parameter setting has practical significance. (2) It needs to satisfy the necessary conditions for platform enterprises and participating enterprises to achieve a stable state $\mathrm{D}(1,1)$ in combination with the equilibrium results presented in Section 2. (3) According to evolutionary game theory, it is necessary to discuss the influence of the change in key parameters on the evolutionary equilibrium results [40]. Therefore, the BCR parameter values are 0.2, 0.3, 0.4, 0.5, and 0.6 from small to large under the condition of a limited parameter value range. The higher the BCR is, the greater the cost input needed to realize an income under the same income level. (4) Parameter assignment does not indicate the actual value of variables but represents only the relative size among variables to ensure practicality and reveal the change law [41].

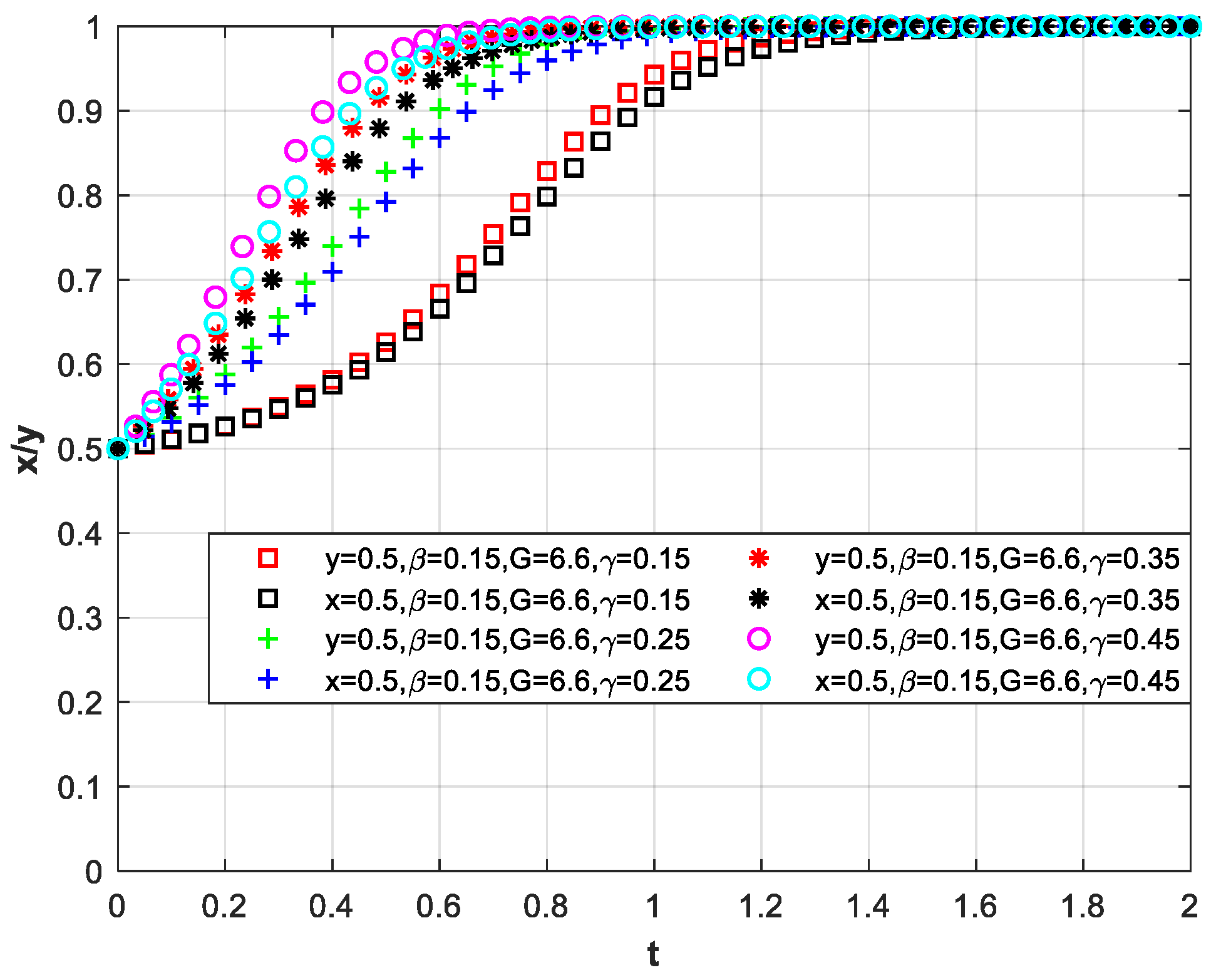
3.1. Collaborative Innovation Costs, Collaborative Innovation Benefits, and Motivation for Co-Innovation

Platform enterprises and participating enterprises make decisions that maximize their own interests on the basis of the benefits and costs of collaborative innovation. Without considering the impact of free-riding benefits and potential risk losses, we analyze the impact of different cost–benefit ratios on the strategic choices of the two parties under the market mechanism. Figure 3 shows the impact of different cost–benefit ratios (BCRs) on the strategic choices of platform enterprises and participating enterprises. The simulation results reveal that the threshold value of the BCR is 0.5. When it is less than 0.5, the players in the game will change from “non-co-innovation” to “co-innovation”, and as the BCR decreases, the evolution speed of two-way “co-innovation” will accelerate.

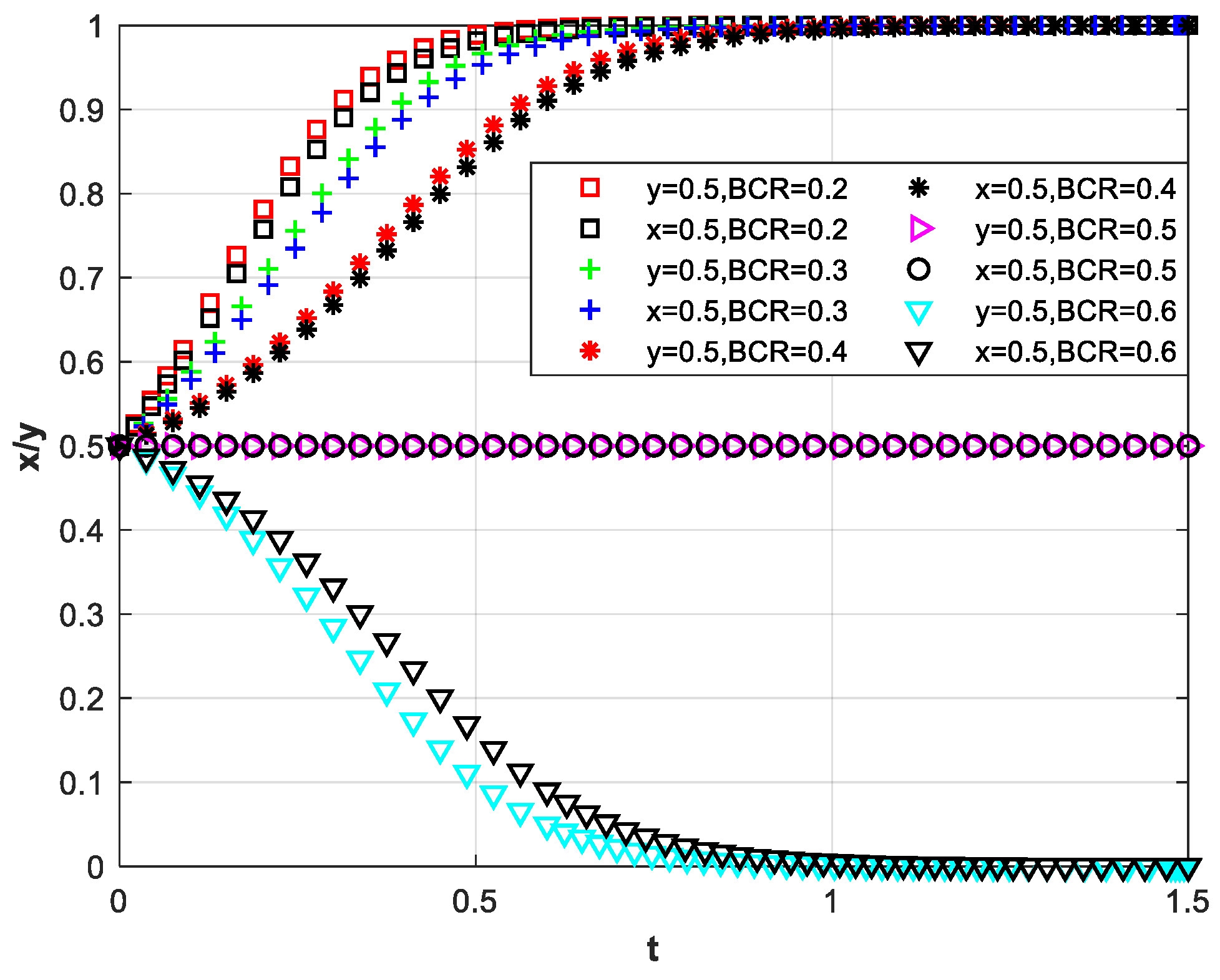
3.2. Operating Cost Subsidies, Government Incentives, and Motivation for Co-Innovation

When enterprises are hesitant to actively choose the “co-innovation” strategy due to their own cost–benefit considerations, government subsidies and direct incentives for enterprises’ operating costs can markedly alleviate the cost–benefit ratio associated with collaborative innovation. According to the simulation results in Figure 3, we select the cost–benefit ratio $\mathrm{BCR}=0.6$. When the system evolves in the direction of non-co-innovation, we analyze the effects of government subsidies and direct incentives on the strategic choices of both sides of the game.

3.2.1. Adopting an Incentive: Subsidizing Operating Costs

When the BCR = 0.6, only operating cost subsidies without government incentives are considered. The parameter values are as follows: $C_1=9$, $C_2=6.6$, $H=10$, $\theta =1$, $\lambda =0.5$, $\mathrm{T}=10$, ${\alpha }_1=1$, ${\alpha }_2=0.6$, $\gamma =0$, $G=0$, $e_1=0$, $e_2=0$, $D_1=0$, $D_2=0$, ${\mathrm{S}}_1=0$, ${\mathrm{S}}_2=0$, $K=0$, $\delta =0$, and $F=0$. Regulating the level of subsidies for operating costs $\beta$, we order the values of $\beta$ as 0.15, 0.25, 0.35, and 0.45, and the evolutionary behaviors of platform enterprises and participating enterprises are shown in Figure 4. The simulation results indicate that there is a threshold between $[0.15,0.25]$ and $\beta$; when it is greater than this threshold, the two sides of the game evolve from “non-co-innovation” to “co-innovation”, and as $\beta$ increases, the rate of convergence to “co-innovation” accelerates.

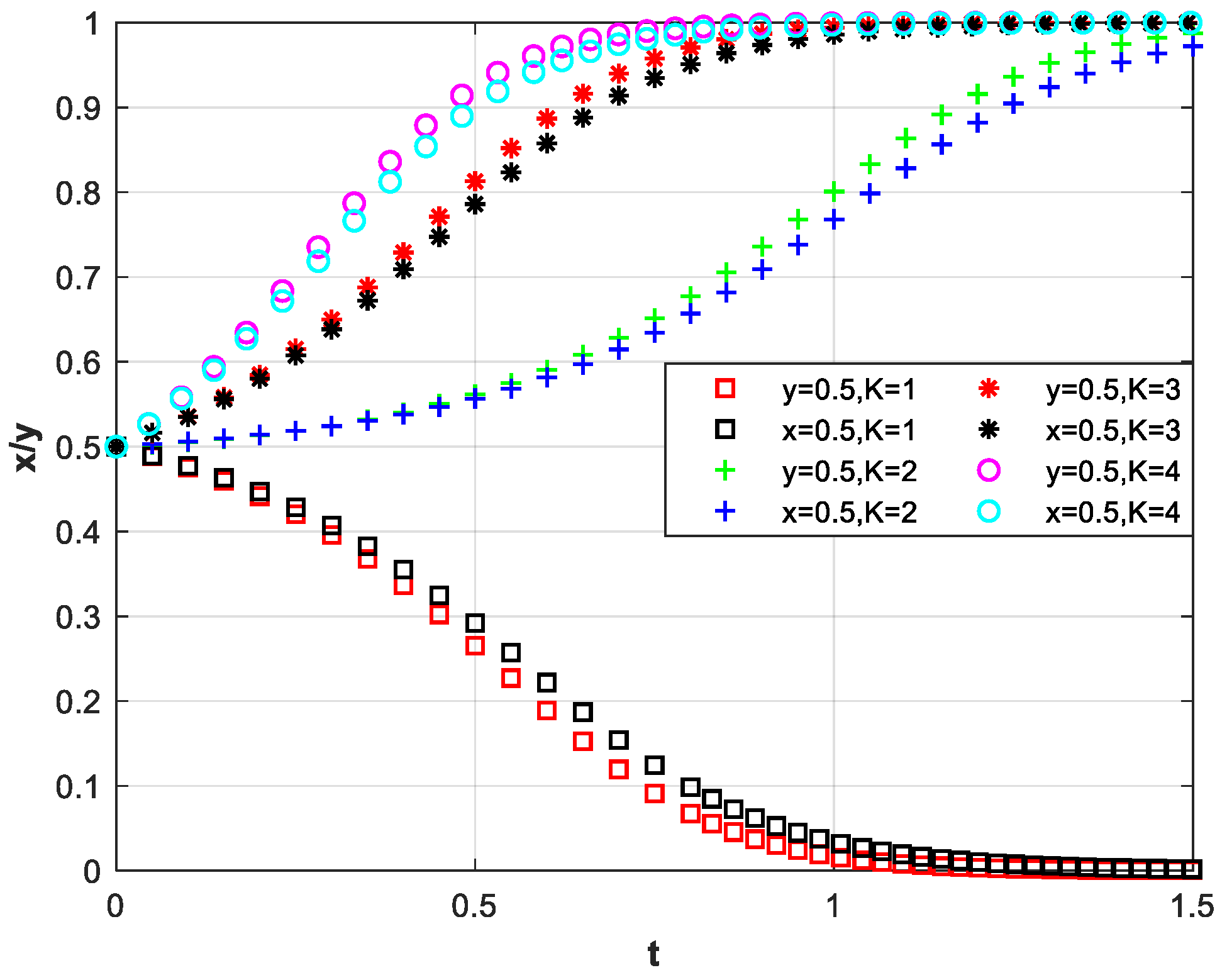
3.2.2. Adopt an Incentive: Governmental Incentives

When the BCR = 0.6, only government incentives are considered without operating cost subsidies. To compare the effects of government incentives and operating cost subsidies, the government incentive base $G$ is set equivalent to the cost of co-innovation $C_2$, $G=6.6$, and the values of the remaining parameters remain unchanged, or $C_1=9$, $C_2=6.6$, $H=10$, $\theta =1$, $\lambda =0.5$, $\mathrm{T}=10$, ${\alpha }_1=1$, ${\alpha }_2=0.6$, $\beta =0$, $e_1=0$, $e_2=0$, $D_1=0$, $D_2=0$, ${\mathrm{S}}_1=0$, ${\mathrm{S}}_2=0$, $K=0$, $\delta =0$, and $F=0$. Regulating the intensity of government incentives $\gamma$, the values of $\gamma$ are 0.15, 0.25, 0.35, and 0.45, respectively, and the simulation results are shown in Figure 5. From the simulation results, it can be seen that there is a threshold between $[0.35,0.45]$ and $\gamma$; when it is greater than this threshold, the two sides of the game evolve from “non-co-innovation” to “co-innovation”, and as $\gamma$ increases, both parties converge to “co-innovation” faster. As evident from Figure 4 and Figure 5, both government incentives and operating cost subsidies actively contribute to the system’s evolution toward collaborative innovation. However, compared with government incentives, the positive impact of government subsidies on the operating costs of platform enterprises and participating enterprises is more pronounced. Moreover, the convergence speed toward “co-innovation” under the influence of operating cost subsidies outpaces that of government incentives.

3.2.3. Adoption of Two Types of Incentives: Subsidized Operating Costs and Government Incentives

Further analysis is conducted on the impact of the two incentive combinations on the outcome of the game between platform firms and participating firms. Selecting $\beta =0.15$ and $G=6.6$ in Figure 4 (where the system evolves towards non-co-innovation), while keeping the values of the remaining parameters constant, we adjust the intensity of governmental incentives $\gamma$. Specifically, we set the values of $\gamma$ to 0.15, 0.25, 0.35, and 0.45, and the simulation results are illustrated in Figure 6. Figure 6 shows that when the government provides enterprises with lower-intensity incentives, the trajectory initially evolving toward “non-co-innovation” gradually shifts toward the stable state of “co-innovation”, and the convergence speed exceeds that of a single means of government cost subsidies. Therefore, relevant government authorities should utilize both government incentives and operating cost subsidies comprehensively to foster the system’s development toward synergistic innovation through judicious policy design, thereby enhancing the competitiveness and sustainable growth of the whole rural e-commerce industry chain.

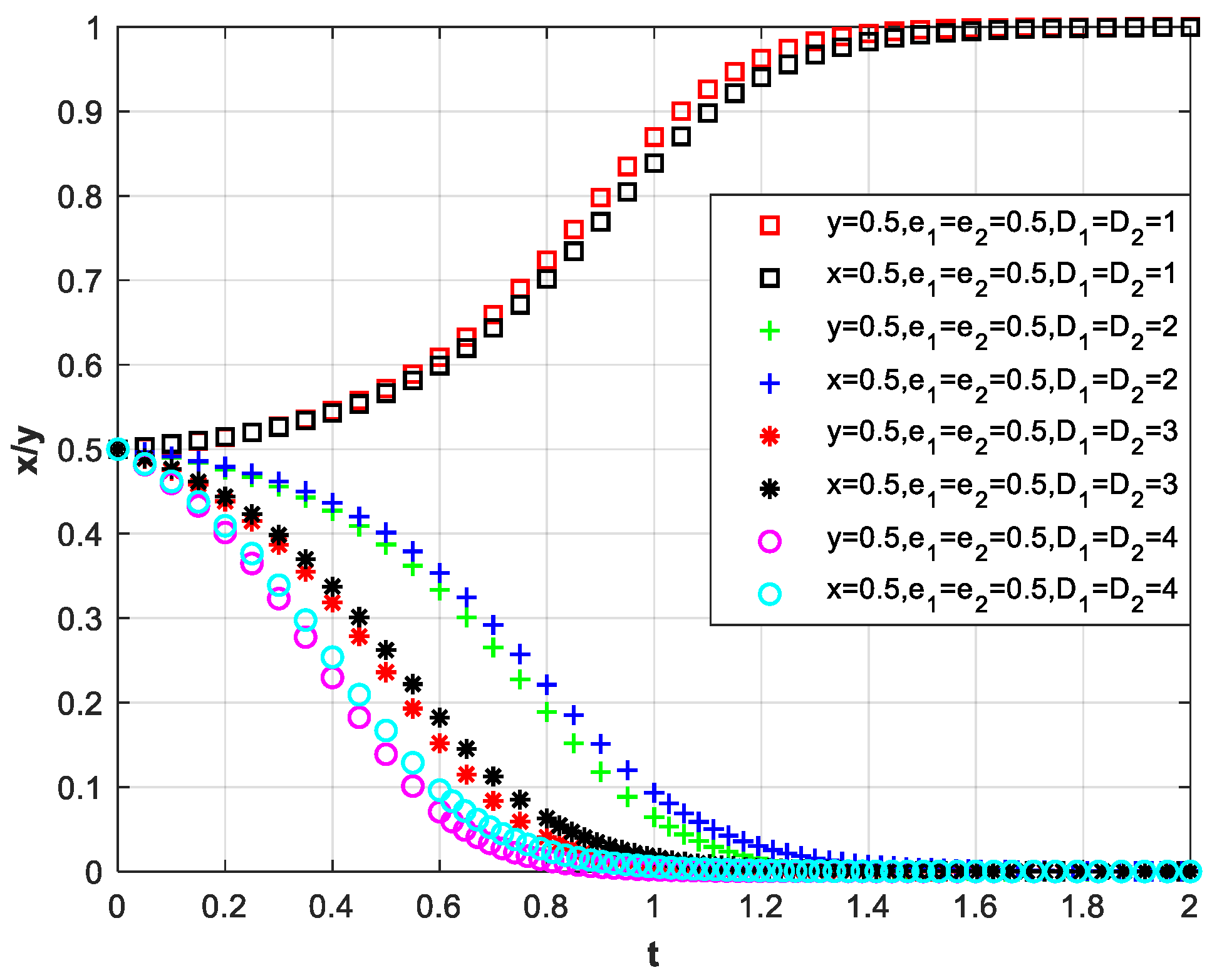
3.3. Potential Risk Losses, Free-Riding Gains, and Motivation for Co-Innovation

3.3.1. Potentially Risky Losses

Selecting $\beta =0.15$, $G=6.6$, and $\gamma =0.25$ in Figure 6 (the system evolves in the direction of co-innovation), taking into account the impact of potential risk losses on the outcome of the system’s evolution, $e_1=e_2=0.5$, and reconciling the potential risk of loss $D_1$ and $D_2$, we order the values of $D_1$ and $D_2$ as 1, 2, 3, and 4, respectively. The rest of the parameter values are kept constant, or $C_1=9$, $C_2=6.6$, $H=10$, $\theta =1$, $\lambda =0.5$, $\mathrm{T}=10$, ${\alpha }_1=1$, ${\alpha }_2=0.6$, $\beta =0.15$, $\gamma =0.25$, $G=6.6$, ${\mathrm{S}}_1=0$, ${\mathrm{S}}_2=0$, $K=0$, $\delta =0$, and $F=0$. The simulation results are depicted in Figure 7. When there is potential risk loss, the trajectory in Figure 6, which initially evolves toward “co-innovation”, gradually converges to the state of “non-co-innovation”. There is a threshold between $[1,2]$ for the potential risk loss of $D_1$ and $D_2$; when it is greater than this threshold, the game transitions from “co-innovation” to “non-co-innovation”, and the speed of convergence accelerates with increasing potential risk.

3.3.2. Free-Rider Gains

$\beta =0.15$, $G=6.6$, and $\gamma =0.25$ in Figure 6 (the system evolves in the direction of co-innovation), and to compare the strength of the roles of free-rider gains and potential risk losses in the direction of system evolution, only the impact of free-rider gains on the outcome of system evolution is taken into account. After adjusting for free-rider gains $S_1$ and $S_2$, we order the values of $S_1$ and $S_2$ to be 0.5, 1, 1.5, and 2, respectively. The remaining parameter values were kept constant, viz., $C_1=9$, $C_2=6.6$, $H=10$, $\theta =1$, $\lambda =0.5$, $\mathrm{T}=10$, ${\alpha }_1=1$, ${\alpha }_2=0.6$, $e_1=0$, $e_2=0$, $D_1=0$, $D_2=0$, $K=0$, $\delta =0$, and $F=0$. The simulation results are displayed in Figure 8. When there is a free-rider gain, the trajectory in Figure 6, which initially progresses toward “co-innovation”, transitions to the state of “non-co-innovation”. Additionally, there exists a threshold between $[1,1.5]$ for the free-rider gain of $S_1$ and $S_2$. When it is greater than this threshold, the game players will change from “co-innovation” to “non-co-innovation”, and the convergence speed will accelerate with increasing free-rider revenue. Comparing Figure 7 and Figure 8, free-rider gains and potential risk losses are not conducive to the evolution of the system toward “co-innovation”, and the negative impact of potential risk losses is more significant; that is, enterprises show greater sensitivity when facing potential risk losses.

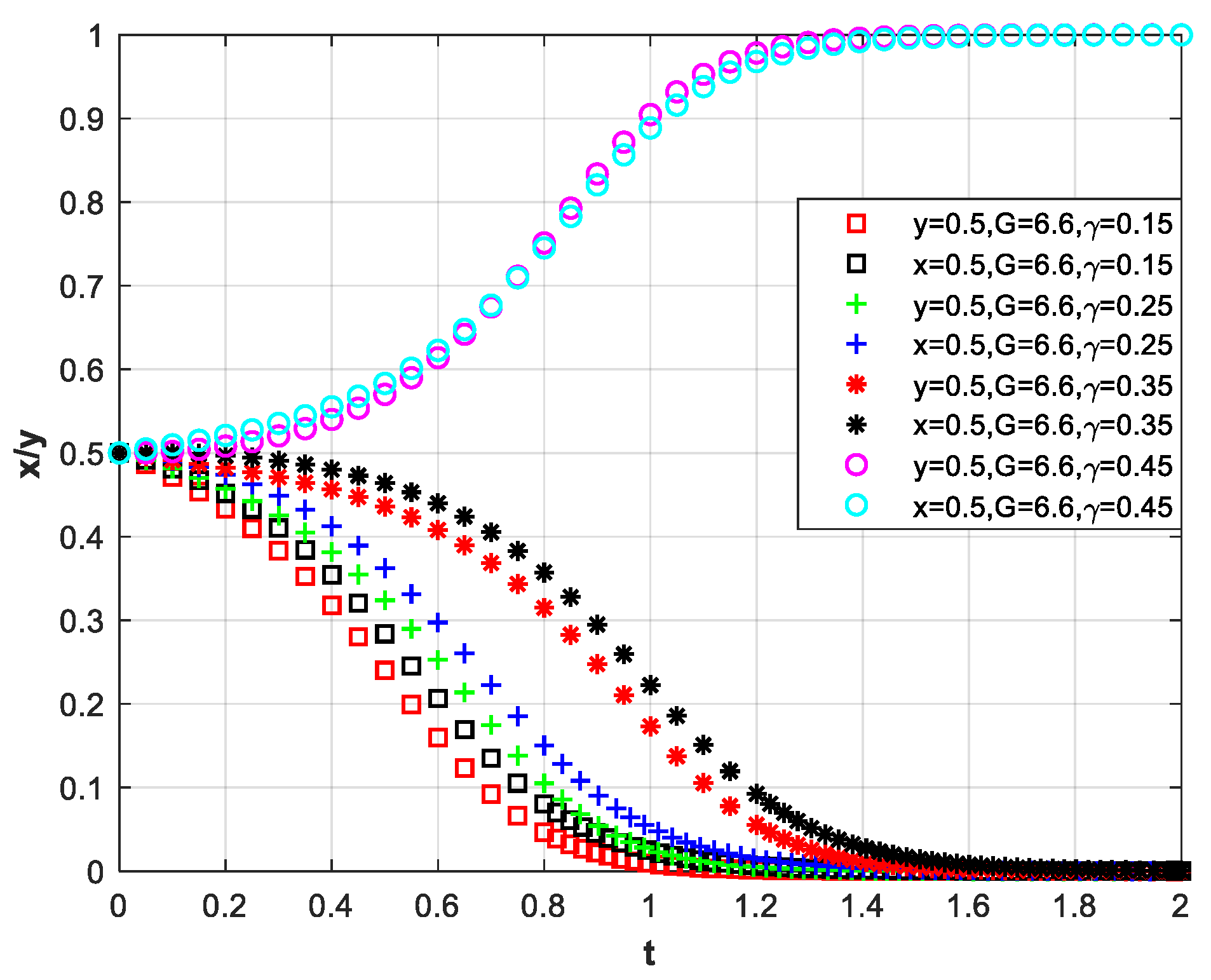
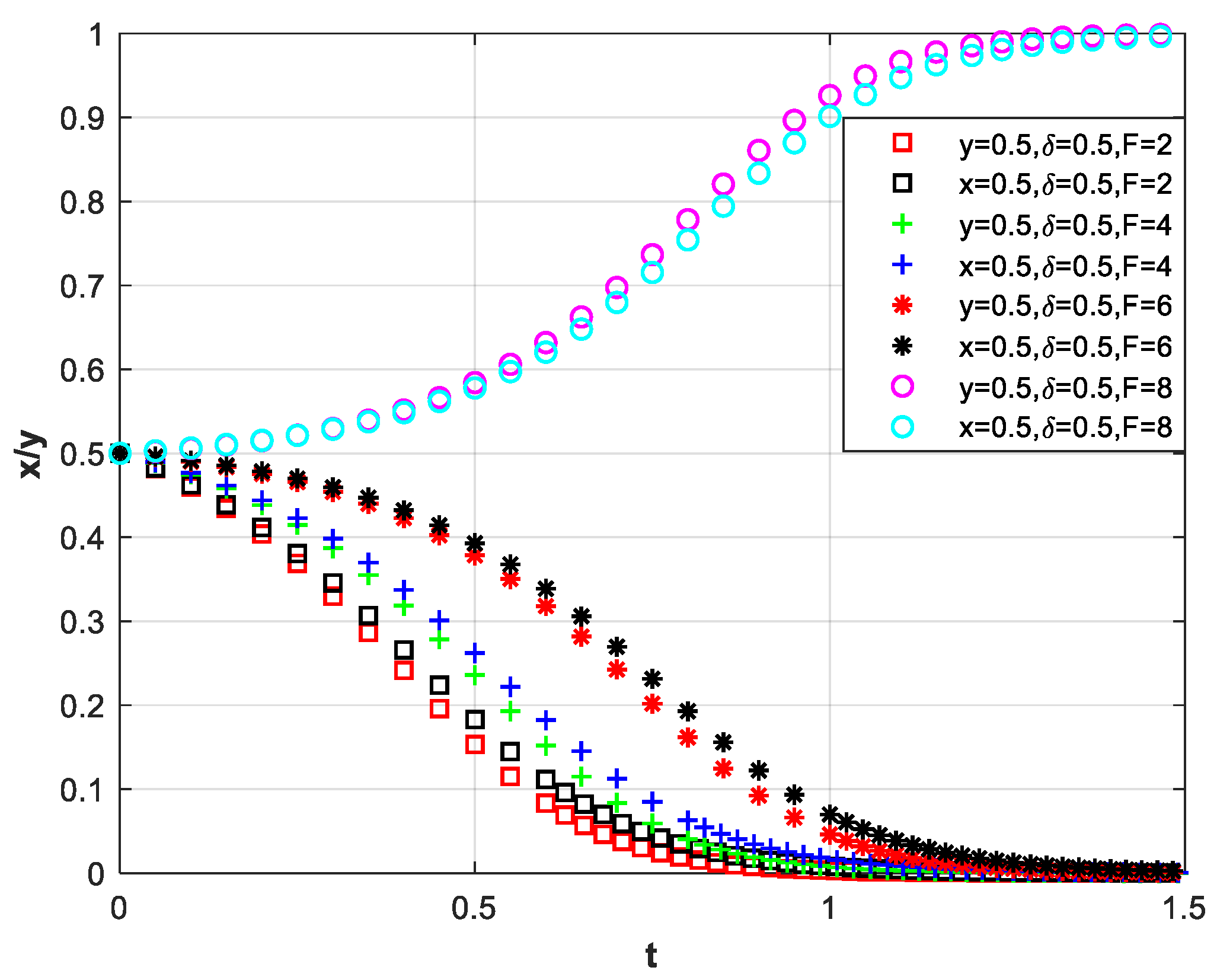
3.4. Liquidated Damage, Government Fines, and Motivation for Co-Innovation

3.4.1. Adoption of a Safeguard: Enterprise Liquidated Damage

In the development of the rural e-commerce industry chain, both parties will formulate a contract. In cases where any one party gains free-rider benefits by not engaging in synergistic innovation, liquidated damage will be imposed. Considering Figure 7 and Figure 8 together, we select $e_1=e_2=0.5$, $D_1=D_2=3$, and $S_1=S_2=2$ (the system evolves in a non-co-innovation direction) and observe the impact of the liquidated damage instrument on the strategic choices of the two parties of the game. Regulating the liquidated damage, we order the values of $K$ as 1, 2, 3, and 4. The remaining parameter values are kept constant, viz. $C_1=9$, $C_2=6.6$, $H=10$, $\theta =1$, $\lambda =0.5$, $\mathrm{T}=10$, ${\alpha }_1=1$, ${\alpha }_2=0.6$, $\beta =0.15$, $\gamma =0.25$, $G=6.6$, $\delta =0$, and $F=0$. The simulation results are shown in Figure 9. The figure shows that there is a threshold value between $[1,2]$ and the default $K$. When K is greater than this threshold, the two sides of the game evolve from “non-co-innovation” to “co-innovation”, and the speed of convergence accelerates with increasing liquidated damage.

3.4.2. Adoption of a Safeguard: Government Fines

The government is actively dedicated to establishing a fair competition mechanism among rural e-commerce enterprises. It aims to implement effective punitive measures against speculative behaviors, such as false propaganda, intellectual property infringement, unfair competition, and other actions that undermine collaborative innovation. Considering Figure 7 and Figure 8 together, we selected $e_1=e_2=0.5$, $D_1=D_2=3$, and $S_1=S_2=2$ (the system evolves in the direction of non-co-innovation) to compare the intensity of the role of government fines and liquidated damage in the direction of the system’s evolution. To consider the effect of government fines on the outcome of the system’s evolution alone, we set $\delta =0.5$. After reconciling the government fines, we ordered the values of $\mathrm{F}$ to be 2, 4, 6, and 8. The remaining parameter values were kept constant, viz.$C_1=9$, $C_2=6.6$, $H=10$, $\theta =1$, $\lambda =0.5$, $\mathrm{T}=10$, ${\alpha }_1=1$, ${\alpha }_2=0.6$, $\beta =0.15$, $\gamma =0.25$, $G=6.6$, and $\mathrm{K}=0$. The simulation results are shown in Figure 10. As shown in Figure 10, when there is a government fine, the trajectory of the system that originally evolved in the direction of “non-co-innovation” will gradually converge to the state of “co-innovation” as the fine increases. Moreover, there is a threshold between $[6,8]$ for the government fine $\mathrm{F}$. When F is greater than this threshold, the game players will change from “non-co-innovation” to “co-innovation”, and the convergence speed will accelerate with increasing government fines. Compared with Figure 9, Figure 10 demonstrates that both enterprise liquidated damage and government fines contribute to the system’s evolution toward “co-innovation”. However, considering the relative proportions of the two values, the assurance effect of liquidated damage appears to be more significant.

3.4.3. Adoption of Two Types of Safeguards: Enterprise Liquidated Damage and Government Penalties

The impacts of the two combinations of safeguards on the outcome of the game for both the platform and the participating firms are further analyzed. By synthesizing Figure 9 and Figure 10, we select $\delta =0.5$ and $\mathrm{F}=2$ in Figure 10 (the system evolves in a nonsynergistic direction) to regulate the liquidated damage $K$, and we order the values of $K$ to 1, 2, 3, and 4. The remaining parameter values are kept constant, viz., $C_1=9$, $C_2=6.6$, $H=10$, $\theta =1$, $\lambda =0.5$, $\mathrm{T}=10$, ${\alpha }_1=1$, ${\alpha }_2=0.6$, $\beta =0.15$, $\gamma =0.25$, and $G=6.6$. The simulation results are depicted in Figure 11. After the government implements a certain degree of regulatory penalties, the threshold value of the default payment is reduced to that of $[0,1]$. Furthermore, the convergence speed toward collaborative innovation surpasses that of a single liquidated damage. Hence, the comprehensive utilization of enterprise liquidated damage and government fines to establish a guarantee mechanism is beneficial for stimulating the innovation vitality and cooperative willingness of all participants in the whole industry chain.

4. Discussion

In this paper, a variety of influencing factors, including the digital technology empowerment coefficient, are included in the research framework, and two collaborative innovation evolution game models between platform enterprises and participating enterprises are constructed. Considering the evolution process of strategy selection by game subjects under both market mechanisms and government supervision, this paper theoretically analyzes the impact of various factors on enterprise behavior decisions. Using case simulation, the study simulates the evolutionary path of the enterprise collaborative innovation game. This study shows that the digital technology empowerment coefficient, technology absorption capacity, information quantity and technology quantity produced by collaborative innovation are important variables affecting the choice of collaborative innovation strategy of enterprises. Potential risk losses and free-rider gains have negative effects on the evolution of the system toward collaborative innovation.

At present, there are few studies on the collaborative behavior of the whole industrial chain of rural e-commerce. To the best of our knowledge, although the literature focuses on the topic of multiagent collaboration in the rural e-commerce industry chain, it generally lacks an in-depth investigation of the dynamic evolution process of microagent behavior decision making, which leads to a lack of convincing demonstrations of multiagent collaboration. Through case studies, Zhang et al. deconstructed the internal logic and driving force of the structural transformation of the rural e-commerce industry chain [15]. Zeng et al. took Shuyang County, Jiangsu Province, as an example, revealed the formation mechanism of rural e-commerce industrial clusters and emphasized the importance of core platform construction [17]. These documents provide support for understanding the multiagent collaborative decision making of the whole industrial chain of rural e-commerce. On this basis, this paper provides a new research perspective and supplements the literature.

Owing to the digital empowerment characteristics and policy-oriented characteristics of the whole rural e-commerce industry chain, this paper not only reveals the key influencing factors of collaborative innovation in the whole rural e-commerce industry chain but also focuses on the impact of regulation on collaborative innovation in the industry chain. With respect to the role of collaborative innovation in the industrial chain, Long et al. [27] and Huo et al. [29] proved that evolutionary game theory is suitable for investigating the role of industrial chain synergy, but all of them are discussed as the main game participants in the model. Unlike their research, which considers the realistic situation of rural e-commerce and the role played by the literature in rural e-commerce [13,25], this paper focuses on the role of external regulators and examines how regulation can improve market failure in the collaborative innovation of the whole industrial chain of rural e-commerce. Our research shows that when the market mechanism fails, the combination of operating cost subsidies and incentives can produce better policy synergy. Compared with the comprehensive application of a single incentive and cost subsidy, it can produce the greatest complementary effect on policy. In addition, when potential risk loss and free-riding income make the whole industry chain tend toward non-collaborative innovation, the introduction of enterprise liquidated damage and fines can effectively promote the evolution of the system toward collaborative innovation. In terms of the relative ratio of the two values, the improvement effect of liquidated damage is more significant. The comprehensive application of enterprise liquid damage and fines can standardize and guide enterprise behavior in many aspects. The findings of this paper provide a useful reference for formulating precise strategies.

However, there are still some shortcomings and limitations in this study. Future research can be carried out from the following two aspects. First, the platform enterprise is the leader of the industrial chain, and other participating enterprises in the chain have certain complementarity and dependence on the platform enterprise, although their respective functions are different. Therefore, the evolutionary game model constructed in this paper focuses solely on the interaction between platform enterprises and participating enterprises and considers the influence of government regulation. We acknowledge that the whole rural e-commerce industry chain involves multiple players. Future research could consider more nuanced stakeholders, such as suppliers and logistics providers. Second, the evolutionary game model constructed in this paper introduces only subsidies, direct rewards and regulatory punishment parameters for regulation and control. Future research can further enrich the parameter settings of regulation and control.

5. Conclusions and Implications

5.1. Conclusions

On the basis of the digital characteristics and strategic attributes of the whole rural e-commerce industry chain, this paper depicts the dynamic game process of the collaborative innovation behavior strategy of the rural e-commerce industry chain under digital empowerment from the perspective of a pure market mechanism and government regulation. The research findings are as follows: (1) Factors such as the digital technology empowerment coefficient, the technology absorptive capacity coefficient, and the amount of information and technology generated by collaborative innovation positively influence the evolution of platform enterprises and participating enterprises toward collaborative innovation. (2) Under the market mechanism, enterprises’ decision making is based on the relative ratio of the benefits and costs of collaborative innovation. When the cost-to-benefit ratio exceeds the threshold, leading to non-collaborative innovation in the whole industry chain, government incentive measures, such as operating cost subsidies and direct incentives to enterprises, can effectively promote collaborative innovation. In particular, the positive incentive effect of operating cost subsidies is notable. (3) Potential risk losses and free-rider gains have negative effects on the evolution of the system toward collaborative innovation. In particular, enterprises are more sensitive to potential risk losses. The introduction of enterprise liquidated damage and government fines can effectively promote the evolution of the system toward collaborative innovation, with the improvement of liquidated damage being particularly significant.

5.2. Contributions to Theoretical Knowledge

The main theoretical contributions of this paper are as follows:

Firstly, this paper establishes evolutionary game models designed for platform enterprises and participating enterprises in the rural e-commerce industry chain under both market-driven and government-regulated scenarios. These models open the black box of the collaborative innovation decision-making mechanism of the rural e-commerce industry chain.

Secondly, this paper integrates various factors such as digital technology empowerment coefficient and technology absorptive capacity into a unified theoretical framework, providing a new theoretical perspective for future research on the collaborative innovation decision-making patterns and mechanisms among enterprises across the whole rural e-commerce industry chain.

5.3. Practical Implications

The findings of this paper practically serve as a reference for enterprises within the industry chain to make both competitive and cooperative decisions and also provide policymakers with a reference for designing effective incentive and supervision strategies aimed at promoting the health of the rural e-commerce industry chain. To provide better management insights, this paper presents a stability mechanism diagram of collaborative innovation in the whole rural e-commerce industry chain in Figure 12.

Our specific management insights are as follows: (1) Control the cost–benefit ratio and improve the benefit distribution mechanism. Both platform enterprises and participating enterprises should enhance their technical research and development to address the diverse demands of the market and achieve greater technological dividends. Simultaneously, enterprises should prioritize refined management practices, optimize processes, and embrace technological innovation to curtail costs. The costs and benefits of enterprises in the innovation process must match to avoid weakening the motivation for collaborative innovation. (2) To enhance information sharing across the whole rural e-commerce industry chain, core platform enterprises should take the lead in establishing enduring and stable cooperative relationships with other enterprises. Using cloud computing, big data, and other modern information technologies, these enterprises can construct a digital platform cooperation system centered on “information sharing and risk sharing”. This system facilitates real-time information dissemination, analysis, and processing, empowering chain enterprises to better comprehend market demand, product development, manufacturing, logistics, and distribution information. (3) Introducing a liquid damage system between platform enterprises and participating entities during cooperation negotiations effectively curbs potential contract breaches. Simultaneously, governments should reduce the cost–benefit ratio threshold of collaborative innovation through diverse incentives, including operational cost subsidies and direct government incentives. To uphold market order and fair competition, governments must increase their supervision and impose penalties to deter unfair competition practices.