Intelligent Assessment of Personal Credit Risk Based on Machine Learning

Abstract

In the 21st-century global economy, the rapid growth of the finance industry, particularly in personal credit, fuels economic growth and market prosperity. However, the rapid expansion of personal credit business has brought explosive growth in the amount of data, which puts forward higher requirements for the risk management of financial institutions. To solve this problem, this paper constructs an intelligent evaluation model of personal credit risk under the background of big data. Firstly, based on the forest optimization feature selection algorithm, combined with initialization based on chi-square check, adaptive global seeding, and greedy search strategies, key risk factors are accurately identified from high-dimensional data. Then, the XGBoost algorithm is used to evaluate the credit risk level of customers, and the traditional Sparrow Search Algorithm is improved by using Tent chaotic mapping, sine and cosine search, reverse learning, and Cauchy mutation strategy to improve the optimization performance of algorithm parameters. Finally, using the Lending Club dataset for empirical analysis, the experiment shows that the model improves the accuracy of personal credit risk assessment and enhances the ability of risk control.

1. Introduction

In recent years, with the rapid development of the economy and the improvement of people’s living standards, personal credit business has experienced rapid growth globally. As an important form of financial service, personal credit not only provides consumers with flexible and diverse channels for obtaining funds but also greatly promotes the prosperity of the consumer market and economic growth. However, with the continuous expansion of the personal credit market, its potential risk factors have become increasingly prominent. In particular, credit risk, as a core issue, has become one of the key factors restricting the healthy development of the market.

Credit risk refers to the risk that borrowers are unable to repay the principal and interest of loans in full and on time due to various reasons. Its origins are complex and diverse, including but not limited to changes in the economic environment, deterioration of personal financial conditions, and decreased willingness to repay. In the traditional credit evaluation system, due to limited information sources and outdated processing methods, financial institutions often find it difficult to comprehensively and accurately grasp the credit status of borrowers, leading to deviations in risk assessment results, which in turn affect the effectiveness and safety of credit decisions. In the event of large-scale defaults, it will bring huge economic losses to banks and may even lead to instability in the entire financial system. Therefore, how to effectively identify and prevent credit risks has become an important issue that financial institutions urgently need to address.

With the rapid development of big data technology and the gradual maturity of intelligent management methods, personal credit risk management is steadily moving towards intelligence and refinement. Using algorithms and big data technology to quickly process massive amounts of information can improve evaluation speed. Using credit risk assessment models to quantify default probability can provide more objective risk assessment results. Therefore, this paper aims to construct an intelligent identification and risk assessment model for personal credit risk factors in the context of big data. It precisely identifies key factors affecting personal credit risk among high-dimensional features, enhancing the comprehensiveness and intelligence of risk factor identification. Based on the specific circumstances of each applicant, such as credit history, income level, consumption behavior, etc., personalized risk assessment results are provided, improving the accuracy of risk assessment. At the same time, this research provides new approaches and methods for promoting the development of big data technology and intelligent management algorithms in the financial field.

The structure of this paper is arranged as follows: the second part introduces relevant research work, including the current application status and existing problems of personal credit risk factor identification and personal credit risk assessment methods; the third part elaborates on the construction process of intelligent identification models for personal credit risk factors and personal credit risk assessment models in the context of big data; the fourth part conducts empirical analysis, including dataset construction, data preprocessing, parameter setting, evaluation indicators, and result analysis, and compares with other commonly used models; and the fifth part summarizes the research results, points out the limitations of the research, and indicates future research directions.

2. Related Work

2.1. Identification of Credit Risk Factors

In the context of big data, intelligent management of personal credit risk has become a focal point for both financial institutions and academia. As the foundation of credit risk management, identifying risk factors in personal credit is of great significance for improving the scientific nature and accuracy of credit decisions.

The identification of risk factors in personal credit primarily relies on theoretical support from multiple disciplines such as statistics, machine learning, and data mining. At the theoretical level, risk factor identification is regarded as a process of feature selection or variable selection, which involves screening out key factors that have a significant impact on credit risk from numerous potential risk factors. This process not only helps simplify the model and improve prediction accuracy but also enhances the interpretability and comprehensibility of the model. In the field of credit risk management, the identification of risk factors in personal credit typically involves multiple dimensions such as borrowers’ basic information, financial status, credit history, and consumption behavior [1]. There may be complex interactions among these factors. Therefore, how to effectively identify and integrate these factors to construct an accurate risk assessment model becomes the focus of research.

In the study of credit risk assessment, macro factors have a significant impact on individual credit risk. Previous studies have shown that changes in the macroeconomic environment can indirectly affect individuals’ credit behavior through various channels. For example, an increase in government deficits may lead to increased economic uncertainty, which in turn weakens individuals’ ability to repay debts and increases the probability of default [2]. Changes in monetary policy, such as interest rate adjustments or quantitative easing, can also alter individuals’ financial stress and borrowing behavior by affecting credit conditions and liquidity [3]. In addition, fluctuations in economic cycles are closely related to credit risk. During an economic recession, an increase in unemployment and a decrease in income significantly increase an individual’s risk of default [4]. Inflation is also an important macro factor, especially during the post-COVID-19 period [5]. It affects credit risk through various channels, among which the most significant are reducing household real income, increasing living costs, and raising interest rates. These changes have led to an increase in borrowing costs and a decrease in funds available for debt repayment, thereby increasing the difficulty of personal debt repayment and increasing the likelihood of default. Macro factors are of great significance in credit risk assessment, and their impact is usually indirectly reflected through personal characteristics such as the income level, employment status, and debt ratio. In addition, macro factors usually exist in the form of time series, and the dataset in this article is mainly based on cross-sectional data, which are difficult to integrate directly. Therefore, this article mainly focuses on individual factors. Therefore, this paper mainly focuses on personal-level data to construct a high-precision credit risk assessment model.

There are various methods for identifying risk factors in personal credit, mainly including expert analysis, traditional statistical methods, and machine learning methods.

Some scholars utilize expert analysis and literature review methods to identify and determine the risk factors affecting personal credit. Wu et al. analyzed the factors influencing the credit risk of P2P online borrowers based on various indicators of personal credit risk assessment in domestic and foreign commercial banks, as well as the characteristics of P2P online lending, and identified unique risk factors in this field [6]. Wang et al. constructed an indicator system for personal credit risk assessment through causal reasoning [7].

Traditional statistical methods such as multiple linear regression and logistic regression are employed. By constructing regression models, the relationship between various risk factors and credit default probability is analyzed, thereby identifying key risk factors. These methods play a significant role in credit risk assessment. Zhu adopted the entropy weight method to determine the weight of each indicator and selected the main factors affecting personal credit risk, avoiding the influence of subjective factors [8]. Zhang et al. constructed a personal credit scoring model based on data from commercial banks’ personal consumer credit and the logistic regression model, using SPSS17.0 statistical software. Through empirical testing, they identified six indicators, including borrower’s age, marital status, and education level, as key factors affecting personal credit risk [9]. However, traditional statistical methods may have limitations when dealing with high-dimensional and nonlinear data.

With the advancement of big data and artificial intelligence technology, machine learning methods are increasingly being applied in the identification of risk factors in personal credit. These methods, including decision trees, random forests, support vector machines, and neural networks, can automatically learn complex patterns from data without prior assumptions about data distribution, thus offering significant advantages in handling high-dimensional and nonlinear data. For instance, Cai et al. extracted combined features from raw data using the GBDT model and then constructed a personal credit risk assessment model using logistic regression [10]. Wu et al. utilized the SHAP method to screen reasonable credit evaluation indicators [11]. Liao et al. employed a series of data preprocessing methods and the feature selection method XGBFS based on the Embedded concept to reduce the dimensionality of user credit data and train an XGBoost evaluation model [12]. Wang et al. used principal component analysis (PCA) in credit risk assessment to transform original variables into higher-level abstract features, thereby completing feature extraction [13]. Zhang et al. proposed an improved BIV value feature screening method [14]. Chen et al. introduced a multi-scale deep feature fusion feature extractor that performs multi-scale convolution on one-dimensional data, fully extracts the inherent connections between features, and performs attention fusion to obtain more critical features [15].

Although significant progress has been made in the methods for identifying risk factors in personal credit, numerous challenges still persist in practical applications. On the one hand, with the rapid advancement of big data technology, the dimensions and scale of personal credit data have surged, posing a significant challenge in effectively handling high-dimensional data and accurately identifying key features [12]. On the other hand, the complexity and diversity of personal credit data also present substantial challenges for feature selection, making the comprehensive consideration of interactions and mutual influences among different features a focal point of research [16].

2.2. Assessment of Credit Risk

Personal credit risk assessment refers to the process in which financial institutions, before deciding whether to provide credit services to individuals, collect and analyze relevant information about borrowers, and utilize certain assessment models and methods to predict and quantify the potential default risks that may arise in the future for borrowers.

The development of personal credit risk assessment can be traced back to the early 20th century, when credit decisions were primarily based on experts’ experience and judgment. With the advancement of statistics and computer technology, credit scoring models have gradually emerged and become the primary tool for personal credit risk assessment. Mu et al. collected data such as borrowers’ basic information, financial status, and credit history, and used statistical principles to construct a scoring model to assess borrowers’ creditworthiness [17]. Additionally, methods such as multiple linear regression and logistic regression are commonly used to analyze the relationship between various variables and credit default risk. For instance, Zhang et al. constructed a logistic regression model and established a personal credit scoring card model based on the logistic regression model, which assists decision makers in formulating reasonable credit extension policies, pricing strategies, and other related business operation strategies [18]. Cai et al. used logistic regression to construct a personal credit risk assessment model [10]. Li et al. drew on the strengths of the Lasso model and Cox model to create the Lasso–Cox model for assessing the credit risk of individual borrowers [19].

With the rise in artificial intelligence technologies such as machine learning, the method of personal credit risk assessment has entered a new stage of intelligent development, and the application of machine learning methods in personal credit risk assessment is becoming increasingly widespread. These methods can automatically learn complex patterns in data without the need for preset data distribution, thus performing well in handling high-dimensional, nonlinear data. Xu established a personal credit risk assessment model based on the random forest algorithm, and through empirical analysis, proved that the personal credit risk assessment capability of the random forest model is significantly better than that of the logistic regression model [20]. The improved LSTM algorithm proposed by Gao et al., with its advantages in sequence data modeling, can more effectively capture the long-term dependency between borrowers’ historical behaviors and risk factors [21]. Li et al. used the XGBoost algorithm to theoretically model credit classification problems, and then applied the XGBoost model to personal loan scenarios based on the open dataset of the US Lending Club platform [22]. Zhao established a personal credit assessment model with the help of blockchain and decision tree technology, improving the transparency of personal credit information in Internet finance [23].

On this basis, the introduction of deep learning technology has further promoted the precision of personal credit risk assessment. Zhou et al. used convolutional neural networks (CNNs) to establish a personal credit default prediction model [24]. Liang et al. established a credit risk prediction model based on graph convolutional neural networks [25]. Li et al. constructed the actual survival time of default and early repayment, and applied the Deep Recurrent Survival Analysis (DRSA) model to predict the probability of risk events in personal credit [26].

Furthermore, the application of hybrid models has also brought new breakthroughs to personal credit risk assessment. Some scholars have combined multiple algorithms to improve the efficiency of risk assessment. For example, Zhong et al. proposed a personal credit risk assessment model based on a combined classification strategy [27]. This model introduces the concept of decision scores; selects commonly used credit assessment classification algorithms such as K-nearest neighbor, random forest, decision tree, and support vector machine as base classifiers; calculates the decision scores of each base classifier from two dimensions: stability and accuracy; and evaluates the creditworthiness of borrowers based on the combined decision scores. Zhang et al. utilized optimized auxiliary classifiers to generate adversarial networks (ACGANs) and gradient boosting decision trees (GBDTs) for data oversampling, learning, and classification, respectively, based on the characteristics of imbalanced personal credit data, inter-class overlap, and type diversity [28]. On this basis, they constructed a personal credit risk assessment model. Yan et al. addressed the challenge of low accuracy in identifying high-default-risk customers during credit risk assessment by small loan companies by using hybrid SMOTE and RF algorithms to simultaneously handle the two problems of high dimensionality and imbalance in business data [29].

Some scholars have combined optimization algorithms with machine learning algorithms to enhance the performance, efficiency, and accuracy of machine learning models. For instance, Shen Guifang employed the artificial bee colony algorithm to optimize the support vector machine (SVM) for finding the optimal penalty coefficient C and kernel parameters, thereby constructing an ABC-SVM personal credit risk assessment model [30]. The performance of this model was validated through experiments, comparing it with grid search SVM, GA-SVM, and PSO-SVM. Rao et al. integrated particle swarm optimization (PSO) with extreme gradient boosting (XGBoost) to form a PSO-XGBoost model for assessing credit risk in personal car loans [31]. Chen et al. proposed a personal credit assessment method based on an improved longicorn swarm algorithm to enhance the accuracy of SVM in personal credit evaluation [32]. Gu et al. tailored their approach to the characteristics of personal credit risk data [33]. Initially, they oversampled the data using an enhanced Borderline SMOTE-2 algorithm, followed by the parameter optimization of the classifier using a grid search algorithm. To identify the optimal model combination, they employed logistic regression to analyze the contribution of the base models, ultimately determining the Stacking model.

Despite the continuous development of personal credit risk assessment methods, there are still many challenges in practical applications. First is the improvement of model architecture and algorithms. How to better capture complex patterns in data in a big data environment and how to self-learn in real-world scenarios to better cope with dynamic changes have become important development directions for personal credit risk assessment. Second is the lack of model overfitting and generalization ability. Financial data often exhibit high complexity and nonlinear characteristics. When constructing risk assessment models, overfitting often occurs, meaning that the model performs well on training data but poorly on new data [34]. How to improve the generalization ability of the model to adapt to data changes in different scenarios and time periods is one of the main challenges faced by current risk assessment models [35].

In addition, some scholars have applied machine learning-based models to fraud detection tasks in personal risk management. For example, Xie et al. proposed a learning method based on transaction behavior representation to improve the accuracy of credit card fraud detection by capturing users’ transaction patterns [36]. Similarly, Xie et al. introduced a time-aware attention mechanism for gated networks, which can effectively extract transaction behavior features and improve detection performance [37]. In addition, some scholars have further explored the spatial and temporal information in transaction data by constructing a spatiotemporal gating network, thereby enhancing the effectiveness of fraud detection [38]. Although these studies have achieved significant results in fraud detection tasks, they mainly focus on identifying and preventing illegal behavior or fraudulent activities in transactions, typically applied to real-time or near-real-time verification processes for each transaction. In contrast, this study focuses more on evaluating the overall credit status of customers and predicting the likelihood of future defaults to support long-term decision-making processes such as credit card application approval and credit limit adjustments.

3. Method

3.1. Credit Risk Factor Identification Model

3.1.1. Overview of Basic Algorithms

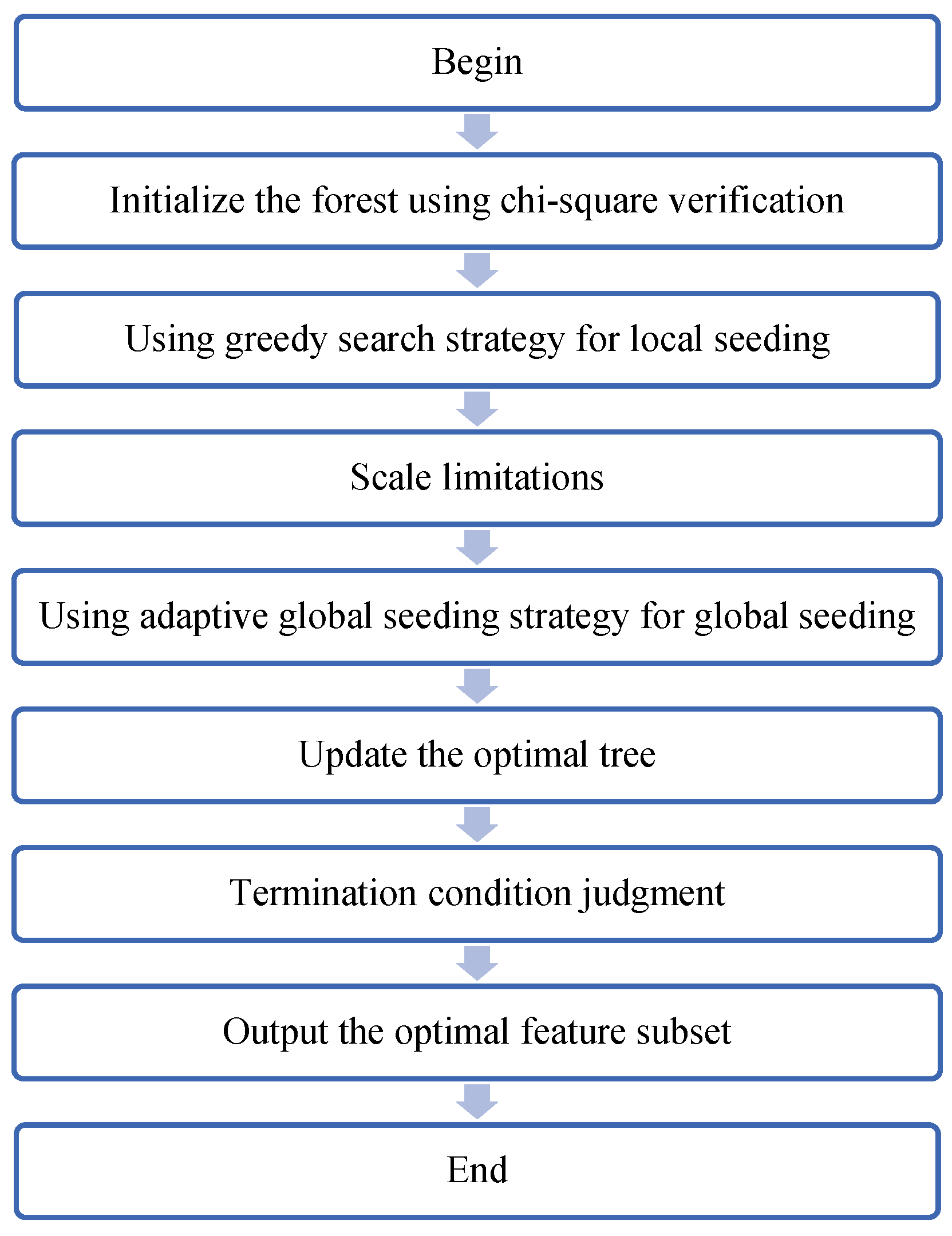
The feature selection using forest optimization algorithm (FSFOA) is an enhanced version of the forest optimization algorithm (FOA), which can be regarded as a forest optimization algorithm for binary discrete vectors. FOA is a bionic evolutionary algorithm proposed by Ghaemi in 2014, inspired by the growth and competition phenomena of trees in nature. In forests, towering trees tend to grow in areas with abundant water and sunlight. The process of trees’ seeds seeking the best habitat is precisely a search and optimization process. By modeling this process, Ghaemi proposed FOA to solve nonlinear optimization problems. In 2016, Ghaemi M and Feizi-Derakhshi M R adapted FOA to discrete vectors by modifying two operators, local seeding and global seeding, and applied it to feature selection, validating the feasibility of FSFOA in the field of feature selection.

FSFOA is a method that utilizes a tree-like structure to represent and select feature subsets. In this approach, each tree explicitly identifies which features are selected for the learning process through a specific 0/1 sequence—where 0 represents a feature that is not selected, and 1 signifies that the feature will be utilized. The entire FSFOA process has been meticulously designed with five core steps to ensure the effectiveness and efficiency of feature selection. The first step involves initializing the forest. During this phase, the system randomly generates N trees, collectively forming the initial forest. Each tree comprises three key components: feature selection status, age, and fitness. The feature selection status is determined by a randomly generated 0/1 sequence, while the age is initialized to 0. Subsequently, the system calculates the fitness of each tree based on the selected features, serving as the basis for subsequent selection and optimization. The second step involves local seeding, which focuses on performing seeding operations on trees with an age of 0. For each tree participating in seeding, the system will replicate LSC trees and reset the ages of these replicated trees to 0. Then, the system will randomly select a feature state to perform a negation operation, in order to explore different feature combinations. After completing these operations, the new tree will be added to the forest, and the ages of all trees in the forest will be incremented by 1. The third step involves size limitation, which aims to control the size of the forest and ensure the efficiency of the algorithm. The system achieves this by setting an age limit (life time) and an area limit. Initially, trees exceeding the age limit are moved to the candidate forest. If, even after this, the number of trees in the forest still exceeds the area limit, the system sorts the trees in descending order of fitness and retains only the area limit trees with the highest fitness in the forest, while the rest are also moved to the candidate forest. The fourth step involves global seeding to further enhance the exploration capability of FSFOA. Based on a preset transfer rate, the system randomly selects a certain proportion of trees for replication. For each replicated tree, the system randomly selects GSO feature states for negation operations, thereby generating new trees, which are then added to the forest. This step aids in exploring a wider range of feature combinations globally. The fifth step involves updating the optimal tree to ensure the continuous optimization of the algorithm. The system identifies the tree with the highest fitness within the current forest, considers it as the optimal tree, and resets its age to 0. Subsequently, this optimal tree is reintroduced into the forest to participate in the next round of local seeding and subsequent optimization processes. By iteratively performing these steps, FSFOA can gradually approach the optimal feature subset selection. Although FSFOA has achieved promising results in feature selection, it still has room for improvement.

Although FSFOA has achieved good results in feature selection, there are still the following issues: (1) When initializing the forest, FSFOA adopts a random selection strategy for feature selection, which introduces high randomness and blindness. This strategy fails to fully cover high-quality feature combinations in the feature space, thereby affecting the algorithm’s subsequent search efficiency and global optimization capabilities. Furthermore, poor initial quality of the forest trees can lead to slow forest convergence and poor adaptability to high-dimensional datasets. (2) During the local seeding stage, FSFOA only randomly selects one feature state for each tree to perform a negation operation. This strategy limits the exploration range of the search space, especially when the LSC (local seeding copy tree count) parameter is small. This limitation reduces the algorithm’s search efficiency, making it difficult to discover potential global optimal feature combinations and being prone to falling into local optima. (3) In the size limitation stage, FSFOA adds all trees with ages exceeding the upper limit to the candidate forest, and retains some trees based on fitness ranking when the forest size exceeds the regional upper limit. However, this approach has computational redundancy issues because the candidate forest may contain a large number of inferior trees with low fitness. These trees may still be selected in the subsequent global seeding stage, increasing the algorithm’s computational cost and potentially leading the algorithm to fall into local solution space. Furthermore, repeatedly using inferior trees may also reduce the algorithm’s global search capability and the quality of the final solution. (4) Experiments have shown that when only considering accuracy as the fitness metric, multiple optimal trees with the same fitness may appear. Moreover, solely using classification accuracy as the optimization objective is too simplistic and cannot effectively improve the feature dimension reduction rate of the feature subset.

Therefore, in order to enhance the overall convergence speed of the forest and strengthen its spatial search and optimization capabilities, this paper proposes a feature selection using the forest optimization algorithm based on hybrid strategies (HSFSFOA).

3.1.2. Initialization Strategy Based on Chi-Squared Test

When initializing the forest, the FSFOA generates the initial solution space in a random manner, resulting in some trees of lower quality. These low-quality trees may fail to discover high-quality populations during subsequent search processes, affecting the quality of the final results. To address this issue, the HSFSFOA proposes a new initialization strategy that selects high-quality features based on the relationship between features and labels, thereby improving the overall quality of the initial solution space.

The HSFSFOA selects features with strong correlation to the label during the initialization stage. This is because such features contribute significantly to classification tasks, while features with weaker correlation to the label are not selected into the optimal feature subset. To achieve this, this paper proposes an initialization method based on the chi-squared test.

The chi-square test is a statistical testing method used to evaluate whether two events are independent or whether there is a significant difference between the actual observed values and the expected values. Its calculation formula is as follows:

$$x^2={\displaystyle \sum _{i=1}^k{\left(A_i-E_i\right)}^2}/E_i$$

(1)

Here, k represents the number of observations, $A_i$ denotes the i-th observation, and $E_i$ signifies the corresponding theoretical value. The larger the value of $x^2$, the greater the deviation between the actual observation and the expected value, indicating a closer correlation between the feature and the prediction target.

The initialization strategy based on the chi-squared test is executed in two steps. Firstly, calculate the chi-squared values for all features and labels in the dataset, and arrange the features in descending order based on the obtained chi-squared values. Then, during the initialization process of each tree, select n features from the sorted feature list as the feature set used by the current tree. Here, n is a randomly generated non-zero integer less than or equal to the total number of features. This method not only ensures that highly relevant features to the labels are selected during initialization, but also promotes exploration diversity by introducing a certain degree of randomness. This helps avoid falling into local optima, thereby improving the overall algorithm performance.

3.1.3. Adaptive Global Seeding Strategy

During the global seeding stage, the GSC (global search control) parameter controls the selection of features, thereby influencing the adjustment of tree morphology. Fixed GSC parameters limit the algorithm’s flexibility in adjusting tree morphology, making it difficult to achieve effective global search and escape from local optima. This paper proposes an improved GSC parameter generation strategy, aiming to fully utilize the global search mechanism to avoid falling into local optima and more effectively find the optimal feature subset.

There are differences in the quality of trees in the candidate forest: some trees perform poorly due to their feature sets being far from the optimal feature subset; others perform better because they have feature sets close to the optimal solution. For the former, more adjustments need to be made to their feature sets; for the latter, only minor adjustments are required.

Inspired by automatic control theory, this paper introduces a method based on a feedback adjustment mechanism to adaptively generate GSC parameter values. This method dynamically sets the GSC value based on the fitness value of each tree (i.e., the classification accuracy of the feature subset determined by the current tree). Specifically, inferior trees will be assigned larger GSC values to allow for more adjustments in feature selection, while superior trees will be assigned smaller GSC values to maintain the stability of their feature sets. Additionally, to distinguish between global and local seeding strategies, upper and lower limits for the GSC parameter are set. In the adaptive global seeding strategy, the GSC parameter value is a function of the tree’s fitness value.

$${\mathrm{mum}}_{GSC}=f( \mathrm{Fitness} )$$

(2)

When evaluating the quality of a tree, not only the performance of the current tree is considered, but also the performance of the ideal optimal tree is referenced to ensure the accuracy of the evaluation. When assessing the quality of a tree, it is necessary to consider not only the quality of the current tree but also the quality of the ideal tree, in order to make an appropriate judgment on the tree’s quality. This article compares the current tree quality $Fitnes{s}_{now}$ with the ideal optimal tree quality $Fitnes{s}_{best}$ to determine the quality of the current tree. When determining the quality of the tree, if there is a large gap between $Fitnes{s}_{now}$ and $Fitnes{s}_{best}$, a conservative evaluation of the tree quality is made; if the gap is small, a more aggressive evaluation of the tree is made. Since the fitness value of the ideal optimal tree is difficult to determine, this article uses the current optimal tree to approximate the ideal optimal tree. The tree quality function is as follows:

$$\mathrm{Fitness} ={\displaystyle \frac{1}{1+e^{-\left({\mathrm{Fithess} }_{\mathrm{best} }-{ \mathrm{Fithess} }_{\mathrm{now} }\right)}}}-{\displaystyle \frac{1}{2}}$$

(3)

After obtaining the quality of the current tree, it needs to be mapped onto the actual number of features that need to be modified. Assuming that the quality of the current tree is directly proportional to the number of features that need to be modified,

$${ \mathrm{num} }_{\mathrm{change} }\propto \mathrm{Fitness}$$

(4)

When finalizing the GSC parameter value, calculate the number of features that should be modified based on the total number of features in the dataset. To ensure that the global seeding process differs from local seeding, set the upper limit of the GSC parameter to 0.5n (where n is the total number of features) and the lower limit to 2. Therefore, the formula for determining the GSC parameter value is as follows:

$${ \mathrm{num} }_{GSC}=1+⌈0.5n\times \mathrm{Fitness}⌉$$

(5)

By adaptively adjusting the GSC value, it can effectively expand the search range of global seeding, helping the algorithm avoid falling into local optima. At the same time, it can more easily find a better search space and promote convergence towards the optimal solution.

3.1.4. Greedy Search Strategy

During the local seeding process of the FSFOA, all trees with a tree age of “0” undergo local search, but this approach limits the overall optimization performance of the algorithm. This paper proposes an improvement to this process, aiming to fully leverage the effectiveness of local search and more efficiently identify the optimal feature subset.

During the local seeding stage, trees with an age of “0” exhibit variations in their morphology. The characteristics of inferior trees differ significantly from those of ideal optimal trees, making it difficult to transform them into high-quality trees by altering individual features. However, the feature subset of high-quality trees is relatively close to the ideal optimal feature subset. Therefore, when conducting multiple local searches, there is a greater likelihood of finding a better feature subset. Based on this, this paper adjusts the local seeding strategy by increasing the selection restrictions on local search trees and expanding the local search range.

Specifically, when selecting a local search tree, we first choose all trees with a tree age of “0” from the forest, and then further filter them based on their quality. Inspired by the greedy strategy, this paper prioritizes selecting trees with higher fitness values for subsequent local search, thereby reducing the search for inferior trees. If only the tree with the highest fitness value is selected, although it can improve the quality of local search, it can lead to a lack of diversity in the forest, potentially causing the algorithm to fall into local optima. Therefore, this paper selects half of the trees in the forest as the objects of local search to maintain the diversity of the forest. For the judgment of tree quality, trees with a tree age of “0” are sorted from high to low according to their fitness values, with the first half marked as high-quality trees for subsequent local search, while the second half are considered inferior trees and do not participate in subsequent local search.

In the FSFOA, the range of local search is controlled by the LSC (local search control) parameter, which is typically set as follows:

$$LSC=⌈{\displaystyle \frac{n}{5}}⌉$$

(6)

To enhance the effectiveness of local search, set the LSC value to twice its original value:

$$LSC=2\times ⌈{\displaystyle \frac{n}{5}}⌉$$

(7)

This not only enables the search for better feature subsets but also ensures the algorithm’s operational efficiency. The local seeding process is essentially a “selecting the best from the good” local search process. With the aforementioned adjustments, the new local seeding strategy fully leverages the “selecting the best from the good” characteristic of local search, eliminates ineffective searches for inferior trees, expands the search range for high-quality trees, and thereby facilitates convergence to the globally optimal or near-optimal feature subset.

The entire flowchart of the risk factor identification algorithm is shown in Figure 1.

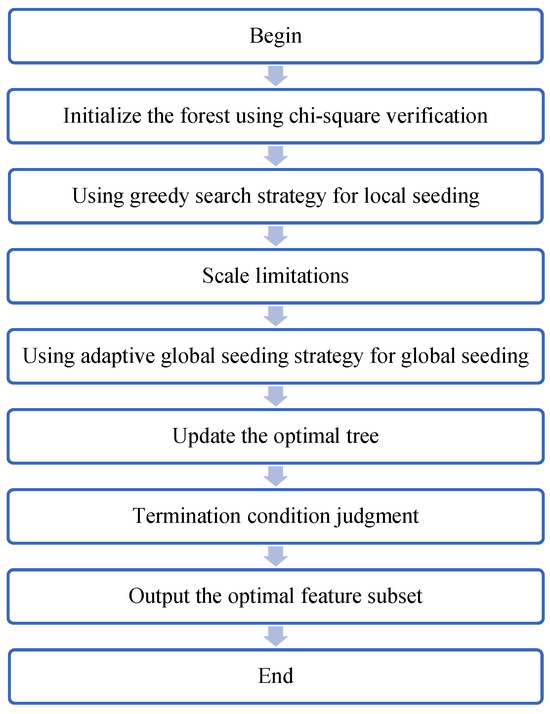
Figure 1. Flowchart of risk factor identification algorithm.

3.2. Credit Risk Assessment Model

3.2.1. Overview of Basic Algorithms

The Sparrow Search Algorithm (SSA), proposed in 2020, is a novel swarm intelligence optimization algorithm that demonstrates strong capabilities in finding optimal solutions. However, compared to most intelligent optimization algorithms, SSA tends to get stuck in local optima during the later stages of iteration, and still faces the issue of low convergence accuracy.

To enhance the global optimization capability of the Sparrow Search Algorithm (SSA), researchers have proposed various improvement strategies. Zhou et al. introduced the TC chaotic mapping to initialize the sparrow population, resulting in a more uniform and diverse population distribution [39]. Liu et al. refined the discoverer position update rule in the SSA by utilizing the Golden Sinusoidal Algorithm, addressing the issue of reduced search dimensions [40]. Xiao et al. introduced a hybrid sine–cosine algorithm to update the discoverer position and incorporated the Levy flight strategy to update the follower positions, thereby improving the SSA and enhancing the scientific nature of parameter selection [41]. Wang et al. proposed a sand cat swarm optimization algorithm that integrates the SSA with the Cauchy mutation strategy [42]. By integrating the search mechanism strategy of the SSA, the algorithm’s search capability is enhanced in the later stages. By adopting the Cauchy mutation strategy, the algorithm changes the position of individuals, improving population diversity and enabling the algorithm to escape local optima. Wang et al. introduced Cauchy mutation and variable spiral search strategies into the follower position update to enhance the algorithm’s search efficiency and global search performance [43]. Xue et al. proposed a multi-strategy improved SSA to address issues such as decreased population diversity and susceptibility to local optima when the algorithm approaches the global optimum [44].

Based on the current research status, this paper improves the traditional Sparrow Search Algorithm (SSA) and proposes an improved Sparrow Search Algorithm to optimize the XGBoost model for credit risk prediction. The improved Sparrow Search Algorithm uses Tent chaotic mapping for initialization; utilizes the sine–cosine search strategy to effectively balance global and local search capabilities; introduces the reverse learning strategy and Cauchy mutation for perturbation to expand the search domain and improve the ability to escape local optima; and adopts greedy rules to determine the optimal solution. By optimizing the XGBoost parameters using the improved Sparrow Search Algorithm, the accuracy of the model in identifying credit risks is improved.

3.2.2. XGBoost Algorithm

XGBoost (extreme gradient boosting) belongs to the Boosting technique in ensemble learning methods. The basic idea of Boosting is to construct a strong learner by combining multiple weak learners. In XGBoost, these weak learners are usually decision trees. Each tree is trained to correct the errors of the previous tree. Each new model is trained based on the difference (residual) between the prediction result of the previous model and the true value, in order to reduce the prediction error of the overall model.

(1) Define the objective function

The core of XGBoost lies in the design of its objective function, which is used to evaluate the quality of the model and guide the learning process of model parameters. The objective function typically consists of two parts: the training loss (loss function) and the regularization term. The training loss measures the difference between the model’s predicted values and the actual values; the regularization term is used to control model complexity and prevent overfitting. For the t-th iteration, the objective function can be expressed as

$${\mathrm{obj}}^{(t)}={\displaystyle \sum _{i=1}^{n}L}\left(y_i,{\widehat{y}}_i^{(t)}\right)+{\displaystyle \sum _{k=1}^t\Omega }\left(f_k\right)$$

(8)

where $L\left(y_i,{\widehat{y}}_i^{(t)}\right)$ is the loss function, $\Omega \left(f_k\right)$ is the complexity of the k-th tree, n is the number of samples, $y_i$ is the true label of the i-th sample, and ${\widehat{y}}_i^{(t)}$ is the predicted value of the i-th sample by the model after the t-th iteration.

(2) Taylor’s second-order expansion

To optimize the objective function, XGBoost performs a second-order Taylor expansion of the loss function. In the t-th iteration, ${\widehat{y}}_i^{(t)}$ is represented as ${\widehat{y}}_i^{(t-1)}+f_t\left(x_i\right)$, where $f_t\left(x_i\right)$ is the predicted value of the t-th tree. Then, the loss function is expanded using Taylor’s formula:

$$L\left(y_i,{\widehat{y}}_i^{(t)}\right)\approx L\left(y_i,{\widehat{y}}_i^{(t-1)}\right)+g_i{f}_t\left(x_i\right)+{\displaystyle \frac{1}{2}}{h}_i{f}_t^2\left(x_i\right)$$

(9)

where $g_i={\displaystyle \frac{\partial L\left(y_i,{\widehat{y}}_i^{(t-1)}\right)}{\partial {\widehat{y}}_i^{(t-1)}}}$ is the first derivative and $h_i={\displaystyle \frac{{\partial }^{2}L\left(y_i,{\widehat{y}}_i^{(t-1)}\right)}{\partial {\left({\widehat{y}}_i^{(t-1)}\right)}^2}}$ is the second derivative.

(3) Simplify the objective function

Substituting the Taylor series expansion into the objective function and removing the constant terms unrelated to $f_t$, we obtain

$${\mathrm{obj}}^{(t)}\approx {\displaystyle \sum _{i=1}^n\left[g_i{f}_t\left(x_i\right)+\frac{1}{2}{h}_i{f}_t^2\left(x_i\right)\right]}+\Omega \left(f_t\right)$$

(10)

(4) Define the complexity of a tree

In XGBoost, the complexity of a tree is composed of the number of leaf nodes and the L2 norm of the leaf node weights:

$$\Omega \left(f_t\right)=\gamma T+{\displaystyle \frac{1}{2}}\lambda {\displaystyle \sum _{j=1}^T{w}_j^2}$$

(11)

where T represents the number of leaf nodes, $w_j$ denotes the weight of the j-th leaf node, and $\gamma$ and $\lambda$ are regularization parameters.

(5) Optimize the objective function

Substituting the complexity of the tree into the objective function, we obtain

$${\mathrm{obj}}^{(t)}\approx {\displaystyle \sum _{i=1}^n\left[g_i{f}_t\left(x_i\right)+\frac{1}{2}{h}_i{f}_t^2\left(x_i\right)\right]}+\gamma T+{\displaystyle \frac{1}{2}}\lambda {\displaystyle \sum _{j=1}^T{w}_j^2}$$

(12)

Since each sample will eventually fall into a leaf node, the objective function can be rewritten as a function of the weights of the leaf nodes. Let $I_j$ be the set of sample indexes contained in the j-th leaf node. Then, the objective function can be expressed as

$${\mathrm{obj}}^{(t)}={\displaystyle \sum _{j=1}^T\left[\left({\displaystyle \sum _{i\in I_j}{g}_i}\right)w_j+\frac{1}{2}\left({\displaystyle \sum _{i\in I_j}{h}_i}+\lambda \right)w_j^2\right]}+\gamma T$$

(13)

To minimize the objective function, we take the derivative of $w_j$ and set it to 0, thereby obtaining the optimal weight of the leaf node:

$$w_j^{*}=-{\displaystyle \frac{{\displaystyle \sum _{i\in I_j}{g}_i}}{{\displaystyle \sum _{i\in I_j}{h}_i}+\lambda }}$$

(14)

Substituting $w_j^{*}$ into the objective function, we obtain the optimal objective function value (also known as the gain):

$$\mathrm{Gain} =-{\displaystyle \frac{1}{2}}{\displaystyle \sum _{j=1}^T\frac{{\left({\displaystyle \sum _{i\in I_j}{g}_i}\right)}^2}{{\displaystyle \sum _{i\in I_j}{h}_i}+\lambda }}+\gamma T$$

(15)

(6) Construct the optimal tree

In XGBoost, the optimal tree is constructed through a greedy algorithm. The specific approach is as follows: starting from the root node, traverse all possible split points for all features, calculate the gain after splitting, and select the split point with the largest gain for splitting. Then, repeat this process for the split child nodes until reaching a preset stopping condition (such as the maximum depth of the tree, the number of samples in the node is below a certain threshold, the gain is less than a certain threshold, etc.).

(7) Model updating and iteration

After completing the construction of a tree, update the model’s predicted values:

$${\widehat{y}}_i^{(t)}={\widehat{y}}_i^{(t-1)}+f_t\left(x_i\right)$$

(16)

Then, proceed to the next iteration and repeat the aforementioned process until the preset number of iterations is reached or the model’s performance no longer shows significant improvement.

XGBoost exhibits high accuracy in classification and regression problems. In this paper, we utilize XGBoost to construct a model for credit risk prediction and employ an enhanced sparrow algorithm to optimize its parameters.

3.2.3. Sparrow Search Algorithm

The Sparrow Search Algorithm is a swarm intelligence optimization algorithm inspired by the foraging behavior of sparrows. In SSA, the sparrow population is divided into three roles: discoverers, joiners, and awareness scouts. These roles exhibit different behavioral patterns during the search process and collaborate to find the optimal solution to the problem.

During the population initialization process, a certain number of sparrow individuals are randomly generated, and each individual is assigned an initial position. These positions are randomly selected within the search space. Parameters such as the maximum iteration count, population size, proportion of discoverers, proportion of vigilantes, vigilance value ($R_2$), and safety threshold (ST) are set.

Then, role division is carried out. Based on the fitness value, a portion of sparrows are selected as discoverers, responsible for exploring new search areas. The remaining sparrows act as joiners, following the discoverers to forage. In each iteration, a random subset of sparrows are chosen as guardians, tasked with monitoring the surrounding environment and avoiding local optima.

The discoverer determines the search direction and range based on its energy reserve (fitness value). Discoverers with high energy explore a wider area, while those with low energy search near their current location. The formula for updating the discoverer’s position is as follows:

$$X_{i,j}^{k+1}=\left\{\begin{array}{l}{X}_{i,j}^k\cdot \exp \left({\displaystyle \frac{-i}{\alpha \cdot { \mathrm{iter} }_{\max }}}\right),R_2<ST\hfill \\ X_{i,j}^k+Q\cdot L,R_2⩾ST\hfill \end{array}\right.$$

(17)

where $X_{i,j}^k$ represents the position of the i-th sparrow in the j-th dimension at the k-th iteration; $\alpha$ is a random number belonging to (0, 1]; ${ \mathrm{iter} }_{\max }$ denotes the maximum iteration count; $R_2$ is the warning value, a random number belonging to [0, 1]; ST is the safety threshold, with a value range of [0.5, 1]; Q is a random number satisfying a normal distribution; and L is an l × d matrix with an average element of 1.

The participant updates their location based on the discoverer’s location and their own location, using the following formula:

$$X_{i,j}^{k+1}=\left\{\begin{array}{ll}Q\cdot \exp \left({\displaystyle \frac{X_{\mathrm{worst} }^k-X_{i,j}^k}{i^2}}\right),\hfill & i>N/2\hfill \\ X_{\mathrm{best} }^k+\left|X_{i,j}^k-X_{\mathrm{best} }^k\right|\cdot A^{+}\cdot L,\hfill & i\le N/2\hfill \end{array}\right.$$

(18)

Among them, $X_{\mathrm{worst} }^k$ represents the current global worst position; $X_{\mathrm{best}}^k$ represents the current global best position; and $A^{+}$ is a matrix calculated by $A^T{\left(A{A}^T\right)}^{-1}$, where A is an l × d matrix with randomly assigned elements of 1 or −1.

The guard decides whether to flee the current location based on the current environment (i.e., the fitness value). The update formula is as follows:

$$X_{i,j}^{k+1}=\left\{\begin{array}{ll}{X}_{\mathrm{best} }^k+\beta \cdot \left|X_{i,j}^k-X_{\mathrm{best} }^k\right|,\hfill & f_i>f_{\mathrm{best} }\hfill \\ X_{i,j}^k+K\cdot \left({\displaystyle \frac{\left|X_{i,j}^k-X_{\mathrm{wost} }^k\right|}{\left(f_i-f_{\mathrm{worst} }^k\right)+\epsilon }}\right),\hfill & f_i=f_{\mathrm{best} }\hfill \end{array}\right.$$

(19)

where $X_{\mathrm{best}}^k$ represents the current global optimal position; $\beta$ is the step size control parameter, satisfying a normal distribution with mean 0 and variance 1; K is a random number with a value range of [−1, 1]; $f_i$ is the current fitness value of the sparrow; $f_{best}$ is the current global optimal fitness value; $f_{worst}$ is the current global worst fitness value; and $\epsilon$ is a minimum constant to prevent the denominator from being zero.

3.2.4. Improved Sparrow Search Algorithm

The traditional Sparrow Search Algorithm (SSA) tends to fall into local optima and exhibits low convergence accuracy in the later stages of iteration. To enhance the global optimization capabilities of SSA, researchers have proposed various improvement strategies. This paper combines the Tent chaotic mapping, sine–cosine search strategy, reverse learning strategy, and Cauchy mutation to improve the traditional Sparrow Search Algorithm. The aim is to balance global and local search capabilities, avoid falling into local optima, and thereby enhance the algorithm’s optimization performance.

During the optimization process of the Sparrow Search Algorithm (SSA), randomly initializing the population can lead to a large number of sparrow individuals clustering together, resulting in uneven distribution. To enhance the diversity of the sparrow population and improve the algorithm’s global search capability, this paper introduces the Tent chaotic mapping function into the SSA. The sine–cosine search strategy is employed to update the position of the discoverer. By combining the periodicity and fluctuation of the sine and cosine functions, it strikes a good balance between global and local search, effectively improving the algorithm’s exploration capability and convergence speed. This strategy effectively balances global and local search capabilities, enhancing the algorithm’s optimization efficiency. The reverse learning strategy expands the search domain by generating the reverse solution of the current optimal solution. In each iteration, the current optimal solution is replaced with its reverse solution with a certain probability, helping the algorithm escape local optima and further explore the solution space. Cauchy mutation perturbs the current optimal solution to generate new candidate solutions. The Cauchy distribution has a long tail, allowing for a wide range of perturbation values, which facilitates a broader search within the solution space, further enhancing the algorithm’s global search capability.

Firstly, the positions of the initial population, including discoverers, joiners, and vigilantes, are generated using the Tent map. Parameters such as population size, maximum iteration count, proportion of discoverers, proportion of vigilantes, vigilance value, and safety threshold are set. The Tent map is used to generate the positions of the initial population, ensuring diversity and uniformity in population distribution. The formula for the Tent map is as follows:

$$X_{n+1}=\left\{\begin{array}{ll}u\times X_n,\hfill & 0\le X_n<0.5\hfill \\ u\times \left(1-X_n\right),\hfill & 0.5\le X_n\le 1\hfill \end{array}\right.$$

(20)

where $X_n$ is the value of the n-th iteration, and u is a constant between 0 and 1, usually set to 0.5 to ensure the uniformity and chaotic characteristics of the mapping.

Then, generate the initial population. Choose an initial value $X_0$, iterate through the Tent mapping formula to generate N random numbers, and linearly map these random numbers between the upper and lower bounds of the search space to generate the positions of the initial population. Assuming that the upper and lower bounds of the search space are lb and ub, the initial position $X_i$ is calculated as follows:

$$X_i=\mathrm{lb}+X_n\times (\mathrm{ub}-\mathrm{lb})$$

(21)

Next, calculate the fitness value of each sparrow. Sort the positions of the sparrows based on their fitness values, and determine the individuals with the current optimal and worst fitness.

Update the position of the discoverer using the sine–cosine search strategy. The position update formula for the sine–cosine search strategy is as follows:

$$X_i^{k+1}=X_i^k+A_1\times \cos \left(B_1\right)\times \left(X_{\mathrm{best} }^k-X_i^k\right)+A_2\times \sin \left(B_2\right)\times \left(X_{\mathrm{best} }^k-X_i^k\right)$$

(22)

where $X_i^k$ represents the position of the i-th explorer in the k-th iteration; $X_{best}^k$ represents the position of the i-th explorer in the k-th iteration; $A_1$ and $A_2$ are two random numbers, each drawn from the interval [0, 1]; and $B_1$ and $B_2$ are angle values randomly selected from the interval [0, 2π].

The positions of the joiner and the guarder are updated according to the traditional SSA formula.

To enable individuals to expand their search domain and find the optimal solution, a reverse learning strategy is introduced into the algorithm. Additionally, Cauchy mutation is introduced to perturb and update the optimal solution position, improving the ability to avoid local optima and enhance the algorithm’s ability to obtain the global optimal solution. To enhance the optimization performance of the algorithm, this paper adopts a dynamic selection strategy, alternating the execution of the reverse learning strategy and Cauchy mutation perturbation strategy at a certain probability. The selection probability q determines whether to use the reverse learning strategy or Cauchy mutation to perturb the current optimal solution. The calculation formula for the selection probability q is

$$q=v_1-v_2\times \left({\displaystyle \frac{{ \mathrm{iter} }_{\max }-k}{{ \mathrm{iter} }_{\max }}}\right)$$

(23)

Among them, $v_1$ is set to 0.5, and $v_2$ is set to 0.1.

When the randomly generated number is less than the selection probability q, the reverse learning strategy is used for position updating, with the formula being

$$X_{\mathrm{best} }^{\prime }(k)=\mathrm{ub}+r\times \left(\mathrm{lb}-X_{\mathrm{best} }(k)\right)$$

(24)

Among them, $X_{\mathrm{best} }^{\prime }(k)$ represents the inverse solution of the optimal solution in the k-th generation; ub and lb denote the upper and lower bounds; r is an l × d random number matrix following a uniform distribution between (0, 1); and r is the information exchange control parameter, with the formula being

$$r={\left({ \mathrm{iter} }_{\max }-{\displaystyle \frac{k}{{ \mathrm{iter} }_{\max }}}\right)}^k$$

(25)

where $ite{r}_{\max }$ represents the maximum iteration count, and k denotes the iteration count.

Otherwise, perform Cauchy mutation perturbation, with the expression as follows:

$$X_{i,j}^{k+1}=X_{\mathrm{best} }^k+\mathrm{cauchy}(0,1)\times X_{\mathrm{best} }^k$$

(26)

Among them, $cauchy\left(0,1\right)$ represents the standard Cauchy distribution function.

Use a greedy selection mechanism to update the optimal solution; that is, compare the fitness values of the old and new optimal solutions, and select the one with a better fitness value as the new optimal solution. The update rule is as follows:

$$X_{\mathrm{best} }=\left\{\begin{array}{l}{X}_{\mathrm{best} },f\left(X_{i,j}^{t+1}\right)⩾f\left(X_{\mathrm{best} }\right)\hfill \\ X_{i,j}^{t+1},f\left(X_{i,j}^{t+1}\right)<f\left(X_{\mathrm{best} }\right)\hfill \end{array}\right.$$

(27)

Finally, determine whether the maximum iteration count has been reached. If the maximum iteration count is reached, output the global optimal solution; otherwise, return to the previous step to continue iterating.

Through the aforementioned improvement strategies, the algorithm achieves a better balance between global and local search capabilities, effectively avoiding the trap of local optima, thereby enhancing the algorithm’s optimization performance. When optimizing the parameters of the XGBoost model, it can search for more optimal parameter combinations, further improving the accuracy of credit risk prediction.

3.2.5. XGBoost Model Combined with Improved Sparrow Search Algorithm

The performance and computational cost of the XGBoost model are influenced by multiple parameters. Among them, setting the learning rate too low can slow down the model’s operation, while setting it too high may affect the model’s prediction accuracy. The maximum depth of the tree (max_depth) serves as a tuning parameter to control overfitting in the model. Optimizing the number of iterations (n_estimators) ensures that the model achieves the best iterative effect. The parameter gamma determines the minimum decrease in the loss function required for node splitting, enabling reasonable node splitting.

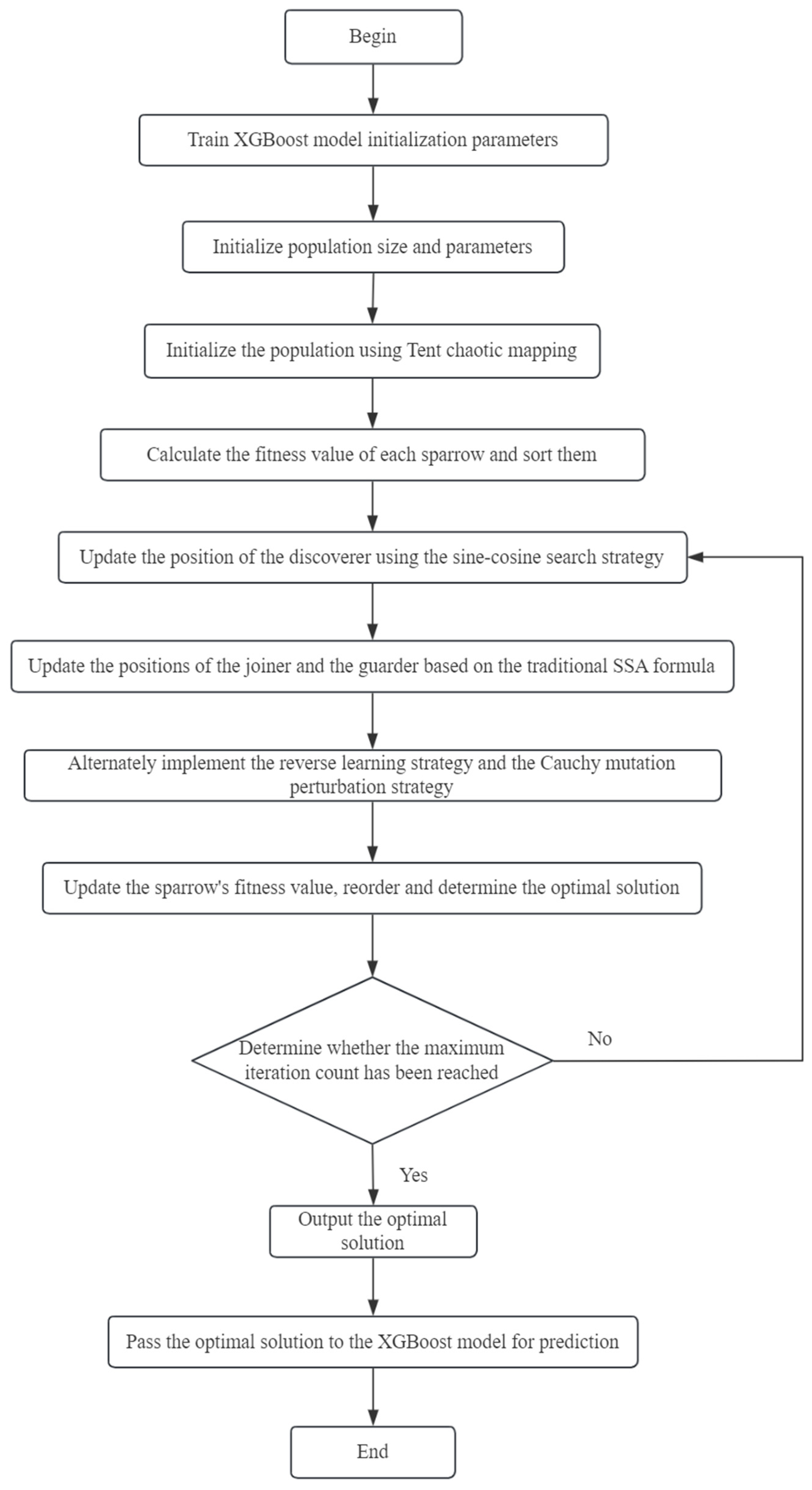
To enhance model performance, this algorithm adjusts these four key parameters. Firstly, the improved Sparrow Search Algorithm is utilized to set the initial parameters of XGBoost, and the position parameters of the sparrows are passed to the model. Subsequently, the fitness value of each individual is calculated, and sorted according to fitness; the position of the sparrows is updated; and the global optimal solution is recorded. When the predetermined number of iterations is reached, the algorithm ends the traversal and outputs the optimal solution, namely the position of the optimal sparrow, which is passed to the XGBoost model as the optimal parameters. Finally, these optimal parameters are used to retrain the XGBoost prediction model. The entire algorithm flow is shown in Figure 2.

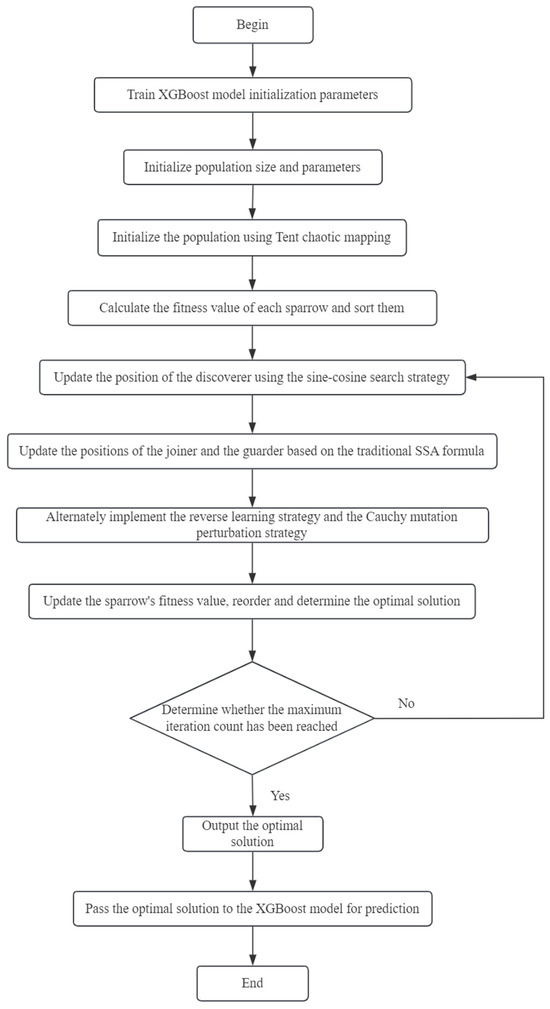
Figure 2. Risk assessment algorithm flowchart.

4. Experiments

4.1. Identification of Credit Risk Factors

4.1.1. Dataset

Lending Club is one of the largest platforms in the United States in terms of total loan volume. The dataset used in the empirical analysis section of this article is a publicly available real-user loan dataset from Lending Club. The dataset is 421 MB in size and contains 887,379 loan records issued from 2007 to 2015. Each loan record has 74 dimensional features, and the Excel file downloaded along with the dataset contains detailed descriptions of the meanings of each field. The data download source is the Kaggle data competition platform.

4.1.2. Data Preprocessing

This dataset encompasses user loan information, economic data, and personal basic information. This section involves data processing, which includes handling missing values, removing irrelevant variables, processing continuous features, handling discrete features, processing time-type features, and handling label features.

(1) Handling missing values

There are a large number of missing values in this dataset. This article deals with variables with missing values in two steps. Firstly, to avoid variables with too many missing values affecting model performance, variables with more than 50% missing values are eliminated, resulting in the deletion of 21 variables in total. Then, for continuous features, missing values are filled using the median. For discrete features, missing values are filled using the mode.

(2) Remove irrelevant variables

In the data preprocessing stage, this paper removed variables that were significantly less correlated with the research content, such as loan ID, member ID, URL, zip code, employee title, zip code, address state, payment plan, title, etc. These variables are either unique identifiers or have significantly lower associations with credit risk, and may even introduce noise or increase the computational complexity of the model. For example, although the zip code may indirectly reflect certain hidden variables such as income level or education level, this paper chooses to directly use individual-level economic and social characteristics to avoid potential biases introduced by proxy variables. By removing variables with significantly lower correlations, the efficiency and interpretability of the model can be improved.

(3) Processing continuous features

For continuous feature values, this paper adopts normalization processing, using the interval scaling method to ensure that the input features have the same magnitude, thereby enabling subsequent algorithms to learn effectively.

(4) Handling discrete features

Due to the presence of text categorical variables such as gender and loan purpose in this dataset, it is necessary to digitize their features by mapping discrete categorical variables to numerical variables. The mapping relationship is shown in Table 1:

Table 1. Map discrete variables to numerical variables.

Variable	The Mapping Relationship Between Discrete Variables and Numerical Variables
grade	A→0, B→1, C→2, D→3, E→4, F→5, G→6
sub_grade	A1→1, A2→2, A3→3, A4→4, A5→5 B1→11, B2→12, B3→13, B4→14, B5→15 C1→21, C2→22, C3→23, C4→24, C5→25 D1→31, D2→32, D3→33, D4→34, D5→35 E1→41, E2→42, E3→43, E4→44, E5→45 F1→51, F2→52, F3→53, F4→54, F5→55 G1→61, G2→62, G3→63, G4→64, G5→65
verification_status	Not Verified→0, Source-Verified→1, Verified→2
purpose	debt_consolidation→0, credit_card→1, home_improvement→2, other→3 major_purchase→4, medical→5, house→6, car→7, vacation→8 small_business→9, moving→10, renewable_energy→11, wedding→12
term	36 months→0, 60 months→1
initial_list_status	w→0, f→1
emp_length	<1 year→0, 1 year→1, 2 years→2, 3 years→3, 4 years→4, 5 years→5 6 years→6, 7 years→7, 8 years→8, 9 years→9, 10+ years→10
home_ownership	MORTGAGE→0, RENT→1, OWN→2, ANY→3, NONE→4
application_type	INDIVIDUAL→0, JOINT→1

(5) Processing of time-type features

Use the to_datetime function in the pandas package to convert the features ‘issue_d’, ‘earliest_cr_line’, ‘last_pymnt_d’, ‘next_pymnt_d’, and ‘last_credit_pull_d’ into datetime types.

(6) Label feature processing

The field used to define good and bad users as labels in the original feature data is loan_status, which contains seven possible values representing seven different loan statuses. For specific explanations, please refer to Table 2.

Table 2. Explanation of loan status fields in Lending Club dataset.

Loan Status	Explanation
Current	The loan has not been closed and is still being repaid normally
Fully Paid	The loan is fully repaid upon maturity or due to early repayment
Charged Off’	Loans for which no further repayments are expected
In Grace Period	The loan is within the grace period, and the overdue time is within 15 days
Late (16–30 days)	The loan is overdue by 16 to 30 days
Late (31–120 days)	The loan is overdue by 31 days to 120 days
Default	The loan is overdue for more than 121 days

In this paper, we define users with loan statuses of ‘Current’ and ‘Fully Paid’ as good users, labeled as 0. Users with loan statuses of ‘In Grace Period’, ‘Late (31–120 days)’, ‘Late (16–30 days)’, ‘Charged Off’, and ‘Default’ are defined as bad users, labeled as 1.

4.1.3. Experimental Environment and Parameter Settings

In terms of the experimental environment, the experimental platform in this paper is a computer with an Intel i9-9880H CPU, 32 GB of memory, and Windows 10 as the operating system. The code runs in Python 3.8, compiled using Jupyter Notebook, and utilizes the scikit-learn machine learning library.

The intelligent recognition algorithm for personal credit risk factors in this article involves parameters such as the upper limit of tree age (life time), the upper limit of forest size (area limit), the global seeding rate (transfer rate), local search control (LSC), and global search control (GSC). Among them, the three parameters of life time, area limit, and transfer rate are used to control the search range and iteration cycle, and are less affected by the dataset. Therefore, the value of life time is fixed at 15, the value of the area limit is fixed at 50, and the value of the transfer rate is fixed at 5%. The remaining parameter setting methods are slightly adjusted, and the parameter values are reset based on the methods in this section.

4.1.4. Evaluation Indicators

To comprehensively evaluate the performance of the improved forest optimization feature selection algorithm, this paper employs three primary evaluation metrics: classification accuracy (CA), dimensionality reduction (DR), and AUC value (Area Under the Curve). Among them, classification accuracy and AUC value are used to assess the algorithm’s classification capabilities, while dimensionality reduction is used to evaluate its dimensionality reduction capabilities.

(1) Classification accuracy: Classification accuracy is a key metric for evaluating the performance of the optimal feature subset on a classifier. It reflects the accuracy of the feature subset selected by the algorithm for classification tasks. The specific definition of classification accuracy is as follows:

$$CA={\displaystyle \frac{\mathrm{CC}}{\mathrm{AC}}}$$

(28)

Among them, CC (Correct Classification) represents the number of instances that can be correctly classified, while AC (All Classification) represents the total number of instances involved in classification. A higher classification accuracy indicates that the feature subset selected by the algorithm performs better in the classification task and can more accurately identify instances of different categories.

(2) Dimensionality reduction rate: The dimensionality reduction rate refers to the proportion of reduction in the number of original features during feature selection or dimensionality reduction. It reflects the algorithm’s ability to effectively reduce the number of features while maintaining classification performance. The specific definition of the dimensionality reduction rate is as follows:

$$DR=1-\left({\displaystyle \frac{\mathrm{SF}}{\mathrm{AF}}}\right)$$

(29)

Among them, SF (selected features) represents the number of selected features in the feature set, while AF (all features) denotes the total number of features in the dataset, which is n. A higher dimensionality reduction rate indicates that the algorithm can select fewer features while maintaining high classification accuracy, thereby achieving more effective feature dimensionality reduction.

(3) AUC value (Area Under Curve): The True Positive Rate (TPR) represents the proportion of true positives that are correctly predicted as positive. The False Positive Rate (FPR) represents the proportion of false positives that are incorrectly predicted as positive. The calculation formula is as follows:

$$TPR={\displaystyle \frac{TP}{TP+FN}}$$

(30)

$$FPR={\displaystyle \frac{FP}{FP+TN}}=1-TPR$$

(31)

The ROC curve can be plotted with FPR as the horizontal axis and TPR as the vertical axis of the coordinate system. The area enclosed by the ROC curve and the coordinate axes is the AUC value. The AUC value represents the strength of the classification performance of the current machine learning algorithm. A higher AUC value indicates that the algorithm’s classification performance is more stable at different thresholds, and its overall classification ability is stronger.

(4) Comprehensive weighted evaluation: In practical business applications, people will comprehensively weigh the benefits brought by classification ability and dimensionality reduction ability. Therefore, in order to unify the evaluation criteria and further verify the effectiveness of the proposed algorithm, this paper adopts comprehensive weighted evaluation to evaluate the effectiveness of the algorithm in practical applications. The definition of comprehensive weighted evaluation is as follows:

$$\mathrm{Fitness} =CA+0.01\times DR$$

(32)

4.1.5. Result Analysis

By utilizing an intelligent identification model for personal credit risk factors, this paper has screened out 19 key features from the original dataset. These features play a crucial role in enhancing the predictive power of the model. For example, if there is a longer employment period (emp_ length), it may mean that the borrower has a more stable source of income to repay the debt. The feature of the last payment amount (last_pymnt_mamnt) reveals the total amount of the last payment received, which helps analyze the borrower’s repayment behavior and habits, and understand whether they have repaid on time and in full, and is crucial for evaluating their credit status. The debt-to-income ratio (DTI) is calculated by dividing the borrower’s monthly total debt payments by their self-reported monthly income. A high DTI indicates that the borrower has a heavy debt burden, which may increase their risk of default. Considering these key factors can provide financial practitioners with a more comprehensive perspective to evaluate the overall credit risk of borrowers and enhance their understanding of borrowers’ debt repayment ability. Compared to the full feature set, the filtered feature set retains only the most predictive features, significantly reducing the dimensionality of the data (with a dimensionality reduction rate of approximately 57.78%). This not only simplifies the model’s complexity but also enhances computational efficiency.

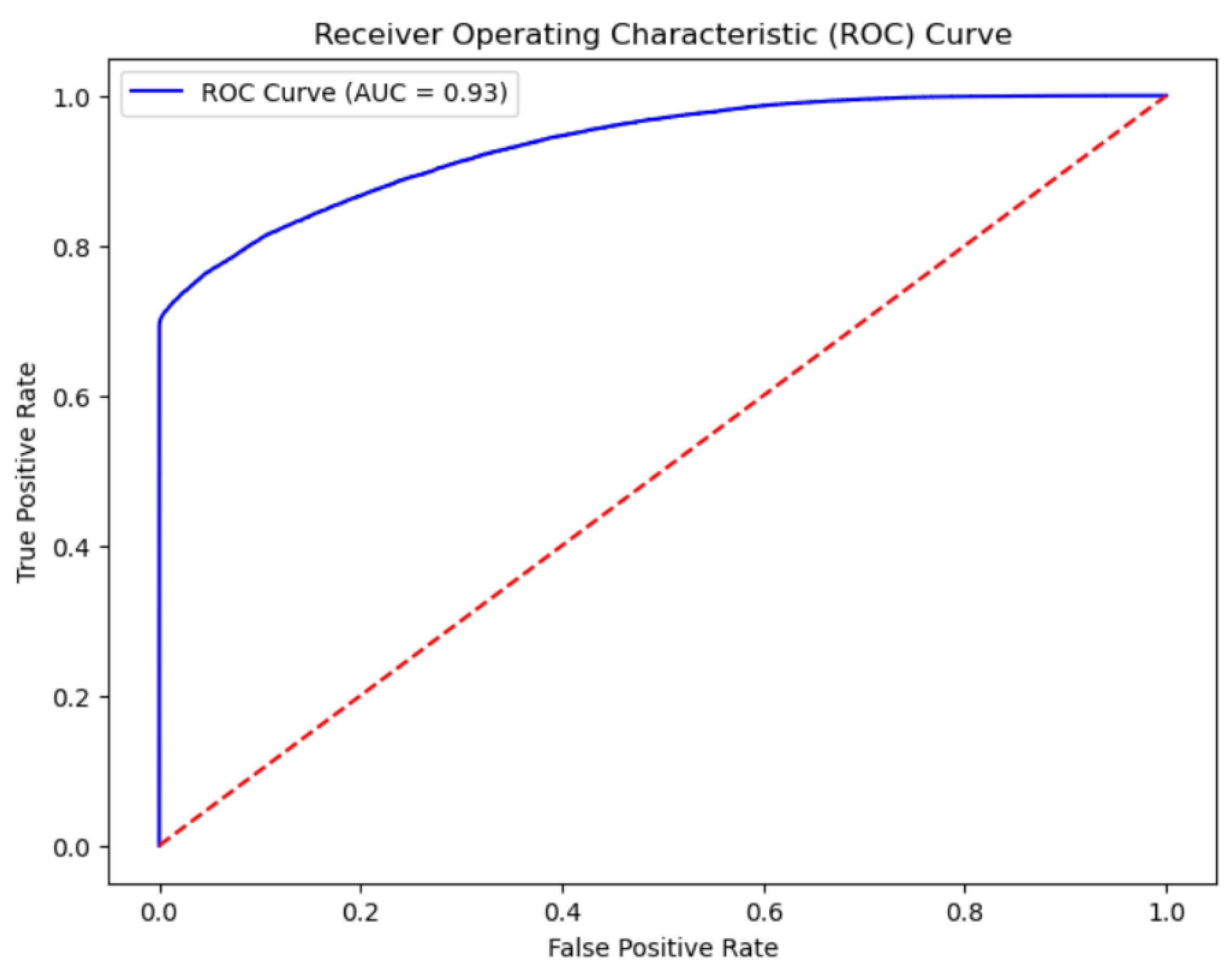
Using key feature data screened out by the intelligent identification model for personal credit risk factors, combined with the XGBoost model for training and testing, this paper obtained the following results: the model’s accuracy reached 97.71%, and the AUC value was 0.93. These data indicate that the model exhibits excellent performance in identifying credit risks, accurately distinguishing between loan default and non-default situations. Furthermore, the high AUC value suggests that the model possesses strong discriminative ability, maintaining good predictive stability even under different threshold settings.

The fitness value, calculated according to the formula, is 0.983. This result indicates that the proposed algorithm exhibits excellent comprehensive performance in practical applications, maintaining high classification capability while achieving certain effectiveness in dimensionality reduction. A fitness value close to 1 signifies that the algorithm has reached a good level in balancing classification accuracy and dimensionality reduction effect, further verifying the effectiveness and practicality of the proposed algorithm.

Finally, by plotting the ROC curve, we visually demonstrate the performance of the model at different thresholds, as shown in Figure 3. The ROC curve closely approaches the upper left corner, and the AUC value is as high as 0.93, proving the superior performance of the model in credit risk identification tasks and the necessity of using an intelligent identification model for personal credit risk factors for feature selection. This result not only provides strong support for credit institutions in identifying personal credit risk factors but also lays a solid foundation for our subsequent further evaluation of personal credit risk.

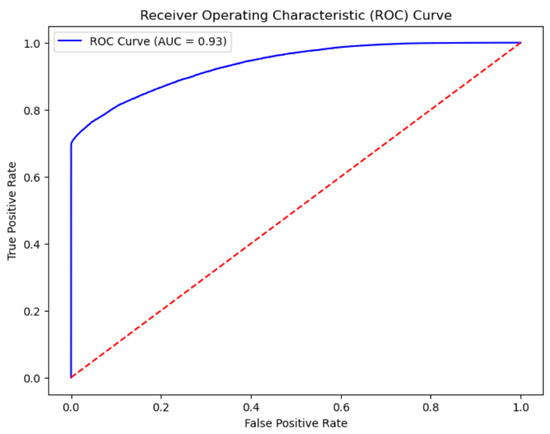
Figure 3. ROC curve.

In addition, this paper selects Recursive Feature Elimination (RFE), random forest, PCA, and Isomap as comparative algorithms for comparative experiments with the HSFSFOA model. The key feature data selected by each feature selection model are utilized, and combined with the XGBoost model for training and testing. The experiments compare the classification accuracy and AUC values of HSFSFOA with those of four other feature selection algorithms on the Lending Club dataset, highlighting the effectiveness of feature selection methods. Detailed experimental data are shown in Table 3.

Table 3. Comparison of evaluation indexes of each model.

	Classification Accuracy	AUC Values
RFE	88.56%	0.89
Random Forest	90.32%	0.90
PCA	86.78%	0.88
Isomap	93.45%	0.92
HSFSFOA	97.71%	0.93

According to the evaluation metrics for each model listed in the table, the HSFSFOA model demonstrates strong performance in both classification accuracy and AUC value. The classification accuracy of the HSFSFOA model reaches as high as 97.71%, surpassing other comparative algorithms, highlighting the model’s robust ability to identify key features in datasets and perform accurate classification based on them. Simultaneously, its AUC value attains 0.93, further validating the model’s high robustness and generalization capability when dealing with complex datasets. This establishes a solid foundation for its widespread application in similar datasets and feature selection tasks.

4.2. Credit Risk Assessment

4.2.1. Dataset

This paper establishes an intelligent identification model for personal credit risk factors in the context of big data, conducts in-depth analysis and screening of 74 dimensional features, and identifies a series of features that have a significant impact on credit risk prediction. Below, we will use these screened important feature data to train an intelligent evaluation model for personal credit risk in the context of big data, and predict and evaluate personal credit risk.

4.2.2. Parameter Settings

The parameter settings for the personal credit risk assessment model are as follows: set the population size (pop_size) to 30; set the maximum iteration count (max_iter) to 100; set the discoverer ratio (discoverer_ratio) to 0.2; set the watcher ratio (watcher_ratio) to 0.1; set the safety threshold (ST) to 0.8; and set the weights (w1, w2) to 0.5 and 0.1. The parameters of the XGBoost model are optimized through an improved Sparrow Search Algorithm, including the learning rate (learning_rate), maximum depth (max_depth), number of estimators (n_estimators), and gamma value (gamma).

4.2.3. Evaluation Indicators

In addition to the evaluation metrics mentioned above, this section will also evaluate the model using precision and recall. In the case of an imbalanced number of sample categories, it is unreasonable to solely use accuracy as a measurement metric. Suppose in a credit dataset, the number of credit defaulters accounts for 1% of the total number of credit borrowers. During the prediction process, if the algorithm simply predicts all predicted data as non-defaulting, its credit risk prediction accuracy will be as high as 99%, which is obviously unreasonable. Therefore, recall and precision are introduced to evaluate the performance of the algorithm. Recall represents the proportion of samples correctly predicted as positive to the total number of positive samples, while precision represents the proportion of samples correctly predicted as positive to the total number of samples predicted as positive. The closer the values of recall and precision are to 1, the better the classification performance of the machine learning algorithm. The calculation formula is as follows:

$$\mathrm{Recall} ={\displaystyle \frac{TP}{TP+FN}}$$

(33)

$$\mathrm{Precision} ={\displaystyle \frac{TP}{TP+FP}}$$

(34)

4.2.4. Result Analysis

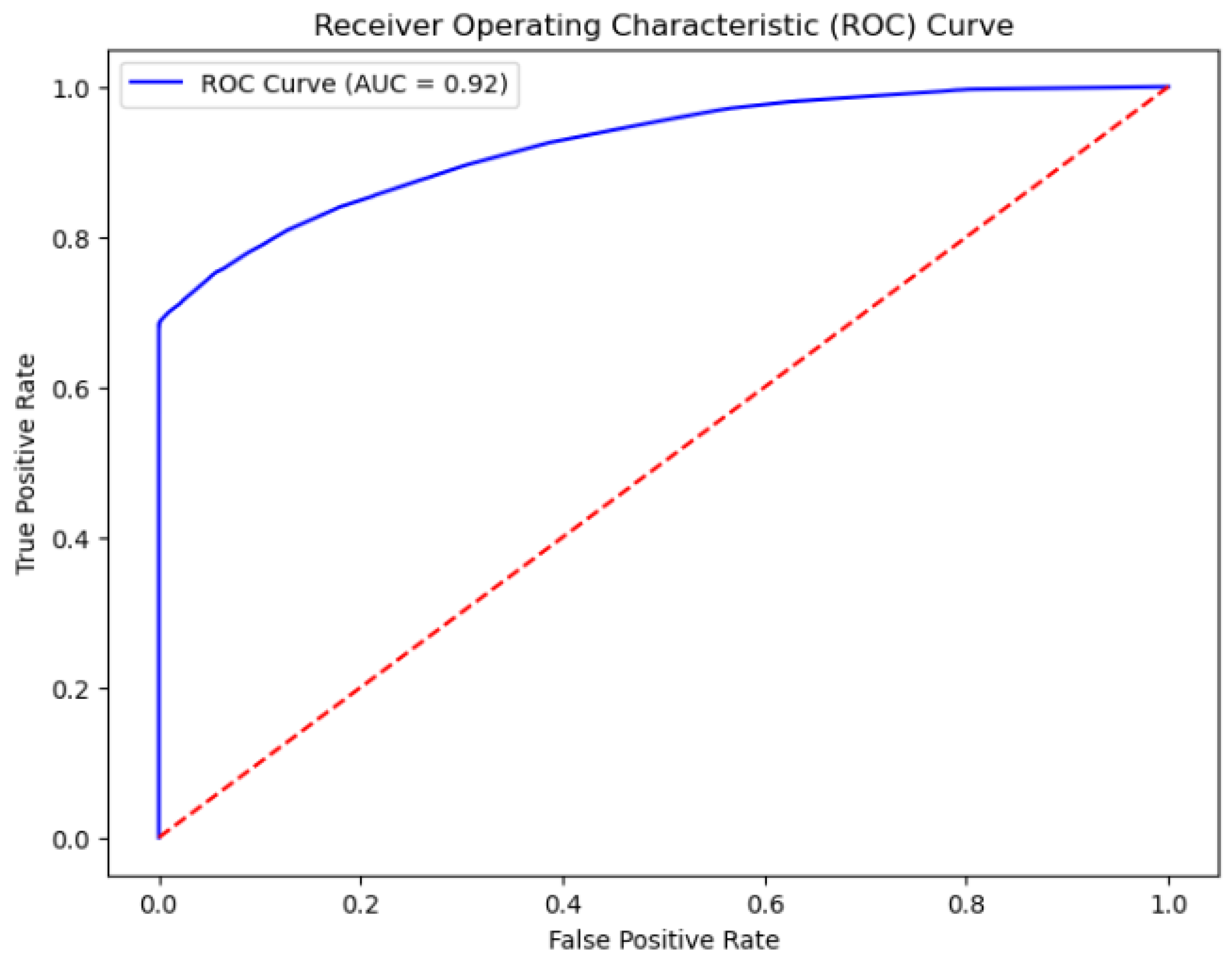
In order to improve the reliability of model evaluation, we adopted a repeated K-fold cross-validation method. Specifically, in the updated experiment, we divided the dataset into five subsets using RepeatedKFold and performed three repetitions on this basis to ensure the stability of the evaluation. At each iteration, one subset of the dataset is used as the test set, while the remaining four subsets are used to train the model. Through this approach, each sample has the opportunity to be a part of the test data, making the evaluation more comprehensive and accurate. After completing all segmentation and repetition, we calculated and output the average accuracy and average AUC values for all iterations to comprehensively evaluate the overall performance of the model. Generally, the AUC value ranges from 0.5 to 1. When the AUC value exceeds 0.75, it indicates that the model is acceptable. AUC values closer to 1.0 signify higher fitting performance of the model. The ROC curve is illustrated in Figure 4. From the figure, it is evident that the AUC of the XGBoost model combined with the improved Sparrow Search Algorithm is 0.923, which is very close to 1. This demonstrates that the model exhibits good performance in assessing credit risk, implying its significant ability to interpret customer performance status. The contributions of variables are fully considered, and the model possesses strong predictive capabilities.

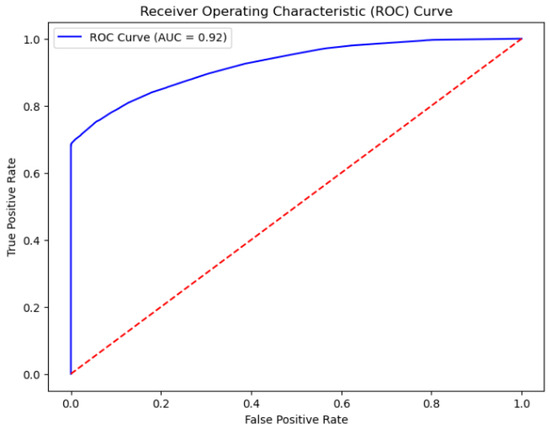
Figure 4. ROC curve.

To comprehensively and deeply evaluate the performance of the XGBoost model combined with an improved Sparrow Search Algorithm in personal credit risk assessment, this paper selects four commonly used machine learning classification algorithms as benchmarks for comparison, namely logistic regression (Logistic Regression), random forest (Random Forest), support vector machine (Support Vector Machine, SVM), K-nearest neighbors (K-Nearest Neighbors, KNNs), Light Gradient Boosting Machine (LightGBM), and Categorical Boosting (CatBoost). The resulting model results are shown in Table 4.

Table 4. Comparison of evaluation indexes of each model.

	Accuracy	Recall	Precision	F1 Score	AUC Value
Logistic regression	0.878	0.650	0.912	0.759	0.857
Random forest	0.898	0.668	0.929	0.776	0.869
Support vector machine	0.889	0.666	0.917	0.771	0.858
K-nearest neighbor	0.872	0.643	0.899	0.749	0.840
XGBoost	0.923	0.676	0.954	0.792	0.878
LightGBM	0.928	0.683	0.958	0.797	0.885
CatBoost	0.931	0.683	0.960	0.799	0.889
XGBoost model combined with improved Sparrow Search Algorithm	0.953	0.685	0.964	0.801	0.921

The XGBoost model combined with the improved Sparrow Search Algorithm achieves an accuracy rate of 0.953, indicating that the model has high accuracy in distinguishing between high and low credit risks, and can provide precise risk assessments for most credit applications, thereby helping financial institutions effectively control credit risks and improve decision-making efficiency. In terms of precision, the model reaches 0.964, meaning that when the model predicts that a credit application is high-risk, the probability that the application is actually risky is extremely high, and it is almost certain to be a genuine risk case. Such high precision not only reduces potential losses caused by misjudgments but also enhances the trust of financial institutions in the model’s prediction results. However, the recall rate of the model is 0.685, which is also at a relatively high level, but compared to the accuracy and precision rates, there is still some room for improvement. The recall rate reflects the model’s ability to identify all actual high-risk cases. A lower recall rate may mean that some high-risk cases are missed by the model, which may pose certain risks in practical applications. To comprehensively evaluate the performance of the model, the F1 score metric is introduced. The F1 score is the harmonic mean of accuracy and recall rates, which can comprehensively reflect the model’s ability to balance the two. The F1 score of this model reaches 0.801, indicating that while maintaining high accuracy and precision rates, the model also achieves relatively good performance in terms of the recall rate, demonstrating excellent overall performance.

Meanwhile, comparing the evaluation data of other models in Table 4, it can be seen that the XGBoost model combined with the improved Sparrow Search Algorithm outperforms other models in all evaluation metrics, indicating that the risk assessment effect of the XGBoost model combined with the improved Sparrow Search Algorithm is superior to other models, which can effectively assist financial institutions in credit risk assessment to a certain extent, improving the scientificity and accuracy of decision making. Furthermore, the XGBoost model combined with the improved Sparrow Search Algorithm is superior to the classic XGBoost model, proving that the model with optimized hyperparameters can better identify the changing trends of specific data, thereby producing better prediction results.

5. Construction of Evaluation Model

This paper constructs an intelligent assessment model for personal credit risk under the background of big data, providing new methodological support for the intelligent assessment of personal credit risk. This model is based on the forest optimization feature selection algorithm, combined with initialization based on chi-square verification, adaptive global seeding, and greedy search strategy, which can automatically identify key risk factors accurately from high-dimensional data. It has made up for the shortcomings of low efficiency and easy omission in traditional manual selection methods, and improved the accuracy of risk factor identification. Then, the model takes personal credit risk factors as input features and uses the XGBoost algorithm to evaluate the customer’s credit risk level. Improve the traditional Sparrow Search Algorithm by using Tent chaotic mapping, sine cosine search, reverse learning, and Cauchy mutation strategy to enhance the optimization performance of algorithm parameters. This model can evaluate personal credit risk and predict customer default probability, making up for the shortcomings of traditional evaluation methods in data processing breadth and risk assessment accuracy, and improving the accuracy of customer default probability prediction.

Based on all the work of this paper, we can draw the following conclusions:

(1) Constructing an intelligent identification model for personal credit risk factors in the context of big data is an effective way to enhance the efficiency of credit risk management. By utilizing machine learning technology to automatically identify potential risk factors, the accuracy and efficiency of risk identification have been significantly improved. The model can extract key features from massive data, providing a solid data foundation and support for subsequent risk assessment and decision making. The establishment of an intelligent identification model not only reduces the time and cost of manual review but also enhances the scientific and systematic nature of risk management.

(2) Developing an intelligent assessment model for personal credit risk in the context of big data can significantly enhance the comprehensiveness and scientific nature of risk assessment. By quantitatively evaluating credit risk and incorporating various advanced algorithms and technologies, such as XGBoost and an improved Sparrow Search Algorithm, this model ensures the objectivity and accuracy of assessment results. It provides a more reliable and comprehensive basis for credit institutions’ risk management decisions, helping institutions better understand and control credit risk, thereby optimizing resource allocation and reducing the non-performing loan ratio.

The method proposed in this paper has broad potential for real-world applications, especially in financial institutions such as banks, which can effectively address the limitations of traditional risk assessment models in processing high-dimensional data and improve the accuracy and efficiency of credit assessment. Traditional credit risk assessment relies on limited historical data and manual experience judgment, making it difficult to comprehensively capture the subtle factors that affect credit risk. Financial institutions can use the method proposed in this paper to mine high-dimensional data, accurately identify key features that affect personal credit risk, and lay a solid foundation for subsequent risk assessment. Financial institutions can use intelligent risk assessment models based on big data to quickly process and analyze complex datasets. This efficiency not only shortens the loan approval cycle and improves user experience, but also provides personalized risk assessment results based on each applicant’s specific circumstances, such as credit history, income level, consumption behavior, etc. This not only enhances the accuracy of risk assessment, but also promotes the diversification and customization of credit products, better meeting the needs of different customer groups. However, potential ethical and technological challenges also need to be considered in practical applications. For example, algorithms may inherit unfair decision-making patterns due to historical biases in training data, which in turn can affect the credit evaluation results of certain groups. To ensure the fairness and transparency of the model, financial institutions should avoid using sensitive features when applying it and strengthen the monitoring and interpretation of the model’s decision-making process.

Although this study has made some progress in the field of personal credit risk assessment, there are still some limitations that need further exploration and improvement. First is the deepening and integration of theoretical frameworks. With the continuous advancement of technology and the accumulation of practical experience, the theoretical system of personal credit risk management in the future will be further deepened and refined. It will further integrate interdisciplinary perspectives such as behavioral economics, psychology, sociology, etc., to comprehensively understand and predict borrower behavior patterns and risk changes. Secondly, multimodal data fusion is an important direction for future research. This article is mainly based on traditional structured data, and in the future, we can further explore the fusion of various unstructured data such as text, images, and videos to more comprehensively capture customers’ credit status and behavioral characteristics. Third is further optimizing the performance of the model. By combining the advantages of deep learning and reinforcement learning, more complex and efficient models can be developed in the future to cope with more dynamic and complex credit risk environments. Fourthly, this article did not directly consider the impact of macro factors on individual credit risk. Future research can explore how to combine macro factors with individual characteristics to construct more comprehensive credit risk assessment models. In addition, there may be complex nonlinear relationships between macro factors and personal characteristics, which provides new research directions for the application of machine learning methods.