Simulation Evaluation and Case Study Verification of Equipment System of Systems Support Effectiveness
Abstract
1. Introduction
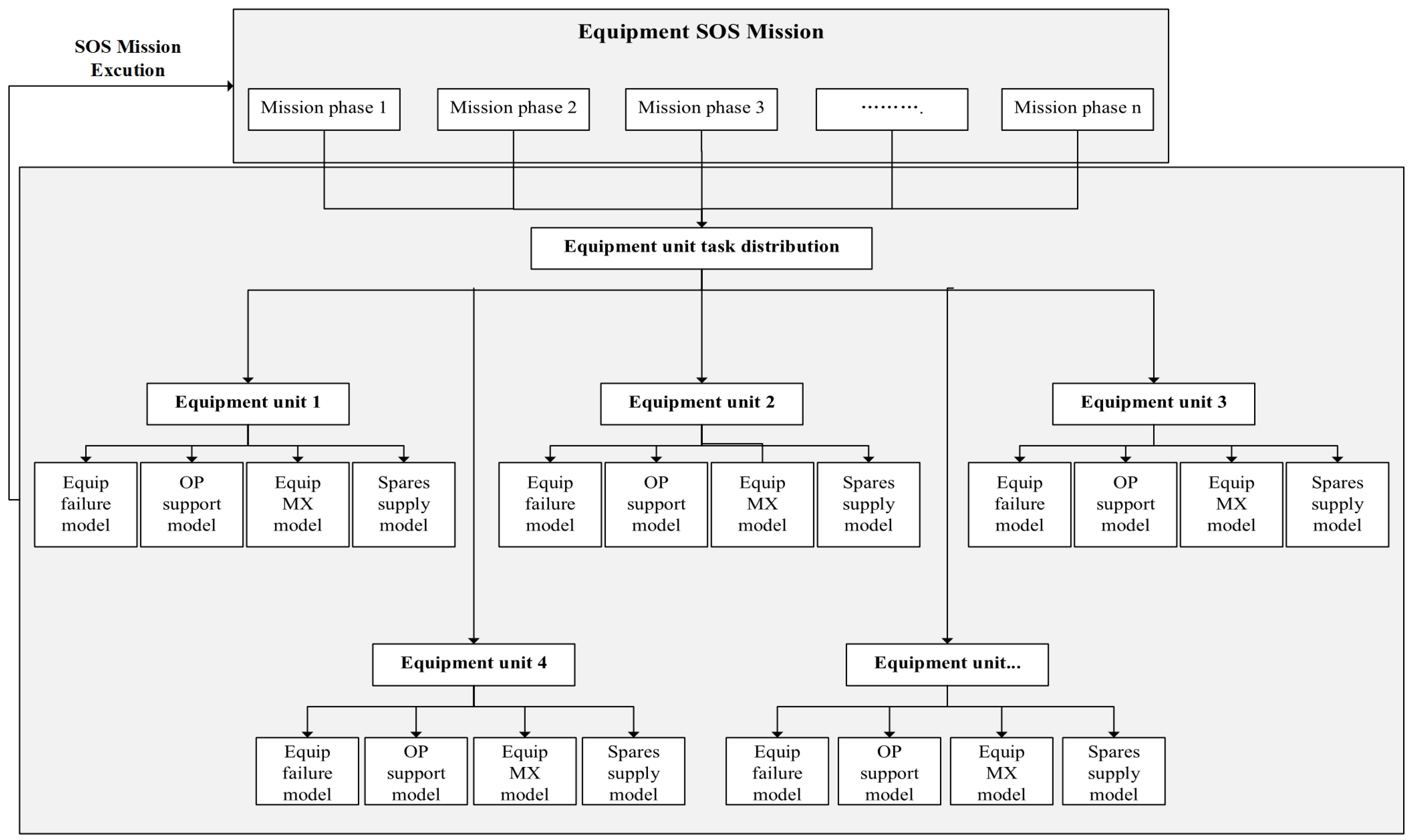
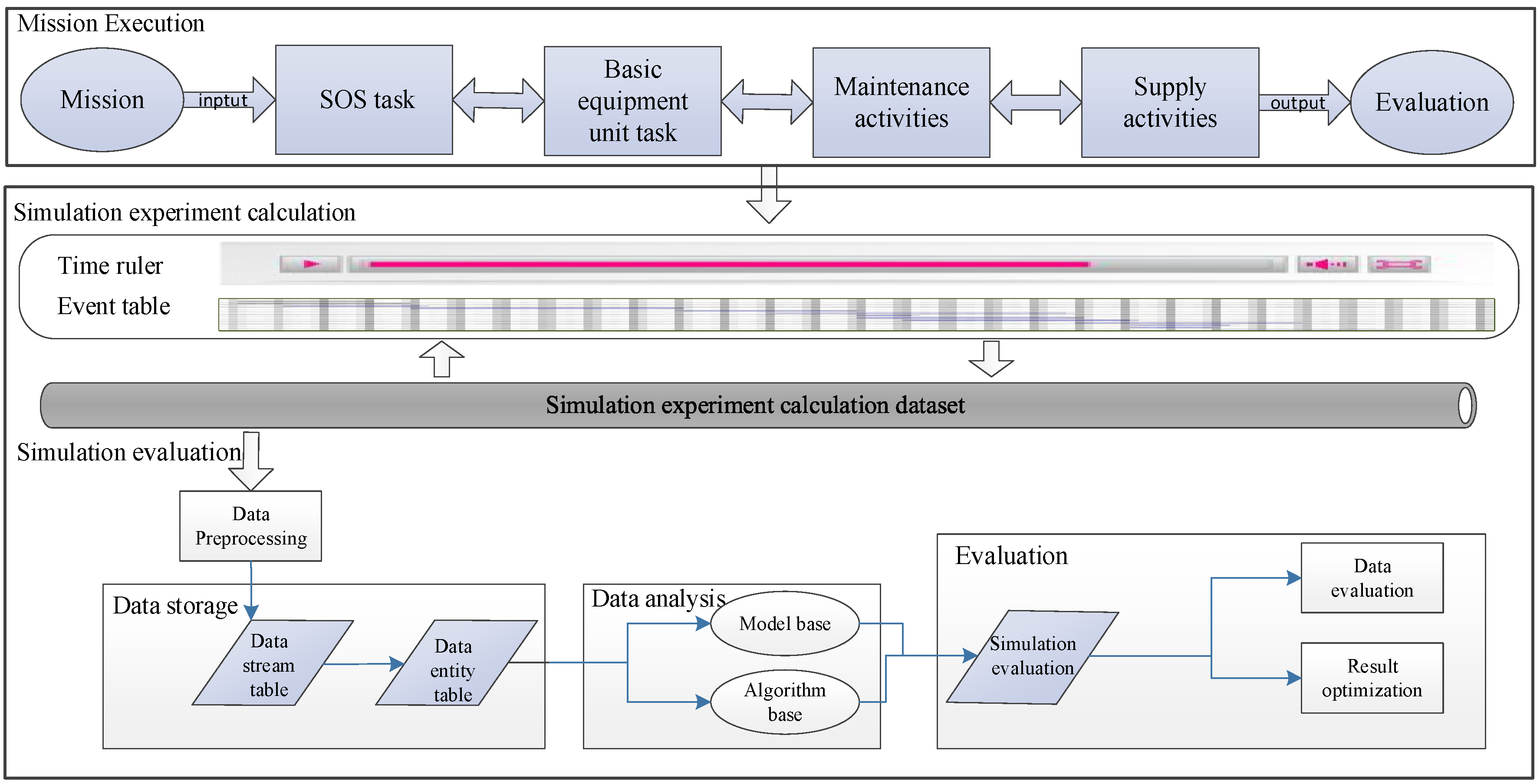
2. Support Task Generation Modeling
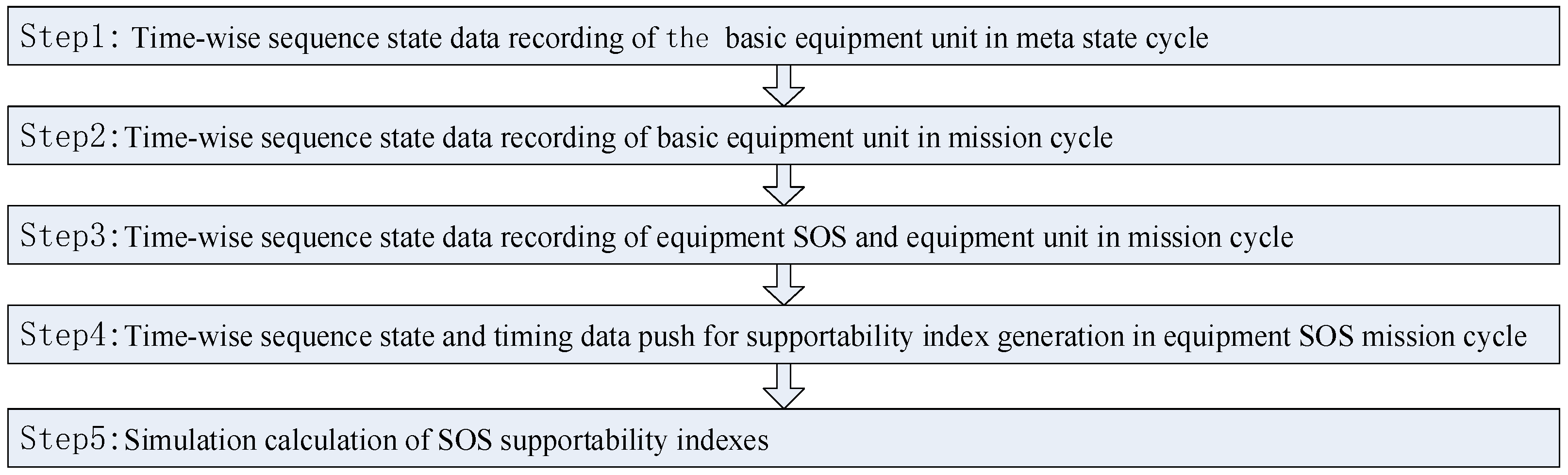
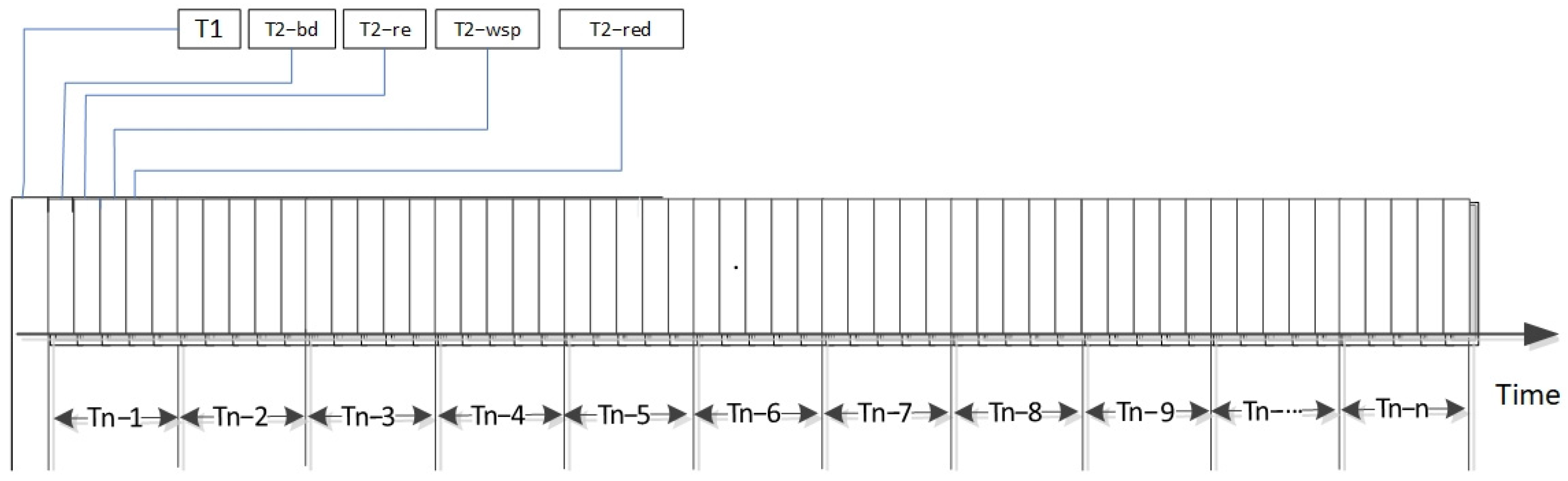
3. Support Effectiveness Evaluation Model
4. Case Study
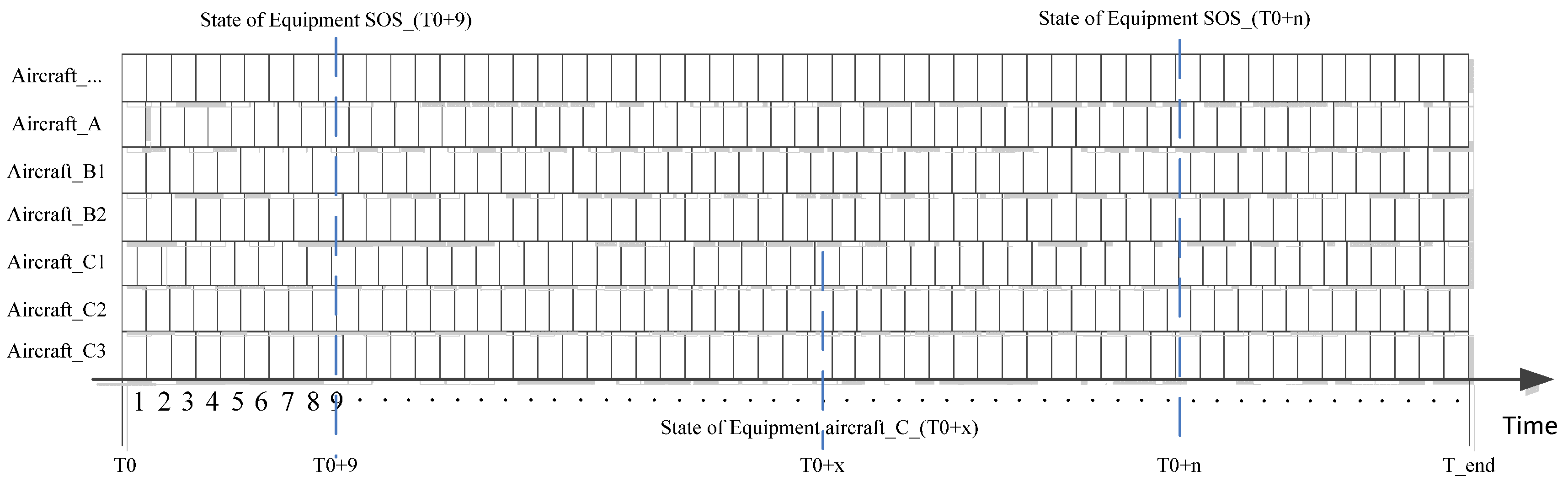
4.1. Mission Background
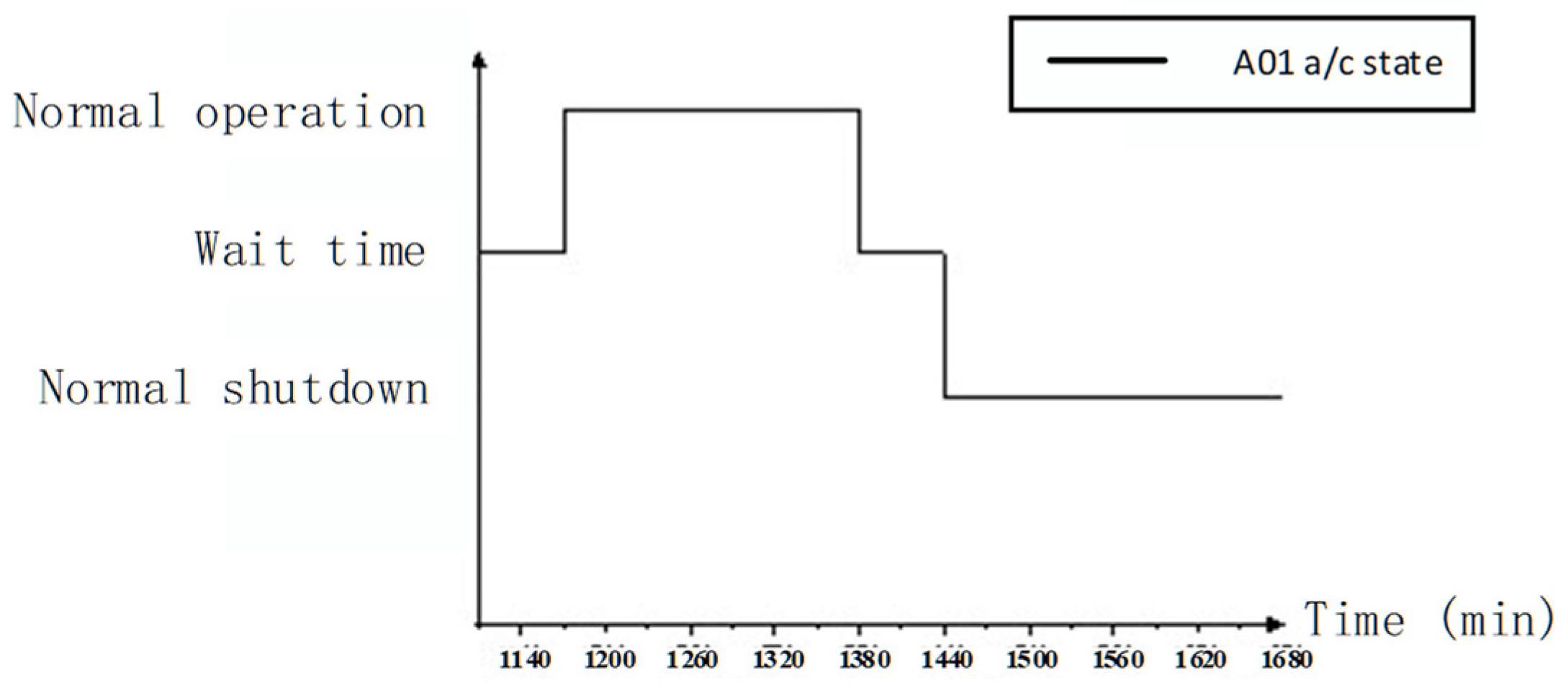
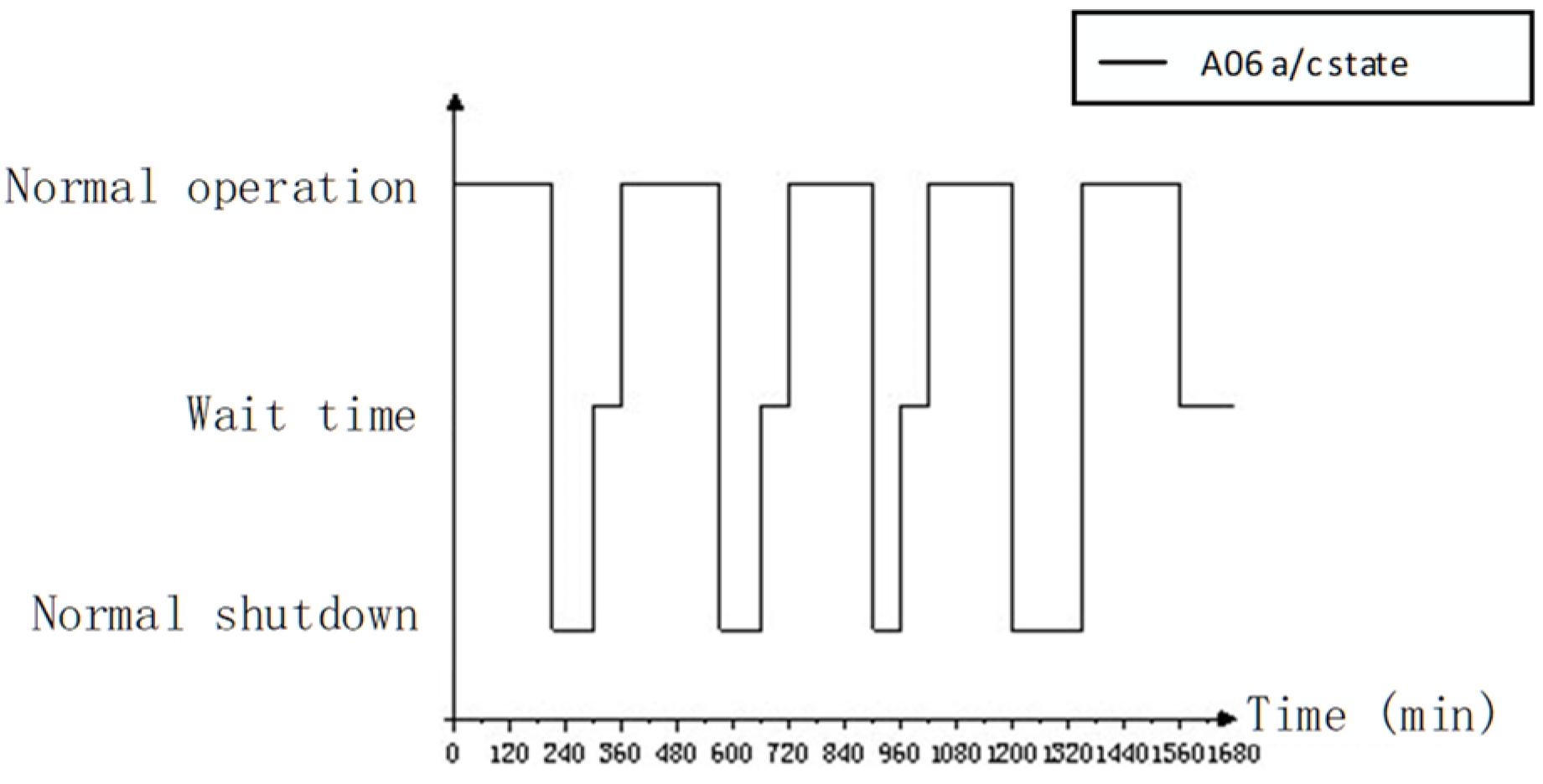
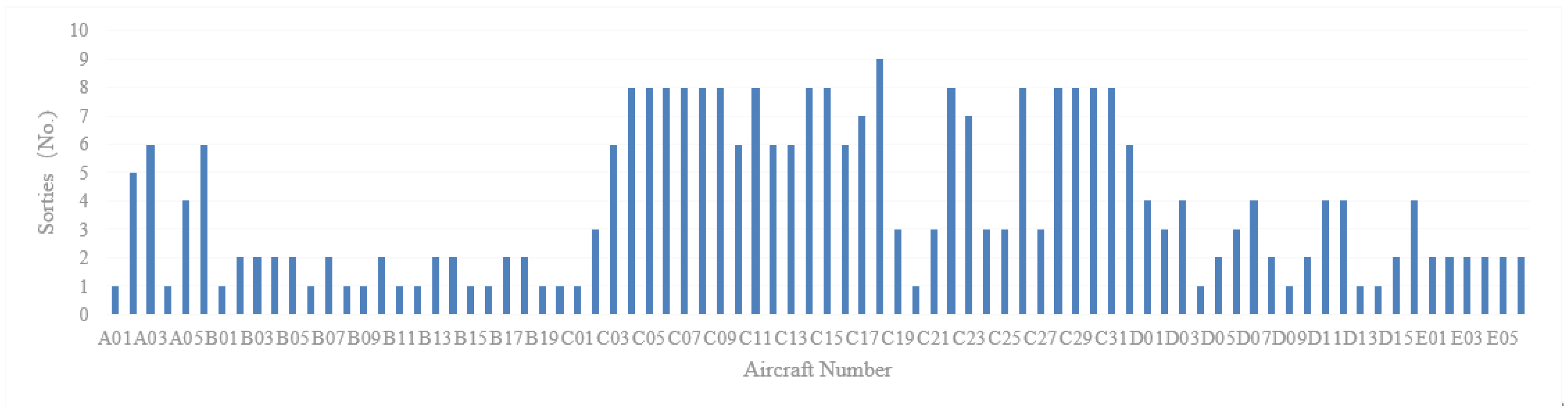
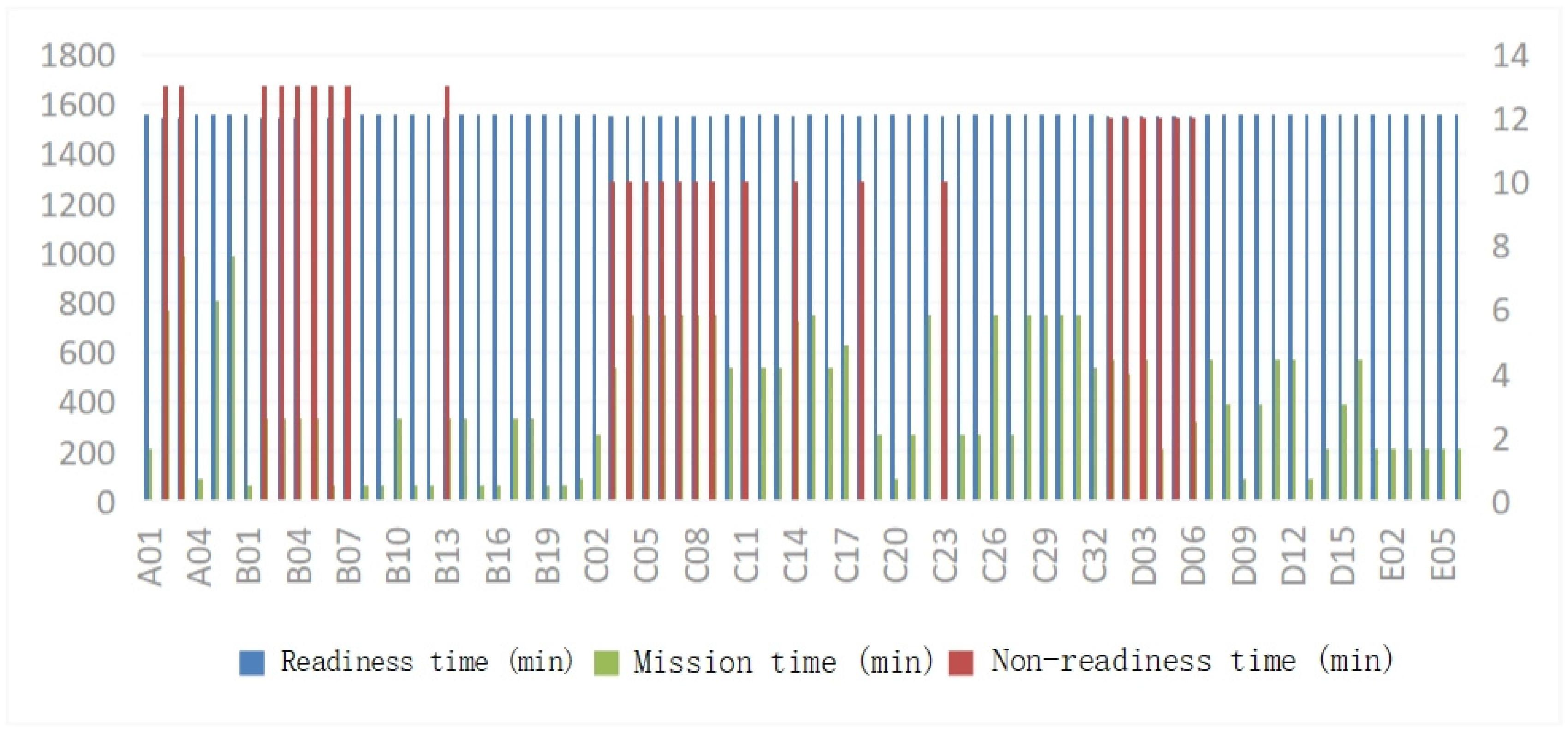
4.2. Simulation Result Analysis
4.3. Experimental Comparison and Verification
- (a)
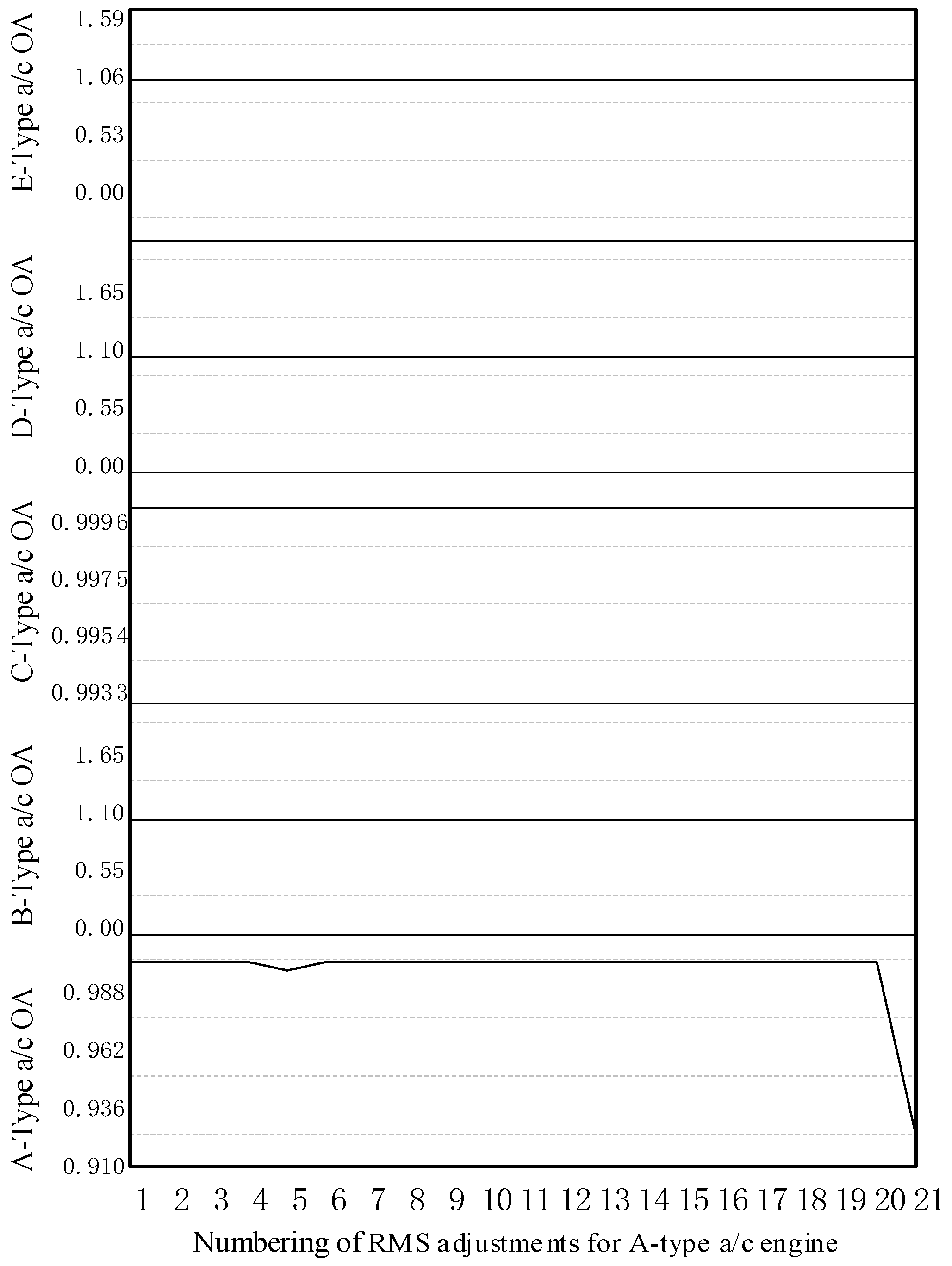
- As the mean time between failures (MTBF) for each aircraft type increased by a step size of 20%, the MSR for aircraft types A, B, C, D, and E within the system support index increased by 9.6%, 8.3%, 10.4%, 20.8%, and 2.1%, respectively, indicating an upward trend. Conversely, as the mean time to repair (MTTR) for each model increased by a step size of 20%, the MSR for aircraft types A, B, C, D, and E in the system support index decreased by 8.3%, 10.4%, 12.5%, 18.8%, and 14.6%, respectively, indicating a downward trend.
- (b)
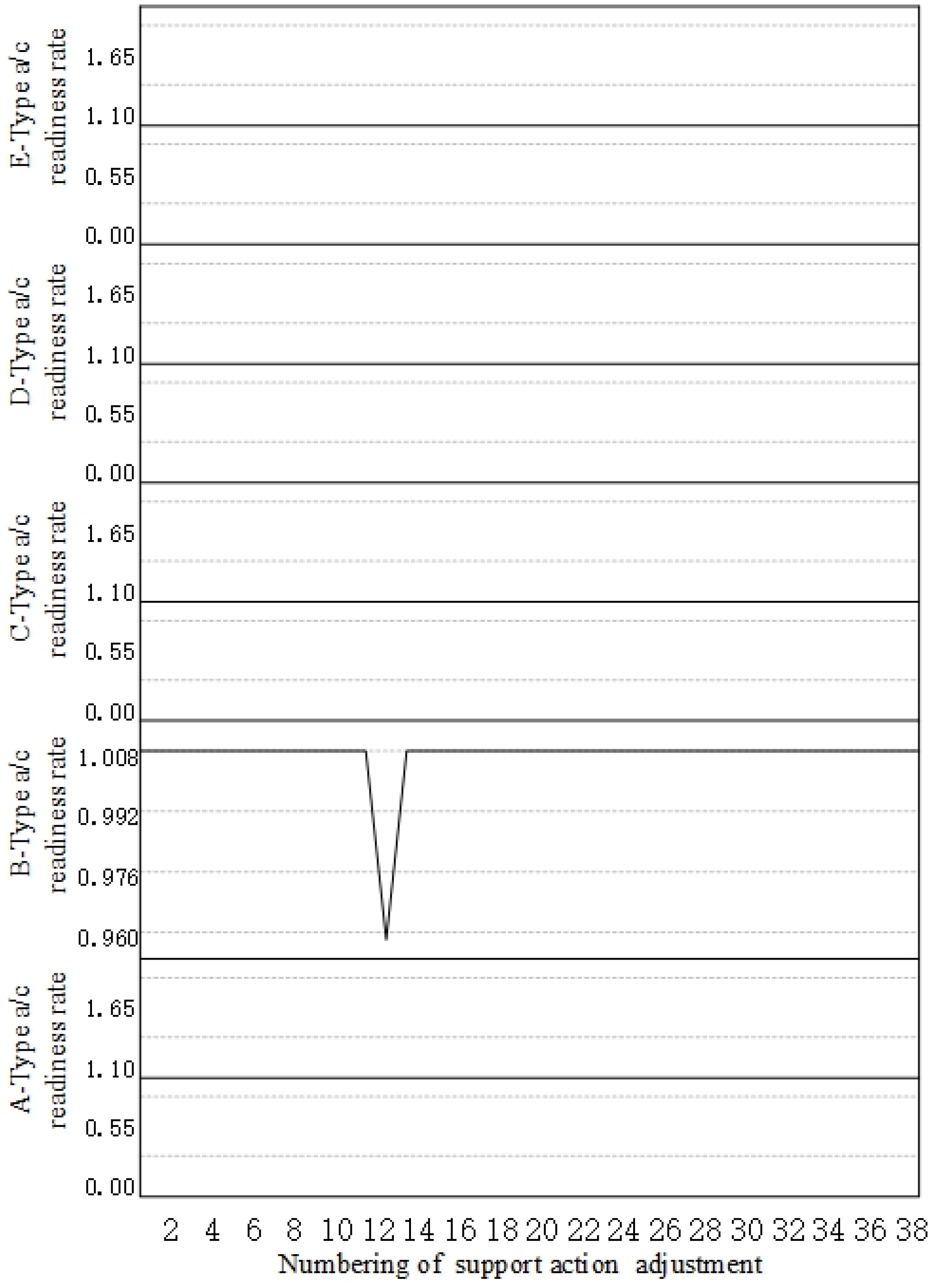
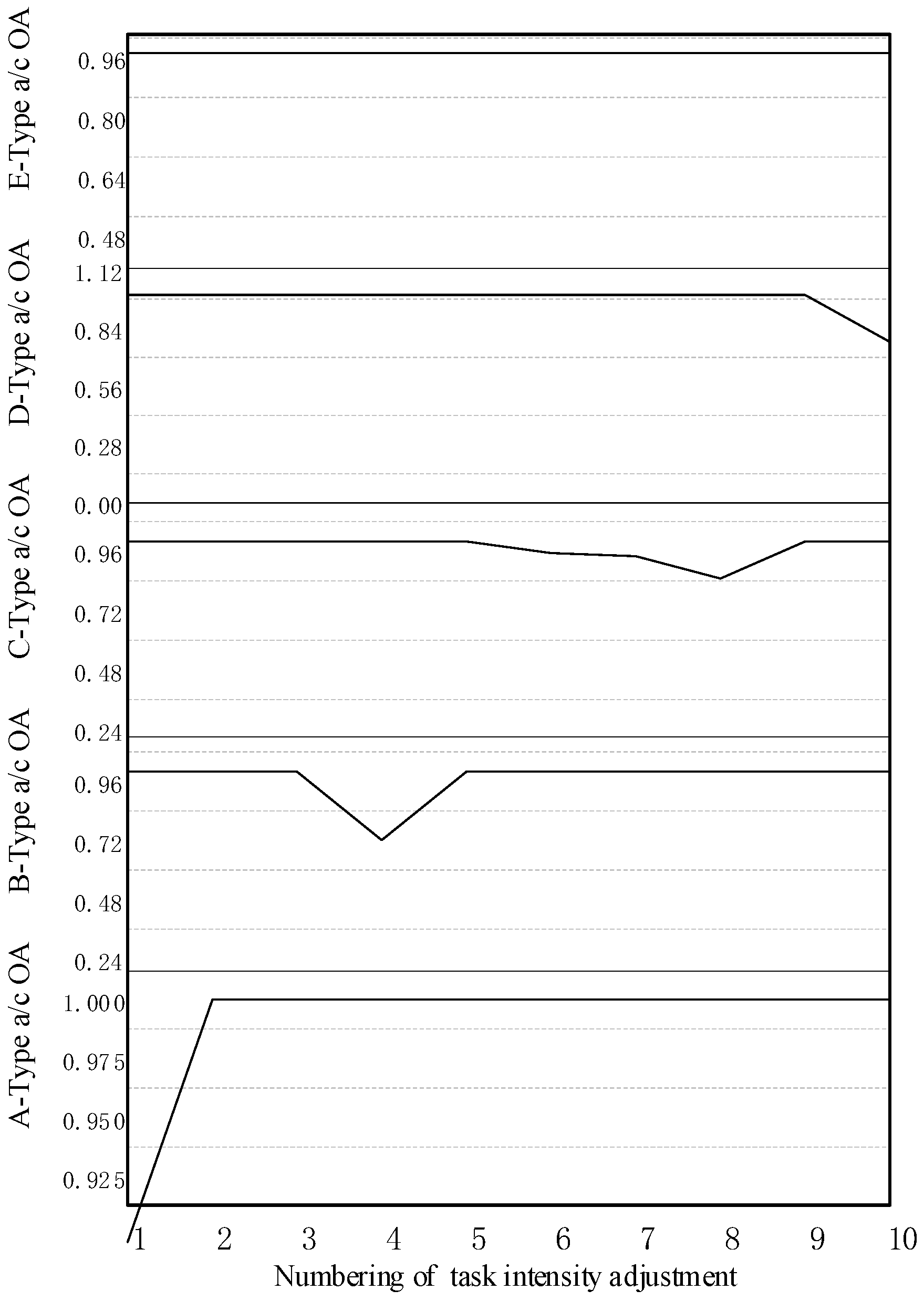
- As the mission intensity for aircraft types A, B, C, D, and E decreased by a step size of 20%, the MSR of the equipment system support index increased by 25.8%, 6.9%, 16.7%, 35.4%, and 6.3%, respectively, indicating an upward trend.
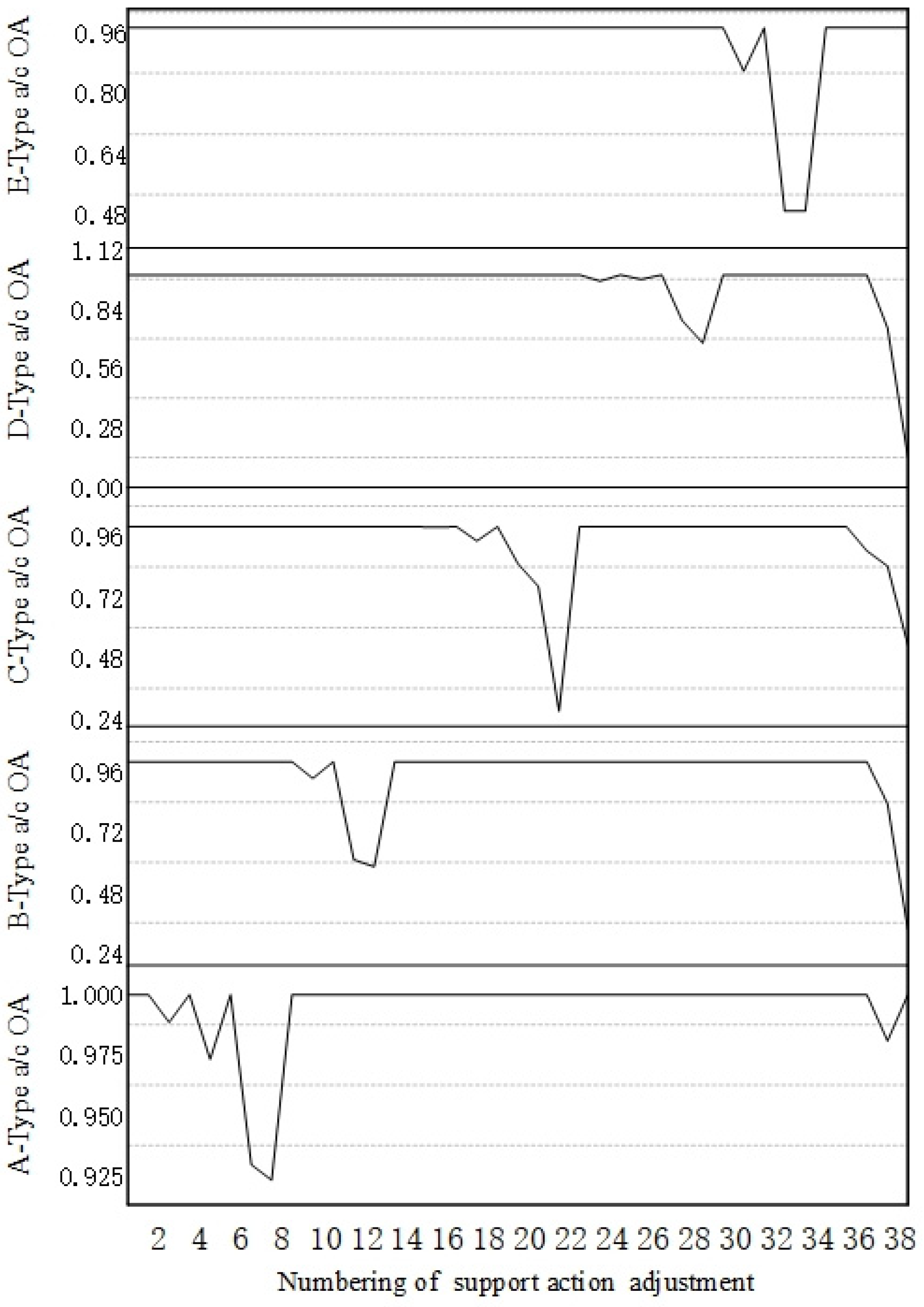
- (c)
- For each task, it is possible to take a comprehensive approach to considering constraints to adjust the input of the optimization system, such as adjusting the phase task time as demonstrated in the literature [30]. The first, second, and third task success rates increased by 8.3%, 4.2%, and 2.1%, respectively, when the time for each task was reduced by 20%. If the task time in each stage is unsuitable for adjustment, the adjustment of task intensity can also help to improve the MSR. For example, when the task intensity for the E-type aircraft was decreased by 20%, the MSR increased by 6.3%. From a system optimization perspective, the optimal operation state of the system is often difficult to obtain, but the impact of local factor adjustment on the operation of the system can be effectively measured.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| No. | Abbreviation/Variables | Description |
| 1 | A, B, C, D, E | Aircraft type |
| 2 | a/c | Aircraft (in figures and tables) |
| 3 | A-MLDT | Mean logistics delay time of the A-type aircraft |
| 4 | A-MTBF | Mean time between failures of the A-type aircraft |
| 5 | A-MTTR | Mean time to repair of the A-type aircraft |
| 6 | LRU | Line replaceable unit |
| 7 | MCP | Mission completion probability |
| 8 | MLDT | Mean logistics delay time |
| 9 | MSR | Mission success rate |
| 10 | MTBF | Mean time between failure. |
| 11 | MTTR | Mean time to repair |
| 12 | MX | Maintenance |
| 13 | OP | Operational support |
| 14 | OA | Operational availability |
| 15 | RMS | Reliability, maintainability, and supportability |
| 16 | RR | Reliability rate |
| 17 | SOS | System of systems |
References
- You, G.R.; Chu, J.T.; Lu, S.Q. Research on Weapon Equipment System. Mil. Oper. Res. Syst. Eng. 2010, 24, 15–22. [Google Scholar]
- Zio, E. Prognostics and Health Management Methods for Reliability Prediction and Predictive Maintenance. IEEE Trans. Reliab. 2024, 73, 41. [Google Scholar] [CrossRef]
- Tan, Y.; Yang, K.; Zhao, Q.; Jiang, J.; Ge, B.; Zhang, X.; Shang, H.; Li, J. Operational Effectiveness Evaluation Method of Weapon Equipment System Combat Network Based on Combat Ring. China. CN201510386251.2, 13 September 2019. [Google Scholar]
- Ding, G.; Cui, L.J.; Zhang, L.; Li, Z.P. Research on key issues in simulation deduction of aviation maintenance support mode. Ship Electron. Eng. 2020, 40, 8–12. [Google Scholar]
- Trivedi, K. Reliability and Availability Assessment. IEEE Trans. Reliab. 2024, 73, 17–18. [Google Scholar] [CrossRef]
- Feng, Z.; Okamura, H.; Dohi, T.; Yun, W.Y. Reliability Computing Methods of Probabilistic Location Set Covering Problem Considering Wireless Network Applications. IEEE Trans. Reliab. 2024, 73, 290–303. [Google Scholar] [CrossRef]
- Gao, L.; Cao, J.; Song, T.; Xing, B.; Yan, X. Distributed equipment support system task allocation model. J. Armored Forces Eng. Acad. 2018, 32, 13–21. [Google Scholar] [CrossRef]
- Luo, L.Z.; Chakraborty, N.; Sycara, K. Multi-robot assignment algorithm for tasks with set precedence constraints. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2526–2533. [Google Scholar]
- Wang, J.H.; Zhang, L.; Shi, C.; Che, F.; Zhang, P.T. Cooperative mission planning for equipment support marshalling based on the optimization of the invading weed bat twin group. Control. Decis. 2019, 34, 1375–1384. [Google Scholar] [CrossRef]
- Xing, B.; Cao, J.H.; Song, T.L.; Chen, S.H.; Liu, F.S. Robustness analysis of complex network of equipment support system for mission success. Comput. Appl. Res. 2018, 35, 475–478. [Google Scholar] [CrossRef]
- Song, T.L.; Xing, L.D. Mission need-based system supportability objectives determination. In Proceedings of the 2011 Proceedings—Annual Reliability and Maintainability Symposium, Lake Buena Vista, FL, USA, 24–27 January 2011. [Google Scholar]
- Li, D. Simulation Modeling and Optimization of the Use of Support Resources for Basic Combat Units Based on Petri Nets. Master’s Thesis, National University of Defense Technology, Changsha, China, 2013. [Google Scholar]
- Li, L.; Xu, C.; Tao, M. Resource Allocation in Open Access OFDMA Femtocell Networks. IEEE Wirel. Commun. Lett. 2012, 1, 625–628. [Google Scholar] [CrossRef]
- Wang, R.; Lei, H.W.; Peng, Y.W. Optimization of multi-level spare parts for naval equipment under wartime mission conditions. J. Shanghai Jiaotong Univ. 2013, 47, 398–403. [Google Scholar]
- Sheng, J.Y. Research on Coordination Evaluation Index of Support Resources Used by Basic Combat Units. Master’s Thesis, National University of Defense Technology, Changsha, China, 2012. [Google Scholar]
- Hooks, D.C.; Rich, B.A. Open systems architecture for integrated RF electronics. Comput. Stand. Interfaces 1999, 21, 147. [Google Scholar] [CrossRef]
- Han, X.Z.; Zhang, Y.H.; Wang, S.H.; Zhang, S.X. Evaluation method of equipment mission success considering maintenance work. Syst. Eng. Electron. Technol. 2017, 39, 687–692. [Google Scholar]
- Cao, L.J. Maintenance decision-making method and application centered on mission success. Firepower Command. Control. 2007, 6, 97–101. [Google Scholar]
- Guo, L.H.; Kang, R. Modeling and simulation of the preventive maintenance support process of basic combat units. Comput. Simul. 2007, 4, 36–39. [Google Scholar]
- Liu, B. Ship Equipment Support Resources and Maintenance Strategy Optimization and Effectiveness Evaluation. Master’s Thesis, Northwestern Polytechnical University, Xi’an, China, 2006. [Google Scholar]
- Zhang, T. Modeling and Analysis of Maintenance Support Capability Assessment During the Use Phase of Equipment. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2004. [Google Scholar]
- Mahulkar, V.; McKay, S.; Adams, D.E.; Chaturvedi, A.R. System-of-Systems Modeling and Simulation of a Ship Environment with Wireless and Intelligent Maintenance Technologies. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2009, 39, 1255–1270. [Google Scholar] [CrossRef]
- Yang, L.B.; Xu, T.H.; Wang, Z.X. Agent based heterogeneous data integration and maintenance decision support for high-speed railway signal system. In Proceedings of the 2014 IEEE 17th International Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 1976–1981. [Google Scholar]
- Cao, Y.; Peng, Y.L.; Wang, T.N. Research on Equipment Support Process Model Based on Multi-Agent System. In Proceedings of the 2009 International Conference on Information Management, Innovation Management and Industrial Engineering, Xi’an, China, 26–27 December 2009; pp. 574–576. [Google Scholar]
- Panteleev, V.; Kamaev, V.; Kizim, A. Developing a Model of Equipment Maintenance and Repair Process at Service Repair Company Using Agent-based Approach. Procedia Technol. 2014, 16, 1072–1079. [Google Scholar] [CrossRef][Green Version]
- Du, X.; Pei, G.; Xue, Z.; Zhu, N. An Agent-Based Simulation Framework for Equipment Support Command. In Proceedings of the 9th International Symposium on Computational Intelligence and Design, Hangzhou, China, 10–11 December 2016; pp. 12–16. [Google Scholar]
- Yang, Y.; Yu, Y.; Zhang, L.; Zhang, W. Sensitivity analysis and parameter optimization of equipment maintenance support simulation system. Syst. Eng. Electron. Technol. 2016, 38, 575–581. [Google Scholar]
- Miranda, P.A.; Tapia-Ubeda, F.J.; Hernandez, V.; Cardenas, H.; Lopez-Campos, M. A Simulation Based Modelling Approach to Jointly Support and Evaluate Spare Parts Supply Chain Network and Maintenance System. IFAC-PapersOnLine 2019, 52, 2231–2236. [Google Scholar] [CrossRef]
- Petrovic, S.; Milosavljevic, P.; Sajic, J.L. Rapid Evaluation of Maintenance Process Using Statistical Process Control and Simulation. Int. J. Simul. Model. 2018, 17, 119–132. [Google Scholar] [CrossRef]
- Pang, S.; Jia, Y.; Liu, X.; Deng, Y. Study on simulation modeling and evaluation of equipment maintenance. J. Shanghai Jiaotong Univ. (Science) 2016, 21, 594–599. [Google Scholar] [CrossRef]
- Ding, G.; Cui, L.J.; Shi, C.; Ding, E.Q. Research on the Construction of Supportability Index of Aviation Equipment System. J. Air Force Eng. Univ. 2019, 19, 55–59. [Google Scholar] [CrossRef]
- Ding, G.; Cui, L.J.; Wang, L.Y.; Hu, R.; Qian, G. Research on the construction of supportability index of aviation equipment system of systems. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1043, 022008. [Google Scholar] [CrossRef]
- Liao, H. Accelerated Testing and Smart Maintenance: History and Future. IEEE Trans. Reliab. 2023, 73, 33–37. [Google Scholar] [CrossRef]
- Ding, G.; Cui, L.J.; Han, C.; Wang, X.H.; Zhang, F. Simulation and evaluation analysis of aviation weapon and equipment system support based on multi agent. J. Beijing Univ. Aeronaut. Astronaut. 2022, 49, 1–15. [Google Scholar] [CrossRef]











| Mission Time | 26 h | ||||||
|---|---|---|---|---|---|---|---|
| Mission Phase Time | 12 h | 8 h | 6 h | ||||
| Phased Mission Requirements | Early Warning and Detection | Forward Reconnaissance | Remote Attack | ||||
| Equipment SOS CF1 | Equipment SOS CF2 | Equipment SOS CF3 | |||||
| Type A a/c | Minimum number | Early warning | 1 | Early warning | 1 | Early warning | 2 |
| Sorties | 2 | 2 | 3 | ||||
| Type B a/c | Minimum number | - | – | - | – | Suppress fire | 7 |
| Sorties | – | – | 10 | ||||
| Type C a/c | Minimum number | Support cover | 5 | Support cover | 7 | Support cover Fire assault | 10 |
| Sorties | 8 | 10 | 16 | ||||
| Type D a/c | Minimum number | - | – | Electronic recon Electronic jamming | 4 | Electronic recon Electronic jamming | 6 |
| Sorties | – | 6 | 8 | ||||
| Type E a/c | Minimum number | - | – | - | – | Air refueling | 4 |
| Sorties | – | – | 6 | ||||
| Case No. | Adjusted Item | Change | Step Size | Before (h/min) | After (h/min) |
|---|---|---|---|---|---|
| 1 | A-MTBF | Decrease | 20% | 1277.43 | 1021.94 |
| 2 | A-MTBF | Decrease | 40% | 1277.43 | 766.46 |
| 3 | A-MTBF | Decrease | 60% | 1277.43 | 510.97 |
| 4 | A-MTBF | Decrease | 80% | 1277.43 | 255.49 |
| 5 | A-MTBF | Decrease | 98.4% | 1277.43 | 20 |
| 6 | A-MTBF | Decrease | 99.20% | 1277.43 | 10 |
| 7 | A-MTTR | Increase | 20% | 13 | 16 |
| 8 | A-MTTR | Increase | 40% | 13 | 18 |
| 9 | A-MTTR | Increase | 60% | 13 | 21 |
| 10 | A-MTTR | Increase | 80% | 13 | 24 |
| 11 | A-MTTR | Increase | 1590% | 13 | 220 |
| 12 | A-MLDT | Increase | 20% | 25 | 30 |
| 13 | A-MLDT | Increase | 40% | 25 | 35 |
| 14 | A-MLDT | Increase | 60% | 25 | 40 |
| 15 | A-MLDT | Increase | 80% | 25 | 45 |
| 16 | A-MLDT | Increase | 780% | 25 | 220 |
| 17 | A-MTBF | Decrease | 20% | 1277.43 | 1021.94 |
| A-MTTR | Increase | 20% | 13 | 16 | |
| A-MLDT | Increase | 20% | 25 | 30 | |
| 18 | A-MTBF | Decrease | 40% | 1277.43 | 776.49 |
| A-MTTR | Increase | 40% | 13 | 18 | |
| A-MLDT | Increase | 40% | 25 | 35 | |
| 19 | A-MTBF | Decrease | 60% | 1277.43 | 510.97 |
| A-MTTR | Increase | 60% | 13 | 21 | |
| A-MLDT | Increase | 60% | 25 | 40 | |
| 20 | A-MTBF | Decrease | 80% | 1277.43 | 225.49 |
| A-MTTR | Increase | 80% | 13 | 24 | |
| A-MLDT | Increase | 80% | 25 | 45 | |
| 21 | A-MTBF | Decrease | 98.40% | 1277.43 | 20 |
| A-MTTR | Increase | 1590% | 13 | 220 | |
| A-MLDT | Increase | 80% | 25 | 45 |
| Case No. | Adjusted Item | Change | Step Size | Before (min/set) | After (min/set) |
|---|---|---|---|---|---|
| 1 | A—Pre-MX | Increase | 20% | 120 | 144 |
| 2 | A—Direct MX 1 | Increase | 20% | 120 | 144 |
| 3 | A—Direct MX 2 | Increase | 40% | 120 | 168 |
| 4 | A—Turnaround 1 | Increase | 20% | 60 | 72 |
| 5 | A—Turnaround 2 | Increase | 60% | 60 | 96 |
| 6 | A—Refueling vehicle | Decrease | 20% | 8 | 7 |
| 7 | A—Air-con vehicle | Decrease | 90% | 8 | 1 |
| 8 | A—Power vehicle | Decrease | 90% | 8 | 1 |
| 9 | A—Pre-MX | Increase | 20% | 120 | 144 |
| 10 | B—Direct MX | Increase | 20% | 120 | 144 |
| 11 | A—Refueling vehicle | Decrease | 20% | 24 | 20 |
| 12 | B—Air-con vehicle | Decrease | 80% | 24 | 5 |
| 13 | B—Power vehicle | Decrease | 80% | 24 | 5 |
| 14 | C—Pre-MX | Increase | 20% | 120 | 144 |
| 15 | C—Direct MX 1 | Increase | 20% | 60 | 72 |
| 16 | C—Direct MX 2 | Increase | 40% | 60 | 84 |
| 17 | C—Turnaround 1 | Increase | 20% | 50 | 60 |
| 18 | C—Turnaround 2 | Increase | 50% | 50 | 75 |
| 19 | C—Refueling vehicle | Decrease | 20% | 39 | 32 |
| 20 | C—Air-con vehicle | Decrease | 80% | 39 | 8 |
| 21 | C—Power vehicle 1 | Decrease | 80% | 39 | 8 |
| 22 | C—Power vehicle 2 | Decrease | 90% | 39 | 4 |
| 23 | D—Pre-MX | Increase | 20% | 120 | 144 |
| 24 | D—Direct MX | Increase | 20% | 120 | 144 |
| 25 | D—Turnaround 1 | Increase | 20% | 60 | 72 |
| 26 | D—Turnaround 2 | Increase | 60% | 60 | 96 |
| 27 | D—Refueling vehicle | Decrease | 20% | 20 | 16 |
| 28 | D—Air-con vehicle | Decrease | 80% | 20 | 4 |
| 29 | D—Power vehicle | Decrease | 80% | 20 | 4 |
| 30 | E—Pre-MX | Increase | 20% | 120 | 144 |
| 31 | E—Direct MX | Increase | 20% | 120 | 144 |
| 32 | E—Refueling vehicle | Decrease | 20% | 14 | 12 |
| 33 | E—Air-con vehicle | Decrease | 80% | 12 | 3 |
| 34 | E—Power vehicle | Decrease | 80% | 12 | 3 |
| 35 | Number of accessory oil vehicles 1 | Decrease | 20% | 9 | 8 |
| 36 | Number of accessory oil vehicles 2 | Decrease | 40% | 9 | 6 |
| 37 | Number of accessory oil vehicles 3 | Decrease | 60% | 9 | 4 |
| 38 | Number of accessory oil vehicles 4 | Decrease | 80% | 9 | 2 |
| 39 | Number of accessory oil vehicles 5 | Decrease | 90% | 9 | 1 |
| Case No. | Mission Phase | Change | Step Size | Before (K/N) | After (K/N) |
|---|---|---|---|---|---|
| 1 | A—1 | Increase | 50% | 1/2 | 2/2 |
| 2 | A—2 | Increase | 50% | 1/2 | 2/2 |
| 3 | A—3 | Increase | 30% | 2/3 | 3/3 |
| 4 | B—3 | Increase | 30% | 7/10 | 10/10 |
| 5 | E—3 | Increase | 50% | 4/6 | 6/6 |
| 6 | C—1 | Increase | 40% | 5/8 | 7/8 |
| 7 | C—2 | Increase | 40% | 7/10 | 10/10 |
| 8 | C—3 | Increase | 40% | 10/16 | 16/16 |
| 9 | D—2 | Increase | 40% | 4/6 | 6/6 |
| 10 | D—3 | Increase | 20% | 6/8 | 8/8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, G.; Cui, L.; Zhang, F.; Shi, C.; Wang, X.; Tai, X. Simulation Evaluation and Case Study Verification of Equipment System of Systems Support Effectiveness. Systems 2025, 13, 77. https://doi.org/10.3390/systems13020077
Ding G, Cui L, Zhang F, Shi C, Wang X, Tai X. Simulation Evaluation and Case Study Verification of Equipment System of Systems Support Effectiveness. Systems. 2025; 13(2):77. https://doi.org/10.3390/systems13020077
Chicago/Turabian StyleDing, Gang, Lijie Cui, Feng Zhang, Chao Shi, Xinhe Wang, and Xiang Tai. 2025. "Simulation Evaluation and Case Study Verification of Equipment System of Systems Support Effectiveness" Systems 13, no. 2: 77. https://doi.org/10.3390/systems13020077
APA StyleDing, G., Cui, L., Zhang, F., Shi, C., Wang, X., & Tai, X. (2025). Simulation Evaluation and Case Study Verification of Equipment System of Systems Support Effectiveness. Systems, 13(2), 77. https://doi.org/10.3390/systems13020077







