Can Government Incentive and Penalty Mechanisms Effectively Mitigate Tacit Collusion in Platform Algorithmic Operations?
Abstract
:1. Introduction
2. Literature Review
2.1. Algorithmic Collusive Behavior
2.2. Governance of Algorithm Collusion and Antitrust Regulation
3. Game Modeling
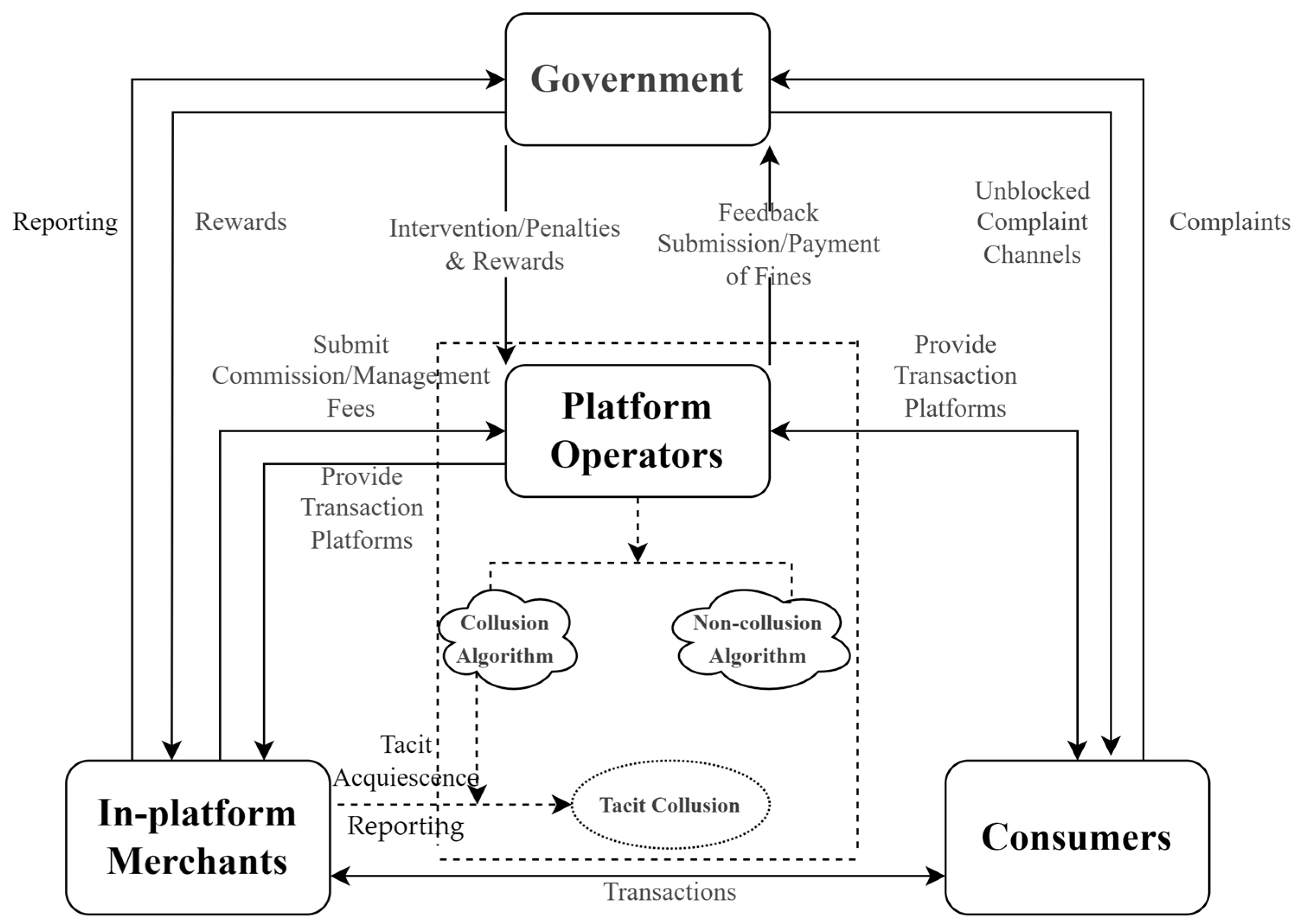
3.1. Scenario Construction and Research Logic
3.2. Parameterization and Underlying Assumptions
3.2.1. Game Subjects and Their Behavioral Strategies
3.2.2. Probability of Behavioral Strategy Adoption
3.2.3. Parameter Assumptions and Meanings in the Model
4. Model Analysis
4.1. Strategy Evolutionary Stabilization Strategy and Analysis
4.2. Stability Analysis of Equilibrium Points of a Four-Way Evolutionary Game System
5. Simulation Analysis
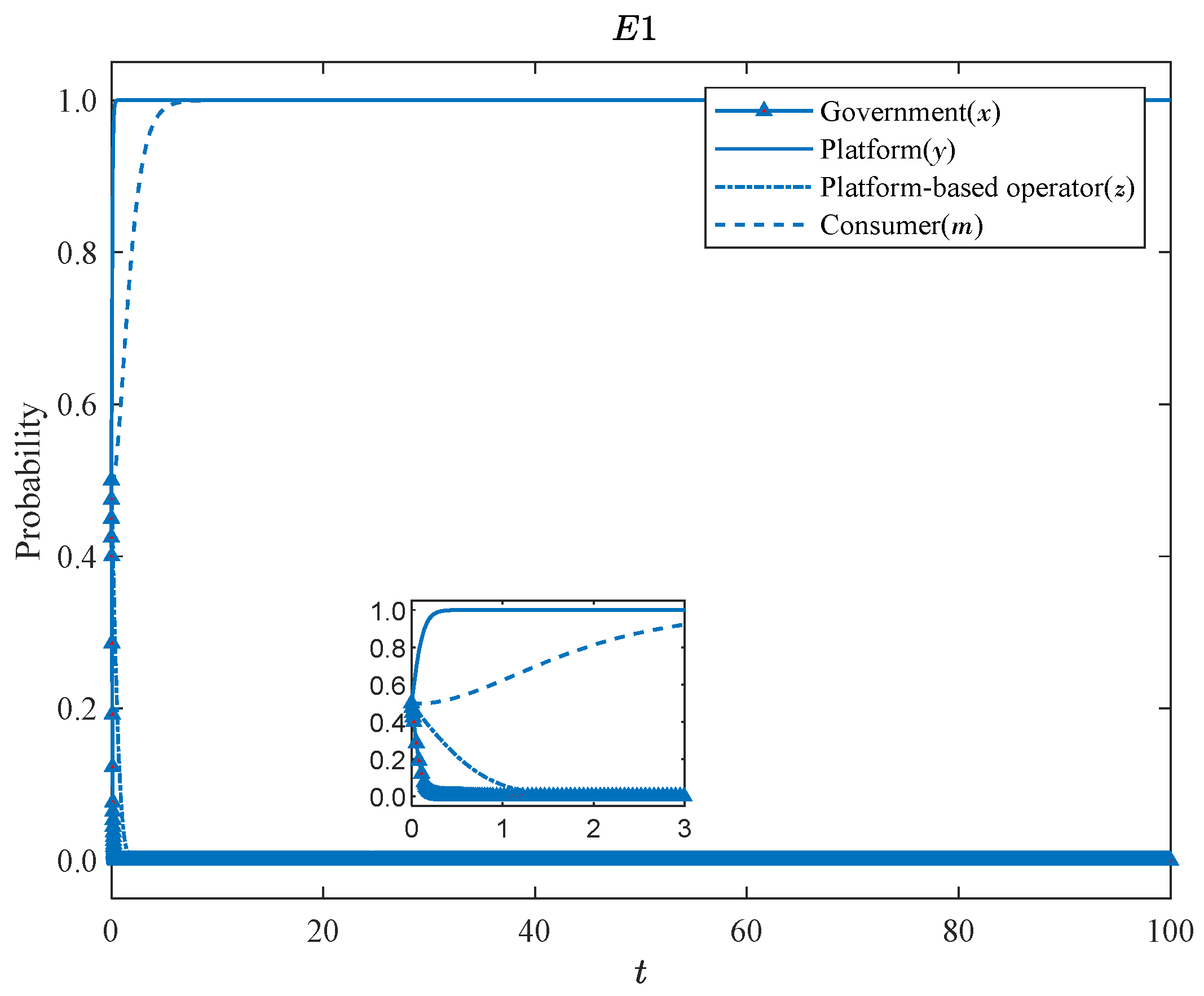
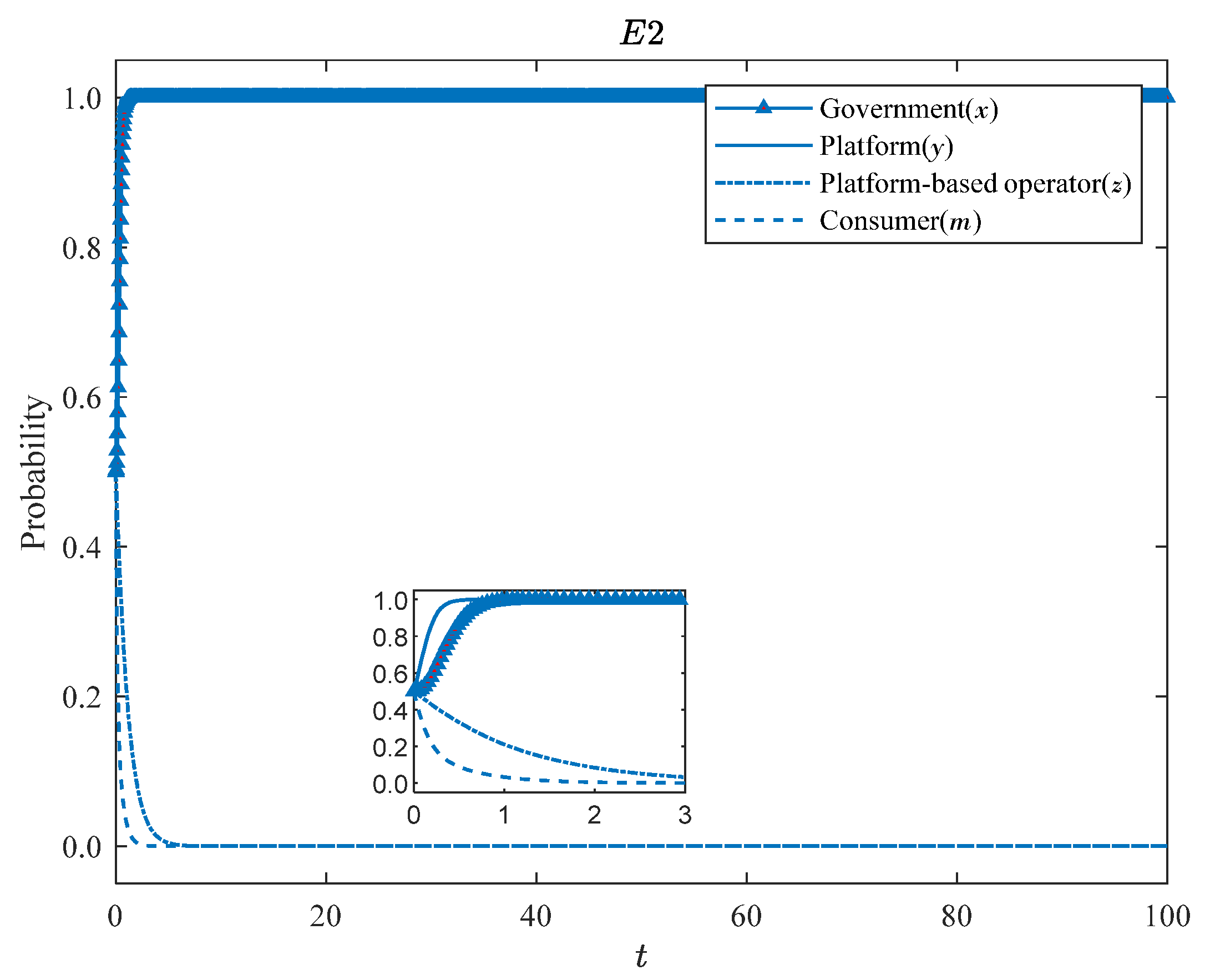
5.1. Validation of the Balanced Results
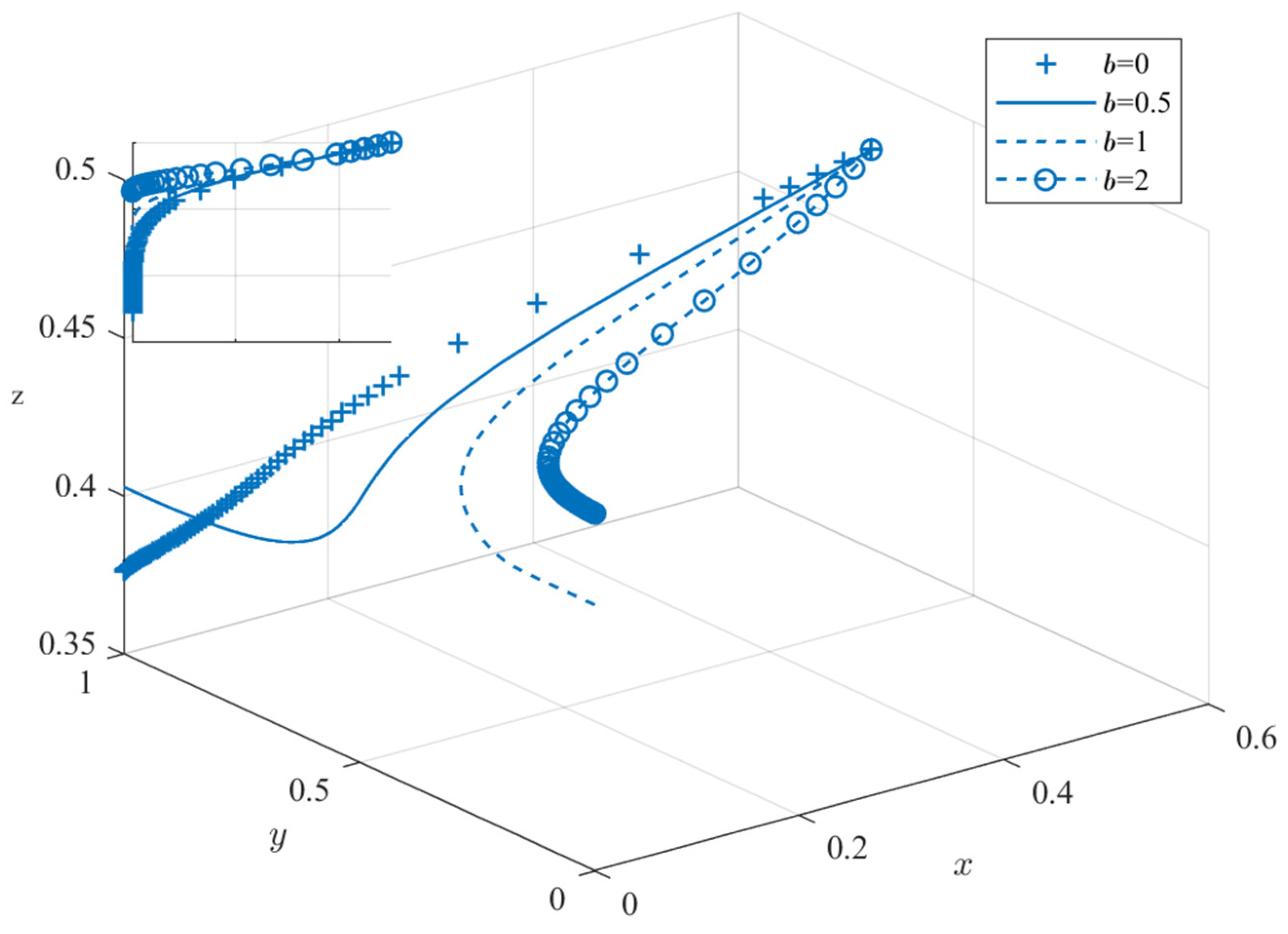
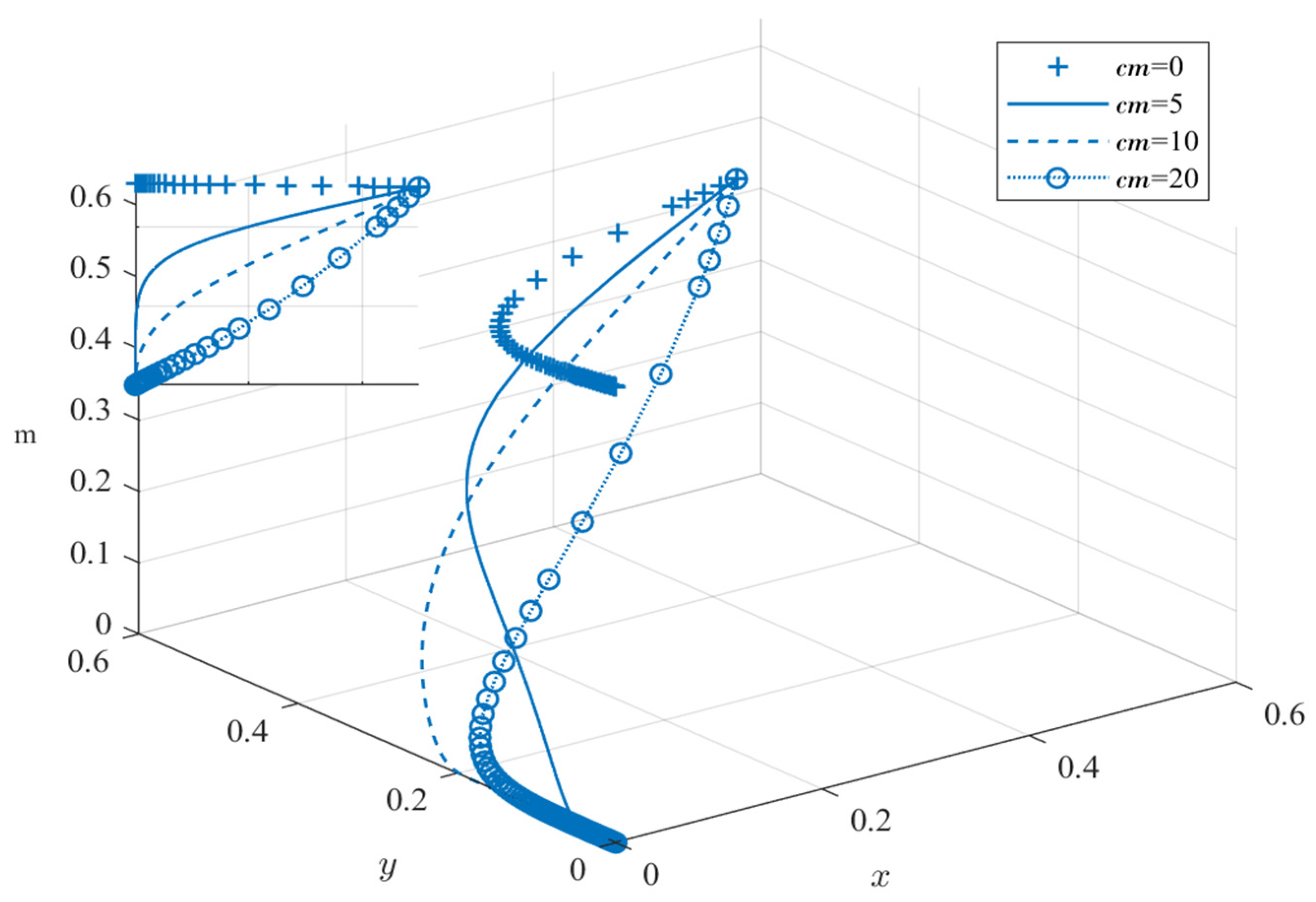
5.2. Impact of Governmental Rewards and Incentives
5.3. A Practical Analysis of Regulatory Cases of Algorithmic Tacit Collusion
5.3.1. The Role of Algorithmic Transparency and Penalty Intensity
5.3.2. Synergistic Governance of Incentives and Complaint Channels
6. Conclusions and Discussions
6.1. Main Conclusions
6.2. Marginal Contributions
6.3. Practical Implications
6.4. Limitations and Future Research
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Strategy Combination | Governmental Revenue | Platform Revenue | Revenue of In-Platform Merchants | Consumer Surplus |
|---|---|---|---|---|
| Model Parameter | Meaning |
|---|---|
| The costs of strong governmental intervention. | |
| The costs of weak governmental intervention. | |
| The covert nature of platform algorithmic collusion increases governmental intervention complexity, necessitating additional scrutiny costs. | |
| The presence of algorithmic collusion within the platform generates total revenue for both the platform and its operators. | |
| Total revenue for platforms and operators in the absence of algorithmic collusion. | |
| Platform commission rate. | |
| Governmental penalty multiplier for platform collusion revenue. | |
| Multiplicative compensation provided by platforms to consumers derived from collusive advantages. | |
| Negative reputational effects of consumer complaints on platforms. | |
| Negative reputational effects of consumer complaints on in-platform merchants. | |
| Cost of consumer complaints. | |
| Governmental rewards for in-platform merchant reporting of algorithmic collusion. |
Appendix B
Appendix B.1. Analysis of the Stability of the Government’s Strategy
Appendix B.2. Strategic Stability Analysis of the Platform
Appendix B.3. Analysis of the Strategic Stability of Merchants Selling Products on the Platform
Appendix B.4. Analysis of the Strategic Stability of Consumers
Appendix C
| Balance Point | Jacobian Matrix Eigenvalues | Stability | Prerequisite | |
|---|---|---|---|---|
| Real Symbol | ||||
| (0, 0, 0, 0) | 0, −, −, X | Point of Instability | -- | |
| (0, 1, 0, 0) | 0, X, X, X | Point of Instability | -- | |
| (0, 0, 1, 0) | 0, −, −, + | Point of Instability | -- | |
| (0, 0, 0, 1) | 0, +, −, X | Point of Instability | -- | |
| (0, 1, 1, 0) | 0, −, −, − | Point of Instability | -- | |
| (0, 1, 0, 1) | X, −, X, X | ESS | ①②③ | |
| (0, 0, 1, 1) | 0, +, −, X | Point of Instability | -- | |
| (0, 1, 1, 1) | +, +, X, X | Point of Instability | -- | |
| (1, 0, 0, 0) | 0, −, +, X | Point of Instability | -- | |
| (1, 1, 0, 0) | X, −, X, X | ESS | ④⑤⑥ | |
| (1, 0, 1, 0) | 0, +, −, + | Point of Instability | -- | |
| (1, 0, 0, 1) | 0, +, +, X | Point of Instability | -- | |
| (1, 1, 1, 0) | +, +, X, − | Point of Instability | -- | |
| (1, 1, 0, 1) | X, −, X, X | ESS | ①③⑥ | |
| (1, 0, 1, 1) | 0, +, +, X | Point of Instability | -- | |
| (1, 1, 1, 1) | +, X, X, X | Point of Instability | -- | |
References
- Hanspach, P.; Galli, N. Collusion by Pricing Algorithms in Competition Law and Economics; Robert Schuman Centre for Advanced Studies Research Paper No. 2024_06; European University Institute: Fiesole, Italy, 2024; Available online: https://hdl.handle.net/1814/76558 (accessed on 20 October 2024).
- Kim, J.; Ahn, S. The platform policy matrix: Promotion and regulation. Policy Internet 2025, 17, e414. [Google Scholar] [CrossRef]
- Yang, Z.; Fu, X.; Gao, P.; Chen, Y.J. Fairness regulation of prices in competitive markets. Manuf. Serv. Oper. Manag. 2024, 26, 1897–1917. [Google Scholar] [CrossRef]
- Calvano, E.; Calzolari, G.; Denicolo, V.; Pastorello, S. Artificial intelligence, algorithmic pricing, and collusion. Am. Econ. Rev. 2020, 110, 3267–3297. [Google Scholar] [CrossRef]
- Deng, A. What do we know about algorithmic tacit collusion. Antitrust 2018, 33, 88. [Google Scholar] [CrossRef]
- Gata, J.E. Controlling algorithmic collusion: Short review of the literature, undecidability, and alternative approaches. SSRN 2018. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3334889 (accessed on 20 October 2024). [CrossRef]
- Cont, R.; Xiong, W. Dynamics of market making algorithms in dealer markets: Learning and tacit collusion. Math. Financ. 2024, 34, 467–521. [Google Scholar] [CrossRef]
- Assad, S.; Calvano, E.; Calzolari, G.; Clark, R.; Denicolò, V.; Ershov, D.; Johnson, J.; Pastorello, S.; Rhodes, A.; Xu, L.; et al. Autonomous algorithmic collusion: Economic research and policy implications. Oxf. Rev. Econ. Policy 2021, 37, 459–478. [Google Scholar] [CrossRef]
- Ferrari, F.; Graham, M. Fissures in algorithmic power: Platforms, code, and contestation. Cult. Stud. 2021, 35, 814–832. [Google Scholar] [CrossRef]
- Sanchez, C.J.M.; Katsamakas, E. AI pricing algorithms under platform competition. Electron. Commer. Res. 2024, 1, 1–28. [Google Scholar] [CrossRef]
- Abada, I.; Lambin, X. Artificial intelligence: Can seemingly collusive outcomes be avoided? Manag. Sci. 2023, 69, 5042–5065. [Google Scholar] [CrossRef]
- Johnson, J.P.; Rhodes, A.; Wildenbeest, M. Platform design when sellers use pricing algorithms. Econometrica 2023, 91, 1841–1879. [Google Scholar] [CrossRef]
- Schwalbe, U. Algorithms, machine learning, and collusion. J. Compet. Law Econ. 2018, 14, 568–607. [Google Scholar] [CrossRef]
- Tripathy, M.; Bai, J.; Heese, H.S. Driver collusion in ride-hailing platforms. Decis. Sci. 2023, 54, 434–446. [Google Scholar] [CrossRef]
- Huang, Y.S.; Wu, T.Y.; Fang, C.C.; Tseng, T.L. Decisions on probabilistic selling for consumers with different risk attitudes. Decis. Anal. 2021, 18, 121–138. [Google Scholar] [CrossRef]
- Sharma, A. Algorithmic Cartels and Economic Efficiencies: Decoding the Indian & EU Perspective. Nuals Law J. 2023, 17, 137. Available online: https://heinonline.org/HOL/P?h=hein.journals/nualsj17&i=169 (accessed on 20 October 2024).
- Frass, A.G.; Greer, D.F. Market structure and price collusion: An empirical analysis. J. Ind. Econ. 1977, 26, 21–44. [Google Scholar] [CrossRef]
- Barta, A.; Molnar, M. Indication of organizational collusion by examining dynamic market indicators. GRADUS 2021, 8, 160–165. [Google Scholar] [CrossRef]
- Aune, F.R.; Mohn, K.; Osmundsen, P.; Rosendahl, K.E. Financial market pressure, tacit collusion and oil price formation. Energy Econ. 2010, 32, 389–398. [Google Scholar] [CrossRef]
- Shimizu, K. “Pricing Game” for Tacit Collusion and Passive Investment. In Proceedings of the CERC 2019; pp. 323–334. Available online: https://www.researchgate.net/publication/332820909_Pricing_Game_for_tacit_collusion_and_Passive_Investment (accessed on 20 April 2024).
- Rock, E.B.; Rubinfeld, D.L. Common ownership and coordinated effects. Antitrust Law J. 2020, 83, 201–252. Available online: https://www.jstor.org/stable/27006859 (accessed on 20 April 2024). [CrossRef]
- Antón, M.; Ederer, F.; Giné, M.; Schmalz, M. Common ownership, competition, and top management incentives. J. Political Econ. 2023, 131, 1294–1355. [Google Scholar] [CrossRef]
- Allain, M.L.; Boyer, M.; Kotchoni, R.; Ponssard, J.P. Are cartel fines optimal? Theory and evidence from the European Union. Int. Rev. Law Econ. 2015, 42, 38–47. [Google Scholar] [CrossRef]
- Ezrachi, A.; Stucke, M.E. Sustainable and unchallenged algorithmic tacit collusion. Northwestern J. Technol. Intellect. Prop. 2019, 17, 217. Available online: https://scholarlycommons.law.northwestern.edu/njtip/vol17/iss2/2/ (accessed on 20 October 2024). [CrossRef]
- Gautier, A.; Ittoo, A.; Van Cleynenbreugel, P. AI algorithms, price discrimination and collusion: A technological, economic and legal perspective. Eur. J. Law Econ. 2020, 50, 405–435. [Google Scholar] [CrossRef]
- Mazumdar, A. Algorithmic collusion. Columbia Law Rev. 2022, 122, 449–488. Available online: https://www.jstor.org/stable/27114356 (accessed on 20 October 2024).
- Epivent, A.; Lambin, X. On algorithmic collusion and reward-punishment schemes. Econ. Lett. 2024, 237, 111661. [Google Scholar] [CrossRef]
- Bernhardt, L.; Dewenter, R. Collusion by code or algorithmic collusion? When pricing algorithms take over. Eur. Compet. J. 2020, 16, 312–342. [Google Scholar] [CrossRef]
- Gata, J.E. Collusion between algorithms: A literature review and limits to enforcement. Eur. Rev. Bus. Econ. 2021, 1, 73–94. [Google Scholar] [CrossRef]
- Abada, I.; Lambin, X.; Tchakarov, N. Collusion by mistake: Does algorithmic sophistication drive supra-competitive profits? Eur. J. Oper. Res. 2024, 318, 927–953. [Google Scholar] [CrossRef]
- Evans, D.S. Basic principles for the design of antitrust analysis for multisided platforms. J. Antitrust Enforcemen 2019, 7, 319–338. [Google Scholar] [CrossRef]
- Farrell, J.; Katz, M.L. Innovation, rent extraction, and integration in systems markets. J. Ind. Econ. 2000, 48, 413–432. [Google Scholar] [CrossRef]
- Xu, Z. From algorithmic governance to govern algorithm. AI Soc. 2024, 39, 1141–1150. [Google Scholar] [CrossRef]
- Spulber, D.F. Unlocking technology: Antitrust and innovation. Compet. Law Econ. 2008, 4, 915–966. [Google Scholar] [CrossRef]
- Yenipazarli, A. On the effects of antitrust policy intervention in pricing strategies in a distribution channel. Decis. Sci. 2023, 54, 64–84. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, L.; Huang, T.; Tang, H. Collaborative governance for responsible innovation in the context of sharing economy: Studies on the shared bicycle sector in China. J. Open Innov. Technol. Mark. Complex. 2020, 6, 35. [Google Scholar] [CrossRef]
- Wachhaus, A. Platform governance: Developing collaborative democracy. Adm. Theory Prax. 2017, 39, 206–221. [Google Scholar] [CrossRef]
- McSweeny, T.; O’Dea, B. The implications of algorithmic pricing for coordinated effects analysis and price discrimination markets in antitrust enforcement. Antitrust 2017, 32, 75. Available online: https://heinonline.org/HOL/P?h=hein.journals/antitruma32&i=76 (accessed on 20 October 2024).
- Balasingham, B. Hybrid restraints and Hybrid tests under US antitrust and EU competition law. World Compet. 2020, 43, 261–282. [Google Scholar] [CrossRef]
- Yekkehkhany, A.; Murray, T.; Nagi, R. Stochastic superiority equilibrium in game theory. Decis. Anal. 2021, 18, 153–168. [Google Scholar] [CrossRef]
- Sun, L.; Li, X.; Su, C.; Wang, X.; Yuan, X. Analysis of dynamic strategies for decision-making on retrofitting carbon capture, utilization, and storage technology in coal-fired power plants. Appl. Therm. Eng. 2025, 264, 125371. [Google Scholar] [CrossRef]
- Su, C.; Zha, X.; Ma, J.; Li, B.; Wang, X. Dynamic optimal control strategy of CCUS technology innovation in coal power stations under environmental protection tax. Systems 2025, 13, 193. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhou, Y. Can Government Incentive and Penalty Mechanisms Effectively Mitigate Tacit Collusion in Platform Algorithmic Operations? Systems 2025, 13, 293. https://doi.org/10.3390/systems13040293
Wang Y, Zhou Y. Can Government Incentive and Penalty Mechanisms Effectively Mitigate Tacit Collusion in Platform Algorithmic Operations? Systems. 2025; 13(4):293. https://doi.org/10.3390/systems13040293
Chicago/Turabian StyleWang, Yanan, and Yaodong Zhou. 2025. "Can Government Incentive and Penalty Mechanisms Effectively Mitigate Tacit Collusion in Platform Algorithmic Operations?" Systems 13, no. 4: 293. https://doi.org/10.3390/systems13040293
APA StyleWang, Y., & Zhou, Y. (2025). Can Government Incentive and Penalty Mechanisms Effectively Mitigate Tacit Collusion in Platform Algorithmic Operations? Systems, 13(4), 293. https://doi.org/10.3390/systems13040293






