An Improved K-Spare Decomposing Algorithm for Mapping Neural Networks onto Crossbar-Based Neuromorphic Computing Systems
Abstract
:1. Introduction
2. Background
2.1. Dynamic Fixed-Point Format
2.2. Crossbar-Based Neuromorphic System
3. Varied-K Decomposition Algorithm
3.1. Problem Definition
3.2. Proposed Method
| Algorithm 1 Varied k-spare neuron decomposition |
| Input pre-trained model, m, t, e, p, q, max_k |
| Output k_hash contains k of all MCAs of the entire network model |
| 1. for each NN layer in a model do |
| 2. if NN layer is CNN do |
| 3. Transform CNN weights to 2d matrix W |
| 4. Decompose M × N sized W to p × q sized Wi,j |
| 5. for each Wi,j do |
| 6. WDFPi,j ← Quantize DFP Wi,j |
| 7. WVDAi,j ← Assign max scaling factor of each column to all scaling factors in the same column in WDFPi,j |
| 8. SWi,j ← Calculate MSQE score of WVDAi,j |
| 9. SW ← [SWi,j] |
| 10. S ← { SW} |
| 11. min, max ← min(S), max(S) |
| 12. step ← (max – min)/max_k |
| 13. Initial k_hash |
| 14. for each NN layer in a model do |
| 15. M, N ← NN layer’s weights W size |
| 16. a ← M/p |
| 17. b ← M % p |
| 18. I (b) = 0 |
| 19. if b > 0 |
| 20. I (b) ← 1 |
| 21. k_list ← [] |
| 22. for i from 1 to a + I (b) do |
| 23. from_column ← 1 |
| 24. while from_column < N do: |
| 25. best_k ← 0 |
| 26. for ki,j from 0 to q − 1 do |
| 27. to_column ← min(from_column + q − ki,j, N) |
| 28. SWi,j ← SW[i, from_column: to_column] |
| 29. temp_k ← Integer((max(SWi,j) – min)/step) |
| 30. if temp_k equals ki,j |
| 31. best_k ← temp_k 32. exit for loop of ki,j |
| 33. k_list ← best_k |
| 34. from_column ← from_column + best_k |
| 35. end while |
| 36. end for |
| 37. k_hash[layer] ← k_list |
| 38. end for |
| 39. return k_hash |
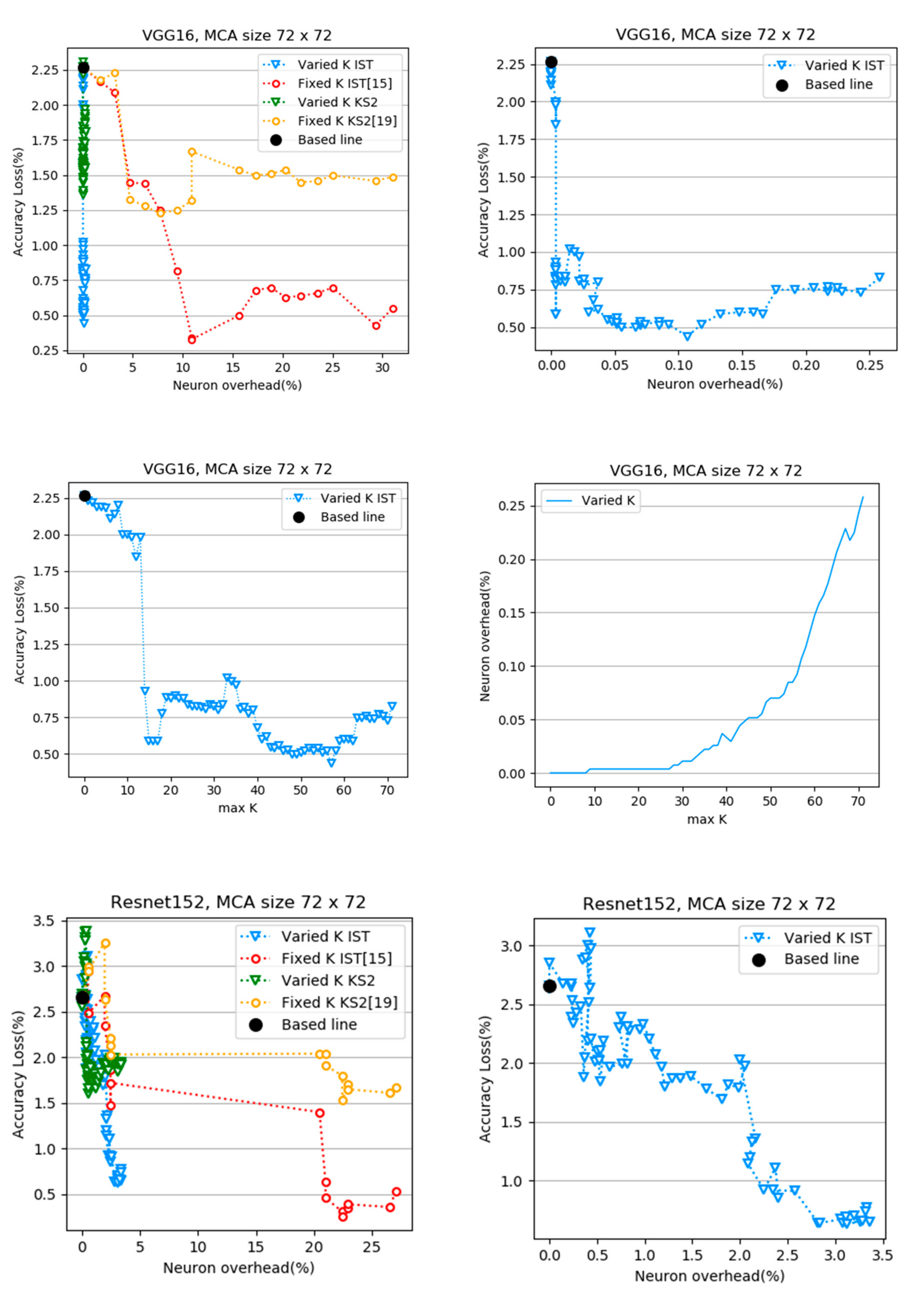
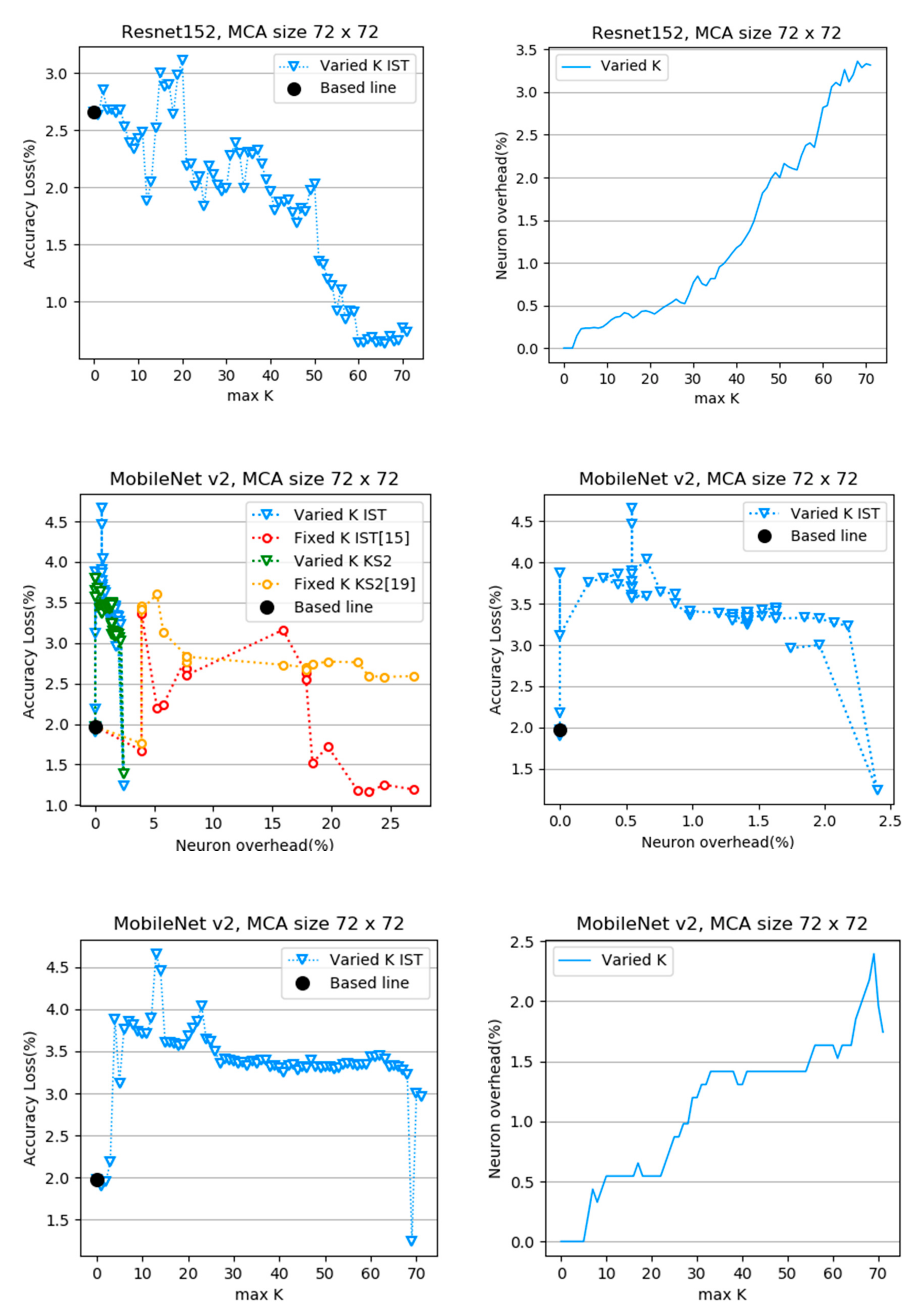
4. Experimental Results
- Small crossbars generally get a better result than big crossbars because the small group of dynamic fixed-point numbers causes a smaller error than the big group
- Optimized network like Resnet and MobileNet need more neuronal overhead to restore the accuracy of models than the sparse network as VGG
- Small-size crossbars cause a small quantization error but it uses plenty of crossbar amount. Therefore, it is more expensive for combination after decomposing.
- Big size crossbar cause a larger quantization error but use a small resource for combination. In addition, the varied k algorithm still works well to restore the accuracy of models in big size crossbars.
- We obtained a better result for MobileNet v2 than the previous size with a larger-sized MCA p = q = 128. We achieve accuracy lost at 0.91% while using 6.11% neuronal overhead.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Abbreviation | Description |
| NN | Neural Network |
| DNN | Deep Neural Network |
| VDA | Vanilla Decomposition Algorithm |
| VSDA | Varied K spare neuron Decomposing Algorithm |
| VGG, VGG16 | Names of very deep convolutional neural networks proposed by Visual Geometry Group [2] |
| CMOS | Complementary Metal Oxide Semiconductor |
| NCS | Neuromorphic Computing System |
| ANN | Artificial Neural Network |
| MCA | Memristor Crossbar Array |
| DFP | Dynamic Fixed-Point |
| DAC | Digital Analog Converter |
| KS2 | K Split-in-Two |
| IST | Iterative Split-in-Two |
| K-SDA | K-Spare neuron Decomposing Algorithm |
| MSQE | Mean Squared Quantization Error |
References
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Wu, C.; Karanasou, P.; Gales, M.J.; Sim, K.C. Stimulated Deep Neural Network for Speech Recognition. Proc. Interspeech 2016, 400–404. [Google Scholar]
- Karpathy, A.; Toderici, G.; Shetty, S.; Leung, T.; Sukthankar, R.; Fei-Fei, L. Large-Scale Video Classification with Convolutional Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1725–1732. [Google Scholar]
- Mead, C. Neuromorphic eletronic systems. Proc. IEEE 1990, 78, 1629–1636. [Google Scholar] [CrossRef] [Green Version]
- Hu, M.; Li, H.; Chen, Y.; Wu, Q.; Rose, G.S.; Linderman, R.W. Memristor crossbar-based neuromorphic computing system: A case study. IEEE Trans. Netw. Learn. Syst. 2014, 25, 1864–1878. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.; Strachan, J.P.; Li, Z.; Grafals, E.M.; Davila, N.; Graves, C.; Lam, S.; Ge, N.; Yang, J.J.; Williams, R.S. Dot-product engine for neuromorphic computing: Programming 1T1M crossbar to accelerate matrix-vector multiplication. In Proceedings of the 2016 53rd ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 5–9 June 2016; pp. 1–6. [Google Scholar]
- Boybat, I.; Le Gallo, M.; Nandakumar, S.R. Neuromorphic computing with multi-memristive synapses. Nat. Commun. 2018, 9, 2514. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.; Shin, T. Simplifying deep neural networks for neuromorphic architectures. In Proceedings of the 53rd Design Automation Conference (DAC), Austin, TX, USA, 5–9 June 2016; pp. 1–6. [Google Scholar]
- Chung, J.; Shin, T.; Kang, Y. INsight: A neuromorphic computing system for evaluation of large neural networks. arXiv 2015, arXiv:1508.01008. [Google Scholar]
- Chi, P.; Li, S.; Xu, C.; Zhang, T.; Zhao, J.; Liu, Y.; Wang, Y.; Xie, Y. PRIME: A novel processing-in-memory architecture for neural network computation in ReRAM-based main memory. Acmsigarch Comput. Arch. News 2016, 44, 27–39. [Google Scholar] [CrossRef]
- Shafiee, A.; Nag, A.; Muralimanohar, N.; Balasubramonian, R.; Strachan, J.P.; Hu, M.; Williams, R.S.; Srijumar, V. ISAAC: A convolutional neural network accelerator with in-situ analog arithmetic in crossbars. ACM Sigarch Comput. Arch. News 2016, 44, 14–26. [Google Scholar] [CrossRef]
- Yao, P.; Wu, H.; Gao, B.; Tang, J.; Zhang, Q.; Zhang, W.; Yang, J.J.; Qian, H. Fully hardware-implemented memristor convolutional neural network. Nature 2020, 577, 641–646. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Tang, T.; Xia, L.; Li, B.; Wang, Y.; Yang, H. Low Bit-Width Convolutional Neural Network on RRAM. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2020, 39, 1414–1427. [Google Scholar] [CrossRef]
- Fatahalian, K.; Sugerman, J.; Hanrahan, P. Understanding the efficiency of gpu algorithms for matrix-matrix multiplication. In Proceedings of the ACM SIGGRAPH/EUROGRAPHICS Conference on Graphics Hardware, Grenoble, France, 29–30 August 2004; pp. 133–137. [Google Scholar]
- Kim, C. A Neural Network Decomposition Algorithm for Crossbar-based Neuromorphic System. Master’s Thesis, Incheon National University, Incheon, Korea, February 2020. [Google Scholar]
- Kim, C.; Abraham, A.J.; Kang, W.; Chung, J. A Neural Network Decomposition Algorithm for Mapping on Crossbar-Based Computing Systems. Electronics 2020, 9, 1526. [Google Scholar] [CrossRef]
- Gysel, P.; Motamedi, M.; Ghiasi, S. Hardware-oriented approximation of convolutional neural networks. arXiv 2016, arXiv:1605.06402. [Google Scholar]
- Kang, Y.; Yang, J.; Chung, J. Weight partitioning for dynamic fixed-point neuromorphic computing systems. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2019, 38, 2167–2171. [Google Scholar] [CrossRef]
- Kang, Y.; Chung, J. A dynamic fixed-point representation for neuromorphic computing systems. In Proceedings of the International SoC Design Conference (ISOCC), Seoul, South Korea, 5–8 November 2017; pp. 44–45. [Google Scholar]
- Fayyazi, A.; Kundu, S.; Nazarian, S.; Beerel, P.; Pedram, M. CSrram: Area-Efficient Low-Power Ex-Situ Training Framework for Memristive Neuromorphic Circuits Based on Clustered Sparsity. In Proceedings of the 2019 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Miami, FL, USA, 15–17 July 2019; pp. 465–470. [Google Scholar]
- Kundu, S.; Nazemi, M.; Pedram, M.; Chugg, K.; Beerel, P. Pre-Defined Sparsity for Low-Complexity Convolutional Neural Networks. IEEE Trans. Comput. 2020, 69, 1045–1058. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.; Li, K.; Li, F. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2009), Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Pytorch. Available online: https://pytorch.org (accessed on 1 February 2019).
- Pytorch Model Zoo. Available online: https://pytorch.org/docs/stable/torchvision/models.html (accessed on 1 February 2019).
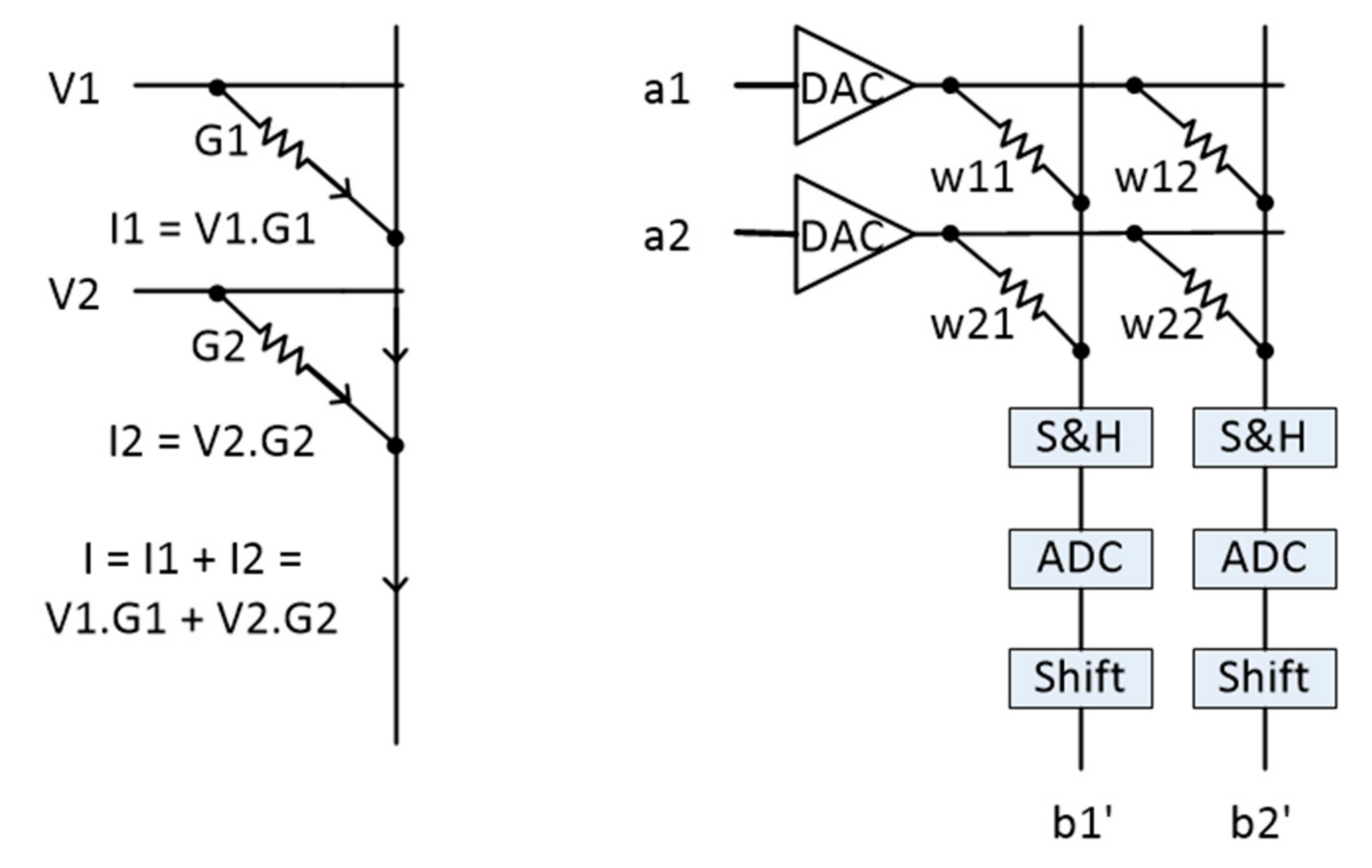
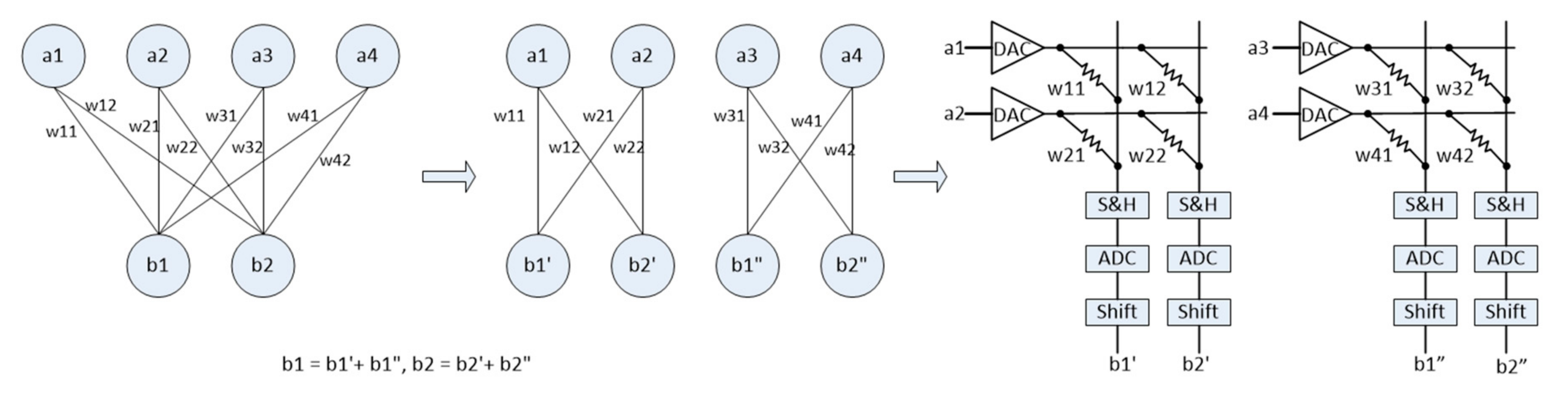
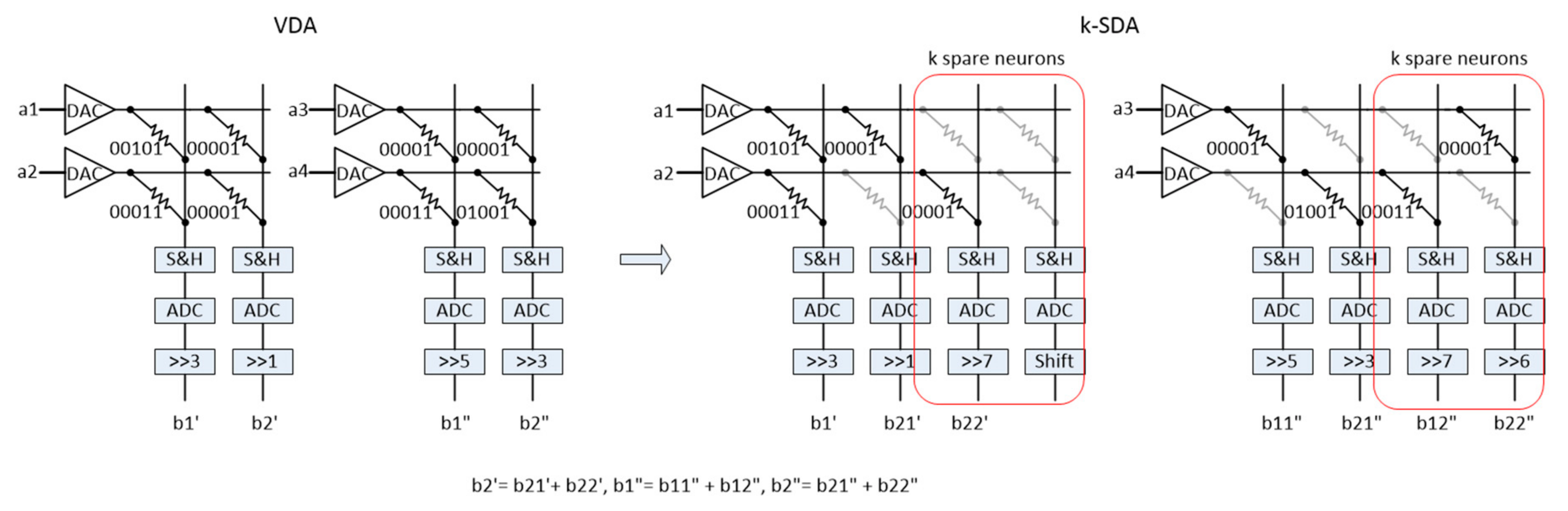

| Floating Point | Fixed Point | Dynamic Fixed Point |
|---|---|---|
| w11 = 0.6027 | 01010(2) × 2−4 | 00101(2) × 2−3 |
| w12 = 0.5012 | 01000(2) × 2−4 | 00001(2) × 2−1 |
| w21 = 0.3528 | 00110(2) × 2−4 | 00011(2) × 2−3 |
| w22 = 0.0062 | 00000(2) × 2−4 | 00001(2) × 2−7 |
| w31 = 0.0352 | 00000(2) × 2−4 | 00001(2) × 2−5 |
| w32 = 0.0251 | 00000(2) × 2−4 | 00011(2) × 2−7 |
| w41 = 0.0178 | 00000(2) × 2−4 | 00001(2) × 2−6 |
| w42 = 1.1098 | 10010(2) × 2−4 | 01001(2) × 2−3 |
| Crossbar Size | 16 × 16 | 32 × 32 | 64 × 64 | ||||
|---|---|---|---|---|---|---|---|
| DNN | Method | Acc (%) | MCAs | Acc (%) | MCAs | Acc (%) | MCAs |
| Vgg16 | Origin | 71.63 | |||||
| VDA | 70.35 | 540,536 | 69.56 | 135,198 | 69.46 | 33,800 | |
| VSDA | 71.43 | 540,543 | 71.23 | 135,273 | 71.21 | 34,100 | |
| L/OH | 0.2 | 0.001% | 0.4 | 0.06% | 0.42 | 0.89% | |
| max_k | 3 | 11 | 47 | ||||
| Resnet152 | Origin | 78.25 | |||||
| VDA | 77.20 | 234,600 | 76.13 | 58,682 | 75.27 | 14,671 | |
| VSDA | 77.82 | 236,480 | 77.60 | 60,092 | 77.65 | 17,026 | |
| L/OH | 0.43 | 0.80% | 0.65 | 2.40% | 0.6 | 16.05% | |
| max_k | 12 | 30 | 63 | ||||
| MobileNet v2 | Origin | 71.85 | |||||
| VDA | 70.14 | 13,806 | 69.74 | 3588 | 69.82 | 1041 | |
| VSDA | 70.20 | 13,808 | 69.76 | 3589 | 69.84 | 1041 | |
| L/OH | 1.65 | 0.01% | 2.09 | 0.03% | 2.01 | 0 % | |
| max_k | 2 | 1 | 1 | ||||
| Crossbar Size | 128 × 128 | 256 × 256 | 512 × 512 | ||||
| DNN | Method | Acc (%) | MCAs | Acc (%) | MCAs | Acc (%) | MCAs |
| Vgg16 | Origin | 71.63 | |||||
| VDA | 69.50 | 8454 | 69.13 | 2121 | 69.04 | 543 | |
| VSDA | 71.29 | 8647 | 71.11 | 2259 | 71.10 | 595 | |
| L/OH | 0.34s | 2.28% | 0.52 | 6.51% | 0.53 | 9.58% | |
| max_k | 92 | 251 | 426 | ||||
| Resnet152 | Origin | 78.25 | |||||
| VDA | 74.23 | 3684 | 74.98 | 968 | 74.97 | 445 | |
| VSDA | 77.64 | 4959 | 77.62 | 1803 | 77.66 | 585 | |
| L/OH | 0.61 | 34.61% | 0.63 | 86.26% | 0.59 | 31.46% | |
| max_k | 116 | 232 | 380 | ||||
| MobileNet v2 | Origin | 71.85 | |||||
| VDA | 69.90 | 360 | 69.91 | 142 | 69.86 | 78 | |
| VSDA | 70.94 | 382 | 71.16 | 164 | 71.12 | 93 | |
| L/OH | 0.91 | 6.11% | 0.69 | 15.49% | 0.73 | 19.23% | |
| max_k | 125 | 253 | 509 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dao, T.D.; Chung, J. An Improved K-Spare Decomposing Algorithm for Mapping Neural Networks onto Crossbar-Based Neuromorphic Computing Systems. J. Low Power Electron. Appl. 2020, 10, 40. https://doi.org/10.3390/jlpea10040040
Dao TD, Chung J. An Improved K-Spare Decomposing Algorithm for Mapping Neural Networks onto Crossbar-Based Neuromorphic Computing Systems. Journal of Low Power Electronics and Applications. 2020; 10(4):40. https://doi.org/10.3390/jlpea10040040
Chicago/Turabian StyleDao, Thanh D., and Jaeyong Chung. 2020. "An Improved K-Spare Decomposing Algorithm for Mapping Neural Networks onto Crossbar-Based Neuromorphic Computing Systems" Journal of Low Power Electronics and Applications 10, no. 4: 40. https://doi.org/10.3390/jlpea10040040
APA StyleDao, T. D., & Chung, J. (2020). An Improved K-Spare Decomposing Algorithm for Mapping Neural Networks onto Crossbar-Based Neuromorphic Computing Systems. Journal of Low Power Electronics and Applications, 10(4), 40. https://doi.org/10.3390/jlpea10040040




