A Simplified Gm − C Filter Technique for Reference Spur Reduction in Phase-Locked Loop
Abstract
:1. Introduction
1.1. Overview of IRNSS PLL
1.2. Reference Spur in PLL
1.3. Spur Reduction Techniques
1.4. Filter Technique for Reference Spur Reduction
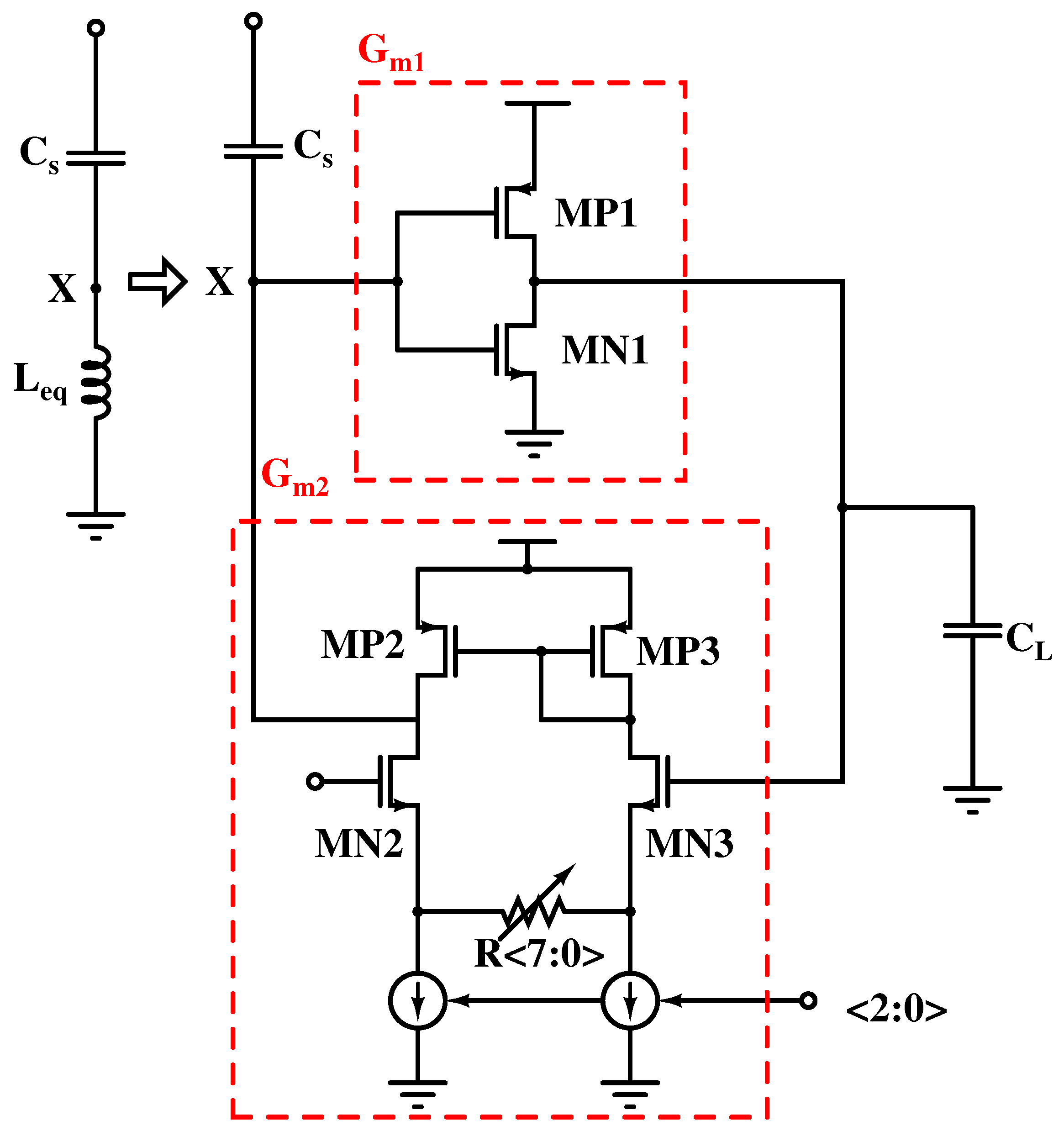
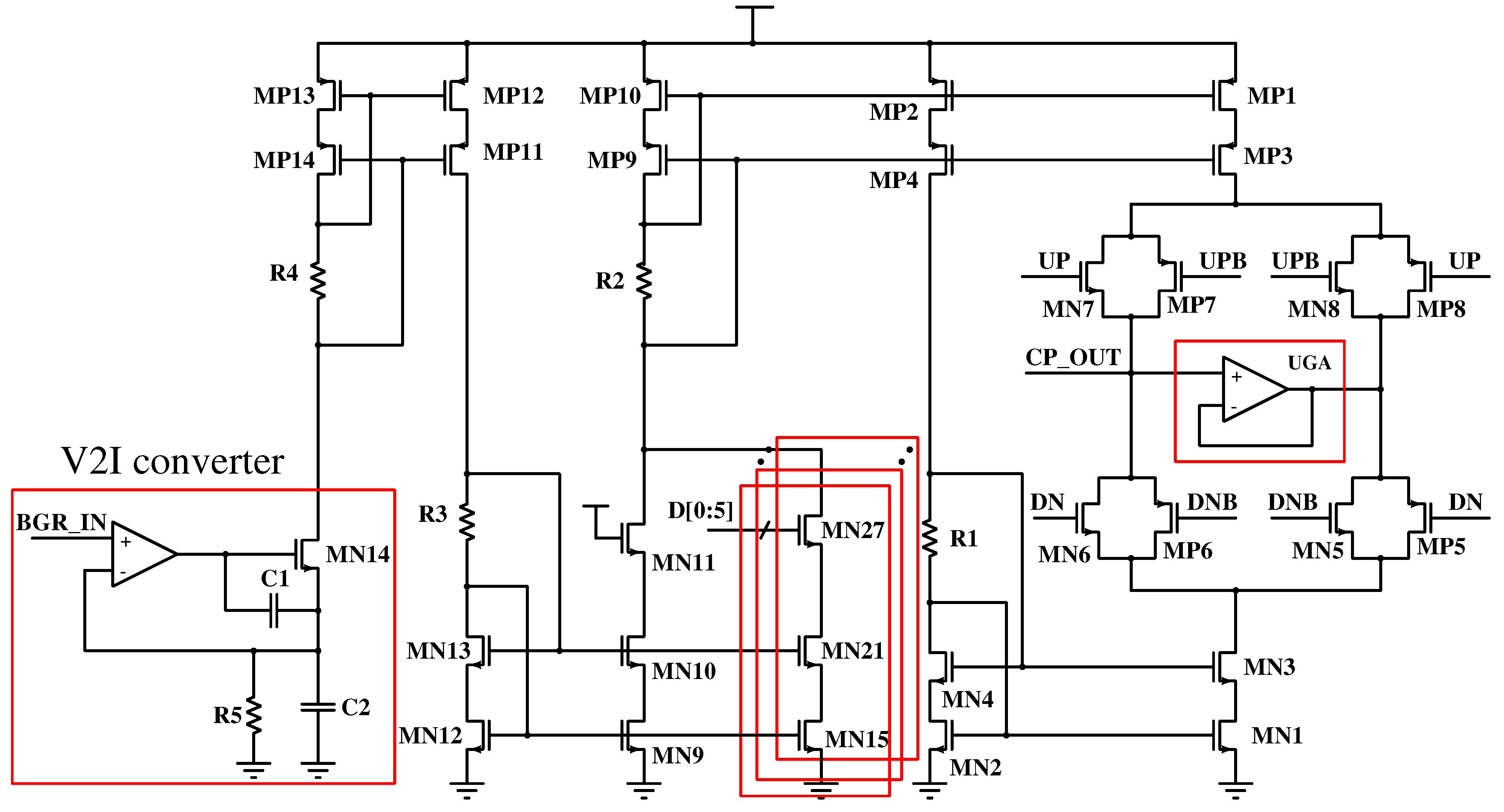
2. Proposed Filter Technique
2.1. Phase-Locked Loop Design
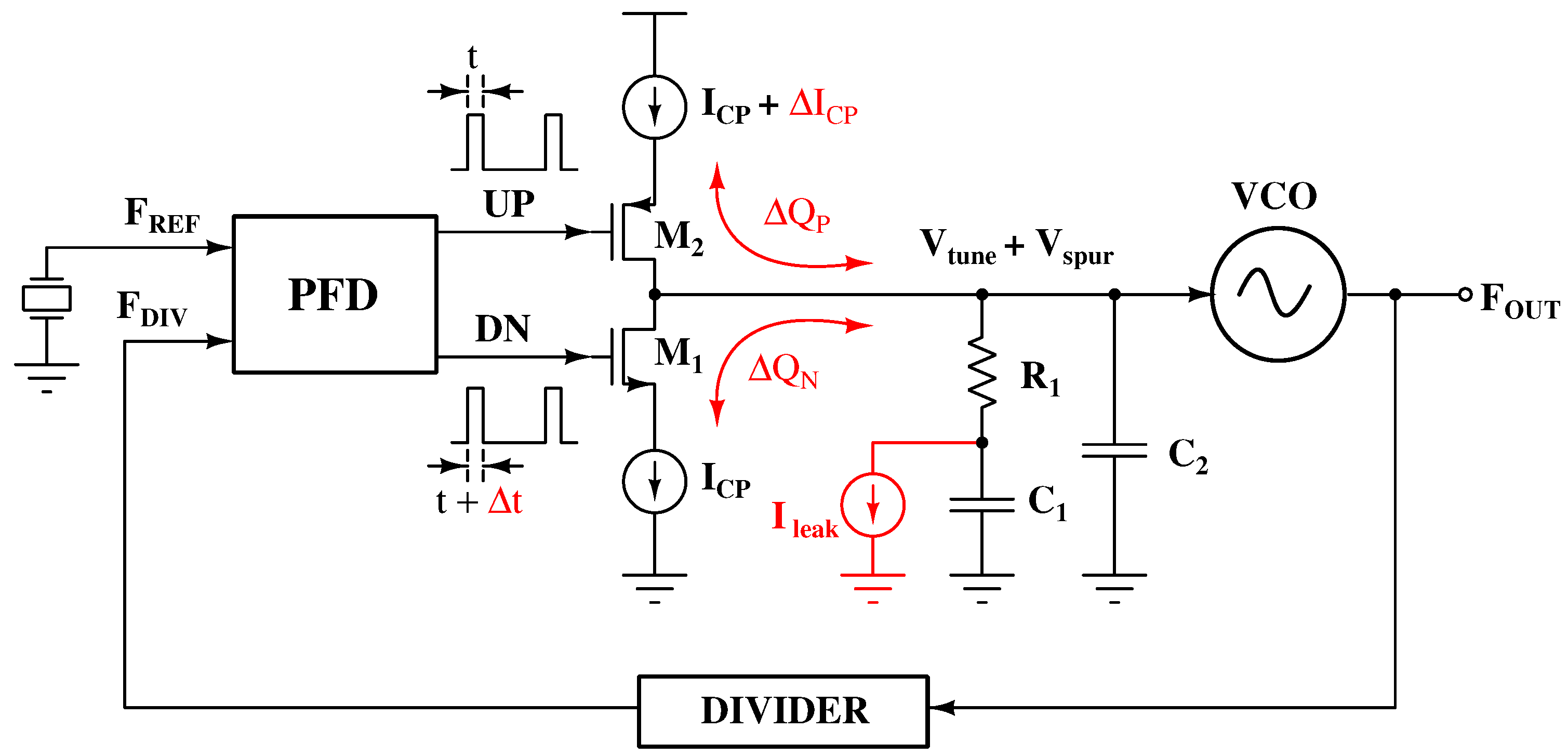
2.1.1. PFD and Charge Pump
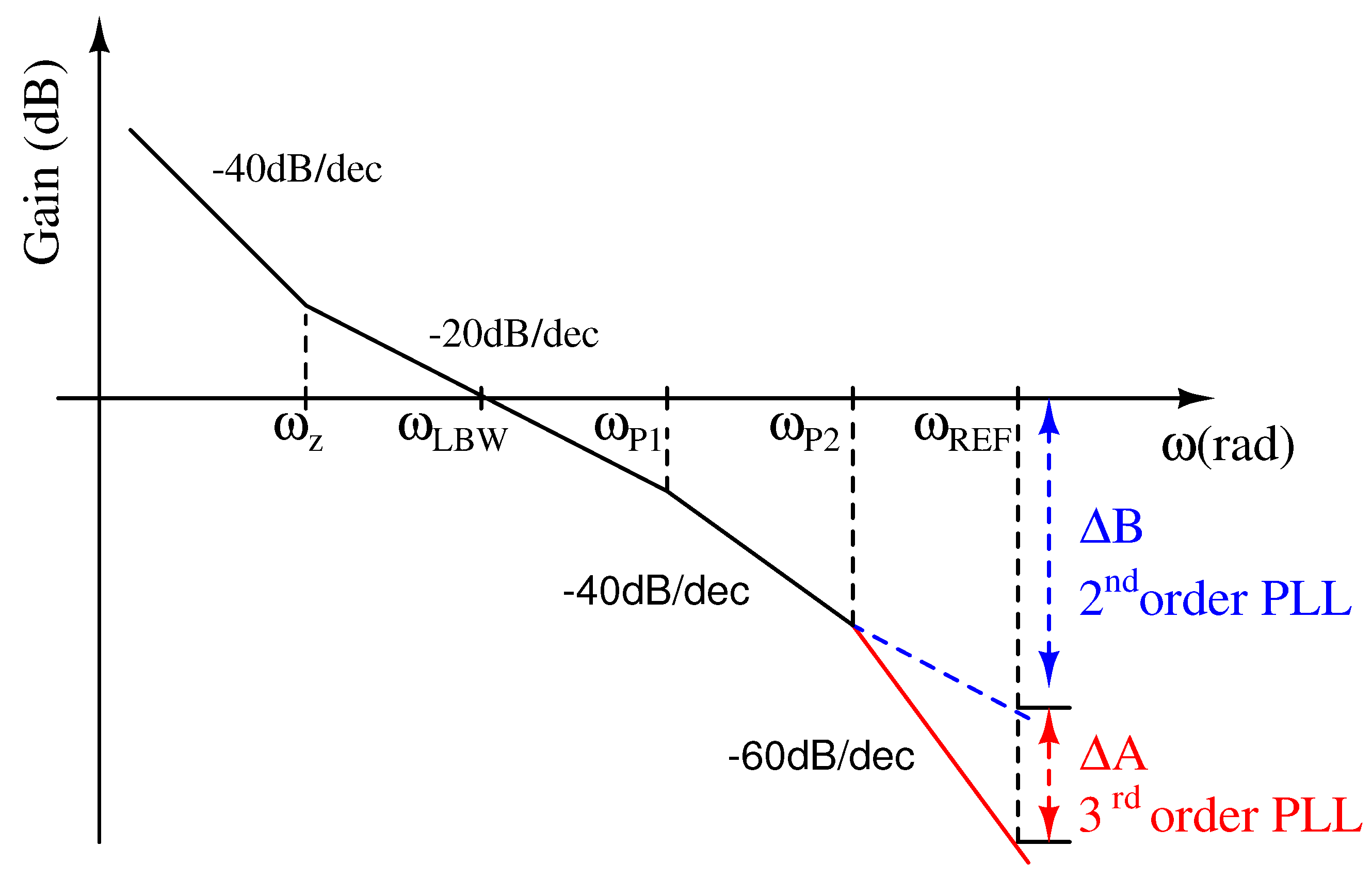
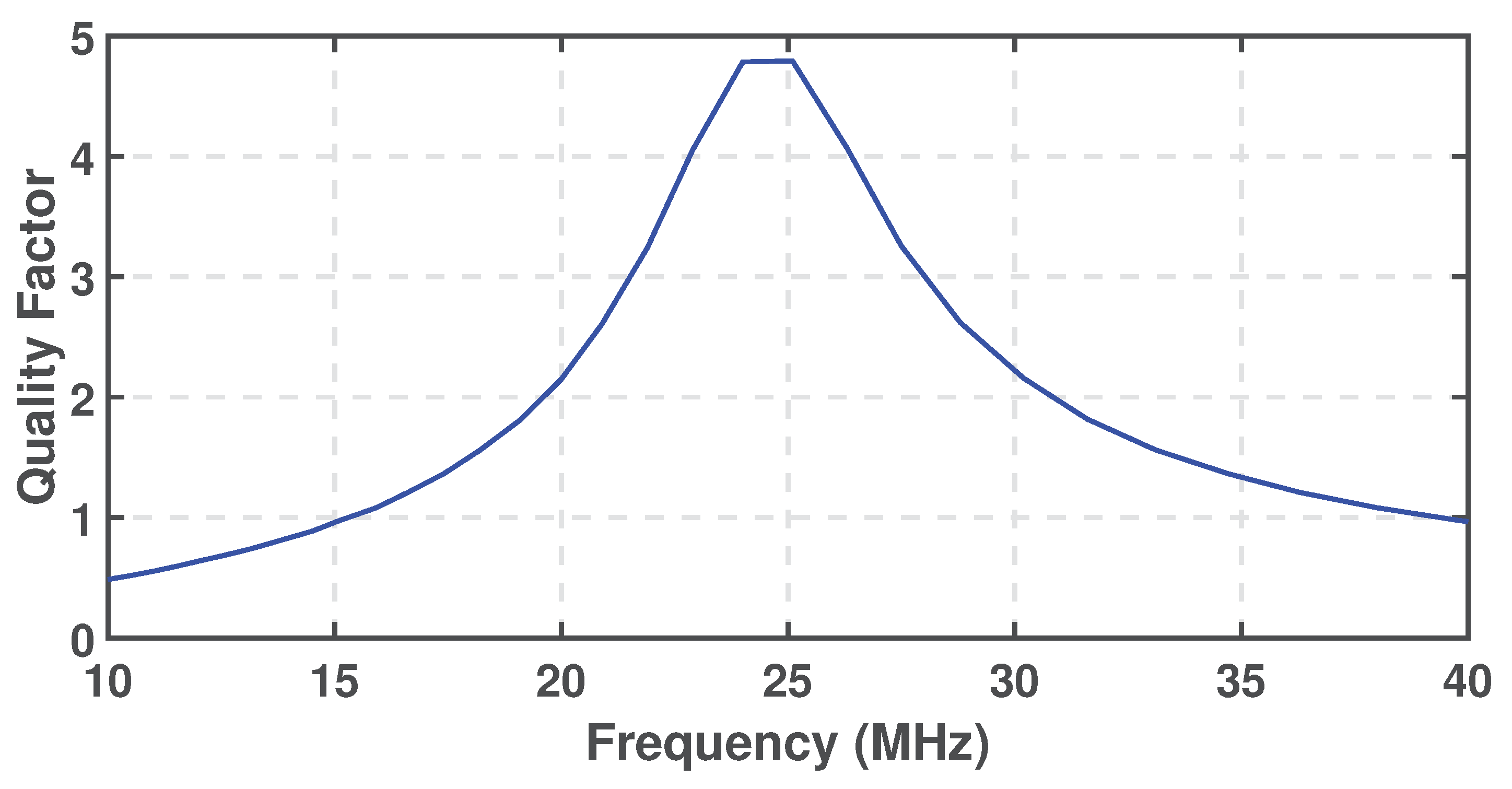
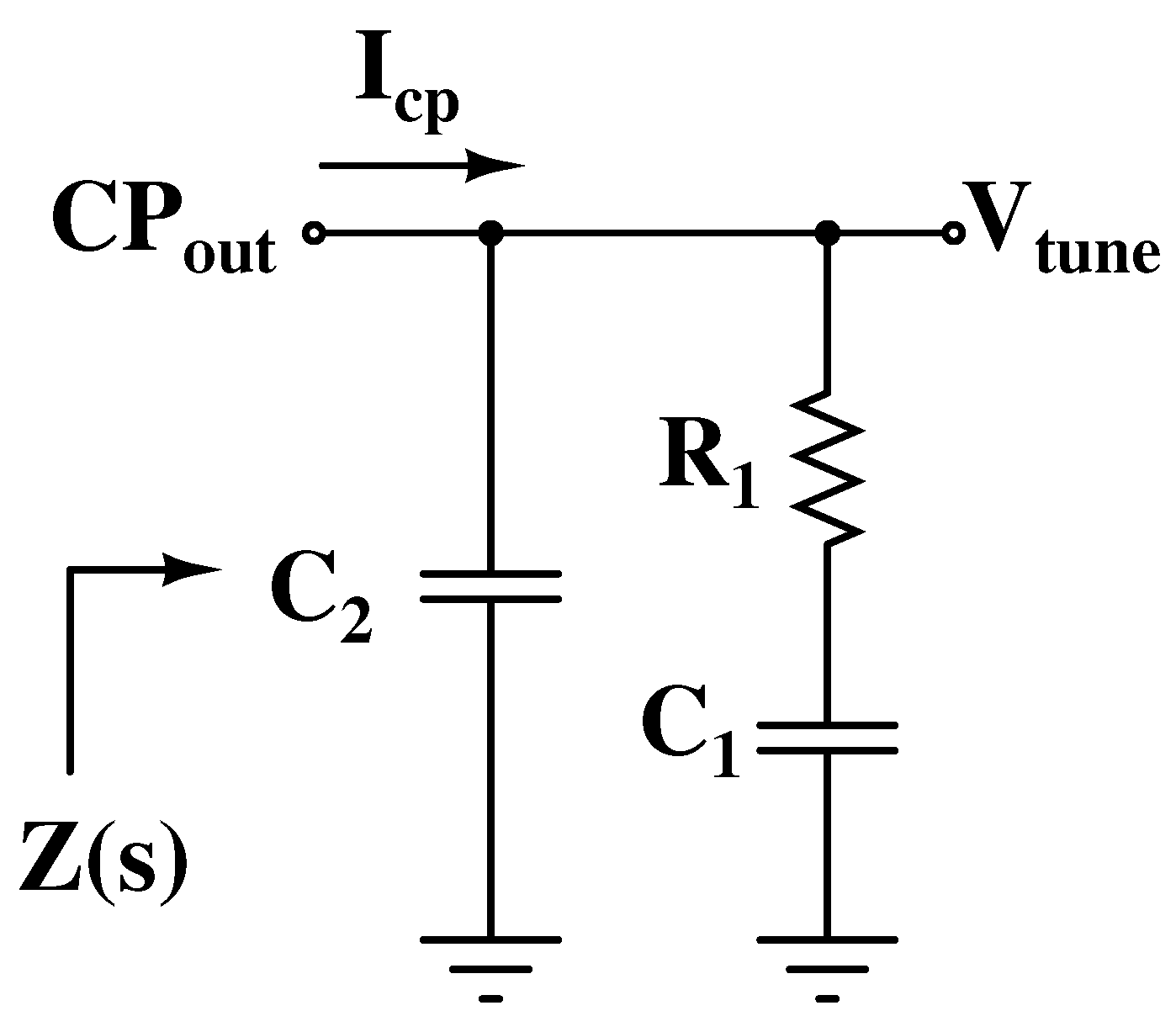
2.1.2. Second-Order Loop Filter
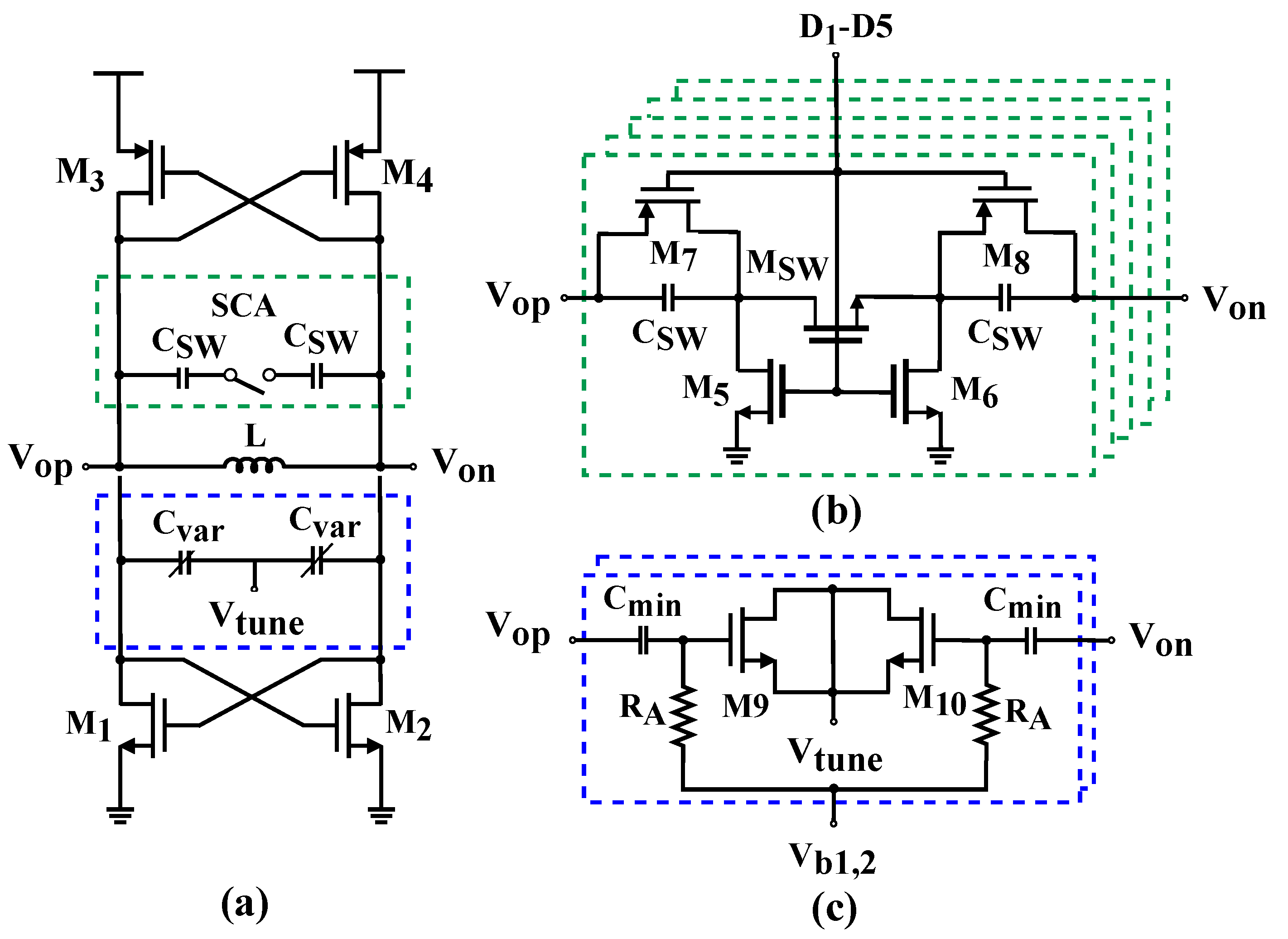
2.1.3. VCO and CML Divider
2.1.4. Feedback Divider
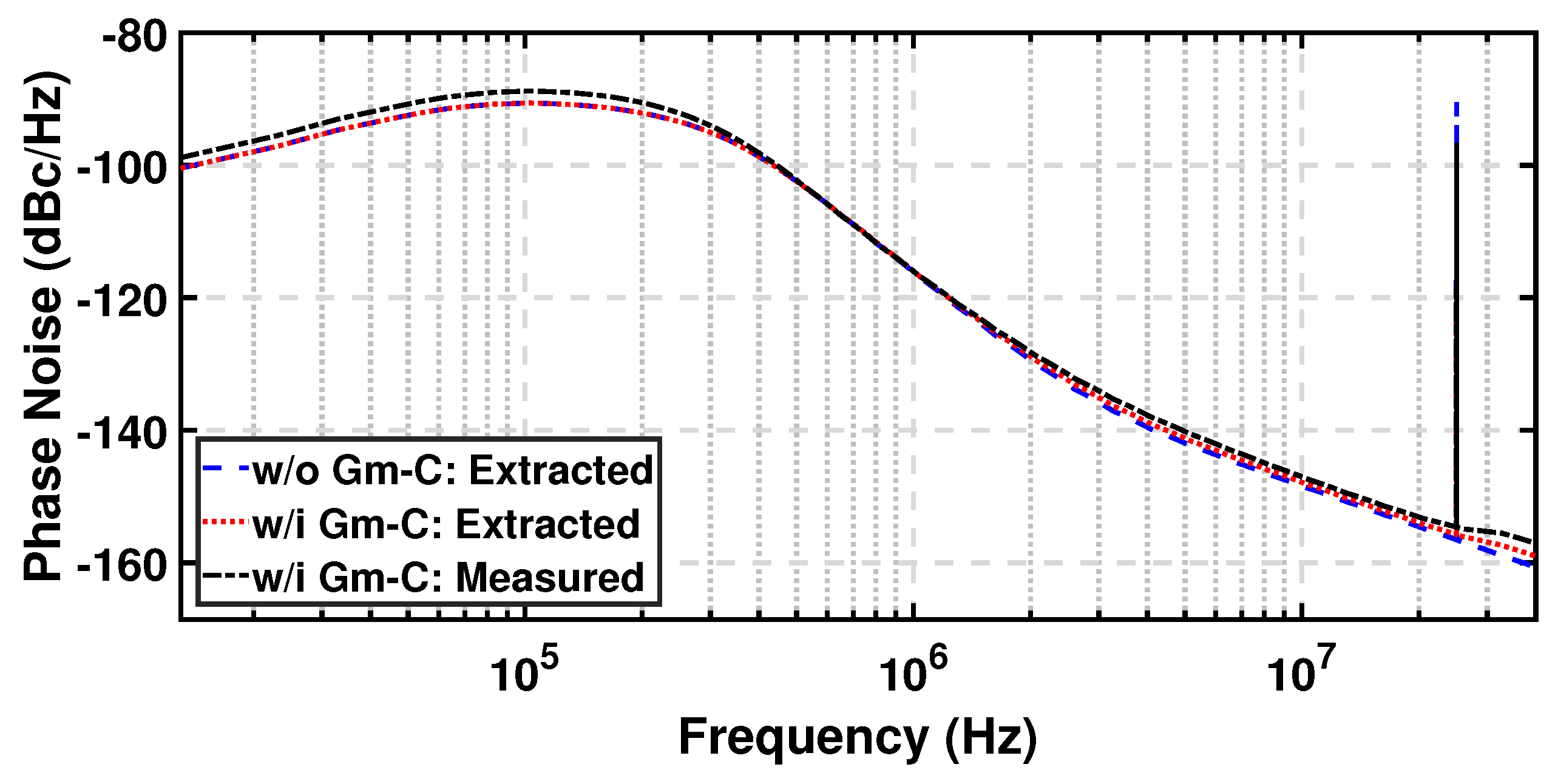
3. Measurement Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ko, J.; Kim, J.; Cho, S.; Lee, K. A 19-mW 2.6-mm/sup 2/ L1/L2 dual-band CMOS GPS receiver. IEEE J. Solid-State Circuits 2005, 40, 1414–1425. [Google Scholar]
- Li, S.; Li, J.; Gu, X.; Wang, H.; Li, C.; Wu, J.; Tang, M. Reconfigurable All-Band RF CMOS Transceiver for GPS/GLONASS/Galileo/Beidou with Digitally Assisted Calibration. IEEE Trans. Very Large Scale Integr. Syst. 2015, 23, 1814–1827. [Google Scholar] [CrossRef]
- Hung, C.-M.; Kenneth, K.O. A fully integrated 1.5-V 5.5-GHz CMOS phase-locked loop. IEEE J. Solid-State Circuits 2002, 37, 521–525. [Google Scholar] [CrossRef]
- Li, A.; Chao, Y.; Chen, X.; Wu, L.; Luong, H.C. A Spur-and-Phase-Noise-Filtering Technique for Inductor-Less Fractional-N Injection-Locked PLLs. IEEE J. Solid-State Circuits 2017, 52, 2128–2140. [Google Scholar] [CrossRef]
- Lee, Y.; Seong, T.; Yoo, S.; Choi, J. A Low-Jitter and Low-Reference-Spur Ring-VCO-Based Switched-Loop Filter PLL Using a Fast Phase-Error Correction Technique. IEEE J. Solid-State Circuits 2018, 53, 1192–1202. [Google Scholar] [CrossRef]
- Seong, T.; Lee, Y.; Yoo, S.; Choi, J. A 320-fs RMS Jitter and −75-dBc Reference-Spur Ring-DCO-Based Digital PLL Using an Optimal-Threshold TDC. IEEE J. Solid-State Circuits 2019, 54, 2501–2512. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, Y.; Mak, P.-I.; Martins, R.P. A Calibration-Free, Reference-Buffer-Free, Type-I Narrow-Pulse-Sampling PLL with −78.7-dBc REF Spur, −128.1-dBc/Hz Absolute In-Band PN and −254-dB FOM. IEEE-Solid-State Circuits Lett. 2020, 3, 494–497. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, Y.; Mak, P.-I.; Martins, R.P. A 0.003-mm2 440fsRMS-Jitter and −64dBc-Reference-Spur Ring-VCO-Based Type-I PLL Using a Current-Reuse Sampling Phase Detector in 28-nm CMOS. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 2307–2316. [Google Scholar] [CrossRef]
- Seol, J.-H.; Choo, K.; Blaauw, D.; Sylvester, D.; Jang, T. Reference Oversampling PLL Achieving −256-dB FoM and −78-dBc Reference Spur. IEEE J. Solid-State Circuits 2021, 56, 2993–3007. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, Y.; Jiao, H.; Mak, P.-I.; Martins, R.P. A 3.36-GHz Locking-Tuned Type-I Sampling PLL with −78.6-dBc Reference Spur Merging Single-Path Reference-Feedthrough-Suppression and Narrow-Pulse-Shielding Techniques. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3093–3097. [Google Scholar] [CrossRef]
- Liang, Y.; Boon, C.C. A 40 GHz CMOS PLL with −75-dBc Reference Spur and 121.9-fsrms Jitter Featuring a Quadrature Sampling Phase-Frequency Detector. IEEE Trans. Microw. Theory Tech. 2022, 70, 2299–2314. [Google Scholar] [CrossRef]
- Liang, Y.; Boon, C.C.; Chen, Q. A 23.4 mW −72-dBc Reference Spur 40 GHz CMOS PLL Featuring a Spur-Compensation Phase Detector. IEEE Microw. Wirel. Components Lett. 2022, 32, 1091–1094. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, Y.; Zhao, B.; Mak, P.-I.; Martins, R.P. A 3.6-GHz Type-II Sampling PLL with a Differential Parallel-Series Double-Edge S-PD Scoring 43.1-fsRMSJitter, −258.7-dB FOM, and −75.17-dBc Reference Spur. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2023, 31, 188–198. [Google Scholar] [CrossRef]
- Verma, A.; Bhagavatula, V.; Singh, A.; Wu, W.; Nagarajan, H.; Lau, P.; Yu, X.; Elsayed, O.; Jain, A.; Sarkar, A.; et al. A 16-Channel, 28/39GHz Dual-Polarized 5G FR2 Phased-Array Transceiver IC with a Quad-Stream IF Transceiver Supporting Non-Contiguous Carrier Aggregation up to 1.6GHz BW. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 18–22 February 2024; pp. 1–3. [Google Scholar]
- Chary, P.P.; Peerla, R.S.; Pula, B.T.; Dutta, A.; Sahoo, B.D. Package Aware LC-VCO with Self-Biased Switched Capacitor Structure for Better Supply Noise Rejection. IEEE TRans. Components Packag. Manuf. Tech. 2022, 12, 1653–1660. [Google Scholar] [CrossRef]
- Shi, C.; Wang, C.; Ye, L.; Liao, H. 99 dBc/Hz @ 10 KHz 1 MHz-step dual-loop integer-N PLL with anti-mislocking frequency calibration for global navigation satellite system receiver. In Proceedings of the 2011 IEEE International Symposium of Circuits and Systems (ISCAS), Rio de Janeiro, Brazil, 15–18 May 2011; pp. 1876–1879. [Google Scholar]
- Bai, Z.; Zhou, X.; Mason, R.D.; Allan, G. A 2-GHz Pulse Injection-Locked Rotary Traveling-Wave Oscillator. IEEE Trans. Microw. Theory Tech. 2016, 64, 1854–1866. [Google Scholar] [CrossRef]
- Kharalkar, A.; Pancholi, M.; Kanchetla, V.K.; Khade, A.; Khyalia, S.; Hameed, S.; Zele, R. A Compact, Low-Phase Noise Fractional-N PLL for Global Navigation Receiver. In Proceedings of the IEEE 19th New Circuits and Systems Conference (NEWCAS), Toulon, France, 13–16 June 2021; pp. 1–4. [Google Scholar]
- Peerla, R.S.; Chary, P.; Dutta, A.; Sahoo, B.D. A Dual VCO Based L5/S Band PLL with Extended Range Divider for IRNSS Application. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Austin, TX, USA, 27 May–1 June 2022; pp. 1699–1703. [Google Scholar]
- Shaik Peerla, R.; Dutta, A.; Sahoo, B.D. An Extended Range Divider Technique for Multi-Band PLL. J. Low Power Electron. Appl. 2023, 13, 43. [Google Scholar] [CrossRef]
- Elsayed, M.M.; Abdul-Latif, M.; Sanchez-Sinencio, E. A Spur-Frequency-Boosting PLL with a −74 dBc Reference-Spur Suppression in 90 nm Digital CMOS. IEEE J. Solid-State Circuits 2013, 48, 2104–2117. [Google Scholar] [CrossRef]
- Rhee, W. Design of high-performance CMOS charge pumps in phase-locked loops. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Orlando, FL, USA, 30 May–2 June 1999; Volume 2, pp. 545–548. [Google Scholar]
- Lin, T.H.; Kaiser, W.J. A 900-MHz 2.5-mA CMOS frequency synthesizer with an automatic SC tuning loop. IEEE J. Solid-State Circuits 2001, 36, 424–431. [Google Scholar]
- Gao, X.; Klumperink, E.A.; Socci, G.; Bohsali, M.; Nauta, B. Spur Reduction Techniques for Phase-Locked Loops Exploiting A Sub-Sampling Phase Detector. IEEE J. Solid-State Circuits 2010, 45, 1809–1821. [Google Scholar] [CrossRef]
- Lee, T.; Lee, W. A Spur Suppression Technique for Phase-Locked Frequency Synthesizers. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 6–9 February 2006; pp. 2432–2441. [Google Scholar]
- Ko, H.G.; Bae, W.; Jeong, G.S.; Jeong, D.K. Reference Spur Reduction Techniques for a Phase-Locked Loop. IEEE Access 2019, 7, 38035–38043. [Google Scholar] [CrossRef]
- Sharma, J.; Krishnaswamy, H. A 2.4-GHz Reference-Sampling Phase-Locked Loop That Simultaneously Achieves Low-Noise and Low-Spur Performance. IEEE J. Solid-State Circuits 2019, 54, 1407–1424. [Google Scholar] [CrossRef]
- Kong, L.; Razavi, B. A 2.4 GHz 4 mW Integer-N Inductorless RF Synthesizer. IEEE J. Solid-State Circuits 2016, 51, 626–635. [Google Scholar] [CrossRef]
- Cheng, X.; Chen, F.J.; Zhang, L.; Gao, H.; Han, J.A.; Han, J.Y.; Yu, Y.; Deng, X.J. A Closed-Loop Reconfigurable Analog Baseband Circuitry with Open-Loop Tunable Notch Filters to Improve Receiver Tx Leakage and Close-in Blocker Tolerance. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 839–843. [Google Scholar] [CrossRef]
- Razavi, B. Design of CMOS Phase-Locked Loops: From Circuit Level to Architecture Level; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Lavrič, A.; Batagelj, B.; Vidmar, M. Calibration of an RF/Microwave Phase Noise Meter with a Photonic Delay Line. Photonics 2022, 9, 533. [Google Scholar] [CrossRef]
- Wu, W.; Yao, C.W.; Guo, C.; Chiang, P.Y.; Chen, L.; Lau, P.K.; Bai, Z.; Son, S.W.; Cho, T.B. A 14-nm Ultra-Low Jitter Fractional-N PLL Using a DTC Range Reduction Technique and a Reconfigurable Dual-Core VCO. IEEE J. Solid-State Circuits 2021, 56, 3756–3767. [Google Scholar] [CrossRef]








| Parameter | Value |
|---|---|
| Crystal frequency (MHz) | 23 to 27 |
| VCO range (GHz) | 1.6 to 3.2 |
| VCO gain (MHz/V) | 80 to 120 |
| (mA) | 0.1 to 1 |
| Division ratio | 64 to 127 |
| Loop bandwidth (kHz) | 160 to 240 |
| Phase margin (°) | 54 to 59 |
| PN @ 100 kHz (dBc/Hz) | −90 to −95 |
| PN @ 1 MHz (dBc/Hz) | −115 to −120 |
| X | 0 | ||
| 0 | 1 | ||
| 1 | 1 |
| This Work | [28] | [29] | |
|---|---|---|---|
| Supply (V) | 2.5 | 1.3 | 1.8 |
| Architecture (V) | Single ended | Differential | Differential |
| Operational amplifier in implementation | No | Yes (Single ended) | Yes (Fully differential) |
| Circuit Complexity | Low | Moderate | High |
| Current (mA) | 0.2 | 0.4 | 1.5 |
| Compatible with lower supply | Yes | No | No |
| Programmability | No † | Yes | Yes |
| This Work | [18] | [26] | [32] | |
|---|---|---|---|---|
| Technology (nm) | 65 | 65 | 65 | 14 |
| Supply (V) | 2.5/1.2 | 1.2 | 1.3 | 1/0.8 |
| Frequency (GHz) | 1.6–3.2 | 1.17–2.5 | 0.8 | 5–7 |
| Reference (MHz) | 23–27 | 23–27 | 50 | 76.8 |
| PN (dBc/Hz) @ 1 MHz | −116/−122 | −116 | −110 | −122 |
| Area () | 0.8 | 0.25 | 0.935 | 0.31 |
| Power (mW) | 30 | 15.7 | 4.8 | 14.2 |
| Ref. spur (dBc) | −64 (−57 ‡) | NA | −68.57 | −69.6 |
| FoM † | 171.3 | 165.4 | 161.25 | 186.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chary, P.P.; Shaik Peerla, R.; Dutta, A. A Simplified Gm − C Filter Technique for Reference Spur Reduction in Phase-Locked Loop. J. Low Power Electron. Appl. 2024, 14, 17. https://doi.org/10.3390/jlpea14010017
Chary PP, Shaik Peerla R, Dutta A. A Simplified Gm − C Filter Technique for Reference Spur Reduction in Phase-Locked Loop. Journal of Low Power Electronics and Applications. 2024; 14(1):17. https://doi.org/10.3390/jlpea14010017
Chicago/Turabian StyleChary, P. Purushothama, Rizwan Shaik Peerla, and Ashudeb Dutta. 2024. "A Simplified Gm − C Filter Technique for Reference Spur Reduction in Phase-Locked Loop" Journal of Low Power Electronics and Applications 14, no. 1: 17. https://doi.org/10.3390/jlpea14010017
APA StyleChary, P. P., Shaik Peerla, R., & Dutta, A. (2024). A Simplified Gm − C Filter Technique for Reference Spur Reduction in Phase-Locked Loop. Journal of Low Power Electronics and Applications, 14(1), 17. https://doi.org/10.3390/jlpea14010017






