An Ultra-Low-Voltage Approach to Accurately Set the Quiescent Current of Digital Standard Cells Used for Analog Design and Its Application on an Inverter-Based Operational Transconductance Amplifier
Abstract
:1. Introduction
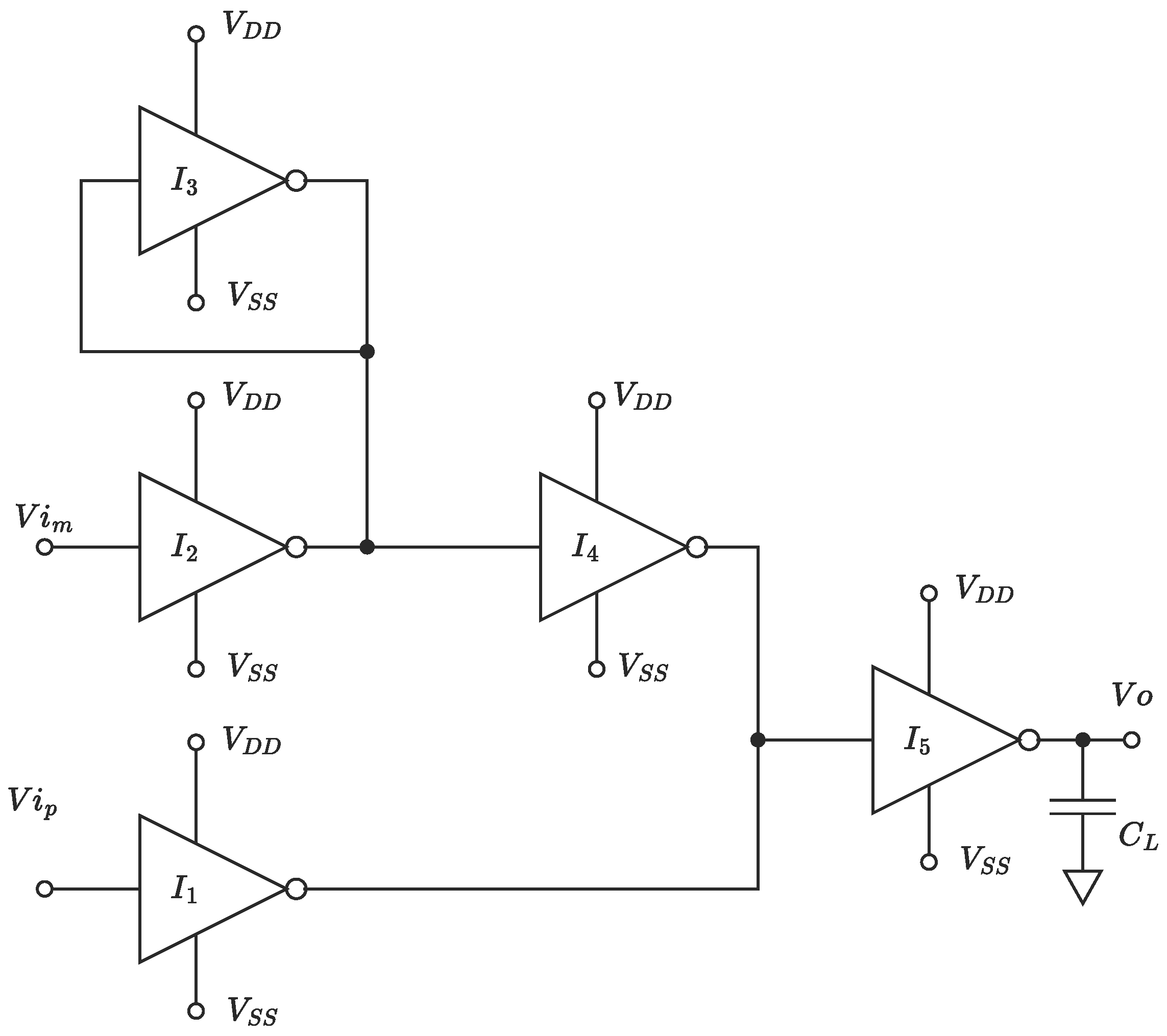
2. Two-Stage Standard-Cell-Based OTA Operating in Sub-Threshold
2.1. Characterization of the CMOS Inverter Operating in Sub-Threshold and Transfer Matrix
2.2. Analytical Characterization of the Standard-Cell-Based Two-Stage OTA
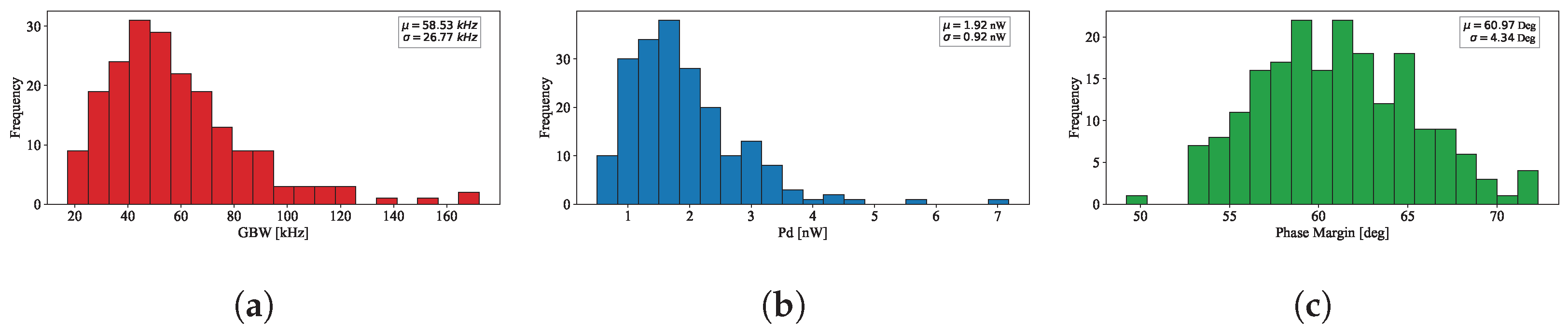
2.3. Simulation Results on the Conventional Standard-Cell-Based Two-Stage OTA Operating in Sub-Threshold without Quiescent Current Control
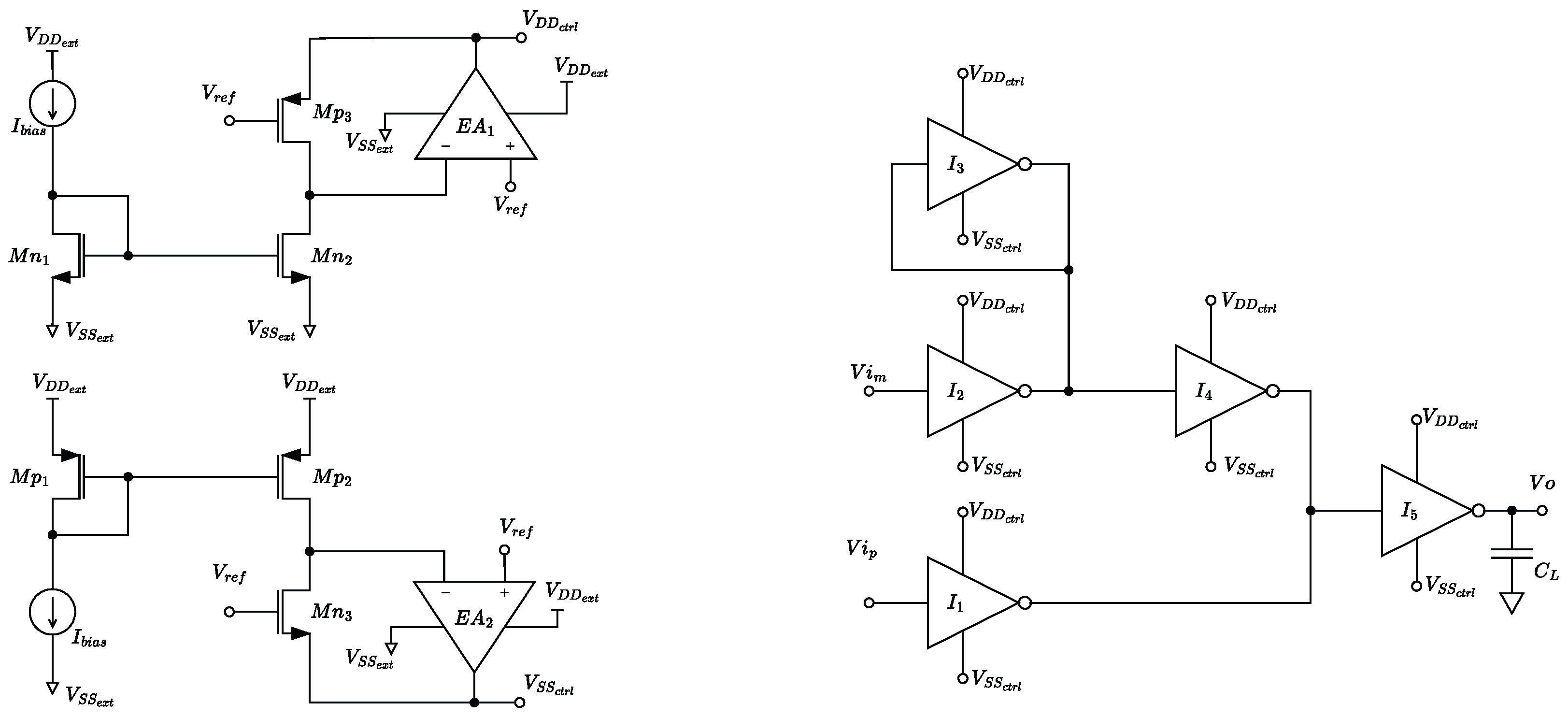
3. Proposed Approach to Set the Quiescent Current of Standard-Cell Inverters and Application to a Standard-Cell-Based OTA
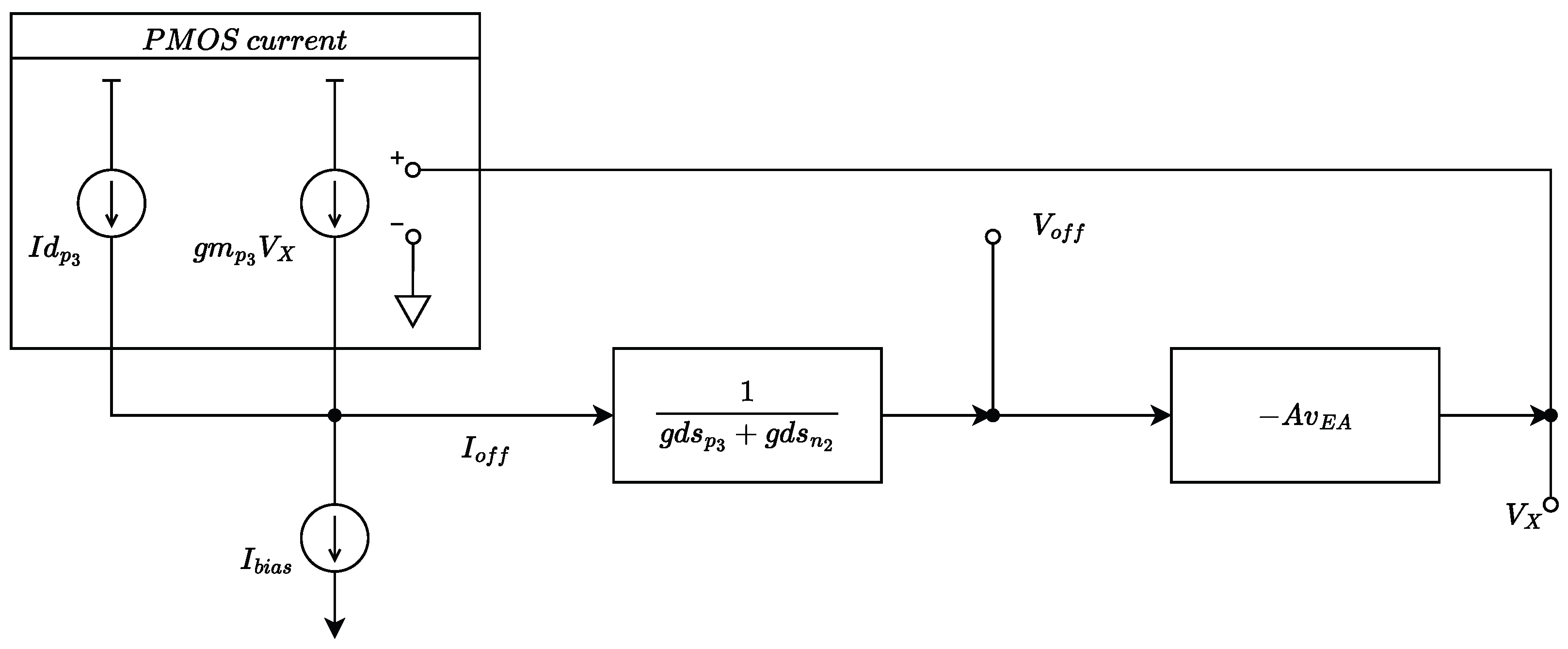
3.1. Analysis of the Feedback Loop in the ASV Generators
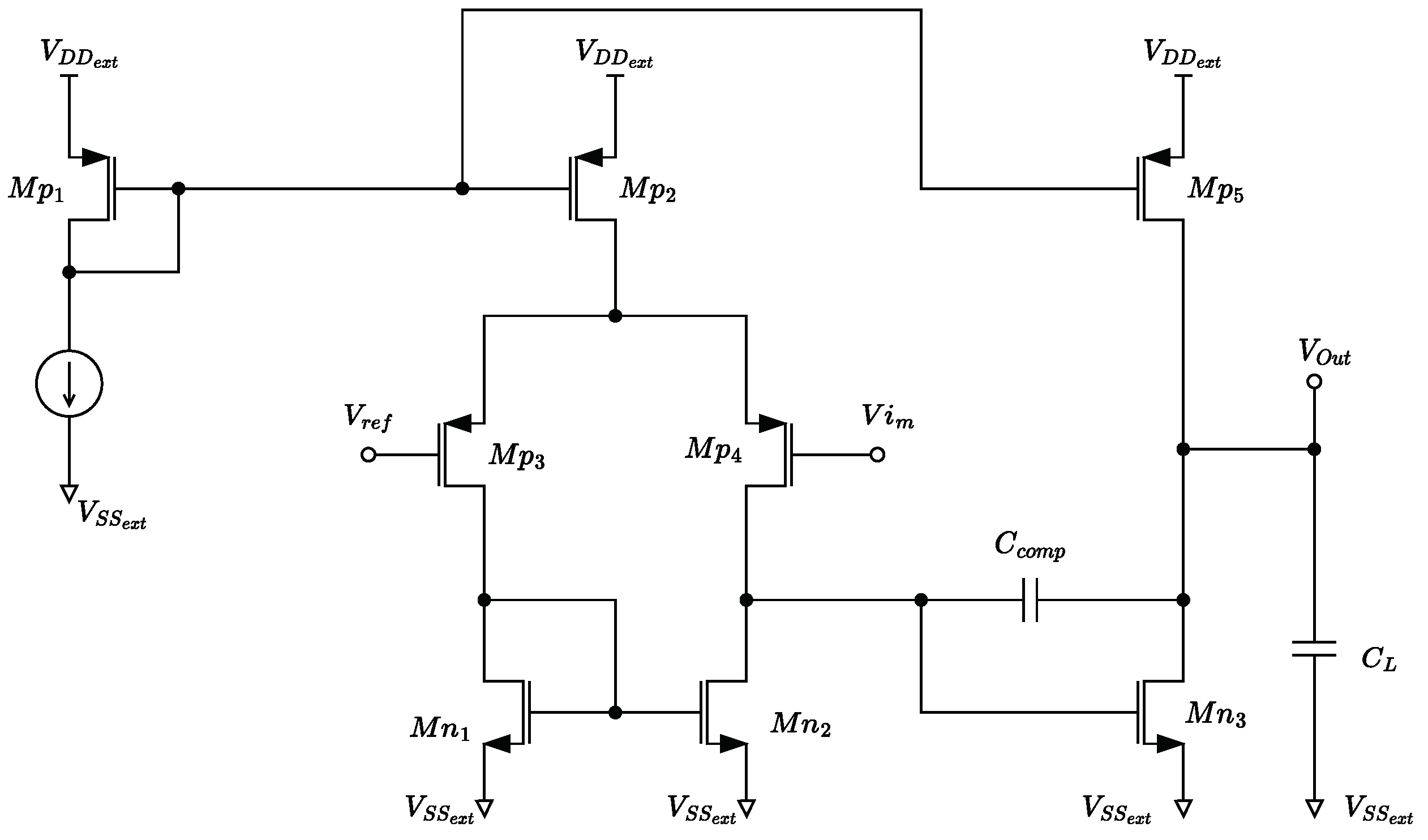
3.2. Implementation of the Error Amplifier
3.3. Impact of the and ASV Generators on the PSRR
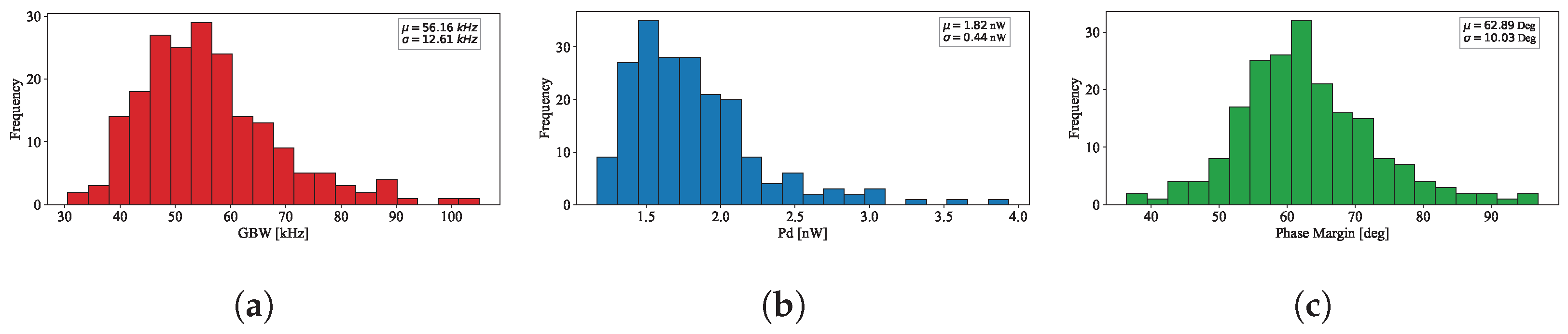
4. Simulation Results on the Standard-Cell-Based Two-Stage OTA Operating in Sub-Threshold with the Proposed Quiescent Current Control
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASV | Adaptive Supply Voltage |
| ASVG | Adaptive Supply Voltage Generator |
| DAC | Digital-to-Analog Converter |
| DIGOTA | Digital Operational Transconductance Amplifier |
| GBW | Gain–Bandwidth Product |
| IoT | Internet of Things |
| OTA | Operational Transconductance Amplifier |
| PSRR | Power Supply Rejection Ratio |
| PVT | Process, Supply Voltage, and Temperature |
| ULP | Ultra-Low Power |
| ULV | Ultra-Low Voltage |
References
- Buzzin, A.; Asquini, R.; Caputo, D.; de Cesare, G. Sensitive and Compact Evanescent-Waveguide Optical Detector for Sugar Sensing in Commercial Beverages. Sensors 2023, 23, 8184. [Google Scholar] [CrossRef] [PubMed]
- Gupta, B.B.; Quamara, M. An overview of Internet of Things (IoT): Architectural aspects, challenges, and protocols. Concurr. Comput. Pract. Exper. 2020, 32, e4946. [Google Scholar] [CrossRef]
- Kadhim, K.T.; Alsahlany, A.M.; Wadi, S.M.; Kadhum, H.T. An Overview of Patient’s Health Status Monitoring System Based on Internet of Things (IoT). Wirel. Pers. Commun. 2020, 114, 2235–2262. [Google Scholar] [CrossRef]
- Barbirotta, M.; Cheikh, A.; Mastrandrea, A.; Menichelli, F.; Vigli, F.; Olivieri, M. A Fault Tolerant soft-core obtained from an Interleaved-Multi- Threading RISC- V microprocessor design. In Proceedings of the 2021 IEEE International Symposium on Defect and Fault Tolerance in VLSI and Nanotechnology Systems (DFT), Athens, Greece, 6–8 October 2021; pp. 6–8. [Google Scholar] [CrossRef]
- Chuah, J.W. The Internet of Things: An overview and new perspectives in systems design. In Proceedings of the 2014 International Symposium on Integrated Circuits (ISIC), Singapore, 10–12 December 2014; pp. 10–12. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.; Alioto, M. Fully Synthesizable Low-Area Analogue-to-Digital Converters with Minimal Design Effort Based on the Dyadic Digital Pulse Modulation. IEEE Access 2020, 8, 70890–70899. [Google Scholar] [CrossRef]
- Di Patrizio Stanchieri, G.; Aiello, O.; De Marcellis, A. A 0.4 V 180 nm CMOS Sub-μW Ultra-Compact and Low-Effort Design PWM-Based ADC. In Proceedings of the 2024 IEEE International Symposium on Circuits and Systems (ISCAS), New Delhi, India, 18–19 October 2024; pp. 19–22. [Google Scholar] [CrossRef]
- Toledo, P.; Aiello, O.; Crovetti, P.S. A 300mV-Supply Standard-Cell-Based OTA with Digital PWM Offset Calibration. In Proceedings of the 2019 IEEE Nordic Circuits and Systems Conference (NORCAS): NORCHIP and International Symposium of System-on-Chip (SoC), Helsinki, Finland, 29–30 October 2019; pp. 29–30. [Google Scholar] [CrossRef]
- Centurelli, F.; Della Sala, R.; Scotti, G. A Standard-Cell-Based CMFB for Fully Synthesizable OTAs. J. Low Power Electron. Appl. 2022, 12, 27. [Google Scholar] [CrossRef]
- Barbirotta, M.; Menichelli, F.; Cheikh, A.; Mastrandrea, A.; Angioli, M.; Olivieri, M. Dynamic Triple Modular Redundancy in Interleaved Hardware Threads: An Alternative Solution to Lockstep Multi-Cores for Fault-Tolerant Systems. IEEE Access 2024, 12, 95720–95735. [Google Scholar] [CrossRef]
- Sood, L.; Agarwal, A. A CMOS standard-cell based fully-synthesizable low-dropout regulator for ultra-low power applications. AEU Int. J. Electron. Commun. 2021, 141, 153958. [Google Scholar] [CrossRef]
- Xu, Z.; Ojima, N.; Li, S.; Iizuka, T. An All-Standard-Cell-Based Synthesizable SAR ADC With Nonlinearity-Compensated RDAC. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2021, 29, 2153–2162. [Google Scholar] [CrossRef]
- Toledo, P.; Crovetti, P.; Aiello, O.; Alioto, M. Design of Digital OTAs With Operation Down to 0.3 V and nW Power for Direct Harvesting. IEEE Trans. Circuits Syst. I 2021, 68, 3693–3706. [Google Scholar] [CrossRef]
- Toledo, P.; Crovetti, P.; Aiello, O.; Alioto, M. Fully Digital Rail-to-Rail OTA With Sub-1000-μm2 Area, 250-mV Minimum Supply, and nW Power at 150-pF Load in 180 nm. IEEE Solid-State Circuits Lett. 2020, 3, 474–477. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.; Sharma, A.; Alioto, M. Fully-Synthesizable Current-Input ADCs for Ultra-Low Area and Minimal Design Effort. In Proceedings of the 2019 26th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Genoa, Italy, 27–29 November 2019; pp. 27–29. [Google Scholar] [CrossRef]
- Liu, J.; Park, B.; Guzman, M.; Fahmy, A.; Kim, T.; Maghari, N. A Fully Synthesized 77-dB SFDR Reprogrammable SRMC Filter Using Digital Standard Cells. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2018, 26, 1126–1138. [Google Scholar] [CrossRef]
- Toledo, P.; Klimach, H.; Bampi, S.; Crovetti, P. A 300 mV-Supply, 144 nW-Power, 0.03 mm2-Area, 0.2-PEF Digital-Based Biomedical Signal Amplifier in 180 nm CMOS. In Proceedings of the 2021 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Lausanne, Switzerland, 23–25 June 2021; pp. 23–25. [Google Scholar] [CrossRef]
- Della Sala, R.; Centurelli, F.; Scotti, G. A High Performance 0.3 V Standard-Cell-Based OTA Suitable for Automatic Layout Flow. Appl. Sci. 2023, 13, 5517. [Google Scholar] [CrossRef]
- Sala, R.D.; Centurelli, F.; Scotti, G. A Novel Differential to Single-Ended Converter for Ultra-Low-Voltage Inverter-Based OTAs. IEEE Access 2022, 10, 98179–98190. [Google Scholar] [CrossRef]
- Toledo, P.; Crovetti, P.; Klimach, H.; Bampi, S.; Aiello, O.; Alioto, M. A 300mV-Supply, Sub-nW-Power Digital-Based Operational Transconductance Amplifier. IEEE Trans. Circuits Syst. II 2021, 68, 3073–3077. [Google Scholar] [CrossRef]
- Angioli, M.; Barbirotta, M.; Cheikh, A.; Mastrandrea, A.; Menichelli, F.; Jamili, S.; Olivieri, M. Design, Implementation and Evaluation of a New Variable Latency Integer Division Scheme. IEEE Trans. Comput. 2024, 73, 1767–1779. [Google Scholar] [CrossRef]
- Privitera, M.; Crovetti, P.; Grasso, A.D. A Novel Digital OTA Topology With 66-dB DC Gain and 12.3-kHz Bandwidth. IEEE Trans. Circuits Syst. II 2023, 70, 3988–3992. [Google Scholar] [CrossRef]
- Crovetti, P.S. All-Digital High Resolution D/A Conversion by Dyadic Digital Pulse Modulation. IEEE Trans. Circ. Syst. I 2016, 64, 573–584. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.; Alioto, M. Standard Cell-Based Ultra-Compact DACs in 40-nm CMOS. IEEE Access 2019, 7, 126479–126488. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.S.; Alioto, M. Fully Synthesizable Low-Area Digital-to-Analog Converter With Graceful Degradation and Dynamic Power-Resolution Scaling. IEEE Trans. Circ. Syst. I 2019, 66, 2865–2875. [Google Scholar] [CrossRef]
- Rubino, R.; Crovetti, P.S.; Aiello, O. Design of Relaxation Digital-to-Analog Converters for Internet of Things Applications in 40nm CMOS. In Proceedings of the 2019 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Bangkok, Thailand, 11–14 November 2019; pp. 11–14. [Google Scholar] [CrossRef]
- Sala, R.D.; Centurelli, F.; Scotti, G. Enabling ULV Fully Synthesizable Analog Circuits: The BA Cell, a Standard-Cell-Based Building Block for Analog Design. IEEE Trans. Circuits Syst. II 2022, 69, 4689–4693. [Google Scholar] [CrossRef]
- Sala, R.D.; Centurelli, F.; Scotti, G. A Novel High Performance Standard-Cell Based ULV OTA Exploiting an Improved Basic Amplifier. IEEE Access 2024, 12, 17513–17521. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.; Alioto, M. Ultra-Low Power and Minimal Design Effort Interfaces for the Internet of Things: Invited paper. In Proceedings of the 2019 IEEE International Circuits and Systems Symposium (ICSyS), Kuantan, Malaysia, 18–19 September 2019; pp. 18–19. [Google Scholar] [CrossRef]
- Buzzin, A.; Cupo, S.; Giovine, E.; de Cesare, G.; Belfiore, N.P. Compliant Nano-Pliers as a Biomedical Tool at the Nanoscale: Design, Simulation and Fabrication. Micromachines 2020, 11, 1087. [Google Scholar] [CrossRef] [PubMed]
- Namdari, A.; Aiello, O.; Caviglia, D.D. 0.5V 32nW Inverter-Based Gm-C Filter for Bio-Signal Processing. In Proceedings of the 2024 IEEE International Symposium on Circuits and Systems (ISCAS), New Delhi, India, 18–19 October 2024; pp. 19–22. [Google Scholar] [CrossRef]
- Sanchotene Silva, R.; Rodovalho, L.H.; Aiello, O.; Ramos Rodrigues, C. A 1.9 nW, Sub-1 V, 542 pA/V Linear Bulk-Driven OTA with 154 dB CMRR for Bio-Sensing Applications. J. Low Power Electron. Appl. 2021, 11, 40. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.; Lin, L.; Alioto, M. A pW-Power Hz-Range Oscillator Operating With a 0.3–1.8-V Unregulated Supply. IEEE J. Solid-State Circuits 2019, 54, 1487–1496. [Google Scholar] [CrossRef]
- Buzzin, A.; Asquini, R.; Caputo, D.; de Cesare, G. Evanescent waveguide lab-on-chip for optical biosensing in food quality control. Photonics Res. 2022, 10, 1453–1461. [Google Scholar] [CrossRef]
- Aiello, O. Electromagnetic Susceptibility of Battery Management Systems’ ICs for Electric Vehicles: Experimental Study. Electronics 2020, 9, 510. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.; Alioto, M. 5.2 Capacitance-to-Digital Converter for Operation Under Uncertain Harvested Voltage down to 0.3V with No Trimming, Reference and Voltage Regulation. In Proceedings of the 2021 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 13–22 February 2021; pp. 13–22. [Google Scholar] [CrossRef]
- Rodovalho, L.H.; Aiello, O.; Rodrigues, C.R. Ultra-Low-Voltage Inverter-Based Operational Transconductance Amplifiers with Voltage Gain Enhancement by Improved Composite Transistors. Electronics 2020, 9, 1410. [Google Scholar] [CrossRef]
- Ballo, A.; Grasso, A.D.D.; Pennisi, S.; Susinni, G. A 0.3-V 8.5-μ a Bulk-Driven OTA. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2023, 31, 1444–1448. [Google Scholar] [CrossRef]
- Ballo, A.; Carvajal, R.G.; Grasso, A.D.; Luján-Martínez, C.I.; Pennisi, S.; Venezia, C. 0.35-V SR-Enhanced Bulk-Driven OTA for Loads up to 10 nF. IEEE Trans. Circ. Syst. I 2024, 1–9. [Google Scholar] [CrossRef]
- Della Sala, R.; Centurelli, F.; Monsurró, P.; Scotti, G. On the Feasibility of Cascode and Regulated Cascode Amplifier Stages in ULV Circuits Exploiting MOS Transistors in Deep Subthreshold Operation. IEEE Access 2024, 12, 73292–73303. [Google Scholar] [CrossRef]
- Kumngern, M.; Aupithak, N.; Khateb, F.; Kulej, T. 0.5 V Fifth-Order Butterworth Low-Pass Filter Using Multiple-Input OTA for ECG Applications. Sensors 2020, 20, 7343. [Google Scholar] [CrossRef] [PubMed]
- Khateb, F.; Kulej, T.; Vlassis, S. Extremely Low-Voltage Bulk-Driven Tunable Transconductor. Circuits Syst. Signal Process. 2017, 36, 511–524. [Google Scholar] [CrossRef]
- Kulej, T.; Khateb, F.; Arbet, D.; Stopjakova, V. A 0.3-V High Linear Rail-to-Rail Bulk-Driven OTA in 0.13 μm CMOS. IEEE Trans. Circuits Syst. II 2022, 69, 2046–2050. [Google Scholar] [CrossRef]
- Jaikla, W.; Khateb, F.; Kumngern, M.; Kulej, T.; Ranjan, R.K.; Suwanjan, P. 0.5 V Fully Differential Universal Filter Based on Multiple Input OTAs. IEEE Access 2020, 8, 187832–187839. [Google Scholar] [CrossRef]
- Rodovalho, L.H.; Ramos Rodrigues, C.; Aiello, O. Self-Biased and Supply-Voltage Scalable Inverter-Based Operational Transconductance Amplifier with Improved Composite Transistors. Electronics 2021, 10, 935. [Google Scholar] [CrossRef]
- Kulej, T. 0.5-V bulk-driven CMOS operational amplifier. IET Circuits Devices Syst. 2013, 7, 352–360. [Google Scholar] [CrossRef]
- Kulej, T.; Khateb, F. Design and implementation of sub 0.5-V OTAs in 0.18-μm CMOS. Int. J. Circuit Theory Appl. 2018, 46, 1129–1143. [Google Scholar] [CrossRef]
- Kulej, T.; Khateb, F. A Compact 0.3-V Class AB Bulk-Driven OTA. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2019, 28, 224–232. [Google Scholar] [CrossRef]
- Kulej, T.; Khateb, F. A 0.3-V 98-dB rail-to-rail OTA in 0.18 μm CMOS. IEEE Access 2020, 8, 27459–27467. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T. Design and Implementation of a 0.3-V Differential Difference Amplifier. IEEE Trans. Circ. Syst. I 2018, 66, 513–523. [Google Scholar] [CrossRef]
- Della Sala, R.; Centurelli, F.; Monsurrò, P.; Scotti, G.; Trifiletti, A. A 0.3V rail-to-rail three-stage OTA with high DC gain and improved robustness to PVT variations. IEEE Access 2023, 11, 19635–19644. [Google Scholar] [CrossRef]
- Kulej, T.; Khateb, F. 0.4-V bulk-driven differential-difference amplifier. Microelectron. J. 2015, 46, 362–369. [Google Scholar] [CrossRef]
- Kulej, T. 0.4-V bulk-driven operational amplifier with improved input stage. Circuits Syst. Signal Process. 2015, 34, 1167–1185. [Google Scholar] [CrossRef]
- Kulej, T. 0.5-V bulk-driven OTA and its applications. Int. J. Circuit Theory Appl. 2015, 43, 187–204. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Akbari, M.; Steffan, P. 0.3-V bulk-driven nanopower OTA-C integrator in 0.18 μm CMOS. Circuits Syst. Signal Process. 2019, 38, 1333–1341. [Google Scholar] [CrossRef]
- Centurelli, F.; Della Sala, R.; Monsurró, P.; Scotti, G.; Trifiletti, A. A novel OTA architecture exploiting current gain stages to boost bandwidth and slew-rate. Electronics 2021, 10, 1638. [Google Scholar] [CrossRef]
- Della Sala, R.; Spinogatti, V.; Bocciarelli, C.; Centurelli, F.; Trifiletti, A. A 0.15-to-0.5 V Body-Driven Dynamic Comparator with Rail-to-Rail ICMR. J. Low Power Electron. Appl. 2023, 13, 35. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.; Toledo, P.; Alioto, M. Rail-to-Rail Dynamic Voltage Comparator Scalable Down to pW-Range Power and 0.15-V Supply. IEEE Trans. Circuits Syst. II 2021, 68, 2675–2679. [Google Scholar] [CrossRef]
- Sala, R.D.; Centurelli, F.; Scotti, G.; Palumbo, G. Rail to Rail ICMR and High Performance ULV Standard-Cell-Based Comparator for Biomedical and IoT Applications. IEEE Access 2024, 12, 4642–4659. [Google Scholar] [CrossRef]
- Sala, R.D.; Bocciarelli, C.; Centurelli, F.; Spinogatti, V.; Trifiletti, A. A Novel Ultra-Low Voltage Fully Synthesizable Comparator exploiting NAND Gates. In Proceedings of the 2023 18th Conference on Ph.D Research in Microelectronics and Electronics (PRIME), Valencia, Spain, 18–21 June 2023; pp. 18–21. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.; Alioto, M. Fully Synthesizable, Rail-to-Rail Dynamic Voltage Comparator for Operation down to 0.3 V. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 27–30. [Google Scholar] [CrossRef]
- Ballo, A.; Pennisi, S.; Scotti, G. 0.5 V CMOS Inverter-Based Transconductance Amplifier with Quiescent Current Control. J. Low Power Electron. Appl. 2021, 11, 37. [Google Scholar] [CrossRef]
- Chen, T.; Naffziger, S. Comparison of adaptive body bias (ABB) and adaptive supply voltage (ASV) for improving delay and leakage under the presence of process variation. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2003, 11, 888–899. [Google Scholar] [CrossRef]
- Eireiner, M.; Henzler, S.; Georgakos, G.; Berthold, J.; Schmitt-Landsiedel, D. Local Supply Voltage Adjustment for Low Power Parametric Yield Increase. In Proceedings of the 2006 32nd European Solid-State Circuits Conference, Montreux, Switzerland, 19–21 September 2006; pp. 98–101. [Google Scholar] [CrossRef]
- Cha, S.; Milor, L. Adaptive supply voltage and duty cycle controller for yield-power optimization of ICs. In Proceedings of the 2017 7th IEEE International Workshop on Advances in Sensors and Interfaces (IWASI), Vieste, Italy, 15–16 June 2017; pp. 133–138. [Google Scholar] [CrossRef]
- Nielsen, L.S.; Niessen, C.; Sparso, J.; van Berkel, K. Low-power operation using self-timed circuits and adaptive scaling of the supply voltage. IEEE Trans. Very Large Scale Integr. VLSI Syst. 1994, 2, 391–397. [Google Scholar] [CrossRef]



| Typ | FF | SS | SF | FS | 90% | 110% | 0° | 80° | |
|---|---|---|---|---|---|---|---|---|---|
| [mV] | 2.2 | 2 | 2.3 | −0.5 | 7.1 | 7.6 | 2.9 | 2.2 | 2.2 |
| Pd [nW] | 1.688 | 6.958 | 0.371 | 1.599 | 3.338 | 1.013 | 1.505 | 0.536 | 9.713 |
| Itot [nA] | 4.221 | 17.39 | 0.927 | 3.998 | 8.345 | 3.217 | 3.909 | 1.341 | 24.28 |
| [dB] | 52.12 | 49.53 | 56.41 | 51.95 | 51.18 | 48.71 | 51.78 | 52.9 | 50.55 |
| GBW [kHz] | 53.56 | 217.8 | 12.12 | 66.63 | 39.58 | 13.32 | 42.22 | 18.05 | 265.8 |
| [deg] | 60.41 | 63.03 | 56.38 | 53.67 | 71.71 | 72.89 | 63.92 | 60.9 | 60.46 |
| [V/ms] | 144.5 | 546.2 | 34.17 | 149.5 | 394.1 | 21.59 | 101.1 | 90.86 | 368.1 |
| Mean | Std Dev | |
|---|---|---|
| [mV] | 2.3 | 0.99 |
| Pd [nW] | 1.92 | 0.92 |
| Itot [nA] | 4.379 | 2.319 |
| [dB] | 51.12 | 0.90 |
| [deg] | 60.97 | 4.34 |
| GBW [kHz] | 58.53 | 26.77 |
| [V/ms] | 147.5 | 80.44 |
| Mean | Std Dev | |
|---|---|---|
| [mV] | 3.1 | 18.11 |
| Pd [nW] | 1.82 | 0.44 |
| Itot [nA] | 4.314 | 1.106 |
| [dB] | 49.11 | 10.11 |
| [deg] | 62.89 | 10.03 |
| GBW [kHz] | 56.16 | 12.61 |
| [V/ms] | 146 | 30.52 |
| W [m] | 1 µ | 1 µ | 440 n | 3.52 µ | 4 µ |
| L [m] | 500 n | 500 n | 1 µ | 220 n | 500 n |
| Typ | FF | SS | SF | FS | 90% | 110% | 0 | 80 | |
|---|---|---|---|---|---|---|---|---|---|
| [mV] | 0.01 | 0.04 | 0.2 | −0.1 | 0.023 | 0.02 | 0.13 | 0.04 | 0.03 |
| Itot [nA] | 2.497 | 2.505 | 2.167 | 2.399 | 2.499 | 2.477 | 2.499 | 1.945 | 3.56 |
| Pd [nW] | 1.249 | 1.253 | 1.084 | 1.199 | 1.249 | 1.239 | 1.25 | 0.972 | 1.78 |
| [dB] | 51.29 | 45.72 | 58.65 | 51.19 | 50.72 | 51.27 | 51.29 | 53.59 | 45.41 |
| [deg] | 57.8 | 69.8 | 40.79 | 58 | 59.12 | 57.83 | 57.82 | 52.75 | 69.71 |
| GBW [kHz] | 33.67 | 27.42 | 36.04 | 31.91 | 33.48 | 33.42 | 33.68 | 31.25 | 31.42 |
| [V/ms] | 30.1 | 12.27 | 114.6 | 19.27 | 55.41 | 33.83 | 29.32 | 70.82 | 7.218 |
| Mean | Std Dev | |
|---|---|---|
| [mV] | 0.03 | 0.022 |
| Pd [nW] | 1.248 | 0.022 |
| Itot [nA] | 2.497 | 0.044 |
| [dB] | 51.22 | 1.90 |
| [deg] | 58.18 | 4.31 |
| GBW [kHz] | 33.41 | 2.03 |
| [V/ms] | 31.49 | 10.48 |
| Mean | Std Dev | |
|---|---|---|
| [mV] | −0.9 | 15.82 |
| Pd [nW] | 1.32 | 0.14 |
| Itot [nA] | 2.62 | 0.27 |
| [dB] | 51.32 | 2.54 |
| [deg] | 58.32 | 7.30 |
| GBW [kHz] | 34.69 | 9.83 |
| [V/ms] | 31.88 | 10.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Della Sala, R.; Centurelli, F.; Scotti, G. An Ultra-Low-Voltage Approach to Accurately Set the Quiescent Current of Digital Standard Cells Used for Analog Design and Its Application on an Inverter-Based Operational Transconductance Amplifier. J. Low Power Electron. Appl. 2024, 14, 39. https://doi.org/10.3390/jlpea14030039
Della Sala R, Centurelli F, Scotti G. An Ultra-Low-Voltage Approach to Accurately Set the Quiescent Current of Digital Standard Cells Used for Analog Design and Its Application on an Inverter-Based Operational Transconductance Amplifier. Journal of Low Power Electronics and Applications. 2024; 14(3):39. https://doi.org/10.3390/jlpea14030039
Chicago/Turabian StyleDella Sala, Riccardo, Francesco Centurelli, and Giuseppe Scotti. 2024. "An Ultra-Low-Voltage Approach to Accurately Set the Quiescent Current of Digital Standard Cells Used for Analog Design and Its Application on an Inverter-Based Operational Transconductance Amplifier" Journal of Low Power Electronics and Applications 14, no. 3: 39. https://doi.org/10.3390/jlpea14030039
APA StyleDella Sala, R., Centurelli, F., & Scotti, G. (2024). An Ultra-Low-Voltage Approach to Accurately Set the Quiescent Current of Digital Standard Cells Used for Analog Design and Its Application on an Inverter-Based Operational Transconductance Amplifier. Journal of Low Power Electronics and Applications, 14(3), 39. https://doi.org/10.3390/jlpea14030039








