Evaluation of the Different Numerical Formats for HIL Models of Power Converters after the Adoption of VHDL-2008 by Xilinx
Abstract
:1. Introduction
2. Materials and Methods
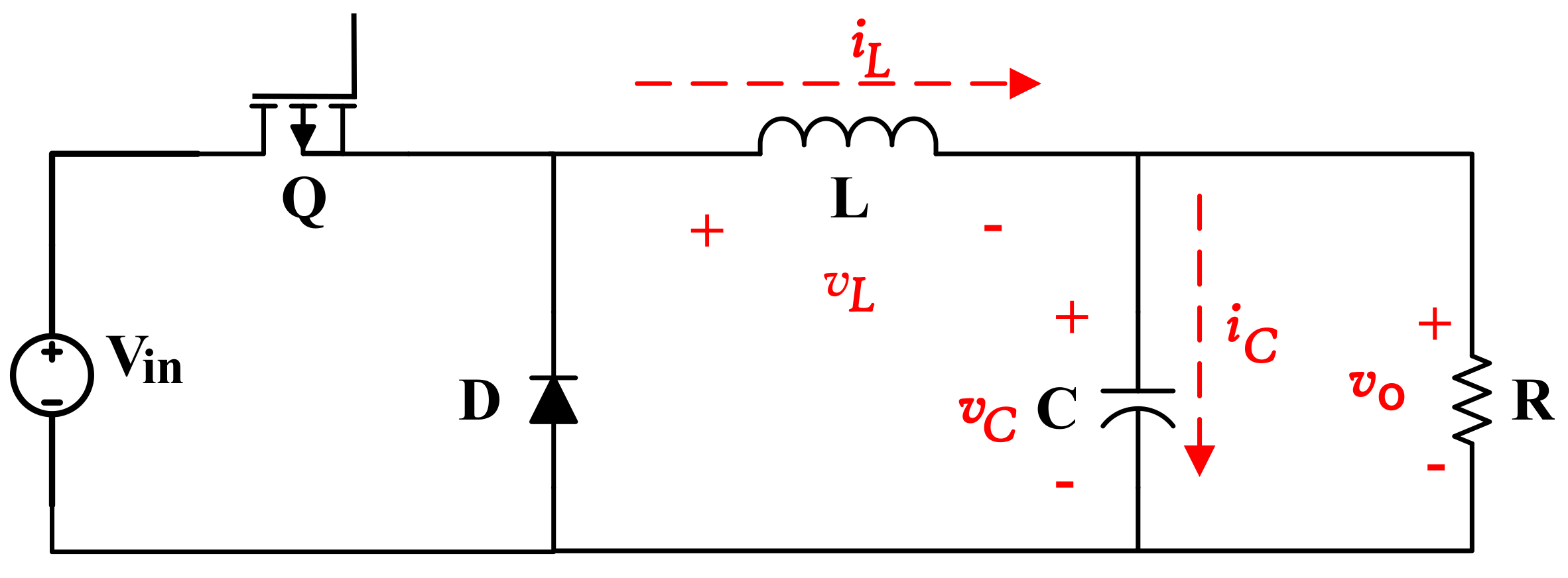
2.1. Buck Power Converter
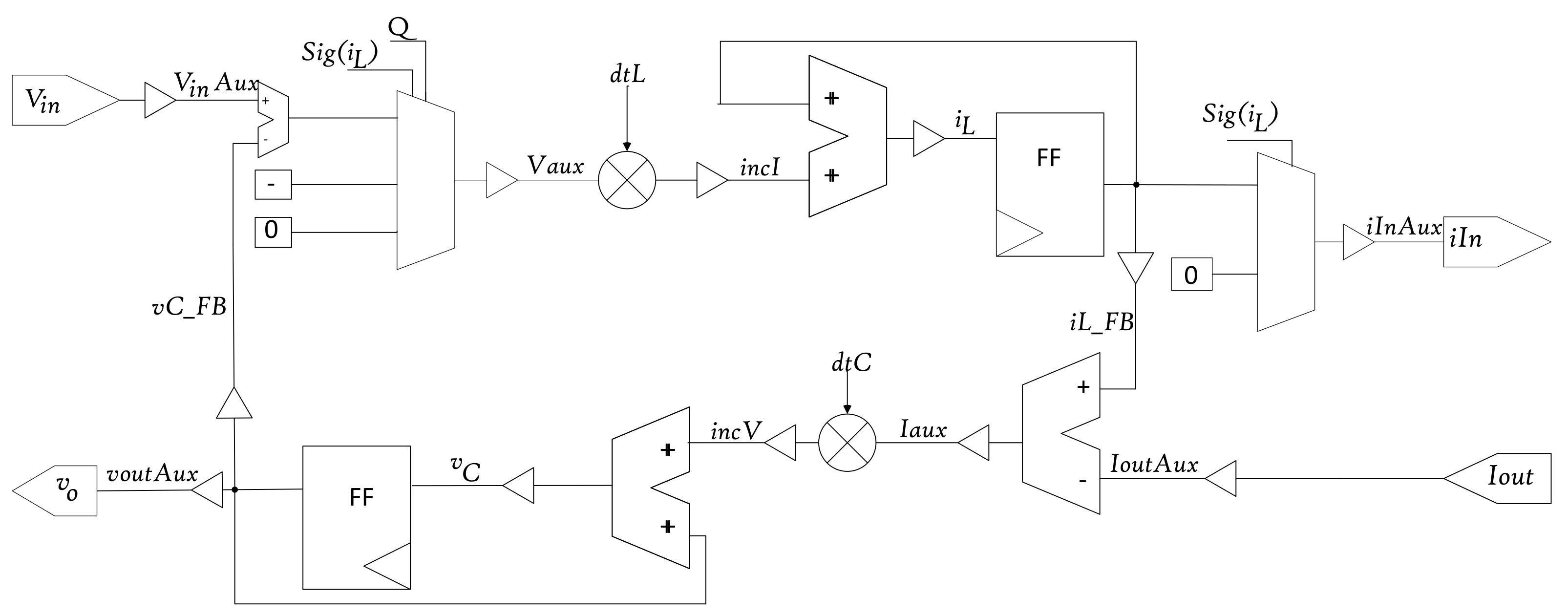
2.2. HIL Model Equations
2.3. Numerical Formats
2.4. Model Evaluation
3. Experiments, Results and Discussion
3.1. Buck Converter HIL Model Simulation
3.2. Synthesis and Implementation Requirements in Terms of Word Length
3.3. Synthesis and Implementation Requirements in Terms of the Rounding and Overflow Modes
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yushkova, M.; Sanchez, A.; de Castro, A. Strategies for choosing an appropriate numerical method for FPGA-based HIL. Int. J. Electr. Power Energy Syst. 2021, 132, 107186. [Google Scholar] [CrossRef]
- Zamiri, E.; Sanchez, A.; Yushkova, M.; Martínez-García, M.S.; de Castro, A. Comparison of Different Design Alternatives for Hardware-in-the-Loop of Power Converters. Electronics 2021, 10, 926. [Google Scholar] [CrossRef]
- Frivaldsky, M.; Morgos, J.; Prazenica, M.; Takacs, K. System Level Simulation of Microgrid Power Electronic Systems. Electronics 2021, 10, 644. [Google Scholar] [CrossRef]
- Saito, K.; Akagi, H. A Power Hardware-in-the-Loop (P-HIL) Test Bench Using Two Modular Multilevel DSCC Converters for a Synchronous Motor Drive. IEEE Trans. Ind. Appl. 2018, 54, 4563–4573. [Google Scholar] [CrossRef]
- Shin, D.C.; Lee, D.M. Development of Real-Time Implementation of a Wind Power Generation System with Modular Multilevel Converters for Hardware in the Loop Simulation Using MATLAB/Simulink. Electronics 2020, 9, 606. [Google Scholar] [CrossRef] [Green Version]
- Montaño, F.; Ould-Bachir, T.; David, J.P. A Latency-Insensitive Design Approach to Programmable FPGA-Based Real-Time Simulators. Electronics 2020, 9, 1838. [Google Scholar] [CrossRef]
- Liu, C.; Bai, H.; Zhuo, S.; Zhang, X.; Ma, R.; Gao, F. Real-Time Simulation of Power Electronic Systems Based on Predictive Behavior. IEEE Trans. Ind. Electron. 2020, 67, 8044–8053. [Google Scholar] [CrossRef]
- Liang, T.; Liu, Q.; Dinavahi, V.R. Real-Time Hardware-in-the-Loop Emulation of High-Speed Rail Power System With SiC-Based Energy Conversion. IEEE Access 2020, 8, 122348–122359. [Google Scholar] [CrossRef]
- Yushkova, M.; Sanchez, A.; de Castro, A. The Necessity of Resetting Memory in Adams–Bashforth Method for Real-Time Simulation of Switching Converters. IEEE Trans. Power Electron. 2021, 36, 6175–6178. [Google Scholar] [CrossRef]
- Lin, N.; Dinavahi, V. Detailed Device-Level Electrothermal Modeling of the Proactive Hybrid HVDC Breaker for Real-Time Hardware-in-the-Loop Simulation of DC Grids. IEEE Trans. Power Electron. 2018, 33, 1118–1134. [Google Scholar] [CrossRef]
- Lauss, G.; Strunz, K. Multirate Partitioning Interface for Enhanced Stability of Power Hardware-in-the-Loop Real-Time Simulation. IEEE Trans. Ind. Electron. 2019, 66, 595–605. [Google Scholar] [CrossRef]
- Dagbagi, M.; Hemdani, A.; Idkhajine, L.; Naouar, M.W.; Monmasson, E.; Slama-Belkhodja, I. ADC-Based Embedded Real-Time Simulator of a Power Converter Implemented in a Low-Cost FPGA: Application to a Fault-Tolerant Control of a Grid-Connected Voltage-Source Rectifier. IEEE Trans. Ind. Electron. 2016, 63, 1179–1190. [Google Scholar] [CrossRef] [Green Version]
- Roshandel Tavana, N.; Dinavahi, V. A General Framework for FPGA-Based Real-Time Emulation of Electrical Machines for HIL Applications. IEEE Trans. Ind. Electron. 2015, 62, 2041–2053. [Google Scholar] [CrossRef]
- Sanchez, A.; Todorovich, E.; de Castro, A. Impact of the hardened floating-point cores on HIL technology. Electr. Power Syst. Res. 2018, 165, 53–59. [Google Scholar] [CrossRef]
- Iranian, M.E.; Mohseni, M.; Aghili, S.; Parizad, A.; Baghaee, H.R.; Guerrero, J.M. Real-Time FPGA-based HIL Emulator of Power Electronics Controllers using NI PXI for DFIG Studies. IEEE J. Emerg. Sel. Topics Power Electron. 2020. [Google Scholar] [CrossRef]
- Lucia, S.; Navarro, D.; Lucia, O.; Zometa, P.; Findeisen, R. Optimized FPGA Implementation of Model Predictive Control for Embedded Systems Using High-Level Synthesis Tool. IEEE Trans. Ind. Inf. 2018, 14, 137–145. [Google Scholar] [CrossRef] [Green Version]
- Mylonas, E.; Tzanis, N.; Birbas, M.; Birbas, A. An Automatic Design Framework for Real-Time Power System Simulators Supporting Smart Grid Applications. Electronics 2020, 9, 299. [Google Scholar] [CrossRef] [Green Version]
- Kumar, P.; Kumar, V.; Pratap, R. FPGA implementation of an Islanding detection technique for microgrid using periodic maxima of superimposed voltage components. IET Gener. Trans. Distrib. 2020, 14, 1673–1683. [Google Scholar] [CrossRef]
- Sanchez, A.; de Castro, A.; Garrido, J. A Comparison of Simulation and Hardware-in-the-Loop Alternatives for Digital Control of Power Converters. IEEE Trans. Ind. Inf. 2012, 8, 491–500. [Google Scholar] [CrossRef]
- Ahmad, J.; Pervez, I.; Sarwar, A.; Tariq, M.; Fahad, M.; Chakrabortty, R.K.; Ryan, M.J. Performance Analysis and Hardware-in-the-Loop (HIL) Validation of Single Switch High Voltage Gain DC-DC Converters for MPP Tracking in Solar PV System. IEEE Access 2021, 9, 48811–48830. [Google Scholar] [CrossRef]
- Nane, R.; Sima, V.M.; Pilato, C.; Choi, J.; Fort, B.; Canis, A.; Chen, Y.T.; Hsiao, H.; Brown, S.; Ferrandi, F.; et al. A Survey and Evaluation of FPGA High-Level Synthesis Tools. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2016, 35, 1591–1604. [Google Scholar] [CrossRef] [Green Version]
- Oruganti, V.S.R.V.; Sarma Dhanikonda, V.S.S.S.; Godoy Simões, M. Scalable Single-Phase Multi-Functional Inverter for Integration of Rooftop Solar-PV to Low-Voltage Ideal and Weak Utility Grid. Electronics 2019, 8, 302. [Google Scholar] [CrossRef] [Green Version]
- Markovska, M.; Taskovski, D.; Kokolanski, Z.; Dimchev, V.; Velkovski, B. Real-Time Implementation of Optimized Power Quality Events Classifier. IEEE Trans. Ind. Appl. 2020. [Google Scholar] [CrossRef]
- Hassan, M.A.; Li, E.p.; Li, X.; Li, T.; Duan, C.; Chi, S. Adaptive Passivity-Based Control of dc–dc Buck Power Converter with Constant Power Load in DC Microgrid Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2029–2040. [Google Scholar] [CrossRef]
- Cristri, A.; Iskandar, R. Analysis and Design of Dynamic Buck Converter with Change in Value of Load Impedance. Procedia Eng. 2017, 170, 398–403. [Google Scholar] [CrossRef]
- Kowalczuk, Z. Discrete approximation of continuous-time systems: A survey. IEE Proc. F Radar Signal Process. UK 1993, 140, 264. [Google Scholar] [CrossRef]
- Xu, F.; Dinavahi, V.; Xu, X. Hybrid analytical model of switched reluctance machine for real-time hardware-in-the-loop simulation. IET Electr. Power Appl. 2017, 11, 1114–1123. [Google Scholar] [CrossRef]
- Xin, Z.; Wang, X.; Loh, P.C.; Blaabjerg, F. Realization of Digital Differentiator Using Generalized Integrator For Power Converters. IEEE Trans. Power Electron. 2015, 30, 6520–6523. [Google Scholar] [CrossRef]
- Park, Y.; Chong, K.T. The numerical solution of the point kinetics equation using the matrix exponential method. Ann. Nucl. Energy 2013, 55, 42–48. [Google Scholar] [CrossRef]
- Chen, B.; Solis, F. Discretizations of nonlinear differential equations using explicit finite order methods. J. Comput. Appl. Math. 1998, 90, 171–183. [Google Scholar] [CrossRef] [Green Version]
- Zamiri, E.; Sanchez, A.; de Castro, A.; Martínez-García, M.S. Comparison of Power Converter Models with Losses for Hardware-in-the-Loop Using Different Numerical Formats. Electronics 2019, 8, 1255. [Google Scholar] [CrossRef] [Green Version]
- Sanchez, A.; de Castro, A.; Martínez-García, M.S.; Garrido, J. LOCOFloat: A Low-Cost Floating-Point Format for FPGAs.: Application to HIL Simulators. Electronics 2020, 9, 81. [Google Scholar] [CrossRef] [Green Version]
- Ashenden, P.J.; Lewis, J. VHDL-2008: Just the New Stuff; The Morgan Kaufmann Series in Systems on Silicon; Elsevier/Morgan Kaufmann: Amsterdam, The Netherlands; Boston, FL, USA, 2008. [Google Scholar]
- Martínez García, M.S.; de Castro, A.; Sanchez, A.; Garrido, J. Analysis of Resolution in Feedback Signals for Hardware-in-the-Loop Models of Power Converters. Electronics 2019, 8, 1527. [Google Scholar] [CrossRef] [Green Version]
- Martínez García, M.S.; de Castro, A.; Sanchez, A.; Garrido, J. Word length selection method for HIL power converter models. Int. J. Electr. Power Energy Syst. 2021, 129, 106721. [Google Scholar] [CrossRef]
- Goni, O.; Sanchez, A.; Todorovich, E.; de Castro, A. Resolution Analysis of Switching Converter Models for Hardware-in-the-Loop. IEEE Trans. Ind. Inf. 2014, 10, 1162–1170. [Google Scholar] [CrossRef]

| Signal | OPT | WL |
|---|---|---|
| Q6.18 | 25 | |
| Q5.19 | 25 | |
| Q-13.24 | 12 | |
| Q-10.21 | 12 | |
| Q-4.18 | 15 | |
| Q-6.19 | 14 | |
| Q6.8 | 15 | |
| Q5.6 | 12 | |
| Q5.6 | 12 | |
| Q6.5 | 12 | |
| Q5.6 | 12 | |
| Q3.8 | 12 | |
| Q5.6 | 12 | |
| Q6.8 | 15 |
| NF | WL | Round and Overflow Modes | MAE | MRE | ||
|---|---|---|---|---|---|---|
| Fixed | 32 | Round, Saturate | 0.0040 | 0.0039 | 0.0008 | 0.0020 |
| 32 | Wrap, Truncate | 0.0077 | 0.0093 | 0.0015 | 0.0047 | |
| 64 | Round, Saturate | 0.0040 | 0.0039 | 0.0008 | 0.0020 | |
| 64 | Wrap, Truncate | 0.0077 | 0.0094 | 0.0015 | 0.0047 | |
| OPT | Round, Saturate | 0.0047 | 0.0042 | 0.0009 | 0.0025 | |
| OPT | Wrap, Truncate | 0.0041 | 0.0049 | 0.0008 | 0.0021 | |
| Float | 32 | Round nearest | 0.0002 | 0.0001 | 0.0000 | 0.0000 |
| 32 | Round zero | 0.0011 | 0.0014 | 0.0005 | 0.0007 | |
| 64 | Round nearest | 0.0002 | 0.0001 | 0.0000 | 0.0000 | |
| 64 | Round zero | 0.0005 | 0.0005 | 0.0001 | 0.0002 | |
| Parameter | Float32 | Float64 | ||
|---|---|---|---|---|
| T (ns) | 83.356 | 84.719 | 124.612 | 116.746 |
| DSP | 4 | 0 | 18 | 0 |
| LUT | 8683 | 9675 | 20,378 | 24,296 |
| FF | 64 | 64 | 128 | 128 |
| IEEE Libraries of VHDL-2008 | ||||||
|---|---|---|---|---|---|---|
| Parameter | Fixed OPT | Fixed32 | Fixed64 | |||
| T (ns) | 16.880 | 17.745 | 16.940 | 20.587 | 31.674 | 34.800 |
| DSP | 2 | 0 | 6 | 0 | 32 | 0 |
| LUT | 242 | 426 | 368 | 1287 | 1225 | 5925 |
| FF | 50 | 50 | 64 | 64 | 128 | 128 |
| IEEE_Proposed Libraries of VHDL-93 | ||||||
| Parameter | Fixed OPT | Fixed32 | Fixed64 | |||
| T (ns) | 17.602 | 17.745 | 17.405 | 20.701 | 32.743 | 34.873 |
| DSP | 2 | 0 | 6 | 0 | 32 | 0 |
| LUT | 241 | 426 | 370 | 1293 | 1216 | 5928 |
| FF | 50 | 50 | 64 | 64 | 128 | 128 |
| Round-Nearest | ||||
|---|---|---|---|---|
| Parameter | Float32 | Float64 | ||
| T (ns) | 83.356 | 84.719 | 124.612 | 116.746 |
| DSP | 4 | 0 | 18 | 0 |
| LUT | 8683 | 9675 | 20,378 | 24,296 |
| FF | 64 | 64 | 128 | 128 |
| Round-Zero | ||||
| Parameter | Float32 | Float64 | ||
| T (ns) | 62.564 | 69.217 | 84.093 | 97.730 |
| DSP | 4 | 0 | 18 | 0 |
| LUT | 4185 | 4782 | 11,754 | 14,850 |
| FF | 64 | 64 | 128 | 128 |
| Round and Saturate | ||||||
|---|---|---|---|---|---|---|
| Parameter | Fixed OPT | Fixed32 | Fixed64 | |||
| T (ns) | 16.880 | 17.745 | 16.940 | 20.587 | 31.674 | 34.800 |
| DSP | 2 | 0 | 6 | 0 | 32 | 0 |
| LUT | 242 | 426 | 368 | 1287 | 1225 | 5925 |
| FF | 50 | 50 | 64 | 64 | 128 | 128 |
| Truncate and Wrap | ||||||
| Parameter | Fixed OPT | Fixed32 | Fixed64 | |||
| T (ns) | 8.558 | 8.576 | 10.525 | 13.863 | 16.933 | 20.462 |
| DSP | 2 | 0 | 6 | 0 | 32 | 0 |
| LUT | 114 | 311 | 241 | 1083 | 731 | 4668 |
| FF | 50 | 50 | 64 | 64 | 128 | 128 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cirugeda-Roldán, E.M.; Martínez-García, M.S.; Sanchez, A.; de Castro, A. Evaluation of the Different Numerical Formats for HIL Models of Power Converters after the Adoption of VHDL-2008 by Xilinx. Electronics 2021, 10, 1952. https://doi.org/10.3390/electronics10161952
Cirugeda-Roldán EM, Martínez-García MS, Sanchez A, de Castro A. Evaluation of the Different Numerical Formats for HIL Models of Power Converters after the Adoption of VHDL-2008 by Xilinx. Electronics. 2021; 10(16):1952. https://doi.org/10.3390/electronics10161952
Chicago/Turabian StyleCirugeda-Roldán, Eva M., María Sofía Martínez-García, Alberto Sanchez, and Angel de Castro. 2021. "Evaluation of the Different Numerical Formats for HIL Models of Power Converters after the Adoption of VHDL-2008 by Xilinx" Electronics 10, no. 16: 1952. https://doi.org/10.3390/electronics10161952
APA StyleCirugeda-Roldán, E. M., Martínez-García, M. S., Sanchez, A., & de Castro, A. (2021). Evaluation of the Different Numerical Formats for HIL Models of Power Converters after the Adoption of VHDL-2008 by Xilinx. Electronics, 10(16), 1952. https://doi.org/10.3390/electronics10161952








