A United Control Strategy of Photovoltaic-Battery Energy Storage System Based on Voltage-Frequency Controlled VSG
Abstract
:1. Introduction
2. The Control Strategy of Voltage-Frequency Controlled VSG
3. The Strategy of Grid-Connected Condition
3.1. Active Power Control Strategy
3.2. Reactive Power Control Strategy
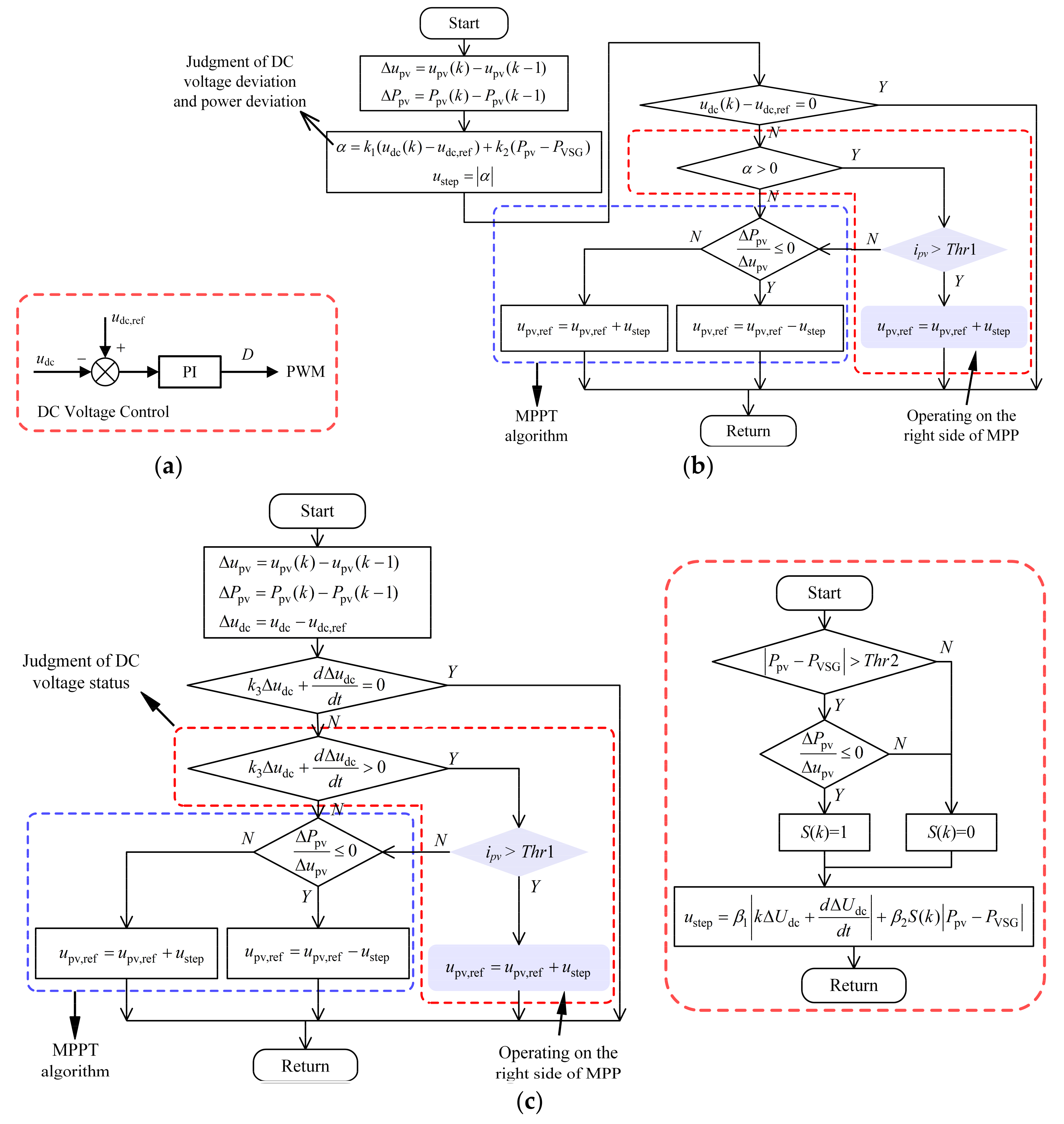
4. The Strategy of the Off-Grid Condition
4.1. Sufficient Irradiance Condition
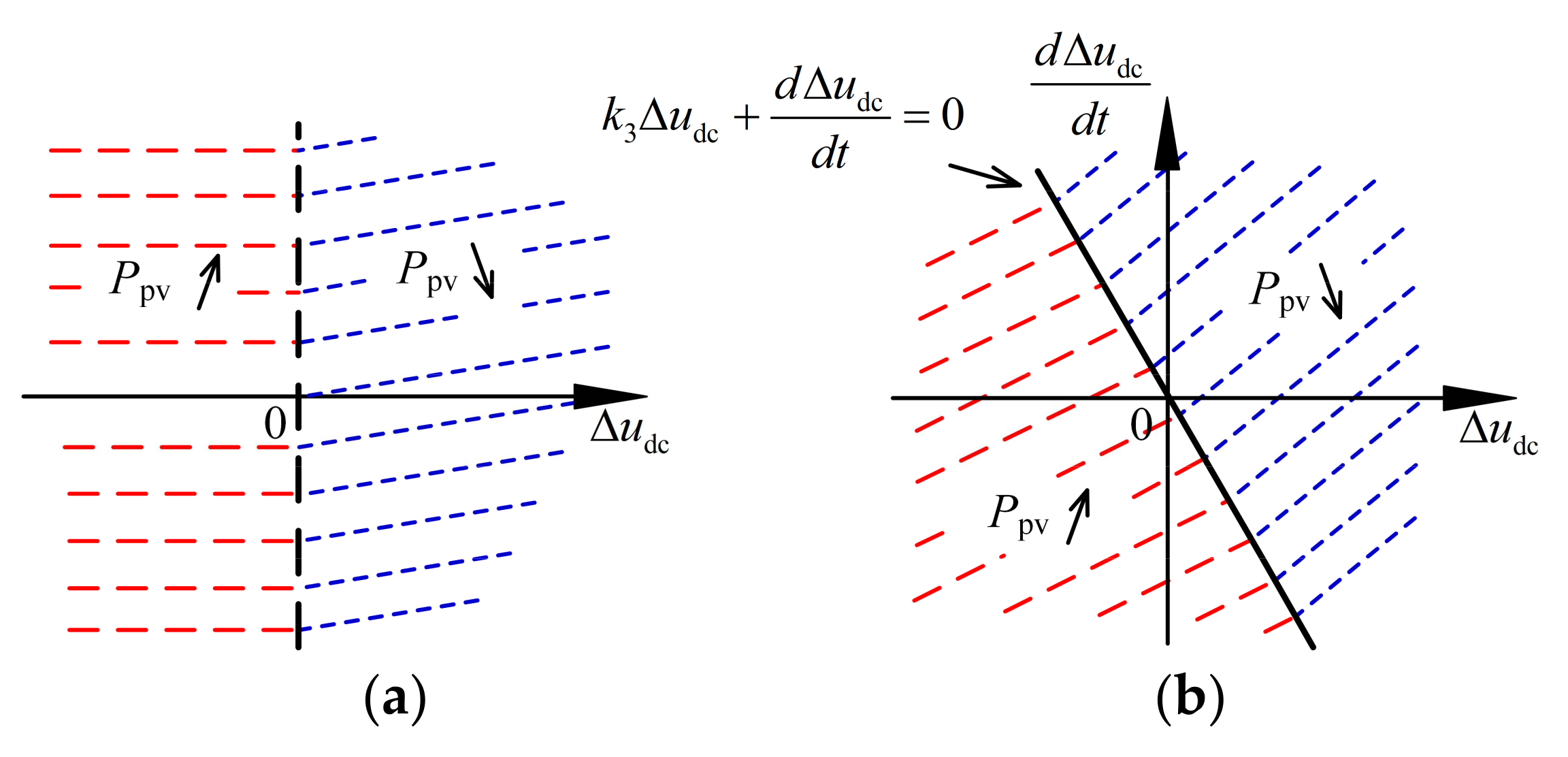
4.2. Insufficient Irradiance Condition
5. The Parameters of the Simulation Model
6. The Analysis of the Simulation
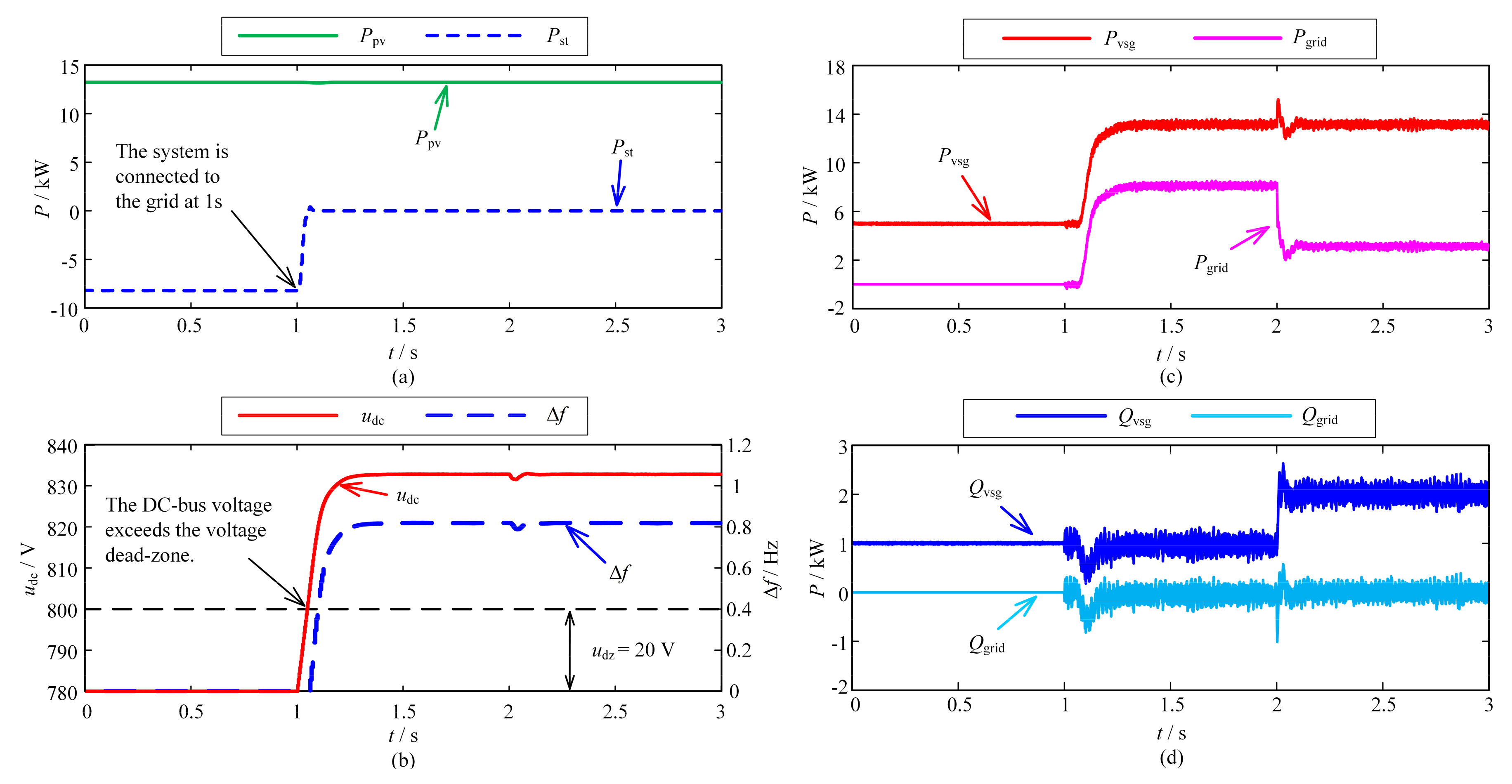
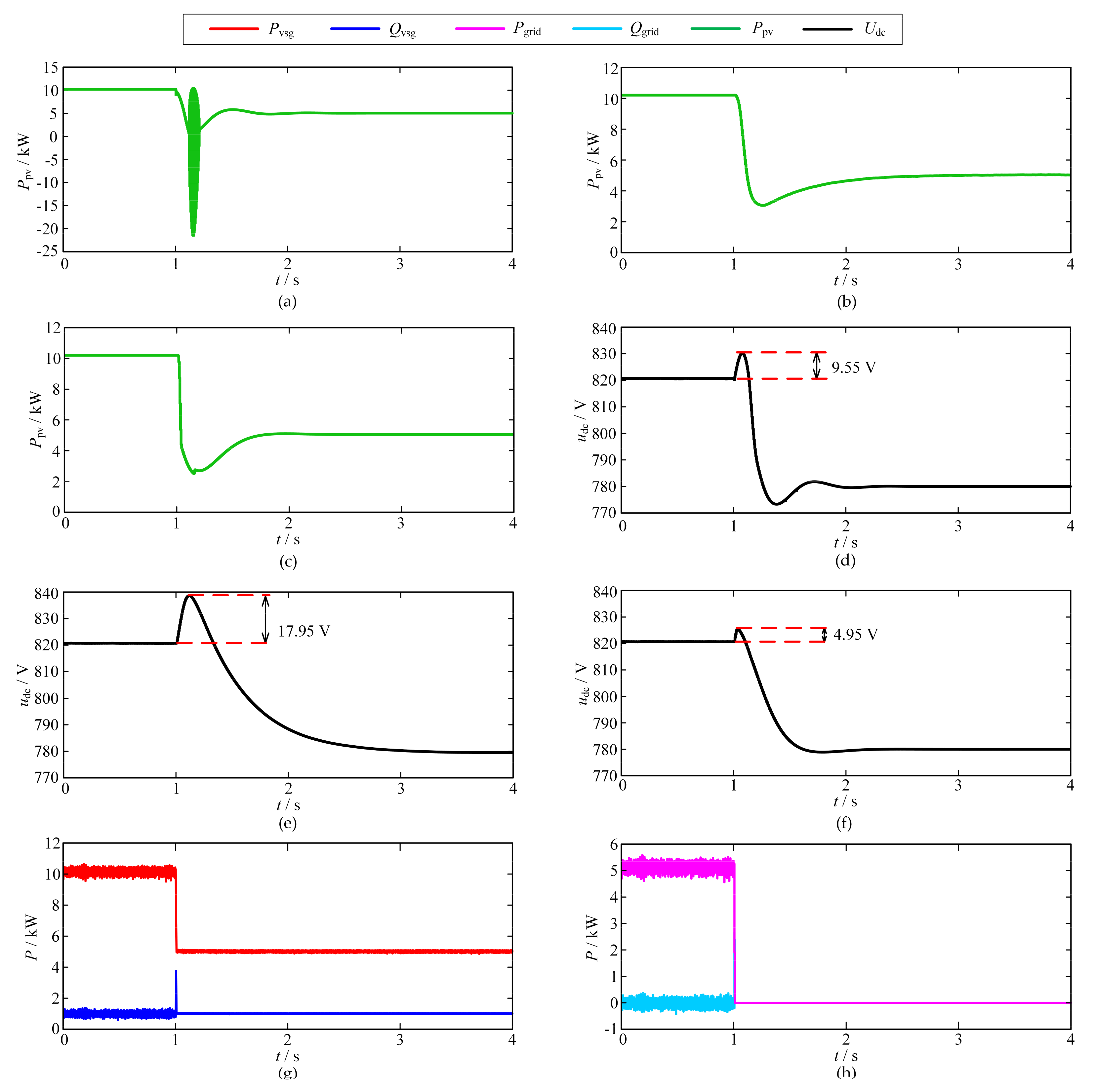
6.1. Verification of Grid-Connected Control Strategy
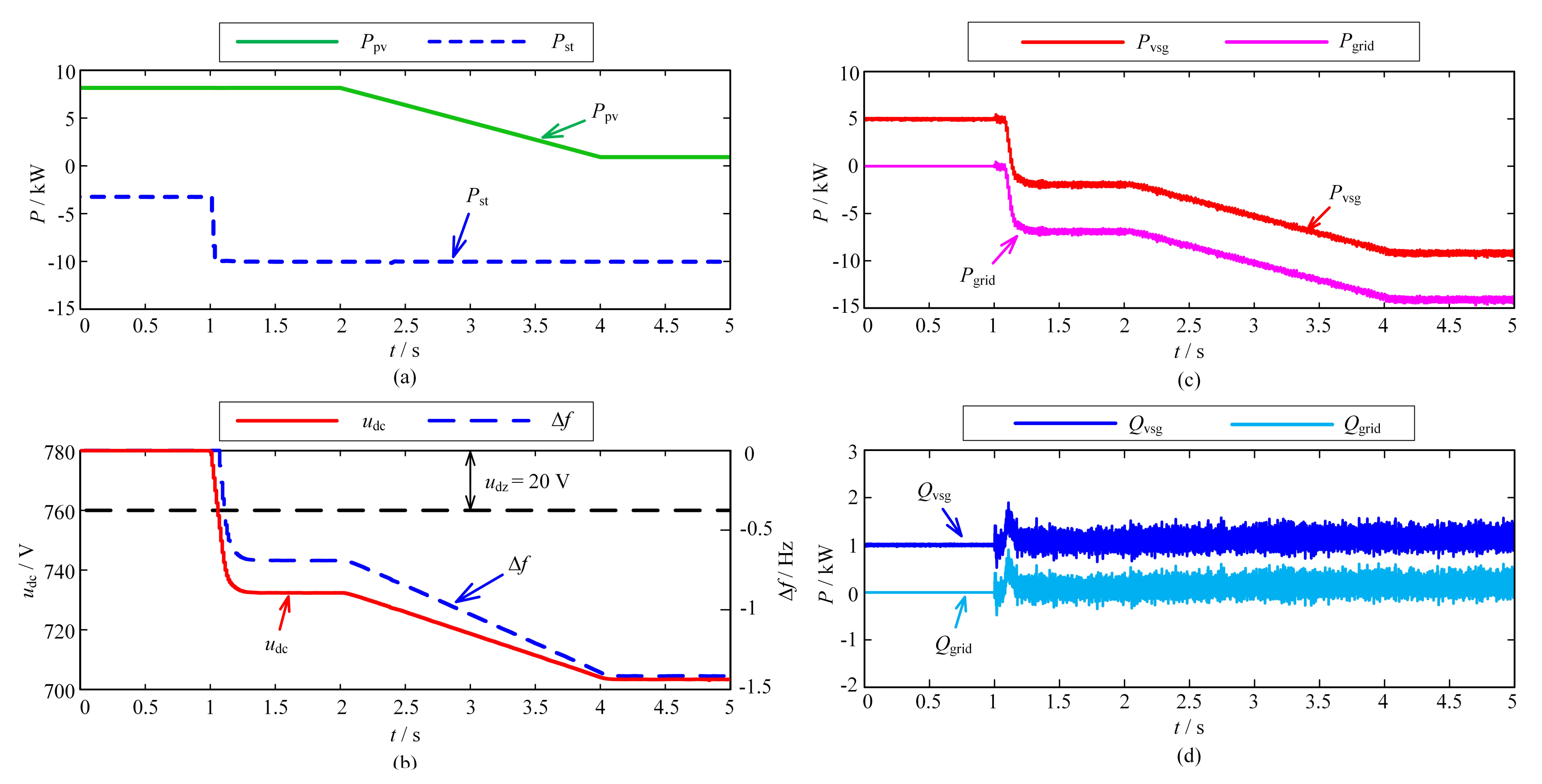
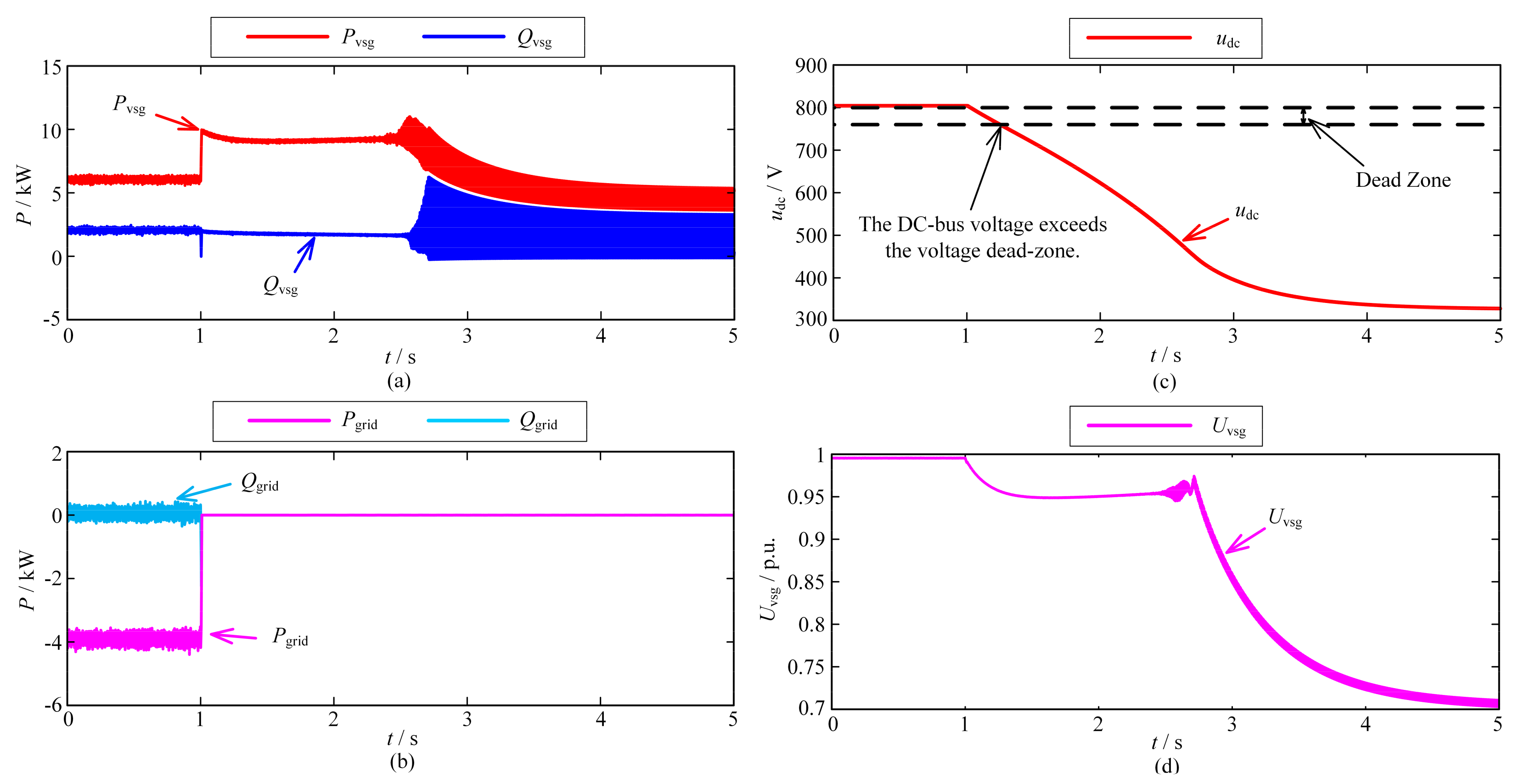
6.2. Verification of Off-Grid Control Strategy
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Renewables 2020: Global Status Report (GSR). Available online: http://www.ren21.net/ (accessed on 16 June 2020).
- Li, X.; Yao, L.; Hui, D. Optimal control and management of a large-scale battery energy storage system to mitigate fluc-tuation and intermittence of renewable generations. J. Mod. Power Syst. Clean Energy 2016, 4, 593–603. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Sun, K.; Guerrero, J.; Vasquez, J.C.; Huang, L. State-of-Charge Balance Using Adaptive Droop Control for Distributed Energy Storage Systems in DC Microgrid Applications. IEEE Trans. Ind. Electron. 2014, 61, 2804–2815. [Google Scholar] [CrossRef] [Green Version]
- Datta, U.; Kalam, A.; Shi, J. Battery Energy Storage System Control for Mitigating PV Penetration Impact on Primary Fre-quency Control and State-of-Charge Recovery. IEEE Trans. Sustain. 2020, 11, 746–757. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Enjeti, P.; Blaabjerg, F.; Wang, H. Wide-Scale Adoption of Photovoltaic Energy: Grid Code Modifications Are Explored in the Distribution Grid. IEEE Ind. Appl. Mag. 2015, 21, 21–31. [Google Scholar] [CrossRef] [Green Version]
- Mao, M.; Qian, C.; Ding, Y. Decentralized coordination power control for islanding microgrid based on PV/BES-VSG. CPSS Trans. Power Electron. Appl. 2018, 3, 14–24. [Google Scholar] [CrossRef]
- Narayanan, V.; Kewat, S.; Singh, B. Solar PV-BES Based Microgrid System With Multifunctional VSC. IEEE Trans. Ind. Appl. 2020, 56, 2957–2967. [Google Scholar] [CrossRef]
- Du, W.; Jiang, Q.; Erickson, M.J.; Lasseter, R.H. Voltage-Source Control of PV Inverter in a CERTS Microgrid. IEEE Trans. Power Deliv. 2014, 29, 1726–1734. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Kumar, P.D.S.; Samanta, S. Steady Output and Fast Tracking MPPT (SOFT-MPPT) for P&O and InC Algorithms. IEEE Trans. Sustain. Energy 2021, 12, 293–302. [Google Scholar]
- Arafat, M.N.; Palle, S.; Sozer, Y. Transition control strategy between standalone and grid-connected operations of volt-age-source inverters. IEEE Trans. Ind. Appl. 2012, 48, 1516–1525. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.; Shadmand, M.B.; Balog, R.S. Model predictive control of a voltage-source inverter with seamless transition be-tween islanded and grid-connected operations. IEEE Trans. Ind. Electron. 2017, 64, 7906–7918. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, B. Seamless Operation and Control of Single-Phase Hybrid PV-BES-Utility Synchronized System. IEEE Trans. Ind. Appl. 2019, 55, 1072–1082. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Nguyen, P.-L.; Ma, Z.; Sheng, W. Self-Synchronized Synchronverters: Inverters Without a Dedicated Synchronization Unit. IEEE Trans. Power Electron. 2014, 29, 619–630. [Google Scholar] [CrossRef]
- Zhong, Q.-C. Power-Electronics-Enabled Autonomous Power Systems: Architecture and Technical Routes. IEEE Trans. Ind. Electron. 2017, 64, 5907–5918. [Google Scholar] [CrossRef]
- Hashmi, K.; Khan, M.M.; Jiang, H.; Shahid, M.U.; Habib, S.; Faiz, M.T.; Tang, H. A Virtual Micro-Islanding-Based Control Paradigm for Renewable Microgrids. Electronics 2018, 7, 105. [Google Scholar] [CrossRef] [Green Version]
- Bai, X.; Miao, H.; Zeng, C. Improved Droop Control Strategy for Reactive Power Sharing of Parallel Inverters in Low-Voltage Microgrid. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 2538–2543. [Google Scholar]
- Zhang, H.; Kim, S.; Sun, Q.; Zhou, J. Distributed Adaptive Virtual Impedance Control for Accurate Reactive Power Sharing Based on Consensus Control in Microgrids. IEEE Trans. Smart Grid 2017, 8, 1749–1761. [Google Scholar] [CrossRef]
- Pranjal, S.; Navdeep, S.; Kumar Pandey, A. Investigating the frequency fault ride-through capability of solar photovoltaic system: Replacing battery via virtual inertia reserve. Int. T. Electr. Energy. 2021, 31, e12791. [Google Scholar]
- Huang, L.; Xin, H.; Wang, Z. Damping Low-Frequency Oscillations Through VSC-HVDC Stations Operated as Virtual Syn-chronous Machines. IEEE Trans. Power Electron. 2019, 34, 5803–5818. [Google Scholar] [CrossRef]
- Dong, S.; Chen, Y.C. A Method to Directly Compute Synchronverter Parameters for Desired Dynamic Response. IEEE Trans. Energy Convers. 2018, 33, 814–825. [Google Scholar] [CrossRef]
- Rasool, A.; Yan, X.; Rasool, H.; Guo, H.; Asif, M. VSG Stability and Coordination Enhancement under Emergency Condition. Electronics 2018, 7, 202. [Google Scholar] [CrossRef] [Green Version]
- Rehman, H.U.; Yan, X.; Abdelbaky, M.A.; Jan, M.U.; Iqbal, S. An advanced virtual synchronous generator control technique for frequency regulation of grid-connected PV system. Int. J. Electr. Power Energy Syst. 2021, 125, 106440. [Google Scholar] [CrossRef]
- Wu, X.; Shen, C.; Iravani, R. Feasible Range and Optimal Value of the Virtual Impedance for Droop-Based Control of Mi-crogrids. IEEE Trans. Smart Grid. 2017, 8, 1242–1251. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Bevrani, H.; Ise, T. A Unified Modeling Method of Virtual Synchronous Generator for Multi-Operation-Mode Analyses. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2394–2409. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Ise, T. Comparison of Dynamic Characteristics Between Virtual Synchronous Generator and Droop Control in Inverter-Based Distributed Generators. IEEE Trans. Power Electron. 2016, 31, 3600–3611. [Google Scholar] [CrossRef]
- Ali, H.; Hussain, A.; Bui, V.-H.; Kim, H.-M. Consensus Algorithm-Based Distributed Operation of Microgrids During Grid-Connected and Islanded Modes. IEEE Access 2020, 8, 78151–78165. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S.; Lee, K. Multistage Stochastic Optimization for Microgrid Operation Under Islanding Uncertainty. IEEE Trans. Smart Grid 2021, 12, 56–66. [Google Scholar] [CrossRef]
- Hoke, A.F.; Shirazi, M.; Chakraborty, S.; Muljadi, E.; Maksimovic, D. Rapid Active Power Control of Photovoltaic Systems for Grid Frequency Sup-port. IEEE J. Emerg. Sel. Topics Power Electron. 2017, 5, 1154–1163. [Google Scholar] [CrossRef]
- Tafti, H.D.; Konstantinou, G.; Townsend, C.D.; Farivar, G.G.; Sangwongwanich, A.; Yang, Y.; Pou, J.; Blaabjerg, F. Extended Functionalities of Photovoltaic Systems With Flexible Power Point Tracking: Recent Advances. IEEE Trans. Power Electron. 2020, 35, 9342–9356. [Google Scholar] [CrossRef]
- Tafti, H.D.; Sangwongwanich, A.; Yang, Y.; Pou, J.; Konstantinou, G.; Blaabjerg, F. An Adaptive Control Scheme for Flexible Power Point Tracking in Photo-voltaic Systems. IEEE Trans. Power Electron. 2019, 34, 5451–5463. [Google Scholar] [CrossRef] [Green Version]
- Sangwongwanich, A.; Yang, Y.; Blaabjerg, F. A Sensorless Power Reserve Control Strategy for Two-Stage Grid-Connected PV Systems. IEEE Trans. Power Electron. 2017, 32, 8559–8569. [Google Scholar] [CrossRef] [Green Version]
- Zhong, C.; Zhou, Y.; Zhang, X.; Yan, G. Flexible power-point-tracking-based frequency regulation strategy for PV system. IET Renew. Power Gener. 2020, 14, 1797–1807. [Google Scholar] [CrossRef]
- Loukriz, A.; Haddadi, M.; Messalti, S. Simulation and experimental design of a new advanced variable step size Incremental Conductance MPPT algorithm for PV systems. ISA Trans. 2016, 62, 30–38. [Google Scholar] [CrossRef] [PubMed]





| Parameter | Value |
|---|---|
| Possible PV maximum power | 15 kW |
| Maximum charging power of energy storage system | 10 kW |
| Maximum discharge power of energy storage system | 15 kW |
| Grid voltage | 6.6 kV |
| Inverter AC voltage | 250 V |
| P&O algorithm tracking frequency | 200 Hz |
| Rated DC-bus voltage (Udc,N) | 780 V |
| Classification | Parameter | Value |
|---|---|---|
| VSG parameters | The droop coefficient of frequency-active power (kf) | 10,000 |
| The droop coefficient of voltage-reactive power (ku) | 66.67 | |
| VSG inertia and damping (J, D) | 0.1, 5 | |
| Grid-connected strategy parameters | DC-bus voltage dead-zone for secondary frequency adjustment (Udz) | 20 V |
| The proportionality coefficient for secondary frequency adjustment (kdc,f) | 0.025 | |
| Off-grid strategy parameters | The proportionality coefficient between voltage component ΔU and DC voltage deviation (kdc,u) | 0.6 |
| Control strategy 1 PI controller parameters: kp, ki | 0.025, 8 | |
| Control strategy 2:Thr1 | 2 | |
| Control strategy 2: k1, k2 | 0.02, 0.0005 | |
| Control strategy 3:Thr1, Thr2 | 2, 500 | |
| Control strategy 3: k3, β1, β2 | 3, 0.0025, 0.003 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Wang, C.; Wang, Z.; Ma, H.; Liang, B.; Wei, X. A United Control Strategy of Photovoltaic-Battery Energy Storage System Based on Voltage-Frequency Controlled VSG. Electronics 2021, 10, 2047. https://doi.org/10.3390/electronics10172047
Yan X, Wang C, Wang Z, Ma H, Liang B, Wei X. A United Control Strategy of Photovoltaic-Battery Energy Storage System Based on Voltage-Frequency Controlled VSG. Electronics. 2021; 10(17):2047. https://doi.org/10.3390/electronics10172047
Chicago/Turabian StyleYan, Xiangwu, Chenguang Wang, Ziheng Wang, Hongbin Ma, Baixue Liang, and Xiaoxue Wei. 2021. "A United Control Strategy of Photovoltaic-Battery Energy Storage System Based on Voltage-Frequency Controlled VSG" Electronics 10, no. 17: 2047. https://doi.org/10.3390/electronics10172047
APA StyleYan, X., Wang, C., Wang, Z., Ma, H., Liang, B., & Wei, X. (2021). A United Control Strategy of Photovoltaic-Battery Energy Storage System Based on Voltage-Frequency Controlled VSG. Electronics, 10(17), 2047. https://doi.org/10.3390/electronics10172047







