A Hybrid-Driven Optimization Framework for Fixed-Wing UAV Maneuvering Flight Planning
Abstract
:1. Introduction
- (1)
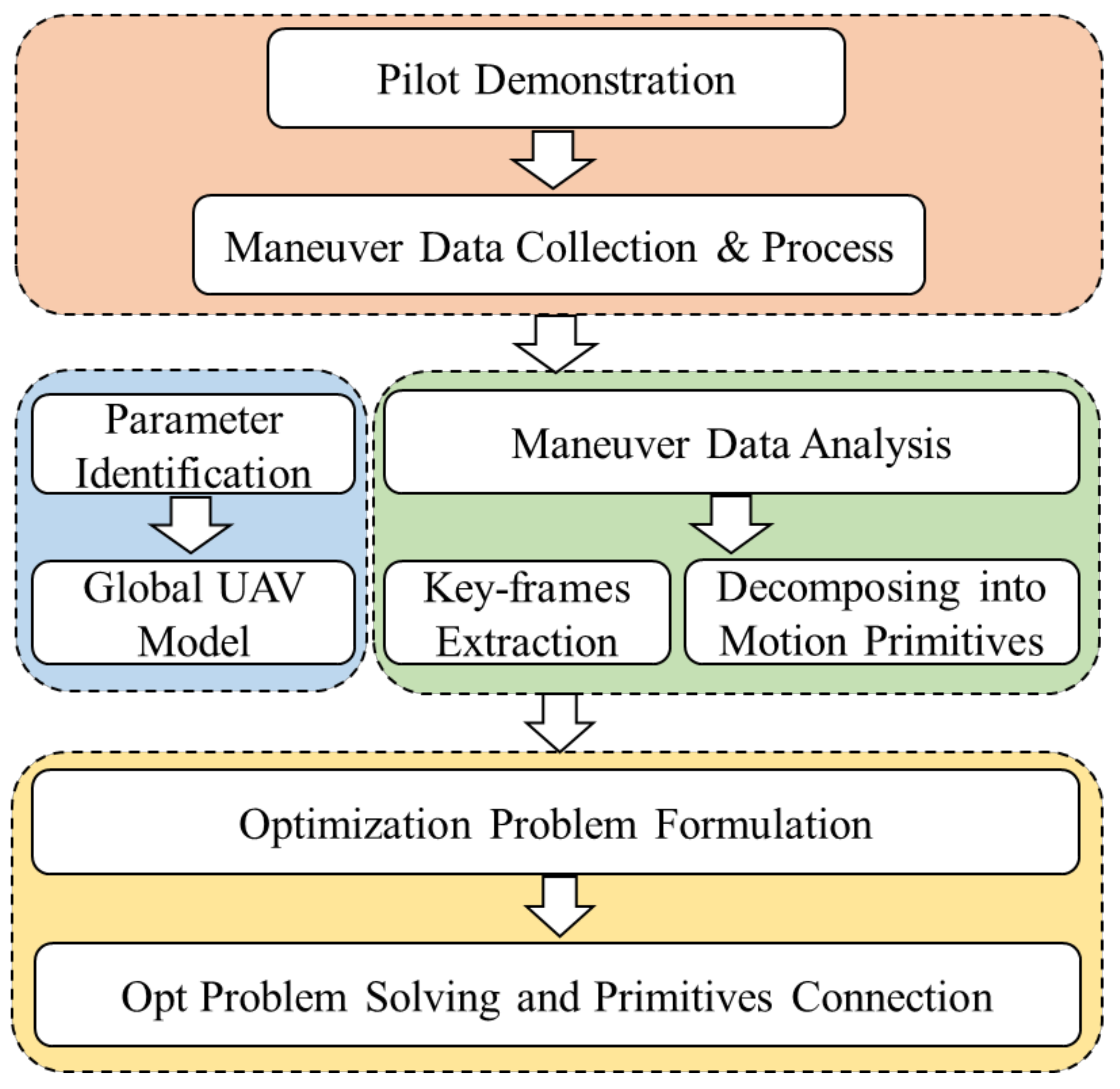
- We proposed a novel data-driven approach for model identification and key-frames extraction using the learning from demonstration principles. Then, complex maneuvers are decomposed into multiple motion primitives;
- (2)
- Based on the motion primitives, the optimal maneuver generation issue is formulated into a time-optimal problem considering key-frames which the UAV must pass by. The connection method of different primitives was also considered in this paper for practicability;
- (3)
- The proposed framework was verified thoroughly in simulation experiments, and it was possible to deduce that this framework is applicable for flight maneuvers in reality.
2. Preliminaries
2.1. Global Fixed-Wing Model
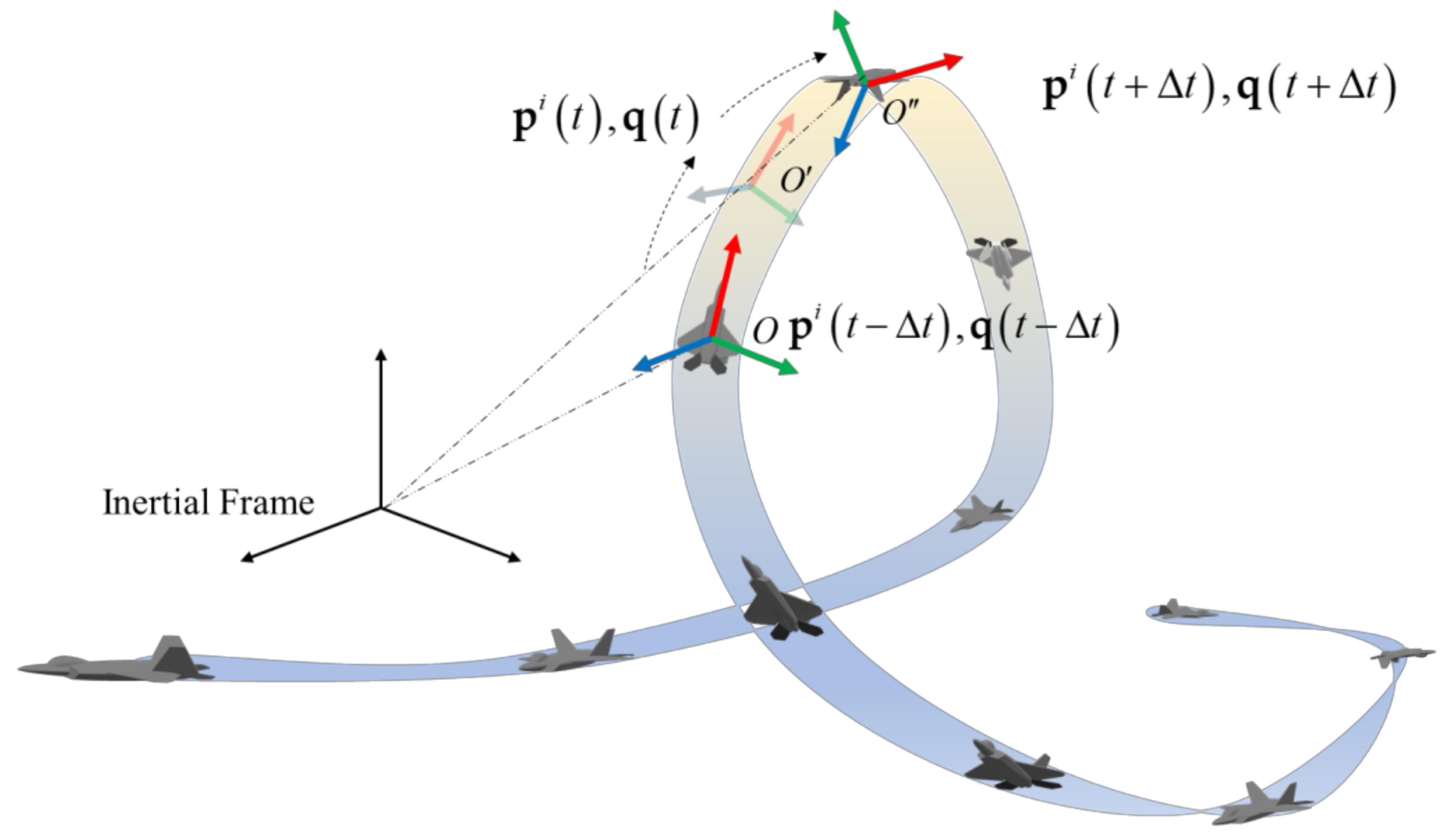
2.2. Acrobatic Maneuver
3. Data Collection and Model Identification
3.1. Acrobatic Maneuver Data Collection
3.2. Model Parameter Identification
4. Optimal Acrobatic Maneuver Design and Generation
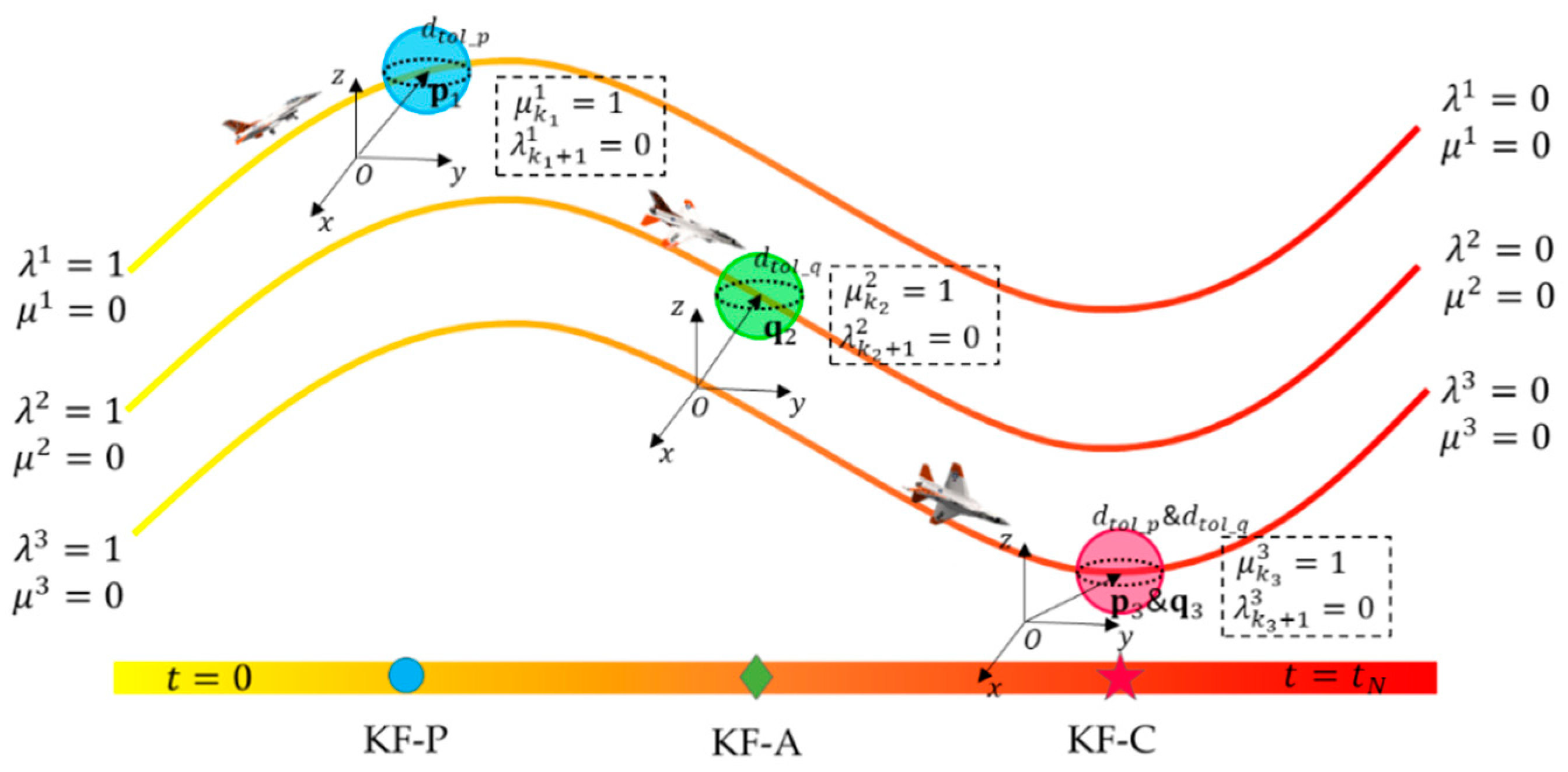
4.1. Key-Frames and Motion Primitives
4.2. Maneuver Optimization
- (1)
- Positional key-frame (KF-P)
- (2)
- Attitude key-frame (KF-A)
- (3)
- Compound key-frame (KF-C)
| Algorithm 1. Fixed-wing UAV optimal maneuver generation. |
|
5. Experiments and Discussion
5.1. Model Identification Results
5.2. Optimization Simulation Setup
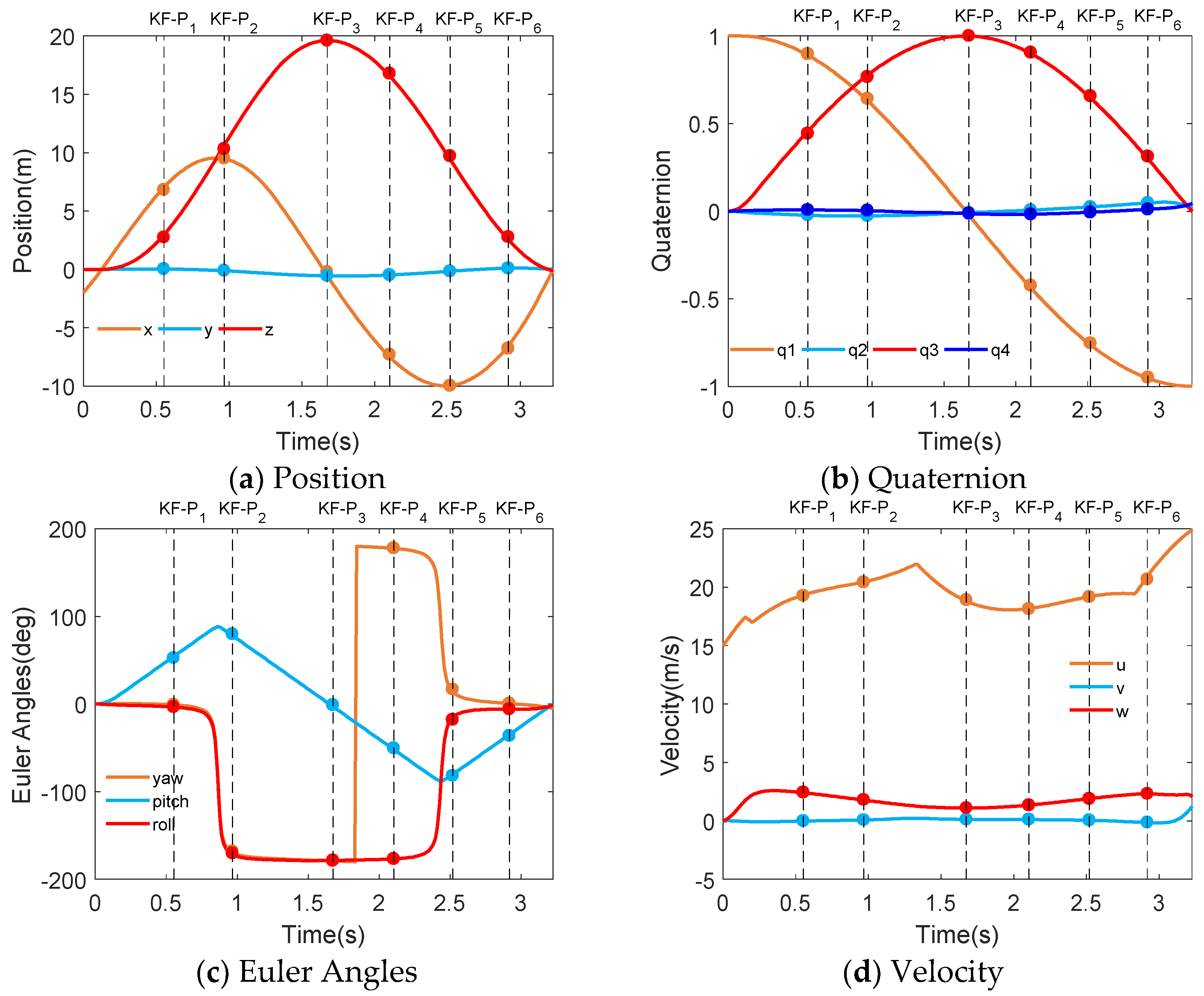
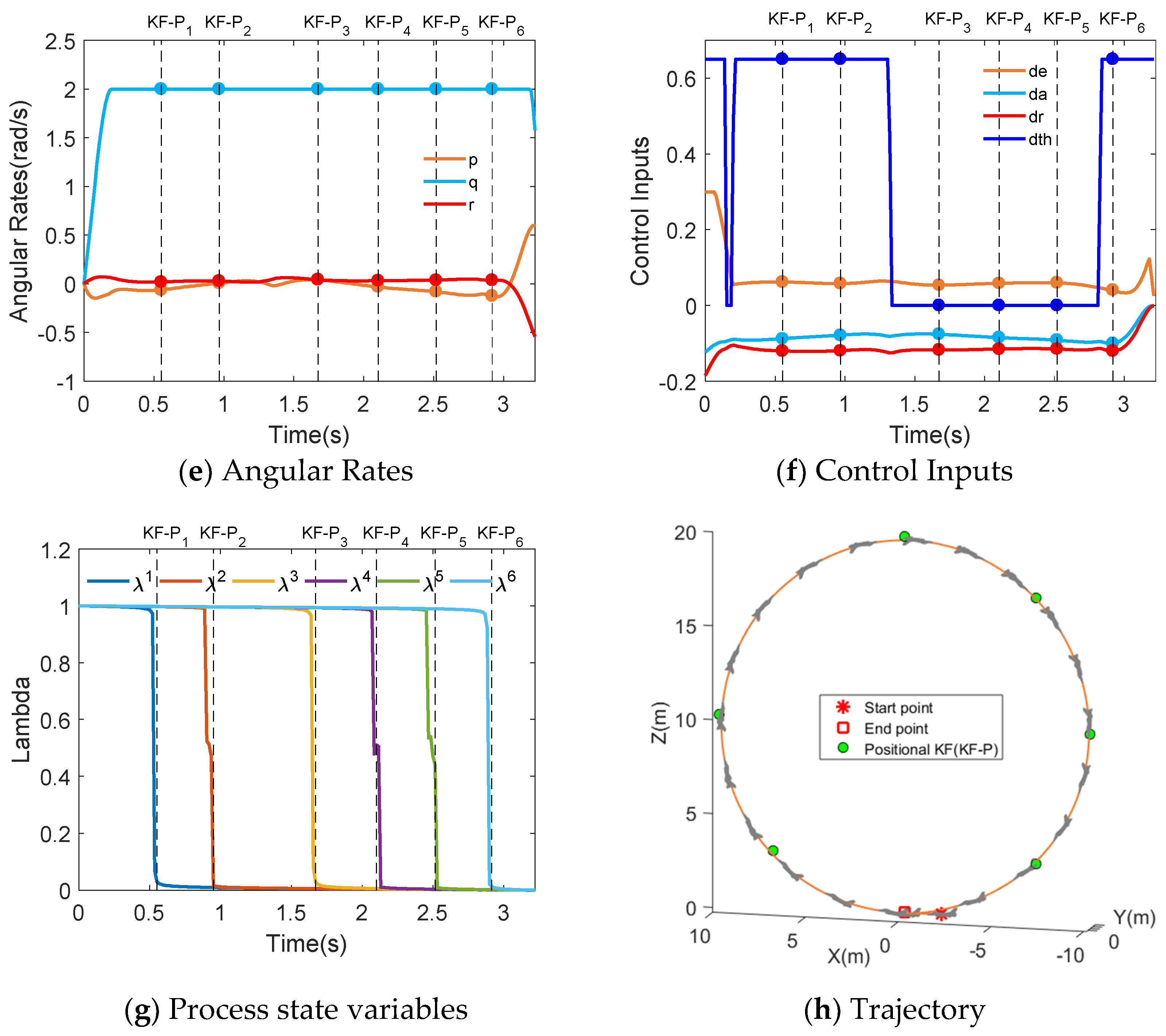
5.2.1. Loop Maneuver
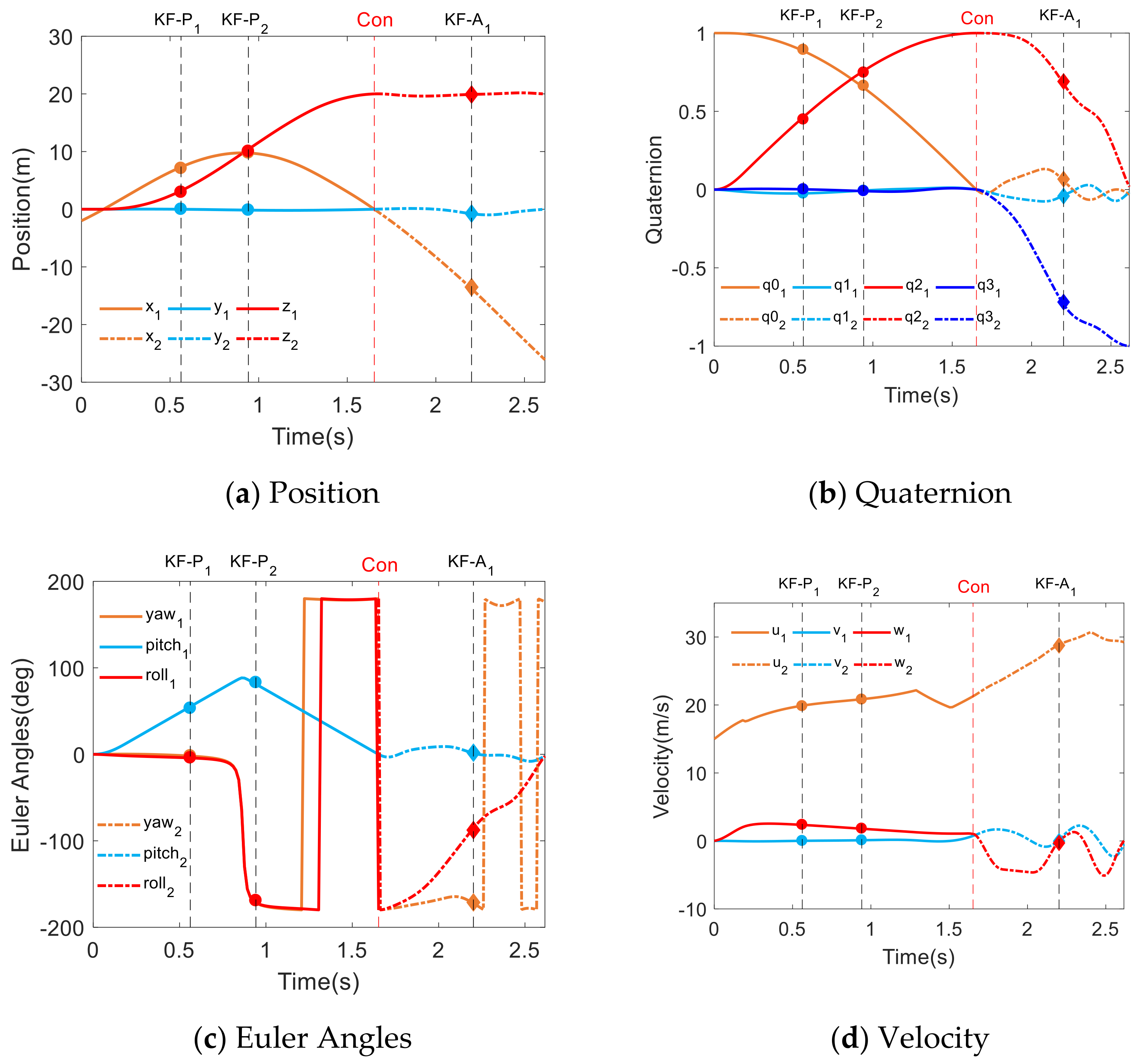
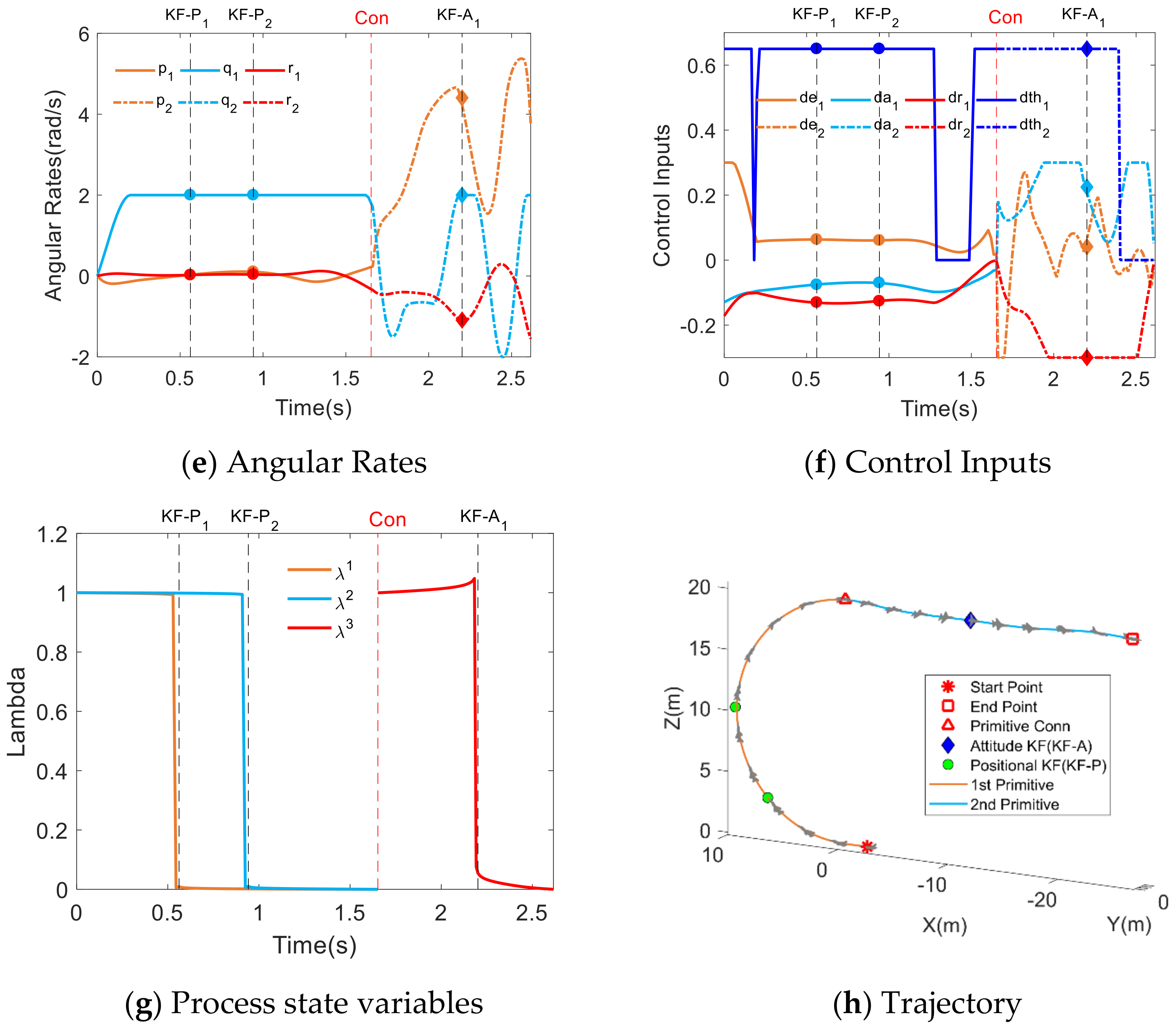
5.2.2. The Immelmann Maneuver
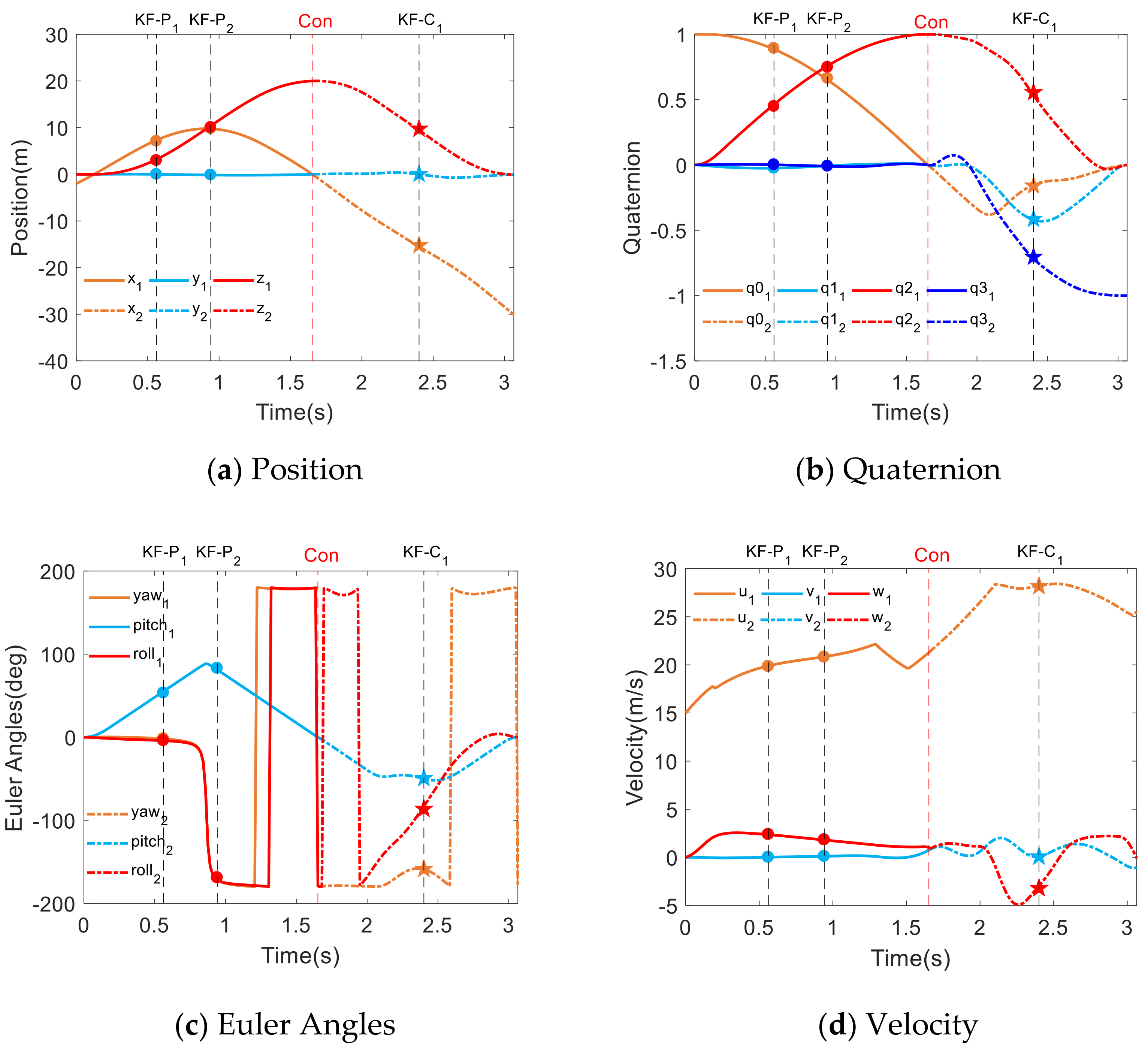
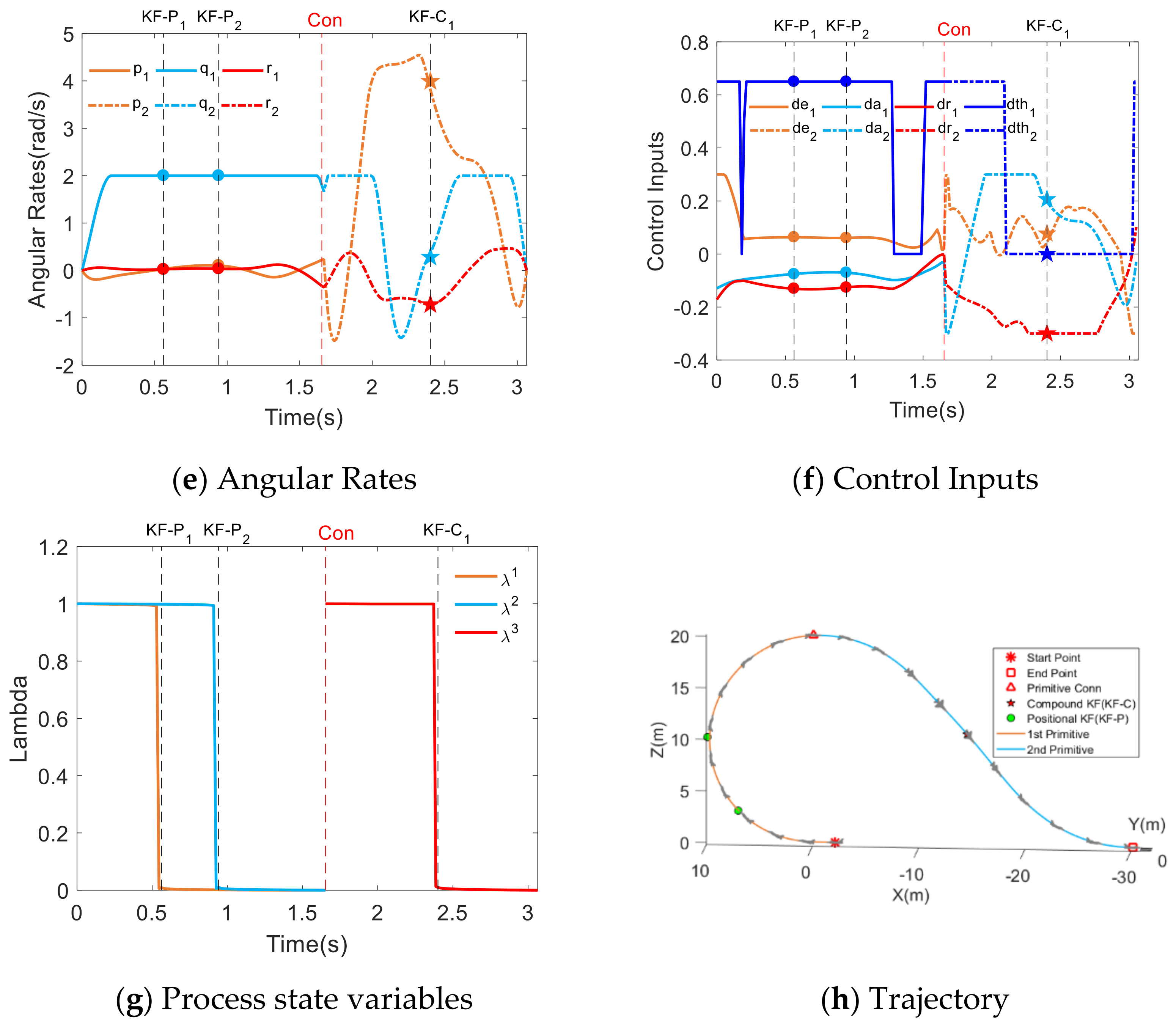
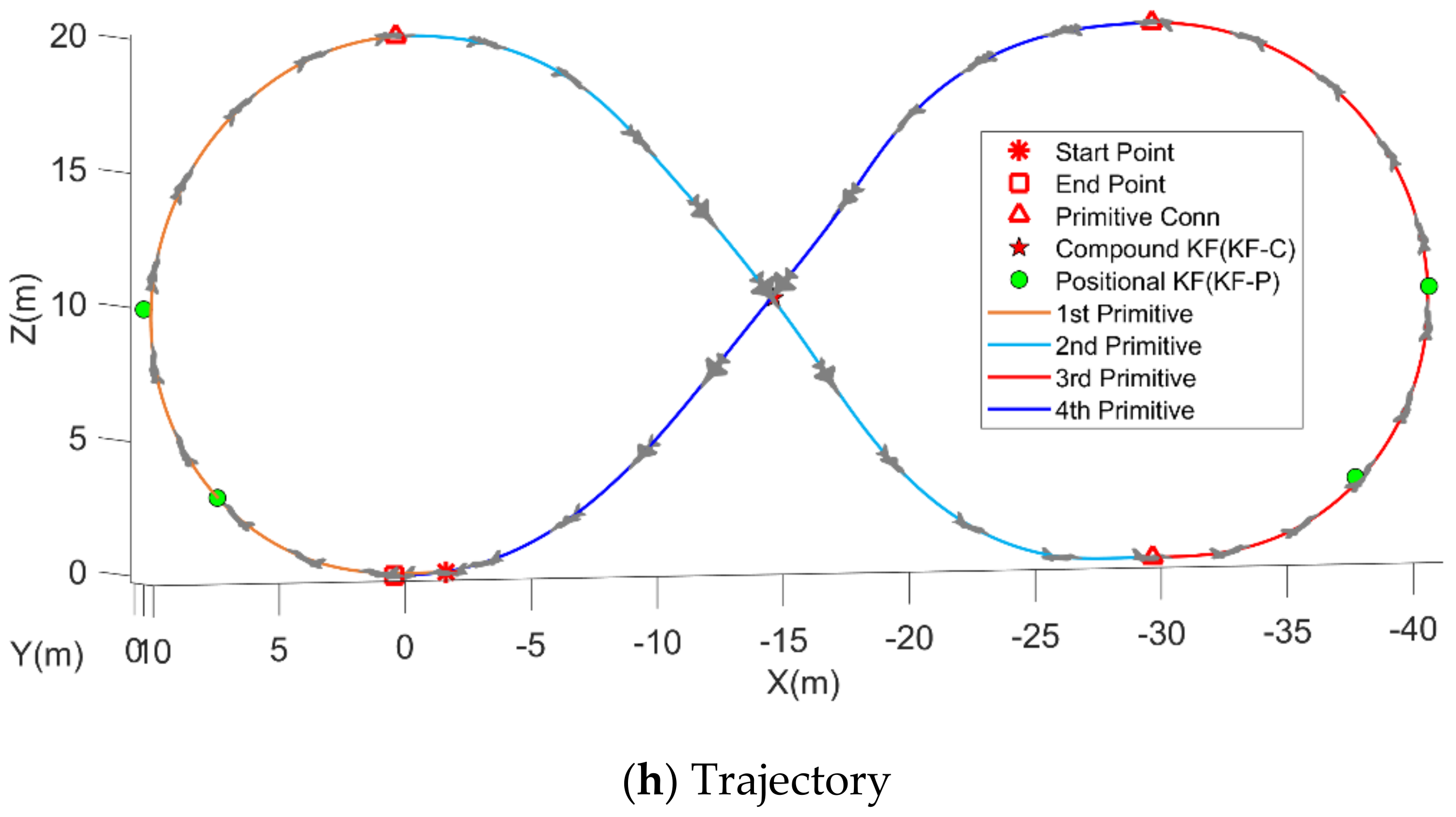
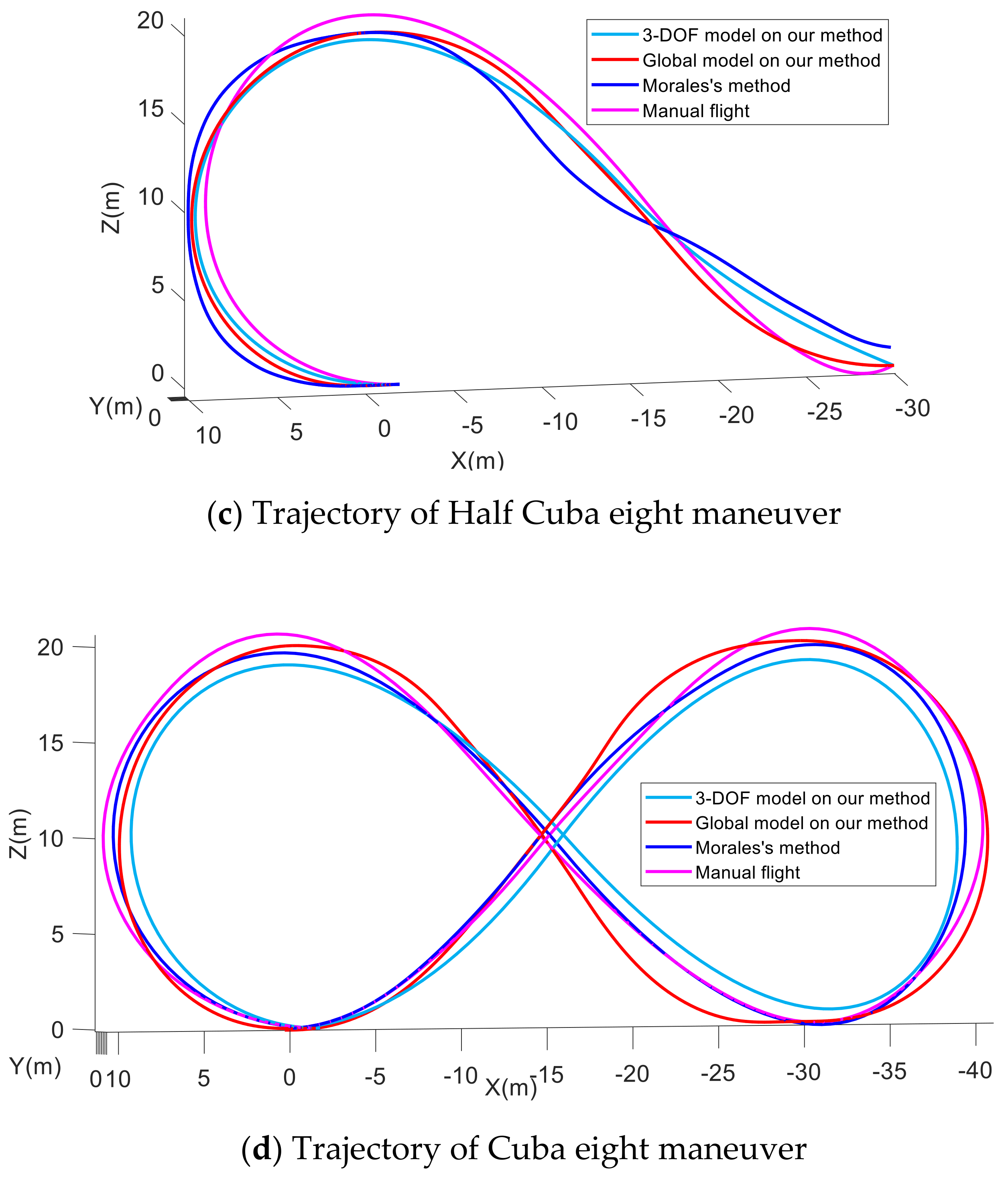
5.2.3. Half Cuban Eight and Cuban Eight Maneuver
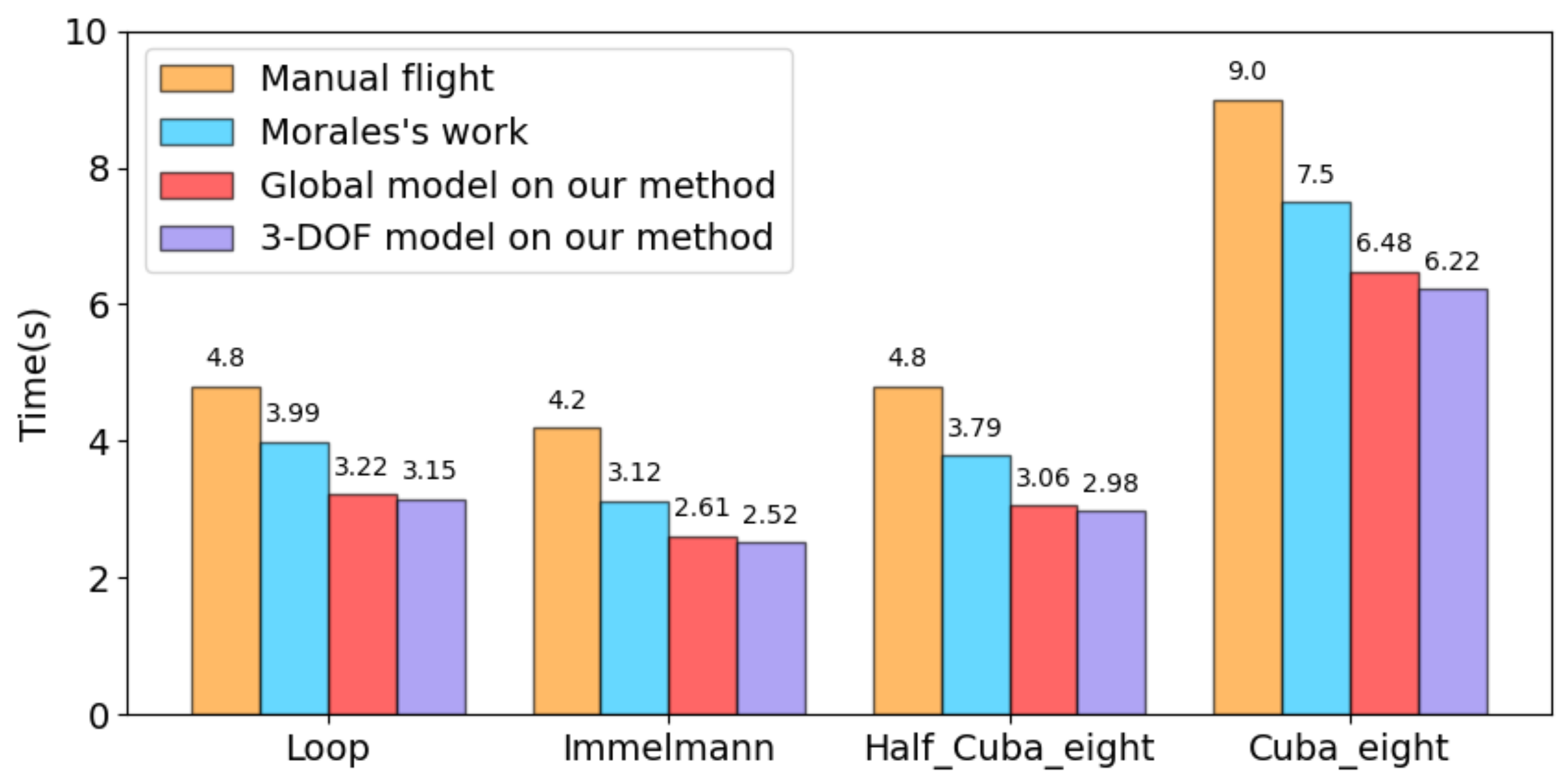
5.3. Benchmark Comparisons
5.4. Analysis of Maneuver Optimization Algorithm
- (1)
- Global Fixed-wing model
- (2)
- Key-frames and primitives design
- (3)
- Initial guess
- (4)
- Optimization constraints
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Ju, C.; Son, H.I. Multiple UAV systems for agricultural applications: Control, implementation, and evaluation. Electronics 2018, 7, 162. [Google Scholar] [CrossRef] [Green Version]
- Tang, T.; Hong, T.; Hong, H.; Ji, S.; Mumtaz, S.; Cheriet, M. An improved UAV-PHD filter-based trajectory tracking algorithm for multi-UAVs in future 5G IoT scenarios. Electronics 2019, 8, 1188. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Wu, C.; Wu, Q.; Eli, Z.M.; Xiong, N.; Zhang, S. Design and analysis of refined inspection of field conditions of oilfield pumping wells based on rotorcraft uav technology. Electronics 2019, 8, 1504. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.L.; Deng, Y.Y.; Weng, W.; Chen, C.H.; Chiu, Y.J.; Wu, C.M. A traceable and privacy-preserving authentication for UAV communication control system. Electronics 2020, 9, 62. [Google Scholar] [CrossRef] [Green Version]
- Stellin, M.; Sabino, S.; Grilo, A. LoRaWAN Networking in Mobile Scenarios Using a WiFi Mesh of UAV Gateways. Electronics 2020, 9, 630. [Google Scholar] [CrossRef] [Green Version]
- Mellinger, D.; Michael, N.; Kumar, V. Trajectory generation and control for precise aggressive maneuvers with quadrotors. Int. J. Robot. Res. 2012, 1–11. [Google Scholar] [CrossRef]
- Hehn, M.; Ritz, R.; DAndrea, R. Performance benchmarking of quadrotor systems using time-optimal control. Auton. Robot. 2012, 33, 69–88. [Google Scholar] [CrossRef]
- Kaufmann, E.; Loquercio, A.; Ranftl, R.; Muller, M.; Koltun, V.; Scaramuzza, D. Deep drone acrobatics. RSS: Robotics, Science, and Systems. arXiv 2021, arXiv:2006.05768. [Google Scholar]
- Gilhyun, R.; Tal, E.; Karaman, S. Multi-fidelity black-box optimization for time-optimal quadrotor maneuvers. RSS: Robotics, Science, and Systems. arXiv 2020, arXiv:2006.02513. [Google Scholar]
- Bry, A.; Richter, C.; Bachrach, A.; Roy, N. Aggressive flight of fixed-wing and quadrotor aircraft in dense indoor environments. Int. J. Robot. Res. 2015, 34, 969–1002. [Google Scholar] [CrossRef]
- Levin, M. Maneuver Design and Motion Planning for Agile Fixed-Wing UAVs. Ph.D. Thesis, McGill University, Montreal, Canada, April 2019. [Google Scholar]
- Tang, J.; Singh, A.; Goehausen, N. Parameterized Maneuver Learning for Autonomous Helicopter Flight. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 4–8 May 2010. [Google Scholar]
- Abbeel, P. Apprenticeship Learning and Reinforcement Learning with Application to Robotic Control. Ph.D. Thesis, Stanford University, Stanford, CA, USA, August 2008. [Google Scholar]
- Abbeel, P.; Coates, A.; Ng, A.Y. Autonomous Helicopter Aerobatics through Apprenticeship Learning. Int. J. Robot. Res 2010, 29, 1608–1639. [Google Scholar] [CrossRef]
- Mueller, M.W.; Hehn, M.; D′Andrea, R. A computationally efficient motion primitive for quadrocopter trajectory generation. IEEE Trans. Robot. 2015, 31, 1294–1310. [Google Scholar] [CrossRef]
- Quan, L.; Han, L.; Zhou, B. Survey of UAV motion planning. IET Cyber-Syst. Robot. 2020, 2, 14–21. [Google Scholar] [CrossRef]
- Liu, S.; Mohta, K.; Atanasov, N.; Kumar, V. Search-based motion planning for aggressive flight in se (3). IEEE Robot. Autom. Lett. 2018, 3, 2439–2446. [Google Scholar] [CrossRef] [Green Version]
- Watterson, M.; Liu, S.; Sun, K.; Smith, T.; Kumar, V. Trajectory optimization on manifolds with applications to quadrotor systems. Int. J. Robot. Res. 2020, 39, 303–320. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, X.; Xu, C.; Gao, F. Geometrically Constrained Trajectory Optimization for Multicopters. arXiv 2021, arXiv:2103.00190. [Google Scholar]
- Basescu, M.; Moore, J. Direct nmpc for Post-Stall Motion Planning with Fixed-Wing uavs. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar]
- Fan, Y.; Lutze, F.H.; Cliff, E.M. Time-optimal lateral maneuvers of an aircraft. J. Guid. Control. Dyn. 1995, 18, 1106–1112. [Google Scholar] [CrossRef]
- Komduur, H.J.; Visser, H.G. Optimization of vertical plane cobralike pitch reversal maneuvers. J. Guid. Control. Dyn. 2002, 25, 693–702. [Google Scholar] [CrossRef]
- Imado, F.; Heike, Y.; Kinoshita, T. Research on a new aircraft point-mass model. J. Aircr. 2011, 48, 1121–1130. [Google Scholar] [CrossRef]
- Morales, M.A.; Silvestre, F.J.; Neto, A.B.G. Equations of motion for optimal maneuvering with global aerodynamic model. Aerosp. Sci. Technol. 2018, 77, 206–216. [Google Scholar] [CrossRef]
- Du, D.; Qi, Y.; Yu, H. The Unmanned Aerial Vehicle Benchmark: Object Detection and Tracking. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Wen, L.; Zhu, P.; Du, D. Visdrone-sot2018: The Vision Meets Drone Single-Object Tracking Challenge Results. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Qi, Y.; Wu, Q.; Anderson, P. Reverie: Remote Embodied Visual Referring Expression in Real Indoor Environments. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Hong, Y.; Rodriguez-Opazo, C.; Qi, Y. Language and visual entity relationship graph for agent navigation. arXiv 2020, arXiv:2010.09304. [Google Scholar]
- Qi, Y.; Pan, Z.; Hong, Y.; Yang, M.H.; Hengel, A.; Wu, Q. Know What and Know Where: An Object-and-Room Informed Sequential BERT for Indoor Vision-Language Navigation. arXiv 2021, arXiv:2104.04167. [Google Scholar]
- Qi, Y.; Pan, Z.; Zhang, S. Object-and-action aware model for visual language navigation. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Gebhardt, C.; Hepp, B.; Nägeli, T. Airways: Optimization-based Planning of Quadrotor Trajectories According to High-Level User Goals. In Proceedings of the 2016 CHI Conference on Human Factors in Computing Systems, San Jose, CA, USA, 7–12 May 2016. [Google Scholar]
- Mellinger, D.; Kumar, V. Minimum Snap Trajectory Generation and Control for Quadrotors. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]
- Foehn, P.; Davide, S. CPC: Complementary progress constraints for time-optimal quadrotor trajectories. arXiv 2020, arXiv:2007.06255. [Google Scholar]
- Foehn, P.; Romero, A.; Scaramuzza, D. Time-optimal planning for quadrotor waypoint flight. Sci. Robot. 2021, 6, eabh1221. [Google Scholar] [CrossRef]
- Rousseau, G.; Maniu, C.S.; Tebbani, S.; Babel, M.; Martin, N. Minimum-time B-spline trajectories with corridor constraints. Application to cinematographic quadrotor flight plans. Control. Eng. Pract. 2019, 89, 190–203. [Google Scholar] [CrossRef] [Green Version]
- Frazzoli, E.; Dahleh, M.A.; Feron, E. Maneuver-Based Motion Planning for Nonlinear Systems with Symmetries. IEEE Trans. Robot. 2005, 21, 1077–1091. [Google Scholar] [CrossRef]
- Bulka, E.; Nahon, M. Autonomous Fixed-Wing Aerobatics: From Theory to Flight. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018. [Google Scholar]
- Bulka, E.; Nahon, M. Automatic Control for Aerobatic Maneuvering of Agile Fixed-Wing UAVs. J. Intell. Robot. Syst. 2019, 93, 85–100. [Google Scholar] [CrossRef]
- Levin, J.M.; Nahon, M.; Paranjape, A.A. Real-time motion planning with a fixed-wing UAV using an agile maneuver space. Auton. Robot. 2019, 43, 2111–2130. [Google Scholar] [CrossRef]
- Wang, B.; Gong, J.; Chen, H. Motion Primitives Representation, Extraction and Connection for Automated Vehicle Motion Planning Applications. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3931–3945. [Google Scholar] [CrossRef]
- Zhang, R.; Hu, Y.; Zhao, K. A Novel Dual Quaternion Based Dynamic Motion Primitives for Acrobatic Flight. In Proceedings of the 2021 5nd International Conference on Robotics and Automation Sciences (ICRAS), Wuhan, China, 11–13 June 2021. [Google Scholar]
- Sonneveldt, L. “Nonlinear F-16 Model Description”,Control and Simulation Div. Faculty of Aerospace Engineering; Delft University of Technology: Delft, The Netherlands, 2006. [Google Scholar]
- Zhang, R.; Zhang, J.; Yu, H. Review of Modeling and Control in UAV Autonomous Maneuvering Flight. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018. [Google Scholar]
- Dutra, D.A. Collocation-Based Output-Error Method for Aircraft System Identification. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar]
- Andersson, J.; Joris, G.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi: A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2018, 11, 1–36. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]




| Property | Value | Property | Value |
|---|---|---|---|
| 3.24 | 0.22 | ||
| 1.225 | 0.31 | ||
| 0.56 | 0.48 | ||
| 1.83 | 0 | ||
| 0.30 | 0 | ||
| 9.8 | 0 | ||
| Property | Value | ||
| Input | Range | State quantity | Range |
| Start | Value | End | Value |
|---|---|---|---|
| Position (m) | [−2,0,0] | Position (m) | [0,0,0] |
| Attitude (quaternion) | [1,0,0,0] | Pitch (deg) | 0 |
| Velocity (m/s) | [15,0,0] | Others | free |
| Angular rate (rad/s) | [0,0,0] | ||
| Key-frame | Value | ||
| Short-term positional key-frame | [7.07,0,2.93], [10,0,10], [0,0,20] [−7.07,0,16.57], [−10,0,10], [−7.07,0,2.43] | ||
| Start | Value | End | Value |
|---|---|---|---|
| Position (m) | [0,0,20] | x (m) | free |
| Attitude (quaternion) | [0,0,1,0] | y (m) | 0 |
| Velocity (m/s) | [21.284,0.748,1.014] | z (m) | 20 |
| Angular rate (rad/s) | [0.226,1.799,−0.326] | Attitude (quaternion) | [0,0,0,−1] |
| Control input | [0.0171,−0.0318,−0.0023,65] | ||
| Key-Frame | Value | ||
| Short-term angle key-frame | |||
| Start | Value | End | Value |
|---|---|---|---|
| Position (m) | [−2,0,0] | Position (m) | [−30,0,0] |
| Attitude (quaternion) | [0,0,1,0] | Pitch (deg) | 0 |
| Velocity (m/s) | [21.284,0.748,1.014] | Roll (deg) | 0 |
| Angular rate (rad/s) | [0.226,1.799,−0.326] | Yaw (deg) | 0 |
| Control input | [0.0171,−0.0318,−0.0023,65] | Angular rate (rad/s) | [0,0,0] |
| Key-Frame | Value | ||
| Short-term Compound key-frame | P = [−15,0,10] | ||
| Long-term attitude key-frame | |||
| Acrobatic Maneuver and Methods | Morales’s Work | Proposed-Global Model | Proposed-3-DOF Model |
|---|---|---|---|
| Loop | 20 min | 10 min | 45 s |
| Immelmann | 6 min | 2 min | 48 s |
| Half Cuban eight | 8 min | 3 min | 42 s |
| Cuban eight | 20 min | 8 min | 2 min |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Cao, S.; Zhao, K.; Yu, H.; Hu, Y. A Hybrid-Driven Optimization Framework for Fixed-Wing UAV Maneuvering Flight Planning. Electronics 2021, 10, 2330. https://doi.org/10.3390/electronics10192330
Zhang R, Cao S, Zhao K, Yu H, Hu Y. A Hybrid-Driven Optimization Framework for Fixed-Wing UAV Maneuvering Flight Planning. Electronics. 2021; 10(19):2330. https://doi.org/10.3390/electronics10192330
Chicago/Turabian StyleZhang, Renshan, Su Cao, Kuang Zhao, Huangchao Yu, and Yongyang Hu. 2021. "A Hybrid-Driven Optimization Framework for Fixed-Wing UAV Maneuvering Flight Planning" Electronics 10, no. 19: 2330. https://doi.org/10.3390/electronics10192330
APA StyleZhang, R., Cao, S., Zhao, K., Yu, H., & Hu, Y. (2021). A Hybrid-Driven Optimization Framework for Fixed-Wing UAV Maneuvering Flight Planning. Electronics, 10(19), 2330. https://doi.org/10.3390/electronics10192330





