Integrating Vehicle Positioning and Path Tracking Practices for an Autonomous Vehicle Prototype in Campus Environment
Abstract
:1. Introduction
2. Related Works
3. Methods
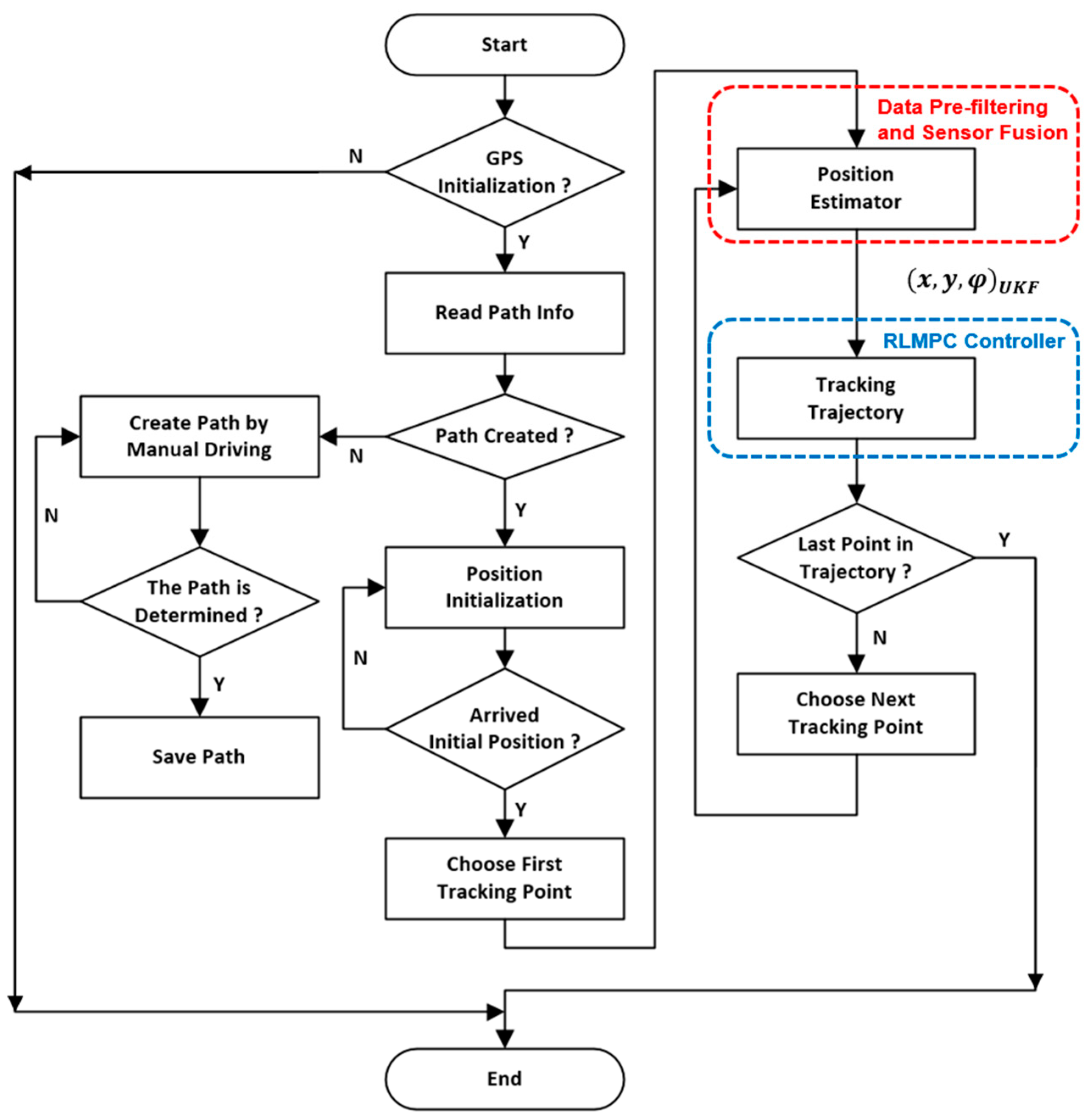
3.1. System Architecture
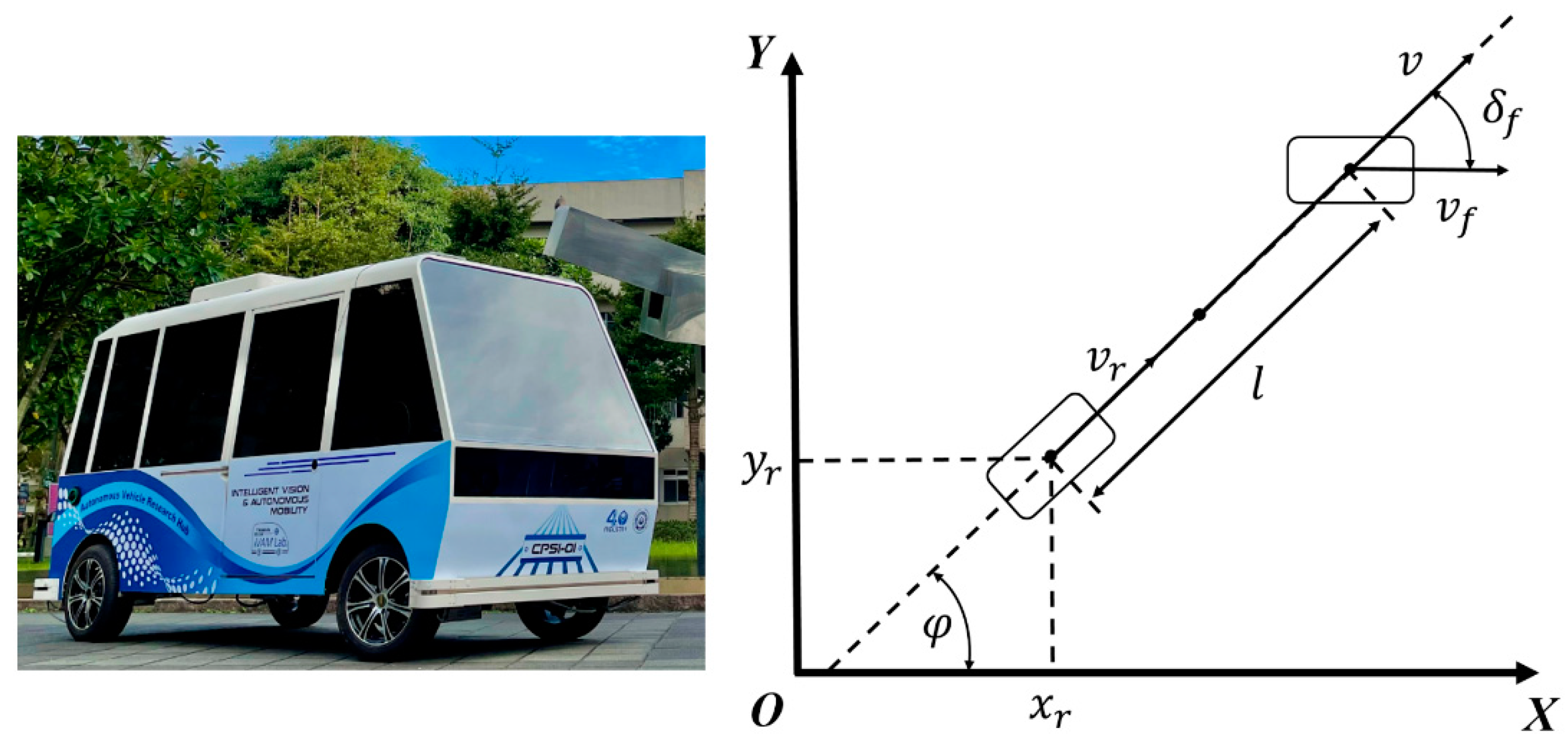
3.2. Vehicle Modeling
3.3. UKF-Based Position Estimation
- Case 1: If and , the correction set of will take into account both position and orientation data from odometry, where and the covariance matrix of measurement noise are defined as in Equations (8) and (9):
- Case 2: If and , the correction set of will only take the position data from odometry, where and the covariance matrix of measurement noise are defined as in Equations (10) and (11):It is noted that is the estimated orientation of the UKF from the last iteration.
- Case 3: If and , the correction set of will only take the orientation data from odometry, where and the covariance matrix of measurement noise are defined as in Equations (12) and (13):It is noted that and are the components of the estimated position of the UKF from the last iteration.
- Case 4: If and , the vehicle will not take the odometry measurement data as the correction input of the UKF.
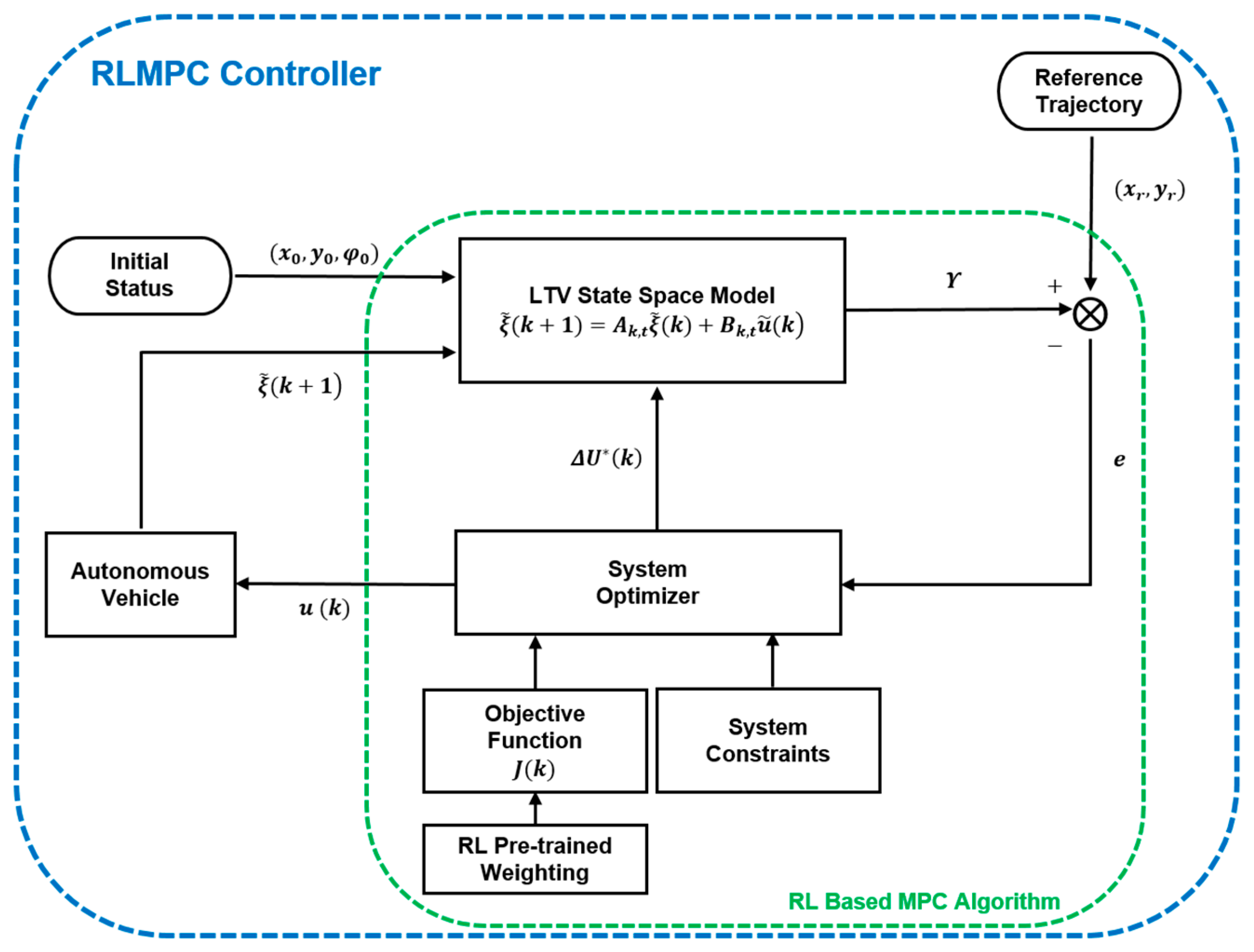
3.4. Reinforcement Learning-Based Model Predictive Control
4. Simulations and Experiments
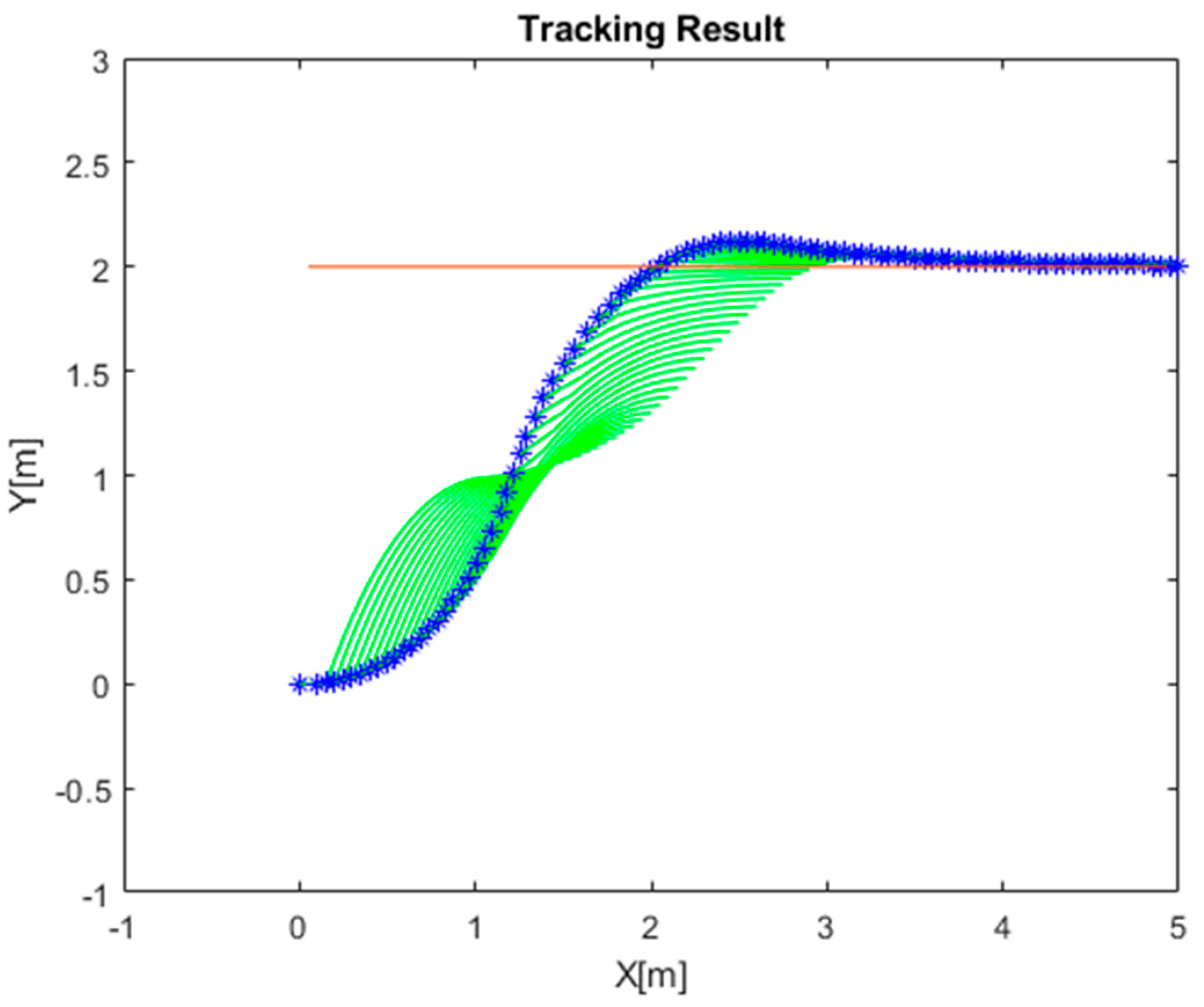
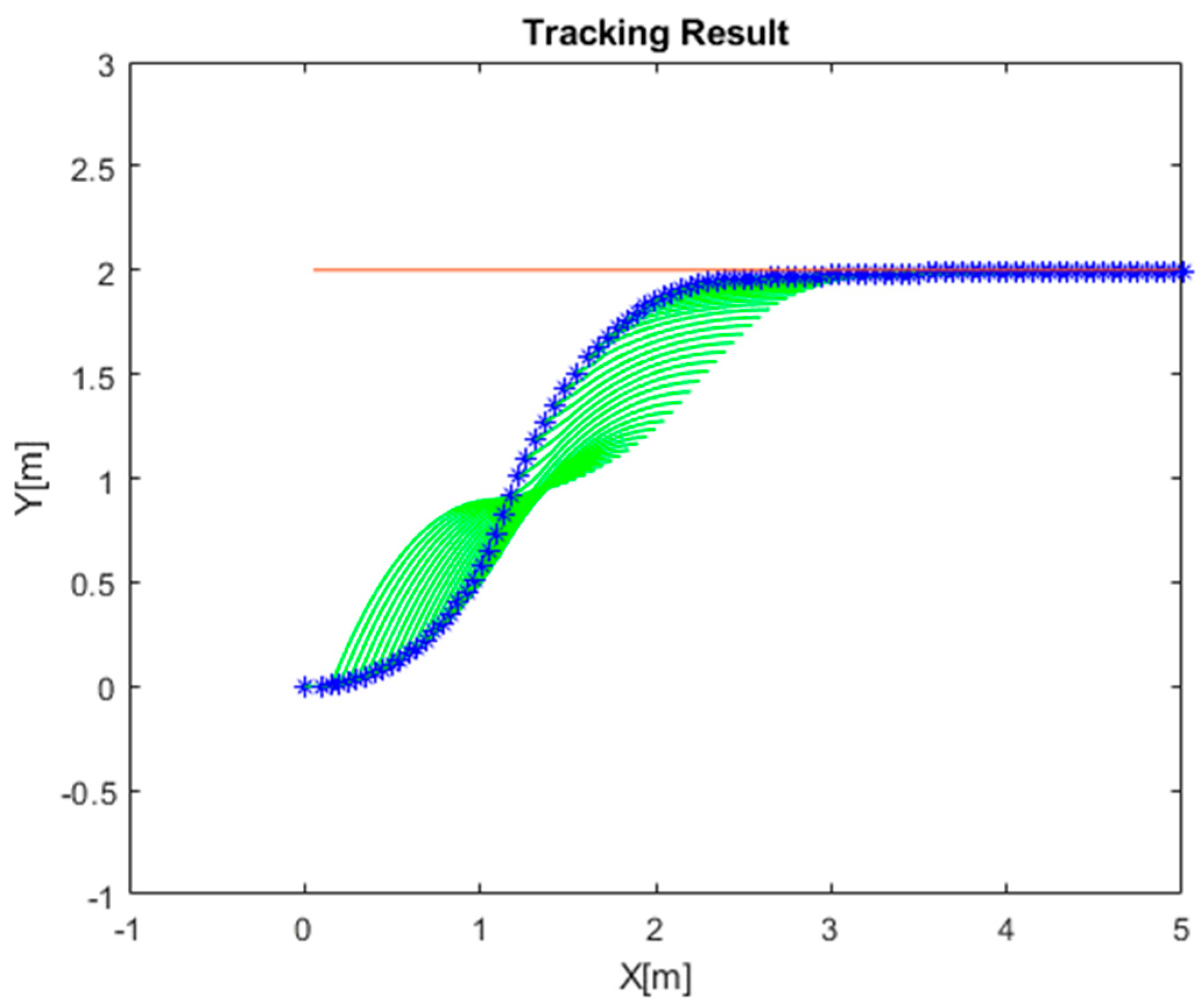
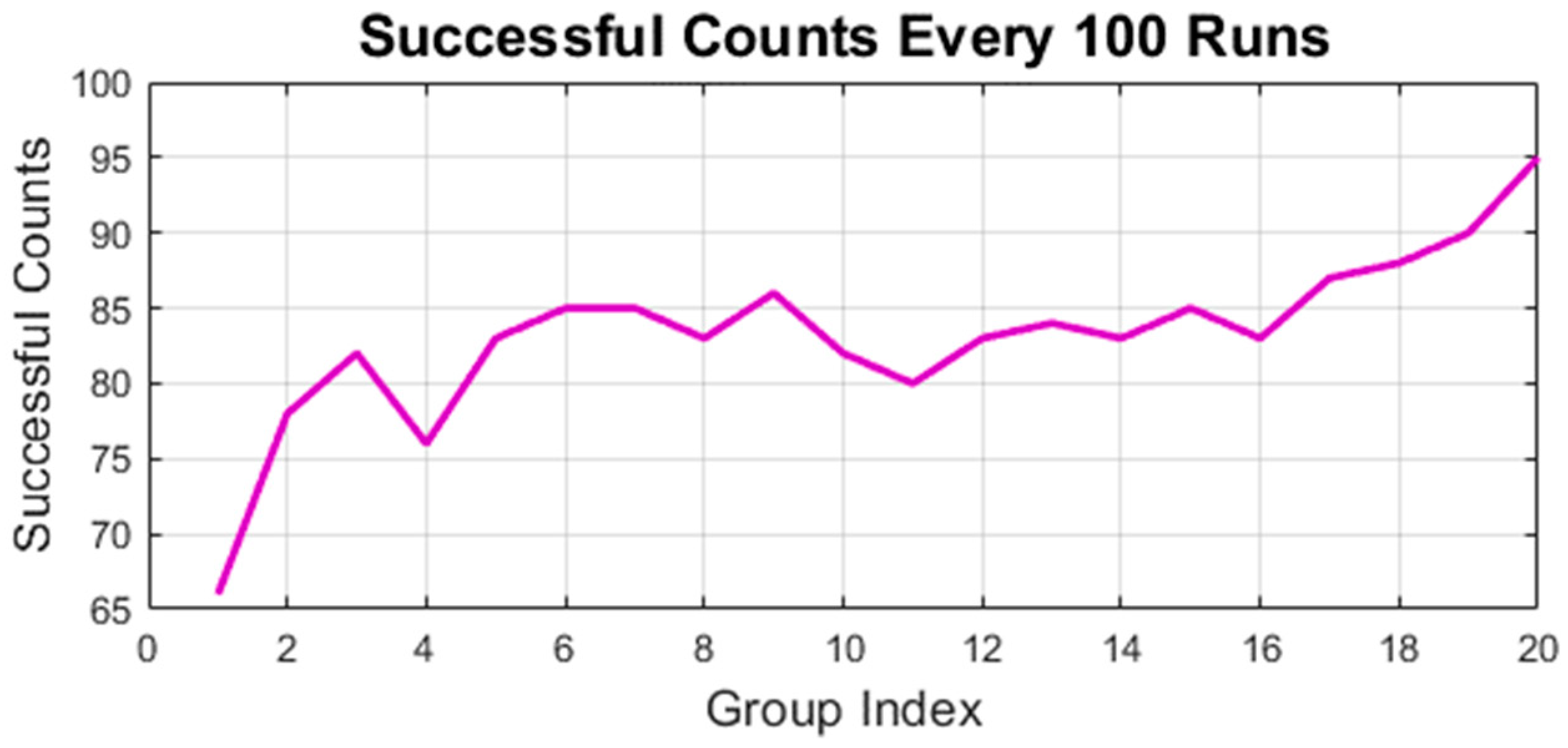
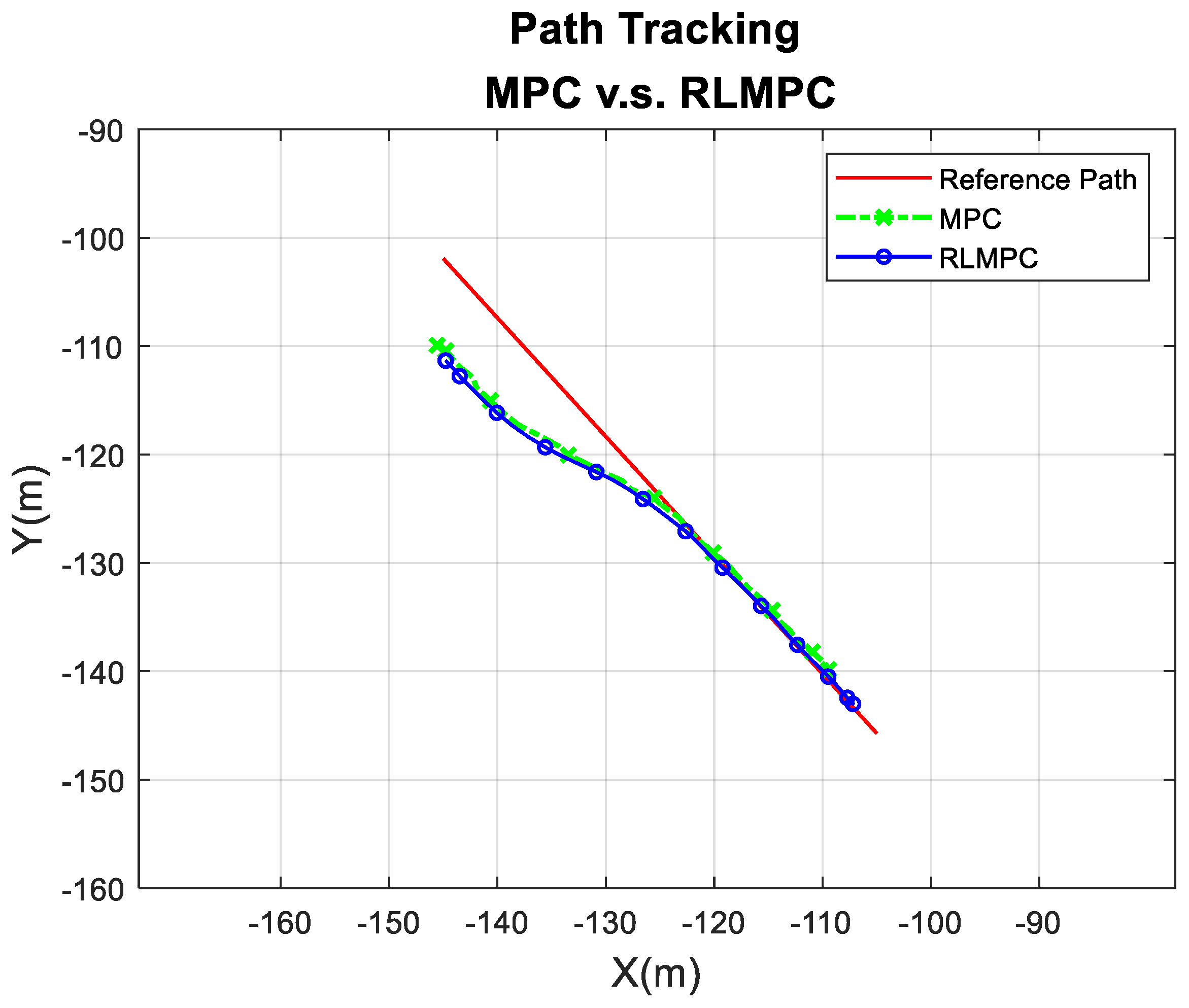
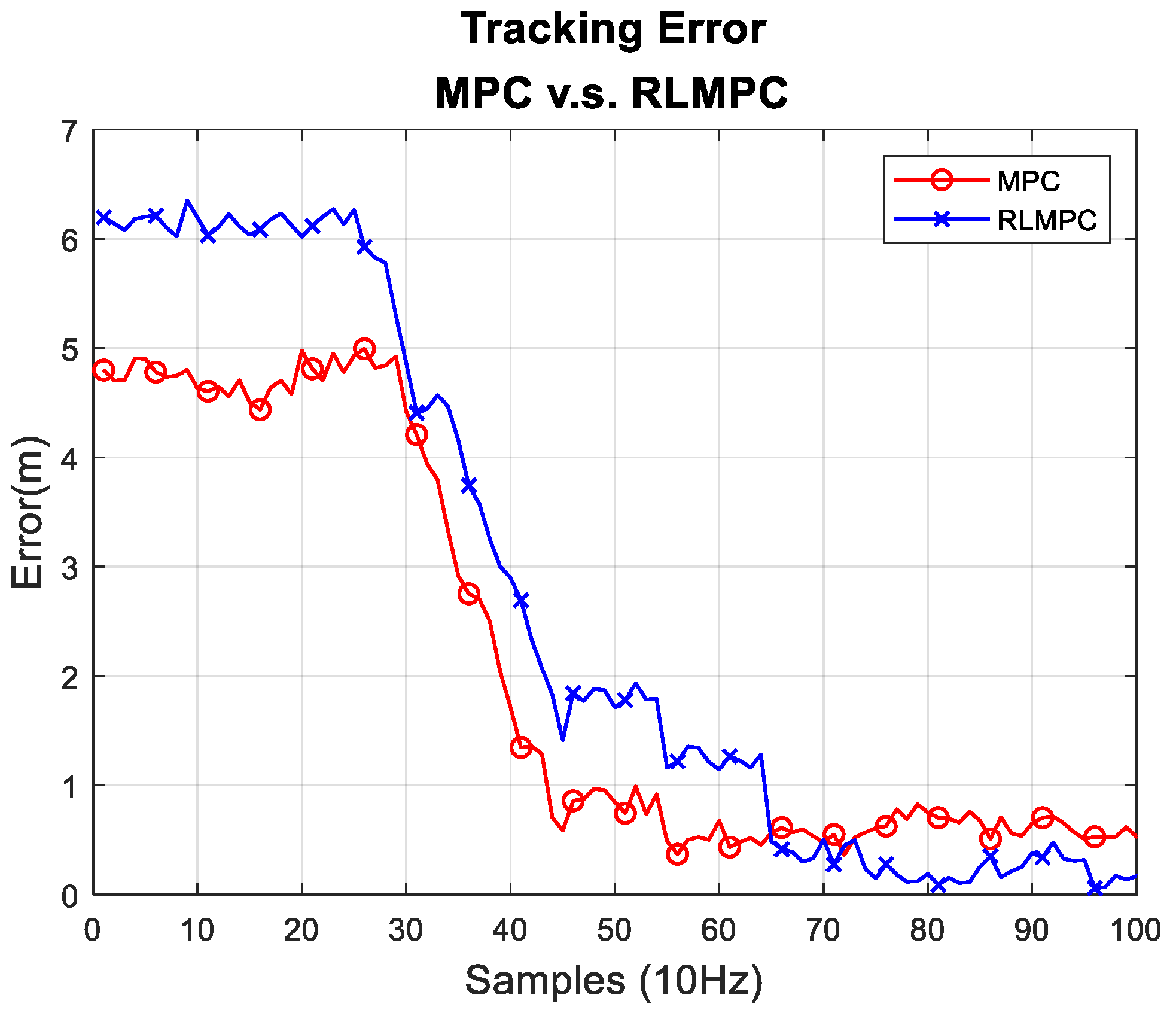
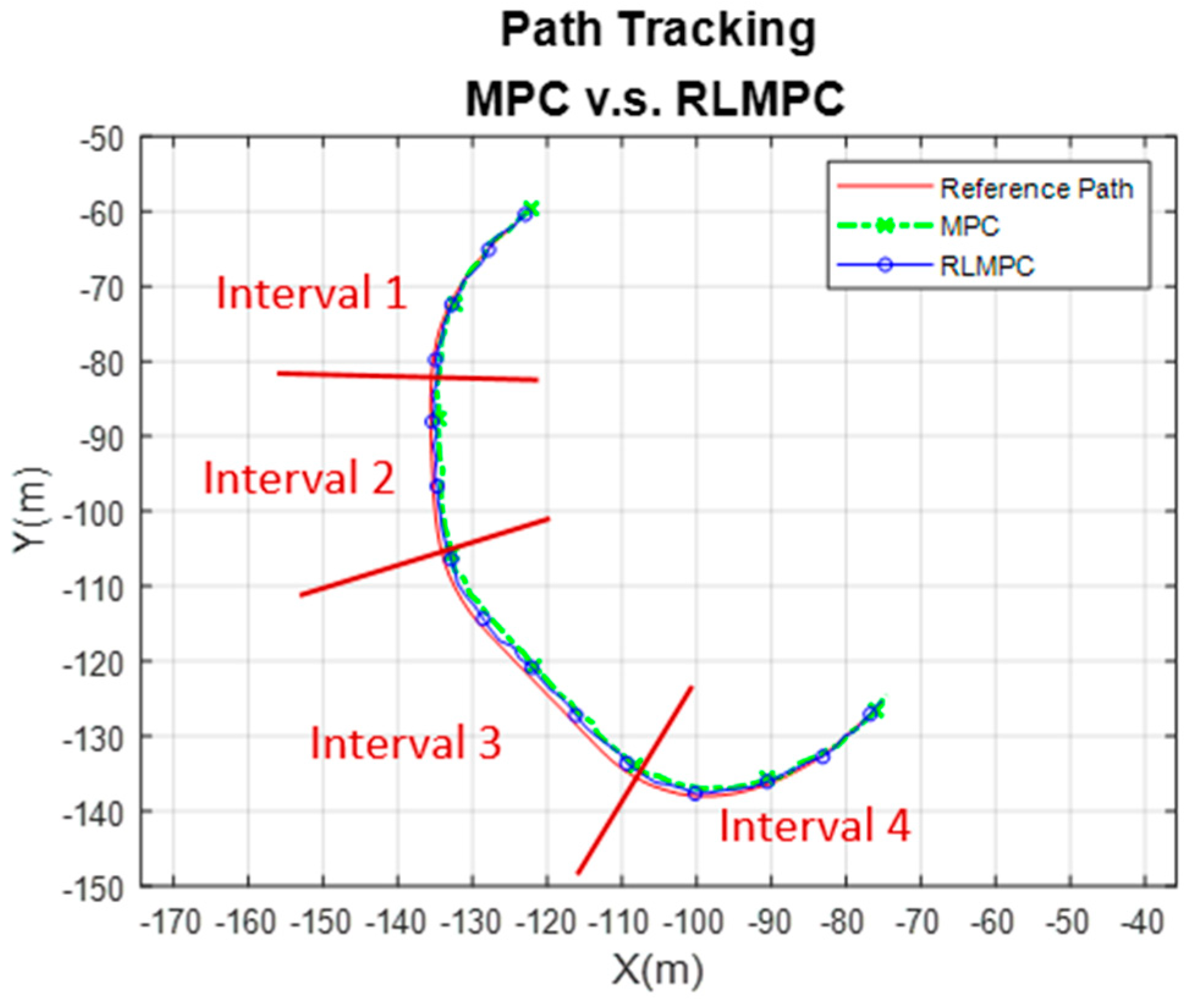
4.1. Simulation of RLMPC-Based Path Tracking
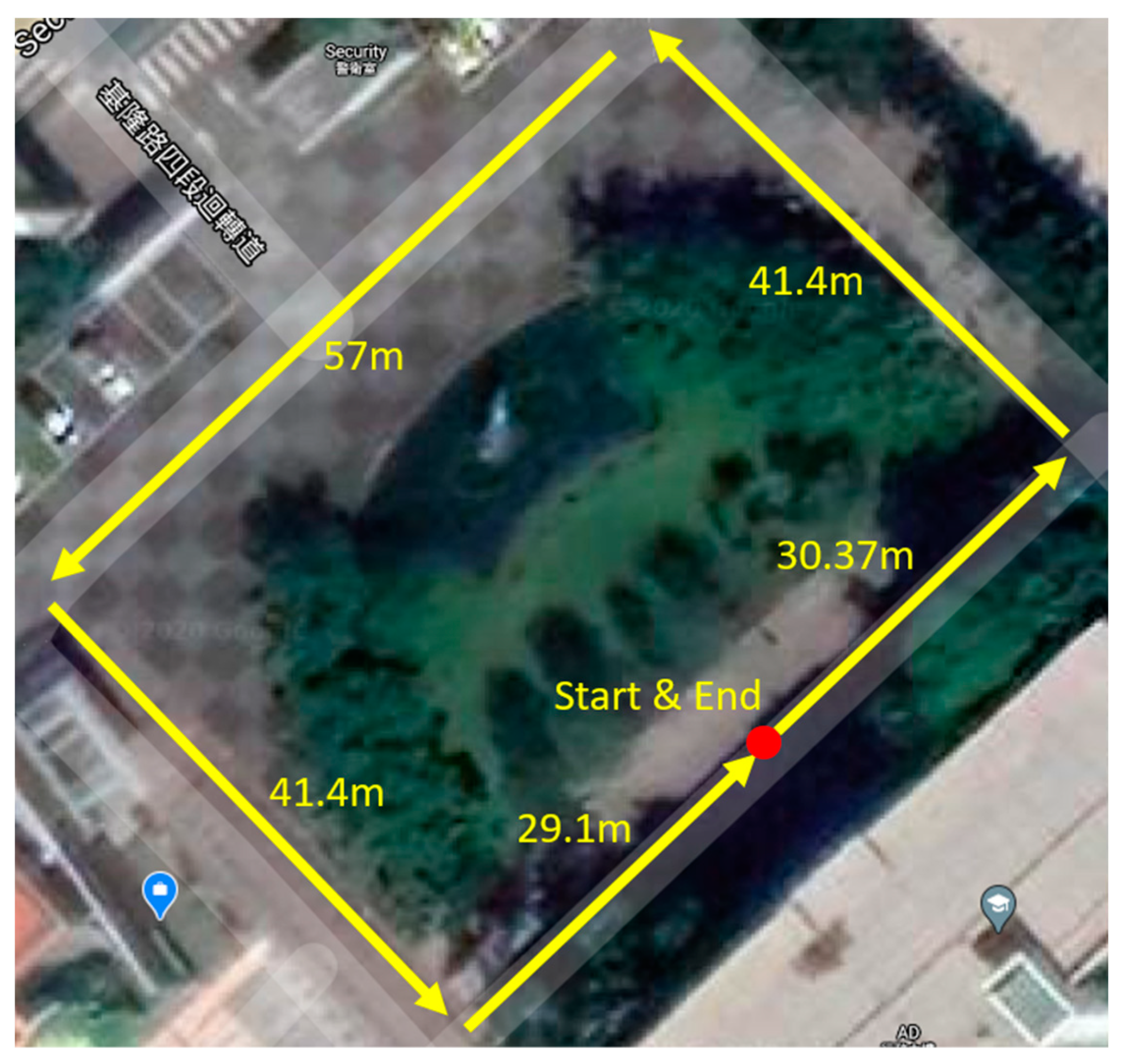
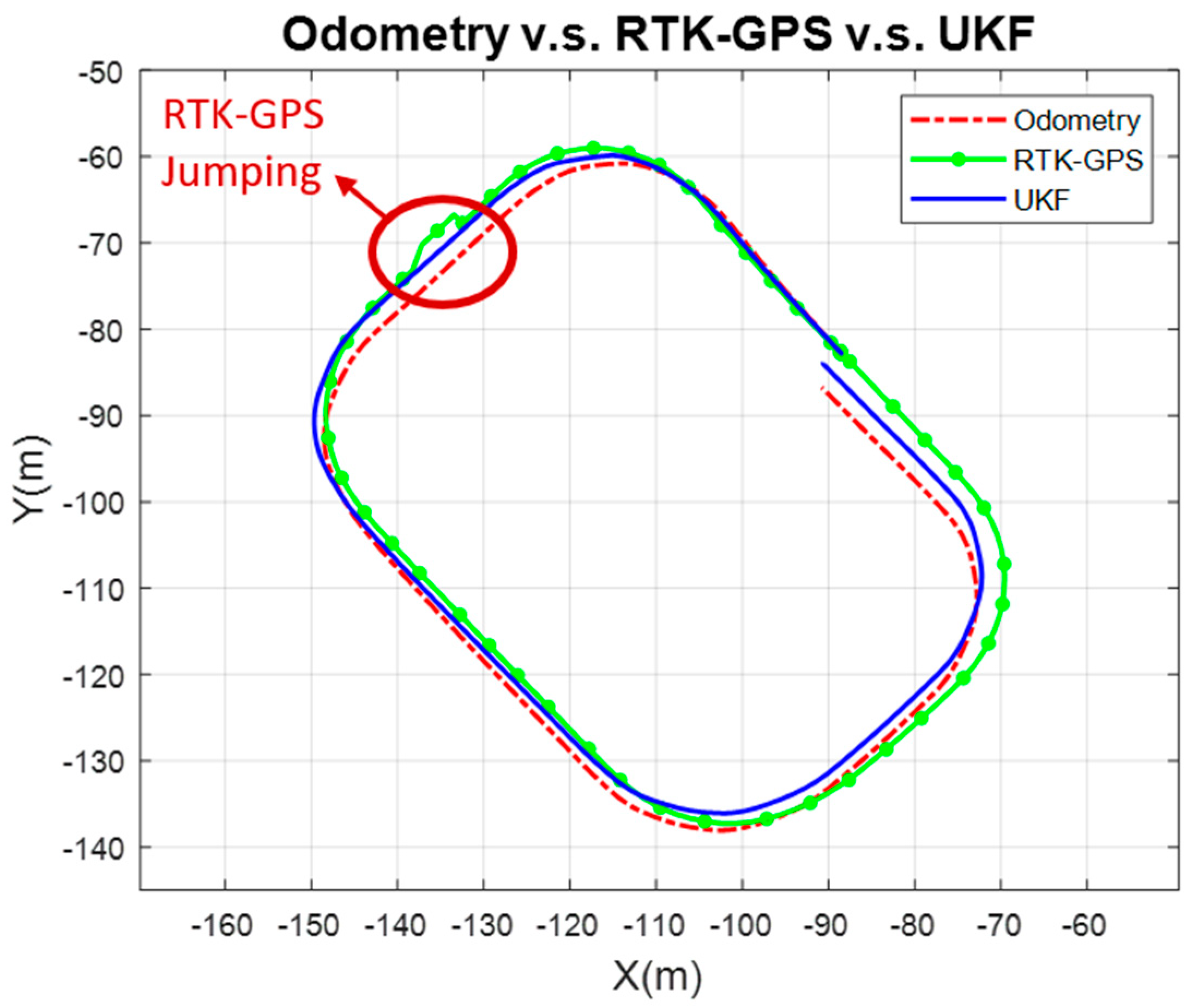
4.2. Validation of Estimated Distance with Position Estimation
4.3. Integrated Experiment with EV by Applying RL-Based MPC
5. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
References
- Wan, E.A.; Van Der Merwe, R. The unscented Kalman filter for nonlinear estimation. In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium (Cat. No.00EX373), Lake Louise, AB, Canada, 4 October 2000; pp. 153–158. [Google Scholar]
- Rose, C.; Britt, J.; Allen, J.; Bevly, D.M. An Integrated Vehicle Navigation System Utilizing Lane-Detection and Lateral Position Estimation Systems in Difficult Environments for GPS. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2615–2629. [Google Scholar] [CrossRef]
- Um, I.; Park, S.; Oh, S.; Kim, H. Analyzing Location Accuracy of Unmanned Vehicle According to RTCM Message Frequency of RTK-GPS. In Proceedings of the 2019 25th Asia-Pacific Conference on Communications (APCC), Ho Chi Minh City, Vietnam, 6–8 November 2019; pp. 326–330. [Google Scholar]
- Kim, J.W.; Lee, D.K.; Bin Cao, S.; Lee, S.S. Availability evaluation and development of network-RTK for vehicle in downtown. In Proceedings of the 2014 International Conference on Information and Communication Technology Convergence (ICTC), Busan, Korea, 22–24 October 2014; pp. 557–558. [Google Scholar]
- Liu, T.; Li, B. Single-frequency BDS/GPS RTK with low-cost U-blox receivers. In Proceedings of the 2017 Forum on Cooperative Positioning and Service (CPGPS), Harbin, China, 19–21 May 2017; pp. 232–238. [Google Scholar]
- Ng, K.M.; Johari, J.; Abdullah, S.A.C.; Ahmad, A.; Laja, B.N. Performance Evaluation of the RTK-GNSS Navigating under Different Landscape. In Proceedings of the 2018 18th International Conference on Control, Automation and Systems (ICCAS), PyeongChang, Korea, 17–20 October 2018; pp. 1424–1428. [Google Scholar]
- Um, I.; Park, S.; Kim, H.T.; Kim, H. Configuring RTK-GPS Architecture for System Redundancy in Multi-Drone Operations. IEEE Access 2020, 8, 76228–76242. [Google Scholar] [CrossRef]
- Maier, D.; Kleiner, A. Improved GPS sensor model for mobile robots in urban terrain. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 4385–4390. [Google Scholar]
- Yi, S.; Worrall, S.; Nebot, E. Geographical Map Registration and Fusion of Lidar-Aerial Orthoimagery in GIS. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 128–134. [Google Scholar]
- Wei, L.; Cappelle, C.; Ruichek, Y.; Zann, F. Intelligent Vehicle Localization in Urban Environments Using EKF-based Visual Odometry and GPS Fusion. IFAC Proc. Vol. 2011, 44, 13776–13781. [Google Scholar] [CrossRef] [Green Version]
- Aftatah, M.; Lahrech, A.; Abounada, A. Fusion of GPS/INS/Odometer measurements for land vehicle navigation with GPS outage. In Proceedings of the 2016 2nd International Conference on Cloud Computing Technologies and Applications (CloudTech), Marrakech, Morocco, 24–26 May 2016; pp. 48–55. [Google Scholar] [CrossRef]
- Henkel, P.; Sperl, A.; Mittmann, U.; Bensch, R.; Farber, P. Precise Positioning of Robots with Fusion of GNSS, INS, Odometry, LPS and Vision. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; pp. 1–6. [Google Scholar]
- Mohamed, S.A.S.; Haghbayan, M.-H.; Westerlund, T.; Heikkonen, J.; Tenhunen, H.; Plosila, J. A Survey on Odometry for Autonomous Navigation Systems. IEEE Access 2019, 7, 97466–97486. [Google Scholar] [CrossRef]
- Mikov, A.; Panyov, A.; Kosyanchuk, V.; Prikhodko, I. Sensor Fusion for Land Vehicle Localization Using Inertial MEMS and Odometry. In Proceedings of the 2019 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Naples, FL, USA, 1–5 April 2019; pp. 1–2. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, Y.; Farrell, J.A. High-Precision Vehicle Navigation in Urban Environments Using an MEM’s IMU and Single-Frequency GPS Receiver. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2854–2867. [Google Scholar] [CrossRef]
- Chen, M.; Ren, Y. MPC based path tracking control for autonomous vehicle with multi-constraints. In Proceedings of the 2017 International Conference on Advanced Mechatronic Systems (ICAMechS), Xiamen, China, 6–9 December 2017; pp. 477–482. [Google Scholar]
- Paden, B.; Cap, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A Survey of Motion Planning and Control Techniques for Self-Driving Urban Vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef] [Green Version]
- Jhang, J.-H.; Lian, F.-L. An Autonomous Parking System of Optimally Integrating Bidirectional Rapidly-Exploring Random Trees* and Parking-Oriented Model Predictive Control. IEEE Access 2020, 8, 163502–163523. [Google Scholar] [CrossRef]
- Shen, C.; Guo, H.; Liu, F.; Chen, H. MPC-based path tracking controller design for autonomous ground vehicles. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 9584–9589. [Google Scholar]
- Tang, W.; Yang, M.; Wang, C.; Wang, B.; Zhang, L.; Le, F. MPC-Based Path Planning for Lane Changing in Highway Environment. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 1003–1008. [Google Scholar]
- Chen, Y.; Wang, J. Trajectory Tracking Control for Autonomous Vehicles in Different Cut-in Scenarios. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 4878–4883. [Google Scholar]
- Dixit, S.; Montanaro, U.; Dianati, M.; Oxtoby, D.; Mizutani, T.; Mouzakitis, A.; Fallah, S. Trajectory Planning for Autonomous High-Speed Overtaking in Structured Environments Using Robust MPC. IEEE Trans. Intell. Transp. Syst. 2020, 21, 2310–2323. [Google Scholar] [CrossRef]
- Liniger, A.; Domahidi, A.; Morari, M. Optimization-based autonomous racing of 1:43 scale RC cars. Optim. Control Appl. Methods 2015, 36, 628–647. [Google Scholar] [CrossRef] [Green Version]
- Rosolia, U.; Carvalho, A.; Borrelli, F. Autonomous racing using learning Model Predictive Control. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 5115–5120. [Google Scholar]
- Lin, F.; Chen, Y.; Zhao, Y.; Wang, S. Path tracking of autonomous vehicle based on adaptive model predictive control. Int. J. Adv. Robot. Syst. 2019, 16, 1–12. [Google Scholar] [CrossRef]
- Görges, D. Relations between Model Predictive Control and Reinforcement Learning. IFAC-PapersOnLine 2017, 50, 4920–4928. [Google Scholar] [CrossRef]
- Xie, H.; Xu, X.; Li, Y.; Hong, W.; Shi, J. Model Predictive Control Guided Reinforcement Learning Control Scheme. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Guan, Y.; Ren, Y.; Li, S.E.; Sun, Q.; Luo, L.; Li, K. Centralized Cooperation for Connected and Automated Vehicles at Intersections by Proximal Policy Optimization. IEEE Trans. Veh. Technol. 2020, 69, 12597–12608. [Google Scholar] [CrossRef]
- Tange, Y.; Kiryu, S.; Matsui, T. Model Predictive Control Based on Deep Reinforcement Learning Method with Discrete-Valued Input. In Proceedings of the 2019 IEEE Conference on Control Technology and Applications (CCTA), Hong Kong, China, 19–21 August 2019. [Google Scholar]
- Modalavalasa, H.K.; Makkena, M.L. Intelligent Parameter Tuning Using Segmented Adaptive Reinforcement Learning Algorithm. In Proceedings of the 2020 International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 2–4 July 2020; pp. 252–256. [Google Scholar]
- Zanon, M.; Gros, S. Safe Reinforcement Learning Using Robust MPC. IEEE Trans. Autom. Control 2021, 66, 3638–3652. [Google Scholar] [CrossRef]


| α-Parameter | ε-Parameter | γ-Parameter | Training Episodes |
|---|---|---|---|
| 0.5 | 0.2 | 0.95 | 2000 |
| Methods | Ground Truth (m) | Estimated Distance (m) | Error (%) | Mean Error (m) | Standard Deviation (m) |
|---|---|---|---|---|---|
| Odometry | 199.27 | 192.882 | 3.205 | 6.387 | 4.856 |
| RTKGPS | 199.27 | 197.462 | 1.684 | 3.356 | 2.243 |
| UKF | 199.27 | 198.201 | 0.826 | 1.646 | 1.198 |
| Proposed Method | Wei [10] | Mikov [14] | |
|---|---|---|---|
| Ground Truth (m) | 199.27 | 674.5 | 10,352 ± 3749 |
| Estimated Distance (m) | 198.201 | 683.18 | 10,404 ± 3777 |
| Error (%) | 0.826 | 1.29 | 0.502 ± 0.746 |
| Mean Error (m) | 1.646 | 1.23 | - |
| Standard Deviation (m) | 1.198 | 1.05 | 28 |
| Method | Maximum Error (m) | Average Error (m) | Standard Deviation (m) | RMSE (m) |
|---|---|---|---|---|
| MPC | 0.671 | 0.291 | 0.138 | 0.257 |
| RLMPC | 0.615 | 0.196 | 0.112 | 0.227 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.-A.; Kuo, C.-H. Integrating Vehicle Positioning and Path Tracking Practices for an Autonomous Vehicle Prototype in Campus Environment. Electronics 2021, 10, 2703. https://doi.org/10.3390/electronics10212703
Yang J-A, Kuo C-H. Integrating Vehicle Positioning and Path Tracking Practices for an Autonomous Vehicle Prototype in Campus Environment. Electronics. 2021; 10(21):2703. https://doi.org/10.3390/electronics10212703
Chicago/Turabian StyleYang, Jui-An, and Chung-Hsien Kuo. 2021. "Integrating Vehicle Positioning and Path Tracking Practices for an Autonomous Vehicle Prototype in Campus Environment" Electronics 10, no. 21: 2703. https://doi.org/10.3390/electronics10212703
APA StyleYang, J.-A., & Kuo, C.-H. (2021). Integrating Vehicle Positioning and Path Tracking Practices for an Autonomous Vehicle Prototype in Campus Environment. Electronics, 10(21), 2703. https://doi.org/10.3390/electronics10212703






