Interleaved High Step-Up Current Sharing Converter with Coupled Inductors
Abstract
:1. Introduction
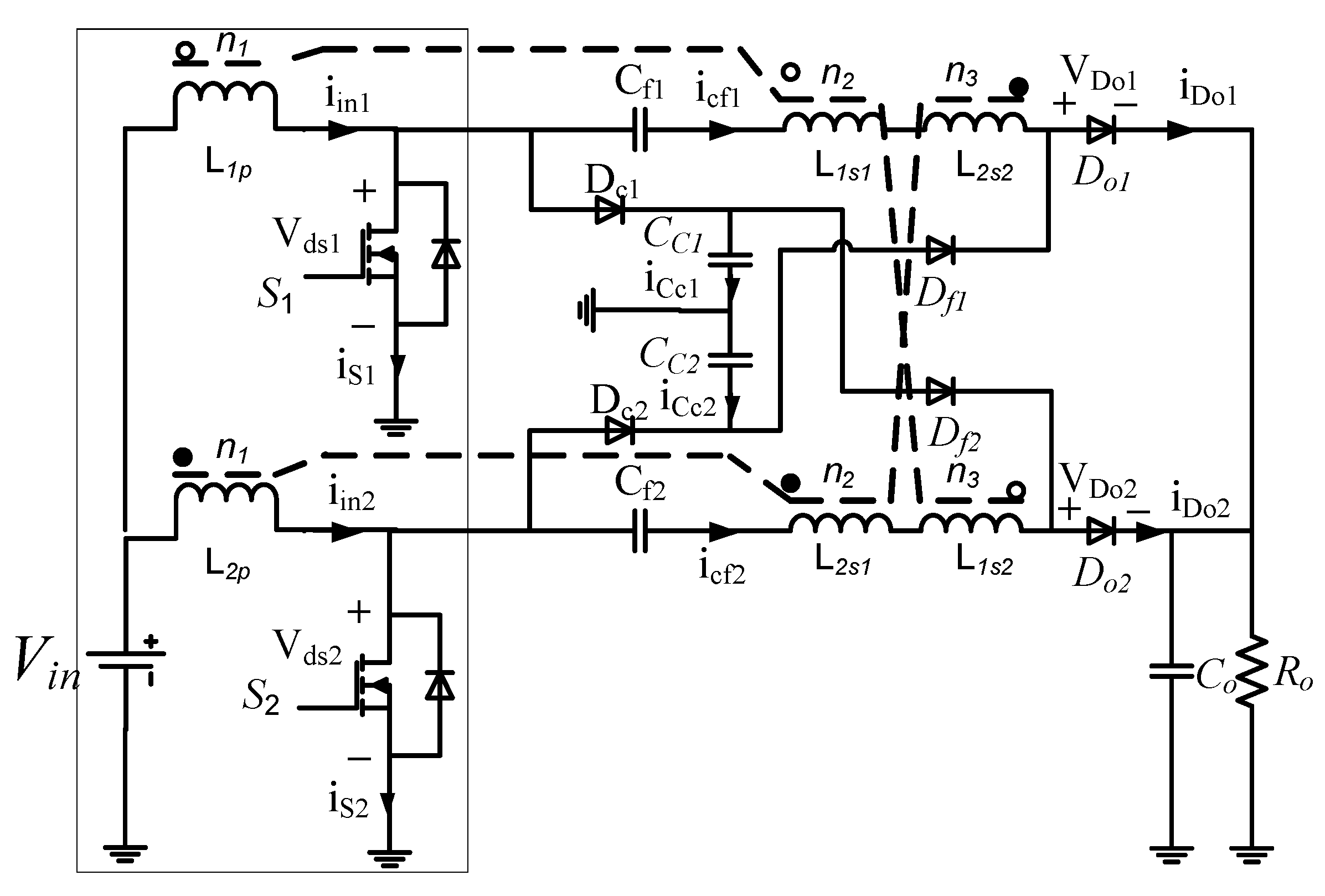
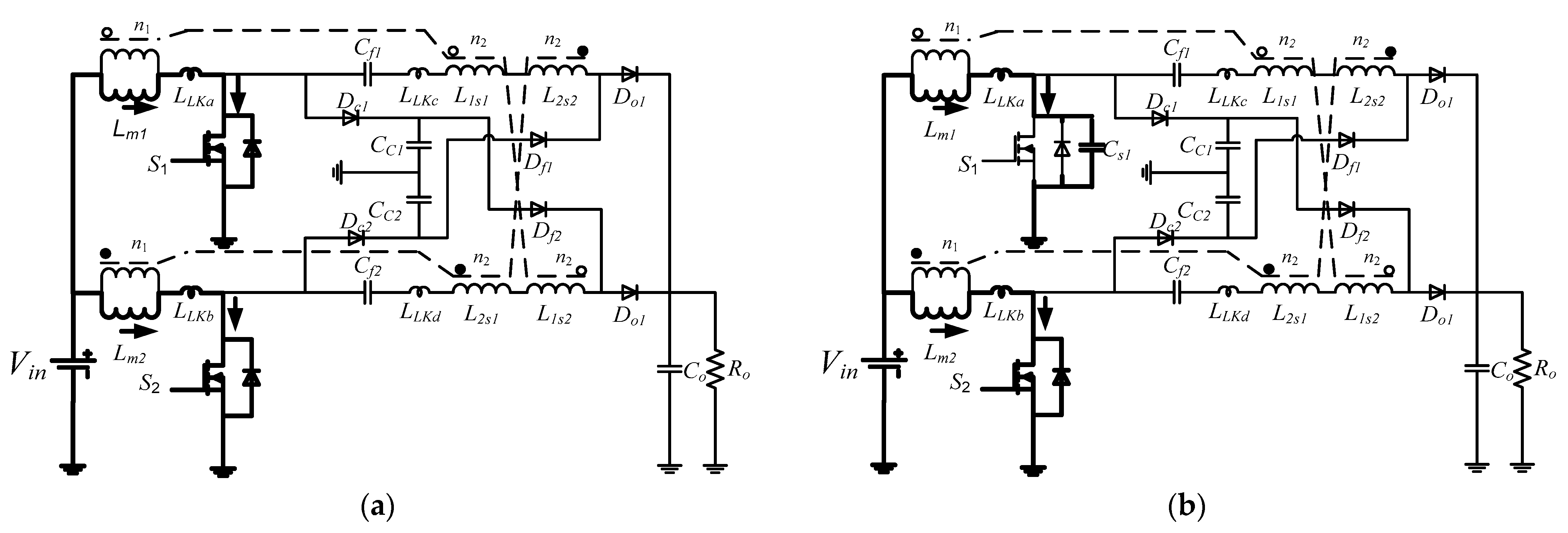
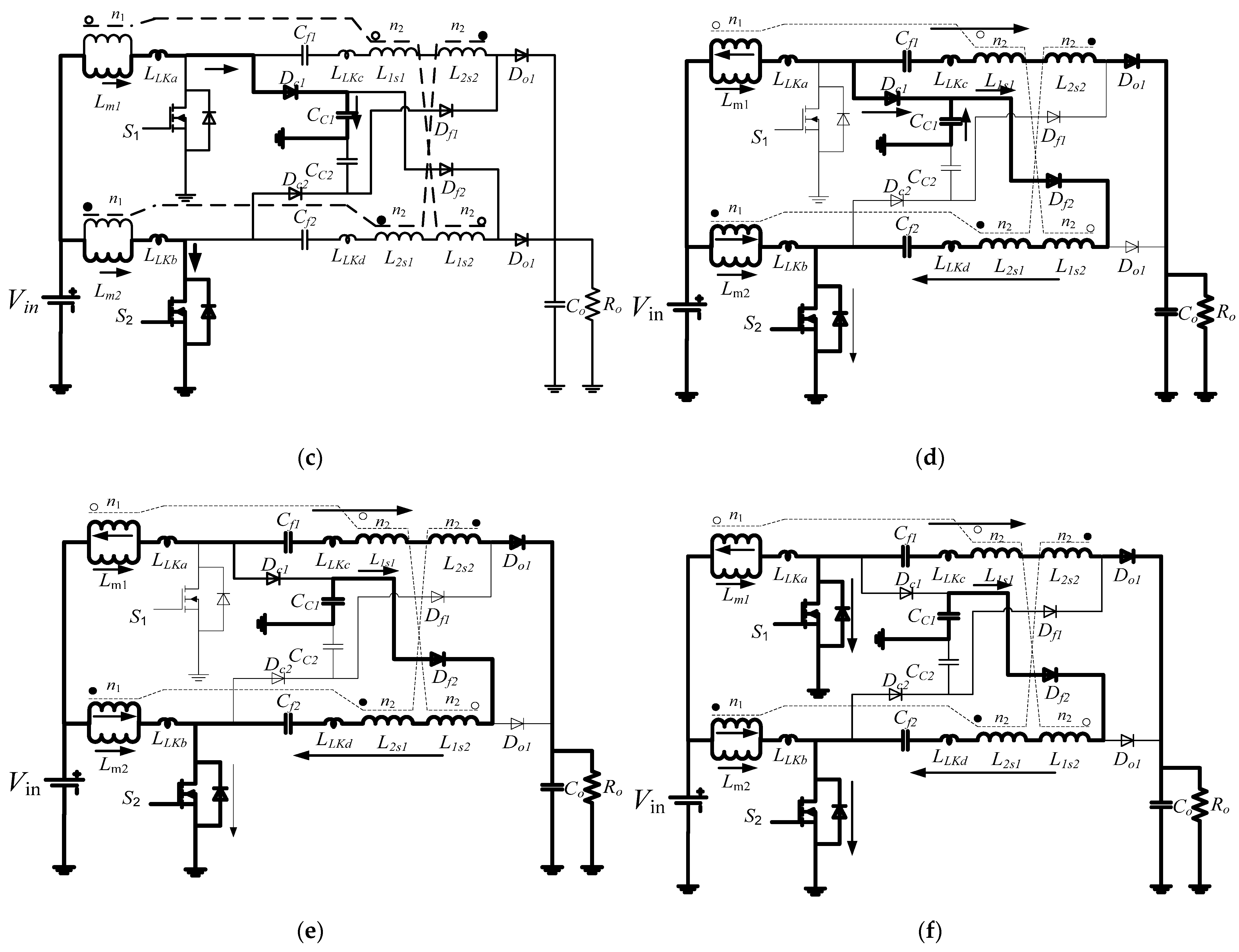
2. Working Principle
3. Steady-State Working Performance Analysis
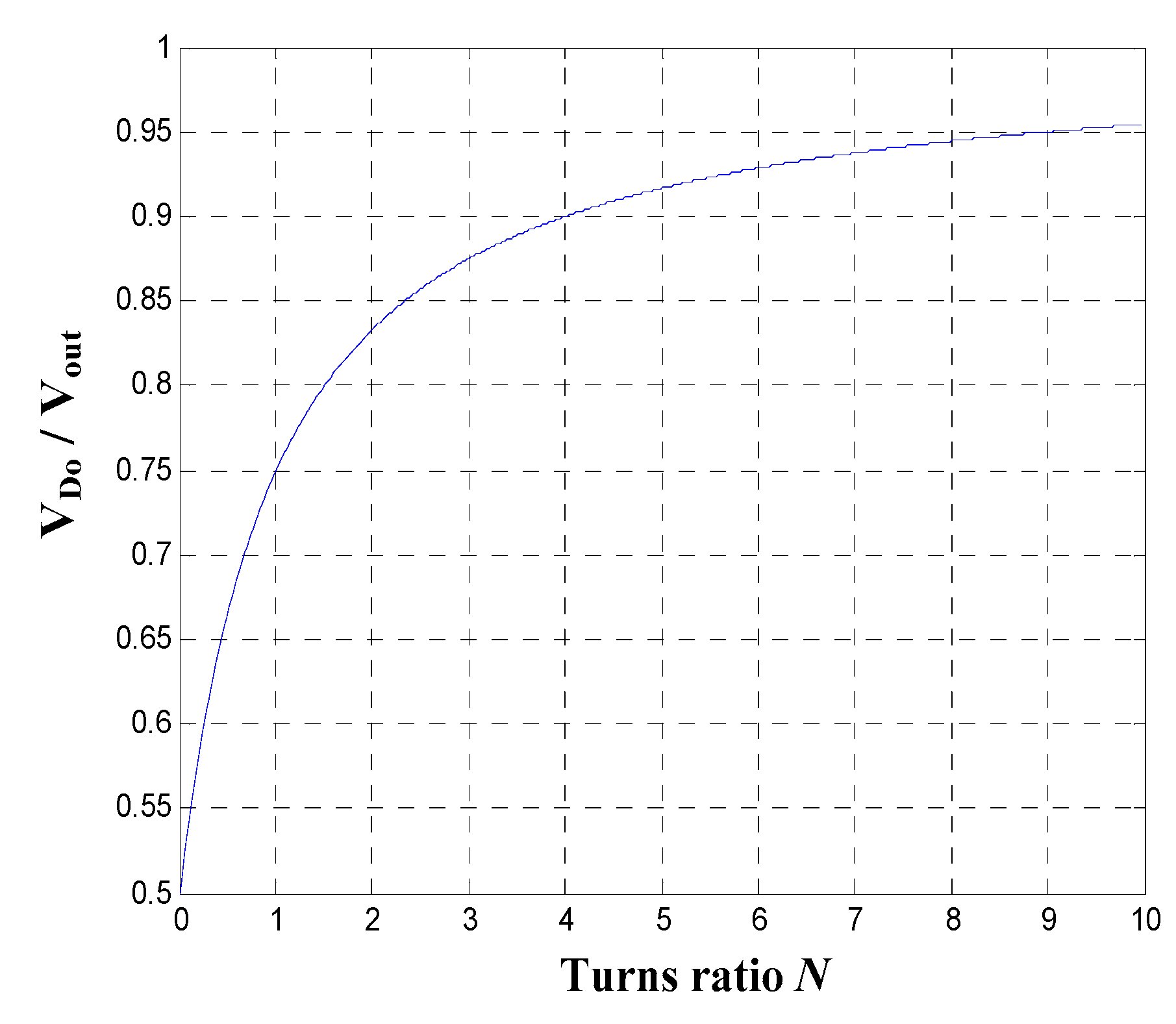
3.1. Voltage Gains
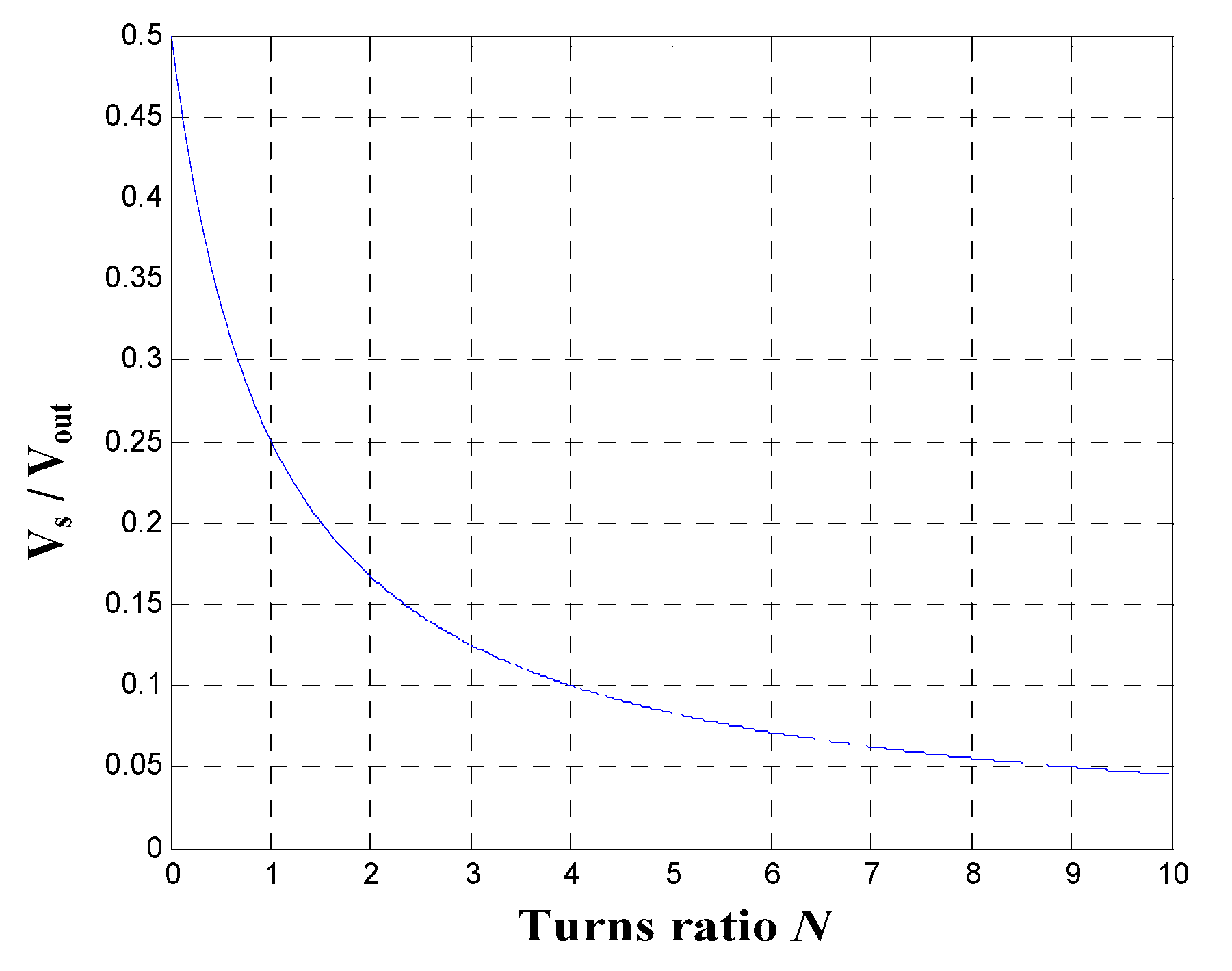
3.2. Switch Voltage Stress
3.3. Realization of Soft Switching
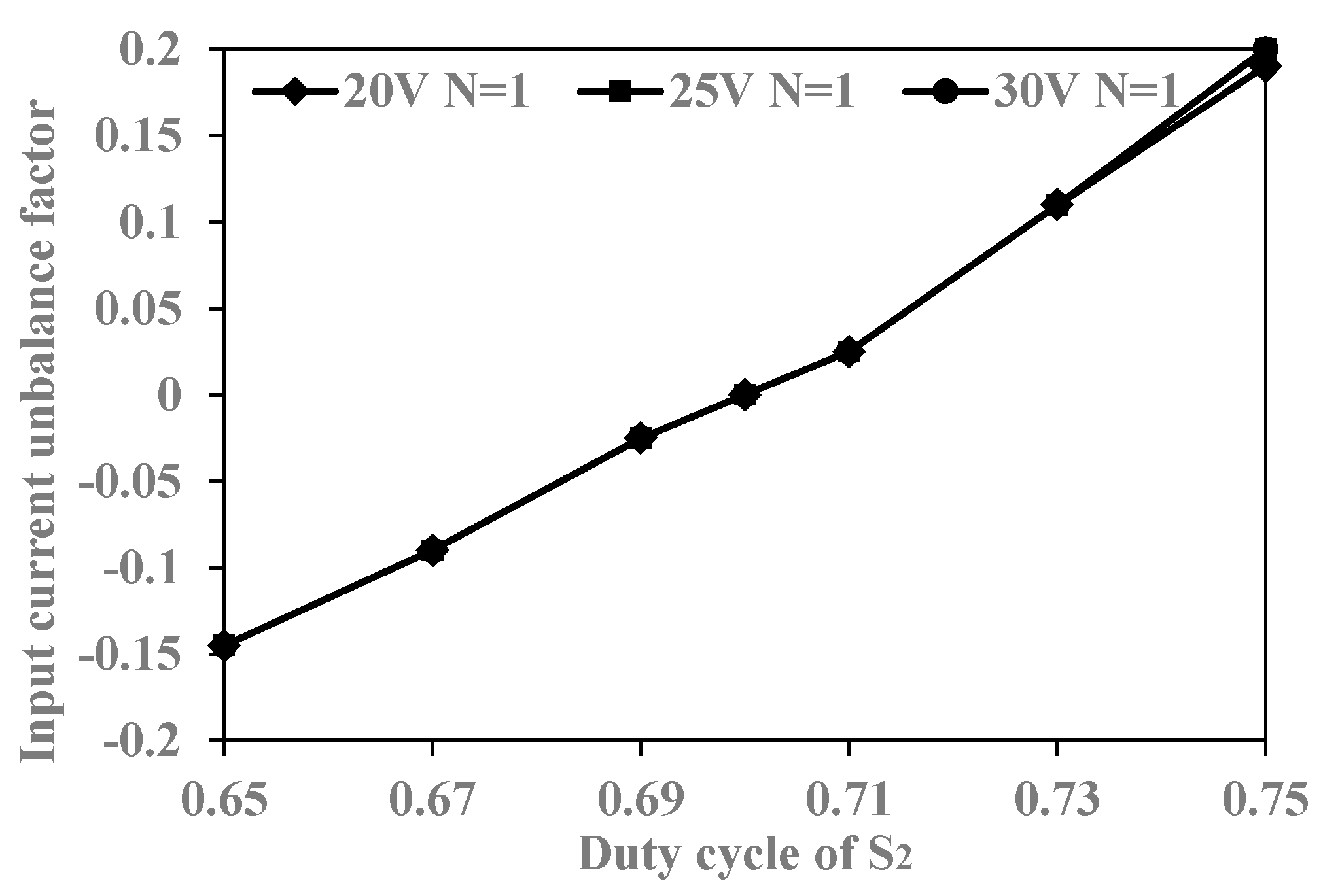
3.4. Current Sharing
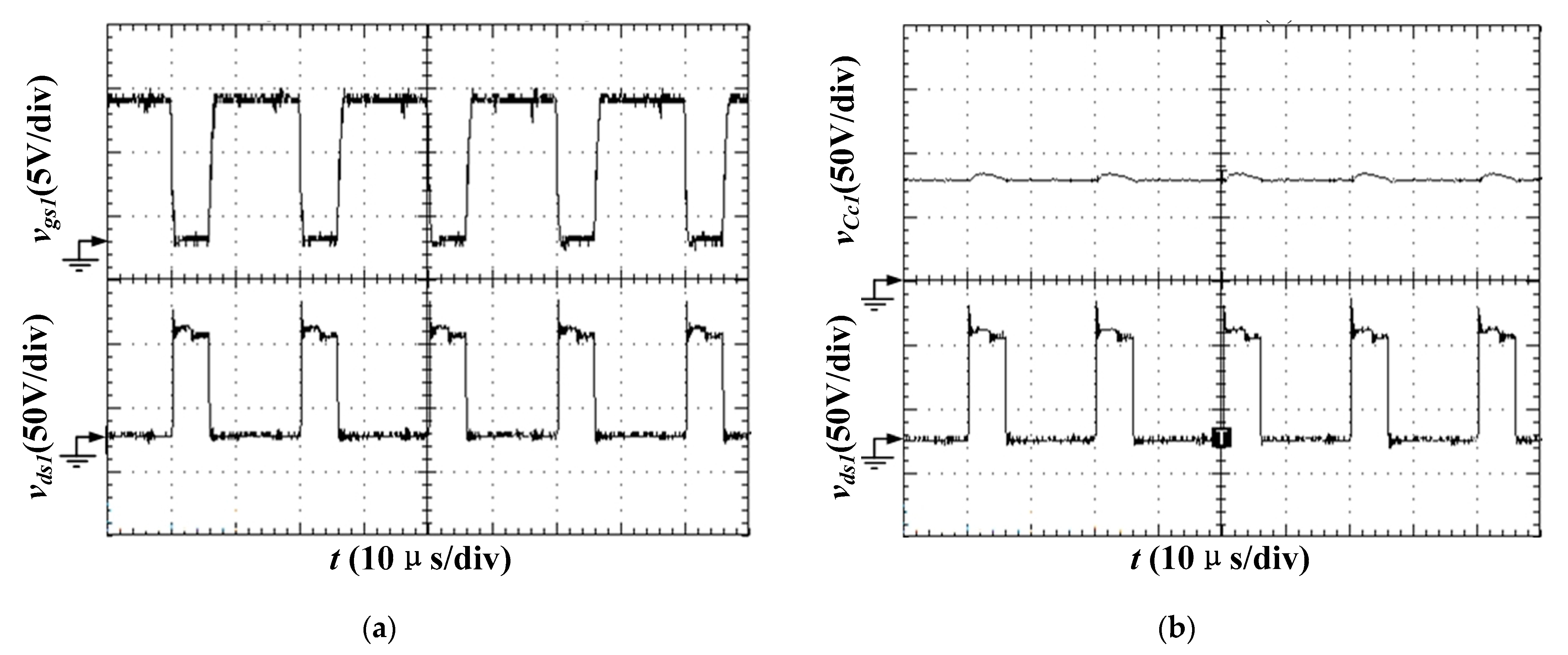
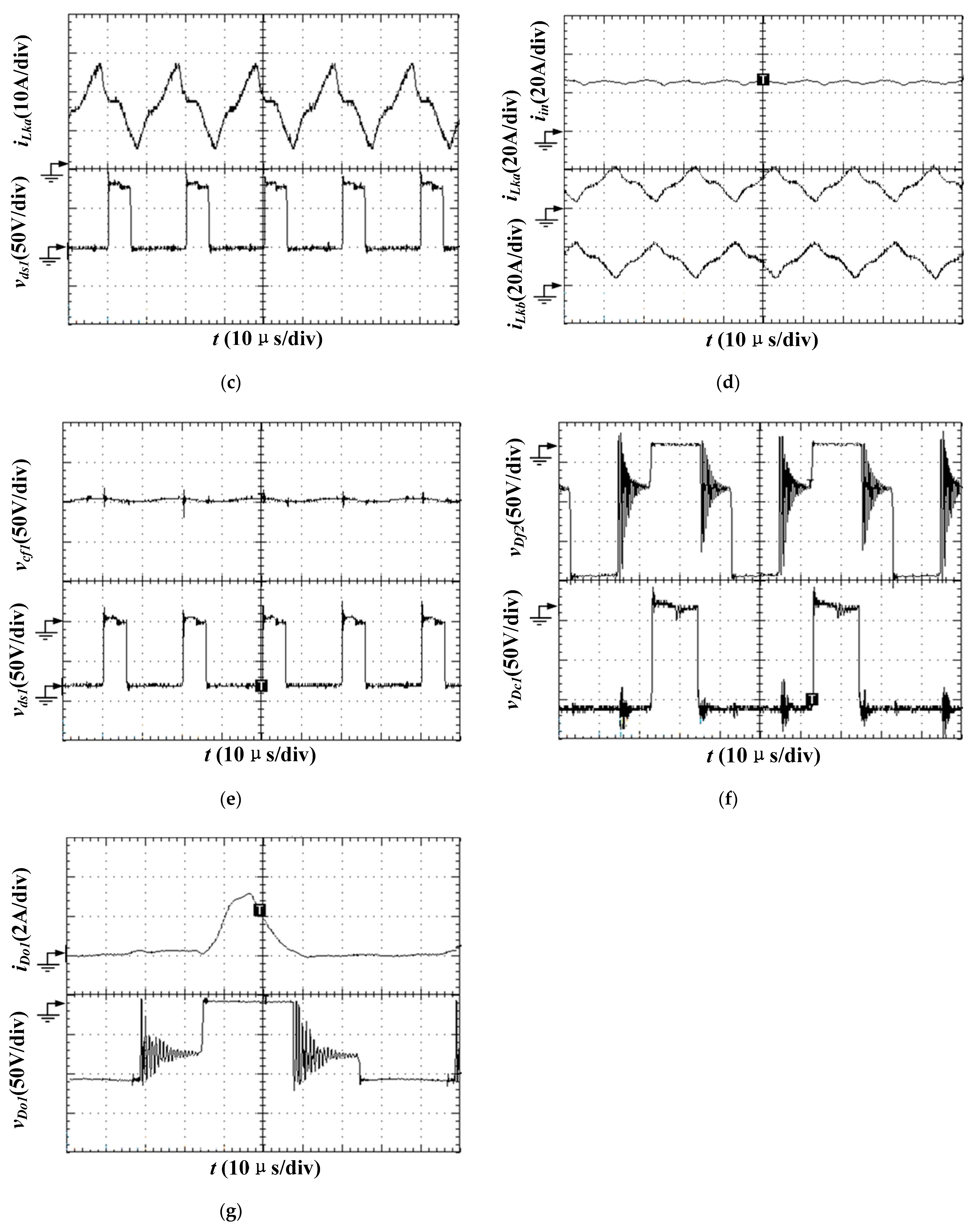
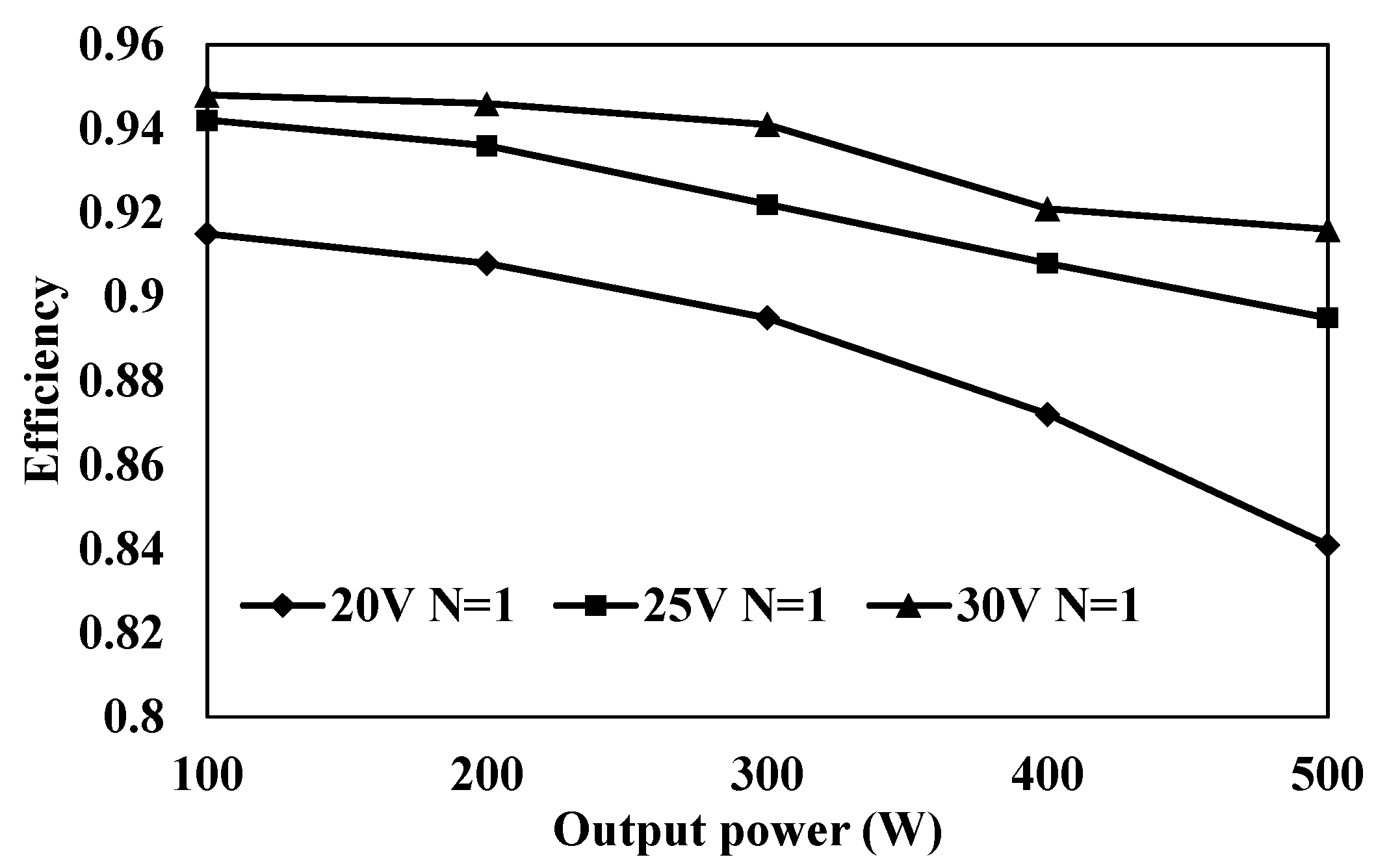
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- D’Ovidio, G.; Masciovecchio, C.; Rotondale, A. Hydrogen fuel cell and kinetic energy recover systems technologies for powering urban bus with zero emission energy cycle. IET Intell. Transp. Syst. 2016, 10, 573–578. [Google Scholar] [CrossRef]
- Nemeș, R.; Ciornei, S.; Ruba, M.; Marțis, C. Real-time simulation of scaled propulsion unit for light electric vehicles. Electr. Eng. 2020, 102, 43–52. [Google Scholar] [CrossRef]
- Ta, L.D.; Dao, N.D.; Lee, D.C. High-efficiency hybrid LLC resonant converter for on-board chargers of plug-in electric vehicles. IEEE Trans. Power Electron. 2020, 35, 8324–8334. [Google Scholar] [CrossRef]
- Snoussi, J.; Elghali, S.B.; Benbouzid, M.; Mimouni, M.F. Optimal sizing of energy storage systems using frequency-separation-based energy management for fuel cell hybrid electric vehicles. IEEE Trans. Veh. Technol. 2018, 67, 9337–9346. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, G. A predictive energy management system for hybrid energy storage systems in electric vehicles. Electr. Eng. 2019, 101, 759–770. [Google Scholar] [CrossRef]
- Lin, C.C.; Yang, L.S.; Wu, G. Study of a non- isolated bidirectional DC-DC converter. IET Power Electron. 2013, 6, 30–37. [Google Scholar] [CrossRef]
- Salvador, M.A.; Lazzarin, T.B.; Coelho, R.F. High step-up DC–DC converter with active switched- inductor and passive switched-capacitor networks. IEEE Trans. Ind. Electron. 2018, 65, 5644–5654. [Google Scholar] [CrossRef]
- Tseng, K.C.; Liang, T.J. Novel high-efficiency step- up converter. IEE Proc. Power Appl. 2004, 151, 182–190. [Google Scholar] [CrossRef]
- Narasimharaju, B.L.; Dubey, S.P.; Singh, S.P. Design and analysis of coupled inductor bidirectional DC–DC convertor for high-voltage diversity applications. IET Power Electron. 2012, 5, 998–1007. [Google Scholar] [CrossRef]
- Liu, H.; Wang, L.; Ji, Y.; Li, F. A novel reversal coupled inductor high-conversion-ratio bidirectional DC–DC converter. IEEE Trans. Power Electron. 2018, 33, 4968–4979. [Google Scholar] [CrossRef]
- Wai, R.J.; Duan, R.Y. High-efficiency power conversion for low-power fuel cell generation system. IEEE Trans. Power Electron. 2005, 20, 847–856. [Google Scholar] [CrossRef]
- Wai, R.J.; Duan, R.Y. High-efficiency DC/DC converter with high voltage gain. IEE Proc. Electric Power Appl. 2005, 152, 793–802. [Google Scholar] [CrossRef]
- Matsuda, A.; Koizumi, H.; Sato, T. Two-stage interleaved DC-DC converter with input-parallel output-series connection. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar]
- Hsieh, Y.C.; Hsueh, T.C.; Yen, H.C. An interleaved Boost converter with zero-voltage transition. IEEE Trans. Power Electron. 2009, 24, 973–978. [Google Scholar] [CrossRef]
- Lee, J.Y.; Kim, G.S.; Oh, K.; Baek, D. Fully integrated low-ripple switched-capacitor DC–DC converter with parallel low-dropout regulator. Electronics 2019, 8, 98. [Google Scholar] [CrossRef] [Green Version]
- Prabhala, V.A.K.; Fajri, P.; Gouribhatla, V.S.P.; Baddipadiga, B.P.; Ferdowsi, M. A DC–DC converter with high voltage gain and two input boost stages. IEEE Trans. Power Electron. 2016, 31, 4206–4215. [Google Scholar] [CrossRef]
- Frivaldsky, M.; Morgos, J.; Hanko, B.; Prazenica, M. The study of the operational characteristic of interleaved boost converter with modified coupled inductor. Electronics 2019, 8, 1049. [Google Scholar] [CrossRef] [Green Version]
- Alzahrani, A.; Ferdowsi, M.; Shamsi, P. A family of scalable non-isolated interleaved DC–DC boost converters with voltage multiplier cells. IEEE Access 2019, 7, 11707–11721. [Google Scholar] [CrossRef]
- Alzahrani, A. A hybrid DC–DC quadrupler boost converter for photovoltaic panels integration into a DC distribution system. Electronics 2020, 9, 1965. [Google Scholar] [CrossRef]
- Hwu, K.I.; Yau, Y.T. High step-up converter based on coupling inductor and bootstrap capacitors with active clamping. IEEE Trans. Power Electron. 2014, 29, 2655–2660. [Google Scholar] [CrossRef]
- Tseng, K.; Lin, J.; Huang, C. High step-up converter with three-winding coupled inductor for fuel cell energy source applications. IEEE Trans. Power Electron. 2015, 30, 574–581. [Google Scholar] [CrossRef]
- Li, W.; Xiang, X.; Li, C.; Li, W.; He, X. Interleaved high step-Up ZVT converter with built-in transformer voltage doubler cell for distributed PV generation system. IEEE Trans. Power Electron. 2013, 28, 300–313. [Google Scholar] [CrossRef]






| Conventional Transformer Included Boost Converter | Conventional Interleaved Boost Converter | Converter in [22] | Proposed Converter | |
|---|---|---|---|---|
| Voltage gain | ||||
| Main switch voltage stress | Vo | |||
| Output diode voltage stress | Vo | Vo | Vo | Less than 2/3 Vo |
| Input current ripple | Large | Large | Small | small (in total) |
| Soft switching | ZCS or ZVS | Hard switching | ZVS | ZCS |
| Reverse recovery | Large | Large | Small | Small |
| Output voltage ripple | Large | Large | Small | Small |
| Current autobalance | No | No | No | Yes |
| Clamp circuit | Natural voltage clamping | Additional circuit | Two MOSFETS two capacitors | Two diodes Two capacitors |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Lin, Z.; Tan, Q.; Lu, F.; Zeng, T. Interleaved High Step-Up Current Sharing Converter with Coupled Inductors. Electronics 2021, 10, 436. https://doi.org/10.3390/electronics10040436
He L, Lin Z, Tan Q, Lu F, Zeng T. Interleaved High Step-Up Current Sharing Converter with Coupled Inductors. Electronics. 2021; 10(4):436. https://doi.org/10.3390/electronics10040436
Chicago/Turabian StyleHe, Liangzong, Zhile Lin, Qingyang Tan, Fengwang Lu, and Tao Zeng. 2021. "Interleaved High Step-Up Current Sharing Converter with Coupled Inductors" Electronics 10, no. 4: 436. https://doi.org/10.3390/electronics10040436
APA StyleHe, L., Lin, Z., Tan, Q., Lu, F., & Zeng, T. (2021). Interleaved High Step-Up Current Sharing Converter with Coupled Inductors. Electronics, 10(4), 436. https://doi.org/10.3390/electronics10040436






