Toward Reliable Compact Modeling of Multilevel 1T-1R RRAM Devices for Neuromorphic Systems
Abstract
:1. Introduction
2. Compact Models Description
2.1. Stanford-PKU Model Extended with Multilevel Capability
2.2. Valence Change Memory Model with Cylindrical Shaped Filament (UGR-VCMCF)
2.3. Valence Change Memory Model with Truncated-Cone Shaped Filament (UGR-VCMTCF)
3. Experimental Samples Characteristics
4. Modeling Results and Discussion
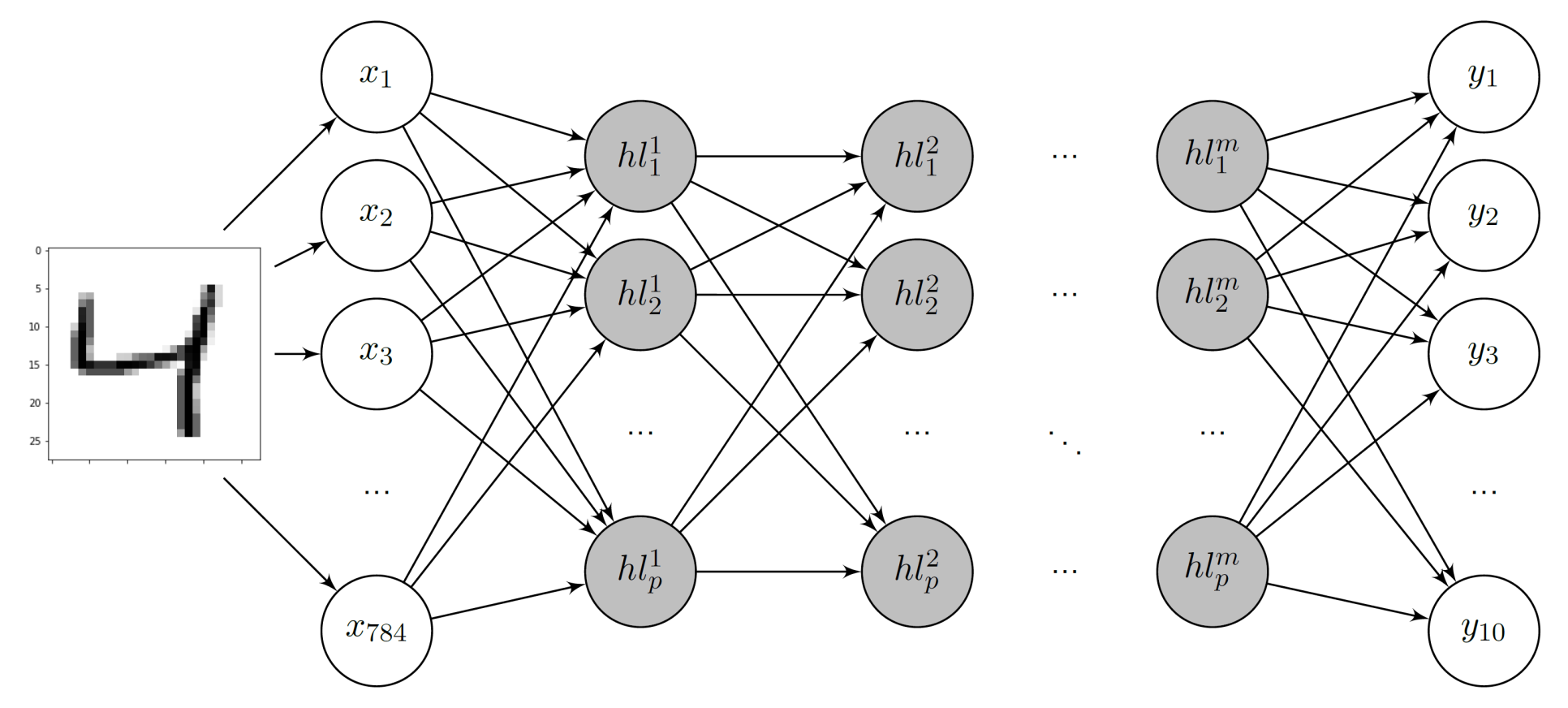
5. A Neural Network Study to Assess the Multilevel Approach
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Valentian, A.; Rummens, F.; Vianello, E.; Mesquida, T.; de Boissac, C.L.; Bichler, O.; Reita, C. Fully Integrated Spiking Neural Network with Analog Neurons and RRAM Synapses. In Proceedings of the IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; pp. 14.3.1–14.3.4. [Google Scholar]
- Yao, P.; Wu, H.; Gao, B.; Tang, J.; Zhang, Q.; Zhang, W.; Yang, J.J.; Qian, H. Fully hardware-implemented memristor convolutional neural network. Nature 2020, 577, 641–646. [Google Scholar] [CrossRef]
- Prezioso, M.; Merrikh-Bayat, F.; Hoskins, B.; Adam, G.; Likharev, K.; Strukov, D. Training and Operation of an Integrated Neuromorphic Network Based on Metal-Oxide Memristors. Nature 2014, 521. [Google Scholar] [CrossRef] [Green Version]
- Kang, J.F.; Gao, B.; Huang, P.; Liu, L.F.; Liu, X.Y.; Yu, H.Y.; Yu, S.; Wong, H.P. RRAM based synaptic devices for neuromorphic visual systems. In Proceedings of the IEEE International Conference on Digital Signal Processing (DSP), Singapore, 21–24 July 2015; pp. 1219–1222. [Google Scholar]
- Zahari, F.; Hansen, M.; Mussenbrock, T.; Ziegler, M.; Kohlstedt, H. Pattern recognition with TiOx-based memristive devices. AIMS Mater. Sci. 2015, 2, 203–216. [Google Scholar] [CrossRef]
- Ginnaram, S.; Qiu, J.T.; Maikap, S. Controlling Cu Migration on Resistive Switching, Artificial Synapse, and Glucose/Saliva Detection by Using an Optimized AlOx Interfacial Layer in a-COx-Based Conductive Bridge Random Access Memory. ACS Omega 2020, 5, 7032–7043. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ziegler, M.; Wenger, C.; Chicca, E.; Kohlstedt, H. Tutorial: Concepts for closely mimicking biological learning with memristive devices: Principles to emulate cellular forms of learning. J. Appl. Phys. 2018, 124, 152003. [Google Scholar] [CrossRef]
- Huang, P.; Zhu, D.; Chen, S.; Zhou, Z.; Chen, Z.; Gao, B.; Liu, L.; Liu, X.; Kang, J. Compact Model of HfOx-Based Electronic Synaptic Devices for Neuromorphic Computing. IEEE Trans. Electron Devices 2017, 64, 614–621. [Google Scholar] [CrossRef]
- Maestro-Izquierdo, M.; Gonzalez, M.; Campabadal, F. Mimicking the spike-timing dependent plasticity in HfO2-based memristors at multiple time scales. Microelectron. Eng. 2019, 215, 111014. [Google Scholar] [CrossRef]
- Kim, W.; Menzel, S.; Wouters, D.J.; Waser, R.; Rana, V. 3-Bit Multilevel Switching by Deep Reset Phenomenon in Pt/W/TaOX/Pt-ReRAM Devices. IEEE Electron Device Lett. 2016, 37, 564–567. [Google Scholar] [CrossRef]
- Larentis, S.; Nardi, F.; Balatti, S.; Gilmer, D.C.; Ielmini, D. Resistive Switching by Voltage-Driven Ion Migration in Bipolar RRAM—Part II: Modeling. IEEE Trans. Electron Devices 2012, 59, 2468–2475. [Google Scholar] [CrossRef]
- Sedghi, N.; Li, H.; Brunell, I.; Dawson, K.; Potter, R.; Guo, Y.; Gibbon, J.; Dhanak, V.; Zhang, W.D.; Zhang, J.; et al. The role of nitrogen doping in ALD Ta2O5 and its influence on multilevel cell switching in RRAM. Appl. Phys. Lett. 2017, 110, 102902. [Google Scholar] [CrossRef] [Green Version]
- Misha, S.H.; Tamanna, N.; Woo, J.; Lee, S.; Song, J.; Park, J.; Lim, S.; Park, J.; Hwang, H. Effect of nitrogen doping on variability of TaOx-RRAM for low-power 3-Bit MLC applications. ECS Solid State Lett. 2015, 4, 25–28. [Google Scholar] [CrossRef] [Green Version]
- Prakash, A.; Deleruyelle, D.; Song, J.; Bocquet, M.; Hwang, H. Resistance controllability and variability improvement in a TaOx-based resistive memory for multilevel storage application. Appl. Phys. Lett. 2015, 106, 233104. [Google Scholar] [CrossRef] [Green Version]
- Pérez, E.; Zambelli, C.; Mahadevaiah, M.K.; Olivo, P.; Wenger, C. Toward Reliable Multi-Level Operation in RRAM Arrays: Improving Post-Algorithm Stability and Assessing Endurance/Data Retention. IEEE J. Electron Devices Soc. 2019, 7, 740–747. [Google Scholar] [CrossRef]
- Milo, V.; Zambelli, C.; Olivo, P.; Pérez, E.; Mahadevaiah, M.K.; Ossorio, O.G.; Wenger, C.; Ielmini, D. Multilevel HfO2-based RRAM devices for low-power neuromorphic networks. APL Mater. 2019, 7, 081120. [Google Scholar] [CrossRef] [Green Version]
- Hajri, B.; Aziza, H.; Mansour, M.M.; Chehab, A. RRAM Device Models: A Comparative Analysis With Experimental Validation. IEEE Access 2019, 7, 168963–168980. [Google Scholar] [CrossRef]
- Kuzum, D.; Yu, S.; Wong, H.P. Synaptic electronics: Materials, devices and applications. Nanotechnology 2013, 24, 382001. [Google Scholar] [CrossRef] [PubMed]
- Lekshmi Jagath, A.; Hock Leong, C.; Kumar, T.N.; Almurib, H.F. Insight into physics-based RRAM models—Review. J. Eng. 2019, 2019, 4644–4652. [Google Scholar] [CrossRef]
- Ielmini, D.; Milo, V. Physics-based modeling approaches of resistive switching devices for memory and in-memory computing applications. J. Comput. Electron. 2017, 16, 1121–1143. [Google Scholar] [CrossRef] [Green Version]
- Linn, E.; Siemon, A.; Waser, R.; Menzel, S. Applicability of Well-Established Memristive Models for Simulations of Resistive Switching Devices. IEEE Trans. Circuits Syst. Regul. Pap. 2014, 61, 2402–2410. [Google Scholar] [CrossRef] [Green Version]
- Menzel, S.; Siemon, A.; Ascoli, A.; Tetzlaff, R. Requirements and Challenges for Modelling Redox-based Memristive Devices. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar]
- Li, H.; Jiang, Z.; Huang, P.; Wu, Y.; Chen, H.; Gao, B.; Liu, X.Y.; Kang, J.F.; Wong, H.P. Variation-aware, reliability-emphasized design and optimization of RRAM using SPICE model. In Proceedings of the Design, Automation Test in Europe Conference Exhibition (DATE), Grenoble, France, 9–13 March 2015; pp. 1425–1430. [Google Scholar] [CrossRef]
- Jiang, Z.; Wu, Y.; Yu, S.; Yang, L.; Song, K.; Karim, Z.; Wong, H.P. A Compact Model for Metal–Oxide Resistive Random Access Memory With Experiment Verification. IEEE Trans. Electron Devices 2016, 63, 1884–1892. [Google Scholar] [CrossRef]
- Reuben, J.; Fey, D.; Wenger, C. A Modeling Methodology for Resistive RAM Based on Stanford-PKU Model With Extended Multilevel Capability. IEEE Trans. Nanotechnol. 2019, 18, 647–656. [Google Scholar] [CrossRef] [Green Version]
- González-Cordero, G.; Roldán, J.B.; Jiménez-Molinos, F. Simulation of RRAM memory circuits, a Verilog-A compact modeling approach. In Proceedings of the Conference on Design of Circuits and Integrated Systems (DCIS), Granada, Spain, 23–25 November 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Panda, D.; Sahu, P.P.; Tseng, T.Y. A collective study on modeling and simulation of resistive random access memory. Nanoscale Res. Lett. 2018, 13, 1–48. [Google Scholar] [CrossRef] [PubMed]
- McPherson, J.; Kim, J.; Shanware, A.; Mogul, H. Thermochemical description of dielectric breakdown in high dielectric constant materials. Appl. Phys. Lett. 2003, 82, 2121–2123. [Google Scholar] [CrossRef]
- González-Cordero, G.; González, M.; García, H.; Campabadal, F.; Dueñas, S.; Castán, H.; Jiménez-Molinos, F.; Roldán, J. A physically based model for resistive memories including a detailed temperature and variability description. Microelectron. Eng. 2017, 178, 26–29. [Google Scholar] [CrossRef]
- AdMOS: Advanced Modeling Solutions. Available online: https://admos.de/en/home-en/ (accessed on 21 September 2020).
- Virtuoso Analog Design Environment. Available online: https://www.cadence.com/ko_KR/home.html (accessed on 21 September 2020).
- Roldán, J.B.; Alonso, F.J.; Aguilera, A.M.; Maldonado, D.; Lanza, M. Time series statistical analysis: A powerful tool to evaluate the variability of resistive switching memories. J. Appl. Phys. 2019, 125, 174504. [Google Scholar] [CrossRef]
- Miranda, E.; Mehonic, A.; Ng, W.H.; Kenyon, A.J. Simulation of Cycle-to-Cycle Instabilities in SiO x -Based ReRAM Devices Using a Self-Correlated Process With Long-Term Variation. IEEE Electron Device Lett. 2019, 40, 28–31. [Google Scholar] [CrossRef]
- Pérez, E.; Maldonado, D.; Acal, C.; Ruiz-Castro, J.; Alonso, F.; Aguilera, A.; Jiménez-Molinos, F.; Wenger, C.; Roldán, J. Analysis of the statistics of device-to-device and cycle-to-cycle variability in TiN/Ti/Al:HfO2/TiN RRAMs. Microelectron. Eng. 2019, 214, 104–109. [Google Scholar] [CrossRef]
- Pérez, E.; Kalishettyhalli Mahadevaiah, M.; Zambelli, C.; Olivo, P.; Wenger, C. Data retention investigation in Al:HfO2-based resistive random access memory arrays by using high-Temperature accelerated tests. J. Vac. Sci. Technol. B 2019, 37, 012202. [Google Scholar] [CrossRef]
- Aldana, S.; Pérez, E.; Jiménez-Molinos, F.; Wenger, C.; Roldán, J.B. Kinetic Monte Carlo analysis of data retention in Al:HfO2-based resistive random access memories. Semicond. Sci. Technol. 2020, 35, 115012. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- LeCun, Y.; Cortes, C.; Burges, C. MNIST Handwritten Digit Database. Available online: http://yann.lecun.com/exdb/mnist (accessed on 21 September 2020).
- Popescu, M.C.; Balas, V.E.; Perescu-Popescu, L.; Mastorakis, N. Multilayer Perceptron and Neural Networks. WSEAS Trans. Circ. Syst. 2009, 8, 579–588. [Google Scholar]
- Nayak, P.; Zhang, D.; Chai, S. Bit efficient quantization for deep neural networks. arXiv 2019, arXiv:1910.04877. [Google Scholar]
- Pérez-Ávila, A.J.; González-Cordero, G.; Pérez, E.; Pérez-Bosch, E.; Kalishettyhalli Mahadevaiah, M.; Wenger, C.; Roldán, J.B.; Jiménez-Molinos, F. Behavioral modeling of multilevel HfO2-based memristors for neuromorphic circuit simulation. In Proceedings of the XXXV Conference on Design of Circuits and Integrated Systems (DCIS), Segovia, Spain, 18–20 November 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Bilbao, I.; Bilbao, J. Overfitting problem and the over-training in the era of data: Particularly for Artificial Neural Networks. In Proceedings of the 8th International Conference on Intelligent Computing and Information Systems (ICICIS), Cairo, Egypt, 5–7 December 2017; pp. 173–177. [Google Scholar]
- Covi, E.; Brivio, S.; Serb, A.; Prodromakis, T.; Fanciulli, M.; Spiga, S. Analog Memristive Synapse in Spiking Networks Implementing Unsupervised Learning. Front. Neurosci. 2016, 10, 482. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jeong, H.; Shi, L. Memristor devices for neural networks. J. Phys. D Appl. Phys. 2018, 52, 023003. [Google Scholar] [CrossRef]
- Tang, J.; Yuan, F.; Shen, X.; Wang, Z.; Rao, M.; He, Y.; Sun, Y.; Li, X.; Zhang, W.; Li, Y.; et al. Bridging Biological and Artificial Neural Networks with Emerging Neuromorphic Devices: Fundamentals, Progress, and Challenges. Adv. Mater. 2019, 31, 1902761. [Google Scholar] [CrossRef] [PubMed]



| (V) | (V) | (V) | Resistance (kΩ) a | |
|---|---|---|---|---|
| LRS1 | 1 | 0.65 | 0.6 | 16 |
| LRS2 | 1.2 | 0.65 | 0.7 | 11 |
| LRS3 | 1.6 | 0.75 | 0.9 | 8 |
| HRS | 2.7 | - | - | 170 |
| Gap Distance (nm) | |||
|---|---|---|---|
| S-PKU | UGR-VCMCF | UGR-VCMTCF | |
| LRS1 | 0.95 | 1 | 0.86 |
| LRS2 | 0.85 | 0.86 | 0.65 |
| LRS3 | 0.73 | 0.75 | 0.25 |
| HRS | 1.88 | 1.88 | 1.88 |
| = 0.28 nm | = 0.35 V | = 854 A |
| = 0.4 m/s | = 0.4 | = 3 |
| = 1.8 nm | = 300 K | = 20 |
| = 1.8 nm | = 6 nm | = 0.52 nm·V |
| = 0.6 eV | = 1500 K/W | C = 0.35 nm |
| = 0.275 nm | = 0.4 V | = 1.7 mA |
| = 0.8 m/s | = 1 | = 3 |
| = 18 | = 1.8 nm | = 0.25 nm |
| = 1.8 nm | = 6 nm | = 300 K |
| = 0.65 eV | = 0.65 eV | = 5 nm |
| h = 0.01 | = 10 | = 500 kS/m |
| = 0.25 nm | = 0.28 nm | = 0.26 V |
| = 0.4 V | = 1.7 mA | = 1.7 mA |
| = 0.8 m/s | = 1 | = 3 |
| = 18 | = 1.8 nm | = 0.25 nm |
| = 1.8 nm | = 6 nm | = 300 K |
| = 0.65 eV | = 0.65 eV | = 5 nm |
| = 1 nm | = 500 kS/m | = 1.65 S/m |
| Hidden Layers a | Levels | No Quantization | U-SYMM | U-ASYMM |
|---|---|---|---|---|
| 1 (32) | 2 | 0.86 | 0.13 | 0.21 |
| 4 | 0.71 | 0.33 | ||
| 8 | 0.88 | 0.88 | ||
| 2 (32) | 2 | 0.80 | 0.09 | 0.33 |
| 4 | 0.79 | 0.49 | ||
| 8 | 0.91 | 0.87 | ||
| 3 (32) | 2 | 0.94 | 0.15 | 0.21 |
| 4 | 0.65 | 0.50 | ||
| 8 | 0.84 | 0.69 | ||
| 1 (64) | 2 | 0.93 | 0.17 | 0.45 |
| 4 | 0.82 | 0.56 | ||
| 8 | 0.93 | 0.93 | ||
| 2 (64) | 2 | 0.92 | 0.15 | 0.48 |
| 4 | 0.79 | 0.39 | ||
| 8 | 0.95 | 0.89 | ||
| 3 (64) | 2 | 0.94 | 0.23 | 0.38 |
| 4 | 0.74 | 0.51 | ||
| 8 | 0.92 | 0.87 | ||
| 1 (128) | 2 | 0.94 | 0.08 | 0.25 |
| 4 | 0.93 | 0.85 | ||
| 8 | 0.97 | 0.96 | ||
| 2 (128) | 2 | 0.94 | 0.18 | 0.26 |
| 4 | 0.92 | 0.45 | ||
| 8 | 0.96 | 0.95 | ||
| 3 (128) | 2 | 0.95 | 0.11 | 0.51 |
| 4 | 0.83 | 0.53 | ||
| 8 | 0.97 | 0.86 | ||
| 1 (256) | 2 | 0.95 | 0.08 | 0.19 |
| 4 | 0.91 | 0.81 | ||
| 8 | 0.97 | 0.96 | ||
| 2 (256) | 2 | 0.95 | 0.11 | 0.84 |
| 4 | 0.90 | 0.74 | ||
| 8 | 0.98 | 0.96 | ||
| 3 (256) | 2 | 0.96 | 0.17 | 0.75 |
| 4 | 0.91 | 0.77 | ||
| 8 | 0.97 | 0.95 | ||
| 1 (512) | 2 | 0.96 | 0.11 | 0.41 |
| 4 | 0.93 | 0.89 | ||
| 8 | 0.97 | 0.97 | ||
| 2 (512) | 2 | 0.97 | 0.10 | 0.77 |
| 4 | 0.95 | 0.70 | ||
| 8 | 0.98 | 0.97 | ||
| 3 (512) | 2 | 0.97 | 0.23 | 0.66 |
| 4 | 0.96 | 0.77 | ||
| 8 | 0.98 | 0.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Bosch Quesada, E.; Romero-Zaliz, R.; Pérez, E.; Kalishettyhalli Mahadevaiah, M.; Reuben, J.; Schubert, M.A.; Jiménez-Molinos, F.; Roldán, J.B.; Wenger, C. Toward Reliable Compact Modeling of Multilevel 1T-1R RRAM Devices for Neuromorphic Systems. Electronics 2021, 10, 645. https://doi.org/10.3390/electronics10060645
Pérez-Bosch Quesada E, Romero-Zaliz R, Pérez E, Kalishettyhalli Mahadevaiah M, Reuben J, Schubert MA, Jiménez-Molinos F, Roldán JB, Wenger C. Toward Reliable Compact Modeling of Multilevel 1T-1R RRAM Devices for Neuromorphic Systems. Electronics. 2021; 10(6):645. https://doi.org/10.3390/electronics10060645
Chicago/Turabian StylePérez-Bosch Quesada, Emilio, Rocío Romero-Zaliz, Eduardo Pérez, Mamathamba Kalishettyhalli Mahadevaiah, John Reuben, Markus Andreas Schubert, Francisco Jiménez-Molinos, Juan Bautista Roldán, and Christian Wenger. 2021. "Toward Reliable Compact Modeling of Multilevel 1T-1R RRAM Devices for Neuromorphic Systems" Electronics 10, no. 6: 645. https://doi.org/10.3390/electronics10060645
APA StylePérez-Bosch Quesada, E., Romero-Zaliz, R., Pérez, E., Kalishettyhalli Mahadevaiah, M., Reuben, J., Schubert, M. A., Jiménez-Molinos, F., Roldán, J. B., & Wenger, C. (2021). Toward Reliable Compact Modeling of Multilevel 1T-1R RRAM Devices for Neuromorphic Systems. Electronics, 10(6), 645. https://doi.org/10.3390/electronics10060645








