Informing Piano Multi-Pitch Estimation with Inferred Local Polyphony Based on Convolutional Neural Networks
Abstract
1. Introduction
2. Related Work
3. Methodology
3.1. Feature Representations
3.1.1. High-Resolution Constant-Q Transform (HR-CQT)
3.1.2. Low-Resolution Constant-Q Transform (LR-CQT)
3.1.3. Folded CQT (F-CQT)
3.2. CNN Models
MPE Model: ConvNet-MPE
3.3. LPE Models
3.3.1. ConvNet-LPE
3.3.2. CQT Model
3.3.3. F-CQT Model
3.3.4. F-CQT 3D Model
4. Datasets
4.1. MIDI Aligned Piano Sounds (MAPS) Dataset
4.2. Saarland Music Data (SMD)
4.3. SMD-Synth
5. Experimental Procedure
5.1. Label Acquisition
5.2. Class Partitioning Strategies
5.3. Model Training and Evaluation
5.4. MPE Postprocessing
6. Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| LPE | MPE | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| base model | cl | krnl | fr | FM | Fµ | Pµ | Rµ | Fµ | Fµ |
| ConvNet-MPE | 88 | (3, 3) | 3 (5) | n/a | n/a | 70.79 | 61.43 | 65.78 | n/a |
| base informed | |||||||||
| LPE-GT | 3 | - | - | 100.0 | 100.0 | 74.20 | 63.03 | 68.16 | +2.38 |
| 6 | - | - | 100.0 | 100.0 | 71.59 | 70.25 | 70.91 | +5.13 | |
| 13 | - | - | 100.0 | 100.0 | 71.25 | 71.25 | 71.25 | +5.47 | |
| ConvNet-LPE | 3 | (3, 3) | 3 (5) | 59.32 | 82.20 | 69.65 | 61.60 | 65.38 | −0.40 |
| 6 | (3, 3) | 3 (5) | 31.00 | 34.48 | 61.83 | 63.58 | 62.69 | −3.09 | |
| 13 | (3, 3) | 3 (5) | 14.30 | 32.58 | 65.01 | 59.38 | 62.07 | −3.71 | |
| HR-CQT | 3 | (1, 24) | 1 (5) | 56.95 | 80.46 | 69.65 | 60.47 | 64.73 | −1.05 |
| 6 | (1, 24) | 1 (5) | 30.34 | 33.11 | 59.12 | 67.40 | 62.99 | −2.79 | |
| 13 | (1, 24) | 1 (5) | 14.47 | 30.15 | 58.49 | 68.06 | 62.91 | −2.87 | |
| 3 | (3, 24) | 3 (5) | 59.12 | 83.93 | 68.80 | 62.85 | 65.69 | −0.09 | |
| 6 | (3, 24) | 3 (5) | 31.88 | 34.70 | 65.39 | 61.51 | 63.39 | −2.39 | |
| 13 | (3, 24) | 3 (5) | 13.55 | 32.85 | 62.90 | 63.43 | 63.16 | −2.62 | |
| 3 | (5, 24) | 5 | 60.39 | 81.60 | 69.83 | 61.26 | 65.26 | −0.52 | |
| 6 | (5, 24) | 5 | 31.27 | 36.15 | 66.32 | 60.22 | 63.12 | −2.66 | |
| 13 | (5, 24) | 5 | 13.95 | 32.33 | 61.33 | 64.88 | 63.06 | −2.72 | |
| LR-CQT | 3 | (3, 24) | 3 | 58.52 | 82.74 | 69.72 | 61.03 | 65.09 | −0.69 |
| 6 | (3, 24) | 3 | 28.32 | 34.25 | 63.72 | 60.12 | 61.87 | −3.91 | |
| 13 | (3, 24) | 3 | 12.98 | 33.30 | 65.88 | 55.53 | 60.26 | −5.52 | |
| F-CQT | 3 | (4, 3) | 1 | 49.16 | 79.21 | 68.65 | 59.82 | 63.93 | −1.85 |
| 3 | (4, 6) | 1 | 52.10 | 79.74 | 68.99 | 59.80 | 64.07 | −1.71 | |
| 6 | (4, 3) | 1 | 21.02 | 25.44 | 58.14 | 53.00 | 55.94 | −9.84 | |
| 13 | (4, 3) | 1 | 7.25 | 22.29 | 71.64 | 31.46 | 43.72 | −22.06 | |
| F-CQT 3D | 3 | (3, 4, 3) | 3 | 53.50 | 80.35 | 69.75 | 59.28 | 64.09 | −1.69 |
| 3 | (3, 4, 6) | 3 | 53.66 | 79.75 | 69.63 | 58.74 | 63.72 | −2.06 | |
| 6 | (3, 4, 3) | 3 | 27.14 | 33.19 | 64.99 | 55.15 | 59.67 | −6.11 | |
| 13 | (3, 4, 3) | 3 | 16.52 | 33.84 | 63.87 | 58.30 | 60.96 | −4.82 | |
| 3 | (3, 4, 3) | 5 | 57.49 | 83.08 | 69.48 | 61.20 | 65.08 | −0.70 | |
| 6 | (3, 4, 3) | 5 | 29.39 | 33.92 | 63.96 | 58.02 | 60.85 | −4.93 | |
| 13 | (3, 4, 3) | 5 | 13.38 | 33.40 | 65.92 | 57.21 | 61.26 | −4.52 | |
| 3 | (5, 4, 3) | 5 | 59.69 | 82.55 | 70.30 | 60.55 | 65.06 | −0.72 | |
| 3 | (5, 4, 6) | 5 | 59.32 | 81.90 | 70.51 | 59.83 | 64.73 | −1.05 | |
| 6 | (5, 4, 3) | 5 | 30.59 | 36.03 | 65.48 | 58.14 | 61.59 | −4.19 | |
| 13 | (5, 4, 3) | 5 | 12.30 | 31.91 | 64.61 | 56.77 | 60.44 | −5.34 | |
References
- Paulus, J.; Müller, M.; Klapuri, A. State of the Art Report: Audio-Based Music Structure Analysis. In Proceedings of the 11th International Society for Music Information Retrieval Conference (ISMIR), Utrecht, The Netherlands, 9–13 August 2010; pp. 625–636. [Google Scholar]
- Schindler, A.; Lidy, T.; Böck, S. Deep Learning for MIR Tutorial. arXiv 2020, arXiv:2001.05266. [Google Scholar]
- Rafii, Z.; Liutkus, A.; Stöter, F.R.; Mimilakis, S.I.; FitzGerald, D.; Pardo, B. An Overview of Lead and Accompaniment Separation in Music. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 26, 1307–1335. [Google Scholar] [CrossRef]
- Mimilakis, S.I.; Drossos, K.; Cano, E.; Schuller, G. Examining the Mapping Functions of Denoising Autoencoders in Singing Voice Separation. IEEE/ACM Trans. Audio Speech Lang. Process. 2020, 28, 266–278. [Google Scholar] [CrossRef]
- Han, Y.; Kim, J.; Lee, K. Deep convolutional neural networks for predominant instrument recognition in polyphonic music. arXiv 2016, arXiv:1605.09507. [Google Scholar] [CrossRef]
- Taenzer, M.; Abeßer, J.; Mimilakis, S.I.; Weiss, C.; Müller, M.; Lukashevich, H. Investigating CNN-Based Instrument Family Recognition For Western Classical Music Recordings. In Proceedings of the 20th International Society for Music Information Retrieval Conference (ISMIR), Delft, The Netherlands, 4–8 November 2019. [Google Scholar]
- Zhou, X.; Lerch, A. Chord Detection Using Deep Learning. In Proceedings of the 14th International Society for Music Information Retrieval Conference (ISMIR), Málaga, Spain, 26–30 October 2015. [Google Scholar]
- Kelz, R.; Dorfer, M.; Korzeniowski, F.; Böck, S.; Arzt, A.; Widmer, G. On the Potential of Simple Framewise Approaches to Piano Transcription. In Proceedings of the 17th International Society for Music Information Retrieval Conference (ISMIR), New York, NY, USA, 7–11 August 2016. [Google Scholar]
- Kim, J.W.; Salamon, J.; Li, P.; Bello, J.P. Crepe: A Convolutional Representation for Pitch Estimation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 161–165. [Google Scholar]
- Duan, Z.; Pardo, B.; Zhang, C. Multiple Fundamental Frequency Estimation by Modeling Spectral Peaks and Non-Peak Regions. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 2121–2133. [Google Scholar] [CrossRef]
- Yeh, C.; Roebel, A.; Rodet, X. Multiple Fundamental Frequency Estimation and Polyphony Inference of Polyphonic Music Signals. Audio Speech Lang. Process. IEEE Trans. 2010, 18, 1116–1126. [Google Scholar]
- Kareer, S.; Basu, S. Musical Polyphony Estimation. In Proceedings of the Audio Engineering Society Convention 144, Milan, Italy, 23–26 May 2018. [Google Scholar]
- Emiya, V.; Badeau, R.; David, B. Multipitch Estimation of Piano Sounds Using a New Probabilistic Spectral Smoothness Principle. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 1643–1654. [Google Scholar] [CrossRef]
- Müller, M.; Konz, V.; Bogler, W.; Arifi-Müller, V. Saarland Music Data (SMD). In Proceedings of the Late-Breaking and Demo Session of the 12th International Conference on Music Information Retrieval (ISMIR), Miami, FL, USA, 24–28 October 2011. [Google Scholar]
- Mesaros, A.; Heittola, T.; Virtanen, T. Metrics for Polyphonic Sound Event Detection. Appl. Sci. 2016, 6, 162. [Google Scholar] [CrossRef]
- Stöter, F.R.; Chakrabarty, S.; Edler, B.; Habets, E.A.P. Classification vs. Regression in Supervised Learning for Single Channel Speaker Count Estimation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018. [Google Scholar]
- Miwa, T.; Tadokoro, Y.; Saito, T. Musical pitch estimation and discrimination of musical instruments using comb filters for transcription. In Proceedings of the 42nd Midwest Symposium on Circuits and Systems (Cat. No.99CH36356), Las Cruces, NM, USA, 8–11 August 1999; Volume 1, pp. 105–108. [Google Scholar] [CrossRef]
- Klapuri, A. Multipitch Analysis of Polyphonic Music and Speech Signals Using an Auditory Model. IEEE Trans. Audio Speech Lang. Process. 2008, 16, 255–266. [Google Scholar] [CrossRef]
- Su, L.; Yang, Y. Combining Spectral and Temporal Representations for Multipitch Estimation of Polyphonic Music. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 23, 1600–1612. [Google Scholar] [CrossRef]
- Kumar, N.; Kumar, R. Wavelet transform-based multipitch estimation in polyphonic music. Heliyon 2020, 6, e03243. [Google Scholar] [CrossRef] [PubMed]
- Benetos, E.; Dixon, S. Joint Multi-Pitch Detection Using Harmonic Envelope Estimation for Polyphonic Music Transcription. IEEE J. Sel. Top. Signal Process. 2011, 5, 1111–1123. [Google Scholar] [CrossRef]
- Boháč, M.; Nouza, J. Direct magnitude spectrum analysis algorithm for tone identification in polyphonic music transcription. In Proceedings of the 6th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems, Prague, Czech Republic, 15–17 September 2011; Volume 1, pp. 473–478. [Google Scholar]
- Brown, J.C. Calculation of a constant Q spectral transform. J. Acoust. Soc. Am. 1991, 89, 425–434. [Google Scholar] [CrossRef]
- Ducher, J.F.; Esling, P. Folded CQT RCNN for Real-Time Recognition of Instrument Playing Techniques. In Proceedings of the 20th International Society for Music Information Retrieval Conference (ISMIR), Delft, The Netherlands, 4–8 November 2019. [Google Scholar]
- McFee, B.; Raffel, C.; Liang, D.; Ellis, D.; McVicar, M.; Battenberg, E.; Nieto, O. Librosa: Audio and music signal analysis in python. In Proceedings of the 14th Python in Science Conference (SCIPY), Austin, TX, USA, 6–12 July 2015; pp. 18–25. [Google Scholar]
- Sigtia, S.; Benetos, E.; Dixon, S. An End-to-End Neural Network for Polyphonic Piano Music Transcription. arXiv 2016, arXiv:1508.01774. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the Difficulty of Training Deep Feedforward Neural Networks. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 11–18 December 2015. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Drossos, K.; Magron, P.; Virtanen, T. Unsupervised Adversarial Domain Adaptation Based on the Wasserstein Distance for Acoustic Scene Classification. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Palz, NY, USA, 20–23 October 2019; pp. 259–263. [Google Scholar] [CrossRef]
- Taenzer, M.; Mimilakis, S.; Abeßer, J. SMD-Synth: A synthesized Variant of the SMD MIDI-Audio Piano Music Subset. 2021. Available online: https://zenodo.org/record/4637908#.YGPUTT8RWUk (accessed on 30 March 2021). [CrossRef]
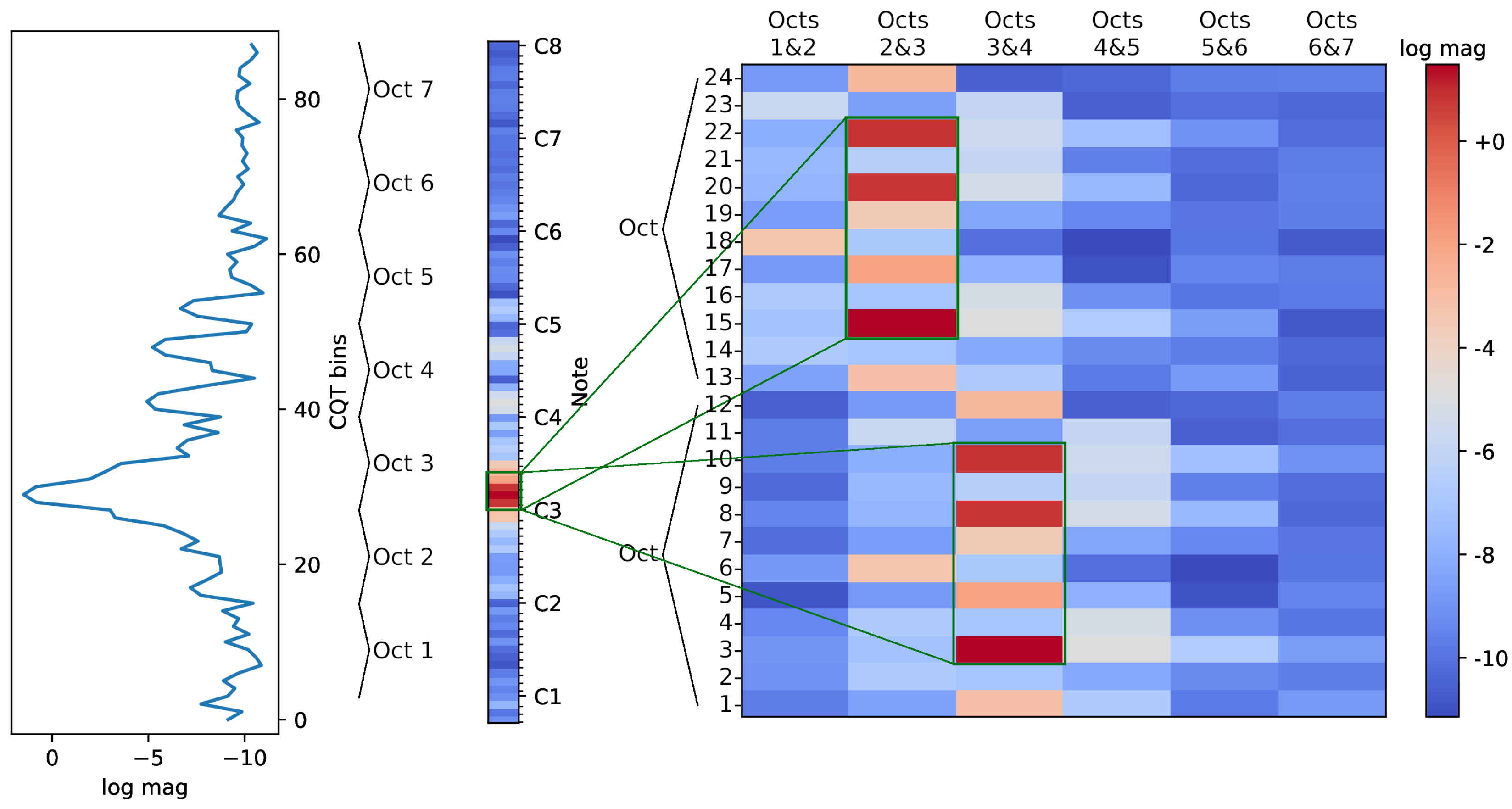

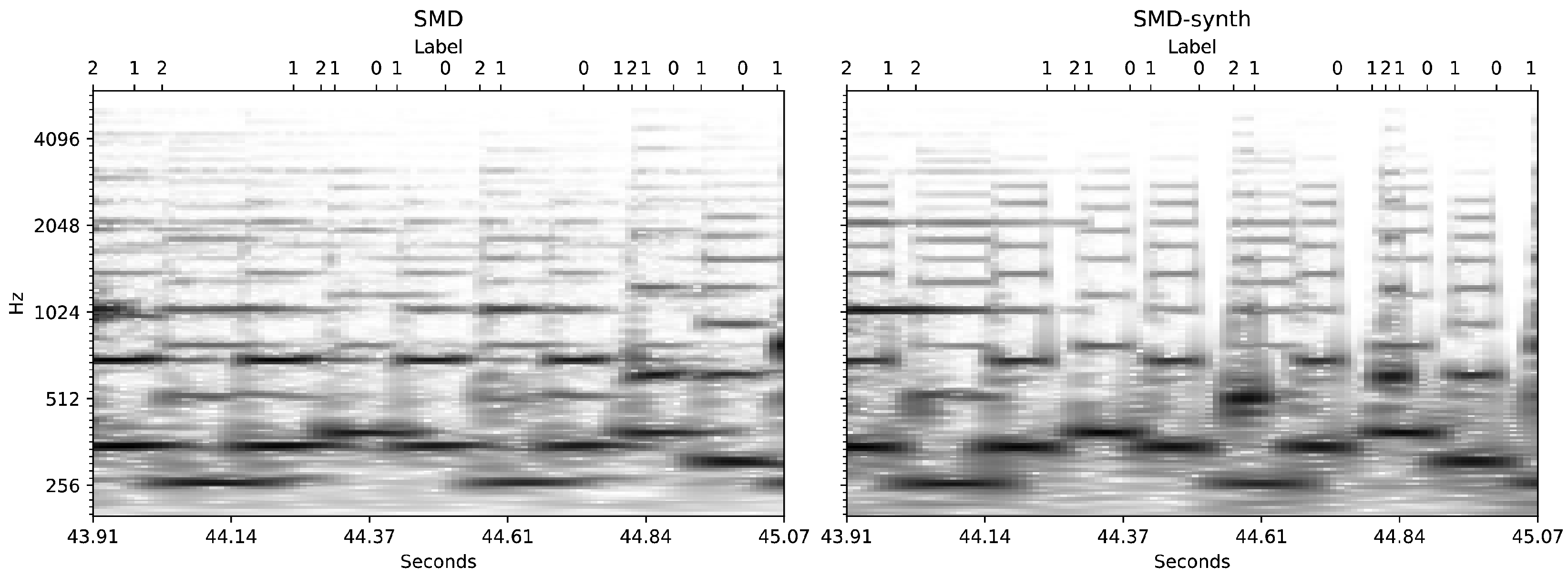
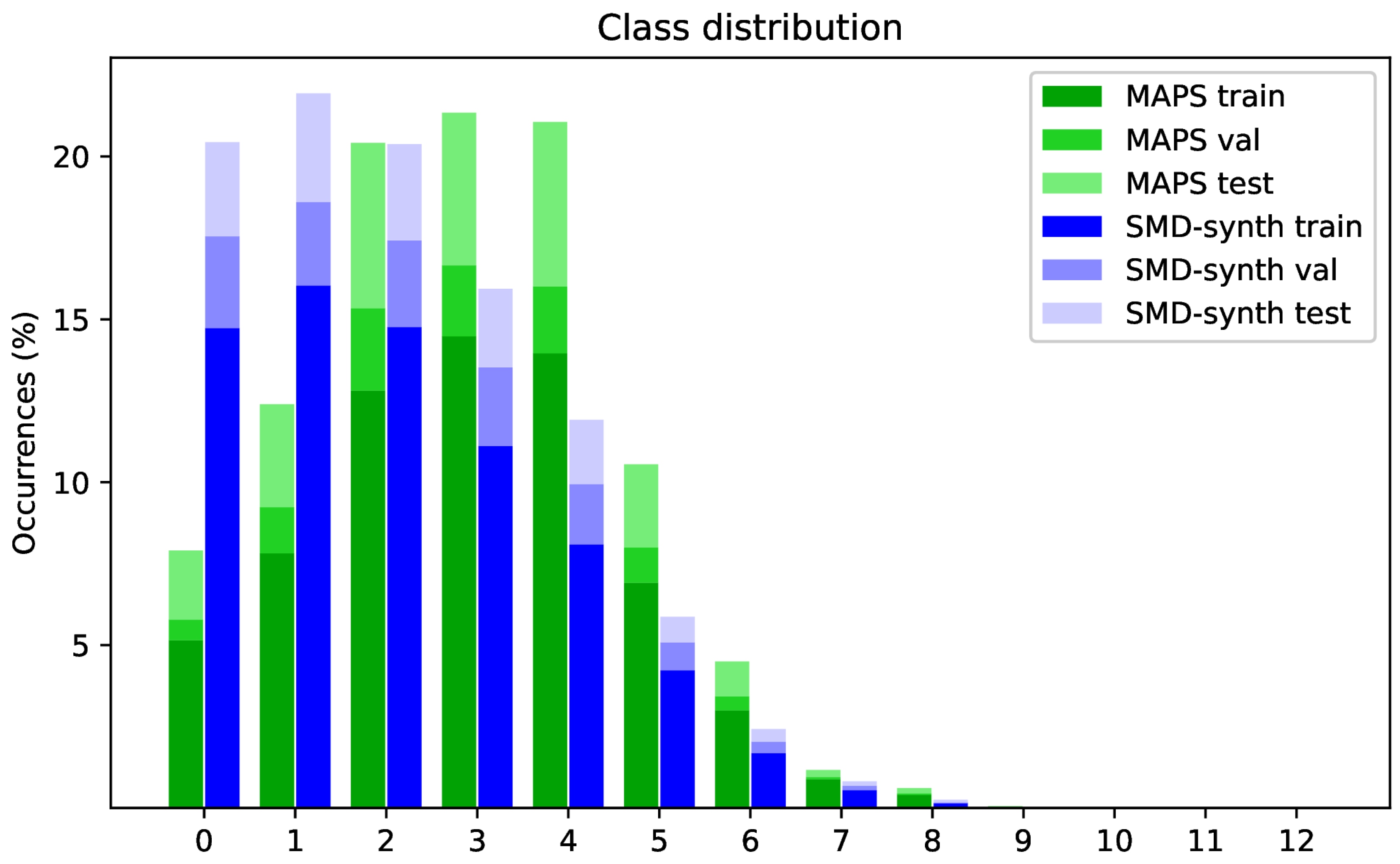

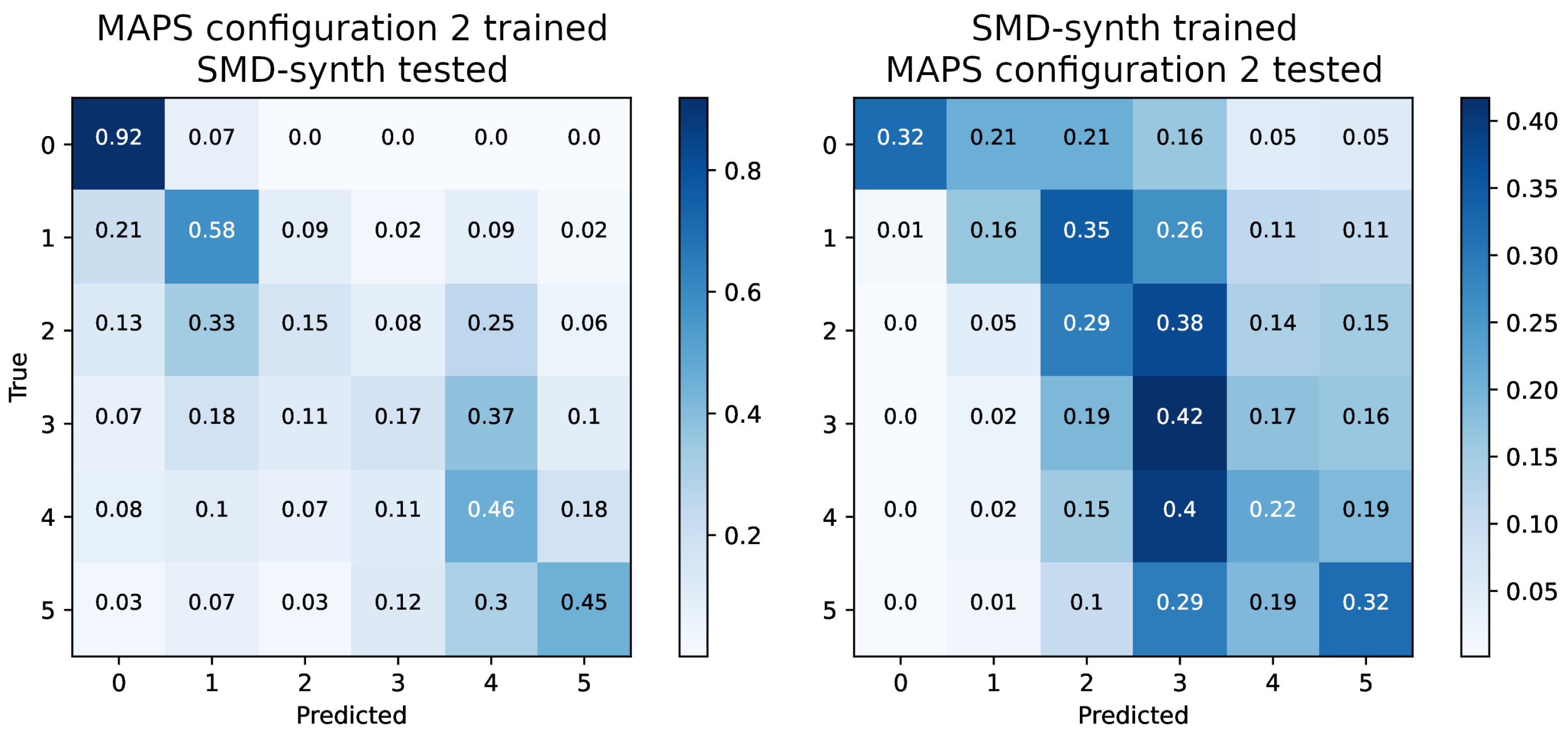
| Parameter | HR-CQT | LR-CQT | F-CQT |
|---|---|---|---|
| Sample rate (kHz) | 44.10 | 22.05 | 22.05 |
| Wave data normalization | - | ✓ | ✓ |
| Log magnitude | - | ✓ | ✓ |
| Data standardization | - | - | - |
| Hopsize (samples) | 512 | 512 | 512 |
| Bins per octave | 36 | 12 | 12 |
| Patch length (frames) | 5 | 1/3/5 | 1 (F-CQT 3D: 1/3/5) |
| Model Name | Task | Features | Kernels | # Classes | # Parameters |
|---|---|---|---|---|---|
| ConvNet-MPE | MPE | HR-CQT | (3, 3) | 88 | 2,158,000 |
| ConvNet-LPE | LPE | HR-CQT | (3, 3) | 3/6/13 | 2,114,000–2,119,000 |
| CQT | LPE | HR-CQT | (1/3/5, 24) | 3/6/13 | 79,000–287,000 |
| CQT | LPE | LR-CQT | (3, 24) | 3/6/13 | 112,000–161,000 |
| F-CQT | LPE | F-CQT | (4, 3/6) | 3/6/13 | 47,000–107,000 |
| F-CQT 3D | LPE | F-CQT | (3/5, 4, 3/6) | 3/6/13 | 221,000–394,000 |
| Dataset | Files per Set Train/Val/Test | Duration [min] Train/Val/Test | Max. Polyphony Train/Val/Test |
|---|---|---|---|
| MAPS config. 2 | 180/30/60 (270) | 711.0/133.5/261.7 | 12/11/12 (@44100/512) |
| 12/11/12 (@22050/512) | |||
| SMD-synth | 35/7/8 (50) | 201.3/38.6/21.2 | 12/11/12 (@44100/512) |
| 12/11/11 (@22050/512) | |||
| LPE | MPE | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| base model | cl | krnl | fr | FM | Fµ | Pµ | Rµ | Fµ | Fµ |
| ConvNet-MPE | 88 | (3, 3) | 3 (5) | n/a | n/a | 70.79 | 61.43 | 65.78 | n/a |
| base informed | |||||||||
| LPE-GT | 3 | - | - | 100.0 | 100.0 | 74.20 | 63.03 | 68.16 | +2.38 |
| 6 | - | - | 100.0 | 100.0 | 71.59 | 70.25 | 70.91 | +5.13 | |
| 13 | - | - | 100.0 | 100.0 | 71.25 | 71.25 | 71.25 | +5.47 | |
| ConvNet-LPE | 3 | (3, 3) | 3 (5) | 59.32 | 82.20 | 69.65 | 61.60 | 65.38 | −0.40 |
| 6 | (3, 3) | 3 (5) | 31.00 | 34.48 | 61.83 | 63.58 | 62.69 | −3.09 | |
| 13 | (3, 3) | 3 (5) | 14.30 | 32.58 | 65.01 | 59.38 | 62.07 | −3.71 | |
| HR-CQT | 3 | (3, 24) | 3 (5) | 59.12 | 83.93 | 68.80 | 62.85 | 65.69 | −0.09 |
| 6 | (3, 24) | 3 (5) | 31.88 | 34.70 | 65.39 | 61.51 | 63.39 | −2.39 | |
| 13 | (3, 24) | 3 (5) | 13.55 | 32.85 | 62.90 | 63.43 | 63.16 | −2.62 | |
| LR-CQT | 3 | (3, 24) | 3 | 58.52 | 82.74 | 69.72 | 61.03 | 65.09 | −0.69 |
| 6 | (3, 24) | 3 | 28.32 | 34.25 | 63.72 | 60.12 | 61.87 | −3.91 | |
| 13 | (3, 24) | 3 | 12.98 | 33.30 | 65.88 | 55.53 | 60.26 | −5.52 | |
| F-CQT | 3 | (4, 3) | 1 | 49.16 | 79.21 | 68.65 | 59.82 | 63.93 | −1.85 |
| 6 | (4, 3) | 1 | 21.02 | 25.44 | 58.14 | 53.00 | 55.94 | −9.84 | |
| 13 | (4, 3) | 1 | 7.25 | 22.29 | 71.64 | 31.46 | 43.72 | −22.06 | |
| F-CQT 3D | 3 | (3, 4, 3) | 5 | 57.49 | 83.08 | 69.48 | 61.20 | 65.08 | −0.70 |
| 6 | (3, 4, 3) | 5 | 29.39 | 33.92 | 63.96 | 58.02 | 60.85 | −4.93 | |
| 13 | (3, 4, 3) | 5 | 13.38 | 33.40 | 65.92 | 57.21 | 61.26 | −4.52 | |
| LPE | MPE | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| base model | cl | krnl | fr | FM | Fµ | Pµ | Rµ | Fµ | Fµ |
| ConvNet-MPE | 88 | (3, 3) | 3 (5) | n/a | n/a | 96.05 | 81.58 | 88.23 | n/a |
| base informed | |||||||||
| LPE-GT | 3 | - | - | 100.0 | 100.0 | 94.56 | 84.04 | 88.99 | +0.76 |
| 6 | - | - | 100.0 | 100.0 | 90.79 | 89.00 | 89.89 | +1.66 | |
| 13 | - | - | 100.0 | 100.0 | 90.02 | 90.02 | 90.02 | +1.79 | |
| ConvNet-LPE | 3 | (3, 3) | 3 (5) | 92.96 | 93.42 | 92.91 | 83.66 | 88.04 | −0.19 |
| 6 | (3, 3) | 3 (5) | 59.73 | 66.81 | 86.81 | 82.84 | 84.78 | −3.45 | |
| 13 | (3, 3) | 3 (5) | 26.80 | 64.14 | 86.67 | 82.79 | 84.69 | −3.54 | |
| HR-CQT | 3 | (3, 24) | 3 (5) | 90.53 | 91.12 | 93.18 | 83.03 | 87.81 | −0.42 |
| 6 | (3, 24) | 3 (5) | 61.35 | 67.54 | 88.80 | 81.93 | 85.23 | −3.00 | |
| 13 | (3, 24) | 3 (5) | 27.68 | 64.83 | 88.49 | 81.76 | 84.99 | −3.24 | |
| LR-CQT | 3 | (3, 24) | 3 | 92.30 | 92.64 | 91.70 | 82.42 | 86.81 | −1.42 |
| 6 | (3, 24) | 3 | 60.36 | 67.73 | 83.33 | 83.03 | 83.18 | −5.05 | |
| 13 | (3, 24) | 3 | 28.59 | 66.52 | 85.30 | 81.92 | 83.57 | −4.66 | |
| F-CQT | 3 | (4, 3) | 1 | 89.73 | 90.23 | 91.01 | 82.14 | 86.35 | −1.88 |
| 6 | (4, 3) | 1 | 54.76 | 61.39 | 81.21 | 81.39 | 81.30 | −6.93 | |
| 13 | (4, 3) | 1 | 24.66 | 59.96 | 83.39 | 79.89 | 81.60 | −6.63 | |
| F-CQT 3D | 3 | (3, 4, 3) | 5 | 92.04 | 92.34 | 91.95 | 81.93 | 86.65 | −1.58 |
| 6 | (3, 4, 3) | 5 | 56.18 | 63.61 | 80.78 | 82.93 | 81.84 | −6.39 | |
| 13 | (3, 4, 3) | 5 | 24.47 | 62.10 | 81.62 | 81.85 | 81.73 | −6.50 | |
| LPE | MPE | ||||||
|---|---|---|---|---|---|---|---|
| Model | cl | FM | Fµ | Pµ | Rµ | Fµ | Fµ |
| Scenario 1: trained on MAPS configuration 2, tested on SMD-synth | |||||||
| ConvNet-MPE | 88 | n/a | n/a | 83.73 | 70.31 | 76.43 | n/a |
| ConvNet-LPE | 3 | 71.08 | 75.47 | 81.17 | 69.52 | 74.89 | −1.54 |
| 6 | 36.71 | 41.37 | 63.03 | 73.44 | 67.83 | −8.60 | |
| 13 | 17.11 | 43.39 | 72.46 | 66.18 | 69.18 | −7.25 | |
| HR-CQT | 3 | 69.70 | 76.32 | 80.06 | 70.13 | 74.77 | −1.66 |
| 6 | 39.51 | 45.51 | 71.03 | 67.02 | 68.97 | −7.46 | |
| 13 | 17.14 | 40.71 | 67.62 | 65.09 | 66.33 | −10.10 | |
| Scenario 2: trained on SMD-synth, tested on MAPS configuration 2 | |||||||
| ConvNet-MPE | 88 | n/a | n/a | 59.54 | 60.28 | 59.91 | n/a |
| ConvNet-LPE | 3 | 42.75 | 80.58 | 57.69 | 61.32 | 59.45 | −0.46 |
| 6 | 26.40 | 29.38 | 54.59 | 63.32 | 58.63 | −1.28 | |
| 13 | 11.79 | 24.65 | 54.54 | 62.97 | 58.45 | −1.46 | |
| HR-CQT | 3 | 47.58 | 80.95 | 58.11 | 61.21 | 59.62 | −0.29 |
| 6 | 25.92 | 27.47 | 56.00 | 61.02 | 58.40 | −1.51 | |
| 13 | 11.81 | 25.18 | 56.73 | 59.76 | 58.21 | −1.70 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taenzer, M.; Mimilakis, S.I.; Abeßer, J. Informing Piano Multi-Pitch Estimation with Inferred Local Polyphony Based on Convolutional Neural Networks. Electronics 2021, 10, 851. https://doi.org/10.3390/electronics10070851
Taenzer M, Mimilakis SI, Abeßer J. Informing Piano Multi-Pitch Estimation with Inferred Local Polyphony Based on Convolutional Neural Networks. Electronics. 2021; 10(7):851. https://doi.org/10.3390/electronics10070851
Chicago/Turabian StyleTaenzer, Michael, Stylianos I. Mimilakis, and Jakob Abeßer. 2021. "Informing Piano Multi-Pitch Estimation with Inferred Local Polyphony Based on Convolutional Neural Networks" Electronics 10, no. 7: 851. https://doi.org/10.3390/electronics10070851
APA StyleTaenzer, M., Mimilakis, S. I., & Abeßer, J. (2021). Informing Piano Multi-Pitch Estimation with Inferred Local Polyphony Based on Convolutional Neural Networks. Electronics, 10(7), 851. https://doi.org/10.3390/electronics10070851





