Development of Electric Drive on the Basis of Five-Phase Synchronous Electric Motor

Abstract

This paper shows a model of a five-phase synchronous motor with permanent magnets and a simulation model of a control device. A simulation model in the SimInTech software product is built. The transient time is 0.03 s when a stepped input is applied. When the load moment of inertia increases by a factor of 10, the accuracy of speed response decreases. The maximum motor speed error is 40% at a time of 0.2 s. This is a consequence of changing the model of the control object. It is suggested to perform model identification and adapt PI controllers according to load parameters.

1. Introduction

Industrial use of electric drives began at the beginning of last century. At that time, direct voltage or alternating voltage on three phases was used. One of the founders of electric drives is considered to be Dane X. Erested, who in 1820 showed the possibility of interaction between a magnetic field and a conductor with a current. The Frenchman A. Ampere in the same year developed the theory and built a mathematical model of this interaction. British scientist M. Faraday in 1821 demonstrated the principle of transformation of electric energy into mechanical energy through the electromagnetic field. Russian scientists B.S. Jacobi and E.H. Lenzu in 1834 created the first direct current electric motor. In 1837 the American Davenport built an electric motor with a simpler commutator. In 1838 B.S. Jacobi improved the design of the electric motor, which is the prototype of the modern electric machine. In 1841, Englishman C. Whitson built a single-phase synchronous electric motor. In 1876, Russian scientist P.N. Yablochkov developed several designs of synchronous generators to power the candles he invented, and also invented a transformer. In 1888, Italian G. Ferraris and Yugoslavian N. Tesla discovered the phenomenon of rotating magnetic fields, which initiated the design of multiphase electric motors. Ferraris and Tesla developed several models of two-phase AC motors. The Russian electrical engineer M.O. Dolivo-Dobrovolsky developed a three-phase alternating current system in 1889. In the same year, he patented an asynchronous electric motor with a squirrel-cage rotor, and a few later with a phase rotor. M.O. Dolivo-Dobrovolsky also developed a 3-phase synchronous generator and 3-phase transformer, the designs of which remain virtually unchanged today.

Most AC motors were designed as three-phase devices. In theory, AC motors can be built with any number of phases. Drives with a large number of phases have a number of advantages compared with conventional three-phase drives: reduction in amplitude and increase in the frequency of moment ripple, reduction in harmonic rotor currents (if there is a rotor winding), reduction in the value of electric current per phase without increasing the voltage per phase, reduction in DC link current harmonics, higher reliability and increased power at the same mass [1].

Paper [2] investigates a kind of five-phase dual-rotor permanent-magnet synchronous motor (DRPMSM), which contains dual rotors and a single stator. This kind of motor has the potential advantages of high power density, high reliability and high efficiency, which make it more appropriate for use in electric vehicles (EVs). In order to evaluate the most suitable power level for this kind of structure, the electromagnetic, thermal and mechanical characteristics are investigated in this paper. The length-to-diameter ratio of motors is researched to obtain the highest power density and then the optimum ratio is obtained. Based on the optimum ratio, the thermal characteristics are researched under natural conditions and forced-air cooling conditions with different wind speeds. In addition, the mechanical characteristics are analyzed under no-load and different load conditions, respectively. All of the results are analyzed by two-dimension (2-D) and three-dimension (3-D) finite element method (FEM) simulation, which provides a good reference to select a suitable power level for this kind of motor structure [2].

The realization of a multiphase motor with more than three phases is possible even on the basis of a stator package of a three-phase machine with insignificant modernization of winding scheme. These factors allow us to consider electric traction on the basis of seven-phase machines as an alternative to the three-phase electric drive. Seven-phase motor (compared to three-phase), depending on the ratio of the number of turns in a phase, has a smaller nominal phase current, or a smaller phase voltage. When the number of phases is increased, a reduction in copper consumption is expected. The level of noise and vibrations of electromagnetic origin in a seven-phase motor is lower in comparison with a three-phase motor, which is a consequence of a number of features of the seven-phase winding. The subject of research is seven-phase motor winding (winding connection diagram—“star”), connected to a bridge converter, namely its ability to reduce vibrations of electromagnetic origin (in comparison with three-phase winding). The mode of pulsation of the common point potential of the seven-phase winding relative to the “zero” of the converter was investigated. The amplitude modulation of the space-time voltage vector of the seven-phase winding under the influence of pulsation of the common point potential relative to the “zero” of the converter was also investigated. During theoretical studies, the Fourier series decomposition method was used, as well as methods of vector analysis. To confirm the theoretical results, experimental studies of model samples of seven-phase and three-phase synchronous motors were carried out. The experiments were carried out on special equipment designed to study control algorithms of converters implementing space-time vector modulation of multiphase machines. The main result of the work is that a seven-phase motor (winding connection diagram—“star”) has a lower value of pulsations of the winding common point potential relative to the converter “zero” as compared to a three-phase motor. The numerical values of the ripple were determined and verified experimentally. This indicates that the level of ripples of electromagnetic origin is reduced when using a simple converter operation algorithm. The obtained results can be used in the creation of electric traction with vector control on the basis of seven-phase motors [3]. It should be noted that the seven-phase motor has more complex power electronics, the core of which are 14 transistors and more complex control algorithms with high computational complexity in vector control compared to a five-phase synchronous motor.

The subject of the study is a five-phase winding of an ABCDE motor with a spatial phase shift connected to a converter that forms a time phase shift of ACEBD. The process of forming the resulting voltage vector with one of the converter control algorithms is investigated, and the voltage ripple level of the common point of the five-phase winding relative to the converter zero is determined. When conducting theoretical studies used the method of decomposition in a Fourier series, as well as methods of vector analysis. To confirm the theoretical results, experimental studies of a prototype model of a five-phase synchronous motor were carried out. The main results are that with a time sequence of alternating ACEBD phases of a symmetrical five-phase winding, the “working” resulting voltage vector is the third harmonic vector, and its rotation frequency is three times the frequency of the converter. The practical significance of the work is that with a single frequency converter, the rotational speed of the resulting voltage vector of the five-phase winding has two values and can change discretely depending on the time sequence of the phase alternation. This property can be used to regulate the engine speed in a modern traction electric drive [4,5].

The most important characteristics of a modern drive are high reliability, good control characteristics, low maintenance and repair requirements, and low operating costs. New power semiconductor elements, such as MOSFETs and IGBTs, increase the control capabilities of electric machines [6]. In our study, a PWM frequency of 20 kHz is chosen, which will provide a good ratio of the quality of the generated signal to the power converter efficiency. FDS9945 transistors were used.

Studies in the field of modern electric drives are given in works [7,8,9,10,11,12,13,14,15,16].

Article [7] reviews the recent advancements of multiphase machines in several aspects such as topology, control, and performance to evaluate the possibility of exploiting them more in electric vehicle (EV) applications in the future.

In papers [8,9,10,11], an optimally-tuned PID control. The parametric synthesis of the PID controller on the basis of continuous and discrete models was performed. Numerical simulations using SimInTech for the adaptive regulator taking into account the cargo weight (from empty to maximum loaded) were carried out. The scheme of automatic selection of actuator PID coefficients considering the cargo weight was proposed. As a result of the parametric synthesis of discrete PID control law, optimum values of its amplification coefficients were determined. In [12], the authors discussed the stability analysis and calculation of oscillatory processes based on a dynamic model, the parametric identification of which was performed on the basis of experimental data and the results of a multidimensional numerical simulation. In our work, we used two PI regulators. The internal fast-acting PI regulator is by electric current in the rotating coordinate system. The external PI regulator is by angular velocity.

In the paper [13], the results of research and model tests of asynchronous induction machines of modular design are presented. Several positive aspects of the practical realization of this design and the characteristic features of its mathematical description in comparison with the synchronous reactive machine of modular design are pointed out. An algorithm for the calculation of the machine parameters is considered and a computer model of the electric drive in the MATLAB-Simulink package is developed.

In [14], the authors have established and solved the problem of the analytical design law of direct adaptive control of the electric actuator. It is shown that the proposed law can be implemented on an analog or computer PID controller platform. In this case, a traditional PID controller can be transformed into an adaptive one by simply changing its setting parameters while keeping the composition of the elements unchanged, which include the integrator, differentiator, and amplifiers.

Article [15,16] discusses the development of advanced electric drive control systems and explores the challenges of modeling real physical objects, including control system design, testing, and the development of working prototypes. An algorithm for executable code development was presented.

The papers [17,18,19,20,21] scientifically discuss the progressive diagnostics of electrical drives with sensor support and the proposed AI (artificial intelligence) model.

This paper builds a model of a five-phase synchronous motor controlled by a transistor voltage converter-regulator based on power semiconductor switches. A prototype motor was made and tested. The influence of motor operating modes and load moment of inertia on the accuracy of the motor speed is investigated.

2. Materials and Methods

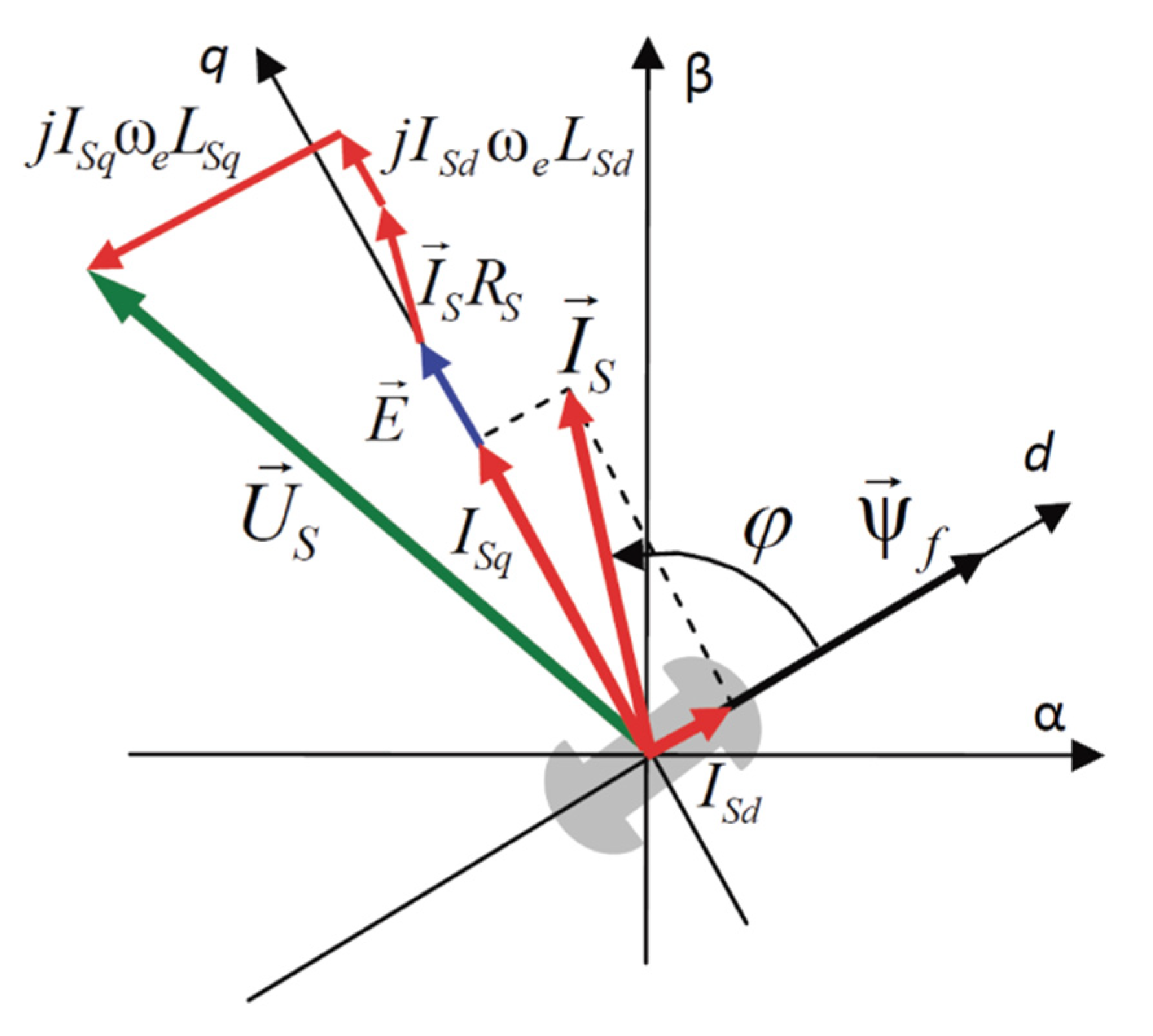
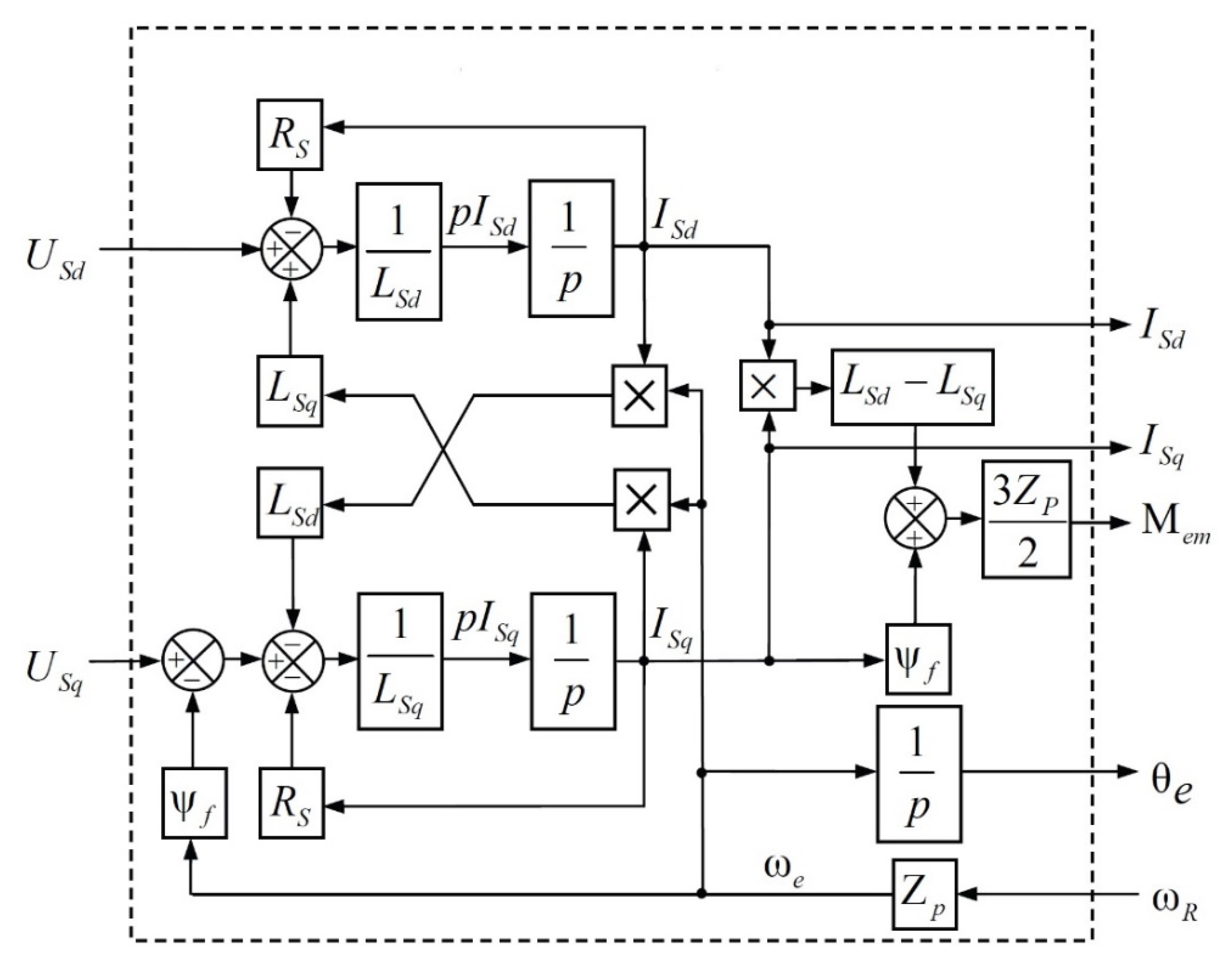
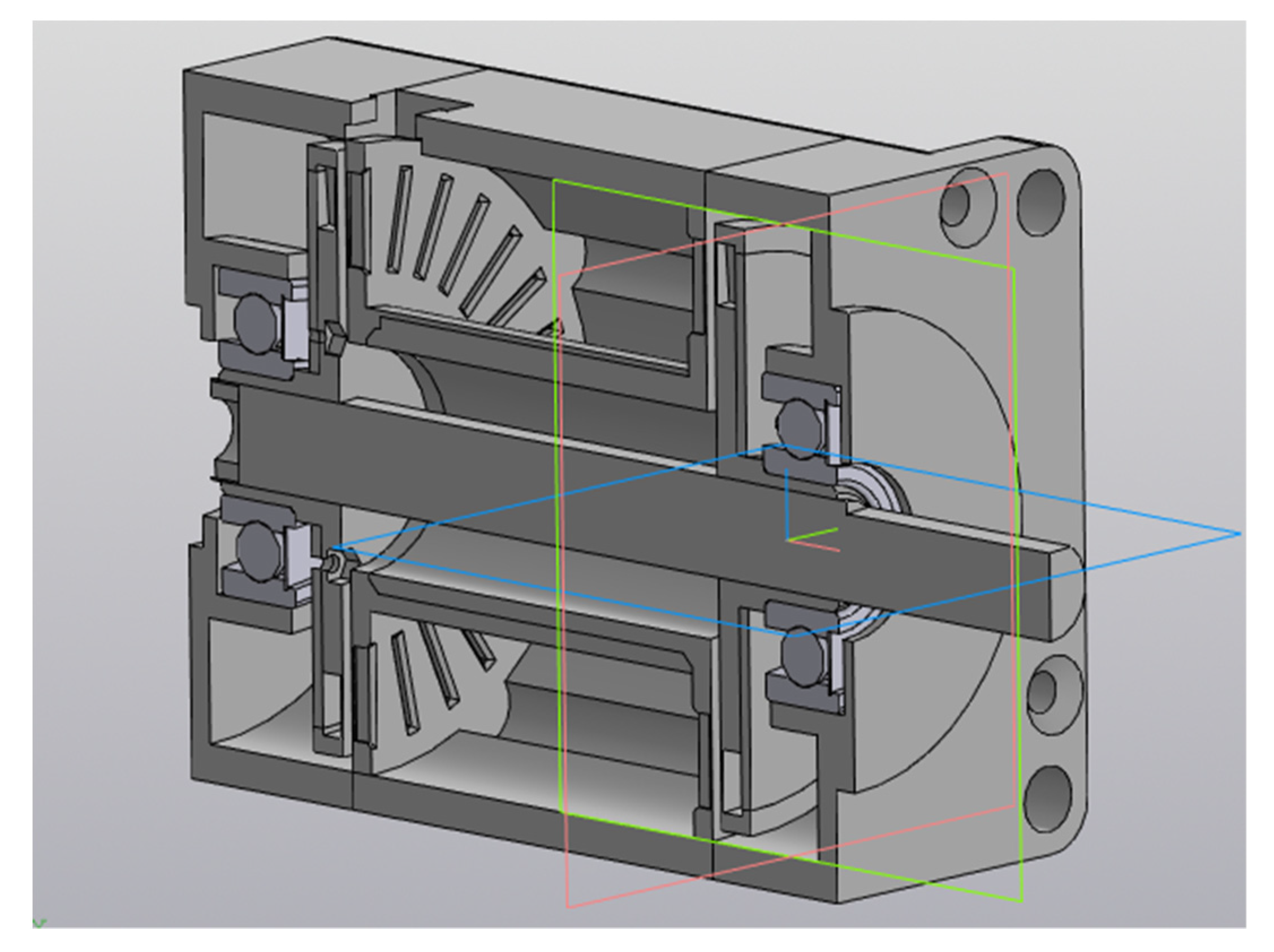
2.1. Mathematical Model of a Five-Phase Synchronous Motor

Figure 1 shows a vector diagram explaining the processes occurring in a synchronous motor. We will consider them in a rotating coordinate system dq, the axis d of which is oriented along the rotor flux [22].

The rotor of the motor, being a permanent magnet, produces a flux capacitance ψ_f, equal to the product of the rotor flux by the number of turns of the stator winding. The vector of this current-circuiting is directed along the rotor axis d from the positive pole to the negative pole and lags behind the stator current vector Is by some angle φ. The constant flux of the rotating rotor creates in stator windings the vector of electromagnetic field (EMF) E directed at a right angle to the flux and leading it by 90 degrees (the derivative of rotor current-current dψ_f/dt) [22].

The amplitude of the EMF vector is determined by the expression:

E = ψ_f ∙ ω_e,

(1)

where ω_e is the rotational speed of the field; ω_e = Z_p ω_R; ω_R is the rotor speed; Z_p is the number of motor pole pairs.

According to Figure 1, we can write the following vector relation [9]:

U_S = E + I_SR_S + jω_e (I_SdL_Sd + I_SqL_Sq),

(2)

where U_S is the stator voltage vector; I_s is the stator current vector; I_Sd and I_Sq are its components; L_Sd and L_Sq are stator inductance along d and q axes; R_S is stator resistance.

According to Figure 1, the stator voltage vector is balanced by the EMF vector and voltage drop on active (R_S) and reactive (L_Sd and L_Sq) resistances of the stator winding.

Motor torque arises as a result of force interaction between current and stator current-current vectors. The torque is determined by the vector product of the effective values of these vectors. Taking into account the phase and the number of pole pairs of the motor (Z_p), the following expression for calculating the motor torque can be written [9]:

$$M_{em}=\frac{3}{2}{Z}_p(I_S\times {\psi }_S)=\frac{3}{2}{Z}_p|I_S|\cdot |{\psi }_S|\sin \phi$$

(3)

where φ is the angle between the current and stator current-current vectors.

The formula for calculating the electromagnetic torque of the motor in the dq coordinate system will look like this [8]:

$$M_{em}=\frac{3}{2}{Z}_p(I_{Sq}{\psi }_f+I_{Sd}{I}_{Sq}(L_{Sd}-L_{Sq}))$$

(4)

The motor stator is a five-phase inductor coil and assuming that magnetic losses are neglected, the following expression can be written for it in the dq coordinate system, rotating with the field.

$$\left\{\begin{array}{l}{U}_{Sd}=L_{Sd}\frac{d{I}_{Sd}}{dt}+R_S{I}_{Sd}-{\omega }_e{L}_{Sq}{I}_{Sq}\\ U_{Sq}=L_{Sq}\frac{d{I}_{Sq}}{dt}+E+R_S{I}_{Sq}+{\omega }_e{L}_{Sd}{I}_{Sd}\end{array}\right.,$$

(5)

Let us write Equation (5) in Cauchy form and add the equation of electromagnetic torque.

$$\left\{\begin{array}{l}\frac{d{I}_{Sd}}{dt}=\frac{1}{L_{Sd}}(U_{Sd}-R_S{I}_{Sd}+{\omega }_e{L}_{Sq}{I}_{Sq})\\ \frac{d{I}_{Sq}}{dt}=\frac{1}{L_{Sq}}(U_{Sq}-R_S{I}_{Sq}-{\omega }_e{L}_{Sd}{I}_{Sd}-{\psi }_f{\omega }_e)\\ M_{em}=\frac{3}{2}{Z}_p(I_{Sq}{\psi }_f+I_{Sd}{I}_{Sq}(L_{Sd}-L_{Sq}))\end{array}\right.,$$

(6)

By Equation (6) we can build a model of electromagnetic processes of the synchronous motor, as shown in Figure 2.

The model is augmented with a rotor field angle calculator (θ_e), which is obtained by integrating the field velocity (ω_e). The input signals of the model are voltages and velocity, and the output signals are currents, electromagnetic moment and field angle.

The rotor speed of the motor in this case is determined by the expression:

$${\omega }_R=\frac{1}{J}{\displaystyle \int (M_{em}-M_L)}dt$$

(7)

where: J is the moment of inertia applied to the rotor; M_L is the load torque applied to the rotor.

Accordingly, the output of the electromagnetic moment of the motor model should be fed to the model of the mechanical system, made on the elements of the “Mechanics” library, which allows us to simulate complex transfer mechanisms and loads. The mechanical system model converts the torque signal into speed, which in turn is fed to the corresponding input of the motor model.

The motor receives a five-phase voltage generated by pulse width modulation, has a load resistance torque with some moment of inertia, and outputs electromagnetic torque and speed. The mathematical model of a five-phase motor is used to simulate a five-phase synchronous machine.

2.2. Synchronous Motor Drive System Based on Five-Phase Voltage Regulator Using IGBT

The simulation model of the motor and control device is developed based on the PI controller of angular speed using position sensors, electric current sensors and IGBT transistors as power switches. The simulation model of the control device in the SimInTech software product is shown in Figure 3. The speed is given in relative units relative to the rated motor speed. The speed equal to 1 corresponds to the nominal speed of the motor. The control unit has two feedback loops. The external feedback loop is implemented as a PI motor speed controller. The internal fast feedback loop is implemented as two PI controllers of the motor electric current projections on the d and q axes.

The motor parameters are given in

Table 1. Motor parameters.

Parameter Name	Parameter Designation	Parameter Value
Number of motor pole pairs	Zp	42
Stator phase resistance, Ohm	RS	16
Stator phase inductance, Hn	LS	0.112
Rotor current coefficient, Vb	F	0.4

. The parameters of the PI controller of motor speed are given in

Table 2. Parameters of PI motor speed controller.

Parameter Name	Parameter Designation	Parameter Value
Proportional coefficient	kp	4
Integral coefficient	ki	150

. Parameters of the PI controller of projections of electric motor current on the d and q axes are given in

Table 3. Parameters of PI controller of projections of electric motor current on the d and q axes.

Parameter Name	Parameter Designation	Parameter Value
Proportional coefficient	kp	4
Integral coefficient	ki	400

.

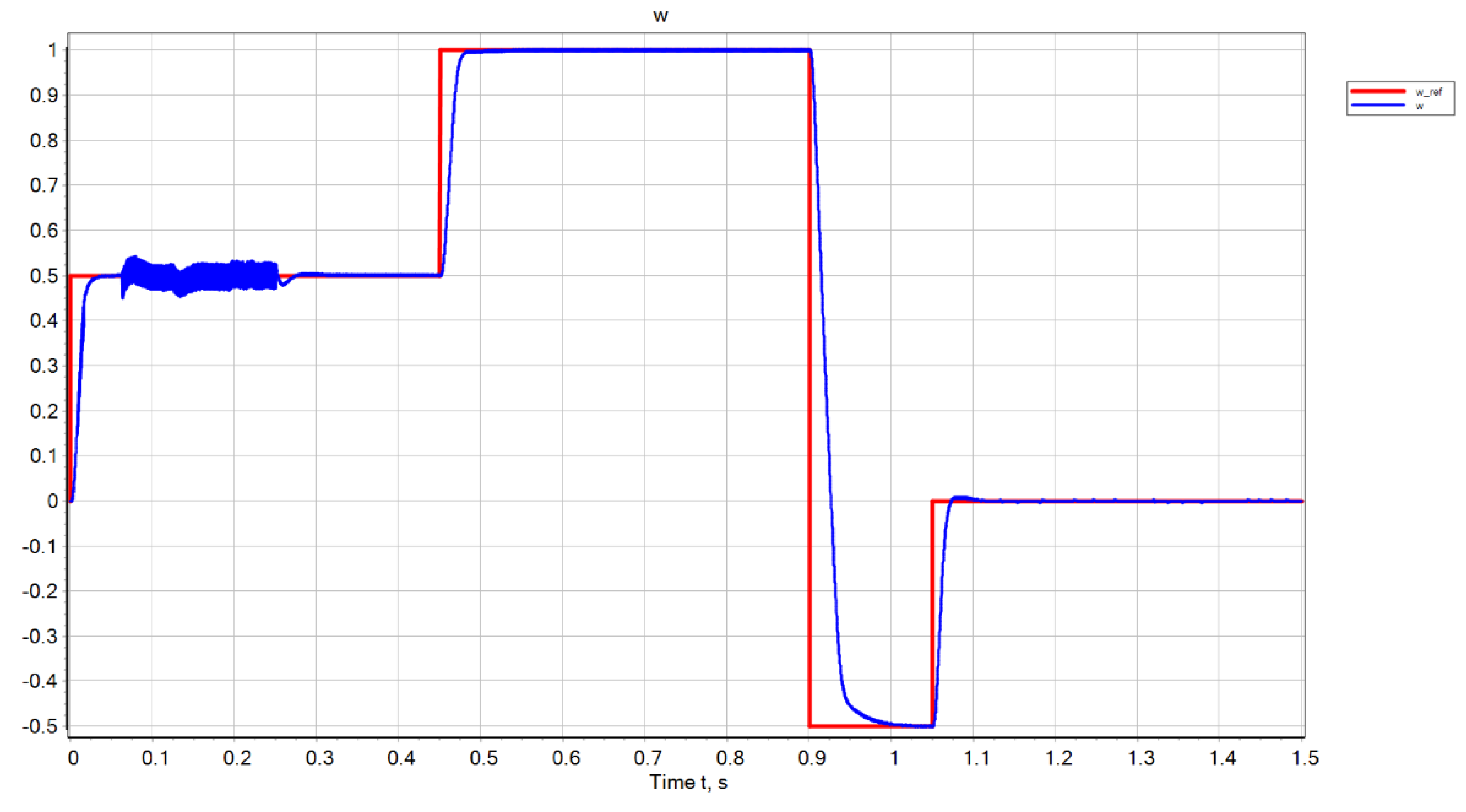
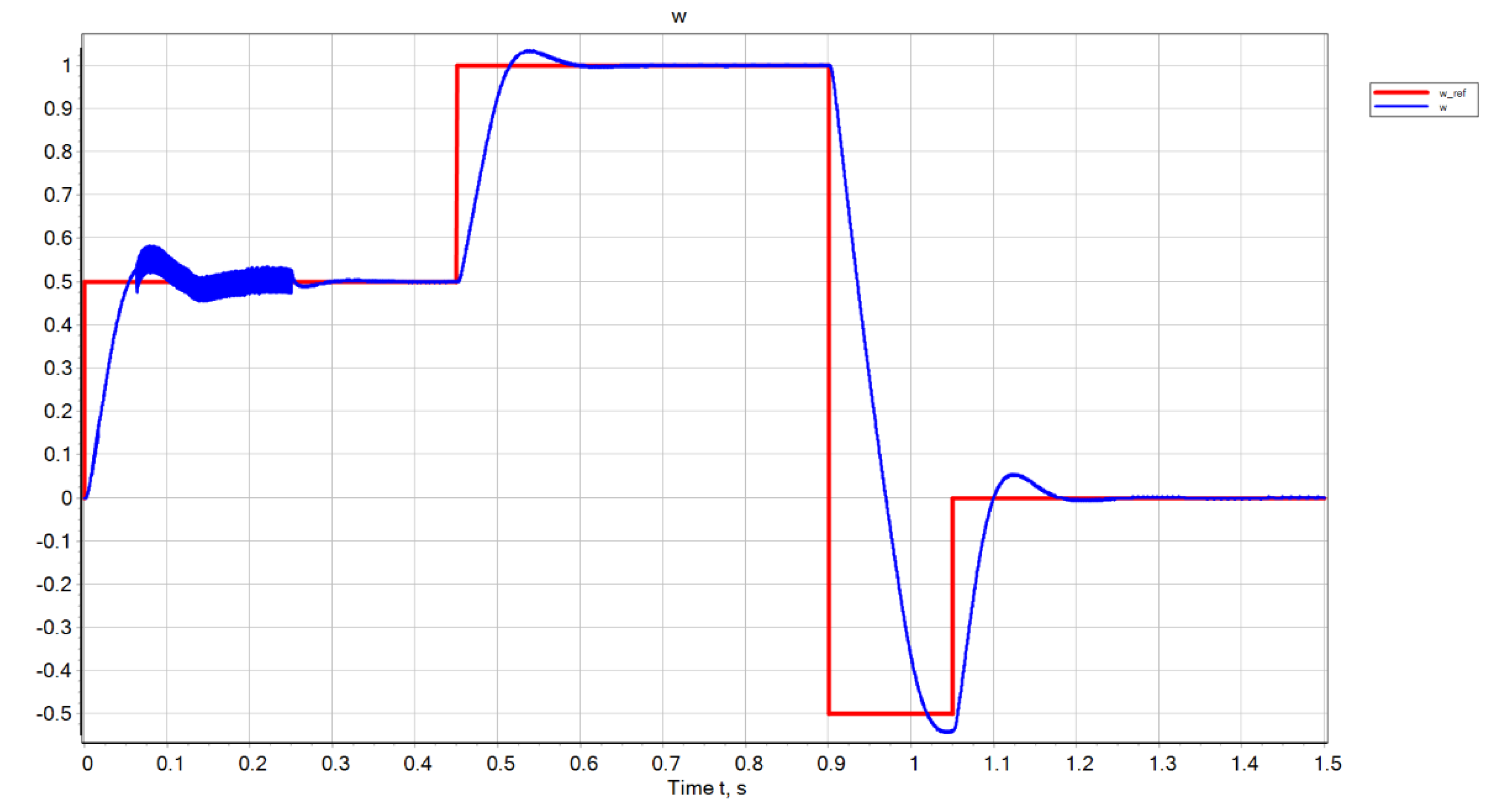
3. Results

Figure 4 shows the given angular speed and angular speed of the motor for a rectangular voltage input signal with a load moment of inertia of 0.7 kg∙m².

When a stepped action is applied to the input, the transient time is 0.03 s. at a load moment of inertia of 0.7 kg∙m².

Figure 5 shows the reference angular speed and angular speed of the motor for a rectangular voltage input signal with a load moment of inertia of 2.1 kg∙m².

When a stepped action is applied to the input, the transient time is 0.1 s. at a load moment of inertia of 2.1 kg∙m².

If the motor is accelerated smoothly, the accuracy of the trajectory increases, as shown in Figure 6.

The smaller error of the angular velocity with its linear change is explained by the fact that the motor rotor together with the load has a certain moment of inertia. The sum of moments (electromagnetic torque with sign ‘+’, load torque with sign ‘–’) is equal to the product of the moment of inertia by the angular acceleration. With a stepped input signal specifying angular velocity, the angular acceleration tends to infinity at the time of the jump, with a linear change in angular velocity, the angular acceleration will be a constant. To provide infinite angular acceleration requires infinite motor torque and therefore infinite electric current. The finite value of the electric current of real devices determines the angular velocity error is smaller when it changes linearly than when the input signal is stepped.

Figure 6 shows the given angular velocity and angular velocity of the motor when applied to the input with a load moment of inertia of 0.7 kg∙m². Figure 7 shows the given angular velocity and angular velocity of the motor when applied to the input with a load moment of inertia of 2.1 kg∙m².

If the load moment of inertia increases by a factor of 10, the speed accuracy decreases. The maximum motor speed error is 40% at a time of 0.2 s. This is a consequence of changing the model of the control object. Therefore, it is necessary to perform model identification and adapt PI controllers. When the load moment of inertia threshold value corresponding to the motor torque parameters is exceeded, an alarm signal must be issued.

To study the principles of control and the development of power boards, a mockup of the motor was developed (Figure 8). To study the control principles and the development of power boards, a mock-up engine was created (Figure 8). The mock-up of the engine has been created with CA support to enable the use of CAD, CAM, DFM, and other systems that help achieve higher product accuracies and help companies develop new products [23,24,25].

The stator is assembled from individual coils in 5 groups, each group is connected to one of the power supply phases, the phases are connected in a “star” pattern (Figure 9).

The rotor is two discs rigidly mounted on the shaft with permanent magnets inside (Figure 10 and Figure 11).

The housing of the layout is made according to the Nema 23 standard, which allows you to test the operation of the device on all systems that have the appropriate attachment (Figure 12).

The AS5600 magnetic encoder is used to control the rotor angle of rotation (Figure 13).

The prototype is fully assembled and functional (Figure 14).

4. Discussion

This paper considers five-phase synchronous motors and their advantages. The mathematical model of a five-phase motor in a rotating dq coordinate system is used to simulate. A simulation model of the control device is implemented in the SimInTech program. The five-phase motor control unit is based on two PI controller loops. The external control circuit is implemented as a PI controller for angular velocity. The internal control circuit is implemented as a PI controller for electric current. The results of the simulation of a five-phase motor with a stepped input signal and with a linear change in angular velocity are shown. As a result of the simulation, the transient times have been established. It is shown that with a linear change in angular velocity, the angular velocity error is smaller than with a step input signal. When the moment of inertia increases by a factor of three, the angular velocity overshoots and the angular velocity error increases. Five-phase synchronous motors with permanent magnets have been developed. Currently, most inverters for AC motors are three-phase. The wide implementation of five-phase motors requires the production of five-phase inverters based on 10 power MOSFET transistors. Further direction of research is related to the development of fault-tolerant control of five-phase motors. This requires the development of a diagnostic system that detects the fault associated with the loss of phase five-phase motor or its short circuit, or fault of power MOSFET transistors. Then the five-phase motor is controlled for 4 phases only, excluding the defective phase or MOSFET transistor.

5. Conclusions

In this paper, a simulation model of five-phase synchronous motors was developed in SimInTech software and the results were evaluated. The five-phase motor control device is implemented on the basis of two PI controller loops. The external control circuit is implemented as a PI controller of angular velocity. The internal control circuit is implemented as a PI regulator of electric current. The results of the simulation of a five-phase motor with a stepped input signal and with a linear change in angular velocity are shown. The transient time is 0.03 s when the step influence is applied to the input. The accuracy of speed response decreases when the load moment of inertia increases by a factor of 10. The maximum error in the motor speed is 40% at a time of 0.2 s. This is a consequence of changing the model of the control object. It is suggested to perform model identification and adapt PI controllers according to load parameters. A design of five-phase synchronous motors with permanent magnets has been developed. The five-phase synchronous motor has the following characteristics:

-

weight of the motor: 0.52 kg;

-

overall dimensions: 61 × 56 × 56 mm³;

-

nominal power: 55 Watts;

-

efficiency: 93%;

-

power supply voltage: 24 V;

-

rated current: 2.5 A;

-

nominal torque: 0.18 N∙m;

-

rated speed of rotation: 2960 rpm;

-

inertia moment of the rotor: 321∙10⁻⁷ kg∙m².

-

All obtained parameters of the motor correspond to the technical specification.