Abstract
Satellite communication systems are increasingly facing serious environmental challenges such as malicious jamming, monitoring, and intercepting. As a current development of artificial intelligence, intelligent jammers with learning ability can effectively perceive the surrounding spectrum environment to dynamically change their jamming strategies. As a result, the current mainstream satellite communication anti-jamming technology based on wide interval high-speed frequency hopping is unable to deal with this problem effectively. In this work, we focus on anti-jamming problems in the satellite communication domain, and reformulate the power allocation problem under two kinds of confrontation scenarios as one-shot and repeated games model. Specifically, for the problem of multi-channel power allocation under a one-shot confrontation scenario, we firstly model the problem of allocating limited power resource between communication parties and a jammer on multi-channel based on a BG (Blotto Game) model. Secondly, a DO-SINR (Double Oracle-Signal to Interference plus Noise Ratio) algorithm is designed to approximate the Nash equilibrium of the game between two parties. Experiments show that the DO-SINR algorithm can effectively obtain the approximate Nash equilibrium of the game. For the problem of multi-channel power allocation under a repeated confrontation scenario, we firstly transform the problem into an online shortest path problem with a graph structure to make the problem solving process more intuitive, and then design the Exp3-U (Exp3-Uniform) algorithm which utilizes the graph structure to solve the multi-channel power allocation problem. Experiments show that our algorithm can minimize the expected regret of communication parties during online confrontation, while maintaining good operating efficiency. The two power allocation problems constructed in this paper are common problem formed in confrontation scenarios. Our research and analysis can simulate some actual confrontation scenarios of the satellite communication power allocation, which can be used to improve the adaptability of satellite communication systems in complex environments.
1. Introduction
Satellite communication systems have the advantages of wide global coverage and are not restricted by complex geographical conditions between two locations; they are an important part of the wireless communication field and are widely used in all aspects of people’s lives, such as navigation and positioning, climate monitoring, satellite radio and television, etc. The above-mentioned characteristics of satellite communication have determined that satellite communication has become an indispensable means of communication technology in the modern high-tech industry, every country in the world attaches great importance to the construction of its satellite communication systems. Yet at the same time, satellite communication systems are also plagued by various aspects, including malicious jamming in the civilian field, monitoring, intercepting, and jamming in the military field. Especially with the current development of artificial intelligence, intelligent jammers with a learning ability can effectively perceive the surrounding spectrum environment to dynamically change their jamming strategy, making it difficult for communication systems to employ effective anti-jamming methods [1].
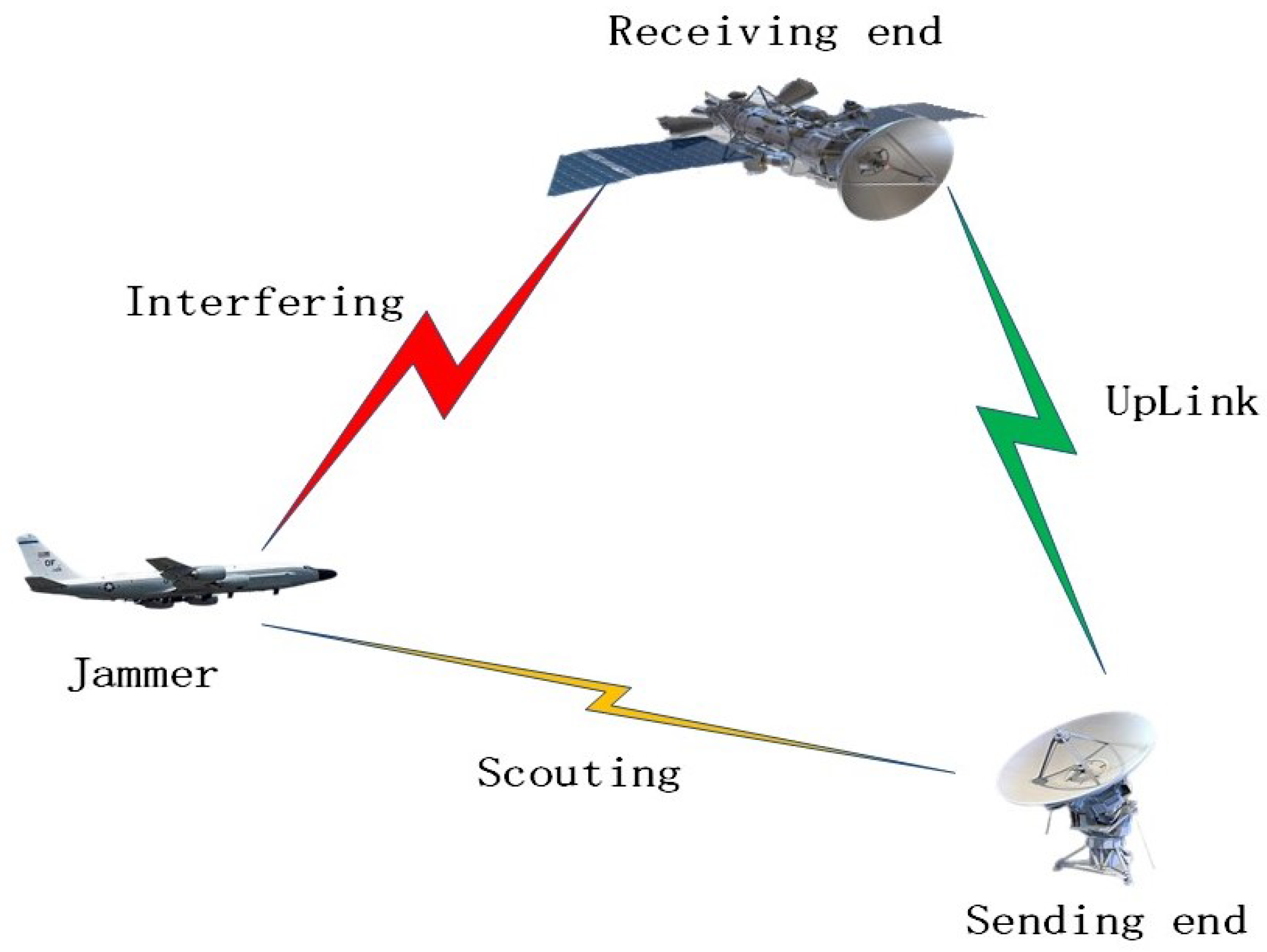
The traditional satellite communication anti-jamming technology is mainly based on wide interval high-speed frequency hopping, combined with different modulation and coding methods to achieve the anti-jamming effect. Although this kind of wide interval high-speed frequency hopping satellite communication system already has a certain anti-jamming capability, its essence is still a blind anti-jamming system, the anti-jamming method it adopts is a passive defense measure, which cannot make optimal decisions based on jamming cognition. The improvement of various anti-jamming performances is at the expense of consuming the frequency resources and power resources of the satellite communication systems. From the perspective of Shannon’s information theory, these methods will eventually lose the total capacity of the communication systems or lead to an increase in the complexity of the systems. This anti-jamming technology is difficult to use to effectively deal with the increasingly intelligent confrontation situation in the context of artificial intelligence [2]. Therefore, it is necessary to explore the research on intelligent anti-jamming technology of satellite communication considering the background of artificial intelligence technology. Moreover, when wide interval high-speed frequency hopping action occurs, only one channel is used, resulting in a relatively low spectrum utilization rate [3], this method is difficult to use to resolve tracking jamming effectively. With the development of the software and hardware technology of communication systems, satellite communication systems can use multiple channels at the same time. For example, in a multi-user synchronous orthogonal frequency hopping satellite communication system, the communication parties can apply for occupying multiple channels at the same time to increase the total capacity of the communication systems. Meanwhile, with the continuous progress of reconnaissance technology, countermeasure equipment such as high-altitude and long-endurance reconnaissance drones and small satellites with close-in reconnaissance capabilities have gradually become practical, and it has become easier for the jammer to track and interfere with communication parties. A schematic diagram of a typical confrontation scenario between the communication parties and the jammer is shown in Figure 1.
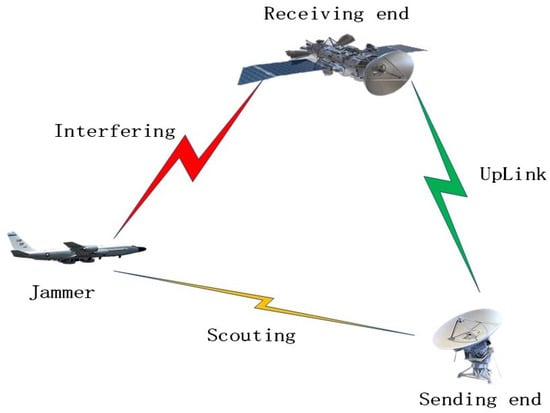
Figure 1.
Schematic diagram of typical confrontation scenario between the communication parties and the jammer.
The challenges faced by occupying multiple channels for information transmission in satellite communication are still very serious, therefore, it is of great significance for us to study the problem of multi-channel power allocation. From the game theory perspective, the strategy selection of the communication parties and the jammer in the multi-channel power allocation confrontation scenario can be modeled as a two-player zero-sum game [4], which is suitable for modeling and solving this problem using knowledge of game theory. For the multi-channel power allocation problem under a one-shot confrontation scenario, we focus on approximating the Nash equilibrium. In an actual confrontation scenario, there may be repeated confrontations between the communication parties and the jammer. In this scenario, it is not necessary for the communication parties to use Nash equilibrium as the adaptive optimal strategy when the jammer does not use Nash equilibrium. Therefore, our goal in this case is to minimize the expected regret of the communication parties after multiple confrontations.
For the multi-channel power allocation problem under a one-shot confrontation scenario, the problem-solving methods are different depending on the optimization objective. For the case with the optimization objective as the communication capacity, the authors of [5] modeled the multi-channel power allocation anti-jamming problem as a Stackelberg game and proved the existence of the Stackelberg equilibrium. In [6], the authors studied the Nash equilibrium under a different channel model. For the AWGN (Additive White Gaussian Noise) channel model, the Nash equilibrium of opposing parties is to equally distribute power on all available channels, while for the frequency selective fading scenario, the Nash equilibrium of opposing parties can be solved by an iterative water-filling algorithm. So far, for multi-channel power allocation problems, the case of optimizing communication capacity has been well solved. However, they are not applicable in the actual communication system, because the actual communication system transmits information at a specific rate, with the SINR (Signal-to-Interference-plus-Noise Ratio) reaching the demodulation threshold, larger communication power cannot further improve the communication capacity. Therefore, the optimization objective of the communication parties should be the number of channels through which information is transmitted successfully. The multi-channel power allocation problem with the optimization objective of the number of successfully transmitted channels can be modeled as BG (Blotto Game) models [7,8,9]. In [7,8], the authors construct the confrontation scenarios with the secondary user and attacker simultaneously being able to access all available channels in cognitive radio networks, and model the power allocation problem between the two parties as a BG model. They obtain the Nash equilibrium of the game by constructing a joint distribution that matches the expected marginal distribution and satisfies the power budget constraint. However, finding the specific Nash equilibrium determined by the joint probability distribution function is still a difficult task. In [9], the author modeled the multi-channel power allocation problem between attacker and defender in cognitive radio as a two-player constant BG model and solved the model using the basic concept of iterative Nash bargaining solution, with the objective of enabling IoT (Internet of Things) systems safety level to reach an effective and stable state. There are few works on multi-channel power allocation problems under a repeated confrontation scenario. We consider the online learning problem under the partially observable model studied in [10], which assumes that the learner is able to obtain the loss of the chosen actions, and observe the loss of some other actions. In [11], the authors modeled different types of bandit feedback information as a graph structure, and proposed definitions of strongly observable graphs, weakly observable graphs, and unobservable graphs, while the multi-channel power allocation problem corresponds to a weakly observable graph. The authors of [12] also considered the partial observable problem of the multi-armed bandit (MAB) with side observation, and modeled it as a graph structure to describe regret according to the dominance and independence numbers of the observability graph.
Based on the above literature survey, we conclude that the multi-channel power allocation problem under a one-shot confrontation scenario with the communication capacity as the optimization objective has been solved well. However, the multi-channel power allocation problem, which takes the number of successfully transmitted channels as the optimization objective, needs to be further studied, and the solution method needs to be further optimized. Therefore, we study the multi-channel power allocation problem based on the BG model with the number of successful transmission channels as the optimization objective, and improve the model solving method to avoid the dilemma of finding a specific Nash equilibrium determined by the joint probability distribution function. For the multi-channel power allocation problem under a repeated confrontation scenario, we are inspired by the online learning problem under the partially observable model and transform the multi-channel power allocation problem under a repeated confrontation scenario into a graph structure problem, and the objective of model solving is to minimize the expected regret of the communication parties after multiple confrontation. It should be noted that each round of interaction in the repeated confrontations is modeled based on the BG model.
A generalized BG is a two-player zero-sum game for competitive resource allocation. Each player has a fixed resource budget and simultaneously allocates their resources to n battlefields. When a participant allocates more resources than the opponent on a certain battlefield, they will gain the battlefield, and the corresponding side that wins more battlefields is the final winner [13]. Although the rules of the game are very simple, the number of potential battlefields and the total resources of each player can vary, so the potential strategies that players can employ are almost limitless. These two kinds of confrontation scenario proposed in this paper can be constructed on the basis of the Blotto Game model, and the models under different problems can be solved respectively.
The main work and contributions of this paper are as follows:
- First, for the problem of multi-channel power allocation under a one-shot confrontation scenario, we model the problem based on the BG model. We also design the DO-SINR (Double Oracle-Signal-to-Interference-plus-Noise Ratio) algorithm with the number of channels as the optimization objective to solve the approximate Nash equilibrium of the game between the two parties, avoiding the dilemma of finding the specific Nash equilibrium determined by the joint probability distribution function. The result can be used in the case of online games, if the jammer adopts an approximate Nash equilibrium, and the communication parties have no prior knowledge of the opponent, then the approximate Nash equilibrium strategy is an optional strategy;
- Second, we study the problem of multi-channel power allocation under a repeated confrontation scenario. We transform the problem into a shortest path problem with a graph structure to make the problem-solving process more intuitive, and then design the Exp3-U (Exp3-Uniform) algorithm based on the graph structure to solve the resource allocation problem under the condition of repeated games. Experiments show the effectiveness of our algorithm in minimizing the expected regret of communication parties during online confrontation while maintaining good operating efficiency.
In these two works, the problem of multi-channel power allocation under a one-shot confrontation scenario can be regarded as offline setting, and the approximate Nash equilibrium of the problem can be used as a blueprint strategy for online setting. The problem of satellite communication power allocation under a repeated confrontation scenario belongs to online learning problems, and the communication parties usually need to continuously and dynamically learn and adjust the trade-off between exploiting the current actions and exploring the new actions. The blueprint strategy and the strategy boost in online learning are important factors for obtaining super performance in two-player zero-sum games [14]. The two works in this paper are the common problem forms in the confrontation scenario. Our research and analysis can simulate the confrontation scenario of the actual satellite communication power allocation, which is of great significance to the research of jamming and anti-jamming in satellite communication.
This paper is arranged as follows. Section 2 presents the basic system model for power allocation between the communication parties and the jammer. Section 3 introduces the solution to the power allocation problem under the condition of one-shot game and experimental verification. Section 4 introduces the solution to the power allocation problem under the condition of repeated games and experimental verification. Section 5 concludes the article.
2. Problem Modeling
2.1. Scenario Description
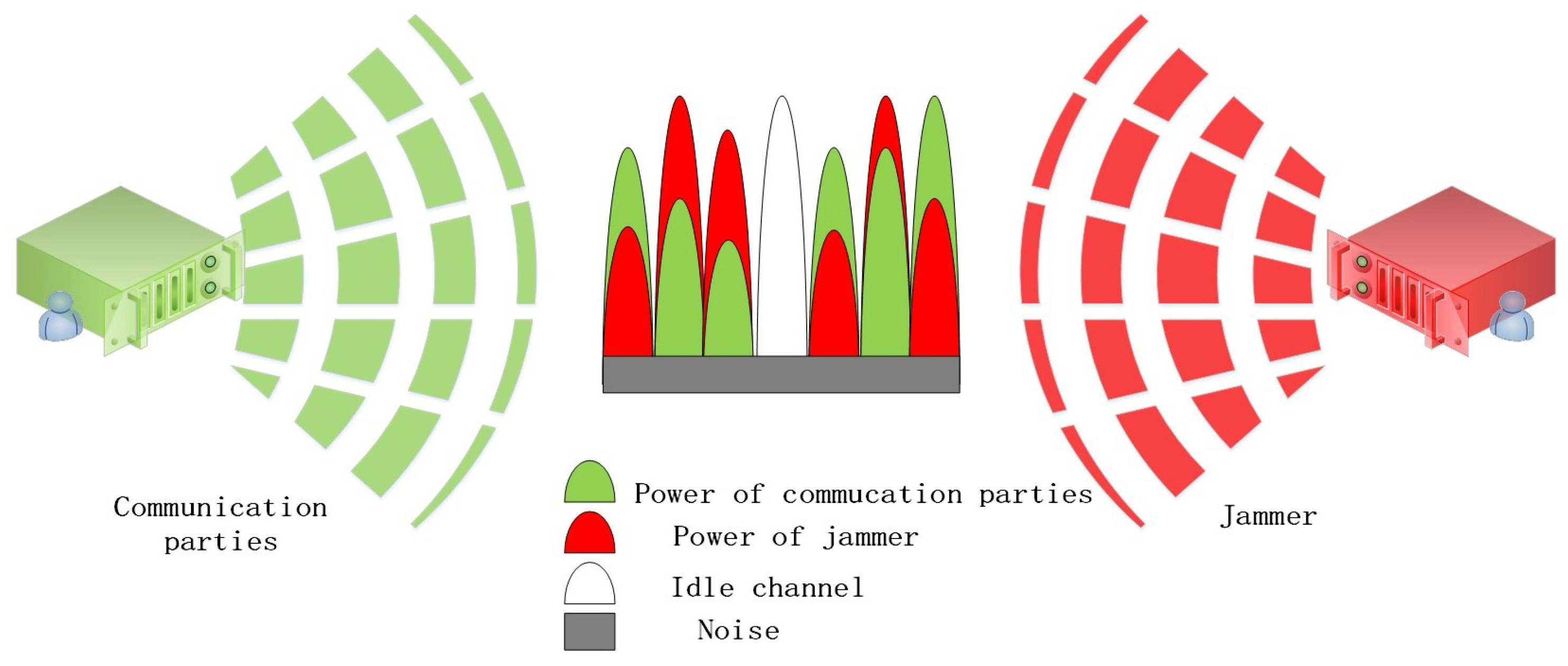
In the confrontation scenario of Figure 1, we assume that the uplink between the satellite communication transmitting terminal and the receiving terminal includes multiple information transmission channels, and the communication parties use the multiple channels for information transmission (there may be idle channels). The jammer implements the technology of tracking interference or barraging interference on the communication parties through effective detection, but due to the limitation of the total interference power, it cannot barrage all the channels of the communication parties at the same time. The schematic diagram of multi-channel power allocation under the confrontation scenario is shown in Figure 2.
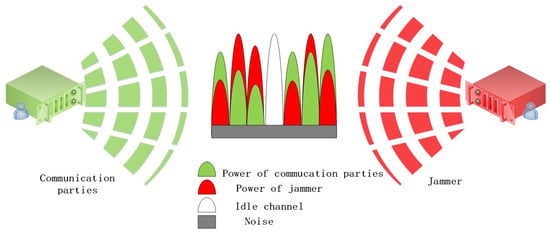
Figure 2.
Schematic diagram of power allocation confrontation between communication parties and jammer. The communication parties on the left adopt a suitable power allocation strategy to maximize the number of information transmission channels, and the jammer on the right transmits a certain interference power to prevent the information transmission of the communication parties.
2.2. Problem Notations
As shown in Figure 2, communication parties (denoted by r) need to find a reasonable power allocation strategy to resist power interference from jammer (denoted by m), so as to maximize information transmission. Assuming that there are n available information transmission channels at time t, r has power budgets of , , the power allocated by the r to channel k is , , , the vector of power allocation is denoted as , . Similarly, m has a power budget of , , the power allocated by m to channel k is , , , the vector of power allocation is denoted as , . As the receiver, if the received SINR exceeds the minimum requirement ( is determined by the type of service), i.e.,
then information can be transmitted successfully; otherwise, the link is too poor to be useful, is the variance of white noise when the receiver receives signal from channel k.
Since the BG is a zero-sum game, the utility functions of r and m can be defined as
where represents the value of available channel k, , and
2.3. Problem Definition
To model the confrontation scenario, we assumed that both r and m can effectively perceive the spectrum environment and have a common understanding of the game rules. r needs to transmit signals on multiple channels with a number of n, but faces interference from m, so r needs to allocate power to the transmission channels to meet the standard of signal transmission (as defined in Equation (1)), and m allocates the interference power to the transmission channels in an attempt to prevent the signal transmission. Both r and m do not know the power allocation strategy adopted by the opponent before taking action, it is a difficult decision to make in this situation. This paper mainly constructs two confrontation scenarios:
- The first is to assume that r and m are completely rational, and they perform power allocation on n channels with the same/different resource budgets; our goal is to solve the approximate Nash equilibrium of the BG model under a one-shot confrontation scenario;
- The second is to assume that m is an oblivious opponent that exists widely in the MAB problem [15], the opponent does not have the ability to remember the interaction history of the game played, and the power allocation strategy obeys a fixed distribution. There are multiple confrontations between r and m. In each round of confrontation, the two parties perform power allocation on n channels. After a complete confrontation process is over, r obtains the losses of this confrontation, that is, the value (vector) of the channels successfully interfered with by m. The goal of r is to achieve the smallest expected regret after multiple rounds of complete confrontation.
3. Equilibrium Approximating of One-Shot Game
We consider the problem of multi-channel power allocation under a one-shot confrontation scenario in this section, r applies for the use of multiple channels for information transmission, and m implements the technology of tracking jamming or barraging jamming on r after performing a reconnaissance mission, but there is a limitation of the total jamming power budgets, which cannot barrage all channels of the user at the same time. Although there may be a time difference for the allocation actions of the two parties, it can be seen that both parties allocate power resources to selected channels at the same time because the allocation strategy is unknown to the opponent. It is not required to allocate power resources for each channel, but all power resources are required to be allocated at one time, and each channel is independent from the others. The purpose of this setting is to obtain an approximate Nash equilibrium of the opposing parties when both r and m are rational, and the approximate Nash equilibrium can be applied to the case of online games, if m adopts approximate Nash equilibrium, and r has no prior knowledge about the opponent, then the approximate Nash equilibrium strategy is optional.
3.1. Best Response Iteration
In this section, we model the problem of multi-channel power allocation under a one-shot confrontation scenario based on the BG model, then we design the DO-SINR algorithm to solve the approximate Nash equilibrium of the game between the two parties, and the optimization objective of the algorithm is to obtain as many channels as possible. In this confrontation scenario of power allocation, r and m select strategies from nonempty compact sets and , respectively. The concept of mixed strategy allows both parties to arbitrarily assign probability weights on their respective sets of strategies. The mixed strategy of r is a Borel probability measure p over , all the mixed strategies of r constitute . Additionally, the mixed strategy of m is a Borel probability measure q over , all the mixed strategies of m constitute . We define the problem of multi-channel power allocation under a one-shot confrontation scenario as .
We suppose that m has pure strategies, denoted as , the probability corresponding to each strategy is , one of the pure strategy is , and the corresponding probability is . Combined with the utility function of r (as defined in Equation (2)), the optimal strategy of r is the solution of Equation (4).
Since is the signum function, this nonlinear optimization problem is reformulated as the following mixed-integer linear problem. We use the SciPy library in Python for the optimal solution.
Similarly, the optimal strategy for m is obtained by solving a similar mixed-integer linear problem.
3.2. Nash Equilibrium Approximation
The Nash equilibrium is such that each player’s strategy is an optimal response to the other players’ strategies. For the two-player zero-sum Blotto Game , its mixed approximate Nash equilibrium should satisfy
According to [16], for , we define the lower value of by
and define the upper value of by
If the lower value is equal to the upper value, then the Nash equilibrium of the problem exists, and . Sometimes, in practical applications, it is difficult to obtain an accurate Nash equilibrium solution. At this time, people solve the that meets the requirements of use. For and , the is defined as,
where is sufficient for our performance needs and can reduce the computational burden. An important principle in designing the approximate Nash equilibrium in large-scale zero-sum games is optimal response dynamic iteration. Two representative algorithms are Double Oracle (DO) [17] and Policy Space Response Oracle (PSRO) [18]. The DO algorithm solves the approximate Nash equilibrium of large-scale zero-sum games by solving a series of subgames, and it has been proven to converge to the Nash equilibrium in finite zero-sum games [19]. Based on the works of Adam [20], we take the SINR formula (as defined in Equation (1)) as the evaluation criterion for winning or losing the game, and design the DO-SINR algorithm to solve the problem of multi-channel power allocation under a one-shot confrontation scenario.
The DO-SINR algorithm is as shown in Algorithm 1. First, setting the initial strategy sets and of r and m, respectively, in each round of iteration, the approximate Nash equilibrium of the subgame is solved, then the best responses and are obtained for and , respectively, and added to and respectively. The process loops until the termination condition is satisfied.
| Algorithm 1 DO-SINR Algorithm for of |
| Input: Game , , , Output: of
|
3.3. Numerical and Experimental Analysis of
To provide empirical game theoretic policy space analysis of , we discretize the continuous strategy space with granularity C and transform it into a discrete BG model to solve. When , it can be regarded as a continuous BG model. According to [21], every finite game has an equilibrium point. In the generalized BG problem, the approximate Nash equilibrium exists under some restrictive conditions (e.g., symmetric resource budgets and equal value for each battlefield), but it is still an open question whether Nash equilibrium exists under general conditions. A discrete Blotto game is a finite game (both the number of players and the strategies are finite), so it has at least one Nash equilibrium or mixed Nash equilibrium. Next, we set up the symmetric game (same resource budgets between r and m) experiment and asymmetric game (different resource budgets between r and m) experiment, respectively, and solved the approximate Nash equilibrium under a one-shot confrontation scenario between the two parties to test the effectiveness of the DO-SINR algorithm.
3.3.1. Symmetric Game Experiment
We consider the case of , assuming that the power budgets of both r and m are equal after conversion, that is, the game between the two parties is symmetric. Assuming that the values of the channels are equal, the Gaussian white noise variance of channel k is = 1 uw, and . Since there is a constraint for channel k, if r decides to allocate power to channel k for information transmission, the power he allocates to channel k is not less than 10 uw. Assuming that w, according to Equation (1), if r and m are assumed to have the same budgets, then w. From the perspective of power consumption, the cost of r for anti-jamming is much higher than that of m.
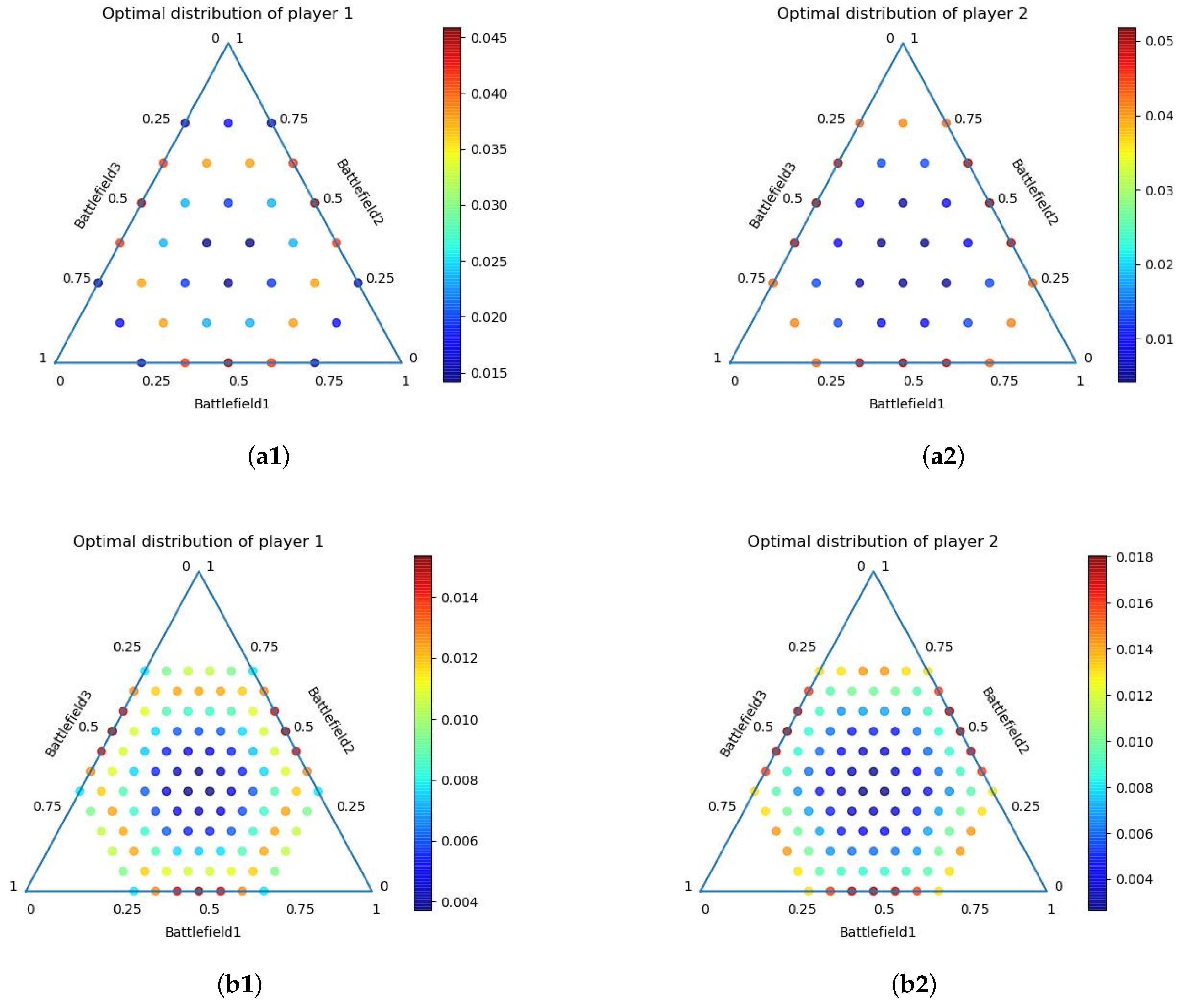
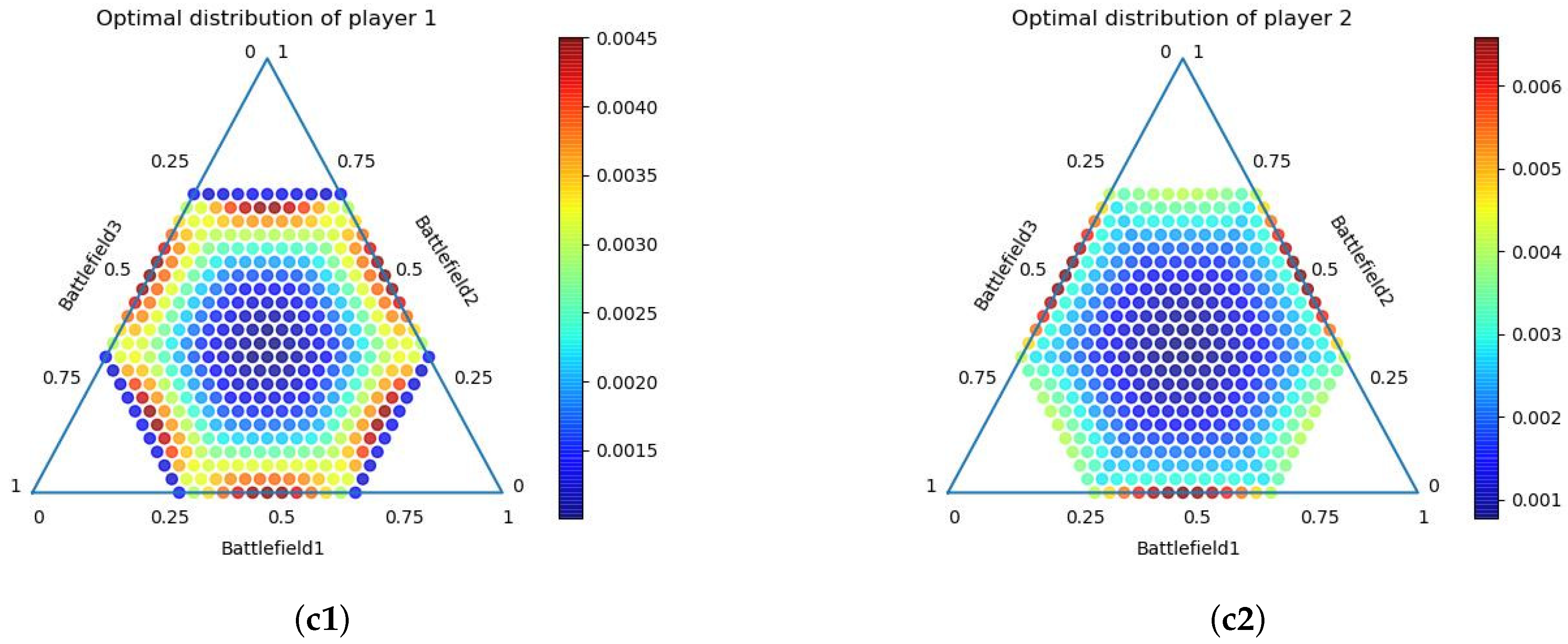
The power range of r allocated to each channel is 1030 w, or 0 w, and the power range of m allocated to each channel is 0∼100 w. To simplify the problem, we now map them to [0, 1]. Since we discretized the continuous policy space, we have tested the experiment with segmentation granularity , respectively. We do not need to consider the case where the power allocated to a channel is less than 10uw because we cannot obtain any number between [0, 1/32] unless the value of C is set very small. We set the termination condition . The experimental results are shown in Figure 3.
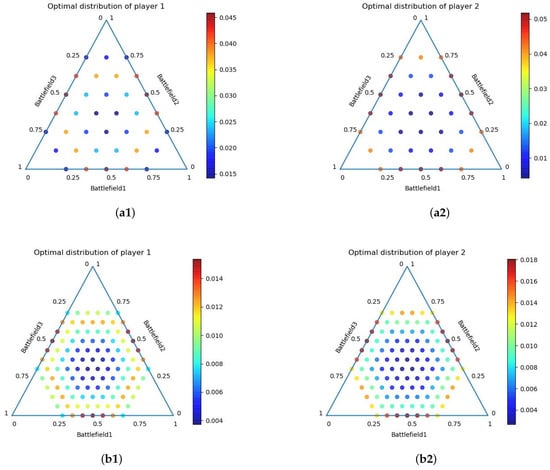
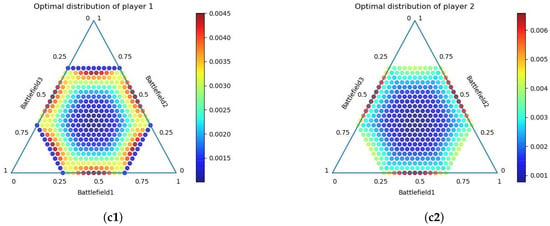
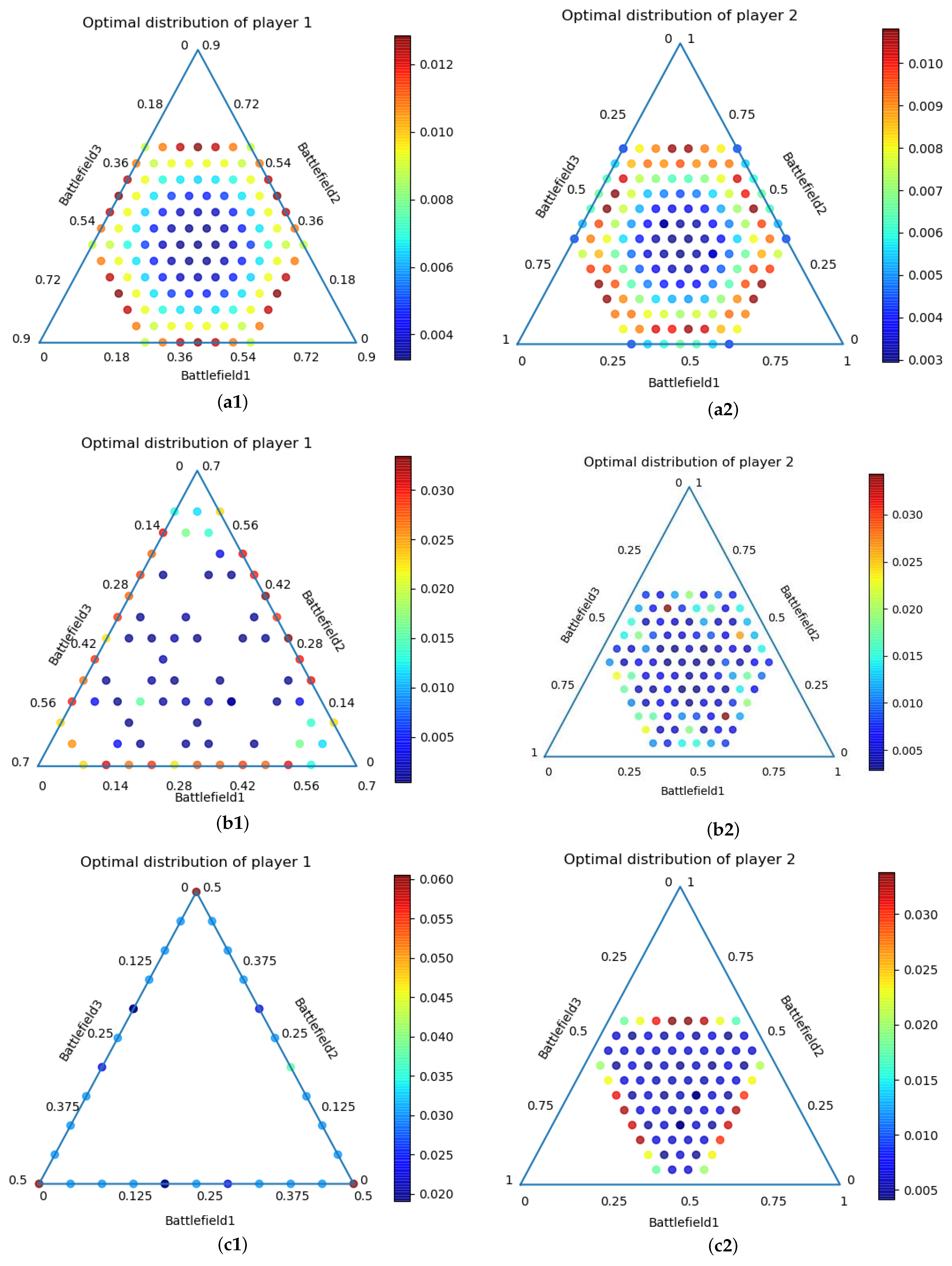
Figure 3.
Schematic diagram of the approximate Nash equilibrium of under symmetric game conditions. The three-dimensional coordinates of each point in the figure represent the power allocation strategy, and the color represents the probability assignment of the strategy. (a1,a2) C = 1/8; (b1,b2) C = 1/16; (c1,c2) C = 1/32.
It can be seen from Figure 3 that when the resource budgets of both parties are equal, the approximate Nash equilibrium evenly distributes the respective resource budgets on each channel. From the perspective of solving the BG model, this conclusion and the results of [22,23] are consistent. In [22], when the resource budgets of the opposing parties are equal, their allocation strategy in each battlefield is the resource budget multiplied by a fixed proportional coefficient, respectively. That is, in the case of the same budgets on both sides of the confrontation, there are few extreme allocation strategies. For example, we can allocate resource budgets on one or a few battlefields (or allocate 0 on some battlefields). This is also consistent with general common sense experience, because if the budget is centrally allocated to a few battlefields, other battlefields that are not allocated resources will be lost, which is not beneficial to the result of the game.
3.3.2. Asymmetric Game Experiment
As mentioned in the symmetric game, from the perspective of power consumption, the cost of r of anti-jamming is much higher than that of m. Asymmetric resource budgets are very common in actual confrontation scenario. We assume that the power budgets of the two parties are not equal after conversion. That is, the game between the two parties is asymmetric.
We keep the power budgets of r as 1030 w and the power budgets of m as w, w, 200 w, w respectively. That is, the power budgets of r is , , , of m, respectively, after conversion, the segmentation granularity , and other conditions are the same as the setting of the symmetric game Section 3.3.1. We set the termination condition .
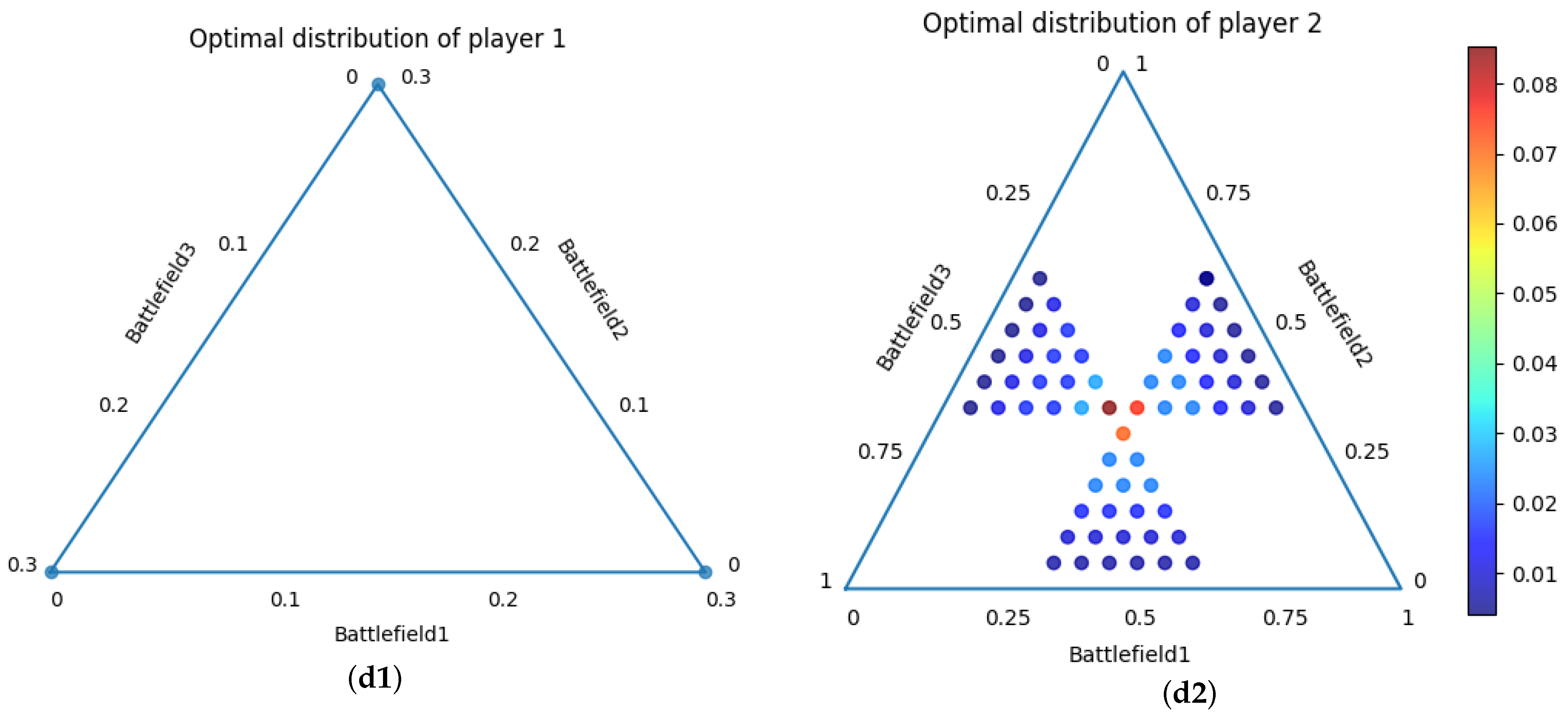
It can be seen in Figure 4 that when the resource budgets of the two parties are not equal, the approximate Nash equilibrium of the two parties also shows different characteristics. When the value of dwindles, r is more inclined to allocate power on 1∼2 channels because they have fewer resource budgets (when , r allocates power resource to one channel), while m tends to allocate power resource evenly across channels due to having sufficient budgets (when , m allocate power resource equally across three channels), which is consistent with general experience.
Figure 4.
Schematic diagram of the approximate Nash equilibrium of under asymmetric game conditions. The three-dimensional coordinates of each point in the figure represent the power allocation strategy, and the color represents the probability assignment of the strategy. (a1,a2) ; (b1,b2) ; (c1,c2) ; (d1,d2).
4. Online Learning of Repeated Games
We consider the problem of multi-channel power allocation under a repeated confrontation scenario in this section. In the actual satellite communication anti-jamming scenario, there may be many instances of confrontations between r and m. Finding ways of adjusting the next allocation strategy according to the previous confrontation results is a problem worth studying. In the problem of multi-channel power allocation under a repeated confrontation scenario, the resource budgets and channel values of each game are the same as in the initial stage, and both parties allocate power resources to the selected channel at the same time. After a complete confrontation process is over, r obtains the losses of this confrontation, that is, the value (vector) of the channels successfully interfered with by m. Additionally, from the loss of selected action, the loss caused by some other actions is calculated (this is the side observation, see Section 4.2 for the specific explanation). The goal of r is to achieve the smallest expected regret after multiple rounds of complete confrontation. In this case, r usually needs to continuously and dynamically learn and adjust the trade-off between exploiting the current actions and exploring the new actions.
We aim to design an online resource allocation algorithm that minimizes the expected regret of r while maintaining good operational efficiency. For each confrontation in the repeated confrontation scenario, we first model the problem of multi-channel power allocation based on the BG model. Then, the SINR (Equation (1)) is used as the criterion to judge the outcome of the allocation strategy of the opposing parties, it is more suitable for the application requirements of satellite communication. The main problem we face is how to design an efficient algorithm that minimizes the expected regret of r after repeated games.
4.1. Online Shortest Path Problem Reformulation
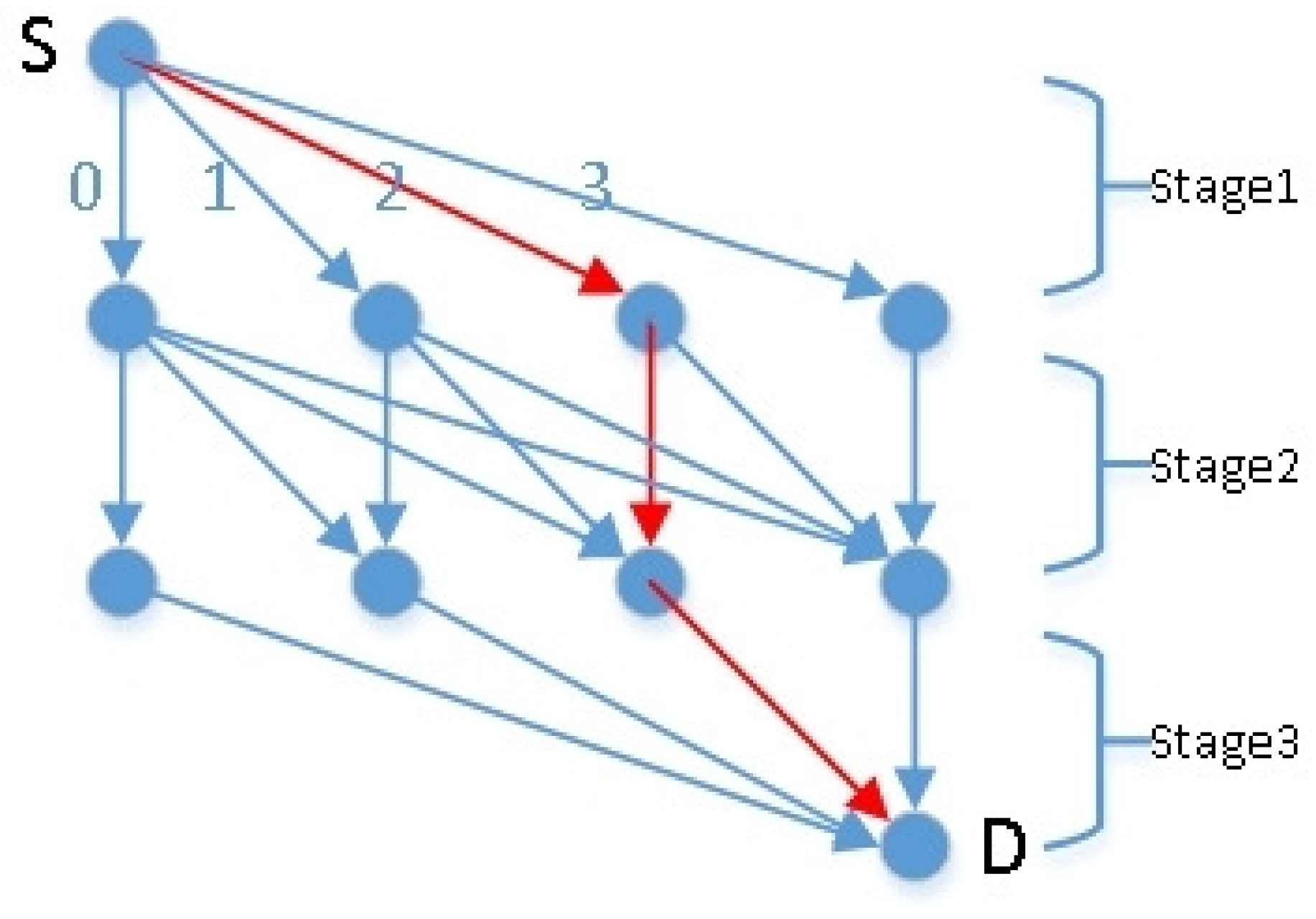
For the convenience of expression, we refer to the problem of multi-channel power allocation under a repeated confrontation scenario as the semi-combinatorial Blotto Game (SCBG) problem. Inspired by the works in [10,11,12], we transform the SCBG problem into an online shortest path (OSP) problem on a graph structure, which makes the solving process more intuitive. The schematic diagram of converting the SCBG problem into the OSP problem is shown in Figure 5.
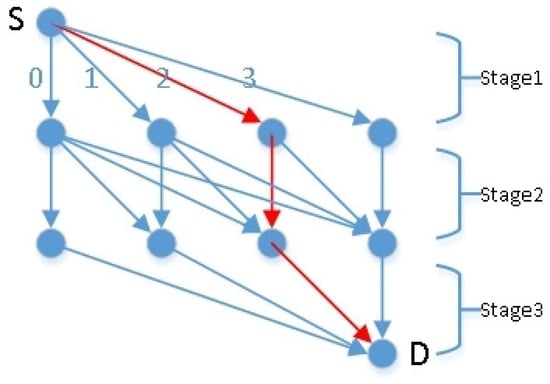
Figure 5.
Schematic diagram of OSP problem represented by graph structure.
We represent the set of actions of r as a set of paths (from initial vertex to terminate vertex) on a directed acyclic graph (DAG). DAG has the following properties—there are two special vertices, the initial vertex and the terminate vertex, they are called S and D, respectively. represents the set of all paths starting from S and ending with D, the vertex set and edge set of the DAG are denoted by and , respectively. Setting and , and each edge belongs to at least one path . Let n denote the longest path length in (n is the number of channels in ), that is, . Figure 5 is the DAG in the case of and . There are 10 paths from the initial vertex S to the terminate vertex D, which represent the resource allocation strategy, where each edge represents the number of resources allocated to the current stage. For example, the red path in the Figure 5 represents the allocation of 2 resources in stage 1, the allocation of 0 resources in stage 2, and the allocation of 1 resource in stage 3, that is, the strategy is (2,0,1). Given the time horizon , the online shortest path (OSP) problem is defined as, in time , r choose a path p to represent its power allocation strategy without knowing the power allocation strategy of m. Each edge on this path corresponds to a scalar loss determined by Formula (1). At the end of a time period t, r observe the loss of all edges on the selected path by themselves. The goal of r is to minimize the expected regret, which is defined by Equation (11).
4.2. Online Learning of the SCBG Problem
We focus on expected regret for the SCBG problem, the expected regret is defined as, over T time periods, the difference between the cumulative loss produced by the actual allocation strategy (represented as a complete path) and the cumulative loss produced by the best single action in hindsight.
where p denotes a best single action and denotes the action chosen by the learner at time t. Our goal is to minimize the expected regret. If there is when , we say that the corresponding algorithm can achieve regret minimization.
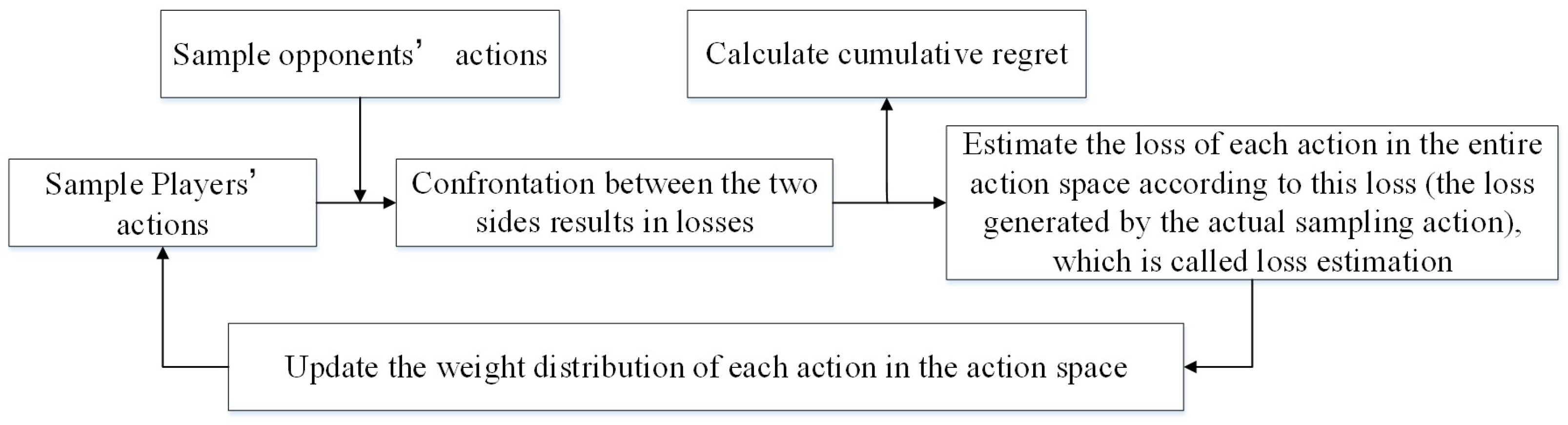
The MAB problem is one of the classic online learning problems, and the solution to the SCBG problem can be inspired by the algorithm for solving the MAB problem. The representative algorithm for solving the MAB problem is the Exp3 algorithm [24,25,26,27]. Exp3 is an exponentially weighted algorithm that concerns exploration and exploitation. The player chooses an action at a mixture of normalized weights with coefficient and uniformly distributed probability with coefficient , then the expected regret is calculated in the process of repeated games, and the algorithm is effective if the growth trend of the cumulative regret gradually slows down. The construction process of Exp3 algorithm is shows as Figure 6.
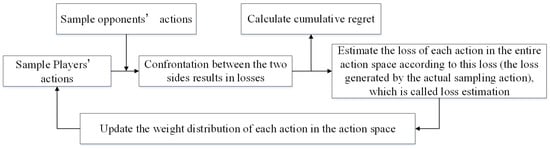
Figure 6.
Schematic diagram of construction process of the Exp3 algorithm.
For the SCBG problem, the author in [28] proposed the Exp3-OE algorithm based on DAG, which can realize the upper regret bound of , where P represents the number of paths in the DAG, but the algorithm still has room for improvement. We improved the performance of the Exp3-OE algorithm by re-proposing the Exp3-U algorithm. The improvements are mainly reflected in the following two aspects:
- In the Exp3-OE algorithm, only the weight of the path when sampling the actions is considered, and it does not considers the exploration of other action with smaller weights. The trade-off between exploration and exploitation is critical in incomplete information games. In the early proposed algorithm of Exp3 [24], the rest actions assigned a fixed probability to maintain the exploration of other action with smaller weights. It has been proven that this kind of algorithm can achieve a better regret guarantee through rigorous mathematical theory. In the SCBG problem, the strategy space is very large, and the path with more weight in the current confrontation stage may not be the optimal strategy in the long run. Therefore, inspired by the type of the Exp3 algorithm, we propose a path sampling method that mixes weight ratio distribution and uniform distribution. It assigns a weight to the edge which belongs to the selected path based on the regret of it in the previous stage, and adds a uniform distribution to ensure that the algorithm tries all actions. Otherwise, the algorithm may miss an action that performs well in the long run.
- We multiply the loss of the revealed edge by the distance coefficient d to cause the different edges (edges corresponding to allocation strategies) to have different losses. The Exp3-OE algorithm does not take this aspect into consideration, but broadly sets equal the loss of the revealed edge to the loss of the selected edge, which cannot reflect the advantages and disadvantages of a different edge. We improve it and conduct experiments to verify the effectiveness of our methods.
Our Exp3-U algorithm is shown in Algorithm 2. We first explain some of the notation,
where represents the set of paths that reveal the loss of edge e, and represents the set of edges whose loss is revealed by path p. Specifically, in Figure 5, if the player fails at stage1, edge2 can reveal the loss of edge1 and edge0 because it represents fewer resources than the selected allocation strategy by the player(the red path represents the allocation strategy chosen by the player). If it wins at stage1, edge2 can reveal the loss of edge3, which is 0, because it represents more resources than the selected allocation strategy; this is the definition of side observation. Through the information obtained from side observation, we can more accurately estimate the loss of some edges, then reasonably update the weights of the corresponding edges, and actions are chosen based on edge weights in the next confrontation.
| Algorithm 2 Exp3-U Algorithm for SCBG problem, based on (Ref. [28], Algorithm 1) |
| Input:n, , , T, graph DAG Output: cumulative loss of SCBG
|
| Algorithm 3 WP Algorithm for path sample, based on (Ref. [28], Algorithms 3 and 4) |
Input:n, , , , graph DAG
|
| Algorithm 4 Algorithm for Computing of edge e at time stage t, (Ref. [28], Algorithm 2) |
| Input:, , and , ; Output:
|
When estimating the loss, we multiply the loss of the selected edge by the distance coefficient d and assign it to the loss of the revealed edge, so that different edges (edges corresponding to allocation strategies) have different losses. Our Exp3-U algorithm can achieve the upper regret bound of . And the proof process refers to the general regret upper bound proof process of [28,29]. The following Algorithm 3 is the path sampling algorithm adopted in step 4 of the Exp3-U algorithm, which is called the WP algorithm in [28], we change it to be the method that mixes weight ratio distribution and uniform distribution.
4.3. Numerical Experimental Analysis of the SCBG Problem
We consider the case of , assuming that the power budgets of both parties are equal after conversion, that is, the game between the two parties is symmetric. Since r has a constraint on the allocated channel, the power should be greater than for the channel selected by r. Assuming that the value of the channels is equal, the Gaussian white noise variance of each channel is 1 uw, and , then, if r decides to allocate power to channel k for information transmission, the power allocated to channel k should be greater than 10 uw.
In the experiment, we set different resource budget conditions, and observe whether the expected regret of the Exp3-U algorithm is improved under different resource budget conditions. The segmentation granularity , , . An oblivious adversary is set in our experiments, it is also widely adopted in the multi-armed bandit problem. In our setting, the adversary’s power allocation strategy obeys a probability distribution, which is set uniformly. At the same time, we set the Uniform algorithm (at the same level as the adversary setting) and the Exp3-OE algorithm [28] to compare the performance with our Exp3-U algorithm. Performance mainly includes two indicators of cumulative regret and operating efficiency.
4.3.1. Experimental Results on Expected Regret
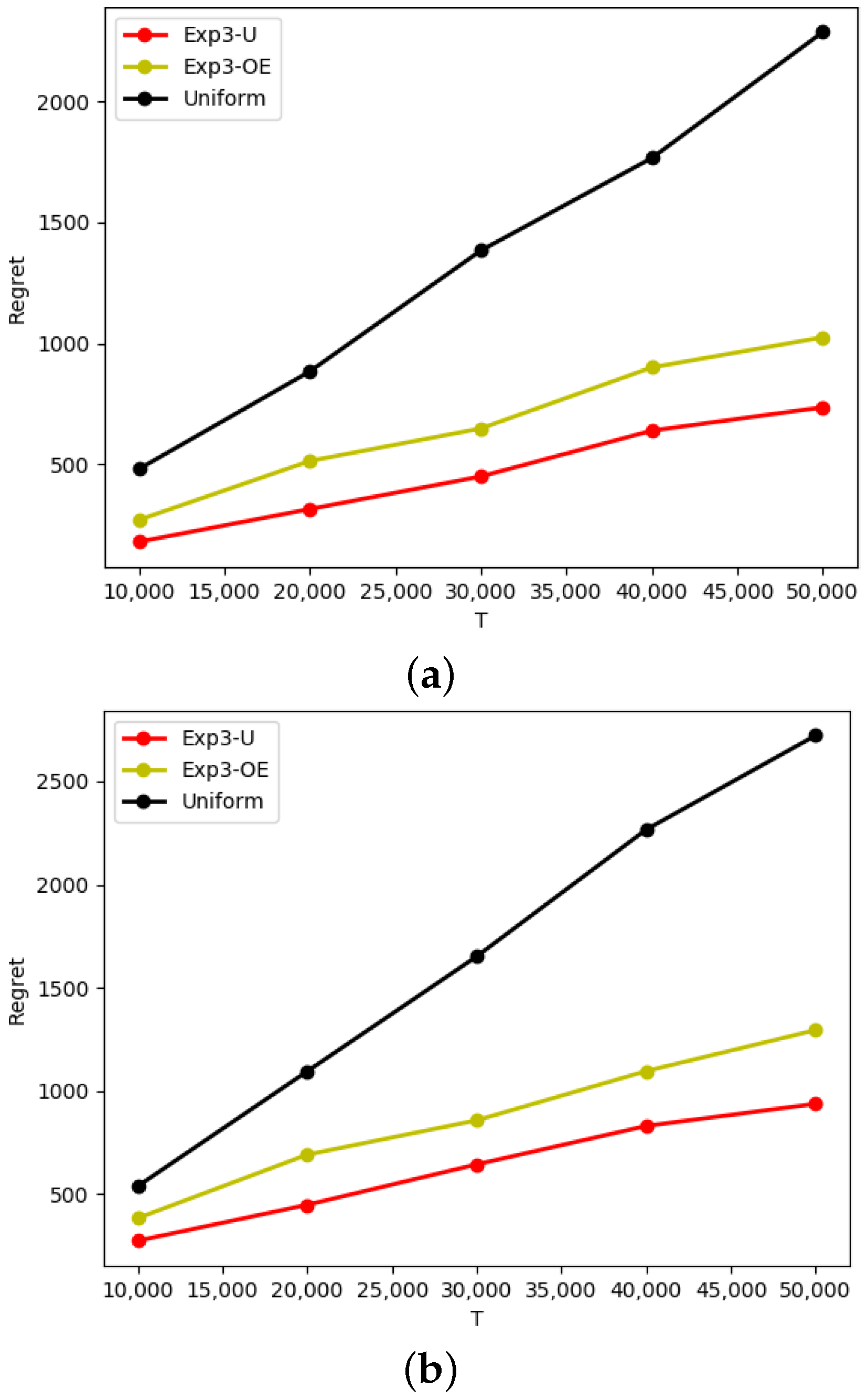
We set the case where the channel values are not equal, that is, set the values of the three channels to be [0.25, 0.4, 0.35], and the results are shown in Figure 7.
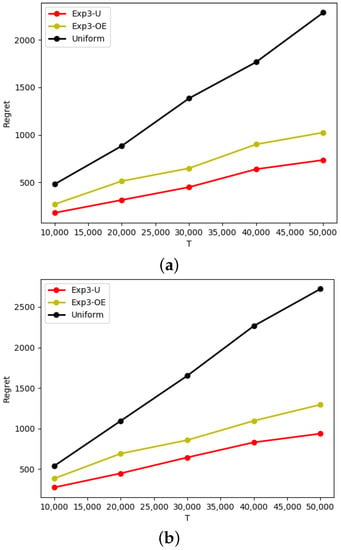
Figure 7.
The expected regret generated by the EXP3-U algorithm for the SCBG problem. (a) 3 w; (b) 6 w.
It can be seen from Figure 7 that under different power resource budgets, the expected regret of the variant form of the Exp3 algorithm is better than that of the Uniform algorithm. Since the algorithm used by the opponent is the Uniform algorithm, the effects of the two parties are equal over a long time, so the expected regret curve of the Uniform algorithm has a linear relationship with T. Further, our Exp3-U algorithm is better than the Exp3-OE algorithm in terms of expected regret. The curve trends of the two algorithms are similar. There is When , which means that Exp3-U algorithm is regret-minimized.
4.3.2. Experimental Results on Operating Efficiency
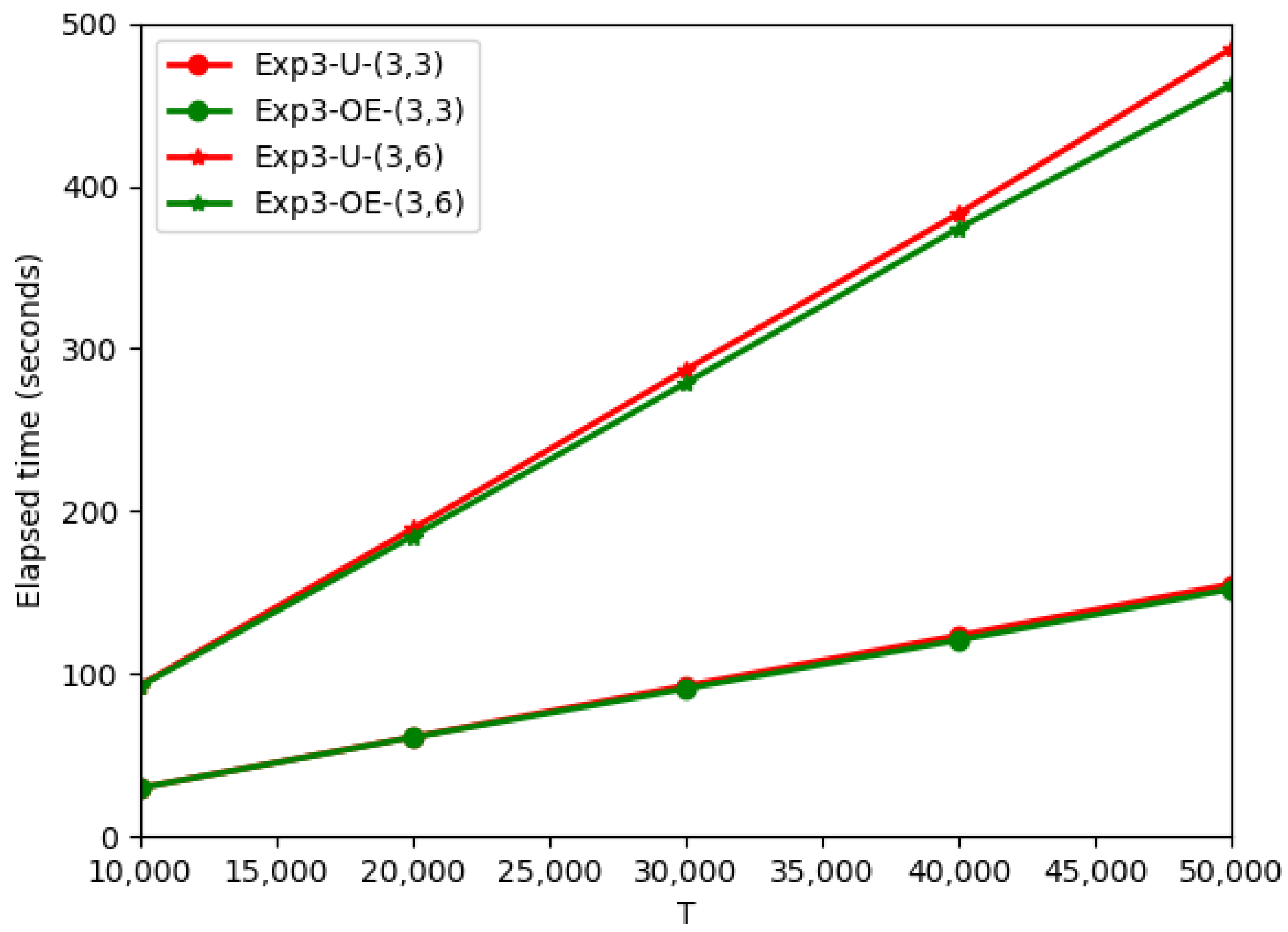
An important measure of the online adversarial algorithm is operating efficiency. In the Exp3-OE algorithm, the operating efficiency is closely related to the number of edges in the DAG. Since our Exp3-U algorithm only improves the loss estimation and path sampling method, and does not change the DAG structure, the operation efficiency is comparable to that of Exp3-OE. Line7 of Algorithm 2 can be performed in at most time and Exp3-U runs in at most time. Figure 8 shows the comparison of the Exp3-U algorithm and the Exp3-OE algorithm in terms of running time.
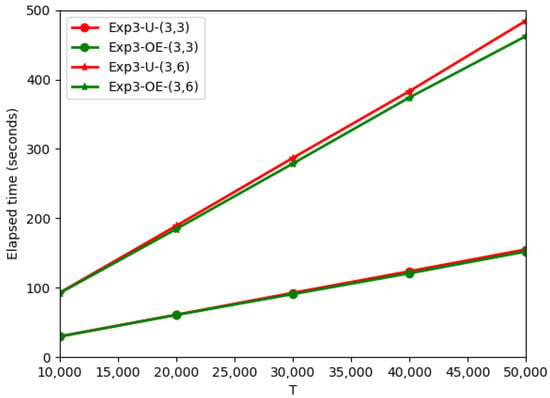
Figure 8.
Comparison of Exp3-U algorithm and Exp3-OE algorithm in running time.
As can be seen from Figure 8, even after 50,000 iterations, the running times of the Exp3-U algorithm and the Exp3-OE algorithm are comparable. Therefore, compared with the Exp3-OE algorithm, the Exp3-U algorithm has the same operating efficiency under the premise that the expected regret is improved.
5. Conclusions
This paper mainly models and solves the problem of multi-channel power allocation under a one-shot confrontation scenario and repeated confrontation scenario. For the problem of multi-channel power allocation under a one-shot confrontation scenario, we model the problem based on the BG model, and design the DO-SINR algorithm with the number of channels as the optimization objective to solve the approximate Nash equilibrium of the game between the two parties. The results obtained in this way are more in line with the application requirements of satellite communication. Concerning the problem of multi-channel power allocation under a repeated confrontation scenario, we transform the problem into an online shortest path problem with a graph structure to transform the problem-solving process more intuitively, and then design the Exp3-U algorithm based on the graph structure to solve the resource allocation problem. Experiments show that our algorithm can minimize the expected regret of communication parties during the online confrontation while maintaining good operation efficiency. The two game problems constructed in this paper are the common forms in the confrontation scenario. Our research and analysis can simulate the confrontation scenario of the actual satellite communication power allocation.
Author Contributions
Conceptualization, M.Z. and J.C.; methodology, M.Z., S.C., and J.L.; validation, S.C. and J.L.; resources, J.L. and Z.H.; data curation, M.Z. and Z.H.; writing—original draft preparation, M.Z.; writing—review and editing, S.C., J.L. and M.Z.; supervision, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grants No. 61806212, No. 61702528, and the Postgraduate Research Innovation Project of Hunan Province No. CX20210011.
Data Availability Statement
Our code will be available at https://github.com/mw-zou/power-allocation (accessed on 1 October 2022).
Conflicts of Interest
The authors declare no conflict of interest and there is nothing else that needs to be declared.
Abbreviations
The following abbreviations are used in this manuscript:
| SINR | Signal to Interference plus Noise Ratio |
| BG | Blotto Game |
| DO | Double Oracle |
| SCBG | Semi-combinatorial Blotto Game |
| OSP | Online shortest path |
| DAG | Directed acyclic graph |
References
- Fourati, F.; Alouini, M.S. Artificial intelligence for satellite communication: A review. Intell. Converg. Netw. 2021, 2, 213–243. [Google Scholar] [CrossRef]
- Wei, P.; Wang, S.; Luo, J.; Liu, Y.; Hu, L. Optimal frequency-hopping anti-jamming strategy based on multi-step prediction Markov decision process. Wirel. Netw. 2021, 27, 4581–4601. [Google Scholar] [CrossRef]
- Yao, F.; Jia, L.; Sun, Y.; Xu, Y.; Feng, S.; Zhu, Y. A hierarchical learning approach to anti-jamming channel selection strategies. Wirel. Netw. 2019, 25, 201–213. [Google Scholar] [CrossRef]
- Straffin, P.D., Jr. Game Theory and Strategy; MAA: New Denver, BC, Canada, 1993. [Google Scholar]
- Yang, D.; Xue, G.; Zhang, J.; Richa, A.; Fang, X. Coping with a smart jammer in wireless networks: A Stackelberg game approach. IEEE Trans. Wirel. Commun. 2013, 12, 4038–4047. [Google Scholar] [CrossRef]
- Li, T.; Song, T.; Liang, Y. Wireless Communications under Hostile Jamming: Security and Efficiency; Springer: Singapore, 2018. [Google Scholar]
- Wu, Y.; Wang, B.; Liu, K.J.R.; Clancy, T.C. Anti-jamming games in multi-channel cognitive radio networks. IEEE J. Sel. Areas Commun. 2011, 30, 4–15. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, B.; Liu, K.J.R. Optimal power allocation strategy against jamming attacks using the Colonel Blotto game. In Proceedings of the GLOBECOM 2009-2009 IEEE Global Telecommunications Conference, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–5. [Google Scholar]
- Kim, S. Cognitive radio anti-jamming scheme for security provisioning IoT communications. KSII Trans. Internet Inf. Syst. (TIIS) 2015, 9, 4177–4190. [Google Scholar]
- Kocák, T.; Neu, G.; Valko, M.; Munos, R. Efficient learning by implicit exploration in bandit problems with side observations. In Advances in Neural Information Processing Systems 27 (NIPS 2014); Curran Associates, Inc.: Red Hook, NY, USA, 2014. [Google Scholar]
- Alon, N.; Cesa-Bianchi, N.; Dekel, O.; Koren, T. Online learning with feedback graphs: Beyond bandits. Conference on Learning Theory. PMLR 2015, 40, 23–35. [Google Scholar]
- Alon, N.; Cesa-Bianchi, N.; Gentile, C.; Mansour, Y. From bandits to experts: A tale of domination and independence. Adv. Neural Inf. Process. Syst. 2013, 26, 1612–1620. [Google Scholar]
- Borel, E. La théorie du jeu et les équations intégralesa noyau symétrique. Comptes Rendus L’Acad. Sci. 1921, 173, 58. [Google Scholar]
- McAleer, S.; Farina, G.; Lanctot, M.; Sandholm, T. ESCHER: Eschewing Importance Sampling in Games by Computing a History Value Function to Estimate Regret. arXiv 2022, arXiv:2206.04122. [Google Scholar]
- Slivkins, A. Introduction to multi-armed bandits. Found. Trends Mach. Learn. 2019, 12, 1–286. [Google Scholar] [CrossRef]
- Glicksberg, I.L. A further generalization of the Kakutani fixed point theorem, with application to Nash equilibrium points. Proc. Am. Math. Soc. 1952, 3, 170–174. [Google Scholar] [CrossRef]
- McMahan, H.B.; Gordon, G.J.; Blum, A. Planning in the presence of cost functions controlled by an adversary. In Proceedings of the 20th International Conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2003; pp. 536–543. [Google Scholar]
- Lanctot, M.; Zambaldi, V.; Gruslys, A.; Lazaridou, A.; Tuyls, K.; Pérolat, J.; Silver, D.; Graepel, T. A unified game-theoretic approach to multiagent reinforcement learning. arXiv 2017, arXiv:1711.00832. [Google Scholar]
- Dinh, L.C.; Yang, Y.; Tian, Z.; Nieves, N.P.; Slumbers, O.; Mguni, D.H.; Ammar, H.B.; Wang, J. Online Double Oracle. arXiv 2021, arXiv:2103.07780. [Google Scholar]
- Adam, L.; Horčík, R.; Kasl, T. Double oracle algorithm for computing equilibria in continuous games. Proc. Aaai Conf. Artif. Intell. 2021, 35, 5070–5077. [Google Scholar] [CrossRef]
- Nash, J. Non-cooperative games. Ann. Math. 1951, 54, 286–295. [Google Scholar] [CrossRef]
- Roberson, B. The colonel blotto game. Econ. Theory 2006, 29, 1–24. [Google Scholar] [CrossRef]
- Min, M.; Xiao, L.; Xie, C.; Hajimirsadeghi, M.; Mandayam, N.B. Defense against advanced persistent threats: A colonel blotto game approach. In Proceedings of the 2017 IEEE international conference on communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Auer, P.; Cesa-Bianchi, N.; Freund, Y.; Schapire, R.E. The nonstochastic multiarmed bandit problem. SIAM J. Comput. 2002, 32, 48–77. [Google Scholar] [CrossRef]
- Cesa-Bianchi, N.; Lugosi, G. Prediction, Learning, and Games; Cambridge University Press: Cambridge, UK, 2006; pp. 156–173. [Google Scholar]
- Bubeck, S.; Cesa-Bianchi, N. Regret analysis of stochastic and nonstochastic multi-armed bandit problems. Found. Trends® Mach. Learn. 2012, 5, 1–122. [Google Scholar] [CrossRef]
- Orabona, F. A modern introduction to online learning. arXiv 2019, arXiv:1912.13213. [Google Scholar]
- Vu, D.Q.; Loiseau, P.; Silva, A.; Tran-Thanh, L. Path planning problems with side observations—When colonels play hide-and-seek. Proc. Aaai Conf. Artif. Intell. 2020, 34, 2252–2259. [Google Scholar] [CrossRef]
- Cesa-Bianchi, N.; Lugosi, G. Combinatorial bandits. J. Comput. Syst. Sci. 2012, 78, 1404–1422. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).